Synaptic and circuit mechanisms promoting broadband transmission of olfactory stimulus dynamics

Abstract

Sensory stimuli fluctuate on many timescales. However, short-term plasticity causes synapses to act as temporal filters, limiting the range of frequencies they can transmit. How synapses in vivo might transmit a range of frequencies in spite of short-term plasticity is poorly understood. The first synapse in the Drosophila olfactory system exhibits short-term depression, and yet can transmit broadband signals. Here we describe two mechanisms that broaden the frequency characteristics of this synapse. First, two distinct excitatory postsynaptic currents transmit signals on different timescales. Second, presynaptic inhibition dynamically updates synaptic properties to promote accurate transmission of signals across a wide range of frequencies. Inhibition is transient but grows slowly, and simulations show that these two features of inhibition promote broadband synaptic transmission. Dynamic inhibition is often thought to restrict the temporal patterns that a neuron responds to, but our results illustrate a different idea: inhibition can expand the bandwidth of neural coding.

Natural stimuli exhibit dynamics on a wide range of timescales. For example, movements of the eye cause visual scenes to fluctuate rapidly when objects are viewed at a distance, but more slowly when viewed from close up¹. Similarly, odors can fluctuate rapidly when plumes are riding on a stiff breeze, but more slowly near surfaces and in low wind^{2, 3}. Thus, sensory systems need ways to transmit information on a broad range of temporal scales.

Transmitting broadband signals is not trivial, because many common biophysical features of neural systems can act as temporal filters that limit transmission to specific frequency ranges^4–6. In particular, short-term synaptic depression is a ubiquitous phenomenon that imposes a bandpass filter on information transmission. Synapses that exhibit short-term depression preferentially transmit rapid modulations in the presynaptic firing rate, while filtering out slow or sustained rate modulations^7–11. Such synapses are common near the sensory periphery^12–15.

Are there mechanisms in vivo that allow sensory systems to overcome the temporal filters imposed by short-term synaptic depression? Several studies in the retina, brainstem, and cortex have shown that a sensory synapse can exhibit strong short-term depression when it is examined in a reduced experimental preparation, but can nonetheless transmit broadband signals in vivo or in a semi-intact preparation^16–20. The mechanisms that might promote broadband synaptic transmission in vivo are poorly understood. Presynaptic inhibition is a likely candidate, as synaptic depression can be reduced by tonic activation of presynaptic GABA receptors in vitro^{21, 22}. In vivo, however, GABAergic neurons are activated dynamically, and so the way that inhibition shapes the frequency characteristics of a synapse will depend on how excitatory and inhibitory neurons are co-activated by dynamic stimuli^{23, 24}.

In this study, we investigated how a sensory synapse in vivo can transmit information on many timescales. We focused on the first synaptic relay of the Drosophila olfactory system, the synapse between olfactory receptor neurons (ORNs) and projection neurons (PNs) in the antennal lobe (Fig. 1a). We describe two mechanisms that enable broadband transmission at this synapse. First, each presynaptic spike elicits two kinetically-distinct excitatory postsynaptic currents that transmit presynaptic firing rate changes on different timescales. Second, presynaptic inhibition dynamically modulates the properties of synaptic transmission to produce a more accurate representation of the stimulus time course across a wide range of frequencies. Because two kinetic components are found at a variety of excitatory synapses, and because presynaptic inhibition is common in many circuits, the mechanisms we describe here should have broad relevance for how neural systems can transmit information on a range of timescales.

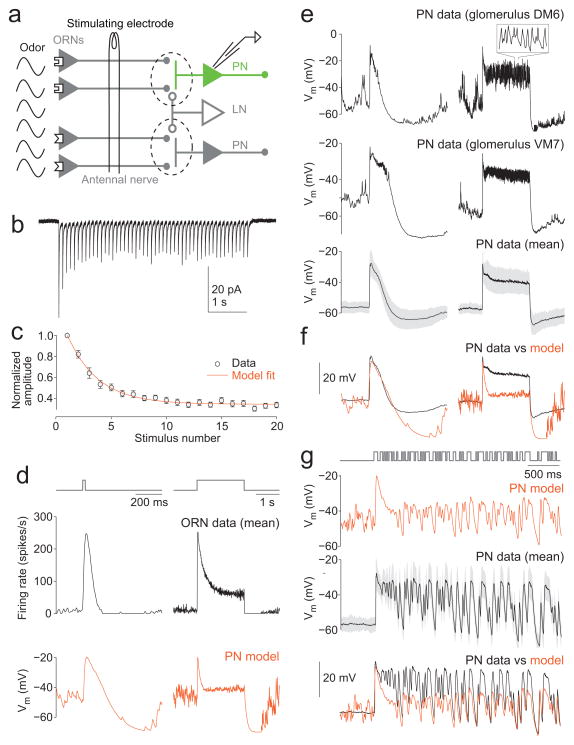
Figure 1. Mismatch between predictions of a simple depression model and PN odor responses.

a, Schematic of the antennal lobe circuit. All the ORNs that express the same odorant receptor project to the same glomerulus (dashed line), where they make synapses with PNs and LNs. In vivo patch clamp recordings are performed in GFP+ PNs that arborize in specific glomeruli. ORN spikes could be elicited using either odor or direct electrical stimulation of ORN axons.

b, Excitatory postsynaptic currents (EPSCs) evoked by electrical stimulation of ORN axons at 10 Hz (average of 7 trials, for a PN in glomerulus DM6).

c, Mean normalized EPSC amplitudes during a 10 Hz train (±s.e.m., n=19 PNs from 19 flies in glomerulus DM6 or VM2). Line is a fit of the simple synaptic depression model (Equation 1, see Methods; f = 0.78 and τ = 893 ms).

d, A simple model of synaptic depression predicts that PN responses to odor should be transient. Top: 20 ms and 2 s stimuli (note different time scales). Middle: firing rates measured in ORNs presynaptic to glomerulus VM7 (n= 4 ORNs in 4 flies). Bottom: predicted PN membrane potential. Note the transient response to the 2 s stimulus. The model PN is described by Equation 1 and 2 (see Methods and Supplementary Fig. 3).

e, Top: example PN responses (single trials, PNs in glomerulus DM6 or VM7). The 2 s stimulus elicits a sustained depolarization and sustained spiking (inset). Bottom, mean (averaged across 17 PNs from 17 flies in glomerulus DM6, VM2, or VM7, ± s.d. across PNs). When many PN recordings are averaged together, spikes make a negligible contribution.

f, Model prediction overlaid on the data. Baselines (pre-stimulus) have been aligned to facilitate comparison. Note that the model predicts a transient response while the data show a sustained response.

g, Model versus data for a dense sequence of odor pulses (odor valve is open 50% of the time). Bottom panel shows traces overlaid with baselines aligned. Again, the model predicts a transient response while the data show a sustained response.

Results

ORN-to-PN synapses show prominent short-term depression¹² (Fig. 1b), which is an intrinsic property of these synapses (Supplementary Fig. 1). Taken at face value, this would predict that PNs should respond only transiently to prolonged odor stimuli. Nonetheless, PNs in other insect species can generate sustained responses to odors²⁵ while also encoding rapidly fluctuating stimuli with high fidelity^{26, 27}.

To illustrate this mismatch, we compared the PN odor responses predicted by a simple model of ORN-to-PN synapses to actual PN odor responses. We focused on PN membrane potential rather than PN firing rate, because we are primarily interested in synaptic dynamics, and because firing rate tracks the membrane potential in these neurons (Supplementary Fig. 2).

To model ORN-to-PN synapses, we began with a well-studied model of synaptic depression^{7, 8}. In this model the amplitude of the unitary postsynaptic conductance decrements by a factor f after each spike, and recovers with a time constant τ between spikes. This model produced a good fit to the depression dynamics of recorded excitatory postsynaptic currents (EPSCs, Figures 1b–c).

To predict PN odor responses, we constructed a model PN that receives input from a population of model ORNs. with firing rates drawn from our data (Figure 1d). The amplitude of the synaptic conductance resulting from each ORN spike was specified by the depression model (i.e., the fitted parameters f and τ). Synaptic conductances from all ORN-to-PN synapses were summed, and the resulting change in PN membrane potential was determined by modeling the PN as a leaky passive integrator with properties fit to published data¹². All the parameters of the model were fit to data (Methods and Supplementary Figure 3).

As we would expect for a depressing synapse, this model predicted transient responses to long odor pulses (Fig. 1d). In contrast, real PNs produced more sustained responses to long odor pulses (Fig. 1e–f). Moreover, real PNs were able to respond continuously to dense fluctuating stimuli, while the model predicted that responses should attenuate after the first few hundred milliseconds (Fig. 1g). Importantly, the PN types used to fit the parameters of the model (f and τ) were a subset of those PN types that we measured odor responses from (see Methods).

This comparison makes clear that the assumptions of this simple depression model are incorrect. In particular, the model assumes that there is one timescale of synaptic dynamics, and that the parameters specifying synaptic dynamics (f and τ) are constant over time. We therefore investigated each of these assumptions experimentally.

Two components of postsynaptic currents

To better understand the dynamics of synaptic transmission, we examined isolated spontaneous EPSCs from PNs. Each EPSC arises from a single ORN spike²⁸, and so any dynamics present in these EPSCs must arise from unitary ORN-to-PN connections. Individual spontaneous EPSCs displayed two decay rates (Fig. 2a). These two kinetic components were also visible in EPSCs evoked by direct electrical stimulation of ORN axons (Fig. 2b). We observed that when ORN axons were stimulated repetitively, the fast component depressed more quickly than the slow component (Fig. 2c).

Figure 2. Two distinct components of EPSCs at ORN-to-PN synapses.

a, Examples of spontaneous EPSCs recorded with ORNs intact, showing a slow component (arrow). These examples come from two PNs having unusually low spontaneous EPSC rates, in order to better show isolated events, but the shapes of these EPSCs are typical of other recordings.

b, Single EPSC evoked by electrical stimulation of ORN axons in a DM6 PN (black, average of 8 trials) and fit of a bi-exponential decay to this trace (orange).

c, EPSCs evoked by electrical stimulation of ORN axons at 10 Hz (mean of 13 PNs from 13 flies in glomerulus DM6 or VM2, all traces normalized to the amplitude of the first EPSC before averaging). Arrow: slow component. The first EPSC is overlaid in gray on the last EPSC, in order to show how the fast component decays more quickly over the train as compared to the slow component.

d, A low concentration of curare (5–10 μM) mainly blocks the fast component (mean across 7 PNs from 7 flies). A low concentration of imidicloprid (IMI, 50–100 nM, n=6 PNs from 6 flies) mainly blocks the slow component. Control traces (gray) are reproduced from panel b. The effects of curare were mimicked by methyllycaconitine (100 nM) or α-bungarotoxin (1 μM; data not shown).

e, Data are presented as in c and d for 50-Hz trains.

f, Percentage of charge transfer remaining in curare or IMI (mean ± s.e.m.). The two drugs together blocked 70±12% of the evoked current during the 50 Hz stimulus (mean±s.e.m, n=8 PNs from 8 flies).

g, Model PN responses to 20 ms and 2 s odor stimuli. PNs were modeled with the fast or slow components alone, or with both components together. Inset at right shows the model response to the 20 ms stimulus on an expanded timescale. Inputs to the model were measured firing rates from ORNs in glomerulus VM7. For the fast component, the EPSC shape was taken from data recorded in IMI, and depression parameters f and τ were fit to the decay at 10 Hz in IMI. Similarly, for the slow component, the EPSC shape and depression parameters were fit to data recorded in curare.

h, Same as panel g, but with the onset of model responses shown on expanded time scale, and with traces vertically offset so that the mean baseline (pre-odor) membrane potential is the same in all cases.

Typical of excitatory central synapses in insects, EPSCs at these synapses are mediated by nicotinic acetylcholine receptors^{12, 29}. Nicotinic currents with distinct kinetics have been isolated pharmacologically from insect central neurons^{30, 31}. We therefore asked whether the two kinetic components at ORN-to-PN synapses might also be pharmacologically separable.

We found that low concentrations of curare preferentially blocked the fast component of EPSCs evoked by electrical stimulation (Fig. 2d). The slow component was preferentially occluded by the nicotinic partial agonist imidacloprid (IMI; Fig. 2d, Supplementary Fig. 4).

The two pharmacological components of EPSCs showed different amounts of short-term depression. In response to a 10 Hz spike train, the slow (curare-resistant) component depressed more slowly than did the fast (IMI-resistant) component (Fig. 2d). We quantified the rate of depression for the two components by fitting each with the parameters f and τ (as described above). For the IMI-resistant component, these parameters were f = 0.77, and τ = 1006 ms, whereas for the curare-resistant component, these parameters were f = 0.91, τ = 629 ms, indicating a much slower rate of depression. These distinctions were even more pronounced during a high-frequency train that is within the range of odor-evoked ORN firing rates³² (50 Hz; Fig. 2e,f). These experiments suggest that ORN-to-PN synapses contain two types of nicotinic receptor with distinct kinetics. Alternatively, the two components might represent different states of the same receptor.

To illustrate the consequences of these findings, we modified our model so that the EPSC was composed of two components fit to our pharmacological data (Supplementary Fig. 3). This two-component model produced a more sustained response than the single component model, reflecting the contribution of the slow component (Fig. 2g,h). The fast component rose more rapidly than the slow component, and contributed to the rapid rise time of the response (Fig. 2h). Thus, the two EPSC components encode distinct temporal features of odor stimuli, allowing the synapse to transmit a wider range of stimulus dynamics.

Inhibition promotes faithful encoding of stimulus dynamics

Thus far, we have assumed that the parameters that specify synaptic dynamics (f and τ) are themselves constant over time. However, the parameters governing depression may be under dynamic control, because presynaptic inhibition at ORN terminals can decrease the rate of synaptic depression, both in the antennal lobe³³, and in the olfactory bulb, the he vertebrate analog of the antennal lobe^34–36. We therefore investigated the hypothesis that GABAergic inhibition modulates the dynamics of synaptic transmission in vivo to produce changes in PN response dynamics.

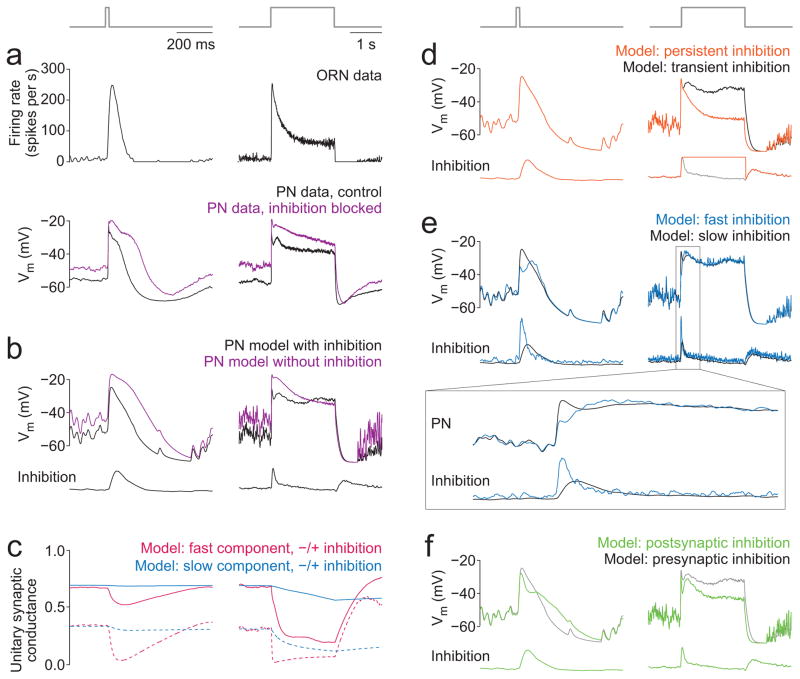
To block inhibition, we bath-applied CGP54626 (a GABA_B antagonist) together with picrotoxin (an antagonist of inhibitory GABA_A and GluCl receptors). Both antagonists are required to block inhibition in this circuit^{33, 37}. This is mainly a presynaptic manipulation, because inhibition in this circuit acts primarily on ORN axon terminals, with a smaller effect on PN dendrites^{33, 38}. When inhibition was blocked, responses to brief stimuli were significantly prolonged (Fig. 3a–c). In addition, responses to long stimuli showed significantly more decay (Fig. 3a–b,d). Thus, inhibition truncates responses to brief stimuli, but stabilizes responses to long stimuli.

Figure 3. Inhibition truncates responses to brief pulses and stabilizes responses to long pulses.

a, Response of an example PN (glomerulus DM6) to 20 ms and 2 s stimuli before and after blocking inhibition with picrotoxin (5 μM) and CGP54626 (50 μM). Blocking inhibition prolongs the response to the short pulse, whereas it causes the responses to the long pulse to decay more steeply over time. The decay in the PN response to a long pulse likely reflects the combined effects of short-term synaptic depression and ORN adaptation (see Discussion).

b, Mean response of 17 PNs to the same stimuli (glomeruli DM6, VM2, and VM7, recorded from 17 different flies). Control data are reproduced from Figure 1e.

c, Duration of the response to a short (20 ms) odor pulse at half-maximal amplitude. Mean duration increases significantly after blocking inhibition (p = 7.0e-6, t-test). Each pair of connected symbols represents a PN.

d, Ratio of the late response to the peak response for a long (2 s) odor pulse. The late response is defined as the depolarization from baseline during the last 100 ms. The mean late/peak ratio decreases significantly when inhibition is blocked (p = 3.8e-4, t-test).

e, Mean PN response to the long stimulus in experiments where additional negative holding current was applied after blocking inhibition to bring the baseline membrane potential to the same level as control (n=8 PNs from 8 flies). Blocking inhibition significantly decreases the mean late/peak ratio for these cells (p=2.5e-3, t-test).

Blocking inhibition depolarized the mean PN membrane potential even in the absence of odors, likely by increasing the amount of spontaneous excitatory synaptic input onto PNs. To control for the effects of depolarization, we injected hyperpolarizing current to return the PN to its original membrane potential; this did not alter the dynamics of PN odor responses or the effect of blocking inhibition (Fig. 3e). This result implies that blocking inhibition directly affects synaptic conductances in PNs.

To examine the role of inhibition in encoding more naturalistic stimuli, we presented long trains of odor pulses that ranged from very sparse to very dense (Fig. 4a). When inhibition was blocked, responses to sparse pulses were prolonged (Fig. 4b), while responses to dense pulse trains decayed more steeply over time (Fig. 4c). Thus, inhibition truncates responses to brief and sparse stimuli, while it also stabilizes responses to long or dense stimuli.

Figure 4. Inhibition truncates responses to sparse stimuli and stabilizes responses to dense stimuli.

a, Mean response to fluctuating stimuli with different densities, before and after blocking inhibition with picrotoxin and CGP54626 (n=17 PNs from 17 flies). The odor valve was randomly selected to be on or off in each 20 ms interval, and the mean percentage of time the odor valve was open varied from 1% to 50%.

b, Duration of the response to a short pulse (at half-maximal amplitude) after blocking inhibition, normalized to the duration before blocking inhibition. Values are plotted for each stimulus density. To compute these values, we selected responses to a relatively isolated pulse late within the random train for each stimulus (gray boxes in panel a). During sparse stimuli, blocking inhibition prolongs odor responses, but this effect decreases with stimulus density.

c, Ratio of peak depolarization during the last second of the stimulus to peak depolarization during the first second of the stimulus. During dense stimuli, blocking inhibition causes responses to decay more with time.

d, Mean impulse response for sparse pulse trains (same PNs as in panel a). The impulse response for each PN was calculated as the mean response to all 20 ms pulses separated by at least 400 ms within the random pulse trains.

e, Duration at half-maximal amplitude of the impulse response for each PN. Blocking inhibition significantly increases response duration (p=5.2e-5, t-test).

f, Mean effective impulse responses for dense pulse trains (same PNs as in panel a, inset schematizes positive and negative components). Here the effective impulse response was calculated by cross-correlating the densest stimulus (50%) with the membrane potential to obtain a linear filter, then using this filter to predict the response to a 20 ms odor pulse.

g. The ratio of the positive and negative components of the linear filter, before and after blocking inhibition. The linear filter was obtained by cross-correlating the densest stimulus (50%) with the membrane potential. This ratio decreases significantly (p=1.4e-3) after blocking inhibition. Each point represents a PN.

A common way to describe a neural code is to calculate the linear filter that relates the stimulus to the response. We can estimate the linear filter in multiple ways. One is to measure the “impulse response”— the response to a brief stimulus that is shorter than the integration time of the system. We measured the impulse response by averaging together all PN responses to 20 ms odor pulses that were separated by at least 400 ms in our trains of sparse stimuli (Fig. 4d). Blocking inhibition prolonged the impulse response (Fig. 4e). This result implies that inhibition normally keeps the impulse response narrow.

A different method of estimating the linear filter is by cross-correlating the time course of the response with the time course of our densest stimulus, where the odor was on 50% of the time (see Methods). This filter can then be used to predict the response to a 20 ms odor pulse – the “effective impulse response” for a dense stimulus (Fig. 4f). This analysis showed that the effective impulse response was narrower during a denser stimulus (Fig. 4f compare with Fig. 4e). Moreover, when the stimulus was dense, blocking inhibition did not prolong the response, but instead slightly decreased the positive component of the response relative to the negative part (Fig. 4g). This ratio dictates the response to a sustained stimulus: if the positive component of the filter is large compared to the negative component, a sustained stimulus will produce a net response that is also large and positive.

Together these analyses show that there is not a fixed relationship between the stimulus time course and the response time course. Rather, this relationship changes depending on the statistics of the stimulus: sparse stimuli produce large and prolonged responses while dense stimuli produce briefer and smaller responses. Inhibition counteracts these effects, creating a more consistent relationship between the stimulus time course and the response time course. Specifically, inhibition enforces brief responses to sparse and brief stimuli, and sustained responses to dense and sustained stimuli. These results suggest that inhibition is recruited differently depending on the statistics of the stimulus. To test this hypothesis we next recorded the responses of inhibitory local neurons (LNs).

Odors elicit transient activity in inhibitory neurons

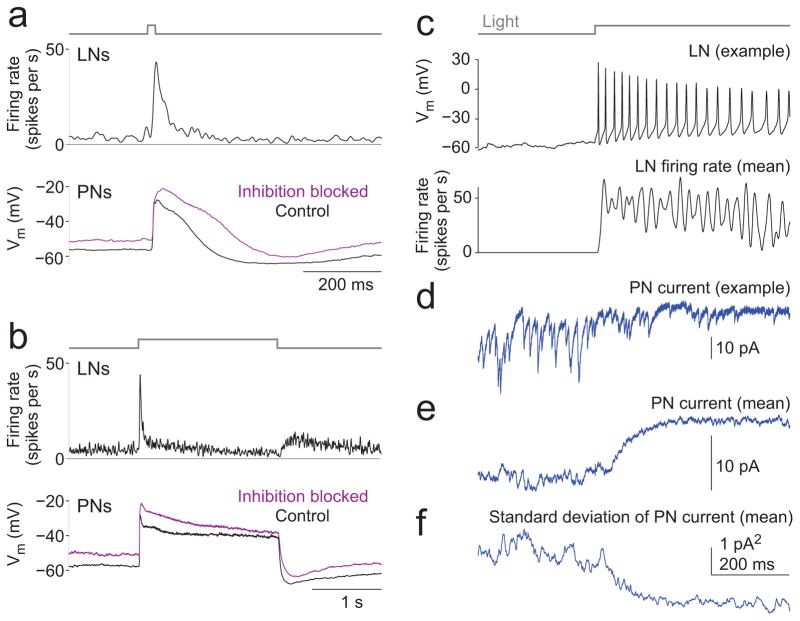
In order to examine how LNs are recruited by stimuli with different temporal properties, we made in vivo cell-attached recordings from a large population of LNs (45 in total). We sampled a diverse population of LNs by labeling three different subsets of LNs with GFP, and recording randomly within these subsets of cells (see Methods). LNs exhibited diverse response dynamics (Fig. 5a). However, certain dynamical features were typical of most LNs. First, nearly all LNs we recorded were spontaneously active (4.6 ± 2.8 spikes/s, mean ± s.d. across cells), consistent with our finding that blocking inhibition depolarized PNs even in the absence of an odor stimulus (Fig. 3a,b). Second, odor-evoked activity in LNs was highly transient, with a sharp burst of spikes at odor onset (Fig. 5a,b). Most LNs did not respond in a sustained manner to long odor pulses. Indeed, responses were actually suppressed during long stimuli in many LNs (Fig. 5a).

Figure 5. LNs respond transiently to odor stimuli.

a, Rasters showing spiking responses of six example LNs recorded in cell-attached mode. Examples were chosen to illustrate the diversity of LN temporal responses.

b, Mean LN firing rates evoked by these stimuli (n=45 LNs from 38 flies), recorded in cell-attached mode. Firing rate was obtained by taking the average number of spikes per 1 ms bin (trial averages for each LN were averaged together) and smoothing with a 20 ms-wide hanning window. On average, both the short stimulus (20 ms) and the long stimulus (2 s) elicit mainly transient excitation, shifting towards inhibition during the later part of the long stimulus.

c, Mean LN firing rates evoked by sparse odor pulse trains (20 ms pulses at 3.2 s intervals) and dense odor pulse trains (20 ms pulses at 100 ms intervals). Sparse pulses elicit reliable bursts in LN spiking, but the dense stimulus elicits a pronounced burst of LN spiking only at the onset of the train.

d, Mean synaptic current in LNs (n=22 LNs from 22 flies) evoked by a long (2 s) odor stimulus and recorded in voltage-clamp mode at a command potential of −60 mV.

e, Same as above for PNs (n=9 PNs from 8 flies, all from glomerulus DM6, VM2 or VM7).

f, The ratio of the synaptic current late in the response to a long pulse (the last 200 ms of the stimulus period) to the peak synaptic current. This ratio is significantly higher in PNs than in LNs (p=1.7e-3, t-test).

g, Synaptic currents in LNs before and after blocking inhibition (with picrotoxin and CGP54626), each averaged across the same 5 LNs.

More complex odor stimuli produced similar results. Sparse, brief odor pulses elicited large and transient increases in LN activity. By contrast, a dense train of intermittent pulses recruited LNs mainly at the onset of the train (Fig. 5c). In this respect LNs differ from PNs, which can show sustained responses to dense pulse trains (Fig. 1g).

To compare LN and PN response dynamics directly, we recorded odor-evoked synaptic currents from both cell types in whole cell voltage-clamp mode, at a holding potential near rest (−60 mV). Because LNs and PNs have different membrane time constants, this approach provided the most accurate comparison of response dynamics in the two cell types. These recordings showed that odor –evoked inward current was more transient in LNs than in PNs (Fig. 5d–f). Inward current in LNs was transient even after pharmacological blockade of inhibition (Fig. 5g), indicating an intrinsic difference between excitatory synapses onto LNs versus PNs. As we will argue below, the transience of LN spiking is relevant to understanding how inhibition stabilizes responses to long stimuli.

Inhibition grows slowly relative to local neuron spiking

The timing of inhibition depends not only on the dynamics of LN spiking, but also on the relationship between LN spiking and the effects of inhibition on target cells. We noted that LN firing rates peak rapidly after odor onset, but the functional effects of inhibition peak ~100 ms later in our PN data. The effects of inhibition also outlast the odor-evoked increase in average LN firing rates (Fig. 6a,b). These observations suggest that there is some slow process between LN spiking and the effects of inhibition on target cells.

Figure 6. Inhibition grows slowly relative to LN spiking.

a, Top: mean LN firing rate evoked by a short (20 ms) odor pulse, averaged over all LNs. Bottom: mean PN membrane potential response to the same stimulus, before and after blocking inhibition. Data reproduced from Figure 5b and Figure 3b. The main effect of blocking inhibition on the PN odor response begins ~100 ms after the peak in LN spiking, and also outlasts the burst in LN spiking.

b, Same as above, but for a long (2 s) odor stimulus. Again, inhibition grows more slowly than does LN spiking.

c, Top, Light evoked spikes in an LN expressing channelrhodopsin-2. Bottom, mean firing rate evoked by light in LNs expressing channelrhodopsin-2 (n=4 LNs from 4 flies).

d, A voltage-clamp recording from an example PN (glomerulus DM6) displaying inhibition in response to optogenetic activation of LNs (V_hold = −60 mV). During the light stimulus, spontaneous EPSCs slowly become smaller and less frequent, and the mean inward current decreases. PNs were recorded separately from LNs.

e, Mean holding current in PNs in response to optogenetic activation of LNs (n=7 PNs from 7 flies, VM2 or DM6). The mean holding current changes slowly compared to the time course of LN spiking.

f, Standard deviation in the PN holding current. The decrease in the standard deviation of the holding current reflects the decrease in both amplitude and frequency of spontaneous EPSCs, and therefore provides a measure of presynaptic inhibition. Note that by this measure, presynaptic inhibition also builds slowly.

Until now, we have been measuring the functional effects of inhibition by comparing PN odor responses before and after pharmacological blockade of GABA receptors. To obtain a more direct measure of the time course of functional inhibition, we expressed channelrhodopsin-2 in a large subset of LNs. This experiment allowed us to directly elicit LN spiking with light and thereby compare the timecourse of LN spiking to the timecourse of inhibition in target cells.

While light-evoked firing rates rose rapidly in LNs (Fig. 6c), inhibition measured in PNs progressed more slowly (Fig. 6d–f). LNs primarily inhibit PNs indirectly, by inhibiting ORN axon terminals^{33, 38}. Because ORNs spike spontaneously and produce spontaneous EPSCs in PNs²⁸, spontaneous EPSCs in PNs provide a sensitive measure of the time course of presynaptic inhibition. The time course of inhibition could be fit with an alpha function with a time constant of about 25 ms. These data provide direct evidence that LNs have slow effects on ORN neurotransmitter release. Below we will describe how the slow growth of inhibition is relevant to how inhibition stabilizes neural activity.

The dynamics of inhibition are functionally relevant

Our findings highlight two dynamical features of inhibition in this circuit. First, LN spiking is transient. Second, the effects of inhibition grow slowly relative to LN spiking. How might these two features be important to recapitulating the functional effects of inhibition?

To address this question, we added inhibition to our model. Presynaptic inhibition at ORN-to-PN synapses decreases both EPSC amplitude and the rate of synaptic depression in experimental data³³. To model these effects, we divided ORN firing rates (recorded in separate experiments) by a parameter I(t) that represents the time-varying amplitude of inhibition. This procedure essentially models inhibition as a decrease in presynaptic release probability. I(t) was estimated by taking the average spiking activity of all LNs, and filtering this signal with a 25 ms alpha function to mimic the slow growth of inhibition relative to LN spiking. As in previous models, ORN-to-PN synapses in this model had both fast and slow components, although we modified how we fit the parameters of the slow component (Supplementary Figure 5; Methods and Discussion).

Similar to our experimental results (Fig. 7a), we found that adding inhibition to our model truncated responses to brief odor pulses and stabilized responses to long pulses (Fig. 7b). Moreover, adding inhibition to the model decreased baseline (pre-odor) activity relative to the steady-state odor response. In this sense, inhibition increased the signal-to-noise ratio of postsynaptic activity. We observed a similar suppression of baseline activity relative to steady-state in our experimental results (Fig. 7a).

Figure 7. The dynamics of inhibition are functionally relevant.

a, Mean ORN responses to a short (20 ms) and long (2 s) stimulus (n=4 ORNs presynaptic to glomerulus VM7). Data reproduced from Figure 1d. Below are mean PN responses with inhibition intact and blocked (n=7 PNs postsynaptic to glomerulus VM7; this is a subset of the data in Figure 3b).

b, Model PN responses to the same stimuli, with and without inhibition. Inhibition is transient, slower than LN spiking, and presynaptic. Shown below each PN response is the time course of inhibition (parameter I(t) in the model). Inhibition truncates the response to the short stimulus and generates a more stable response to the long stimulus; it also hyperpolarizes the pre-odor baseline.

c, Time course of the amplitude of the unitary postsynaptic conductance for fast and slow components of ORN-to-PN synapses (parameter A(t) in Equation 3, Methods). Solid traces show this parameter with inhibition while dashed traces show this parameter without inhibition. Without inhibition, synapses are weaker both before and during the stimulus.

d, Model PN responses with transient inhibition (black trace, same as panel b) compared to persistent inhibition (I(t) is clamped at its peak throughout the stimulus). Persistent inhibition causes the PN response to decay during the long stimulus.

e, Model PN responses with inhibition that is slow (LN firing rate smoothed with a 25 ms alpha function, same as panel b) versus inhibition that is faster (LN firing rate smoothed with 5 ms alpha function). Inset shows the onset of the response to the long stimulus on an expanded timescale. When the onset of inhibition is faster, inhibition begins to act before the initial PN depolarization is complete.

f, Model PN responses with presynaptic inhibition (black trace, same as panel b) versus postsynaptic inhibition. I(t) was the same in both models, and the gain of postsynaptic inhibition was set so the level of pre-odor hyperpolarization was matched. Postsynaptic inhibition decreases the sustained odor response relative to the pre-odor baseline.

In this model, there are two distinct reasons why inhibition stabilizes neural activity. First, because inhibition is transient, it preferentially cancels excitation in the epoch when excitation is strongest – that is, when ORN-to-PN synapses are strongest, and when ORN firing rates are highest. Moreover, because inhibition is presynaptic, it decreases the rate of synaptic depression, thereby preserving synaptic resources (e.g., vesicles or receptors) for later epochs. This latter effect is clearest in the evolution of the amplitude of the unitary postsynaptic conductance over time (Fig. 7c).

What would happen if odors evoked sustained rather than transient activity in LNs? When we clamped LN firing rates at their peak level throughout the odor stimulus, the PN response ran down during a long stimulus (Fig. 7d).

Is it important that inhibition grows slowly? When we filtered LN activity less strongly (thereby making the time course of inhibition more similar to the time course of LN activity), inhibition began to act on the synapse before the PN response had peaked, and so the peak response was attenuated and response onset was slowed (Fig. 7e).

What would change if inhibition were postsynaptic rather than presynaptic? To examine this question, we replaced presynaptic inhibition in the model with an inhibitory conductance in the PN that reversed at −70 mV. As before, inhibition at each time point was proportional to I(t). Postsynaptic inhibition decreased the size of the sustained PN odor response relative to the pre-odor baseline (Fig. 7f), whereas presynaptic inhibition had the opposite effect (compare with Fig. 7b). This occurs because postsynaptic inhibition is strongest when the PN is depolarized and sits far from the reversal potential for the inhibitory current; by contrast, presynaptic inhibition has a stronger effect on low presynaptic firing rates than on high presynaptic firing rates (Supplementary Fig. 6).

This model clarifies the role that inhibitory dynamics play in shaping the time course of PN responses. Because inhibition—like excitation—is transient, it cancels out many of the transient distortions produced by synaptic depression and ORN adaptation. However, because inhibition grows slowly, it preserves the rapid onset of the response when the stimulus onset is also rapid. Dynamic inhibition thus allows the circuit to encode both rapid and sustained stimuli more accurately.

Inhibition flattens the frequency response of the circuit

In this study, we have described synaptic and circuit mechanisms that counteract short-term depression (Fig. 8a). Since short-term synaptic depression acts as a bandpass temporal filter^{7, 8}, we would expect these mechanisms to also broaden the frequency response of the circuit, making postsynaptic response amplitude more constant across a range of stimulus timescales. Modeling allows us to test this idea by probing responses to stimuli that are difficult to generate experimentally. To model LN spiking responses to novel stimuli, we used a formalism similar to the feedforward component of our PN model (see Methods). LN spike rates were then translated into a time-varying inhibitory signal as before.

Figure 8. Inhibition flattens the frequency response of synaptic transmission.

a, Schematic of the antennal lobe circuit illustrating the temporal characteristics of each synapse. ORN-to-PN synapses include two components: a fast component that depresses rapidly, and a slow component that depresses more slowly. Excitation onto LNs depresses more completely than excitation onto PNs, and LN inhibition of ORN axon terminals is slow. As a consequence, the dynamics of ORN-to-PN synapses are modulated by an inhibitory signal that is a more transient and delayed version of excitation onto PNs.

b, Model PN responses to a train of brief and sparse odor pulses. The fast component has a faster rise and decay than the slow component, and the sum of both components is intermediate. Inhibition speeds the decay of these responses. The time course of inhibition (parameter I(t)) is shown below.

c, Model PN responses to a dense train of odor pulses. The slow component generates a more sustained response than the fast component, but decays slowly over time. The sum of both components is intermediate. Inhibition regulates the slow component to produce a more stable response over time.

d, Impulse responses calculated by averaging model responses to sparse pulses, as in Figure 4d.

e, Impulse responses for dense pulse trains, calculated by computing the linear filter and convolving it with a 20-ms stimulus pulse, as in Figure 4f.

f, Model PN responses to a slowly-modulated stimulus (a sine squared function). The fast component of excitation generates a transient response when the stimulus starts to increase, while the model with inhibition tracks the stimulus more accurately.

g, Amplitude of model PN responses at the stimulus frequency, plotted versus stimulus frequency (sine squared functions, as in f). Inhibition flattens the frequency response function, decreasing responses at intermediate frequencies, while also boosting responses at low and high frequencies.

We used this approach to examine four models: a model with the fast component of excitation only, with slow excitation only, with both fast and slow excitation, and with inhibition added. We began by examining model responses to the sparse and dense pulse stimuli shown in Figure 4. In this case, the inputs to the model were measured ORN firing rates.

Brief and sparse odor pulses (Fig. 8b) highlighted the importance of fast excitation: the fast component allowed the PN to respond quickly to a pulse onset and to faithfully resolve pulses in quick succession. Adding slow excitation prolonged the PN response, but subsequently adding inhibition made PN responses more transient again (Fig. 8b). In this regime, inhibition improved encoding of high-frequency stimuli, insofar as it shortened the response to brief stimuli.

Conversely, a long train of dense odor pulses (Fig. 8c) highlighted the importance of slow excitation. Here, the slow component provided long-lasting excitation, while the fast component produced a more transient response. Adding inhibition increased the stability of the PN response over the duration of the long dense train because inhibition selectively canceled the strong early response. In this regime, inhibition improved encoding of low-frequency stimuli, by creating more stable responses to a prolonged stimulus.

To quantify the contribution of inhibition in these different regimes, we calculated impulse responses based on the model output. As in our data (Fig. 4), the shape of the impulse response in the absence of inhibition depended on stimulus statistics, with dense stimuli producing smaller and briefer responses than sparse stimuli (Fig. 8d,e). One reason why this occurs is that the slow component of ORN-to-PN synapses decays slowly, so the ratio of fast to slow increases over time. Also similar to our data (Fig. 4), the effects of inhibition depended on stimulus statistics. In a sparse regime, modeled inhibition decreased the duration of the impulse response (from 145 to 90 ms at half-maximum). In a dense regime, it increased the ratio of positive to negative filter components (from 1.25 to 1.41), meaning that a sustained stimulus produces a larger sustained response.

Together, these observations suggest that inhibition enables the model PN to encode stimulus time course more consistently across frequencies. To test this idea explicitly, we probed our model with sinusoidally-modulated stimuli at different frequencies (Fig. 8f). We modeled ORN responses to these stimuli using a linear filter extracted from ORN data (see Methods and Supplementary Figure 3). The slow component of excitation followed this stimulus rather faithfully, whereas the fast component was recruited only transiently during the rising phase of the sinusoid. Adding inhibition cancelled the transient of excitation, producing a more sinusoidal response.

To quantify the ability of each model to follow sinusoidal stimuli, we measured the power in the response at the frequency of the stimulus (Fig. 8g). As expected, low frequencies were best encoded by the slow component of excitation, whereas high frequencies were best encoded by the fast component. In a model with both components, inhibition decreased power at intermediate frequencies, and slightly increased power at both high and low frequencies. Thus, the net effect of inhibition was to flatten the frequency response of the system.

Discussion

Near the sensory periphery, synapses must fulfill two competing demands. On the one hand, they need to signal rapidly, because reaction times for all subsequent neurons depend on fast peripheral transmission. Accordingly, many synapses near the sensory periphery are relatively strong^12–15. On the other hand, synapses near the periphery ought to encode stimuli as faithfully as possible, because information discarded at the periphery cannot be regained. Strong synapses often exhibit profound depression, because they are subject to vesicle depletion and/or postsynaptic desensitization. These considerations suggest that there may be mechanisms at work that mitigate the effects of synaptic depression, especially near the periphery. In this study we show how the interaction of multiple synaptic and circuit mechanisms can reduce synaptic depression to promote faithful coding of both fast and slow stimuli.

Why not simply build a synapse that does not depress at all? Synapses that depress only modestly have been reported previously^{39, 40}, but even in these cases depression is nonzero. Thus, there might be reasons to reduce and modulate depression without eliminating it. Indeed, depression can be useful when the goal of the system is to encode relative intensity or contrast^{7, 9–11}. Synaptic depression may also be a useful way to limit the metabolic demands of neural activity. At a synapse where the level of depression is tuneable, the tradeoffs are most flexible⁸.

Fast and slow receptors together increase transmission bandwidth

One mechanism that promotes broadband coding is having two components to excitatory synaptic transmission. We found that that each presynaptic spike elicits an EPSC with two kinetically separable and pharmacologically separable components. The fast component mediates rapid responses at stimulus onset, while the slow component provides sustained responses to ongoing stimuli. The Drosophila genome encodes 10 distinct nicotinic subunits, and so the fast and slow components could represent molecularly distinct receptors. Alternatively, they could represent two conductance states of the same receptor.

EPSCs at many vertebrate central synapses also display two phases of decay. These two components are mediated by fast and slow ionotropic glutamate receptors (AMPA and NMDA receptors). Although most studies of NMDA receptors have focused on their role in triggering long-term plasticity, they can also carry sensory signals. Specifically, NMDA receptors carry the steady-state response to a prolonged stimulus, while AMPA receptors mediate the transient onset response^41–44. Thus, our results may have broad conceptual relevance to vertebrate neural circuits, although the details of implementation are different.

By using two receptors with different kinetics, neurons can adjust their temporal selectivity. For example, mammalian retinogeniculate synapses contain variable ratios of AMPA to NMDA conductances, allowing postsynaptic neurons to encode diverse temporal features⁴³. Moreover, both AMPA/NMDA receptors⁴⁵ and insect nicotinic acetylcholine receptor subtypes³⁰ can be can be differentially regulated by second messenger pathways.

Dynamic inhibition promotes broadband synaptic transmission

Many in vitro studies have shown that presynaptic inhibition can counteract short-term synaptic depression^{8, 21, 22}. However, in previous studies, presynaptic receptors were activated tonically using bath-applied agonists, while in vivo these receptors are likely activated dynamically. For this reason, it is important to study how the dynamics of inhibition shape excitatory transmission.

We can separate inhibition into two processes: the activation of inhibitory interneurons, and synaptic transmission from interneurons onto target neurons. Here we measured the dynamics of both processes. First, we found that odor-evoked synaptic currents in LNs are transient—more transient than in PNs. Strongly depressing excitatory synaptic currents have also been reported in inhibitory interneurons in somatosensory cortex⁴⁶, olfactory cortex⁴⁷, and hippocampus⁴⁸.

Second, we found that the effects of LNs on target neurons grow slowly. Many studies have described a delay between excitation and inhibition^49–51. This delay is often thought to arise from the additional synapse present in a feedforward inhibitory circuit, as compared to a feedforward excitatory circuit. Here we show that synaptic transmission from LNs onto ORN terminals is intrinsically slower than transmission from ORNs onto PNs.

Our model shows that the dynamics of inhibition matter. Because inhibition is transient, it cancels out many of the transient distortions produced by synaptic depression and ORN adaptation, while preserving the sustained response to a sustained stimulus. Because inhibition grows slowly, it preserves the fast onset of the response to a rapid-onset stimulus, while also truncating responses to brief stimuli. Finally, because inhibition is presynaptic, it increases the difference between the sustained odor response and the pre-odor baseline.

Our conclusion that inhibition can promote broadband coding is based on both experimental results and simulations. Experimentally, we observed that inhibition enforces brief responses to brief stimuli but sustained responses sustained stimuli (Figure 4). This is consistent with the idea that inhibition flattens the frequency response of the circuit, because both high frequency (brief) and low frequency (sustained) stimuli are represented more faithfully in the presence of inhibition. Modeling allowed us to make this idea explicit, by exploring responses to odor stimuli that we could not easily deliver in the laboratory, such as sinusoidal odor fluctuations, and longer trains of random pulses.

Dynamic inhibition has often been interpreted as conferring selectivity for specific temporal patterns of excitation^46–50. In other words, inhibition is thought to restrict the range of temporal waveforms that a neuron responds to. Our results provide a different perspective: dynamic inhibition can actually expand the range of frequencies that a neuron can encode. This can occur when the frequency characteristics of a synapse are restricted by short-term depression, and when presynaptic inhibition is tuned to counteract this limitation on bandwidth. Our results may thus provide insight into the function of local inhibitory circuits in many systems.

Strengths and limitations of our models

In this study, we employed relatively simple models whose parameters were heavily constrained by experimental measurements. In any model that is constrained by data, the intepretation of the model is of course limited by the limitations of the data itself. A case in point is the slow component of the EPSC at ORN-to-PN synapses. We initially fit this to EPSCs recorded in curare. This exercise showed that a model fit to pharmacologically-defined EPSC components can roughly reproduce PN odor responses (Fig. 2). However, this simple model did not fully capture the dynamics of real PN odor responses in the absence of inhibition (compare Figs. 2 and 3). It is likely that curare incompletely blocks the fast component, so when we fit the slow component to the curare data, it depressed too quickly. We therefore subsequently fit the slow component to PN odor response data with inhibition blocked (Figs. 7 and 8; Supplementary Fig. 5). Here the fit was better because the modeled slow component depressed more slowly. In the future, it would be interesting to use genetic manipulations to isolate these EPSC components more precisely.

Any model is also a simplification. For example, to model the dynamics of LN activity, we simply took the summed spiking activity of all LNs (Figure 6), which neglects the diversity of spiking dynamics across the LN population (Fig. 5). In the future, it will be interesting to determine whether LNs with different dynamics have different postsynaptic targets or weights. Our model may be useful to future studies of interneuron diversity because it provides a new way of thinking about interneuron dynamics: they can serve to minimize the distortions produced by the dynamics of excitatory synaptic input. As such, a diversity of LN dynamics may allow the network to more accurately remove distortions on multiple timescales.

METHODS

Fly stocks

Flies were raised at 25°C on a cornmeal-agar based medium under a 12 hr/12 hr light/dark cycle. All experiments were performed on adult female flies 1-3 days post-eclosion. All stocks used have been originally published as follows: UAS-CD8:GFP (ref. ⁵²), NP3481-Gal4 (ref. ⁵³), GH298-Gal4 (ref. ⁵⁴), NP3056-Gal4 and LCCH3-Gal4 (ref. ⁵⁵), UAS-ChR2::EYFP (ref. ⁵⁶).

Electrophysiology

Whole-cell patch clamp recordings from PNs and LNs were performed as previously described⁵⁷. Briefly, the fly was positioned in a horizontal platform, with the dorsal part of the fly head above the platform and most of the fly below the platform. The dorsal part of the fly head was dissected to expose the brain and bathed in external saline containing 103 mM NaCl, 3 mM KCl, 5 mM TES, 8 mM trehalose, 10 mM glucose, 26 mM NaHCO₃, 1 mM NaH₂PO₄, 4 mM MgCl₂, and 1.5mM CaCl₂. Cell bodies were visualized using infrared optics and a 40× water-immersion objective on an upright compound microscope (Olympus BX51). Patch pipettes (5–7 MΩ) were pulled the day of the recording and filled with internal solution containing 140 mM KOH, 140 mM aspartic acid, 10 mM HEPES, 1 mM EGTA, 1 mM KCl, 4 mM MgATP, 0.5 mM Na₃GTP, and 13 mM biocytin hydrazide. The pH of the internal solution was adjusted to 7.2 ± 0.1 and osmolarity to 265 ± 3 mOsm. The internal solution for voltage clamp recordings contained 140 mM CsOH in place of KOH. In a subset of voltage clamp experiments, 5 mM QX-314•Cl⁻ was added to the internal solution to reduce the occurrence of unclamped spikes. For these recordings, the osmolarity of the internal solution was readjusted to 265 ± 3 mOsm after addition of QX-314•Cl⁻. During current clamp recordings a small negative holding current (~10 pA) was applied to bring the resting membrane potential to between −50 and −60 mV, thereby counteracting the small depolarizing current created by the seal conductance⁵⁸. Recordings from labeled PNs were performed in the genotype NP3481-Gal4,UAS-CD8:GFP (which labels PN in glomeruli DM6, VM2, VM7, and DL5). LN recordings in Figure 5 were performed in the following genotypes: GH298-Gal4,UAS-CD8:GFP or UAS-CD8:GFP;NP3056-Gal4 or NP3056-Gal4,UAS-CD8:GFP, and LCCH3-Gal4,UAS-CD8:GFP (corresponding to lines 4, 5, and 7 from ref. ⁵⁵; these Gal4 lines collectively label eight of the nine major morphological types of GABAergic LNs).

After each PN recording, the identity of the recorded cell was confirmed post hoc by immunohistochemistry with a fluorescent conjugate of streptavidin (to visualize the recorded cell), rat antibody to CD8 (to visualize GFP-positive neurons; Invitrogen, MCD0800, 1:40 dilution) and mouse nc82 antibody (to visualize glomerular volumes; Developmental Studies Hybridoma Bank, nc82-s, 1:50 dilution)⁵⁷. In odor stimulation experiments, unless otherwise indicated, we pooled data from PNs in glomeruli DM6, VM2, and VM7, because we obtained similar results for all three glomeruli. For experiments where we electrically stimulated the antennal nerve, we pooled data from PNs in glomeruli DM6 and VM2 (VM7 was not included here because it receives input from ORNs in the maxillary palp, not the antenna, and so direct EPSCs cannot be evoked by antennal nerve stimulation). In a small subset of experiments, the filled PN was not recoverable, but because PNs in only four glomeruli were GFP-labeled (DM6, VM2, VM7, DL5), and because DL5 PNs have a distinctive large size and low input resistance, it is nonetheless very likely that the recorded PN arborized in one of the three glomeruli we were intending to target (DM6, VM2, VM7). Recordings in Fig. 2a were made in random PNs, and one antenna was removed prior to the experiment to decrease the rate of spontaneous EPSCs and thereby better resolve the kinetics of individual events.

In a subset of PN recordings, we observed very little depolarization of PNs in response to odor. This type of response was associated with very low or absent spontaneous activity, and generally all the PNs in the preparation exhibited the same behavior. Recordings in which the GFP-labeled PNs did not spike in response to odor presentation were terminated immediately and these preparations were discarded.

To measure LN spiking, we chose to make cell-attached recordings because they are less invasive than whole cell recordings, and because it is relatively easy to detect LN spikes in cell-attached mode. Cell-attached recordings from LNs were performed using saline-filled patch pipettes, in voltage-clamp mode, with the command voltage adjusted so that the holding current was essentially zero. Positive pressure was released before the pipette encountered the cell body to prevent formation of a tight seal. The cell body was then gradually drawn into the pipette with weak negative pressure until a stable extracellular spike waveform was obtained. Recordings that showed signs of membrane rupture were discarded.

For ORN recordings, the fly was immobilized in a modified plastic pipetter tip such that the maxillary palps (which contain the ORNs presynaptic to glomerulus VM7) were exposed to air. A reference electrode was placed in the eye and the palp was stabilized using a cover slip and a glass pipette. Sensilla containing the dendrites of specific ORNs were visualized using a 50× air objective on an upright compound microscope. ORN spikes were recorded using high impedence pulled-glass capilliaries filled with external saline and inserted into the sensillum lymph surrounding the ORN dendrites. VM7 ORNs were readily identified based on their characteristic spike shape and odor response profile.

All electrophysiological recordings were performed with an Axopatch 200B amplifier. Data was filtered at 2 kHz and then digitized at 10 kHz.

Olfactory stimulation of ORNs

Odor stimulation was designed to produce rapid and reliable delivery of odor pulses of various durations. On the day of the experiment, the odor 2-heptanone was diluted 1:100 (vol:vol) in 990 μL of paraffin oil and placed in a fresh plastic screw-cap vial (1 mL). The odor 2-heptanone was chosen because it strongly activates ORNs presynaptic to the 3 PN types we recorded from in this study (VM7, DM6, and VM2) and because it activates a large number of ORNs, thereby making it likely that it recruits a substantial amount of LN-mediated inhibition. Charcoal-filtered air was continuously flowed through the odor tube at 0.7 L/min until the concentration of the odor at the outlet tube reached a steady-state that was lower than the initial concentration when the air was turned on; thus, the effective concentration of the odor at the outlet tube was less than 1:100. During most of the experiment, the odor vapor was diverted into an open tube with a vacuum at one end (vacuum flow rate 0.6 L/min) to avoid contaminating the room air. In order to send the odor to the fly, a valve (LFAA1201610H, The Lee Company, Essex, CT) rapidly switched the odor stream from the vacuum tube to a delivery tube aimed at the fly’s head. The delivery tube was 3 cm long and had an inner diameter of 1.5 mm. Two miniature video cameras (Unibrain) were used to position the odor tube reliably in relationship to the fly’s head. Photo-ionization detector measurements (miniPID, Aurora Scientific) were used to verify that this device could reliably deliver square pulses of durations from 20 ms to 2 s, and that the concentration of the odor at the fly’s location was reasonably stable throughout the experiment (Supplementary Fig. 7). Each odor stimulus was presented several times consecutively in each recording, with 2–7 trials per stimulus in an ORN recording, and typically 4 trials per stimulus in a PN recording, and responses to trials were averaged before averaging data across recordings.

Electrical stimulation of ORN axons

The third segments of both antennae were removed with fine forceps just prior to opening the head capsule. The antennal nerve ipsilateral to the recorded PN was drawn into a large-diameter saline-filled pipette and stimulated with 50 μs pulses using a stimulus isolator (AMPI, Iso-Flex) in constant current mode. The stimulus amplitude was adjusted for each experiment to produce a reliable EPSC waveform with minimal unclamped spiking (7.5–150 μA). Empirically, we found that recordings with initial EPSCs larger than 80 pA tended to produce unclamped spikes. We therefore analyzed only recordings in which the initial EPSC amplitude was less than 80 pA. Except for this criterion we did not attempt to remove unclamped spikes from our data, as these made little contribution to the average response. Cells for which we were unable to obtain a stable EPSC waveform in response to electrical stimulation were discarded. In the EPSC waveforms shown in Fig. 2 and Supplementary Fig. 1b–c, the brief electrical artifact caused by the stimulus was deleted for display purposes, and the trace was mended by linear extrapolation between the cut ends; the maximum time blanked was 1.5 ms.

Optogenetic stimulation of LNs

Experiments in Fig. 6c–f were performed in the genotype shakB²/Y; UAS-ChR2::EYFP-C/+; UAS-ChR2::EYFP-B/NP3056-Gal4. This fly harbors UAS-ChR2::EYFP insertions on both chromosome 2 (insertion “C”) and chromosome 3 (insertion “B”)⁵⁶. NP3056-Gal4 drives expression in a large fraction of GABAergic LNs⁵⁵. These experiments were performed in a shakB² background in order to eliminate lateral excitation, thereby isolating the kinetics of lateral inhibition alone⁵⁹. PNs were not GFP-labeled in these experiments, and so PNs were selected randomly, and then the glomerulus they innervated was identified post hoc using immunohistochemistry (see above). For consistency with our other PN recordings, we included only PNs that innervated one of the three glomeruli that we focused on in this study; we obtained a total sample of seven such PNs (six from DM6 and one from VM2). Light stimuli were provided by a 100 W mercury arc lamp, bandpass filtered at 460–500nm, and delivered to the specimen focused through a 40× water-immersion objective. Light was gated by a shutter (Uniblitz) controlled by a TTL pulse. Neutral density filters were used to attenuate the light to a power density of 17–20 mW/mm². Power density was measured using an optical power meter (Newport 1916-C) with the photodetector (818P-015-19) positioned behind a pinhole aperture placed at the level of the specimen. Light was presented for 5–7 trials in each recording, at an interval of 60 sec for PN recordings and 30 sec for LN recordings.

Pharmacology

Tubocurarine chloride (Tocris) was dissolved in water to make a 25 mM stock which was stored at 4°C. Imidacloprid (Sigma-Aldrich, item # 37894) was dissolved in DMSO to make a 1 mM stock which was at room temperature. Methyllycaconitine citrate salt hydrate (Sigma) was dissolved in water to make a 2mM stock and kept at 4°C. Alpha-bungarotoxin (Tocris) was dissolved in water to make a 5mM stock and kept at 4°C. Picrotoxin (Tocris) was dissolved in aqueous 100 mM NaCl to make a 5 mM stock solution which was stored in the dark at room temperature. CGP54626 (Tocris) was dissolved in DMSO to make a 50 mM stock solution which was stored at −20°C.

Modeling

In Fig. 1, we modeled PN membrane potential responses to ORN spike trains. We recorded ORN firing rates in separate experiments, and we modeled ORN spike trains as inhomogeneous Poisson processes governed by these firing rates. Both spontaneous and odor-evoked firing rates were taken from our data. Because experimental measurements indicate that ORNs spike are independently²⁸, we generated spike trains for each of the 40 model ORNs independently. The number of ORNs in this population follows published data indicating that there are on average ~40 ORNs that express each odorant receptor, and each of these ORNs synapses onto every PN in its cognate glomerulus^{28, 32, 60}.

Each ORN spike produced a postsynaptic conductance whose shape was determined by the average normalized EPSC in response to nerve stimulation. We used the first EPSC produced by a 10 Hz stimulus, so the first 100 ms was taken from data, and the shape from t = 100 ms to t = 500 ms was extrapolated from a bi-exponential fit to the first 100 ms. The maximum amplitude of this conductance (0.28 nS) was set such that the amplitude of a unitary EPSC prior to depression was ~13.5 pA and the amplitude of a unitary EPSP was ~7 mV, given the passive membrane properties described below. These EPSC and EPSP amplitudes are consistent with published measurements of unitary EPSCs and EPSPs in PNs located in glomeruli DM6 and VM2¹².

To model short-term synaptic depression at ORN-to-PN synapses, we used a well-studied formalism^{7, 8, 61}. We scaled the amplitude of each unitary post-synaptic conductance by a factor A(t), which represents the synaptic resources (e.g., vesicles or receptors) available at time t. After each ORN spike, A decreased by a factor f which then recovered with time constant τ.

$$\begin{array}{l}ifs(t)=1,A(t+\mathrm{\Delta }t)=f\ast s(t)\ast A(t)\\ ifs(t)=0,A(t+\mathrm{\Delta }t)=A(t)+(1-A(t))\mathrm{\Delta }t/\tau \end{array}$$ (Equation 1)

where s(t) is a binary vector, sampled with a time step (Δt) of 1 ms, that takes a value of 1 if a spike occurred in the presynaptic ORN and 0 otherwise. The parameters f (which is unitless) and τ (which has units of ms) were fit to the mean normalized amplitude of EPSCs recorded in PNs in response to electrical stimulation of the antennal nerve at 10 Hz (Fig. 1c). The synaptic conductance arising from each ORN spike train was calculated by first computing A(t), and then convolving A(t) with the standard conductance waveform described above.

Conductances arising from each ORN-to-PN synapse were summed to produce the total excitatory synaptic conductance in the model PN (g_syn(t)). Membrane potential responses of PNs were modeled according to

$$\frac{dV}{dt}=\frac{-(V(t)-E_{\mathit{leak}}+g_{\mathit{syn}}(t)·R_m·\left(V(t)-E_{\mathit{syn}})\right)}{{\tau }_m}$$ (Equation 2)

where V(t) is the membrane voltage, E_leak is the reversal potential for leak currents, R_m is the membrane resistance, E_syn is the reversal potential for synaptic currents, and τ_m is the membrane time constant. E_leak was set to −70 mV, which is close to the resting potential of PNs in tetrodotoxin⁵⁸ and E_syn to −10 mV, which is close to the measured reversal potential for nicotinic acetylcholine receptors⁶². The constant R_m was set at 800 MΩ, which is close to published measurements⁶³, while τ_m (5 ms) was adjusted so that a unitary EPSP decayed with a half-width of about 50 ms, in agreement with published data¹². Membrane potential was simulated using the Euler method at a time resolution of 0.1 ms. Total excitatory synaptic conductance (g_syn(t)) was upsampled from 1 kHz to 10 kHz prior to simulation. Supplementary Fig. 3a shows synaptic currents and voltages generated by this model. This model was also used in Supplementary Fig. 5d.

In Figure 2, ORN input was modeled in the same way as for Fig. 1, but each spike elicited a conductance with two components, fast and slow. The parameters governing depression of the fast component (f and τ) were fit to EPSC amplitudes evoked by a train of electrical stimuli at 10 Hz in IMI, and the shape of the unitary synaptic conductance was taken from the average EPSC evoked by the first stimulus of the train in IMI. Similarly, f, τ, and the shape of the unitary synaptic conductance for the slow component were taken from data recorded in curare. The slow conductance waveform was extrapolated to 500 ms using a single exponential and the fast conductance waveform was extrapolated to 500 ms using a bi-exponential. The amplitudes of the two conductances prior to depression were set to 0.22 nS (fast component) and 0.06 nS (slow component) such that the summed conductance had an amplitude of 0.28 nS as in the single component model. The ratio of fast and slow conductances was set by the fit of a bi-exponential decay to the first average normalized control EPSC in response to a 10 Hz stimulus. Supplementary Fig. 3b shows synaptic currents and voltages generated by the two-component model.

In Figs. 7 and 8, we fit the parameters of the slow component to PN odor response data (in picrotoxin and CGP54626) rather than to nerve stimulation data. This fitting procedure allowed the model to capture the slow decay in response to long stimuli and the prolonged response to brief stimuli, both of which are prominent in the data when inhibition is blocked (Figures 3a,b and 4a; Supplementary Figure 5). Another change (relative to the model in Fig. 2) is that the input to the model in Figs. 7 and 8 was ORN firing rate rather than ORN spikes. This modification allowed the model to run more rapidly and facilitated fitting to odor response data. Each component of the synaptic conductance was described by a pair of equations:

$$\frac{dA}{dt}=-r·s(t)·A(t)+(1-A(t))/{\tau }_A$$ (Equation 3)

$$\frac{dg}{dt}=k·s(t)·A(t)-g(t)/{\tau }_g$$ (Equation 4)

As in Equation 1, A(t) governs the amplitude of the postsynaptic conductance. Here s(t) is a measured ORN firing rate with units of spikes ms⁻¹, rather than a binary vector. The parameter r governs the rate of depression and is equivalent to (1- f) in Equation 1, and τ_A is equivalent to τ in Equation 1. The conductance is g(t), where k controls the amplitude of the conductance and τ_g specifies the rate of decay of the conductance. For the fast component, we used r = 0.23 spike⁻¹, τ_A = 1006 ms, k = 20 nS/spike, and τ_g = 9.3 ms. The values for r and τ_A were taken from the fits of EPSC amplitude as a function of stimulus number in IMI, while the parameter τ_g was taken from the faster exponential fit to the EPSC shape in IMI. The parameters of the slow component were fit (using the MATLAB routine nlinfit.m) in order to minimize the difference between the predicted PN membrane potential in response to 55% density stimulus and the actual disinhibited response (Supplementary Fig. 5c-e). ORN spikes were delayed by a fixed amount (10 ms) such that the model and measured PN responses commenced with the same delay relative to the stimulus. Fitted parameters for the slow component were r = 0.0073 spike⁻¹, τ_A = 33247 ms, k = 1.8 nS/spike, and τ_g = 80 ms. The two conductances were summed to yield the total synaptic conductance (g_syn). This was then used to model the model PN membrane potential according to Equation 2.

Although it was useful for illustrative purposes in Figs. 7 and 8 to fit the slow component to PN odor response data rather than evoked EPSCs in curare, this choice did not affect any of our major conclusions regarding the model. When the model was fit to nerve stimulation data, as in Fig. 2, rather than PN odor response data, we observed qualitatively similar effects of inhibition on model PN odor responses in simulations analogous to those in Figs.7 and 8f–g (not shown).

Dynamic inhibition was added to the model in Fig. 7 by taking the average recorded spiking activity of all LNs (Fig. 5b), and then convolving this signal with a 25 ms alpha function to generate a measure of functional inhibition at each time point (I(t), labeled as “inhibition” below each of the corresponding model PN responses in Fig. 7). This inhibitory signal divided the input to the model (ORN firing rate) at each point in time. Note that this is equivalent to inhibition decreasing the probability of synaptic release, which governs both the rate of depression r and the amplitude of the synaptic conductance g_syn. The magnitude of I(t) that we computed in this manner provided a good qualitative fit to the data, so its scale was not adjusted.

In Fig. 8b–g, we needed to model LN firing rates (rather than taking LN firing rates from our data). Our model needed to capture the transience of LN firing rates, so to achieve this, we used a depression model similar to our model of depression at ORN-to-PN synapses – i.e a pair of equations with the same form as Equation 3–4. The parameters of this model were r = 0.3 spike⁻¹, τ_A = 1000 ms, k = 100 and τ_C = 15 ms. We chose f and τ to produce LN activity that depressed at about the same rate as PN excitation, but with a lower steady-state level, motivated by our finding that steady-state currents are smaller in LNs than in PNs (Fig. 5f). A positive offset of 1 spike per ms⁻¹ was added to LN(t) to match measured baseline LN activity. LN activity was simulated at a time resolution of 1 ms. As before, we convolved LN activity with an alpha function (25 ms) in order to obtain the time course of inhibition (I(t)).

In Fig. 8f–g, ORN firing rates in response to sinusoidal odor concentration fluctuations were modeled as linearly filtered versions of the stimulus waveforms. We extracted the best-fit linear filter from the spiking responses of VM7 ORNs to a plume of 2-heptanone (1:100 dilution in paraffin oil, ref. ⁶⁴). The filter (Supplementary Fig. 3c) was extracted by cross-correlation of ORN spikes and simultaneously-recorded odor concentration measurements (miniPID, Aurora Scientific), followed by decorrelation by the power spectrum of the odor concentration fluctuations^{61, 64}.

In our models, ORNs are the only source of excitation to PNs. In reality, PNs also receive lateral excitation from a specialized LNs^{59, 65}. Lateral excitation can contribute to the slow component of EPSCs evoked by electrical stimulation of ORN axons¹², and it also contributes to PN odor responses^{53, 59, 65}. However, its overall contribution is small in most cases, relative to the contribution of feedforward excitation. We verified this in pilot experiments in VM7 PNs by comparing the magnitude of steady-state odor responses during a dense sustained stimulus with feedforward excitation intact (i.e., with the maxillary palps intact) or with feedforward excitation removed (with the maxillary palps removed just before the experiment).

Data analysis

No formal statistical calculations were used to pre-determine sample sizes. Sample sizes were qualitatively governed by the observed cell-to-cell reliability in the measurements we performed in pilot experiments. Our sample sizes are similar to those generally employed in the field. Data distribution was assumed to be normal but this was not formally tested. No blinding was performed during experiments or analysis. A statistical methods checklist is available with the supplementary materials”. All statistical tests are 2-sided. Measurements of membrane potential were downsampled to 1 kHz prior to analysis and averaging.

To compute the PN impulse response for sparse stimuli (Figs. 4d and 8d), all responses to isolated 20 ms odor pulses (defined as pulses preceded by >400 ms of clean air) were extracted and averaged together. To estimate the effective impulse response for dense stimuli (Figs. 4f and 8e), we first calculated linear filters relating the odor to the PN response. We presented a 10 s long binary stimulus in which the valve switched randomly between open and closed states every 20 ms, with an equal probability of being open and closed. Filters were obtained by cross-correlating the valve state with PN membrane potential. Because this stimulus was close to white, and because correcting for stimulus correlations increases noise in filter estimates, we did not correct for stimulus correlations. Correcting for stimulus correlations should make these filters narrower and should have the same effect on filters derived from control and anatagonist data. Filters were then scaled to obtain the best linear fit to the response. The effective impulse response in Fig. 4f and 8e was generated by convolving this filter with a 20 ms pulse stimulus.

To measure presynaptic inhibition (Fig. 6f), we took the standard deviation in PN holding current, because it is sensitive to both the amplitude and frequency of spontaneous EPSCs in PNs. We first computed the standard deviation over 20 ms windows sliding in 0.1 ms increments. For each window we then computed the median value across trials for that cell. Finally, we calculated the mean value for each window across cells.

To obtain the frequency response of model PN responses in Fig. 8f, we modeled responses to sine-squared stimuli at different frequencies (for a stimulus frequency ω, the stimulus amplitude was sin(2π(ω/2)t)²). These responses r(t) were projected onto a sinusoid at frequency ω to obtain a measure of response amplitude at that frequency:

$$F(\omega )=\frac{1}{t_{\mathit{max}}}\ast \mid {\sum }_{t=1}^{t_{\mathit{max}}}r(t)e^{-2\pi i\omega t}\mid$$ (Equation 5)