The Pot Calling the Kettle Black? A Comparison of Measures of Current Tobacco Use

Abstract

Researchers often use the discrepancy between self-reported and biochemically assessed active smoking status to argue that self-reported smoking status is not reliable, ignoring the limitations of biochemically assessed measures and treating it as the gold standard in their comparisons. Here, we employ econometric techniques to compare the accuracy of self-reported and biochemically assessed current tobacco use, taking into account measurement errors with both methods. Our approach allows estimating and comparing the sensitivity and specificity of each measure without directly observing true smoking status. The results, robust to several alternative specifications, suggest that there is no clear reason to think that one measure dominates the other in accuracy.

1. Introduction

Tobacco use remains the single largest preventable cause of death in the US as well as globally. Controlling tobacco use is a policy priority of most governments and having accurate measures of tobacco use is an important prerequisite for measuring the success of such efforts. Insurance service providers and many employers too desire accurate reports of individual smoking behavior. But that raises a key question; can we accurately measure an individual’s active tobacco use status? Without undue intrusion, a researcher can never observe nor know with certainty the active tobacco use status of an individual. Instead she much relies on an imperfect measure. Most commonly she has two alternatives; self-reported current smoking status or biochemically assessed smoking status. The choice often depends on the researcher’s comparative valuation, based on her heuristics, of the two measures. When a biochemical measure is used to identify active smokers researchers face an additional issue; the threshold to be used to separate smokers and nonsmokers. Researchers use a wide range of thresholds for declaring a person a smoker.¹

The reliability of the measure used to predict tobacco use is can have significant clinical (and therefore policy) implications. For example, McPherson, et al. (2013) suggest that behavioral treatments for smoking cessation tailored on cotinine levels would differ significantly from those predicated on self-reported smoking. They argue that more reliance should be placed on cotinine measures of smoking behavior than on self-reported data. But, if cotinine measures are as subject to error as self-reported data, such a conclusion would not hold.

The reliability of self-reported smoking data has been widely questioned. Social desirability and other biases may lead respondents to misrepresent their smoking status. In particular, in the aftermath of increased anti-tobacco legislation and more hostile social norms against smoking, some survey respondents are believed to feel uncomfortable admitting that they currently smoke. When reported smoking status is linked to a direct financial incentive as in the case of insurance premiums, a smoker has additional reasons to misreport. Smokers typically pay a higher insurance premium than nonsmokers and face unfavorable labor market outcomes including higher unemployment and wage penalties (Levine et al., 1997; van Ours, 2004; Auld, 2005) providing financial motivation for smokers to hide their true status.

Biochemical measures of smoking behavior are often used instead of self-reported data because of this intrinsic bias². Among the biochemical measures used to identify active smokers are the levels of carbon monoxide, NNAL (4-(methylnitrosamino)-1-(3-pyridyl)-1-butanol), and cotinine in various body fluids. Cotinine is the most popular biomarker for identifying smokers due to its perceived high accuracy. Nicotine, the main addictive ingredient in tobacco is metabolised into cotinine within the body in addition to being available directly in tobacco. Its longer half-life compared to nicotine makes it a better candidate to detect tobacco use more accurately (Perez-Stable et al., 1995). Cotinine concentration is typically measured in blood, urine or saliva samples and occasionally in breast milk or hair (Florescu et al., 2009). Blood cotinine concentration, in particular, is considered a reliable indicator of exposure to tobacco smoke. However, biochemical measurements are subject to a variety of measurement and interpretation errors and thus do not provide the surety often attributed to them³. In this paper we employ recent advances in econometric techniques to estimate the accuracy of each measure in predicting true smoking status. We also investigate the impact of the threshold value of a biochemical measure on its error probabilities.

There is a wealth of research assessing the relationship between self-reported smoking data as referenced to biochemical assessments. Any discrepancies between the two measures are almost always attributed to the unreliability of self-reported data (West et al. 2007; Gorber et al., 2009) and only in few instances to the limitations of the biochemical measure (Yeager and Krosnick, 2010, for example). The majority of research comparing the two measures has found little discrepancy between the two approaches, although biochemical measures generally report more smokers than does self-assessment. However, many exceptions show large discrepancies one way or the other, almost always attributing the difference to misreporting by self-reported smokers (Gorber et al., 2009).

The accuracy of biochemically assessed tests is often expressed in terms of sensitivity and specificity. These statistical measures of biochemically assessed smoking tests depend on the biomarker used as well as the type of body fluid tested. Various measures that use different biomarkers are highly correlated but do not always produce the same result. The sensitivity and specificity of a given biochemically assessed test are often considered fixed in practice. However, these statistical measures depend on the chosen threshold point which moderates the trade-off between type I and type II errors. Yet, there are no universally agreed upon standards for these values. For example, 20 studies that use serum cotinine concentration to identify active smokers (Gorber et al., 2009) had threshold values that varied from 8 ng/mL to 50 ng/mL. The manual for the laboratory procedures used for the National Health and Nutrition Examination Survey (Gunter et al., 1996) suggests two thresholds, a serum cotinine concentration less than 5 ng/mL as an indication of a nonsmoker and a concentration of more than 15 ng/mL as an indication of an active smoker. The range in between, according to the manual, may indicate exposure to passive smoking. While most researchers use a cotinine threshold within the above range, Benowitz el al. (2009) proposes a significantly lower threshold of 3 ng/mL arguing that the currently accepted threshold (14 ng/mL according to them) overestimates the number of nonsmokers. Wide disagreement about the cotinine threshold suggests that a cotinine (or any other biomarker) based indicator may not perfectly identify an active smoker.

In spite of broad differences between various biochemical measures used to identify active smokers some researchers have assumed their chosen measure as a gold standard; deviations from these measures and self-reported smoking status is considered a bias in the self-reported data. For example, West et al. (2007) dispute the usual assumption that the estimates based on self-reported data are ‘sufficiently accurate for policy purposes’, arguing that ‘this assumption has not been adequately tested’ but ignores potential errors in biochemical measures. Comparing self-assessed smoking behavior used to compute national prevalence estimates in the US, UK and Poland with cotinine concentration in serum for US and in saliva for UK and Poland they estimate that the national prevalence rates in the US, UK and Poland are underestimated by 0.6, 2.8 and 4.4-percentage points respectively. Gorber et al. (2009) systematically review 54 previous studies on adult smoking behavior each comprising the self-reported and biochemically assessed smoking prevalence estimates. Assuming that the biochemical measure is correct, the authors find an overall trend of underestimation when self-reported smoking status is used to derive smoking prevalence rates. Yeager and Krosnick (2010), using the data from National Health and Nutrition Examination Surveys conducted during 2001–2002 to 2007–2008, estimate the discrepancy in prevalence rates based on self-reported smoking status and serum cotinine concentration levels to be slightly less than 1%. They, however, believe that the self-reported data could be more accurate and attribute this discrepancy to errors in the biochemical measurement.

The wide variation in results reported in previous studies that compares self-reported and biochemical measures show the dependence of each measure on underlying attributes. The accuracy of self-reported data depends on the characteristics of the target population, survey method, framing of the questionnaire and the survey environment. The accuracy of the biochemical measure depends on the biomarker used, type of body fluid tested and, perhaps most importantly, the threshold used to separate smokers and nonsmokers. While these factors could explain the observed differences between self-reported and biochemical measures in the rates of smoking, they do not give any indication of the bias that results with either method, and thus we emphasize the fallacy of comparing self-reported and biochemically measured data to investigate the accuracy of one or the other. In practice, many researchers and practitioners often tend to supplement self-reported data with biochemical measures than doing it the other way. Besides the accuracy issue raised earlier, an important policy issue related to this popular practice is whether the costs associated with biochemical data collections would justify any potential benefits in a given situation.

We found only two studies that evaluate the self-reported and serum-cotinine based measures of smoking status without comparing them to each. The first is Perez-Stable et al. (1995). Their strategy is to compare each measure to other biochemical measures such as hemoglobin, red and white blood cells, iron, lead, cholesterol, vitamin A and vitamin E, physical examination results including body mass index, pulse rate and blood pressure and depression assessments. However, since the association of these measures with smoking intensity could be a result of the elevated cotinine level rather than the smoking behavior itself, it still raises the identification problem, although once removed. The other, more recent, study is Ma et al. (2013) where self-reported and parent-reported active smoking status of Chinese adolescents is analyzed using the capture-recapture method. This method, however, ignores that the probabilities of misclassification across two self-reported sources could be correlated.

In this study we use an econometric approach to separately predict the probabilities of misclassification in self-reported and biochemically assessed data in absolute terms. This is the first attempt to evaluate the reliability of self-reported and biochemically measured smoking status by independently estimating, without reference to the other, that the predicted behavior is in error⁴. The paper contributes to the literature in several ways. First, we propose a method to estimate the extent of misreporting in self-reported smoking data without requiring any biochemical assessments for comparison. The method measures two types of misreporting probabilities (smokers reporting as nonsmokers and vice versa) separately, not just the net effect at the population level, by predicting the likelihood that a particular respondent misreports, again without using any ‘gold standard’. Second, by using the same method on biochemical measures of smoking behavior, we estimate the proportion of type I and type II errors. Finally, by looking at the causes of systematic errors for both measures, the results provide some insights when one should rely on self-reported data and when such data should be validated using a separate biochemical measure.

II. The study sample

We use data from National Health and Nutrition Examination Survey (NHANES) for our analysis. The survey is a continuing program of the US National Center for Health Statistics that examines a national sample of about 5000 persons each year and has both a survey component and a laboratory examination component. The availability of self-reported answers to smoking related questions as well as the levels of serum cotinine concentrations which can be used to construct biochemically assessed measure of smoking behavior makes this dataset a perfect choice for our study. The sampling procedure of NHANES is complicated as certain categories (for example Mexican Americans and other Hispanics) are oversampled. Accordingly, we use survey weights in our estimations and analysis.

We used data from NHANES 2009-10 as our main study sample and eliminated the observations without both objective and self-reported measures. The final sample included 5051 observations from adults (aged 20 years or older) of both genders⁵. The survey was administered as a face to face interview for this sample. Smoking related questions were asked at two points; first at their homes and then at a Mobile Examination Center, just before collecting the laboratory samples that were used to identify the presence of biomarkers we used in this study. For this study, we use the responses at the second interview to avoid the impact of changes in active smoking (and more broadly, tobacco use) status after the initial interview and before the conduct of laboratory procedures.

The series of questions asked at this interview covers the usage of the entire range of tobacco products, not just cigarettes. More specifically, a respondent faces the question ‘During the past 5 days, did you use any product containing nicotine including cigarettes, pipes, cigars, chewing tobacco, snuff, nicotine patches, nicotine gum, or any other product containing nicotine?’. This question is followed by additional questions regarding the current usage of each of these different tobacco products.

In general, a biomarker used to identify an active smoker doesn’t identify a cigarette smoker differently from another type of tobacco user. Hence the inclusion or exclusion of types of tobacco use other than cigarette smoking could explain differences between self-reported and biochemically assessed indicators (West et al., 2007). In our dataset, for example, there are 21.73% cigarette smokers. When we add cigar and pipe smokers the number increases to 23.40%. When we count all types of tobacco users the number jumps to 25.18% which corresponds to an estimated prevalence rate of 25.01% after adjusting for the differences in sampling rates. The cotinine-based indicator identifies 24.17% active smokers at the widely used threshold of 15 ng/mL and 24.85% active smokers at a more aggressive threshold of 10 ng/mL. It is clear that if we compare the number of self-identified active cigarette smokers with an alternative estimate that uses a cotinine threshold of 10-15 ng/mL (as most researchers do) the self-reported measure tend to produce a lower estimate. This result prevails even after adding self-identified current pipe and cigar smokers. However, when we count all self-reported tobacco users the number is comparable and could even be higher than the biochemical measure.

In our analysis, therefore, we include all types of tobacco users, not just cigarette smokers, and includes people who chew tobacco, or use nicotine patches, nicotine gum, or any other product containing nicotine. If someone answered ‘Yes’ to the above question about different forms of tobacco use during the last 5 days, we coded that person’s reported tobacco use status as 1. If they answered ‘No’ to using every form of tobacco the variable was coded 0.

The next issue we face is choosing an appropriate threshold for the cotinine-based measure. We chose a threshold value of 8 ng/mL to define tested tobacco use status based on the measured serum cotinine concentration. This threshold value minimizes the discrepancy between the proportion of self-reported tobacco users and the proportion assessed biochemically. A visual inspection of the bimodal distribution of the serum cotinine level (Figure 1) shows that a threshold of 8 ng/mL (or even lower) provides a clearer break than the more popular threshold of 15 ng/mL for separating two groups⁶. The variable was coded as 1 if the cotinine measurement exceeded the threshold and as 0 otherwise. When coded in this manner there were 1,272 (25.18%) reported tobacco users and 1,276 (25.26%) tested tobacco users. After applying survey weights, the percentages of reported and tested tobacco users in the population were estimated as 25.01% and 24.91% respectively.

Figure 1.

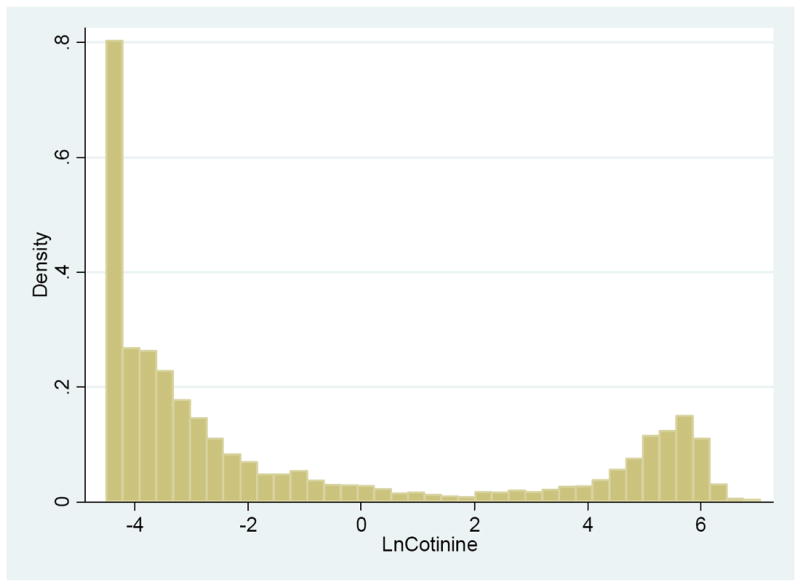
Distribution of Log Values of Serum Cotinine Level

Given that the number of active tobacco users identified by the biochemical measure at this threshold is close to the number of self-reported tobacco users one might expect that the two measures would agree at the individual level too. However, despite the similarity in aggregate numbers we still find a reasonable discrepancy at the individual level. Both measures unambiguously identify 1,190 (23.56%) active tobacco users and 3,693 (73.11%) nonusers but do not agree on the active tobacco use status of the remaining 168 (3.33%) individuals. There are 82 (1.62%) self-reported tobacco users with a cotinine level below 8ng/mL, while another 86 (1.70%) individuals tested as active tobacco users do not admit being so. Because neither method is fully objective, this information is not sufficient to infer whether the self-reported data is misclassified for 168 cases, the cotinine-based measure is inaccurate for those cases, or it is a combination of these two possibilities. We have comparable results even if we derive these statistics using the more recent NHANES 2011-2012 dataset (Table 1).

Table 1.

Comparison of Tested and Reported Data

Reported Status	Tested Status	NHANES 2009-2010	NHANES 2011-2012
Nonuser	Nonuser	3693 (73.1%)	3228 (74.1%)
Nonuser	Tobaccouser	86 (1.7%)	77 (1.8%)
Tobacco user	Nonuser	82 (1.6%)	83 (1.9%)
Tobacco user	Tobacco user	1190 (23.6%)	967 (22.2%)
		5051 (100.0%)	4355 (100.0%)

III. Quantifying the measurement error in current tobacco use indicators

Three approaches have been used by previous researchers to reconcile differences between self-reported and biochemical assessment of “true” tobacco use, which we denote S_i:

• Assume that the biochemical measure (denoted T_i) is true and attribute the entire discrepancy to underreporting of self-reported tobacco use, so (S_i = T_i).

• Assume that the self-reported data (denoted R_i) is accurate and attribute the deviations to the limitations of the biochemical test, hence (S_i = R_i).

• Assume that when either of the measures identifies a tobacco user it is correct but a person is considered a nonuser only if both self-reported and cotinine based measures indicate the person is not a tobacco user, i.e., (S_i = (T_i = 1) ∪ (R_i = 1)). This is the usual practice of insurance service providers.

As the researcher never observes true tobacco use status, verifying the validity of any assumption above is a challenge. In fact, S_i can take any value irrespective of the values of T_i and R_i. Even if T_i and R_i agree for all observations, it does not prove that S_i is accurately measured since both measures could be wrong. Our approach here is to independently estimate the expected error probabilities of each measure with respect to the (unobserved) true value using an econometric approach. We begin our analysis assuming that the measurement error in each indicator is random, although the probability of being mismeasured may depend on the true tobacco use status. We then extend our analysis allowing the measurement error to be systematically different across various subgroups.

The strength of any indicator used to identify an active tobacco user can be defined in terms of two statistical measures, specificity and sensitivity. Sensitivity is the probability that a true smoker being identified correctly and specificity is the probability that a true nonsmoker being identified so. Our first approach assumes that the sensitivity and specificity of a measure are fixed and do not vary across different observations. Let $S_i^0$ be the measured behavior (the self-reported or biochemically assessed current tobacco use status) equal to 1 if classified as a tobacco user and 0 otherwise and S_i be the true (unobserved) tobacco use status, also a binary variable equal to 1 if the person is a current tobacco user and 0 otherwise. Define the sensitivity and the specificity of $S_i^0$ as ${\lambda }_1=\mathrm{Pr}(S_i^0=1\mid S_i=1)$ and ${\lambda }_0=\mathrm{Pr}(S_i^0=0\mid S_i=0)$ respectively.

Let the true proportion of current tobacco users is p and the proportion of current nonusers is (1 − p). Given the sensitivity of the measure is λ₁, λ₁ p proportion of current tobacco users are identified correctly. In addition, given the specificity is λ₀, λ₀ (1 − p) current nonusers also are misidentified as current tobacco users. Altogether, we observe λ₁ p + λ₀ (1 − p) tobacco users when the true proportion is p. The probability that the measured smoking status being 1 can be expressed as,

$$\begin{array}{l}\mathrm{Pr}(S_i^0=1)={\lambda }_1\left(\mathrm{Pr}(S_i=1)\right)+\left(1-{\lambda }_0\right)\left(\mathrm{Pr}\left(S_i=0\right)\right)\\ ={\lambda }_1\left(\mathrm{Pr}(S_i=1)\right)+\left(1-{\lambda }_0\right)\left(1-\mathrm{Pr}\left(S_i=1\right)\right)\\ =\left(1-{\lambda }_0\right)+\left({\lambda }_1+{\lambda }_0-1\right)\left(\mathrm{Pr}\left(S_i=1\right)\right)\end{array}$$ (1)

We can also define this probability in terms of false positives and false negatives. Let α₁ fraction of active tobacco users are not identified so by a given measure while α₀ fraction of nonusers are incorrectly measured as active tobacco users. Now, we correctly identify (1 − α₁) p active tobacco users and mismeasure α₀ (1 − p) additional non users as active users. Altogether, we observe (1 − α₁) p + α₀ (1 − p) active tobacco users while the true proportion is p, By rearranging the terms we can write,

$$\begin{array}{l}\mathrm{Pr}(S_i^0=1)={\alpha }_0+\left(1-{\alpha }_0-{\alpha }_1\right)\left(\mathrm{Pr}\left(S_i=1\right)\right),\mathit{where}\\ {\alpha }_0=1-{\lambda }_0=\mathrm{Pr}(S_i^0=1\mid S_i=0)\mathit{and}\\ {\alpha }_1=1-{\lambda }_1=\mathrm{Pr}(S_i^0=0\mid S_i=1)\end{array}$$ (2)

If we replace Pr(S_i = 1), the propensity to be a current smoker in (2), by F(X_i, β) where X_i is a vector of causal factors affecting the smoking status and β is a vector of coefficients, we have $\mathrm{Pr}(S_i^0=1)={\alpha }_0+\left(1-{\alpha }_0-{\alpha }_1\right)F\left(X_i,\beta \right)$. When X_i and β are entering F as a linear index, F(X_iβ) = F(X_iβ), and our model is equivalent to the binary choice model with two-sided misclassification presented in Hausman et al. (1998). In that framework, S_i can be thought as a derived variable based on another unobserved variable, $S_i^{\ast }$, the latent propensity to be a current smoker. The relationship between $S_i^{\ast }$, X_i, β and S_i under that interpretation is given by,

$$S_i=1.(S_i^{\ast }>0),\mathit{where}{S}_i^{\ast }=X_i\beta +{\epsilon }_i$$ (3)

The result can directly be obtained from the relationship in (3) assuming that the cumulative distribution function of the stochastic error term ε_i is F.

Hausman et al. (1998) demonstrated that the parameters α₀, α₁ and β can be consistently estimated by maximum likelihood when the functional form of F is known and α₀ + α₁ < 1, in addition to the linear index form assumption we already made. They also proposed a semiparametric approach to partially identify the model when the functional form of F is not known.

In our case, however, we have two measurements of the same phenomenon, each with its own sensitivity and specificity. Thus, we can express the expected probabilities of detecting an active smoker (correctly or incorrectly) by each indicator as,

$$\mathrm{Pr}(R_i=1)={\alpha }_0^R+\left(1-{\alpha }_0^R-{\alpha }_1^R\right)F\left(X_i\beta \right)$$ (4)

$$\mathrm{Pr}(T_i=1)={\alpha }_0^T+\left(1-{\alpha }_0^T-{\alpha }_1^T\right)F\left(X_i\beta \right)$$ (5)

As in the previous section, R_i is the self-reported smoking status and T_i is the smoking status derived using the biochemical measure. The error probabilities of each measure, which corresponds to the sensitivity and the specificity of respective measures, are expressed as $\mathrm{Pr}(R_i=1\mid S_i=0)={\alpha }_0^R$, $\mathrm{Pr}(R_i=0\mid S_i=1)={\alpha }_1^R$, $\mathrm{Pr}(T_i=1\mid S_i=0)={\alpha }_0^T$ and $\mathrm{Pr}(T_i=0\mid S_i=1)={\alpha }_1^T$. Since both indicators measure the true smoking status assumed to be a result of the data generating process given by (3), the parameter β does not vary across equations (4) and (5). Therefore, it is more appropriate to estimate the parameters of those two equations jointly if we employ the parametric method of Hausman et al. (1998).

The joint maximum likelihood of (4) and (5) produces consistent estimates of the error probabilities if we correctly specify the model and not otherwise. Therefore, it is important to be cautious on each assumption we make. Given that the smoking status is a binary variable our assumption of a Bernoulli process cannot be wrong. The linear index form assumption is in general restrictive. However, when x_i is a binary indicator the function F(x_iβ) has the same level of flexibility as F(x_i, β). Given that most of the covariates of our empirical specification (presented later) are binary, we do not make a strong assumption when we assume a linear index function. The most restrictive assumption we have to make when identifying above model parametrically is about the functional form of F.

Since the exact distribution of the stochastic error term, ε_i, in (3) is not known, we first consider normality because many other finite distributions are normally distributed asymptotically. Then, we have ε_i ~ N(0, 1), $\mathrm{Pr}(S_i=1)=(S_i^{\ast }>0)=1-\mathrm{\Phi }\left(-X_i\beta \right)=\mathrm{\Phi }(X_i\beta )$ where Φ is the cumulative distribution function of a standard normal distribution. It is customary to arbitrary normalize the normally distributed error term to be mean zero with unit variance in probit models as these parameters are not identified otherwise. If the true distribution is ε_i ~ N(μ,σ²), this arbitrary normalization results in estimating $\raisebox{1ex}{$\beta $}\!\left/ \!\raisebox{-1ex}{$\sigma $}\right.$ instead of the true coefficient vector β. The mean of the true distribution, μ, as well as any non-zero threshold that transforms $S_i^{\ast }$ to S_i in (3) mixes up with the estimated constant term in addition to being scaled.

In our application, the parameters of interest are ${\alpha }_0^R$, ${\alpha }_1^R$, ${\alpha }_0^S$ and ${\alpha }_1^S$ and the identification of β is secondary. An additional advantage of the Hausman et al. (1998) framework is that the model identifies the two types of misclassification probabilities consistently even under the relatively weak assumption of ε_i ~ N(μ,σ²), notwithstanding the fact that μ and σ² are not identified separately from the estimates of β because we can redefine F(X_iβ) as $\mathrm{\Phi }\left(\frac{X_i\beta +\mu }{\sigma }\right)$ without distorting the relationships in (4) and (5). However, the consistency of our estimates still depends on the normality assumption. Therefore, we also need to consider alternative functional form assumptions.

Other common cumulative distribution functions used to estimate binary choice models are inverse logistic, log-log and complementary log-log cumulative functions. Logit estimates, in general, are qualitatively similar to probit estimates except at the tails and may not produce different results if the misclassification probabilities are large. In our application, however, we do not anticipate large misclassification probabilities and it may be worth pursuing a logit specification. Again, we use a standard model but the results are robust to scaled and shifted versions of the distribution function.

Both probit and logit models assume symmetric distributions and may fail to produce consistent estimates if the true distribution is asymmetric. The log-log and complementary log-log models allow checking the possibility of an asymmetric distribution of the error term. The first is positively skewed and the second is negatively skewed. Since the exact nature of the potential asymmetry of the distribution is not known, we consider both positively skewed log-log distribution and the negatively skewed complementary log-log distribution as our third and fourth alternatives respectively. The robustness of the estimates to changes in scale and location parameters still holds. The Hausman et al. (1998) procedure we discussed above assumes that the measurement error is not correlated with observed covariates. An extension to this parametric estimator to incorporate dependence on one or more covariates is discussed briefly in section 5.5 of Hausman et al. (1998) and with more details in Tennekoon and Rosenman (forthcoming).

This Tennekoon and Rosenman procedure involves simultaneous estimation of the parameters of the outcome equation, together with the parameters of two latent relationships defining each type of misclassification probability. More specifically, in Tennekoon and Rosenman, the two types of misclassification probabilities are functions of observed covariates given by, $\mathrm{Pr}\left(S_i^0=1\mid S_i=0\right)=F_0\left(Z_i^0{\gamma }_0\right)$ and $\mathrm{Pr}\left(S_i^0=0\mid S_i=1\right)=F_1\left(Z_i^1{\gamma }_1\right)$. This approach allows estimating sensitivity and specificity of a measure differently for various groups if the functional forms F₀ are F₁ known in addition to F. The functions F₀ and F₁ need not be nonlinear and the model is identifiable when $F_0\left(Z_i^0{\gamma }_0\right)=Z_i^0{\gamma }_0$ and $F_1\left(Z_i^1{\gamma }_1\right)=Z_i^1{\gamma }_1$, if the misclassification probabilities are not large and the two vectors $Z_i^0$ and $Z_i^1$ each is comprised of few variables. We follow the parametric procedure of Tennekoon and Rosenman to ascertain the robustness of our results under covariate dependent misclassification.

IV. Empirical specification and estimation results

However current tobacco use is measured, there should be no difference in what factors predispose someone to use tobacco. Hence, whether we use self-reported or biochemically assessed behavior to indicate whether an individual uses tobacco, we use the same set of explanatory variables for the X_i in equations (4) and (5). Our set of explanatory variables cover age, race/ethnicity, education level, marital status, body structure, pregnant or not, number of smokers at home, whether or not the respondent consumes alcohol, and whether the respondent was an early smoker. The point is to identify those socioeconomic characteristics which best help predict smoking behavior. All of these variables have been used in earlier studies to identify predisposition to smoking (Oh et al., 2010; Hosseinpoor et al., 2011). Summary statistics including the weighted averages of these variables are presented in Table 2. We also present on the same table the corresponding statistics for the NHANES 2011-2012 dataset that we used to check the robustness of our estimates.

Table 2.

Descriptive statistics

Variable	NHANES 2009-2010		NHANES 2011-2012
	Mean	Weighted Mean	Mean	Weighted Mean
Measures of current tobacco use
Reported tobacco user	0.252	0.250	0.241	0.245
Tested tobacco user (cotinine level > 15 ng/mL)	0.242	0.239	0.231	0.229
Tested tobacco user (cotinine level >8 ng/mL)	0.253	0.249	0.240	0.237
Tested tobacco user (cotinine level >3 ng/mL)	0.263	0.259	0.257	0.250
Gender
Male	0.495	0.494	0.507	0.493
Race/Ethnicity
Mexican American	0.186	0.086	0.095	0.073
Other Hispanic	0.103	0.050	0.103	0.063
Non Hispanic Black	0.168	0.105	0.258	0.107
Non Hispanic White	0.487	0.697	0.388	0.686
Mixed or other race/ethnicity	0.049	0.062	0.157	0.072
Age
20-25 years	0.090	0.092	0.108	0.102
25-50 years	0.455	0.503	0.447	0.486
50-65 years	0.232	0.243	0.247	0.256
Over 65 years	0.224	0.162	0.204	0.157
Education
College graduate or above	0.205	0.281	0.260	0.316
Some college or AA degree	0.284	0.305	0.307	0.326
High school graduate/ GED or equivalent	0.230	0.229	0.211	0.203
9-11th grade	0.159	0.124	0.136	0.105
Less than 9th grade	0.121	0.061	0.086	0.050
Marital status
Married	0.523	0.569	0.482	0.532
Widowed	0.084	0.059	0.079	0.054
Divorced	0.108	0.099	0.104	0.108
Separated	0.032	0.023	0.036	0.022
Never married	0.168	0.173	0.219	0.200
Living with a partner	0.084	0.078	0.079	0.084
Body structure
Underweight	0.014	0.017	0.018	0.015
Normal	0.262	0.284	0.290	0.287
Overweight	0.341	0.338	0.324	0.341
Obese	0.383	0.362	0.367	0.357
Other
US citizen	0.846	0.900	0.862	0.912
Number of (additional) smokers at home	0.244	0.229	0.221	0.201
Pregnant	0.011	0.011	0.009	0.010
Exposed to tobacco smoke at home	0.160	0.148	0.142	0.123
Exposed to tobacco smoke at work	0.077	0.085	0.080	0.087
Early initiator (before 16 years)	0.151	0.143	0.139	0.148
Consume Alcohol	0.736	0.780	0.737	0.803

Although predisposition to tobacco use is independent of how tobacco use is measured, misclassification of tobacco users and nonusers is not – it could depend on the measure used. Accordingly, we allow each type of misclassification probability to vary across measures. In Tables 3 and 4 we present our maximum likelihood estimates including the coefficient estimates of the outcome equation and estimated misclassification probabilities of each measure under normal, logistic, log-log and complementary log-log functional form assumptions.⁷

Table 3.

Probit and Logit Models under Random Misclassification

Variable	Probit			Logit
Outcome: Tobacco user
Constant	-1.370	(0.111)	***	-2.276	(0.191)	***
Gender
Male	0.424	(0.053)	***	0.707	(0.091)	***
Age (Excluded: 25-50 years)
20-25 years	0.076	(0.098)		0.141	(0.168)
50-65 years	-0.288	(0.068)	***	-0.479	(0.114)	***
Over 65 years	-0.895	(0.098)	***	-1.519	(0.171)	***
Race/Ethnicity (Excluded: Non Hispanic White)
Mexican American	-0.390	(0.077)	***	-0.664	(0.131)	***
Other Hispanic	-0.176	(0.081)	***	-0.321	(0.140)	**
Non Hispanic Black	0.044	(0.065)		-0.080	(0.111)
Mixed or other race/ethnicity	0.233	(0.111)	**	0.377	(0.190)	**
Education (Excluded: Less than 9th grade)
College graduate or above	-0.783	(0.097)	***	-1.346	(0.169)	***
Some college or AA degree	-0.299	(0.070)	***	-0.509	(0.118)	***
High school graduate/ GED or equivalent	-0.050	(0.068)		-0.086	(0.114)
Marital status (Excluded: Married)
Widowed	0.424	(0.117)	***	0.725	(0.207)	***
Divorced	0.634	(0.079)	***	1.062	(0.132)	***
Separated	0.670	(0.134)	***	1.140	(0.228)	***
Never married	0.304	(0.074)	***	0.513	(0.127)	***
Living with a partner	0.539	(0.098)	***	0.916	(0.163)	***
Body structure (Excluded: Normal)
Underweight	0.592	(0.190)	***	0.998	(0.330)	**
Overweight	-0.108	(0.061)	*	-0.180	(0.103)	*
Obese	-0.310	(0.067)	***	-0.533	(0.117)	***
Other
Early initiator	0.617	(0.068)	***	1.037	(0.114)	***
Consume Alcohol	0.561	(0.080)	***	0.972	(0.140)	***
Number of (additional) smokers at home	1.475	(0.134)	***	2.482	(0.233)	***
Pregnant	-0.090	(0.361)		-0.202	(0.602)
Conditional probability of identifying a tobacco user as a nonuser
Self-reported data	0.085	(0.023)	***	0.083	(0.024)	***
Biochemical measure	0.080	(0.024)	***	0.078	(0.025)	***
Conditional probability of identifying anonuser as a user
Self-reported data	0.019	(0.009)	**	0.011	(0.009)
Biochemical measure	0.017	(0.008)	**	0.010	(0.008)
Number of observations	5,051			5,051
Log likelihood	-3936.97			-3937.10

^***p<0.01;

^**p<0.05;

^*p<0.10

Table 4.

Loglog and Complementary Loglog Models under Random Misclassification

Variable	Loglog			Cloglog
Outcome: Tobacco user
Constant	-2.139	(0.160)	***	-1.006	(0.111)	***
Gender
Male	0.540	(0.081)	***	0.402	(0.049)	***
Age (Excluded: 25-50 years)
20-25 years	0.083	(0.157)		0.100	(0.086)
50-65 years	-0.346	(0.092)	***	-0.302	(0.069)	***
Over 65 years	-1.153	(0.140)	***	-0.881	(0.100)	***
Race/Ethnicity (Excluded: Non Hispanic White)
Mexican American	-0.496	(0.110)	***	-0.391	(0.073)	***
Other Hispanic	-0.257	(0.114)	**	-0.321	(0.076)	**
Non Hispanic Black	-0.024	(0.093)		-0.065	(0.059)
Mixed or other race/ethnicity	0.281	(0.157)	*	0.237	(0.107)	**
Education (Excluded: Less than 9th grade)
College graduate or above	-1.078	(0.138)	***	-0.716	(0.111)	***
Some college or AA degree	-0.403	(0.100)	***	-0.290	(0.111)	***
High school graduate/ GED or equivalent	-0.062	(0.094)		-0.053	(0.111)
Marital status (Excluded: Married)
Widowed	0.548	(0.162)	***	0.416	(0.113)	***
Divorced	0.892	(0.103)	***	0.574	(0.079)	***
Separated	0.903	(0.189)	***	0.624	(0.126)	***
Never married	0.463	(0.103)	***	0.257	(0.069)	***
Living with a partner	0.725	(0.148)	***	0.517	(0.093)	***
Body structure (Excluded: Normal)
Underweight	0.703	(0.299)	**	0.603	(0.181)	**
Overweight	-0.156	(0.085)	*	-0.089	(0.059)
Obese	-0.478	(0.096)	***	-0.248	(0.061)	***
Other
Early initiator	0.808	(0.101)	***	0.597	(0.068)	***
Consume Alcohol	0.775	(0.115)	***	0.516	(0.078)	***
Number of (additional) smokers at home	1.807	(0.215)	***	1.553	(0.128)	***
Pregnant	-0.308	(0.446)		-0.018	(0.462)
Conditional probability of identifying a tobacco user as a nonuser
Self-reported data	0.109	(0.027)	***	0.048	(0.022)	**
Biochemical measure	0.105	(0.030)	***	0.042	(0.022)	*
Conditional probability of identifying anonuser as a user
Self-reported data	0.003	(0.008)		0.030	(0.009)	***
Biochemical measure	0.001	(0.008)		0.029	(0.009)	***
Number of observations	5,051			5,051
Log likelihood	-3955.19			-3930.43

^***p<0.01;

^**p<0.05;

^*p<0.10

The coefficient estimates of the outcome equation under the four different functional form specifications are very similar qualitatively, except for scaling differences. Results show that the propensity to use tobacco is higher for male than for female but drops with age, education and BMI. Mexican Americans and Hispanics are less likely be tobacco users than non-Hispanic Whites but Blacks do not have an identifiable difference. The other and mixed category is more likely to be active tobacco users. Married people are less likely use tobacco than all other marital status categories. The propensity to use tobacco increases with risk factors identified in previous literature including early initiation, number of smokers at home and being an alcohol consumer. The effect of pregnancy is not significant. All these estimates agree with previous literature.

Our main intention here is not the estimation of causal factors affecting current tobacco use, but the error probabilities of self-reported and biochemically assessed measures. The four models produce different estimates of misclassification probabilities. The conditional probability of identifying an actual tobacco user as a nonuser when self-reported measure is used is 8.5%, 8.3%, 10.9% and 4.8% respectively with probit, logit log-log and complementary log-log specifications. The same error probabilities with the tested measure (based on a threshold of 8 ng/mL) are 8.0%, 7.8%, 10.5% and 4.2%. All four models suggest that the tested measure is marginally better than self-reported data but the gap is very narrow. We make a similar observation with the conditional probability of identifying a nonuser as a tobacco user too. The error probabilities in self-reported and tested measures are statistically insignificant at conventional levels when the errors are inverse logistic or log-log. Normal assumption leads to 1.9% misreporting in self-reported data and 1.7% errors with the tested measure. With complementary log-log errors the respective probabilities are 3.0% and 2.9%.

It is unsurprising that the predicted misclassification probabilities whether one uses the self-reported or tested measure are almost the same no matter which model is used. The 8 ng/ML threshold for classifying a tobacco user left the number of self-reported tobacco users (82) with a cotinine level classifying them as non-users almost equal to the number of individuals tested as active tobacco users who do not admit being so (86). This near symmetry in the direction of disagreements between the two measures coupled with choosing the threshold to minimize the difference in the proportion smokers with each measure almost assures us that misclassification probabilities would be similar.

Since the only difference between these four models is the functional form of the error term and they all share exactly the same covariates the log-likelihood values are directly comparable across models. The complementary log-log model has the best fit among the four models with the lowest log-likelihood value. The probit specification produces the second highest log-likelihood value while the logit model too follows the probit model very closely. The log-log model has the weakest model fit. This comparison suggests that both types of error probabilities are likely to be positive as indicated by complementary log-log and probit models and the error distribution is more likely to be negatively skewed than positively skewed, which indicates that the deterministic part of the probability of being an active smoker is positively skewed.

Robustness to different thresholds

Our preferred models (complementary log-log and probit) find that tobacco users are much more likely to be misreported as nonusers than nonusers are to be misreported as tobacco users. For self-reported tobacco use, a random bias towards abstaining could explain this result. With the tested tobacco use behavior, one possibility is that our chosen threshold, 8 ng/mL, could be too high. While this value is lower than the threshold values typically used by most researchers and practitioners it is still higher than the threshold of 3 ng/mL suggested in Benowitz el al. (2009) after a detailed analysis of NHANES data. Therefore, next we investigate how these error probabilities change with the chosen threshold. The estimated sensitivity and specificity of the cotinine-based measure with different threshold values (3, 8 and 15 mg/nL respectively) are presented in Table 5. Since our interest here is on the error probabilities of the biochemical measure we do not report other parameters. The comparable figures for the self-reported measure too are reported on the same table.

Table 5.

Impact of the Selected Threshold on the Accuracy of Measure

Measure	Performance Measure	Probit Model	Logit Model	Log-log Model	Complementary Loglog Model
Cotinine threshold of 3 ng/mL	Sensitivity	0.9307***	0.9335***	0.9042***	0.9678*
		(0.0186)	(0.0190)	(0.0220)	(0.0167)
	Specificity	0.9805***	0.9883	0.9969	0.9689***
		(0.0071)	(0.0072)	(0.0072)	(0.0070)
Cotinine threshold of 8 ng/mL	Sensitivity	0.9200***	0.9221***	0.8951***	0.9584*
		(0.0237)	(0.0248)	(0.0292)	(0.0225)
	Specificity	0.9826**	0.9903	0.9986	0.9711***
		(0.0082)	(0.0082)	(0.0077)	(0.0088)
Cotinine threshold of 15 ng/mL	Sensitivity	0.8967***	0.8983***	0.8728***	0.9348***
		(0.0216)	(0.0221)	(0.0239)	(0.0218)
	Specificity	0.9844**	0.9916	0.9995	0.9734***
		(0.0065)	(0.0064)	(0.0059)	(0.0074)
Self-reported data	Sensitivity	0.9147***	0.9168***	0.8909***	0.9525**
		(0.0226)	(0.0237)	(0.0278)	(0.0219)
	Specificity	0.9813**	0.9890	0.9973	0.9704***
		(0.0086)	(0.0086)	(0.0083)	(0.0091)

Note:

^***p < 0.01;

^**p < 0.05;

^*p < 0.10.

It is obvious that the sensitivity of the cotinine-based measure increases when the threshold is lowered, but at the cost of specificity. When the threshold was lowered to 3 ng/mL the estimated sensitivity of the biochemical measure improves by 0.84-1.14 percentage points while the specificity drops by 0.17-0.22 percentage points. Given that there are 3 to 4 nonusers for each active tobacco user the overall impact of this change on the accuracy of the measure is not significant. When we increase the threshold to 15 ng/mL, a value more popular among researchers, we notice that the specificity improves by 0.09-0.23 percentage points while the sensitivity drops by 2.23-2.38 percentage points. Probably, the cost of the drop in sensitivity when a threshold of 15 ng/mL is used compared to a threshold of 8 ng/mL is too high than the gain in specificity.

No matter which functional form assumption we make, we clearly observe a few facts about the biochemical measure in comparison to self-reported data. At a moderate threshold value of 8 ng/mL, both types of error rates of the biochemical measure are lower than but very close to self-reported data. More specifically, the sensitivity of the biochemical measure is 0.42-0.59 percentage points higher compared to reported data while the specificity is 0.07-0.13 percentage points higher. At a more conservative threshold of 15 ng/mL the specificity of the biochemical measure is slightly higher (0.22-0.31 percentage points) but the sensitivity is 1.76-1.85 percentage points lower. With a more aggressive threshold of 3 ng/mL, the sensitivity of the biochemical measure improves to 1.33-1.67 percentage points over reported data, while the specificity is 0.04-0.15 percentage points less. Clearly, it is not possible to overcome the limitations of the biochemical measure simply by changing the threshold. Our results suggest that the accuracy of the biochemical measure is higher when the threshold is 8 ng/mL than at the two extremes. Therefore, we continue to use 8 ng/mL, which minimizes the discrepancy between the biochemical measure and self-reported data, as our preferred threshold value.

Covariate dependent misclassification

The results we presented so far are based on various models that assume that the sensitivity and specificity of a given measure do not vary across individuals. However, these statistics for a given measure may vary across individuals due to a variety of reasons. The variability of nicotine metabolism across individuals due to genetic differences is well documented (Nakajima et al., 2006 for example) and it suggests that the sensitivity of a cotinine based indicator may differ across different ethnic groups if the same threshold is used to screen active smokers of different ethnicities. The error probabilities of self-reported data also are likely to differ across different sub populations. We allowed for covariate dependent misclassification by generalizing our preferred model from the previous stage, the complementary log-log model, to a more robust model following Tennekoon and Rosenman (2014).

According to Benowitz et al. (2009), the optimum threshold values for identifying active smokers are 5.92 ng/mL, 4.85 ng/mL, and 0.84 ng/mL for non-Hispanic blacks, non-Hispanic whites, and Mexican Americans, respectively. If their findings are correct and can be extended to all types of tobacco users, we should miss some of active tobacco users at our chosen threshold of 8 ng/mL. Moreover, the percentage of missing cases has to be larger among the Mexican Americans than compared to Blacks and Whites. Therefore, we estimated this error probability separately for five race/ethnic categories we have. On the other hand, a biochemical measure is likely to identify a nonuser as a current tobacco user if that person’s environmental tobacco exposure is high. In our dataset, we have information about the extent of environmental tobacco exposure both at home and at the workplace. We estimated the probabilities of misclassifying a nonuser as a current tobacco user for four groups; with no environmental tobacco exposure at home or workplace, exposed at home only, exposed at the workplace only and exposed both at home and at the workplace.

When tobacco use is self-reported, social desirability bias may make it more likely that an active user reports as a nonuser. Noncitizens have social, economic, and political reasons to show that they have good moral character, perhaps motivating them to appear as nonusers when they really use tobacco. They are also likely to misunderstand a survey item than US citizens due to the limitations in language skills and cultural awareness. At the same time, US citizens may understand the importance of a national survey than a noncitizen and complete a survey more responsibly. The former may increase the misclassification probability of noncitizen active tobacco users and the latter may increase the errors among both current tobacco users and nonusers compared to US citizens. We estimated each type of error probability in self-reported data separately for US citizens and noncitizens⁸.

The results of our complementary loglog model that incorporates covariate dependent misclassification are reported in Table 6 (first three columns). The results show that noncitizens are in fact very much likely to self-report as nonuser while actively consuming tobacco. The respective probability is 34.8% compared to the error rate of 3.4% for US citizens. Noncitizen nonusers also have higher error rates than citizens but the difference is smaller. The probability of reporting as an active tobacco user when not is 2.9% with US citizens and 3.8% with noncitizens. The biochemical indicator too shows significant disparities among various subgroups. With a threshold of 8 ng/mL the probability of missing an active smoker by the cotinine test is 36.7% among Mexican Americans and 18.6% among other Hispanics but only 5.5% among non-Hispanic Whites. The effect is not statistically significant among non-Hispanic Blacks. With no environmental tobacco exposed there’s a 2.8% chance that a nonuser will be identified as an active tobacco user. If exposed to tobacco smoke at home (but not at the workplace) this probability is 14.0%. When exposed to tobacco smoke at the workplace a person is 9.8% likely to be identified as a tobacco user when not. If exposed at both home and the workplace this probability is 60.7%. Overall, neither of the measures appears to be better than the other.

Table 6.

Complementary Loglog Models under Covariate Dependent Misclassification

Variable	NHANES 2009-2010			NHANES 2011-2012
Outcome: Tobacco user
Constant	-1.029	(0.122)	***	-0.663	(0.174)	***
Gender
Male	0.412	(0.052)	***	0.351	(0.049)	***
Age (Excluded: 25-50 years)
20-25 years	0.090	(0.091)		-0.351	(0.131)	***
50-65 years	-0.312	(0.070)	***	-0.372	(0.088)	***
Over 65 years	-0.930	(0.117)	***	-1.072	(0.147)	***
Race/Ethnicity (Excluded: Non Hispanic White)
Mexican American	-0.181	(0.087)	**	-0.777	(0.073)	***
Other Hispanic	-0.035	(0.104)		-0.329	(0.076)	**
Non Hispanic Black	-0.084	(0.066)		-0.069	(0.059)
Mixed or other race/ethnicity	0.278	(0.120)	**	-0.172	(0.107)
Education (Excluded: Less than 9th grade)
College graduate or above	-0.749	(0.101)	***	-0.716	(0.111)	***
Some college or AA degree	-0.323	(0.070)	***	-0.290	(0.111)	***
High school graduate/ GED or equivalent	-0.080	(0.068)		-0.053	(0.111)
Marital status (Excluded: Married)
Widowed	0.455	(0.126)	***	0.016	(0.156)	***
Divorced	0.592	(0.084)	***	0.236	(0.110)	**
Separated	0.684	(0.141)	***	0.332	(0.148)	**
Never married	0.269	(0.073)	***	0.162	(0.097)	*
Living with a partner	0.576	(0.105)	***	0.475	(0.126)	***
Body structure (Excluded: Normal)
Underweight	0.661	(0.191)	***	0.339	(0.175)	*
Overweight	-0.086	(0.063)		-0.299	(0.092)	***
Obese	-0.261	(0.064)	***	-0.277	(0.094)	***
Other
Early initiator	0.614	(0.073)	***	0.653	(0.088)	***
Consume Alcohol	0.548	(0.088)	***	0.901	(0.152)	***
Number of (additional) smokers at home	1.496	(0.151)	***	1.387	(0.372)	***
Pregnant	-0.003	(0.516)		-2.670	(0.593)	***
Conditional probability of identifying a tobacco user as a nonuser
Self-reported data
US Citizen	0.034	(0.024)		0.041	(0.048)
Noncitizen	0.348	(0.084)	***	0.269	(0.116)	**
Biochemical measure
White	0.055	(0.033)	*	0.070	(0.045)
Mexican American	0.367	(0.067)	***	0.355	(0.124)	***
Other Hispanic	0.186	(0.113)	*	0.249	(0.118)	**
Non Hispanic Black	0.015	(0.016)		0.013	(0.045)
Mixed or other race/ethnicity	0.066	(0.076)		0.022	(0.034)
Conditional probability of identifying a nonuser as a user
Self-reported data
US Citizen	0.029	(0.010)	***	0.043	(0.012)	***
Noncitizen	0.038	(0.021)	*	0.054	(0.029)	*
Biochemical measure
No environmental tobacco exposure	0.028	(0.009)	***	0.033	(0.009)	***
Exposed at home	0.140	(0.086)		0.190	(0.153)
Exposed at the workplace	0.098	(0.038)	***	0.174	(0.050)	***
Exposed both at home and at the workplace	0.607	(0.293)	**	0.345	(0.300)
Number of observations	5,051			4,355
Log likelihood	-3907.31			-3408.51

^***p<0.01;

^**p<0.05;

^*p<0.10

Robustness to a different dataset

We checked the robustness of our model using the more recent NHANES 2011-2012 dataset. Since, the two datasets share the same variables and survey methodology the error probabilities too are expected to be comparable. The percentage of active tobacco users is less in 2011-2012 compared to 2009-2010 according to both reported and cotinine based measures, suggesting that tobacco use has dropped during the two years⁹. Overall, prevalence may drop through two mechanisms; smoking cessation by all age groups and a reduction in initiation by young people. The results reported in the last three columns of Table 6 (last three columns) are qualitatively not different from the results using our original dataset.

Robustness to a different biomarker

Finally, we check the robustness of our results to a different biomarker. The NHANES survey measures the concentration of NNAL in addition to cotinine. We repeated two of our previous exercises, the complementary log-log models with random and covariate dependent misclassification. Since the NNAL level is missing in 90 observations our sample size is now 4,961. Surprisingly, our previous findings are also valid for this biochemical measure. As our results presented in Table 7 show, if there’s any efficiency gain over self-reported data when a biochemical measure is used that gain is not substantial, no matter whether the biomarker used is cotinine or NNAL.

Table 7.

Complementary Loglog Models with an Alternative Biochemical (NNAL > 0.025 ng/mL)

Variable	Random Misclassification			Covariate Dependent Misclassification
Outcome: Tobacco user
Constant	-1.033	(0.116)	***	-1.057	(0.122)	***
Gender
Male	0.395	(0.050)	***	0.396	(0.052)	***
Age (Excluded: 25-50 years)
20-25 years	0.052	(0.090)		0.041	(0.094)
50-65 years	-0.295	(0.072)	***	-0.300	(0.072)	***
Over 65 years	-0.849	(0.100)	***	-0.885	(0.114)	***
Race/Ethnicity (Excluded: Non Hispanic White)
Mexican American	-0.429	(0.076)	***	-0.235	(0.091)	***
Other Hispanic	-0.141	(0.075)	*	-0.063	(0.102)
Non Hispanic Black	-0.018	(0.060)		-0.065	(0.065)
Mixed or other race/ethnicity	0.266	(0.110)	**	0.307	(0.121)	**
Education (Excluded: Less than 9th grade)
College graduate or above	-0.768	(0.096)	***	-0.785	(0.100)	***
Some college or AA degree	-0.299	(0.068)	***	-0.315	(0.070)	***
High school graduate/ GED or equivalent	-0.031	(0.065)		-0.047	(0.069)
Marital status (Excluded: Married)
Widowed	0.401	(0.116)	***	0.432	(0.127)	***
Divorced	0.570	(0.080)	***	0.577	(0.083)	***
Separated	0.581	(0.128)	***	0.621	(0.139)	***
Never married	0.246	(0.071)	***	0.255	(0.073)	***
Living with a partner	0.491	(0.095)	***	0.527	(0.101)	***
Body structure (Excluded: Normal)
Underweight	0.558	(0.189)	***	0.595	(0.196)	***
Overweight	-0.061	(0.061)		-0.060	(0.063)
Obese	-0.218	(0.063)	***	-0.233	(0.064)	***
Other
Early initiator	0.636	(0.069)	***	0.645	(0.073)	***
Consume Alcohol	0.505	(0.084)	***	0.531	(0.091)	***
Number of (additional) smokers at home	1.642	(0.132)	***	1.468	(0.148)	***
Pregnant	0.230	(0.271)		0.246	(0.289)
Conditional probability of identifying a tobacco user as a nonuser
Self-reported data	0.055	(0.022)	**
US Citizen				0.028	(0.023)
Noncitizen				0.308	(0.087)	***
Biochemical measure	0.037	(0.020)	*
White				0.041	(0.031)
Mexican American				0.341	(0.078)	***
Other Hispanic				0.097	(0.125)
Non Hispanic Black				0.013	(0.013)
Mixed or other race/ethnicity				0.061	(0.072)
Conditional probability of identifying a nonuser as a user
Self-reported data	0.034	(0.009)	***
US Citizen				0.033	(0.010)	***
Noncitizen				0.041	(0.021)	**
Biochemical measure	0.030	(0.008)	***
No environmental tobacco exposure				0.028	(0.008)	***
Exposed at home				0.256	(0.089)	***
Exposed at the workplace				0.089	(0.036)	**
Exposed both at home and at the workplace				0.244	(0.283)
Number of observations	4,961			4,961
Log likelihood	-3836.20			-3817.33

^***p<0.01;

^**p<0.05;

^*p<0.10

Notwithstanding the similarity of results when each of the two biomarkers were used, as our data shows, the two measures disagree on a significant number of cases (2.88%), just as the cotinine indicator and self-reported data do. The NNAL based measure identifies 74 (1.49%) individuals as active tobacco users when the cotinine based meaure doesn’t. The cotinine based measure identifies 69 (1.39%) individuals as active tobacco users when the NNAL based measure doesn’t. At the same time, the NNAL based measure agrees with the cotinine based measure more often than it agrees with self-reported data as shown in Table 8.

Table 8.

Comparison of Two Indicators with the NNAL Based Measure

Reported Tobacco Use	Tobacco Use Based on Cotinine Level	Percentage of Active Tobacco Users Based on NNAL Level
Nonuser	Nonuser	1.80%
Nonuser	Current User	84.71%
Current User	Nonuser	10.98%
Current User	Current User	95.24%
		25.54%

v. Discussion and conclusions

Tobacco use remains one of the leading preventable causes of premature death and a major burden on healthcare budgets. A sizable amount of money is spent on tobacco cessation and avoidance programs every year. Reliable indicators of current tobacco use are needed if the efficacy of these programs is to be accurately assessed, and self-reported smoking status from national or regional surveys is most commonly used to identify active smokers. However, self-reported smoking behavior is often believed to be underreported. As a result, biochemical assessment, thought to be a more objective measure of smoking status is increasingly used by policy makers and insurance service providers.

Our results that survives many robustness checks show that biochemical assessment may not be superior to self-assessment when trying to measure tobacco use; it depends primarily on the use of the information and how much it matters that some individuals may be falsely and unfairly treated as tobacco users. Although our findings confirm that self-reported tobacco use is underreported we do not find that the biochemically assessed measure we studied is clearly a better indicator. Differences between the two measures often considered due to misreporting in most research may, in fact, be explained more (and almost equally) by the errors that occur in both measures. It may be reasonable to correct self-reported data statistically in order to eliminate the bias, instead of switching to a potentially equally unreliable biochemical assessment. As West et al. (2007) have shown previously and we show here, any underreporting of active smoking status in self-reported data could be partly due to ignoring other types of tobacco use (chewing tobacco, nicotine patches, nicotine gum, snuff, pipes and cigars). The reliability of self-reported data and thereby the accuracy of national smoking prevalence estimates can be improved by asking a broad question that includes all types of tobacco use, not just cigarette smoking.

The results we present here are also useful when the interest is not the prevalence rate but the current smoking status, including other tobacco use, of a given individual. Whether the observed indicator is self-reported or biochemically assessed, the model that we implement there can be used to identify the true propensity to be a smoker as well as to estimate the probability that the observed data could be misclassified. When determining an appropriate insurance premium, for example, a provider may use the estimated propensities to calculate a customized contract amount for each individual based on the estimated risk rather than proposing one of the two values pre-assigned for smokers and nonsmokers.

The choice of measure is not simply an academic exercise; false positives and false negatives on smoking behavior have real and important economic impacts – both with regards to efficiency and the distribution of welfare. With regard to the distribution of welfare, individuals falsely classified as smokers through biochemical assessment face higher insurance costs and fewer employment opportunities, while those smokers who either lie when self-reporting or show up as false negatives with a biochemical assessment unfairly impose costs on insurance companies and employers. This misallocation of risk carries efficiency impacts. At the aggregate level, efficient policies against smoking are best served with an accurate assessment of smoking prevalence. As noted in the introduction, clinical practitioners argue smoking cessation programs tailored on cotinine levels should differ from those predicated on self-reported smoking, but if the measures are in error, so too will be the intervention. Thus, understanding how much misreporting occurs with both self-reporting and biochemical assessment of smoking behavior will allow a better and more efficient allocation of resources.