Latent State-Space Models for Neural Decoding

Abstract

Ensembles of single-neurons in motor cortex can show strong low-dimensional collective dynamics. In this study, we explore an approach where neural decoding is applied to estimated low-dimensional dynamics instead of to the full recorded neuronal population. A latent state-space model (SSM) approach is used to estimate the low-dimensional neural dynamics from the measured spiking activity in population of neurons. A second state-space model representation is then used to decode, via a Kalman filter, from the estimated low-dimensional dynamics. The latent SSM-based decoding approach is illustrated on neuronal activity recorded from primary motor cortex in a monkey performing naturalistic 3-D reach and grasp movements. Our analysis show that 3-D reach decoding performance based on estimated low-dimensional dynamics is comparable to the decoding performance based on the full recorded neuronal population.

I. Introduction

Spiking activity in ensembles of single neurons is known to show strong low-dimensional collective dynamics [1, 2]. These low-dimensional collective dynamics (‘neural trajectories’) are likely to reflect spontaneous and evoked activity in highly recurrent neuronal networks. In the case of motor cortex, they also likely reflect task complexity and the fact that the motor system ultimately controls a system, the skeletal-muscle system, with many fewer degrees of freedom. In the case of simple motor tasks, estimated neural trajectories are typically embedded in a much lower dimensional space than the number of neurons commonly recorded by microelectrode arrays (MEAs). It is not known, however, how much information these neural trajectories carry about movement parameters (e.g. kinematics), relative to the information available in the recorded full population.

Here, we address this problem on ensembles of single neurons simultaneously recorded via 96-MEAs implanted in primary motor (MI) cortical area in monkeys performing a naturalistic 3D reach and grasp task. The task consisted of reaching a selected object and grasping it in a specific way after a go cue was presented. Here we focus on decoding 3-D position at the wrist during reaches from estimated low-dimensional neural trajectories, and compare it with decoding from full recorded population. The estimation of these low-dimensional dynamics was based on non-discriminative (unsupervised) latent state-space methods, i.e. without knowledge of the related kinematics. An advantage of estimating low-dimensional dynamics with latent SSMs over more commonly used dimensionality reduction methods such as principal components analysis and factor analysis is that SSMs incorporate temporal structure (dynamics) in the latent state evolution.

This paper is organized as follows. Section II describes the method to extract the low-dimensional dynamics from population activity using latent state-space models. Section III describes decoding using Kalman filters in which the observations are either the full population activity or the estimated low-dimensional dynamics. Section IV describes the behavioral setup for the free reach/grasp task and the preprocessing steps to obtain the neural activity. Comparison between decoding from full population and low-dimensional dynamic is presented in Section V, followed by conclusions in Section VI.

II. Low-Dimensional Dynamics

Low-dimensional dynamics is a k-dimensional representation of the population activity of p neurons, such that k ≤p. Latent state space models (SSMs) can be used to estimate these low dimensional dynamics, denoted as x_t ∈ ℝ^k, at any time point t. Here we adopt Gaussian-Markov state-space models, linear dynamic systems (LDS), where the states evolve accordingly to

$$x_{t+1}={\mu }_x+A{x}_t+{\xi }_t,$$ (1)

where μ_x corresponds to the mean, A ∈ ℝ^k×k is the state transition matrix, and the {ξ_t}'s are independently and identically distributed (i.i.d.) Gaussian noise, ξ_t∼ 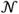(0,Q), with covariance matrix Q ∈ ℝ^k×k. The population activity or observations, y_t ∈ ℝ^p, are linearly related to the states as

$$y_t={\mu }_y+B{x}_t+{\epsilon }_t,$$ (2)

where μ_y is the mean, B ∈ ℝ^k×p is the observation matrix, and ε_t∼ 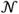(0, R) is i.i.d. Gaussian noise with covariance matrix R ∈ ℝ^pxp. The objective is to estimate the hidden states, x_t, and the time-invariant model parameters, A, B, Q, and R given the observations. Here, we use a combination of subspace identification [3] and Expectation Minimization (EM) [4] methods to estimate the latent state-space model and states.

EM learning is typically computationally intensive requiring a large number of iterations before convergence is achieved. To significantly reduce the number of required iterations, we initialize the latent SSM parameters in the EM learning with the solution obtained from subspace identification. This substantially reduces the number of iterations. Although, we could in some cases go ahead in our decoding analysis with the solutions based only on the subspace identification approach, we found that EM typically results in improved decoding performance.

III. Decoding from Full Population and Low-Dimensional Dynamics

To decode kinematics from the full population activity, we use an additional SSM, such that the observations are the population activity, y_t, and the states are the kinematics, z_t, expressed as

$$\begin{array}{c}{z}_{t+1}={\mu }_z+C{z}_t+{\zeta }_t\\ y_t={\mu }_y+D{z}_t+{\eta }_t,\end{array}$$ (3)

where ζ_t∼ 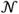(0,S) and η_t∼ 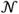(0,T) are i.i.d. noise with covariance matrices S and T, respectively, C and D are the state and observation matrices, and μ_z is the mean of the kinematics. Given the full population activity and measured kinematics in a training dataset, the time-invariant model parameters, C, D, S, and T are estimated by maximum likelihood estimation (MLE). Using Kalman filter recursions, the kinematics can be estimated (decoded) on test trials from the corresponding full population activity and the estimated SSM parameters.

To decode kinematics from the low dimensional dynamics, another SSM is used such that the observations then correspond to the estimated low-dimensional dynamics as described in the previous section, x_t. The SSM is expressed as

$$\begin{array}{c}{x}_t={\mu }_x+E{z}_t+{\varrho }_t\\ z_{t+1}={\mu }_z+F{z}_t+{\varsigma }_t,\end{array}$$ (4)

where ϱ_t∼ 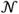(0,W) and ς_t∼ 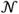(0,V) are i.i.d. noise with covariance matrices W and V, respectively, and E and F are the observation and state matrices, respectively. SSM parameters are estimated via MLE as before and similar Kalman filter recursions are used to decode kinematics from the estimated low-dimensional dynamics and SSM parameters.

IV. Free Reach/Grasp Task

A. Neural Recordings and Signal Pre-processing

Neural recordings were obtained from a microelectrode array implanted in the primary motor cortex (MI) of a monkey performing a 3-D reach and grasp task. Surgery and experimental details are described elsewhere [5, 6].

Field potentials (0.3 Hz – 7.5 kHz, sampled at 30 kHz) were processed offline. A series of zero-phase filters (5 order Butterworth, 250 Hz high-pass) and IIR notch-filters (60, 120 and 180 Hz) were applied to obtain the high-pass activity signal. Neuronal spikes were extracted as events that pass the detection threshold, and then aligned with respect to the minimum peak. Extracted spikes for each channel were hand sorted into individual units/neurons, including both single unit and multiunit activities. Only neurons with an average firing rate > 1 spike/second were selected. A total of 55 single units were used in this study. Neuronal spiking activity was further converted into spike counts in 50-ms time bins. Finally, a square-root transformation was applied to the spike counts so that the single–neuron count distribution could be better approximated by a Gaussian function.

B. Reach/Grasp Task

In this task, the monkey sits on a chair, and the experimenter brings forward an object hanging from a string. Upon go cue, the monkey starts to reach for this object, while the object can still be swinging in space. This allowed us to explore a wide range of hand positions as the monkey tries to continuously reach for the object. Once the object was successfully grasped for ∼1 second, a juice reward was given. A total of 86 successful trials using three different objects were recorded in the session examined in this report.

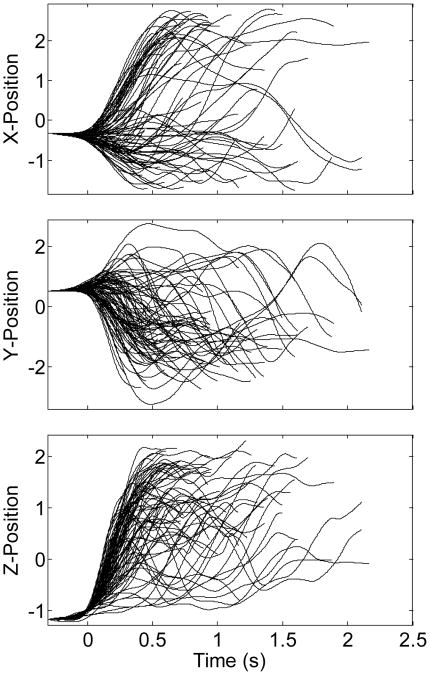
Reflective markers on the arm and hand were used to track the kinematics via Vicon optical motion capture system. This allowed us to collect the 3D wrist position along the X- (horizontal right-left), Y- (horizontal forward-backward) and Z- (vertical upward-downward) axes, as demonstrated in Figure 1. It takes a variable amount of time for the subject to start movement after the go cue. As a result, we estimated the movement onset in each trial as the time the wrist Z-position has been elevated by 10 mm. All kinematics were sampled at ∼240 Hz. For decoding purposes, kinematics were down-sampled to the same sampling rate as that for the population activity (20 Hz).

Figure 1.

3-D wrist position along the X-, Y- and Z- axes for 86 trials. Positions along each axis are z-scored, i.e. zero mean and one standard deviation. Each trial starts from the reference point at time zero. Decoded segments start at -300 ms. Movement onset corresponds to time zero and end at the time the object is grasped. Segments had a variable length ranging from 1 to 2.5 seconds.

V. Results

Decoding performances based on low-dimensional dynamics and based on population activity are compared as means to evaluate the relative amount of information available in the estimated low-dimensional dynamics. Comparable decoding performances indicate that the necessary information for representation/computation involving 3-D positions is preserved in these low-dimensional dynamics.

We estimated the low-dimensional dynamics from population activity using a SSM as described above and set the number of dimensions to k = 12. This is less than 4 times the size of the population with p = 55 neurons. We initialized the model parameters with the solution from subspace identification, and repeated EM learning for 500 iterations.

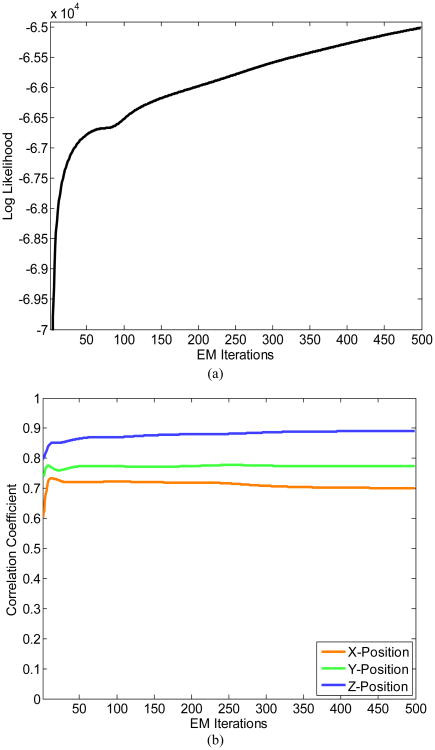
Figure 2a shows the data log-likelihood with increasing EM iterations. We note that, although the log-likelihood increases monotonically as a function of EM iterations (as expected), there can be fluctuations in the correlation coefficient between the actual and decoded 3-D positions as the EM iterations progress. That can happen especially during the first 10-30 EM iterations, as seen in Figure 2b. In addition, the correlation coefficient can actually decrease slightly as it happened in the case of X-position.

Figure 2.

(a) The log-likelihood function at different EM iterations. (b) Fluctuations in the correlation coefficient between true and decoded 3-D positions versus the number of EM iterations.

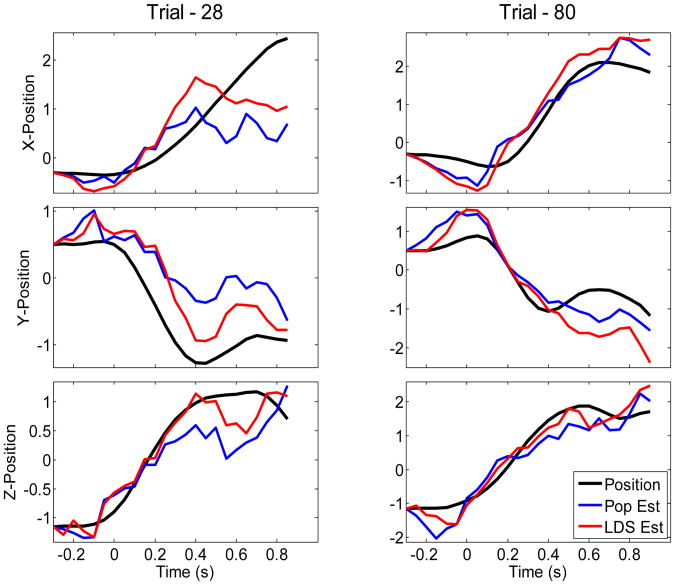
We then used the estimated 12-dimensional dynamics for decoding and compared it with decoding from the full population. Decoding analysis was performed under leave-one-out trial cross-validation. Figure 3 shows a few examples of decoded 3-D positions based on the low-dimensional dynamics and full population. Table 1 compares decoding performances obtained from the full population and from the estimated low-dimensional dynamics. Decoding performances are assessed in terms of average correlation coefficients between the actual and decoded kinematics across all trials. Two main observations can be drawn. First, decoding along the Z-position is in general better than X-position or Y-position in both decoding approaches. Second, decoding from low-dimensional dynamics with a small number of dimensions, i.e. k = 12 in this case, is comparable, and sometimes slightly better than decoding from the full population

Figure 3.

Examples for Kalman decoding of 3-D wrist position from full population activity and from low-dimensional dynamics. The actual kinematic trace is displayed in black for reference. All kinematics are z-scored.

Table 1. Decoding performance as average correlation coefficient between actual and estimated kinematics.

	Population Decoding	LDS Decoding
X-position	0.51	0.54
Y-position	0.84	0.84
Z-position	0.90	0.91

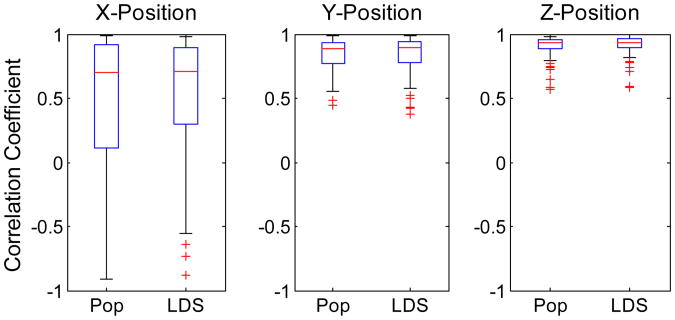
In Figure 4, we report on the distribution of correlation coefficient over all 86 trials for X-, Y-, and Z- positions using boxplots. The central mark in each box is the median performance, and the edges are the 25^th and 75^th percentiles. Whiskers demonstrate the range of the lowest and highest performance, while outliers are performances that pass beyond a certain threshold from the edges of the box, and are illustrated with crosses.

Figure 4.

Comparison of 3-D wrist position decoding based on full population (Pop) and based on the low- dimensional dynamics (LDS). The center red line and edges of the box in each plot indicate the median, and the 25th and 75th percentiles, respectively.

VI. Conclusion

This paper explores a new approach for neural decoding based on low-dimensional neuronal dynamics, where these low-dimensional dynamics are estimated from full population activities via latent state-space models. Decoding performance was used to assess the amount of information in the low-dimensional dynamics compared to the information in the full population. Decoding of 3D hand positions during reach/grasp movements based on low-dimensional dynamics (dimension = 12) was comparable to the performance based on the full recorded population. Overall our findings indicate that information about task-related kinematics is preserved on the low-dimensional dynamics estimated from the recorded neuronal ensembles. We anticipate using this approach to develop more efficient decoders for brain-machine interfaces.