Abstract
Optical interactions with biological tissue provide powerful tools for study, diagnosis, and treatment of disease. When optical methods are used in applications involving tissue, scattering of light is an important phenomenon. In imaging modalities, scattering provides contrast, but also limits imaging depth, so models help optimize an imaging technique. Scattering can also be used to collect information about the tissue itself providing diagnostic value. Therapies involving focused beams require scattering models to assess dose distribution. In all cases, models of light scattering in tissue are crucial to correctly interpreting the measured signal. Here, we review a versatile model of light scattering that uses the Whittle–Matérn correlation family to describe the refractive index correlation function Bn (rd). In weakly scattering media such as tissue, Bn (rd) determines the shape of the power spectral density from which all other scattering characteristics are derived. This model encompasses many forms such as mass fractal and the Henyey–Greenstein function as special cases. We discuss normalization and calculation of optical properties including the scattering coefficient and anisotropy factor. Experimental methods using the model are also described to quantify tissue properties that depend on length scales of only a few tens of nanometers.
Index Terms: Biophotonics, continuous random media, mass fractal, scattering, tissue optics
I. Introduction
In Biology and medicine, optical techniques enable non-invasive measurements of living tissue. Microscopy is particularly ubiquitous because it enables visualization of individual cells and even organelles. There is a continuous effort to resolve ever finer detail to assess the most fundamental properties of living organisms. However, resolution in optical imaging systems poses a challenge to studying length scales less than the diffraction limit (about half the wavelength). Some very clever techniques have been developed to sidestep this issue, including STED, STORM, and other super resolution methods [1]. These methods enable imaging or reconstruction of extraordinary detail, but typically require contrast agents and careful tissue preparation. Therefore, a niche remains available for additional methods of quantifying fine length scales. Several methods with potential to fill that niche rely on analysis of scattering.
Many applications are critically affected by light scattering in tissue. Sometimes scattering is considered a nuisance, and research has been devoted to optical clearing of tissue [2]. At the same time, in many imaging techniques, scattering provides the image contrast, for example, in confocal microscopy or optical coherence tomography (OCT). Diffuse optical tomography is perhaps the best example of using measurement of light propagation in tissue to reconstruct tissue features that cannot otherwise be imaged and relies on reconstructing tissue properties based on transport theory due to multiple scattering [3]. Models of scattering are also important in treatment methods such as photodynamic therapy where carefully controlling the distribution of energy is crucial for successful treatment [4].
Clearly, methods of modeling radiative transport in tissue are needed for a wide range of applications including treatment or therapy, imaging, and characterization or diagnosis. One of the most widely used modeling methods is to numerically solve the radiative transport equation using Monte Carlo (MC) simulations. MC works by simulating a large number of rays as they propagate by sampling two probability distribution functions: 1) The path length traveled between scattering events is described by a decaying exponential associated with mean free path (Beer–Lambert law). 2) The angular distribution of scattered light for a single scattering event is called the phase function. The shape of the phase function is highly dependent on the scattering model. While MC is a powerful simulation method, the results are only as good as the model it is based on.
In this paper, we describe the use of a particularly flexible choice for modeling tissue scattering. The model assumes that tissue can be described as a continuous random media rather than discrete particles, which agrees with observations of material distribution such as electron microscopy. The model is based on the Whittle–Matérn (WM) correlation family and is highly flexible, encompassing several other models previously used to describe tissue including mass fractals and the Henyey– Greenstein (HG) phase function. While direct measurements of the refractive index correlation function would provide the best model of tissue, such measurements are currently not possible with the necessary resolution of a few tens of nanometers. In the meantime, the WM provides a good alternative. We summarize the choices to make within this model and show how optical properties are calculated. Finally, we demonstrate several techniques where this model provides both excellent agreement with data and also a means to quantify the distribution of length scales well below the diffraction-limited resolution.
II. Tissue, Structure, and Refractive Index
Tissue is made up of many interconnected, arbitrarily shaped structures that span a wide range of length scales. Many texts can provide an overview of the components of cells or tissue [5]. For example, the extracellular matrix (ECM) is composed primarily of collagen and elastin fibers ranging in size from 10 to 500 nm in diameter. Cells themselves are of various shapes and sizes on the order of tens of micrometers. Cells are in turn comprised of smaller structures such as membranes (10 nm) and organelles including the nucleus (5–10 µm), mitochondria (0.2–2 µm), and many others. Cells also contain a cytoskeleton made of filaments from 7 to 25 nm in diameter. The nucleus contains nucleoli (0.5–1.0 µm) and DNA in the form of chromatin. The organization of chromatin is the subject of active research, but electron microscopy reveals that chromatin is found in the form of heterochromatin and euchromatin and appears to have different densities. These form globules with length scales of hundreds of nanometers.
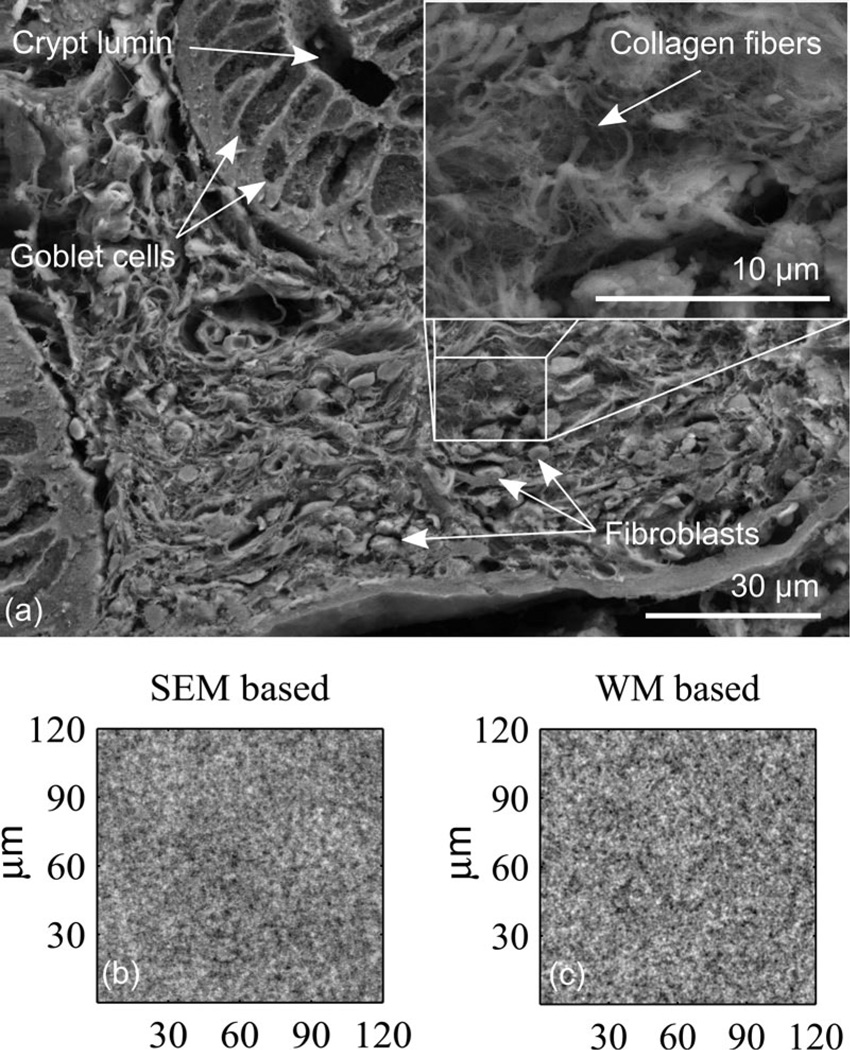
These various structures span several orders of magnitude in size and are composed of a wide range of materials. While the exact refractive index of each component in living tissue is not known, the heterogeneity of material nonetheless results in a range of refractive index values with a complicated spatial distribution. It is this heterogeneity that gives rise to scattering. Fig. 1 shows an image of tissue highlighting the dramatic range of length scales and the interconnected nature of the material. This interconnected material means that refractive index is a continuous function of position and supports the modeling of tissue as a continuous random medium like that of turbulence [6], [7].
Fig. 1.
A scanning electron microscope (SEM) image of colon biopsy showing some of the structural features ranging in size from tens of nanometers to tens of microns (top). The wide range of length scales present and the complex interconnected nature of the components mean that tissue is best modeled as a continuous random medium. Statistically, the scattering depends not on the exact arrangement of material, but instead on the correlation Bn (rd). By calculating the spectral density of the SEM (cropped to a square array), a medium can be constructed that has the same autocorrelation shape as the SEM and is shown on the lower left. The WM model can be used to generate simulated media that have a very similar appearance, an example for D = 3.7 is shown on the lower right. This illustrates how a medium can be constructed with a given autocorrelation function, but the reader is cautioned that the SEM is not a measurement of refractive index and so direct comparison of the SEM autocorrelation and Bn (rd) shape would not be valid.
When it comes to modeling light scattering, the exact distribution for a particular ensemble of material is less important than the statistical properties. What matters most is the shape of the excess refractive index correlation function Bn (rd) discussed below. By considering the spectral density of the SEM image, an artificial medium can be generated that has the same correlation function as the SEM as shown in the lower left of Fig. 1. A medium can also be generated from the WM model using the method described in [8, Ch. 2] and an example is shown in the lower right of Fig. 1 with remarkable similarity. Caution should be taken in and quantitative comparison would not be valid since the SEM does not directly represent refractive index, but qualitatively the SEM represents the structure of tissue containing a wide range length scales.
While it is not yet possible to directly measure refractive index at the resolution of the smallest length scales mentioned above, there are ways to relate local mass density to refractive index. Since mass density can in principle be determined at high resolution using electron microscopy techniques, mass density can be converted to refractive index using the Gladstone–Dale relation [9], [10]:
| (1) |
where ρ is the density of the solute [g/ml] and α is the refractive increment, usually α ≈0.17 ml/g.
Future research using electron microscopy methods may enable direct measurement of mass density and thus refractive index at high resolution so that scattering may be more accurately modeled and related to specific components of tissue. In the meantime, we must be satisfied with empirical models that provide good fits to observable data.
A. Models of Tissue Scattering
Scattering in tissue is the result of light interacting with random variations in refractive index. To better understand scattering in tissue, it is helpful to develop and evaluate models of light propagation in a medium comprised of a spatially random distributions of refractive index. This distribution could be in the form of a continuous function of refractive index (like atmospheric turbulance) or in the form of discrete particles. Many models of tissue scattering approximate tissue as a collection of randomly placed spheres or spheroids [11]–[13]. This is plausible considering that organelles such as nuclei, mitochondria, lysosomes, vacuoles, and even whole cells are approximately spherical (or spheroidal) in shape. The scattering from such isolated particles can be analytically described by the Mie solution to scattering from spheres [14], [15]. Scattering from a random medium made up of many such spheres (i.e., a cloud of rain-drops) is calculated by then incoherently summing the scattering from many spheres according to the number density. However, in many cases, it is hard to argue that the shape is spherical so Mie theory is inherently limited.
Another ubiquitous model of tissue scattering is based on the empirical observation that tissue scattering is usually anisotropic. That is, a very small volume of tissue scatters more light in the forward direction at small angles than in the backward direction. A simple model of such anisotropic scattering was developed by Henyey and Greenstein to describe scattering of interstellar dust and is now referred to as the HG phase function [16]. Counterintuitively, the phase function has little to do with the phase of a scattered ray. Instead, the term is historical and refers to the apparent brightness of celestial bodies such as the moon or planets as they pass through their phases. The function is a normalized intensity as a function of the angle between incident and scattered direction.
Observing tissue scattering using methods such as goniometer and integrating sphere, Jacques et al. found the HG function provided a good model to match their observations [17]. It has since become one of the most common models of tissue scattering. However, this model is limited in that it does not include the dipole factor (discussed in Section IV-A) that leads to a nonmonotonically decreasing function of angle that is typically observed in scattering [11], [18] and it does not provide a physical connection to the structures which generated it.
Other models of tissue scattering have been put forth and used with success and include delta-Eddington proposed by Joseph et al. [19] and discussed in detail by Prahl [20] that uses the sum of a Dirac-δ function and cos θ dependence to describe the phase function, and the P3-approximation [21] that takes the first three terms in an expansion of the solution to the radiative transport equation.
In choosing a model for tissue scattering, it is a good idea to use the simplest model that matches the experimental method employed to avoid over fitting. For example, when using an integrating sphere and the inverse adding doubling (IAD) method [20], the experimental data are well modeled by the HG function. However, as experimental methods evolve, some measurements cannot be explained with such a simple model, and it is necessary to invoke a more complex model of scattering.
B. As New Methods Emerge, Better Models Are Needed
One challenge facing those wishing to model tissue scattering is determining what model to use. Any model of scattering will inherently contain approximations. Choosing the right model is all about choosing the most appropriate set of approximations.
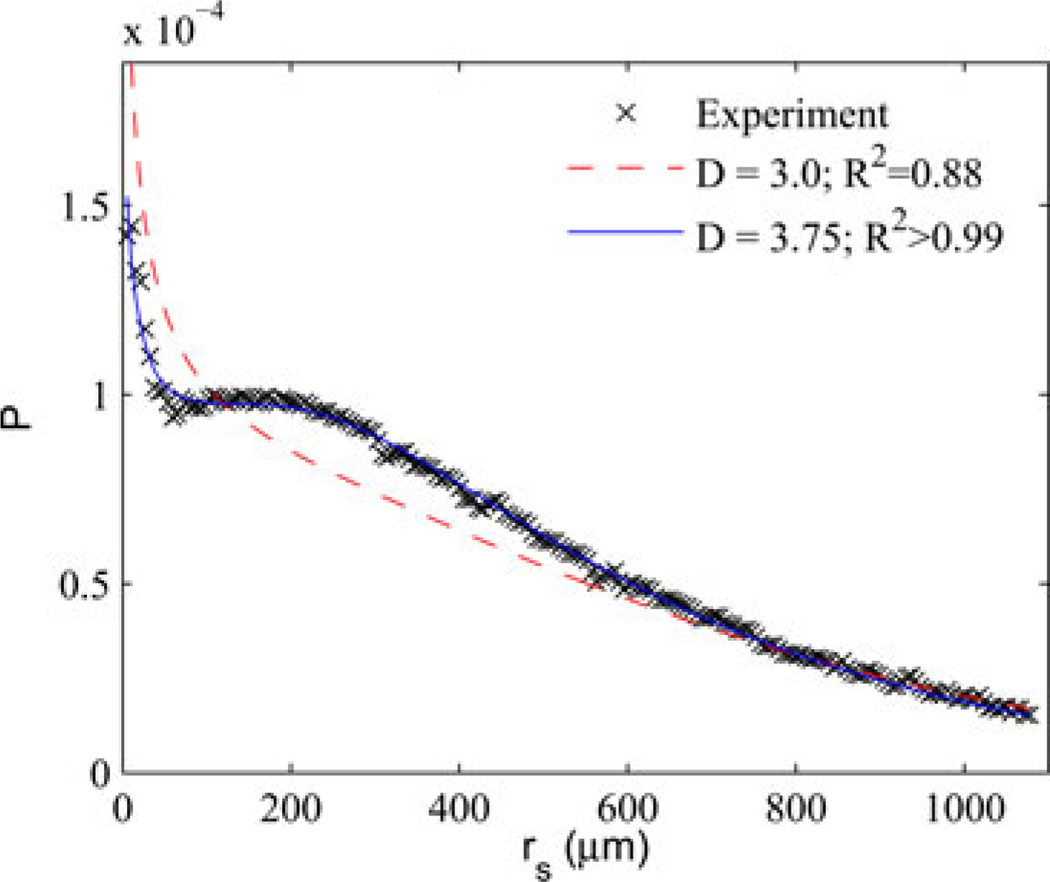
Fig. 2 shows an example where a simple model of scattering based on the HG function is not sufficient to explain the experimental data. In these data, radiative transport is measured with enhanced backscattering (EBS) at length scales ranging from much less than the transport mean free path to much greater than , which for this tissue is about 200 µm. EBS measures the probability distribution P(rs) of ray exit distances relative to the point of entry in a scattering medium, in other words the spatial impulse response of diffuse reflectance [22].
Fig. 2.
Example of experimental data that cannot be explained using the HG function. Radiative transport in rat lung tissue is measured with EBS to produce a probability distribution P (rs) of the entrance/exit separation of rays scattered in the tissue and eventually exiting. Two best fit models of P (rs) computed numerically using MC are also shown based on WM (blue solid) and the special case of D = 3 which is equivalent to the HG phase function commonly used to model tissue. Fitting with a two parameter HG function produces a poor fit to the small rs, while a three-parameter WM-based model results in an excellent fit to the experimental.
Most methods that measure radiative transport via backscattering are only sensitive to separations larger than where the propagation of light can be accurately modeled using the diffusion approximation [23]. The figure shows that the different models tend to converge at these larger length scales, while small distances exhibit more significant differences because in this region, P(rs) is dominated by low order scattering and is, therefore, more sensitive to the shape of the phase function. The model curves are calculated by using the scattering model in MC simulations of scattering to build a catalog of curves for ranges of parameters. Fits to experimental data are obtained by interpolating the model simulation space to produce a lookup table. The dashed red line corresponds to the best fit obtained using the HG phase function, while a much better fit is obtained using the WM model with D = 3.75 highlighting the need for more a more advanced model for measurement methods that are capable of discriminating between different correlation functional forms.
III. Rayleigh–Gans–Debye Approximation
One of the most useful approximations that can be made in scattering from biological tissue is that of “weak” scattering. In this approximation, it is assumed that the scattered field is much less significant than the incident field. This approximation is also known as Rayleigh–Gans–Debye (RGD) scattering, the first Born approximation, or single scattering approximation. Here, we will use “RGD scattering” for brevity. This approximation can be used to describe discrete particles as well as continuous media and has been extensively investigated by Ishimaru for other refractive index correlation functions, so we will follow his derivation for continuous random media [24]. Excellent discussions of RGD scattering in particles are provided by Hulst and van de Hulst [25] as well as Bohren and Huffman [15].
A brief conceptual summary of the RGD approximation is as follows: When a plane wave traveling in free space passes through a particle, the dipoles that make up the particle are excited and begin to oscillate reradiating electromagnetic energy according to the Rayleigh or dipole radiation pattern [26]. In the RGD approximation, the scattered field is insignificant relative to the incident field, so secondary scattering events can be ignored. This is equivalent to saying that the electric field arriving at any point inside the particle is approximately the same as the incident field. In other words, there is no phase delay or refraction inside the particle. The phase of each dipole is then determined by its position along the z-axis (direction of incident wave). The total effect of all the dipoles can then be treated by coherently summing the field from each dipole to obtain the scattering amplitude function f(θ, ϕ). This summation can be mathematically written as an integral of relative excess refractive index as a function of position nΔ(r⃗) = (n(r⃗) − 〈n〉)/〈n〉, where 〈n〉 is the expected value or average refractive index. The spherical wave can be written as a complex exponential so that the operation takes the form of a Fourier transform. We are typically interested in the intensity of scattering, since this is the observable quantity. The intensity is proportional to the square of the amplitude scattering function, which is the Fourier transform of nΔ(r). By applying the Wiener–Khinchin theorem, we see that the scattered intensity per unit volume as a function of angle (known as the differential scattering cross section σ(θ, ϕ)) is proportional to the spectral density Φs (ks), which is the Fourier transform of the autocorrelation of the excess refractive index Bn (rd):
| (2) |
where is a displacement vector between any two points in the medium. When the medium is statistically isotropic, Bn () is radially symmetric and can be represented as a 1-D function of scalar displacement rd. The result simplifies to the product of a dipole factor 1 − sin2 (θ) cos2 (ϕ) multiplied by the spectral density evaluated at ks = 2〈n〉k sin(θ/2), where k is the freespace wavenumber:
| (3) |
Note that this relation works for a suspension of particles as well as continuous media. For particles, the weak scattering approximation is valid when , where a is the particle radius. That is to say, the excess refractive index must be small and the phase delay as the wave traverses the particle must be much less than the wavelength.
It is important to note that while the RGD scattering approximation is often referred to as the single scattering approximation, this does not mean that it cannot be used to model large volumes such as clouds or tissue where multiple scattering takes place. What is required in the case of a particle is that single scattering is valid for a single particle. When a medium is composed of many such particles, light transport can be very accurately computed numerically by methods such as MC [27]. The key is to accurately compute the angular probability for each scattering event and then propagate rays according to mean free path with subsequent scattering events. Interestingly, the same is true for continuous media.
The RGD approximation should, therefore, not be used to model an entire region of tissue, but rather to statistically model a representative volume just large enough to cause one scattering event. Multiple scattering can then be treated as decoupled events that can be summed according to the mean free path and scattering function using computational methods like MC. Such simulations can be made even more accurate by using the Extended Huygens–Fresnel principle to account for the propagation of coherence in the case of multiple scattering, and an excellent review of such treatment developed by Anderson and Thrane is provided in [28, Ch. 17].
A. Validity of the RGD Approximation for Continuous Media
Unlike a particle, there is no clear boundary in continuous media over which the concept of single scattering can be applied. Instead, in continuous media, the single scattering approximation must be valid for a representative small volume of material. By representative, we mean that the volume must be large enough to represent statistical ensemble of the medium, but small enough that single scattering approximation holds. As long as the volume can be defined for which small changes in the volume result in the same differential scattering cross section per unit volume, the RGD approximation is valid. One could also say that ls > Ln must be true, where ls is the mean free path and Ln is the outer length scale of the correlation beyond which the medium is not significantly correlated. In other words, a wave of propagating light must, on average, pass through enough media to be statistically representative before being scattered. This was rigorously investigated using finite-difference time domain and the validity criterion can be written as [29].
B. An Illustrative Example: Suspension of Spheres
While we are most interested in modeling continuous media in this paper, it is instructive to follow through an example using a suspension of spheres. We can then compare the resulting scattering functions to those obtained with the Mie solution. Incidentally, it is just such media in the form of polystyrene microsphere suspensions that are often used as tissue phantoms in research labs.
To begin, we must consider Bn (rd) for a suspension of spheres. For a sphere of radius a, the autocorrelation function can be computed analytically, so Bn (rd) is simply scaled by the variance of the refractive index:
| (4) |
We must next calculate the expected value of refractive index 〈n〉 and the variance of the relative excess refractive index nΔ = n/〈n〉 − 1. These values depend on the refractive index of the spheres ns, surrounding medium nm, and the volume fraction Cv occupied by spheres
| (5) |
| (6) |
The Fourier transform of this function can be calculated analytically
| (7) |
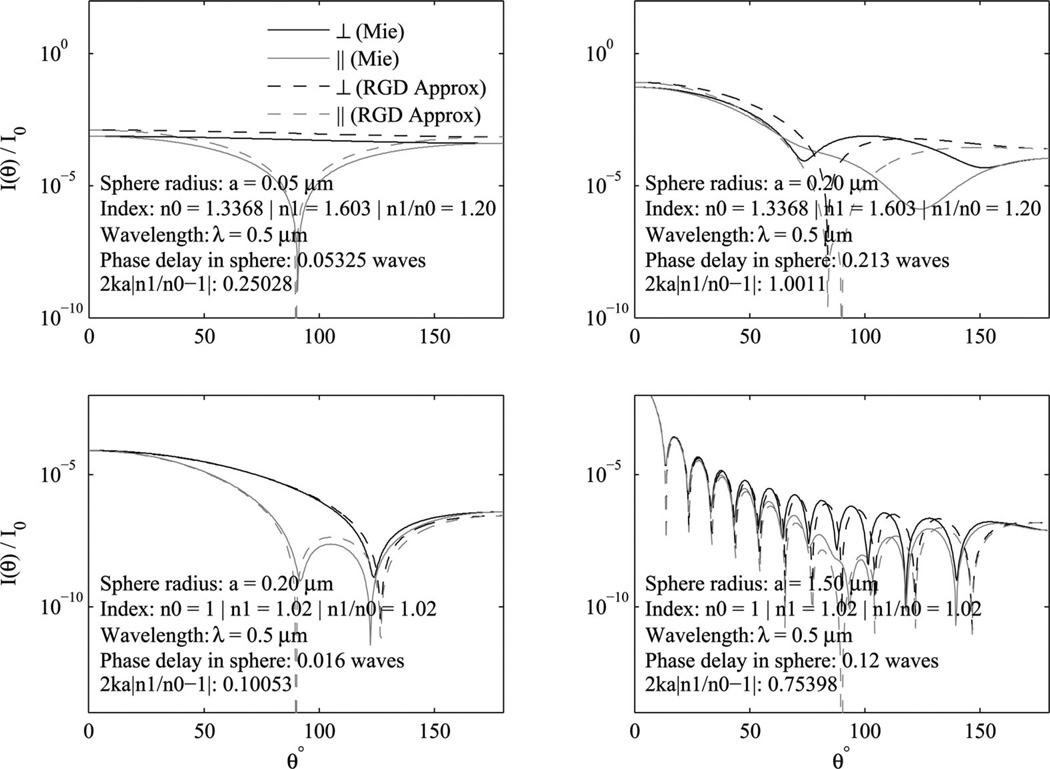
and substituted into (3) to calculate the differential scattering cross section. If we plot the results and compare to the Mie solutions as in Fig. 3, we can see excellent agreement for very small particles (top left) or very small refractive index contrast (bottom left). The accuracy begins to decrease as particle size increases a little (top right). For weaker refractive index contrast, the particle size can get much larger before the agreement breaks down (bottom row). This is consistent with the requirements of the single scattering approximation described in Section III-A.
Fig. 3.
Comparison of the Mie solution for a suspension of microspheres to σ(θ, ϕ) calculated using the RGD approximation. The top two panels show the calculation for polystyrene microspheres in water and while the 100 nm diameter spheres (upper left) show good agreement, the approximation breaks down for 400 nm spheres (upper right). However, when the index contrast is low n1/n0 = 1.02 as in the bottom row, the agreement holds for 400 nm spheres (lower left) and even for large spheres of 3.0 µm (lower right). Calculations used a wavelength of 500 nm.
IV. Quantifying Structure With a Refractive Index Correlation Function
Scattering from a medium can be computed analytically or numerically for a known distribution of dipoles or, equivalently, a known distribution of refractive index. This is rarely if ever the case for biological tissue. It is, therefore, of interest to determine statistical average scattering from a random medium where the exact distribution of index is unknown, but the statistical properties are known, or can be approximated. One way to describe the average scattering properties of a random medium is to describe the average shape of differential scattering cross section from a small representative volume of material. As seen in Section III, an expected value of the differential scattering cross section σ(θ, ϕ) can be directly calculated from the refractive index correlation function Bn (rd).
A. WM Correlation Family
The best model of tissue scattering would be based on a direct measurement of refractive index correlation over the entire range of lengths scales to which scattering is sensitive. This is currently not possible, and so lacking a catalog of refractive index correlation functions in tissue, we can choose to model the correlation function using a functional form to approximate the actual statistical correlation function.
Several correlation functions have been used to model continuous random media. Chapter 16 in Ishimaru’s text describes exponential correlation that leads to the Booker–Gordon formula, the Gaussian model, and the Kolmogorov spectrum also known as the von Kármán spectrum which is based on a power law with a specific power [24], [30]. A number of papers have proposed a fractal model for tissue [6], [7]. Mass fractals are characterized by power law correlation functions where the mass fractal dimension is related to the power. Interestingly, all of these models as well as the HG function can be described by the WM correlation family [30], which is the product of a power law and a modified Bessel function of the second kind of order (D − 3)/2,
| (8) |
The fact that the WM family of correlation functions is so flexible and encompasses many other models makes it an attractive choice. The parameter D controls the shape of function and can be used to represent a wide range of plausible correlations including:
Gaussian: D → ∞;
exponential: D = 4;
stretched exponential: 3 < D < 4;
Kolmogorov/von Karman: D = 11/3;
HG: D = 3;
power law:D < 3.
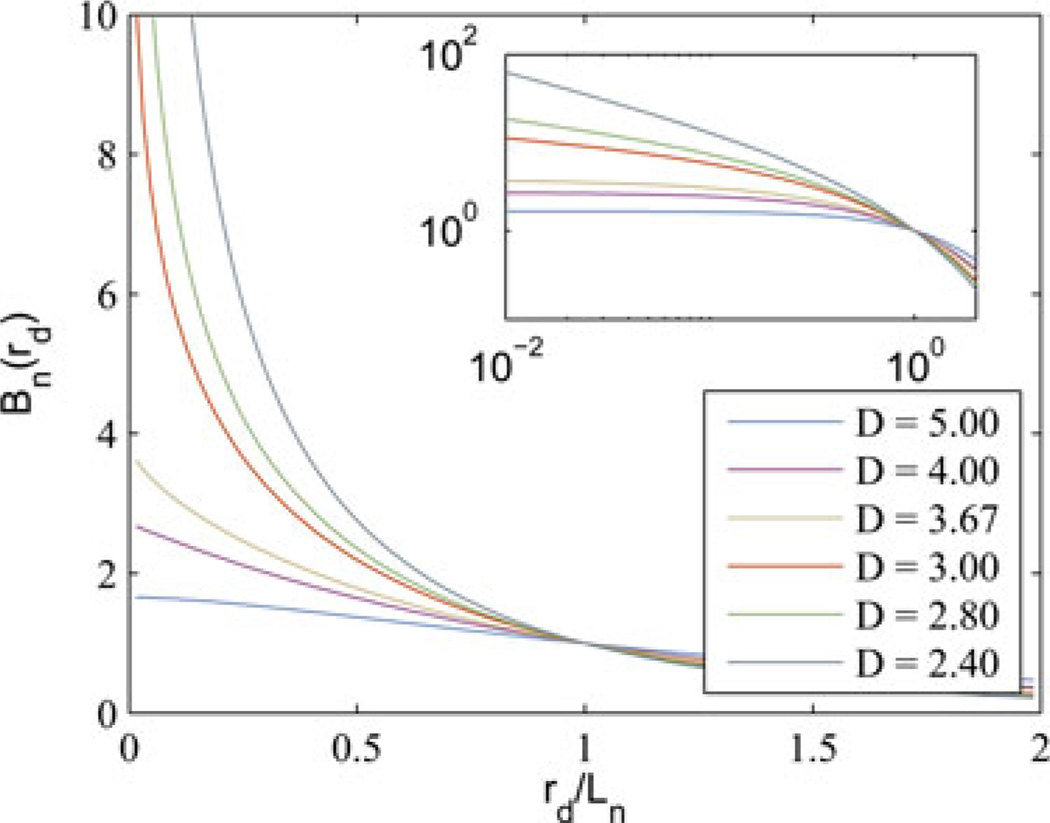
Examples of the functional form for several values of D are shown in Fig. 4. Note that when D < 3, the medium can be considered a mass fractal and the parameter D takes on the special meaning of mass fractal dimension.
Fig. 4.
Examples of the WM function for different values of D normalized such that Bn (rd = Ln) = 1. Inset shows the same functions on a log–log scale.
Fig. 5 shows an example of the differential scattering cross section σ(θ, ϕ) (3) calculated for vertically polarized light and D = 3. For this case, the shape around the equator at σ (θ, ϕ = 90°) corresponding to the shape of the HG phase function. However, an important difference is the inclusion of the dipole factor. When incident light is unpolarized, the phase function can be calculated by averaging over ϕ resulting in a phase function with a minimum at θ = 90° [31]. This extension of the HG phase function more accurately reflects physical measurements. For example, Mourant reported goniometer measurements of tissue along with fitting of the HG function, but the HG phase function could not match the measurements in the backscattering direction [11], [18].
Fig. 5.
An example of the differential scattering cross section σ(θ, ϕ) for left to right propagating vertically polarized light. This example is computed using the WM function discussed below with parameter D = 3 in which case the shape around the equator (ϕ = 90°) corresponds to the HG phase function. The dipole factor produces the dimples oriented in the plane of the electric field polarization.
B. Normalization
The WM correlation family is useful because it can take on so many different functional forms. This does, however, create some challenges in terms of normalizing the function. The convention typically used in signal processing is that correlation functions are normalized such that the value at the origin (rd = 0) is equal to 1, while in statistical disciplines, it is equal to the variance—in our case, the variance of excess refractive index . However, since power laws are unbounded at the origin, this convention is impossible to implement for D < 3. Therefore, no single normalization can be used to satisfy convention in the bounded case D > 3 and the unbounded case D < 3.
The WM function has three parameters: D, An, and Ln. The shape is determined by D, while the latter two can be thought of as scaling parameters. Ln scales the horizontal axis, while An scales the vertical axis. Ln also represents a transition point beyond which the function decays as an exponential. There are several options for the normalization coefficient An, and each has advantages and disadvantages.
It should be noted that these normalization options only affect the interpretation of the coefficient as the variance of refractive index. The function Bn (rd) is not arbitrary and actually represents a physical function that could, in principle, be physically measured. In media where the best fit of Bn (rd) is for D ≤ 3, the actual physical value of is still finite, but the power law only extends down to some small length scale below which the shape is irrelevant. This is sometimes called the inner scale of turbulence. When this inner scale is much smaller than the wavelength, the error in Φs between the unbounded model function and the actual refractive index correlation function is small [31]. Nevertheless, it is useful to explore several options for normalizing Bn (rd).
1) Whittle and Matérn Normalization
Bn (0) = 1 for D > 3: A brief description of the history of the WM function and some closely related functions used in modeling atmospheric turbulence is provided by Guttorp and Gneiting [30]. These authors describe the normalization that Whittle and Matérn used. In this case, the function is normalized to 1 () at rs = 0 for values of D > 3 that result in a bounded function. In other words, is the variance for D > 3, and just a parameter for D <3:
| (9) |
The advantage of this normalization is that it is normalized at the origin when it is bounded, as any actual correlation function should be. The disadvantage is that as D gets smaller and approaches 3, the narrow shape of the function forces the magnitude to zero at any finite value of rd. This, in turn, results in the total scattering cross section collapsing to zero. Additionally, the function is identically zero for D = 3, and so we lose the ability to model the HG function. Guttorp and Gneiting argue that (D − 3)/2 must be greater than 0 for this correlation to be valid (eliminating the need for the absolute value of the gamma function). This is true in that cannot be defined when D ≤ 3, but many interesting cases occur for these values of D, including a power law corresponding to mass fractals. When D ≤ 3, the function Bn (rd) approaches a power law for small rd and so is infinite at the origin.
2) Normalized at a Minimum Length Scale
One possible normalization is to attempt to mimic reality. When D < 3, Bn (rd) approximates a power law corresponding to a mass fractal organization of material. In nature, fractals occur that exhibit self-similarity over a range of scales and, therefore, are described by a power law correlation function. However, the range of scales over which the true function closely follows a power law is not infinite. For example, in tissue, one may observe length scales corresponding to the size of a cell. Zooming in, one observes a similar organization in organelles, but at a length scale an order of magnitude smaller. Zooming in yet further, one might observe globule organization of macromolecules. This approximate self-similarity over several magnitudes of length scales is what gives rise to a power law correlation function. However, this power law cannot extend to infinitely small length scales. At some small scale, only molecules are left and the very definition of refractive index becomes difficult to interpret. If the actual correlation function were known, the mode could be fit by defining a minimum length scale rmin and normalize the function at this value:
| (10) |
Provided that rmin is chosen correctly, the value of the model function at rmin can be close to the true value . The advantage of this normalization is that there is an intuitively satisfying notion that the correlation always starts at for some arbitrarily small value regardless of the value of D. One problem with this normalization is that it introduces a fourth parameter rmin that must be arbitrarily chosen. Since rmin is arbitrary, the value of is also arbitrary which makes interpretation of difficult since it is no longer a material property but depends on the chosen rmin. For a power law, a small change in the chosen value of rmin could result in a large change in the model’s value of and it does not necessarily correspond to the actual variance of the real medium.
3) Normalized to Value c at rd = Ln
Since the previous normalization can lead to a misinterpretation of the meaning of , one alternative is to simply normalize the model at a finite value of rd that is already defined in the model, namely Ln. The normalization constant c is not interpreted as variance of refractive index; it is simply the value that scales the model to match the actual medium:
| (11) |
This normalization has the advantage that the it is well behaved for all values of D. Of course, the function is infinite at rd = 0 for value of D ≤ 3 as expected. When D > 3, the function is indeterminate at rd = 0, but the limit is bounded, so this poses no problem for modeling scattering. The disadvantage is that relating this scaling parameter to requires an extra step, but this can be easily dealt for values of D > 3:
| (12) |
When D ≤ 3, could be determined for the actual medium, but is not explicitly part of the model.
These first three choices do not depend on scattering: they simply describe the properties of a medium. There are, however, a few additional options for normalization that amount to normalizing the spectral density independent of the scale of Bn (rd). These retain the dependence on the shape of Bn (rd), but not the magnitude.
4) Normalized Spectral Density
: Another option is to normalize the spectral density Φs such that . In this case, the function takes the form of a Pearson distribution type VII:
| (13) |
The advantage is that the spectral density is never unbounded for any value of D. One disadvantage is that because Φs is a probability function, it has no dependence on the variance of refractive index . This choice of normalization requires D > 1 and has zeros, singularities, or is indeterminate at rd = 0 for values of D = 2, 3, 4.
5) Rayleigh Scattering Normalized
| (14) |
Another option is to normalize such that the scattering coefficient µs converges to the same value for any value of D in the Rayleigh limit where Ln ≪ λ. This is appealing in that as the correlation function becomes much smaller than the wave-length, there should not be any dependence of the shape of the correlation function (or particle). This normalization is then equivalent to saying that all small particles look the same to long waves and scattering depends only on the mean free path independently of the shape of the correlation function. The disadvantage is that the scattering coefficient is indeterminate for values of D = 2, 4.
V. Calculating Optical Properties From Differential Scattering Cross Section
Armed with a method to calculate the differential scattering cross section per unit volume σ(θ, ϕ), we can calculate the optical parameters typically used to characterize a scattering medium. These parameters include the scattering coefficient µs = 1/ls which is the inverse of mean free path ls. The scattering coefficient is equal to the total scattering cross section per unit volume and is easily obtained by integrating,
| (15) |
The anisotropy coefficient g = 〈cos θ〉 is the average of the cosine of the scattering angle,
| (16) |
Anisotropy determines the degree to which scattering is forward directed where g = 1 corresponds to completely forward scattering, 0 < g < 1 corresponds to scattering that is forward directed, and g = 0 corresponds to isotropic scattering. Another parameter commonly used to describe media such as tissue that are typically strongly forward scattering with values of g ≈ 0.9 is the reduced scattering coefficient, Also of interest is the backscattering coefficient,
| (17) |
Also of interest is the backscattering coefficient,
| (18) |
When the WM model is used, these relationships can be calculated analytically in terms of the model parameters. This was shown by Sheppard [32] and later extended by Rogers et al. to include the effect of the dipole factor [31]. What is particularly interesting is the spectral relationship of the optical properties that can be readily measured. For example, the spectral dependence of can be measured and then related to the model parameter D. For example, in biological tissue, the fact that g is large indicates that the medium contains structure large compared to the wavelength, or kLn ≫ 1. In this regime, for D < 4.
VI. Experimental Methods for Quantification of Model Parameters
There are a number of experimental methods capable of measuring scattering properties of tissue, for example, Goniometer, integrating sphere (with the IAD method), Confocal, OCT/ISOCT, and P(rs)/EBS. Of these, the first two require significant tissue preparation to create a thin uniform slab of tissue that is then measured in transmission and reflection. Although Hall et al. showed that thicker tissue samples can be used if multiple scatting is corrected using MC [33], prepared tissue is still required. The remaining methods are attractive because they can be used in reflection and so have potential to be used in vivo. Jacques et al. recently demonstrated quantification of properties including and anisotropy g using confocal and OCT methods [34]. As illustrated in Fig. 2, some methods such as EBS are particularly sensitive to the shape of σ(θ, ϕ) and, therefore, enable measurement of parameter D.
While EBS measurement of P(rs) provides an excellent quantification of tissue properties and demonstrates the advantages of a more complex 3 parameter model, one limitation is the assumption that the medium is statistically homogeneous. We know that tissue is often a layered medium, so methods capable of quantifying the optical properties locally at different positions and depths would be of great utility. One such method is based on OCT and allows assessment of properties in an imaging modality, a technique referred to as inverse spectroscopic OCT (ISOCT).
The unique advantage of ISOCT is that it is capable of imaging tissue structures in 3-D space, while simultaneously providing complete quantification of the optical properties and (by assuming the WM model) the correlation functional form [35], [36]. The depth resolving capability in OCT is realized by interferometry between the reference field and the sample scattering field. The primary contrast is the coherent elastic scattering from the tissue heterogeneity on which the WM scattering model applies. In addition, OCT requires a broadband source to eliminate the 2π ambiguity, providing an opportunity to analyze the scattering spectrum from a scattering medium such as tissue.
The signal in OCT can be approximated to be proportional to the backscattering coefficient µb [see (18)]. Also the signal decay along the penetration depth is exponential and scales with µs. Thus, the OCT image intensity can be modeled as [35]
| (19) |
where I0 is the illumination intensity, r is the reflectance of the reference arm, L is the temporal coherence length of the source, z is the penetration depth, and the mean refractive index of the medium is 〈n〉 ≈ 1.38. Further, a short-time Fourier transform (STFT) can be performed to obtain the spatially resolved spectra, and thus, the wavelength dependence of µb and µs can be obtained. By combining the power law dependence of µb with the absolute values of µb and µs, the three parameters of the model An, D, and Ln can be determined [35]. This allows calculation of anisotropy factor g from (16).
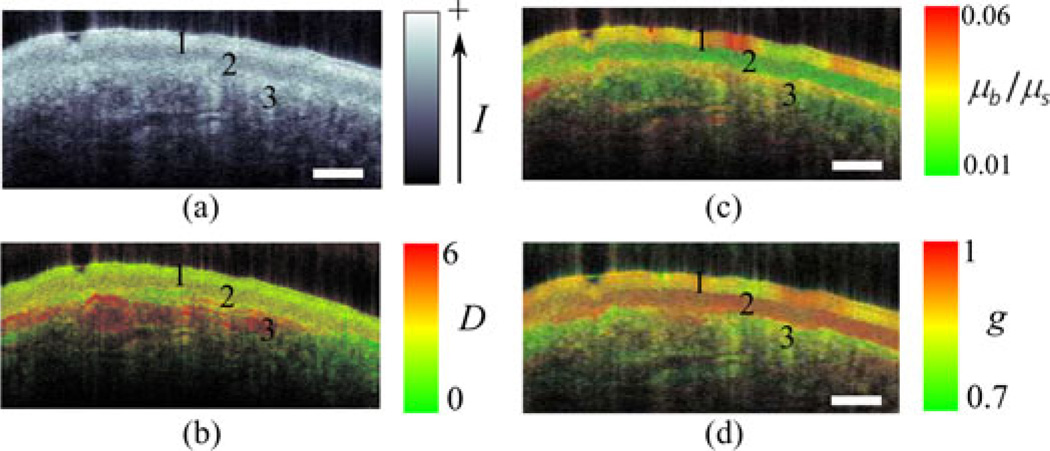
Fig. 6 shows an example of imaging optical and physical properties in a stratified tissue. Fig. 6(a) shows a traditional OCT image of rat buccal tissue. Three distinct layers can be identified: keratinized epithelium, stratified squamous epithelium, and submucosa. For each layer, we assume a statistically homogeneous scattering medium and then applied the ISOCT algorithm on each layer. Fig. 6(c) and (d) shows the capability of imaging D, the ratio of µb and µs, and the anisotropy factor g in a spatially resolved 3-D volume.
Fig. 6.
An example application of the model: The ISOCT method uses the model to quantify optical and ultrastructural properties in an image map from ex vivo rat buccal sample (adapted with permission from [35]). (a) Conventional OCT images. Three layers were labeled as (1) Keratinized epithelium, (2) stratified squamous epithelium, and (3) submucosa. (b)–(d) Pseudocolor ISOCT images encoded with D, µb/µs, and g. Bar = 200 µm.
The advantage of ISOCT lies in the fact that the spatially resolved spectrum reflects the random interference of the scattering field within the resolution volume, even though the axial resolution was sacrificed by performing STFT due to the trade-off between the spectral bandwidth and temporal resolution. The random interference gives rise to the granular “speckle” pattern in the OCT B-scan image. On one hand, many treat OCT speckle as an artifact and developed various ways to eliminate it. On the other hand, speckle can be informative because the random interference can be modeled by Bn (rd) for structures even below the image resolution limit.
Consider a simple example where there are two reflective surfaces along the axial direction with position of zs and zs + Δz; the combined reflected field from these surfaces (E1 + E2) interferes with the reference field (Er) which is reflected by a mirror located at zr. For simplicity, we arbitrarily set all the reflectance values to unity. Thus, the interference part of the spectral intensity is written as
| (20) |
where k is the wave number, Re(·) indicates the real part of a complex number, and superscript * indicates the complex conjugate. The equation shows that interference between a reference and two reflections separated by a small phase difference (small z) creates spectral oscillations modulated by a beat frequency determined by the two surface separation. When the separation is within the axial resolution, the OCT intensity profile cannot differentiate (resolve) any slight changes in separation. However, a change in the separation that is not resolved does change the spectra. In this way, spectral analysis provides more information about the statistical separation, which of course for a random medium is related to the correlation function Bn (rd).
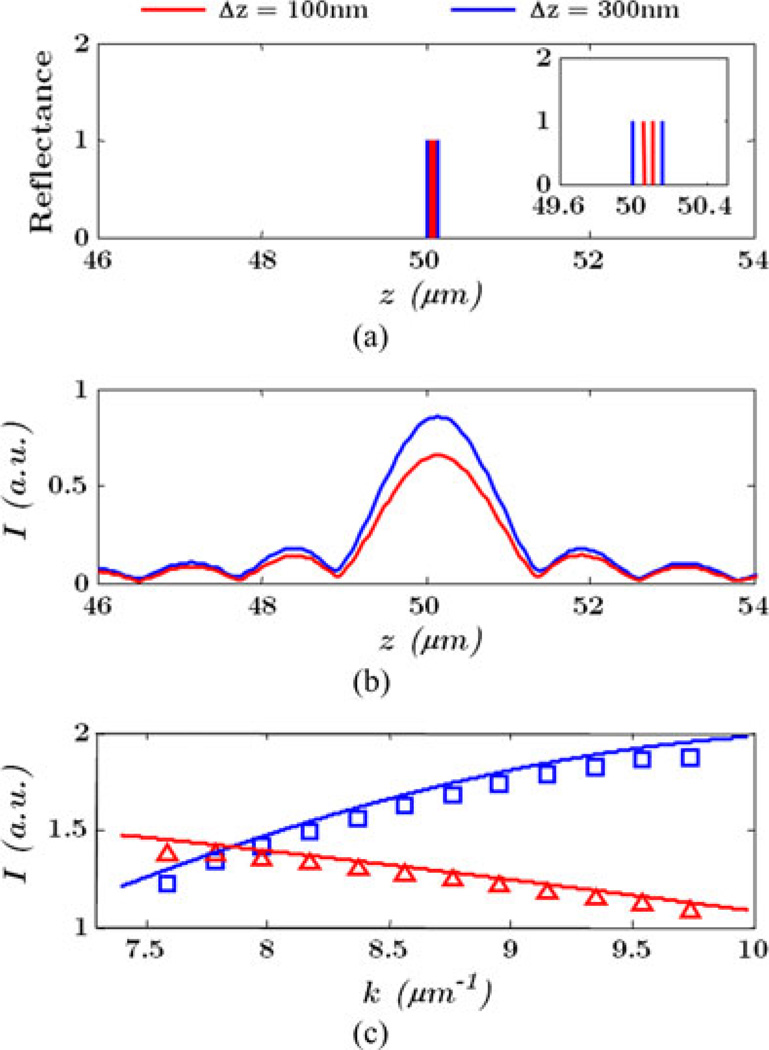
Fig. 7 illustrates the concept by simulating OCT and ISOCT for the two surfaces. In one case, two surfaces were located 50 µm apart from the reference and separated by 100nm; in the second case, the separation was enlarged to 300 nm [see Fig. 7(a)]. The interference spectrum is simulated from 630 to 850 nm and the OCT A-line signal is reconstructed in Fig. 7(b). Further, the ISOCT spectra at z = 50 µm is numerically extracted by STFT and compared for the two cases in Fig. 7(c). It is clear that the conventional OCT A-line signal in Fig. 7(b) has almost identical form, while the beating spectra obtained in ISOCT shows the difference in these two cases. While the details for continuous media are more complex, this simple example illustrates the basic concept that small length scales need not be resolved to be quantified spectroscopically.
Fig. 7.
Illustration of the advantage of spectral analysis in ISOCT. (a) One-dimensional two surface reflectance located at 50 µm from the reference. Case 1 (red): two surface separation is 100 nm. Case 2 (blue): two surface separation is 300 nm. (b) Simulated OCT A-line intensity from two surface separation. (c) Spectral profile extracted at z = 50 µm by ISOCT (squares and triangles), and beating spectra from two surfaces in solid line.
VII. Structural Length-Scale Sensitivity
One of the advantages of performing tissue characterization using optical spectroscopy is the ability to detect and quantify structures smaller than the diffraction limit, even though such structures cannot be resolved using conventional microscopy. This ability arises from the fact that scattering contrast is largely dependent on the spatial distribution of refractive index at structural length-scales smaller than the diffraction limit. Still, the question arises: which range of structural length-scales can optical spectroscopy sense?
While this problem appears straight-forward, the answer is complicated in part by the fact that there is a nonlinear relation between the spatial refractive index distribution nΔ(r⃗) and σ(θ). As a result, it is not possible to independently assess the contribution of different structural length-scales to σ(θ) in order to determine the sensitivity range. Instead, it becomes necessary to consider the interaction between structural length-scales of all sizes at once.
One way to approach such a problem is through the perturbation study first presented in [37]. Under this approach, we begin with a continuous random media specified by the WM model (other models or actual data can easily be considered as well). We then perturb the medium by convolving with a 3-D Gaussian function in order to remove small structural length-scales and observe how the scattering characteristics change in the perturbed medium. This approach treats a medium as “blurred” below a particular length scale and then determines the length for which a notable change in optical properties occurs.
Mathematically, the volume normalized Gaussian function can be expressed as
| (21) |
where W is the full-width at half-maximum. Conceptually,G(r⃗) represents some process (e.g., drug treatment, carcinogenesis, etc.) which transforms the original medium by removing structures smaller than W.
Applying the convolution theorem, the modified medium can be expressed as
| (22) |
where 𝓕 indicates the Fourier transform operation and the superscript l indicates that lower spatial frequencies are retained. The autocorrelation of is then [37]
| (23) |
where is the power spectral density for and can be expressed analytically as
| (24) |
While (23) has no closed-form solution, it can be evaluated numerically in order to observe the functional form.
Similarly, the upper bound of sensitivity can be determined by filtering larger structural length-scales. However, the upper bound is highly dependent on the shape of the correlation function, for example, on D in this model. Conceptually, the upper bound is related to the point at which the value of the correlation function is insignificant in the presence of the rest of the correlation function. This point depends on the magnitude of the function at small length scales. Further, introduction of large length scales that scatter significantly will always affect the scattering measurements, but their presence will also change the correlation function at all smaller length scales, and so cannot be considered a perturbation. It is therefore not particularly meaningful to characterize the upper limit.
A. Length Scale Sensitivity of EBS
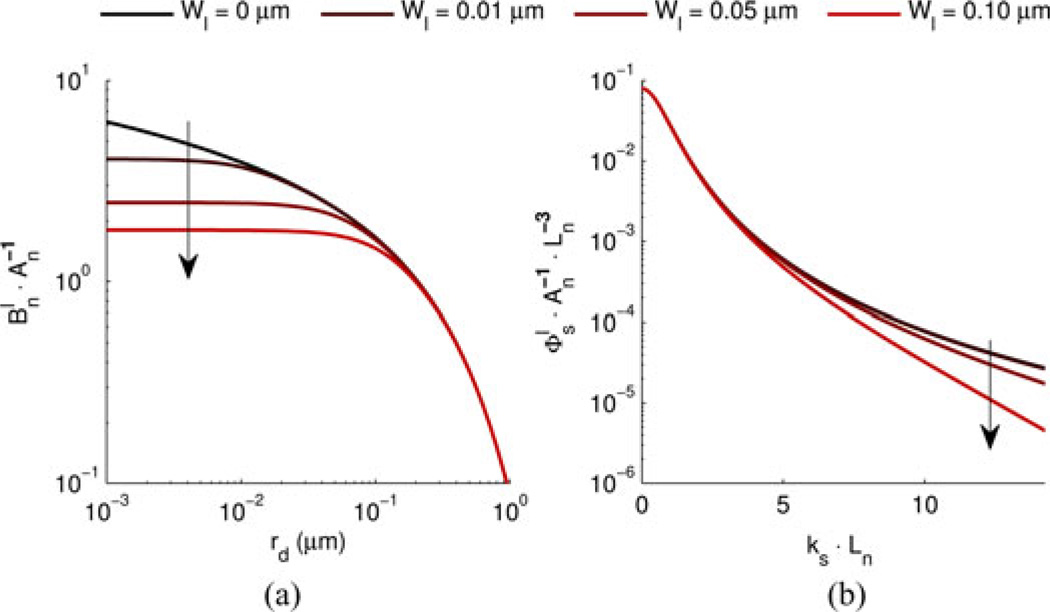
As a demonstration of the shape of the functions described by (23) and (24), we begin with a general approximation of tissue structure using D = 3 (i.e., HG case) and Ln = 0.452 µm (chosen such that g = 0.9 at λ = 0.550 µm with 〈n〉 = 1.38). After perturbing this medium with Gaussian’s of different width, Fig. 8 shows the resulting change in shape of and .
Fig. 8.
Structural length-scale perturbation analysis for D = 3.0 and Ln = 0.452 µm (chosen such that g = 0.9 at λ = 0.550 µm with 〈n〉 = 1.38). (a) . (b) . Arrows indicate direction of increasing Wl.
Under the structural length-scale perturbation analysis, we see a reduction in at smaller values of rd as the width of G(r⃗) widens [see Fig. 8(a)]. The location at which diverges from Bn (rd) occurs at ~ Wl. Conceptually, this indicates a loss of correlation at structural length-scales smaller than Wl. After Fourier transformation of to obtain , this loss of short structural length-scales correlation corresponds to a reduction in scattered power at higher spatial light frequencies [see Fig. 8(b)].
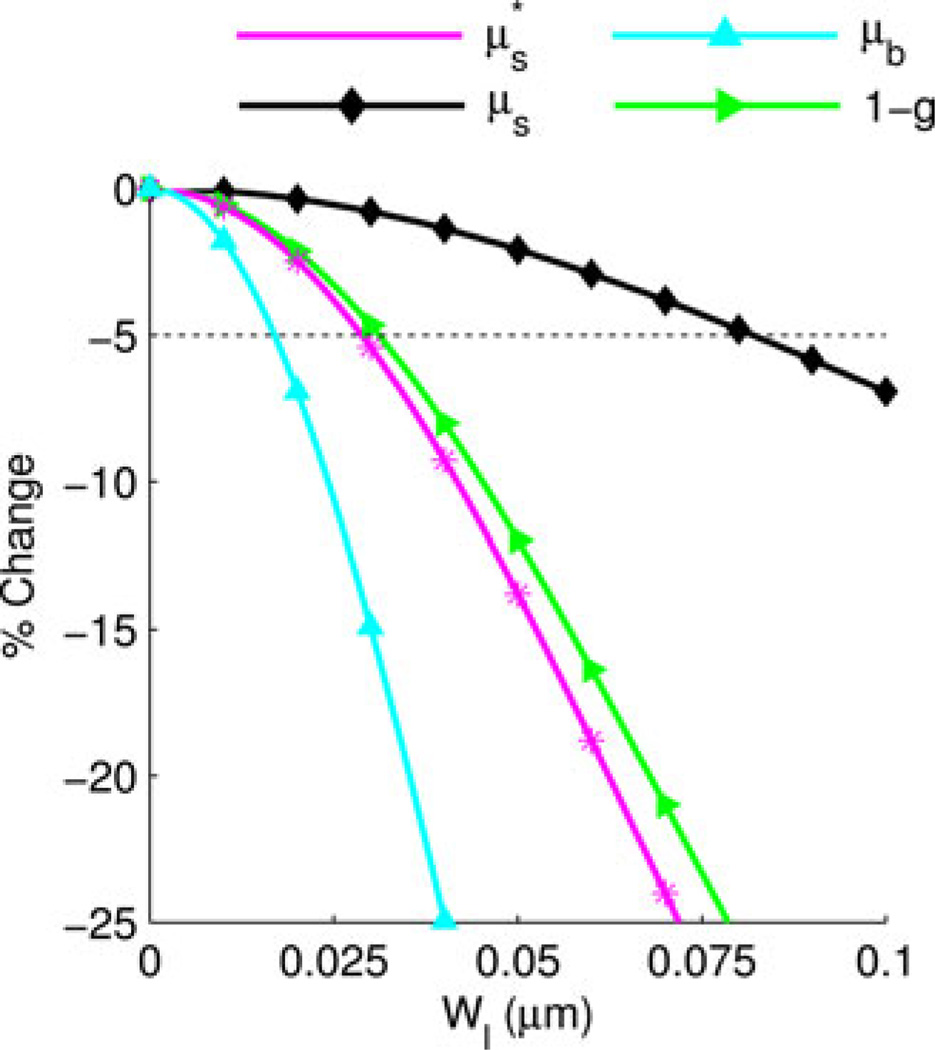
In order to relate the curves in Fig. 8 to observable light scattering characteristics, we first evaluate σ(θ, ϕ) according to (3) and then calculate µs, µb, g, and according to (15)–(18). Fig. 9 shows the percent change in the four optical properties under the structural length-scale perturbation analysis. Defining a 5% change level as the threshold for detecting an alteration in the measured optical properties, we find that µs is sensitive to length scales above 0.082 µm, is sensitive above 0.029 µm, and µb is sensitive above 0.017 µm.
Fig. 9.
% change in the scattering coefficients under the structural length-scale perturbation analysis for D = 3.0 and Ln = 0.452 µm at λ = 0.550 µm with 〈n〉 = 1.38. The dotted line indicates the 5% change threshold.
Next, we extend this analysis to quantify the sensitivity of the shape of P(rs). In order to do this, we performed a series of MC simulations using the open source code detailed in [38]. For these simulations, we implemented the modified scattering phase functions described by and tracked the reflected intensity in bins from to 5 with 0.005 resolution.
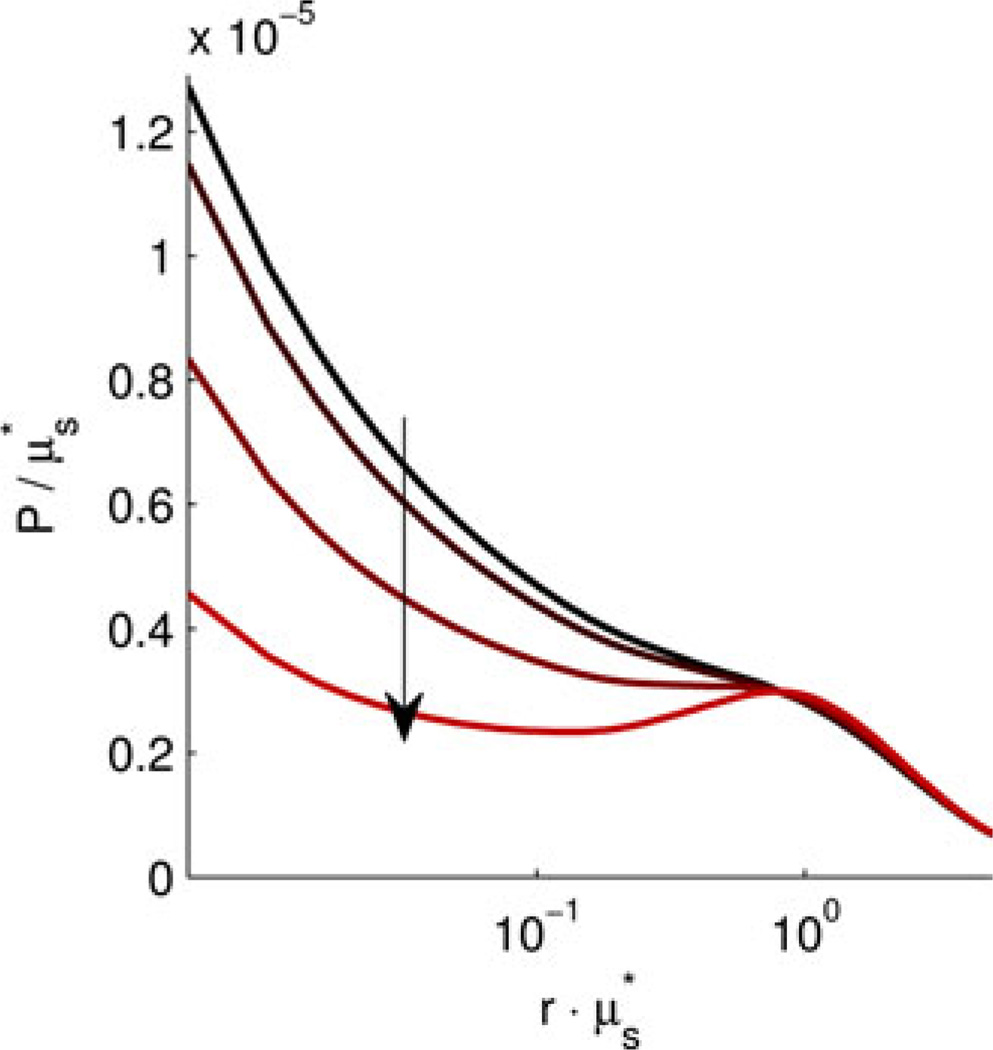
Fig. 10 shows the shape of calculated under the structural length-scale perturbation analysis. The curves are plotted as a function of the unitless in order to isolate the change in shape from the change in . There is a prominent change in the shape of for values of less than 1. It is well known that within this regime is extremely sensitive to the shape of the phase function [39]. We determine the structural length-scale sensitivity limit of by finding the values of Wl for which the value of at any changes by more the 5%. Using this criterion, is sensitive to length scales above 0.018 µm.
Fig. 10.
Change in the shape of under the structural length-scale perturbation analysis for D = 3.0 and Ln = 0.452 µm at λ = 0.550 µm with 〈n〉 = 1.38. Arrows indicate the direction of increasing Wl.
A summary of the structural length-scale sensitivity of various scattering characteristics is shown in Table I. Assuming the best-case scenario of conventional optical microscopy with violet wavelength illumination (λ = 0.400 µm), the diffraction limit is at ~ λ/2 = 0.200 µm. In each case, quantification of the various scattering characteristics provides sensitivity to structures smaller than the diffraction limit.
TABLE I.
Structural length-scale sensitivity of various scattering characteristics in continuous random media
| Scattering characteristic | Sensitivity limit (µm) | |
|---|---|---|
| µs | 0.082 | |
|
|
0.029 | |
| µb | 0.017 | |
|
|
0.018 | |
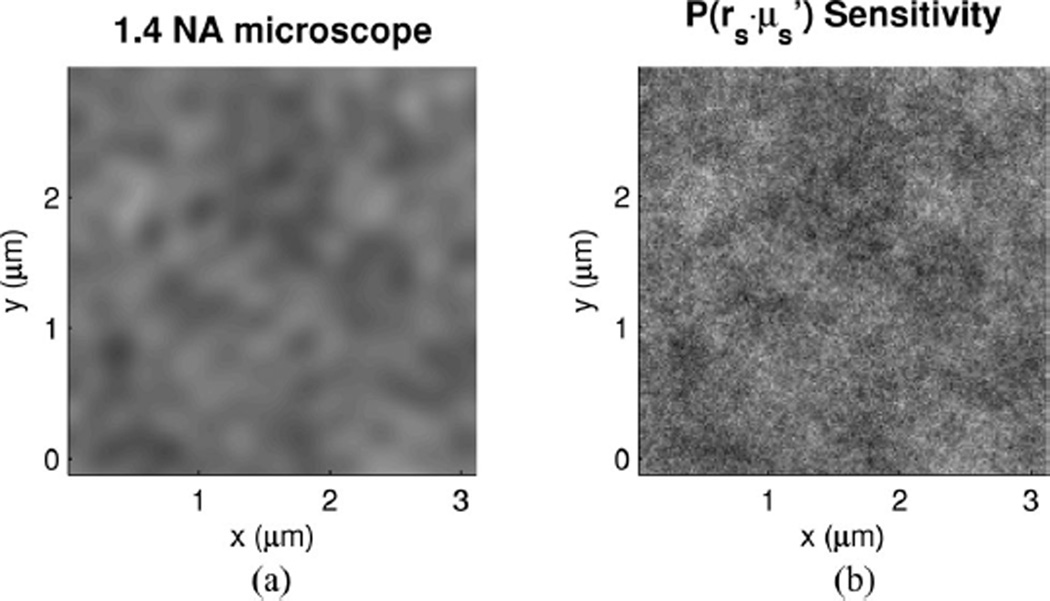
To visualize the meaning of the length scale sensitivity, a continuous random medium that has a desired Bn (rd) can be generated using the method described by Capoglu [8]. Since conventional microscopy is diffraction limited, the microscopically measured medium would at best result in a blurred version of the actual medium with features on the order of λ/2. Fig. 11(a) provides a demonstration of the range of length scales that a conventional microscope would visualize for a single random medium realization. For this same realization, Fig. 11(b) shows the range of length scales that the EBS method would detect using a spatial resolution corresponding to the lower sensitivity of . While the EBS method does not directly resolve the smallest length scales, changes in the shape of nonetheless provide a means to quantify fine structure that is not possible with standard imaging methods.
Fig. 11.
Rendering the continuous random media used in the structural length scale sensitivity analysis. (a) Medium realization with 1.4 NA microscope resolution at λ = 0.4 µm. (b) Medium realization corresponding to the sensitivity range of (where pixel size corresponds to the sensitivity limit).
We note that the sensitivities provided in this section assume that the experimental instrument used to measure such scattering characteristics has sufficiently high signal-to-noise ratio to distinguish a 5% change in value. Given a specific instrument noise level, the analysis presented in this section can be repeated with a different threshold value to determine the structural length-scale sensitivity of that particular instrument.
In the above numerical analysis, we used a particular operation by convolving the medium with 3-D Gaussian function to smooth window. The rationale is that suppression of small length scales without otherwise altering the correlation functional form provides a reasonable comparison. However, it is not be the only way to introduce the perturbation. Other methods such as adding random noise or changing the functional shape may be more appropriate depending on the application and can be performed to assess the length scale sensitivity.
Experimental confirmation of the sensitivities provided in this section is dependent on the fabrication of a continuous medium model whose distribution of length-scales is well controlled. Such phantoms have proven difficult to construct. As such, in the following section, we use a superposition of polystyrene micro-spheres to simulate a power-law distribution of length-scales.
B. Length Scale Sensitivity of ISOCT
ISOCT can be used to measure the value of D by determining the power law dependence of µb on wavelength. In this case, the length scale sensitivity is not exactly the same as that of µb itself. If Bn (rd) is perturbed as before by removing small lengths scales, the value of µb drops quickly, but the spectral dependence changes more slowly requiring a change at slightly larger length scales to produce a measurable change in D using ISOCT, although other methods of measuring D may have different sensitivity.
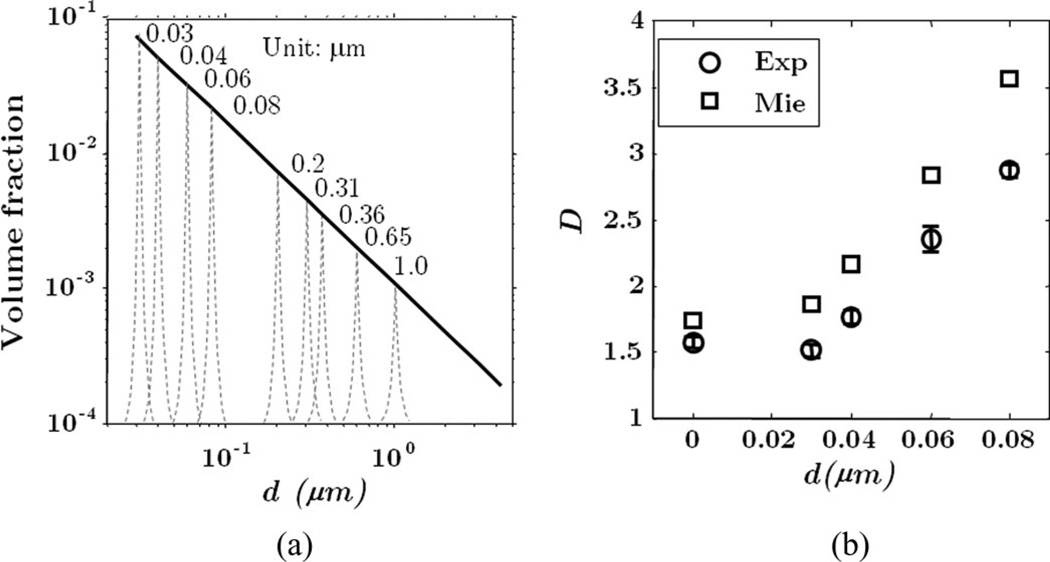
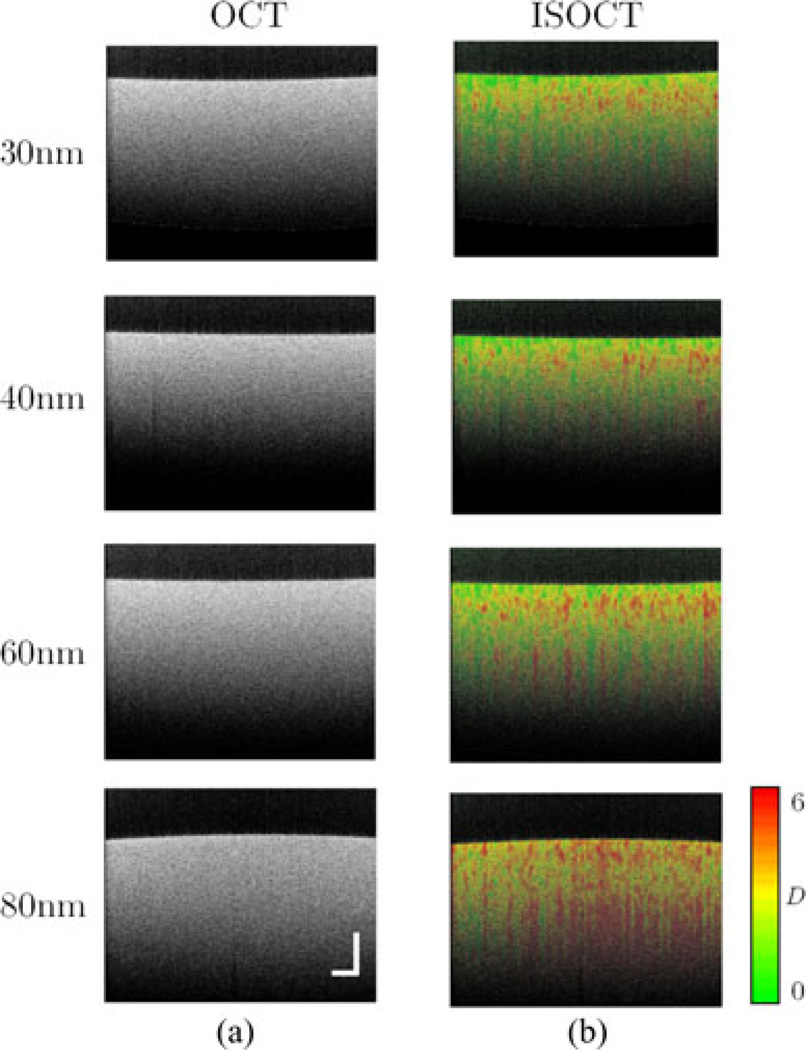
To demonstrate this experimentally, a phantom study consisting of various sizes of polystyrene microspheres was designed to verify the nanometer scale sensitivity. The volume fraction of the spheres is a power law relationship with their diameters as in Fig. 12(a). To determine the smallest length scale to which D measured with ISOCT is sensitive, a series of phantoms was constructed by successively excluding the smallest microspheres included in the previous phantom. For example, the first phantom (No.1) consisted of microspheres from 30nm to 1 µm. The second phantom (No. 2) consisted of microspheres from 40 nm to 1 µm by excluding 30 nm size spheres. The third phantom (No. 3) consisted of microspheres from 60 nm to 1 µm by excluding 30 and 40 nm spheres, and so on.
Fig. 12.
Sensitivity analysis for the dependence of the measured value of D on changes at subdiffractional length scales. Phantoms were made by mixing a suspension of microspheres spanning a range of diameters. (a) The volume fraction of each sphere size present in the suspension forms a power law relative to the diameters. (b) The measured value of D for each phantom is plotted against the value of the smallest sphere diameter present in that phantom. Error bars indicate standard error of measurements for each phantom. Value predicted using Mie theory is also shown. Adapted with permission from [36].
The values of D were measured with ISOCT and compared with Mie theory prediction as in Fig. 12(b). As expected, an increase in the measured value of D was observed as smaller sphere sizes were excluded. When 40 nm spheres were removed, D was measured to be 1.78 ± 0.06 compared to that from the first phantom (No. 1) 1.57 ± 0.04. The increase of 0.21 is above the experimental uncertainty of ±0.2 for measuring D, which corroborates that the perturbation at ≈40 nm can be detected by measuring D with ISOCT, a value well below the resolution limit for OCT. The error bars in Fig. 12(b) indicate the standard error for the measurements of a particular phantom, while the experimental uncertainty of ±0.2 corresponds to the 90% confidence interval for linear regression described in earlier work [35].
The pseudocolor encoded OCT images from above phantom studies demonstrated the advantages of the ISOCT method. While the conventional OCT B-scan images in Fig. 13(a) exhibit no discernible differences, the increase in D is readily appreciated for changes of length scale at 60 nm (No. 3) and 80 nm (No. 4) in Fig. 13(b). These phantoms also highlight the fact that Bn (rd) is a statistical property of the medium. Locally, voxels will have a deterministic correlation function that differs from adjacent voxels. The value of a particular pixel is not particularly meaningful. But upon averaging, the local correlation functions converge to the expected value. This is the reason for the spatial variation seen in the statistically homogeneous sphere suspension shown here. Spatial averaging results in more precise values, but at the cost of spatial resolution. Ideally, imaging is used as in Fig. 6 to map tissue structure, and then, contiguous regions or layers are segmented to report average values of optical properties within a region or layer.
Fig. 13.
OCT and tomographic D maps from phantoms. Gray scale OCT image (a) and pseudocolor D map (b) in low length scale sensitivity studies. Bar = 200 µm. Adapted with permission from [36].
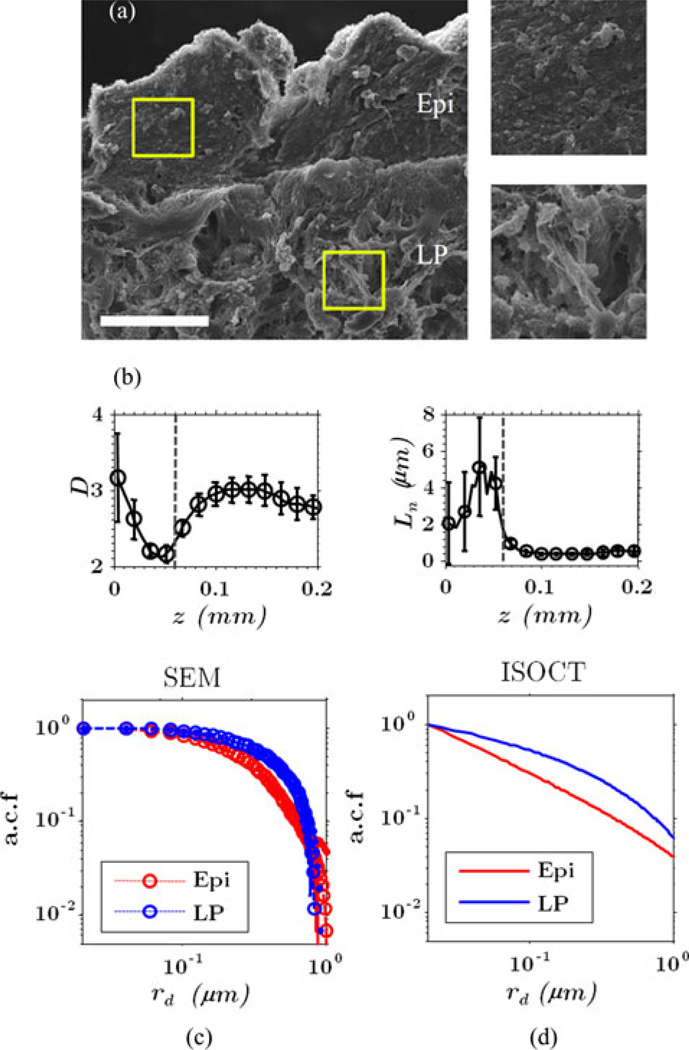
The nanometer scale sensitivity of ISOCT in biological tissue was previously demonstrated using scanning electron microscopy (SEM) [36]. As shown in Fig. 14(a), high-resolution SEM images were taken from ex vivo human rectal mucosa as well as ISOCT measurements shown in Fig. 14(b). Two types of tissue components were identified: epithelium (Epi) and lamina propria (LP). Magnified regions of each are shown in the insets. The image correlation functions calculated from these SEM image regions show that Epi has sharper functional form which coincides with increased presence of small features in Fig. 14(c). Meanwhile, ISOCT measured the depth dependent D and Ln can be plugged back in to Bn (rd) and plotted as in Fig. 14(d). Again, while SEM images do not represent refractive index, this comparison can only be made qualitatively. However, the result is in qualitative agreement with SEM findings: the Epi has a sharper correlation function than LP.
Fig. 14.
ISOCT measurement from human colon biopsy. (a) SEM image of a colon cross section. The resolution is 40 nm. Bar = 10 µm. (b) The ISOCT measurement on D ± SE and Ln ± SE as a function of penetration depth where SE is standard error. The boundary between the epithelial cells and the collagen network is around 50 µm from the surface. (c) and (d) A qualitative comparison between the correlation function obtained by the SEM image (c) and ISOCT (d). The 2-D image autocorrelation function (ACF) ±SE from SEM is calculated from different regions on the image with image dimension 5 × 5 µm. The ISOCT index correlation functions were calculated using averaged value of D and Ln from Epi and LP to reconstruct Bn (rd). Epi: epithelium, LP: lamina propria. Adapted with permission from [36].
VIII. Conclusion
Models of light scattering in tissue are important for a number of applications including imaging, therapy, and diagnosis. Many models have been previously used with good success, the most common being the HG phase function. Several groups have shown evidence that tissue is organized in a way that can be described as a mass fractal. A model based on the WM correlation family has the advantage of being flexible and actually includes many previously used models as special cases.
The model is based on the weak scattering approximation (RGD) which allows a the intensity scattering function from random media to be calculated by taking the Fourier transform of refractive index correlation function. This approximation can be made for clouds of particles or continuous random media provided that the scattered field is weak compared to the incident field over paths longer than the distance over which the medium is correlated. Once the refractive index correlation function can be determined independently, models of scattering can be based on a true correlation function for tissue. However, when the function cannot be independently determined, the WM model may provide a good alternative.
Several experimental methods have been developed that employ the WM model to quantify the optical scattering properties. These methods are shown to be sensitive to length scales an order of magnitude smaller than the diffraction limit. While these methods do not resolve length scales on the order of tens of nanometers, they do provide a means to quantify changes that occur in tissue at these lengths scales. This is of particular significance in diagnostic applications. For example, it is well known that morphological changes occur in tissue during carcinogenesis, but mounting evidence shows that these gross changes are presaged by subtle changes in ECM and chromatin organization [8].
Acknowledgment
The authors would like to thank Sam Norris for the SEM image.
This work was supported by the National Institutes of Health under Grant R01CA128641, Grant R01CA155284, and Grant R01EB003682, and the National Science Foundation under Grant CBET-1240416. The work of A. J. Radosevich was supported by a National Science Foundation Graduate Research Fellowship under Grant DGE-0824162.
Biographies

Jeremy D. Rogers received the B.S. degree in physics from Michigan Technological University, Houghton, MI, USA, in 1999, and the M.S. and Ph.D. degrees in optical sciences from the College of Optical Sciences, University of Arizona, Tucson, AZ, USA, in 2003 and 2006, respectively. He completed Postdoctoral training and continued as Research Assistant Professor in biomedical engineering at Northwestern University, Evanston, IL, USA. He is currently an Assistant Professor in biomedical engineering at the University of Wisconsin, Madison, WI, USA. His research interests include theoretical and numerical modeling of light scattering as well as lens design and development of instrumentation for basic research and application to optical metrology of cells and tissue for diagnostics.

Andrew J. Radosevich received the B.S. degree in biomedical engineering from Columbia University, New York, NY, USA, in 2009. He is currently working toward the Ph.D. degree in biomedical engineering at Northwestern University, Evanston, IL, USA. His research interests include the numerical modeling and experimental observation of enhanced backscattering spectroscopy for use in the early diagnosis and treatment of colon and pancreatic cancers. Mr. Radosevich received a three-year National Science Foundation graduate research fellowship in 2011.

Ji Yi received the B.S. degree from Tsinghua University, Beijing, China, in 2005, and the Ph.D. degree from Northwestern University, Evanston, IL, USA, in 2012, both in biomedical engineering. He is currently a joint Postdoctoral Fellow in Hao F. Zhang and Vadim Backman’s laboratory. His research interests include using optical coherence tomography to quantify tissue ultrastructural properties and explore functional contrast from OCT. He is also interested in optical biosensing for tumorous cell detection and ultraresolution multimodal imaging techniques.

Vadim Backman received the Ph.D. degree in medical engineering from Harvard University, Cambridge, MA, USA, and the Massachusetts Institute of Technology, Cambridge, in 2001. He is currently a Professor of biomedical engineering at Northwestern University, Evanston, IL, USA, a Program Leader in cancer bioengineering, nanotechnology, and chemistry at the Robert H. Lurie Comprehensive Cancer Institute, Chicago, IL, and a member of the Professional Staff in the Division of Gastroenterology, NorthShore University Health-Systems, Evanston, IL. He is involved in translational research, which is focused on bridging these technological and biological innovations into clinical practice. His research interests include biomedical optics, spectroscopy, microscopy, development of analytical approaches to describe light transport in biological media, and optical microscopy for nanoscale cell analysis. Dr. Backman has received numerous awards, including being selected as one of the top 100 young innovators in the world by the Technology Review Magazine and the National Science Foundation CAREER Award.
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Jeremy D. Rogers, Email: jdrogers5@wisc.edu, Department of Biomedical Engineering, University of Wisconsin, Madison, WI 53706 USA.
Andrew J. Radosevich, Email: andrewradosevich2014@u.northwestern.edu, Department of Biomedical Engineering, Northwestern University, Evanston, IL 60208 USA.
Ji Yi, Email: ji-yi@u.northwestern.edu, Department of Biomedical Engineering, Northwestern University, Evanston, IL 60208 USA.
Vadim Backman, Email: v-backman@northwestern.edu, Department of Biomedical Engineering, Northwestern University, Evanston, IL 60208 USA.
References
- 1.Huang B, Bates M, Zhuang X. Super-resolution fluorescence microscopy. Annu. Rev. Biochem. 2009;78(1):993–1016. doi: 10.1146/annurev.biochem.77.061906.092014. [Online]. Available: http://www.annualreviews.org/doi/abs/10.1146/annurev.biochem.77.061906.092014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tuchin VV. Optical Clearing of Tissues and Blood. Bellingham, WA, USA: SPIE Press; 2006. [Google Scholar]
- 3.Boas DA, Brooks DH, Miller EL, DiMarzio CA, Kilmer M, Gaudette RJ, Zhang Q. Imaging the body with diffuse optical tomography. IEEE Signal Process. Mag. 2001 Nov;18(6):57–75. [Google Scholar]
- 4.Wilson B, Patterson M, Lilge L. Implicit and explicit dosimetry in photodynamic therapy: A new paradigm. Lasers Med. Sci. 1997;12(3):182–199. doi: 10.1007/BF02765099. [DOI] [PubMed] [Google Scholar]
- 5.Hausman RE, Cooper GM. The Cell: A Molecular Approach. Washington, DC, USA: ASM; 2004. [Google Scholar]
- 6.Schmitt JM, Kumar G. Turbulent nature of refractive-index variations in biological tissue. Opt. Lett. 1996 Aug;21(16):1310–1312. doi: 10.1364/ol.21.001310. [Online]. Available: http://ol.osa.org/abstract.cfm?URI=ol-21-16-1310. [DOI] [PubMed] [Google Scholar]
- 7.Xu M, Alfano RR. Fractal mechanisms of light scattering in biological tissue and cells. Opt. Lett. 2005 Nov;30(22):3051–3053. doi: 10.1364/ol.30.003051. [Online]. Available: http://ol.osa.org/abstract.cfm?URI=ol-30-22-3051. [DOI] [PubMed] [Google Scholar]
- 8.Wax A, Backman V. Biomedical Applications of Light Scattering. New York, NY, USA: McGraw-Hill (McGraw-Hill biophotonics Series); 2009. [Google Scholar]
- 9.Davies H, Wilkins M, Chayen J, La Cour L. The use of the interference microscope to determine drymass in living cells and as a quantitative cytochemical method. Q. J. Microsc. Sci. 1954;3(31):271–304. [Google Scholar]
- 10.Barer R, Tkaczyk S. Refractive index of concentrated protein solutions. Nature. 1954;173:821–822. doi: 10.1038/173821b0. [DOI] [PubMed] [Google Scholar]
- 11.Mourant JR, Freyer JP, Hielscher AH, Eick AA, Shen D, Johnson TM. Mechanisms of light scattering from biological cells relevant to noninvasive optical-tissue diagnostics. Appl. Opt. 1998;37(16):3586–3593. doi: 10.1364/ao.37.003586. [DOI] [PubMed] [Google Scholar]
- 12.Perelman LT, Backman V, Wallace M, Zonios G, Manoharan R, Nusrat A, Shields S, Seiler M, Lima C, Hamano T, Itzkan I, Van Dam J, Crawford JM, Feld MS. Observation of periodic fine structure in reflectance from biological tissue: A new technique for measuring nuclear size distribution. Phys. Rev. Lett. 1998 Jan;80:627–630. [Google Scholar]
- 13.Wax A, Yang C, Backman V, Kalashnikov M, Dasari RR, Feld MS. Determination of particle size by using the angular distribution of backscattered light as measured with low-coherence interferometry. J. Opt. Soc. Amer. A. 2002;19(4):737–744. doi: 10.1364/josaa.19.000737. [DOI] [PubMed] [Google Scholar]
- 14.Mie G. Beiträge zur optik trüber medien, speziell kolloidaler metall ösungen. Annalen der Physik. 1908;330(3):377–445. [Google Scholar]
- 15.Bohren CF, Huffman DR. Absorption and Scattering of Light by Small Particles. New York, NY, USA: Wiley; 1983. [Google Scholar]
- 16.Henyey LG, Greenstein JL. Diffuse radiation in the Galaxy. Astrophys. J. 1941;93:70–83. [Google Scholar]
- 17.Jacques S, Alter C, Prahl S. Angular dependence of HeNe laser light scattering by human dermis. Lasers Life Sci. 1987;1(4):309–333. [Google Scholar]
- 18.Mourant JR, Fuselier T, Boyer J, Johnson TM, Bigio IJ. Predictions and measurements of scattering and absorption over broad wavelength ranges in tissue phantoms. Appl. Opt. 1997;36:949–957. doi: 10.1364/ao.36.000949. [DOI] [PubMed] [Google Scholar]
- 19.Joseph J, Wiscombe W, Weinman J. The Delta-Eddington approximation for radiative flux transfer. J. Atmospher. Sci. 1976;33(12):2452–2459. [Google Scholar]
- 20.Prahl SA. Ph.D. dissertation. Austin, TX, USA: Univ. Texas at Austin; 1988. Light transport in tissue. [Google Scholar]
- 21.Hull EL, Foster TH. Steady-state reflectance spectroscopy in the p3 approximation. J. Opt. Soc. Amer. A. 2001 Mar;18(3):584–599. [Online]. Available: http://josaa.osa.org/abstract.cfm?URI=josaa-18-3-584. [Google Scholar]
- 22.Radosevich AJ, Mutyal NN, Turzhitsky V, Rogers JD, Yi J, Taflove A, Backman V. Measurement of the spatial backscattering impulse-response at short length scales with polarized enhanced backscattering. Opt. Lett. 2011 Dec;36(24):4737–4739. doi: 10.1364/OL.36.004737. [Online]. Available: http://ol.osa.org/abstract.cfm?URI=ol-36-24-4737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Farrell TJ, Patterson MS, Wilson B. A diffusion theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo. Med. Phys. 1992;19:879–888. doi: 10.1118/1.596777. [DOI] [PubMed] [Google Scholar]
- 24.Ishimaru A. Wave Propagation and Scattering in Random Media. Piscataway, NJ, USA: IEEE Press; 1997. [Google Scholar]
- 25.Hulst HC, Van De Hulst H. Light Scattering: By Small Particles. New York, NY, USA: Dovers; 1957. [Google Scholar]
- 26.Born M, Wolf E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. 7th ed. Cambridge, U.K.: Cambridge Univ. Press; 1999. [Google Scholar]
- 27.Ramella-Roman J, Prahl S, Jacques S. Three MonteCarlo programs of polarized light transport into scattering media—Part I. Opt. Exp. 2005;13(12):4420–4438. doi: 10.1364/opex.13.004420. [DOI] [PubMed] [Google Scholar]
- 28.Tuchin V. Handbook of Coherent-Domain Optical Methods: Biomedical Diagnostics, Environmental Monitoring, and Materials Science. New York, NY, USA: Springer-Verlag; 2013. [Google Scholar]
- 29.Ç apoǧlu 00130;Ilker R, Rogers JD, Taflove A, Backman V. Accuracy of the born approximation in calculating the scattering coefficient of biological continuous random media. Opt. Lett. 2009 Sep;37(17):2679–2681. doi: 10.1364/OL.34.002679. [DOI] [PubMed] [Google Scholar]
- 30.Guttorp P, Gneiting T. On the Whittle-Matérn correlation family. NRCSE-TRS. 2005;80 [Google Scholar]
- 31.Rogers J, Çapoǧlu İ, Backman V. Nonscalar elastic light scattering from continuous random media in the Born approximation. Opt. Lett. 2009;34(12):1891–1893. doi: 10.1364/ol.34.001891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sheppard CJR. Fractal model of light scattering in biological tissue and cells. Opt. Lett. 2007;32(2):142–144. doi: 10.1364/ol.32.000142. [DOI] [PubMed] [Google Scholar]
- 33.Hall G, Jacques SL, Eliceiri KW, Campagnola PJ. Goniometric measurements of thick tissue using Monte Carlo simulations to obtain the single scattering anisotropy coefficient. Biomed. Opt. Exp. 2012;3(11):2707–2719. doi: 10.1364/BOE.3.002707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jacques SL, Wang B, Samatham R. Reflectance confocal microscopy of optical phantoms. Biomed. Opt. Exp. 2012;3(6):1162–1172. doi: 10.1364/BOE.3.001162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yi J, Backman V. Imaging a full set of optical scattering properties of biological tissue by inverse spectroscopic optical coherence tomography. Opt. Lett. 2012 Nov;37(21):4443–4445. doi: 10.1364/OL.37.004443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yi J, Radosevich AJ, Rogers JD, Norris SC, Çapoǧlu İlker R, Taflove A, Backman V. Can OCT be sensitive to nanoscale structural alterations in biological tissue? Opt. Exp. 2013 Apr;21(7):9043–9059. doi: 10.1364/OE.21.009043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Radosevich AJ, Yi J, Rogers JD, Backman V. Structural length-scale sensitivities of reflectance measurements in continuous random media under the born approximation. Opt. Lett. 2012 Apr;37(24):5220–5222. doi: 10.1364/OL.37.005220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Radosevich AJ, Rogers JD, Capoǧlu IR, Mutyal NN, Pradhan P, Backman V. Open source software for electric field Monte Carlo simulation of coherent backscattering in biological media containing birefringence. J. Biomed. Opt. 2012;17(11):115 001–115 001. doi: 10.1117/1.JBO.17.11.115001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Vitkin E, Turzhitsky V, Qiu L, Guo L, Itzkan I, Hanlon EB, Perelman LT. Photon diffusion near the point-of-entry in anisotropically scattering turbid media. Nature Commun. 2011;2:587. doi: 10.1038/ncomms1599. p. 587. [DOI] [PMC free article] [PubMed] [Google Scholar]