Meta-analysis of Correlated Traits via Summary Statistics from GWASs with an Application in Hypertension

Abstract

Genome-wide association studies (GWASs) have identified many genetic variants underlying complex traits. Many detected genetic loci harbor variants that associate with multiple—even distinct—traits. Most current analysis approaches focus on single traits, even though the final results from multiple traits are evaluated together. Such approaches miss the opportunity to systemically integrate the phenome-wide data available for genetic association analysis. In this study, we propose a general approach that can integrate association evidence from summary statistics of multiple traits, either correlated, independent, continuous, or binary traits, which might come from the same or different studies. We allow for trait heterogeneity effects. Population structure and cryptic relatedness can also be controlled. Our simulations suggest that the proposed method has improved statistical power over single-trait analysis in most of the cases we studied. We applied our method to the Continental Origins and Genetic Epidemiology Network (COGENT) African ancestry samples for three blood pressure traits and identified four loci (CHIC2, HOXA-EVX1, IGFBP1/IGFBP3, and CDH17; p < 5.0 × 10⁻⁸) associated with hypertension-related traits that were missed by a single-trait analysis in the original report. Six additional loci with suggestive association evidence (p < 5.0 × 10⁻⁷) were also observed, including CACNA1D and WNT3. Our study strongly suggests that analyzing multiple phenotypes can improve statistical power and that such analysis can be executed with the summary statistics from GWASs. Our method also provides a way to study a cross phenotype (CP) association by using summary statistics from GWASs of multiple phenotypes.

Introduction

Genome-wide association studies (GWASs) have been a major design to discover the genetic determinants of complex traits, with thousands of common genetic variants thus uncovered. The identification of genetic variants reveals important biological insights into the genetic architecture of complex traits such as hypertension (MIM 145500), human height (MIM 606255), and blood lipids.^1–3 It is well known that the effect sizes of identified common variants are often small and that a large sample size is necessary to ensure sufficient power to detect such variants. A common strategy is to perform a meta-analysis, combining the effect and variance estimates from as many independent studies as possible with the same or similar phenotypes, which does not require one to pool the individual-level data, thereby reducing the logistical and regulatory burden associated with transferring individual data across centers,⁴ as well as avoiding the need to explicitly model study design differences or manage confounding by genotyping batch effects and trait ascertainment that differentially affect allele frequency estimates across studies. Notably, GWASs are generally performed with single traits (at a univariate level), although multiple related phenotypes are often collected and studied and are expected to reflect common physiological processes. For example, a hypertension study often measures systolic blood pressure (SBP), diastolic blood pressure (DBP), and hypertension status (HTN), and these phenotypes are analyzed separately.^1,5 It has been suggested that univariate analysis could suffer low statistical power compared with multivariate analysis.⁴ Systematic simultaneous analysis of multiple traits could improve the quality of inferences from analysis of outcomes that all relate to the biological construct of interest.

The joint analysis of multiple phenotypes within a cohort has recently become popular for improving statistical power to detect genetic linkage and association. Solovieff et al. provided a detailed summary of such kinds of approaches.⁴ Most multivariate methods are based on a multivariate regression framework and require both genotypes and phenotypes at the individual level, with an assumption of approximately normally distributed phenotypes. Extensions to allow for nonnormally distributed phenotypes and categorical phenotypes have also been developed based on generalized estimating equations (GEEs), ordinal regression, and a Bayesian framework.^6–10 On the other hand, approaches have been developed based on a dimension reduction technique on the phenotypes, such as principal-components (PCs) analysis and canonical correlation analysis.^11,12 However, it has been reported that testing only the top PCs has lower power than the combined-PC approach.¹³

In contrast to multivariate analysis, a method for integrating the results from standard univariate analyses across various phenotypes in GWASs has recently been developed. The Fisher’s combined p value method can be applied to independent studies but is not straightforward when aggregating p values of different but correlated phenotypes within the same cohort, which will result in inflated type I error. The cross-phenotype meta-analysis (CPMA) was developed for testing whether there is association of a SNP to multiple phenotypes, rather than directly evaluating the aggregated association evidence between a SNP and multiple phenotypes.¹⁴ Although the method can be applied to multiple independent studies, it does not allow overlapping or correlated samples among studies. Standard fixed and random effects meta-analysis methods are also used to combine association across multiple phenotypes but are not well suited to situations where a genetic variant has opposite effects on different phenotypes. As an example, psoriasis (MIM 309480) and Crohn disease (CD) have been reported to be positively correlated, with the prevalence of CD in individuals with psoriasis significantly higher than in controls.¹⁵ However, the G allele of SNP rs12720356 in TYK2 (MIM 176941) increases risk for Crohn disease and decreases risk for psoriasis.^16,17 For HTN-related traits, SBP rises linearly with age, in the absence of treatment, whereas DBP has an inverted “U” pattern with a zenith around age 50. Although SBP and DBP are positively correlated, a genetic variant might have opposite effect for the two traits. An extension of fixed effects meta-analysis is the subset-based meta-analysis,¹⁸ which allows opposite effects and is able to test association to a subset of phenotypes. This method exhaustively searches all possible phenotype subsets and identifies the subset of traits with the strongest association, but with the cost of exponentially increased multiple tests. In addition, the method does not allow for heterogeneity across cohorts for the same phenotype. Several methods have also been developed based on a linear combination of the univariate test statistics.^19,20 These methods have been further used to test for association between correlated traits and genetic markers.^21,22 However, the authors focus on only a single study with multiple traits measured in the same individuals. In addition, individual-level genotype and phenotype data are also required for the method by Yang et al.²² The trait-based association test that uses an extended simes (TATES) procedure combines p values obtained in univariate analysis of traits measured in the same individuals while correcting for correlations among phenotypes.²³ This approach can be challenging when combining association evidence across multiple independent studies because the phenotype correlation matrix can change from cohort to cohort. Another approach, the pleiotropy regional identification method (PRIMe),²⁴ evaluates pleiotropic loci in a genomic region with multiple phenotypes based on results of GWASs. This method calculates a pleiotropic index defined by the number of traits with low association p values in a genomic region. The flipping sign test uses p values obtained from individual trait analysis to combine association from multiple correlated traits but requires computationally intensive simulations to obtain combined p values at the genome-wide significance level.⁵

In this study, we propose a general approach that can integrate association evidence from multiple correlated continuous and binary traits from one or multiple studies. We allow for heterogeneity of effects for the same trait in different studies that might result from different populations, environmental exposures, or designs. We also allow heterogeneity effects for different phenotypes, which is not unexpected in practice. In addition, population structure and cryptic relatedness can be controlled. For cryptic relatedness, we also allow for overlapping or related subjects between the different cohorts studied. Although the proposed method is not specifically designed for identifying subsets of associated traits, we will offer insight into how to detect such subsets of traits.

Material and Methods

Assume we have summary statistical results of GWASs from J cohorts with K phenotypic traits. In each cohort, single SNP-trait association was analyzed for each trait separately. Let T_ijk be a summary statistic for the i^th SNP, j^th cohort, and k^th trait. Let T_i = (T_i11,...,T_iJ1,...,T_i1K,...,T_iJK)^T. For simplification, we omit the SNP index. Thus, T = (T₁₁,...,T_J1,...,T_1K,...,T_JK)^T represents a vector of test statistics for testing the association of a SNP with K traits. Let β = (β₁₁,..., β_J1,..., β_1K,..., β_JK)^T be the effect sizes of the SNP. The null hypothesis is H₀: β = 0 and the alternative hypothesis H₁ is that at least one of the elements of β is not equal to zero. We use a Wald test statistic $T_{jk}=\left({\hat{\beta }}_{jk}/{\hat{s}}_{jk}\right)$, where ${\hat{\beta }}_{jk}\text{and}{\hat{s}}_{jk}$ are the estimated coefficient and corresponding standard error for the k^th trait in the j^th cohort. It is reasonable to assume that T follows a multivariate normal distribution with mean 0 and correlation matrix R under the null hypothesis. In practice, R needs to be estimated and we will address that later. A standard method to test β = 0 is the test statistic S_JK = T^TR⁻¹T, which has asymptotically a χ² distribution with J × K degrees of freedom. This test is omnibus with respect to the alternative hypothesis. When heterogeneous effects exist, in particular if a variant contributes to only a subset of traits, this test is less powerful because of the large number of degrees of freedom. When the effect is homogeneous, i.e., the effect sizes are all the same regardless of traits or cohorts, the most powerful test statistic is

$$S_{Hom}=\frac{e^T{\left(RW\right)}^{-1}T{\left(e^T{\left(RW\right)}^{-1}T\right)}^T}{e^T{\left(WRW\right)}^{-1}e},$$ (Equation 1)

which follows a χ² distribution with one degree of freedom, where e^T = (1,...,1) has length J × K and W is a diagonal matrix of weights for the individual test statistics.^19,20 When the statistics in T are mutually independent and W is diagonal with inverses of variances as elements, S_Hom is equivalent to an inverse variance weighted meta-analysis. A similar method to S_Hom has previously been proposed but it is not specifically for combining the effects across multiple traits.²⁴ Equivalently, we can take the sample sizes for the weights, i.e., $w_{jk}=\sqrt{n_j}$ for the sample size n_j of the j^th cohort. Here we assigned more weight to a large study because a large study carries more information than a small study. The advantage of using sample size over inverse variance is that then we do not need to worry about the traits being on different scales, because a variance is dependent on the scale of measurement. In this study we take $w_{jk}=\sqrt{n_j}$.

The homogeneous effect size assumption is unlikely to be true, especially when multiple phenotypes are analyzed together. We introduce a test statistic based on S_Hom, which is more powerful than S_JK for homogenous data, because it has one degree of freedom. Ideally, we would like to have a test statistic that includes only the cohorts and traits with a true contribution to the association of a genetic variant under the alternative hypothesis H₁. The truncated statistic methods for combining statistical evidence have been suggested for such an analysis.^25,26 We adopt a similar idea here. For a given τ > 0, we let T(τ) be the subvector of T satisfying |T_jk| > τ. That is, only the statistics in the vector T with an absolute value larger than τ will be kept. Similarly, we let R(τ) be a submatrix of R representing the correlation matrix and W(τ) to be the diagonal submatrix of W, corresponding to T(τ). To further allow for different effect directions of a variant for different traits in different cohorts, we let $w_{jk}=\sqrt{n_j}\times sign\left(T_{jk}\right)$. Thus, the signed weights will lead to adding evidence to the association, whether or not the effects of a variant are in the same or different directions. Define

$$S\left(\tau \right)=\frac{e^T{\left(R\left(\tau \right)W\left(\tau \right)\right)}^{-1}T\left(\tau \right){\left(e^T{\left(R\left(\tau \right)W\left(\tau \right)\right)}^{-1}T\left(\tau \right)\right)}^T}{e^{T}W{\left(\tau \right)}^{-1}R{\left(\tau \right)}^{-1}W{\left(\tau \right)}^{-1}e}.$$ (Equation 2)

When τ is large, S(τ) can be undefined if |T_jk| ≤ τ for all j and k. In this case we define S(τ) = 0. Our test statistic is then

$$S_{Het}=\underset{\tau >0}{\max }S\left(\tau \right).$$ (Equation 3)

The asymptotic distribution of S_Het does not follow a standard distribution but can be evaluated by simulation (see the section Evaluating the Distribution of S_Het under the Null Hypothesis). We can rank the statistics |T_jk| for all j and k and evaluate S(τ) at these values to obtain ${\max }_{\tau >0}S\left(\tau \right)$. Because S_Het gives more weight to the large trait-cohort specific statistics, it can maintain statistical power when heterogeneity exists.

Estimation of the Correlation Matrix R among Test Statistics

We assume that the traits are quantitative but we can apply the same argument for qualitative traits. Let Y₁ and Y₂ be two trait vectors and G₁ and G₂ be two genotype vectors. Without loss of generality, we assume no covariates. If Y₁ and Y₂ come from the same study cohort, G₁ and G₂ are the same. We assume that linear regressions were applied to evaluate the association evidence between Y₁ and G₁ and between Y₂ and G₂. That is, we have Y₁ = G₁ β₁ + ε₁ and Y₂ = G₂ β₂ + ε₂, where ${\epsilon }_1\sim N\left(0,I{\sigma }_1^2\right)$ and ${\epsilon }_2\sim N\left(0,I{\sigma }_2^2\right)$. Assume least-squares estimates were obtained and let T₁ and T₂ be the corresponding Wald test statistics for testing β₁ = 0 and β₂ = 0, respectively. Then $T_1=G_1^T{Y}_1/\sqrt{G_1^T{G}_1{\sigma }_1^2}$ and $T_2=G_2^T{Y}_2/\sqrt{G_2^T{G}_2{\sigma }_2^2}$. The correlation between T₁ and T₂ is

$$corr\left(T_1,T_2\right)=\frac{G_1^{T}cov\left(Y_1,Y_2\right)G_2}{\sqrt{G_1^T{G}_1{\sigma }_1^2}\sqrt{G_2^T{G}_2{\sigma }_2^2}}.$$ (Equation 4)

If Y₁ and Y₂ are two traits from the same cohort, then we have G₁ = G₂ and cov(Y₁,Y₂) = r₁₂Iσ₁σ₂, where r₁₂ is the correlation between trait 1 and trait 2. We then have

$$corr\left(T_1,T_2\right)=r_{12}.$$ (Equation 5)

If Y₁ and Y₂ are from different cohorts, then a correlation can be induced only by either overlapping samples or related subjects in the two cohorts. In either case, Equation 5 can capture the correlation. We note that Equation 5 does not depend on individual genotypes but only on the correlation between the two traits. Thus, corr(T₁,T₂) can be estimated from the summary statistics for all the independent SNPs in a genome-wide association study. That is,

$$corr\left(T_1,T_2\right)=\frac{{\sum }_i\left(T_{i1}-{\mu }_1\right)\left(T_{i2}-{\mu }_2\right)}{\sqrt{{\sum }_i{\left(T_{i1}-{\mu }_1\right)}^2{\left(T_{i2}-{\mu }_2\right)}^2}},$$ (Equation 6)

where T₁,T₂ are the test statistics for the SNP for traits 1 and 2 in their corresponding cohorts, and μ₁ and μ₂ are their corresponding means. We suggest using independent SNPs across the genome in Equation 6 rather than all the SNPs regardless of the LD among them, which will lead to inflated correlation estimation.²⁷

Evaluating the Distribution of S_Het under the Null Hypothesis

Although S_Hom follows a χ² distribution with one degree of freedom, S_Het does not have a closed form under the null hypothesis because of the data-adaptive approach we are using. However, S_Het can be viewed as the maximum of weighted sum of trait-specific test statistics satisfying different thresholds, which is closely related to a gamma distribution.²⁸ We assume under the null hypothesis that S_Het follows a gamma distribution with a mean shift and we use simulations to estimate this gamma distribution. Under the null, a correlation between two test statistics T₁,T₂ is determined by the trait correlation in Equation 2 and is independent of the SNP. Instead of generating genotype and phenotype data, we can directly simulate the test statistic T from a multivariate normal distribution $N\left(0,\hat{R}\right)$, where $\hat{R}$ is the estimated correlation matrix given by Equation 6. We use the following steps to evaluate the distribution under the null hypothesis:

• (1)Estimate the correlation matrix $\hat{R}$ by Equation 6 with the observed test statistics across the common genome-wide SNPs for all cohorts and traits.
• (2)Generate L random vectors from the multivariate normal distribution $N\left(0,\hat{R}\right)$.
• (3)For the l^th realization in step 2, calculate the test statistic S_Het,l as in Equation 3. The weight matrix in Equation 2 is calculated with the cohort sample sizes.
• (4)Fit S_Het,1, S_Het,2, ...S_Het,L to a gamma distribution gamma(α, β) + c, where α, β are the shape and scale parameters and c is a constant, and we estimate parameters α, β, and c by matching the first three moments to the data. The estimated parameters are represented by $\hat{\alpha }$, $\hat{\beta }$, and $\hat{c}$, respectively.
• (5)For any observed statistic S_Het,o, the p value is calculated by $p=Prob\left(S_{Het,o}-\hat{c}>S_0\right)$, where S₀ is the fractile corresponding a significance level α₀ of the distribution $gamma\left(\hat{\alpha },\hat{\beta }\right)$.

The above procedure is not dependent on the particular SNP and this null distribution $gamma\left(\hat{\alpha },\hat{\beta }\right)$ can be used for testing any SNP association, which drastically reduces the computation time. Notably, we can also directly use simulated S_Het,1, S_Het,2, ...S_Het,L as the distribution under the null hypothesis. However, the computation is still intensive for GWASs because of the need to evaluate test statistics at a significance level of 5 × 10⁻⁸. We therefore suggest the use of the estimated gamma distribution.

Simulations

We conducted simulations to evaluate the type I error and power of the proposed method. Five cohorts with 3,000 individuals each and three blood pressure traits were generated. We allowed a portion of the samples to overlap among the cohorts, which simulated cryptic relatedness between samples from different cohorts. The simulated data mimicked the blood pressure data from the COGENT BP consortium,⁵ which included SBP, DBP, and HTN. The correlations between SBP and DBP was obtained from the CARe data. We first simulated a genotype g_i for the i^th individual with a minor allele frequency being sampled from a uniform distribution between 0.01 and 0.5, with the assumption of Hardy-Weinberg equilibrium.

To simulate the phenotype data, we first generated latent phenotypes by using a linear additive model

$$Y_i^{\text{′}}=\mu +\beta g_i+{\epsilon }_i,$$ (Equation 7)

where $Y_i^{\prime }$, μ, β, and ε_i are column vectors of length 2, representing traits, intercepts, trait-specific effect sizes of a genotype, and random errors. We used parameters estimated from actual African American data. In our simulation, we simulated $Y_i^{\prime }$ consisting of SBP and DBP, with population means 127 and 78, respectively, and ${\epsilon }_i\sim MVN\left(0,\left[\begin{array}{cc}{\sigma }_1^2& \rho {\sigma }_1{\sigma }_2\\ \rho {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\right]\right)$, where we let ${\sigma }_1^2=412$, ${\sigma }_2^2=132$ and ρ is the correlation between SBP and DBP, which we varied. To simulate HTN, we assumed that individuals with either $Y_{i1}^{\prime }$ > 140 or $Y_{i2}^{\prime }$ > 90 have antihypertensive medications. The effects of antihypertensive medications for SBP and DBP followed the normal distributions $N\left(10,{\sigma }_1^2/4\right)$ and $N\left(5,{\sigma }_2^2/4\right)$, respectively. These effects of medications mimic the current GWASs for which ten and five units are often added to SBP and DBP when an individual is on antihypertensive medications.^5,29 The observed phenotype values for SBP and DBP are

$$Y_i=Y_i^{\prime }-{\epsilon }_i^{\prime }\text{when}\text{the}{\mathit{i}}^{\text{th}}\text{individual}\text{is}\text{on}\text{medication},$$ (Equation 8)

$$Y_i=Y_i^{\prime }\text{when}\text{the}{\mathit{i}}^{\text{th}}\text{individual}\text{is}\text{not}\text{on}\text{any}\text{medication},$$

where ${\epsilon }_i^{\prime }\sim MVN\left(\left[\begin{array}{c}10\\ 5\end{array}\right],\left[\begin{array}{cc}{\sigma }_1^2/4& 0\\ 0& {\sigma }_2^2/4\end{array}\right]\right)$. The hypertensive case is defined as either observed SBP > 140 (equivalently Y_i1 > 140), observed DBP > 90 (equivalently Y_i2 > 90), or on antihypertensive medication. Otherwise, a control is defined. The above simulation process was used to generate the data under both the null and alternative hypotheses for five cohorts. For data under the null hypothesis, we simply let β = 0 in Equation 7. For data under the alternative hypothesis, we set the phenotypic variance explained by a variant as 0.3% of total variance and calculated the β value according to the simulated causal variant allele frequency assuming an additive model of inheritance. In the case of heterogeneity across cohorts, we set β with the calculated value in one cohort and 0 in the rest of the cohorts.

Results

We first examined whether the correlation among phenotypes can be well estimated by the corresponding genome-wide test statistics, as represented in Equations 5 and 6. We simulated three correlated traits (SBP, DBP, and HTN) via the method above but with genetic effects β = 0 and ρ = 0.7 for 3,000 subjects. We also simulated 100,000 independent SNPs for each individual with minor allele frequencies being sampled from a uniform distribution between 0.01 and 0.5, with the assumption of Hardy-Weinberg equilibrium. We performed association tests for all the SNPs with the software Plink.³⁰ Table 1 shows the estimated correlation among the three traits using trait values and the estimated correlation matrix based on the test statistics of 100,000 SNPs. We observed that the trait correlations can be approximated through the calculation of correlations of test statistics of SNPs corresponding to traits (Table 1).

Table 1.

Comparison of Trait Correlations Used for Simulation and Estimated by Test Statistics from SNPs of GWASs

	SBP	DBP	HTN
SBP	–	0.76	0.73
DBP	0.69	–	0.70
HTN	0.66	0.60	–

Values above diagonal are generating correlation coefficients, and under diagonal are estimated based on the test statistics of 100,000 SNPs.

We next examined the type I error of statistics S_Hom and S_Het under three scenarios: (1) ρ = 0, (2) ρ = 0.25, and (3) ρ = 0.5. For each scenario, we simulated 5 independent cohorts each with 3,000 subjects, 100,000 SNPs, and three traits (SBP, DBP, and HTN) under the null hypothesis of no genetic contribution to any of the three traits. We performed the association tests for all the SNPs with the software Plink³⁰ to obtain the test statistics in each cohort separately. We next calculated S_Het for all the 100,000 SNPs and estimated the parameters α, β, and c for the shifted gamma distribution by matching the first three moments. Figure 1 depicts the empirical distributions of $S_{Het}-\hat{c}$ under the three scenarios when no overlapping subjects were generated between the five cohorts. We observed that the estimated $gamma\left(\hat{\alpha },\hat{\beta }\right)$ fits the empirical distribution of $S_{Het}-\hat{c}$ well (Figure 1). In particular, we did not observe a departure in the tail of the gamma distribution. We observed similar results when there were 500 overlapping subjects among the five simulated cohorts (Figure 2). We next used these estimated gamma distribution parameters to evaluate the type I error rates correspondingly.

Figure 1.

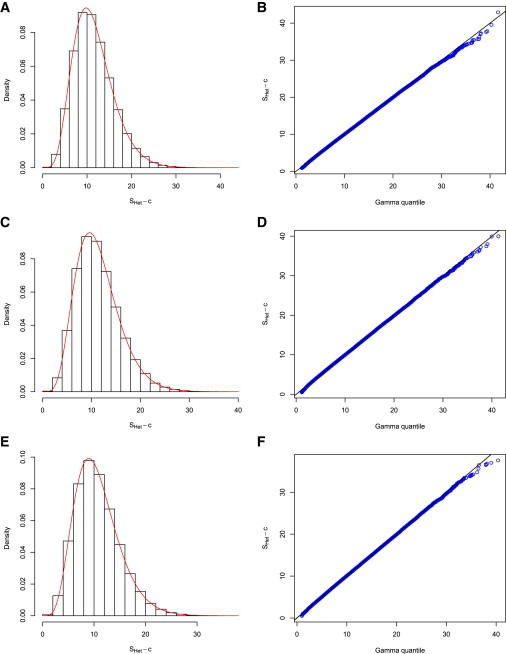
S_Het Distribution

Distribution of the test statistic S_Het under three scenarios: trait correlation is 0 (A and B), trait correlation is 0.25 (C and D), and trait correlation is 0.5 (E and F). We generated 5 cohorts, each with sample size 3,000, with no overlapping samples between cohorts. Left panel is the histogram of S_Het based on 100,000 replications and the red curve represents the theoretical distribution gamma(α,β), where α,β are the shape and scale parameters that were estimated by matching the first two moments. Right panel is a QQ plot of S_Het.

Figure 2.

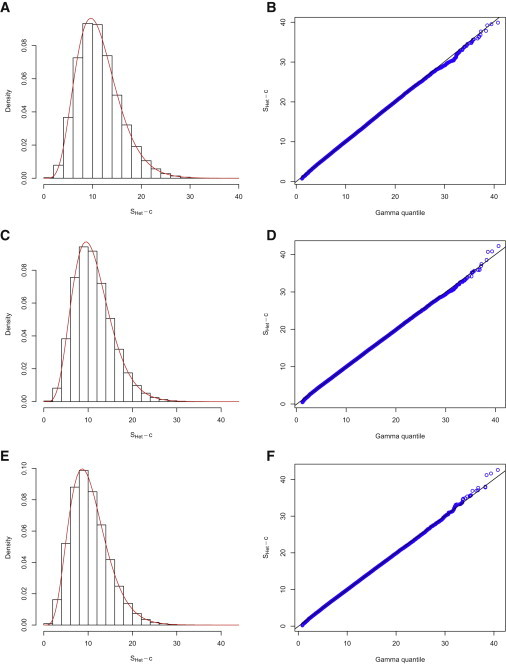
S_Het Distribution when Cohorts Have Overlapping Subjects

Distribution of the test statistic S_Het under three scenarios as in Figure 1. We generated 5 cohorts, each with sample size 3,000; 500 subjects were overlapping between cohorts. Left and right panels are as in Figure 1.

Under each of six scenarios (ρ = (0, 0.25, 0.5) × (nonoverlapping, overlapping sample)), we repeated the above process 100 times, which led to 10⁷ S_Hom and S_Het statistics. We calculated p values of S_Hom statistics by ${\chi }_1^2$ and S_Het statistics by using the shift gamma distribution with previous estimated corresponding parameters, respectively. We then calculated the type I error rates by evaluating the proportion of the p values less than a significance level. Table 2 presents the type I error rates at different significance levels. We observed that the type I error rates were well controlled for S_Hom. For S_Het, type I error rates were slightly inflated when significance levels were less than 10⁻⁵. Thus, the proposed S_Het test statistics can be fitted reasonably well by an estimated shift gamma distribution under the null hypothesis. Because the distribution of S_Het under the null hypothesis depends only on the correlation matrix among traits and number of cohorts and does not depend on a SNP, we can estimate the gamma (α, β) + c that can be used for testing any SNP. This method is computationally feasible. We also observed that the type I error can be well controlled for S_Hom, which follows ${\chi }_1^2$ under the null hypothesis. The well-controlled type I error rates for both S_Hom and S_Het regardless of nonoverlapping or overlapping samples among cohorts indicates that correlations estimated by Equation 6 are well enough for approximating the induced correlations among the summary statistics by overlapped samples.

Table 2.

Type I Error Rates for S_Hom and S_Het

ρ	No. of Overlapped Samples	Significance Level
		0.05	10−2	10−3	10−4	10−5	10−6	10−7
SHom
0.00	0	5.03 × 10−2	9.99 × 10−3	9.96 × 10−4	9.74 × 10−5	1.00 × 10−5	8.00 × 10−7	3.00 × 10−7
	500	4.76 × 10−2	9.18 × 10−3	9.02 × 10−4	9.05 × 10−5	6.50 × 10−6	8.00 × 10−7	2.00 × 10−7
0.25	0	5.04 × 10−2	1.02 × 10−2	1.03 × 10−3	1.07 × 10−4	1.12 × 10−5	7.00 × 10−7	0.00 × 100
	500	4.94 × 10−2	9.81 × 10−3	9.52 × 10−4	9.57 × 10−5	9.50 × 10−6	7.00 × 10−7	1.00 × 10−7
0.50	0	5.06 × 10−2	1.02 × 10−2	1.03 × 10−3	1.06 × 10−4	1.23 × 10−5	1.10 × 10−6	0.00 × 100
	500	4.74 × 10−2	9.21 × 10−3	8.65 × 10−4	7.97 × 10−5	7.30 × 10−6	7.00 × 10−7	2.00 × 10−7
SHet
0.00	0	4.99 × 10−2	1.00 × 10−2	1.03 × 10−3	1.10 × 10−4	1.17 × 10−5	2.00 × 10−6	1.00 × 10−7
	500	4.99 × 10−2	1.00 × 10−2	1.01 × 10−3	1.06 × 10−4	1.30 × 10−5	1.70 × 10−6	1.00 × 10−7
0.25	0	4.98 × 10−2	9.98 × 10−3	1.04 × 10−3	1.11 × 10−4	1.25 × 10−5	1.10 × 10−6	2.00 × 10−7
	500	4.98 × 10−2	1.00 × 10−2	1.02 × 10−3	1.11 × 10−4	1.28 × 10−5	8.00 × 10−7	0.00 × 100
0.50	0	4.99 × 10−2	1.01 × 10−2	1.05 × 10−3	1.10 × 10−4	1.23 × 10−5	1.30 × 10−6	1.00 × 10−7
	500	4.99 × 10−2	1.01 × 10−2	1.05 × 10−3	1.15 × 10−4	1.26 × 10−5	1.30 × 10−6	2.00 × 10−7

Type I error rate was calculated from the asymptotic χ² distribution with 1 d.f. for S_Hom, and the shift gamma distribution parameters were estimated by matching the first three moments for S_Het. We simulated ten million replications for each scenario.

Power

We evaluated the power of the statistics S_Hom and S_Het by simulating three traits, SBP, DBP, and HTN. To simulate the three traits, a SNP was simulated and its genetic effect was added correspondingly. For illustration, we simulated two scenarios: ρ = 0 and ρ = 0.5. In both scenarios, HTN is always correlated with SBP and DBP because of the way the data were simulated. In each scenario, we generated 5 cohorts, each with a sample size of 3,000 subjects. We allowed different genetic contributions to the traits: a genetic variant contributes to a trait in only one of five cohorts (heterogeneity across cohorts within the same trait) or in all five cohorts (no heterogeneity within a trait), and a genetic variant affects SBP only (heterogeneity between traits) or affects both SBP and DBP. After both genotypes and phenotypes were simulated, we perform association tests for all SNPs with the software Plink and calculated S_Hom and S_Het. We calculated the p values for S_Hom by a ${\chi }_1^2$ and with the previous estimated shift gamma distribution for S_Het, respectively. Power was defined as the proportion of test statistics with p values less than a corresponding significance level. We also examined the power when there were 500 overlapping subjects between cohorts. We analyzed the power of S_Hom for SBP, DBP, and HTN, separately as well as combined, and this is denoted as S_Hom−SBP, S_Hom−DBP, S_Hom−HT, and S_Hom, respectively. Power analysis was calculated based on 1,000 replications.

We first examined the power when SBP and DBP were simulated independently. Figure 3 shows the power when a genetic variant contributes to only one of the five cohorts, which represents heterogeneity across cohorts for the same trait. When a genetic variant contributes only to SBP, S_Het has the best power, followed by S_Hom−SBP, S_Hom, and S_Hom−HT (Figure 3A). S_Hom−DBP did not have power because there was no genetic contribution to DBP. This result suggests that the proposed statistic S_Het is able to capture association evidence even when the data include noise because of heterogeneity among traits and cohorts. S_Hom−SBP has more power than S_Hom, which is not surprising because S_Hom included DBP, which had no genetic contribution. The overlap of subjects across the five cohorts is equivalent to reducing the number of subjects who did not have a genetic contribution from SBP. It is thus not surprising that S_Hom−SBP had the most power in this situation (Figure 3B). When a genetic variant contributes to both SBP and DBP in one cohort with the effect sizes in the same direction, the combined trait analyses by S_Hom and S_Het had much improved power although S_Het still had the greatest power (Figure 3C). The power for S_Hom was further improved when there were overlapping samples between studies (Figure 3D), which could be attributed to reduced heterogeneity across cohorts. When a genetic variant contributed to both SBP and DBP in one cohort but with the effects in opposite directions, S_Het still maintained power, whereas S_Hom had almost no power because of the cancellation of the SBP and DBP contributions whether or not there were overlapping samples among cohorts (Figures 3E and 3F).

Figure 3.

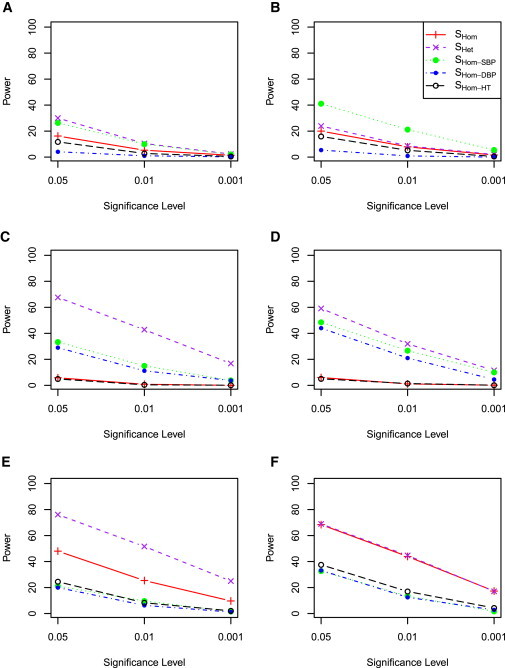
Power Comparison of S_Hom and S_Het when One Cohort Has Genetic Contribution

SBP and DBP were simulated independently. HTN was simulated according to SBP and DBP and simulated medication status. Five cohorts were simulated, but only one of the five cohorts has a genetic contribution. Left: No overlapping samples among the five cohorts. Right: 500 samples were the same in each cohort and a genetic variant contributes phenotypic variation for the same samples.

(A and B) A genetic variant affects only SBP.

(C and D) A genetic variant affects both SBP and DBP but with opposite effect directions.

(E and F) A genetic variant affects both SBP and DBP with the same effect direction.

Figure 4 shows the power when a genetic variant contributes to all five cohorts, which represents no heterogeneity across cohorts for the same trait. When a genetic variant contributed only to SBP, S_Hom−SBP had the most power, regardless of whether there were overlapping samples or not between cohorts (Figures 4A and 4B). The power of S_Hom and S_Het were comparable, with S_Het outperforming S_Hom for no overlapping samples between cohorts. When a genetic variant contributed to both SBP and DBP and the effects were in the same direction (no trait or cohort heterogeneity), S_Het performed similarly to S_Hom (Figures 4C and 4D). However, S_Hom had no power although S_Het maintained power when the genetic effects were in opposite directions (Figures 4E and 4F).

Figure 4.

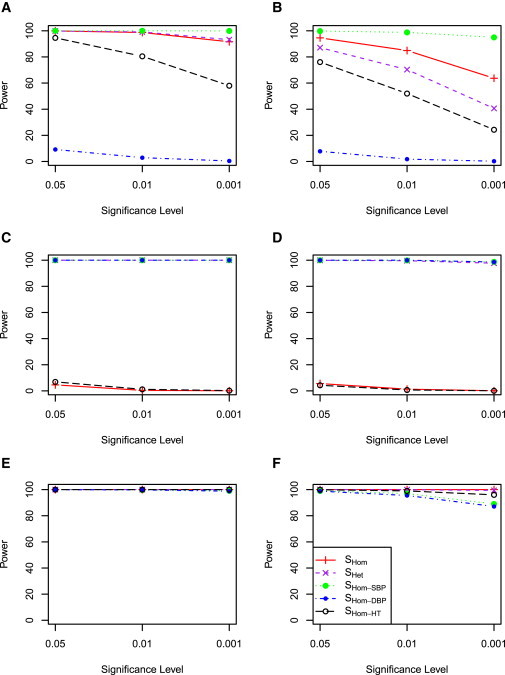
Power Comparison of S_Hom and S_Het when Five Cohorts Have Genetic Contribution

Five cohorts were simulated and the genetic variant has contribution in all five cohorts. Details as in Figure 3.

The results were similar when SBP and DBP were highly correlated (correlation coefficient = 0.5). That is, S_Het usually outperformed or performed equivalently well as the other test statistics when heterogeneity due to cohorts or traits were present in our simulated data (Figures 5 and 6). Interestingly, S_Het improved power substantially when a genetic variant contributed to SBP and DBP in opposite directions but SBP and DBP were positively correlated, compared with no correlation (Figures 3E and 3F versus Figures 5E and 5F). Intuitively, if two traits are highly positively correlated, we are less likely to observe the estimated effects for a variant in opposite directions under the null hypothesis. The same is true if two traits are highly negatively correlated, wherein we will less likely observe the estimated effects for a variant in the same directions under the null hypothesis. The test statistic S_Het apparently captures this information whereas S_Hom does not.

Figure 5.

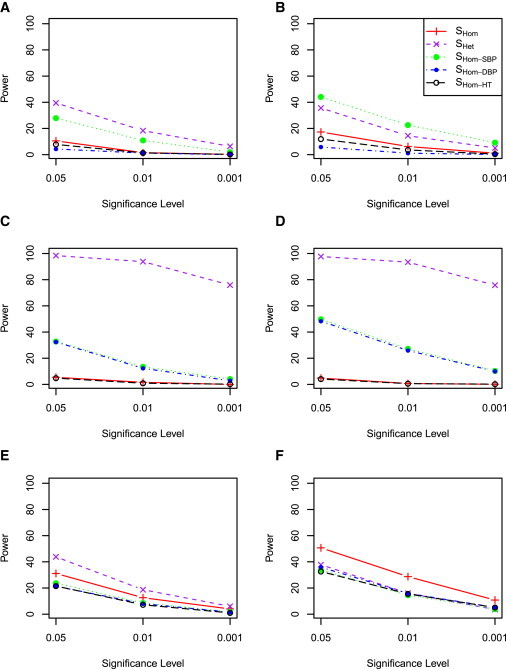
Power Comparison of S_Hom and S_Het with Correlation 0.5 when One Cohort Has Genetic Contribution

SBP and DBP were simulated with correlation 0.5. Five cohorts were simulated but only one of the five cohorts has a genetic contribution. Details as in Figure 3.

Figure 6.

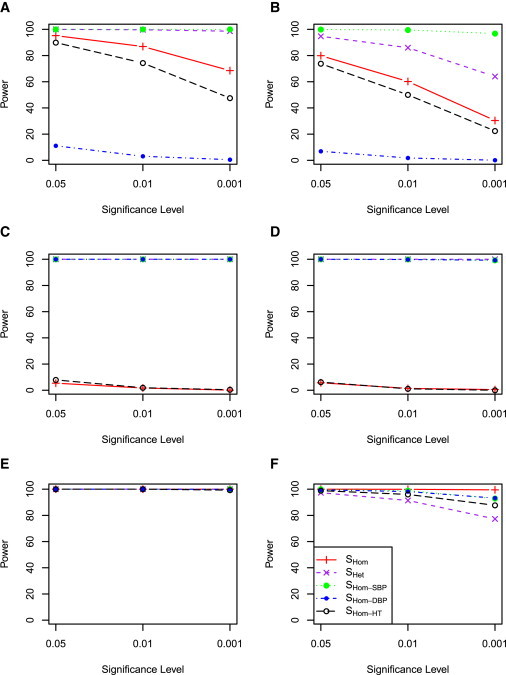
Power Comparison of S_Hom and S_Het with Correlation 0.5 when Five Cohorts Have Genetic Contribution

SBP and DBP were simulated with correlation 0.5. Five cohorts were simulated and the genetic variant has a contribution in all five cohorts. Details as in Figure 3.

Application to the BP GWAS Data from the Continental Origins and Genetic Epidemiology Network

We applied S_Het and S_Hom to the BP data from COGENT BP, which consists of 19 African ancestry cohorts, as detailed in Franceschini et al.⁵ In brief, the COGENT study includes 29,378 subjects, 20 years or older, from 18 U.S. African American cohorts and one cohort from Yoruba, Nigeria. The African American cohorts include Biological bank of Vanderbilt University (BioVU), Atherosclerosis Risk In Communities (ARIC), Coronary Artery Risk Development in Young Adults (CARDIA), Cleveland Family Study (CFS), Jackson Heart Study (JHS), Multi-Ethnic Study of Atherosclerosis (MESA), Cardiovascular Health Study (CHS), Genetic Study of Atherosclerosis Risk (GeneSTAR), Genetic Epidemiology Network of Arteriopathy (GENOA), Healthy Aging in Neighborhoods of Diversity Across the Life Span Study (HANDLS), Health, Aging, and Body Composition (Health ABC) Study, the Hypertension Genetic Epidemiology Network (HyperGEN), the Mount Sinai study (New York City, NY, USA), the Women’s Health Initiative SNP Health Association Resource (WHI-SHARe), the Howard University Family Study (HUFS), the Bogalusa Heart Study (Bogalusa), the Sea Islands Genetic NETwork (SIGNET) and REGARDs, and the Loyola Maywood study (Maywood). Each study received IRB approval of its consent procedures, examination and surveillance components, data security measures, and DNA collection and its use for genetic research. All participants in each study gave written informed consent for participation in the study and to conduct genetic research. Genotyping for the 19 cohorts was performed with either Affymetrix or the Illumina whole-genome SNP genotyping arrays. Quality control of genotyping data and imputation were performed in each cohort separately. Uniform protocols for analysis were conducted by each study. The summary statistics from the GWASs, including the SNP estimated effect sizes and their corresponding standard errors for SBP, DBP, and HTN, were collected for meta-analysis.⁵ In this analysis, we applied S_Het and S_Hom to these summary statistics. Because we observed many unexpected large estimated effect sizes for the HTN analysis in SIGNET, we excluded the HTN results of SIGNET. Thus, our analysis included 56 trait-specific results from GWASs.

We obtained the inverse variance weighted meta-analysis results with the software METAL³¹ for SBP, DBP, and HTN from the original report,⁵ where SNP rs11041530 at CYB5R2 (MIM 608342) is the only variant reaching genome-wide significance (SBP, p = 4.0 × 10⁻⁸). We calculated the proposed statistics S_Het and S_Hom for each SNP and the corresponding p values with a gamma distribution for combining SBP, DBP, and HTN. Figure 7 presents the QQ plots and Manhattan plots of S_Het and S_Hom. The genomic control (GC) inflation factors are 1.08 and 1.05 for S_Het and S_Hom, respectively. A possible reason for the slightly inflated GC factors could be that the hypertension traits are polygenic with a large number of genetic variants of small effect sizes contributing to the phenotypic variation. Combining SBP, DBP, and HTN would further aggregate these variants. S_Hom detected the HOXA-EVX1 (MIM 142996) locus on chromosome 7 at a genome-wide significance level (Table 3 and Figure 7, p = 2.35 × 10⁻⁹). This locus was also reported in the original study and was replicated in Asian and European populations, although SBP, DBP, or HTN trait-specific meta-analyses did not reach genome-wide significance in the discovery phase.⁵ In comparison, S_Het was able to detect four loci at genome-wide significance level (p < 5.0 × 10⁻⁸), including HOXA-EVX1 on chromosome 7, CHIC2 (MIM 604332) on chromosome 4, IGFBP1-IGFBP3 (MIM 146730, 146732) on chromosome 7, and CDH17 (MIM 603017) on chromosome 8 (Table 3 and Figure 7). The regional plots for these four loci are presented in Figure 8. Figure S1 (available online) shows forest plots of the cohort-specific effect sizes of SBP, DBP, and HTN for these four loci. Note that these loci have opposite directions in SBP and DBP meta-analysis except HOXA-EVX1 (Table 3), suggesting that the same genetic variant increases SBP but decreases DBP level (i.e., increases pulse pressure) or vice versa. Interestingly, CHIC2 has been reported to be associated with pulse pressure by large GWASs in a European population.³² The most significant variant, rs11725861 in CHIC2, is located 3 kb away from the sentinel SNP rs871606 reported in Wain et al.,³² and these two SNPs are in strong linkage disequilibrium in HapMap CEU data (r² = 0.35, D’ = 1). Because pulse pressure is defined as the difference between SBP and DBP, the opposite effect sizes of SBP and DBP in this study are thus consistent with the reported association evidence with pulse pressure in European population. The IGF system is implicated in the development of cardiovascular disease. Low circulating levels of IGFBP1 have been reported to be associated with the presence of macrovascular disease and hypertension in type 2 diabetes,^33,34 although there is no direct report of association evidence between the variants at IGFBP1 and blood pressure. However, a recent meta-analysis of European cohorts identified IGFBP3 as being associated with long-term averaging of pulse blood pressure.³⁵ The most significant variant, rs11977526 near IGFBP3, is located 43 kb away from the sentinel SNP rs2949837 reported in Ganesh et al.³⁵ and these two SNPs are in strong linkage disequilibrium in HapMap CEU data (r² = 0.66, D’ = 0.94). There has been no association reported between CDH17 on chromosome 8q21 and blood pressure, although linkage evidence was reported for this locus to essential hypertension in European population.³⁶

Figure 7.

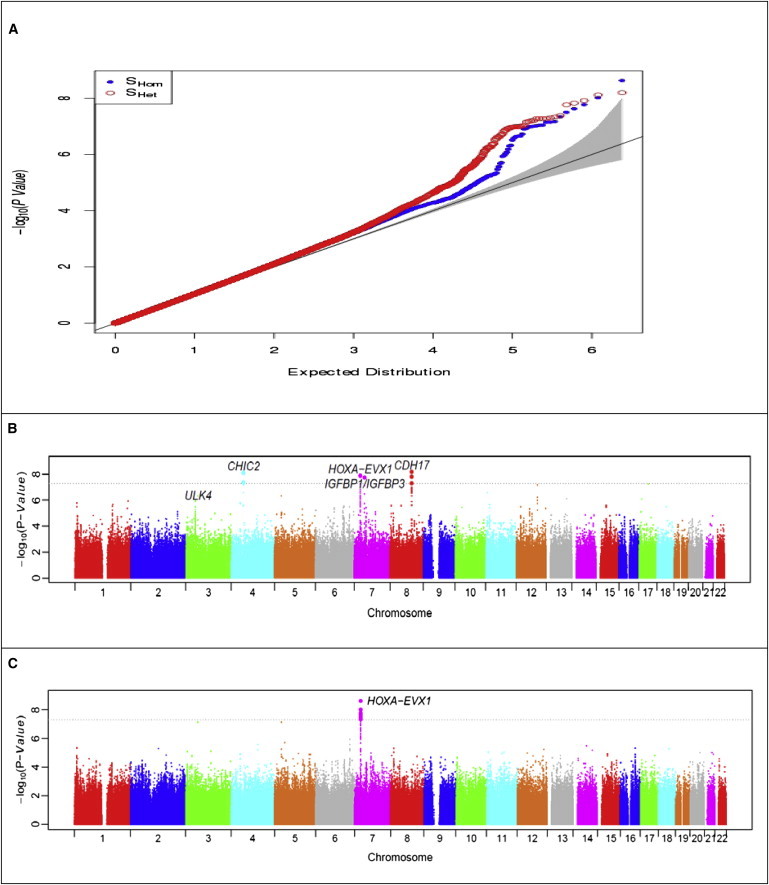
QQ Plots and Manhattan Plots after Combining SBP, DBP, and HTN via S_Hom and S_Het for the COGENT BP GWAS Data

Shown are QQ plots (A), Manhattan plot of S_Het (B), and Manhattan plot of S_Hom (C).

Table 3.

The Top Genetic Variants Identified by S_Het and S_Hom in the COGENT BP Consortium by First Performing Meta-analysis and then S_Het and S_Hom

Chr	SNP	POS	Genes	Effect Allele	Freq	Meta-analysis HTN			Meta-analysis SBP			Meta-analysis DBP			SHom	SHet
						beta	SE	p	beta	SE	p	beta	SE	p	p	p
Loci Reaching Genome-wide Significance
4	rs11725861	54497062	CHIC2	A	0.84	0.04	0.03	2.16 × 10−1	0.79	0.22	2.89 × 10−4	−0.18	0.13	1.63 × 10−1	2.56 × 10−1	8.45 × 10−9
7	rs11564022	27303571	HOXA-EVX1	T	0.23	−0.12	0.02	2.16 × 10−6	−0.89	0.19	1.83 × 10−6	−0.60	0.11	7.66 × 10−8	2.35 × 10−9	1.34 × 10−8
7	rs11977526	45974635	IGFBP1, IGFBP3	A	0.32	−0.01	0.02	5.30 × 10−1	−0.37	0.18	3.73 × 10−2	0.30	0.11	4.62 × 10−3	8.21 × 10−1	1.87 × 10−8
8	rs2446849	95172673	CDH17	T	0.80	−0.06	0.03	3.00 × 10−2	−0.63	0.20	2.00 × 10−3	0.22	0.12	6.75 × 10−2	2.11 × 10−1	7.01 × 10−9
Loci Reaching Suggestive Significance
3	rs10049492	53571572	CACNA1D	A	0.74	0.12	0.03	1.42 × 10−5	0.85	0.19	1.74 × 10−5	0.57	0.12	1.77 × 10−6	7.11 × 10−8	4.60 × 10−7
5	rs6886515	30702383	none	A	0.61	0.11	0.02	4.61 × 10−7	0.71	0.17	2.46 × 10−5	0.40	0.10	6.02 × 10−5	7.15 × 10−8	4.63 × 10−7
6	rs9401512	122707473	HSF2/PKIB	T	0.30	0.00	0.02	9.17 × 10−1	0.44	0.17	1.04 × 10−2	−0.23	0.10	2.75 × 10−2	9.43 × 10−1	5.75 × 10−8
11	rs11041530	7658079	CYB5R2	C	0.12	−0.09	0.03	9.83 × 10−3	−1.35	0.25	4.04 × 10−8	−0.54	0.15	2.65 × 10−4	9.08 × 10−6	2.55 × 10−7
12	rs11837544	93192534	PLXNC1	A	0.20	−0.01	0.03	5.89 × 10−1	−0.50	0.20	1.36 × 10−2	0.27	0.12	2.28 × 10−2	9.37 × 10−1	6.89 × 10−8
17	rs430685	42214309	GOSR2/WNT3	T	0.02	−0.42	0.14	2.65 × 10−3	1.26	0.84	1.33 × 10−1	1.51	0.50	2.64 × 10−3	8.07 × 10−1	5.77 × 10−8

Figure 8.

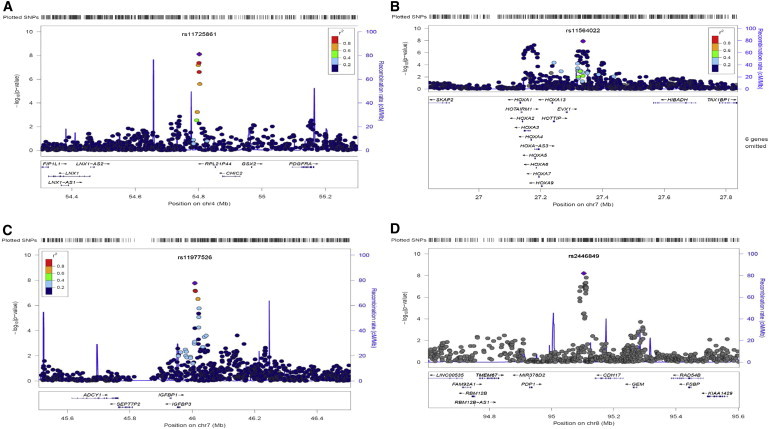
Regional Association Plots

Regional association plots of the four SNPs reaching genome-wide significance (p < 5 × 10⁻⁸) by S_Het for the COGENT BP GWAS data. The most significant SNP at each locus is shown in purple. The fine-scale recombination rate is shown as a blue vertical line. Gene positions are shown at the bottom.

Six additional loci were also identified by S_Het with suggestive evidence (p < 5 × 10⁻⁷, Table 3). The mutations in CACNA1D (MIM 114206), encoding Cav1.3, were reported to regulate Na⁺, K⁺, and Ca²⁺ and to underlie a common subtype of adrenal hypertension.³⁷ The SNP rs6886515 on chromosome 5 is located in an intergenic region. SNP rs9401512 is in HSF2/PKIB (MIM 140581, 606914) on chromosome 6 and has not been reported to be associated with hypertension-related traits. However, this region has been reported to harbor BP variants in admixture mapping analyses.^38,39 SNP rs11041530 in CYB5R2 was reported in the original study but was not significant in a replication analysis.⁵ We have not seen any report of PLXNC1 (MIM 604259) and hypertension. SNP rs430685 locates in WNT3 (MIM 165330) on chromosome 17 and this locus is close to the locus GOSR2 (MIM 604027) reported in Ehret et al.¹ SNP rs430685 is 153 kb away from the sentinel SNP rs17608766 reported in Ehret et al.¹ with D’ of 1.0 but r² value of 0.003 between these two SNPs in HapMap CEU data, indicating that these two signals might be different. WNT3 belongs to the Wnt/frizzled receptor signaling pathway, which has been suggested to have an important functional role in cardiovascular and renal disorders.⁴⁰

Discussion

The observations from GWASs suggest that many genetic variants are associated with multiple correlated or even distinct traits, and such associations have been termed cross-phenotype (CP) associations,⁴ which is relevant to pleiotropy in complex disease. We proposed a statistic S_Het and compared it with S_Hom, and both methods can integrate association evidence of multiple continuous and binary traits from multiple GWASs and thus detect CP associations. Both methods need only the summary statistics obtained from GWASs. S_Hom is an extension of the linear combination of the univariate test statistics^19,20 but allows for sample size as weights. S_Het is a further extension of S_Hom allowing for heterogeneous effects of a trait from different studies, which could be due to different designs, environmental factors, or populations, as well as heterogeneity effects for different phenotypes, which are not unexpected in practice. Under the null hypothesis, S_Hom is asymptotically distributed as chi-square with 1 degree of freedom, although the asymptotical distribution of S_Het is less clear but related to a gamma distribution.²⁸ Our simulations indeed suggest that S_Het can be well approximated by a shift gamma distribution with parameters that can be estimated from the data.

The simulations indicated that the type I error rate is reasonably controlled for both methods (Table 2 and Figures 1 and 2). The estimated gamma distributions well fitted the corresponding empirical distributions as observed from both histograms and the Q-Q plots of S_Het (Figures 1 and 2). When we applied both methods to the data from COGENT BP African ancestry GWASs for blood pressure traits, we did not observe any substantial inflation of the type I error rate (Figure 7), further indicating that both methods are valid.

Our simulations suggest that when heterogeneity is of less concern, S_Hom is more powerful than S_Het. In contrast, when heterogeneity is present, S_Het is more powerful than S_Hom. This property can also be observed from the application of both statistics to the data from COGENT BP African ancestry GWASs for blood pressure traits. S_Hom was able to detect the HOXA-EVX1 locus (p = 2.35 × 10⁻⁹) whereas S_Het identified four loci (CHIC2, HOXA-EVX1, IGFBP1/IGFBP3, and CDH17; p < 5.0 × 10⁻⁸) at a genome-wide significance level. All four loci were missed by single-trait analysis at genome-wide significance level (p < 5.0 × 10⁻⁸) and only the HOXA-EVX1 locus was identified by the flipping sign test in the original report,⁵ suggesting that S_Het is more powerful than combined p values methods when heterogeneity is present. The flipping sign test is similar to Fisher’s method for combining the p values for different traits but requires a large number of simulations to estimate the null distribution to account for the trait correlations. Thus the flipping sign test is similar to S_Hom but S_Hom is more flexible and requires substantially less computational time because of using the estimated asymptotic distribution. The HTN-, SBP-, and DBP-specific meta-analysis of the HOXA-EVX1 locus did not show any heterogeneity (Table 3), which is the reason that this locus was detected by S_Hom. As suggested by our simulations, S_Het is more applicable to heterogeneous data and was able to identify three additional loci, CHIC2, IGFBP1/IGFBP3, and CDH17. This is also consistent with the fact that the effect sizes estimated in the SBP- and DBP-specific meta-analyses were in opposite directions for all three of these loci (Table 3). In addition, S_Het was able to identify six loci with suggestive association evidence for hypertension-related traits. Among the identified loci, CHIC2, HOXA-EVX1, IGFBP1/IGFBP3, CACNA1D, and GOSR2/WNT3 have been confirmed to be associated with hypertension-related traits,^5,32–35 suggesting that our methods powerfully identify true signals.

Compared with existing methods, S_Hom and S_Het have multiple advantages for identifying cross-phenotype (CP) associations. Both methods are able to combine traits measured on different scales, including continuous and binary traits. Further, S_Het allows for heterogeneous effects. Both methods are able to accommodate overlapping or related subjects within and among different studies or cohorts, as our simulations suggested. We assumed that the trait-specific summary statistics have already well accounted for the confounding effect caused by either population structure or cryptic relatedness within a cohort. Since our approach accounts for correlations of test statistics among traits or cohorts, S_Hom and S_Het are able to control the effect of cryptic relatedness occurring among cohorts, as observed in the simulations when overlapping samples were simulated among cohorts (Figures 3, 4, 5, and 6). S_Hom and S_Het are in principal able to control the effect of population structure occurring between cohorts, although this property of the methods has not been formally evaluated in our simulation studies.

In contrast, a fixed or random effect meta-analysis is able to combine results from multiple studies but is limited to the same traits and no overlapping or related subjects across studies. The cross-phenotype meta-analysis¹⁴ is able to test CP association but cannot be applied when there are overlapping subjects. The linear combination of univariate test statistics applies only to a single study with multiple traits and requires individual-level genotype and phenotype data.^17,18 The TATES requires only p values, not the individual-level genotype and phenotype data, but cannot be applied to multiple studies.²³ The scaled marginal model proposed by Schifano et al.⁴¹ requires individual-level genotype and phenotype data. Thus, S_Hom and S_Het are quite general and can be applied to a wide range of data and study designs, and they require only that estimates exist for a given SNP.

In contrast to the subset-based meta-analysis,¹⁸ S_Hom and S_Het do not specifically identify a subset of associated traits. However, trait-specific meta-analysis results can be examined after a SNP is identified by S_Het, which will allow one to see whether the association evidence from S_Het is contributed by only a subset of the traits. When maximizing the statistic in Equation 3, we can record which trait or cohort contributed to the final statistic. The current S_Hom and S_Het test CP associations for only one SNP. Huang et al.²⁴ developed an interesting method, PRIMe, which can test a pleiotropic effect for multiple variants in a genomic region. It should not be difficult to extend S_Hom and S_Het to test for multiple variants in a genomic region by using a similar idea as the PRIMe uses, although further studies are warranted to investigate this.

Our proposed statistics S_Hom and S_Het use the summary statistics to estimate the correlation coefficients among traits and cohorts. If trait correlations are known, S_Hom and S_Het can also be applied by supplying the correlation matrix in Equation 3 without using genome-wide summary statistics. There are advantages to using summary statistics instead of individual-level data. First, as pointed out by Lin and Zeng,⁴² there is no asymptotic efficiency gain by analyzing individual-level data compared with meta-analysis when the parameter of interest has a common value across studies, although this aspect of performance is less clear when heterogeneity is present. Second, in practice it is easier and more feasible to obtain summary statistics than individual-level data. Finally, study-specific analysis is better to control the confounding within different study designs by environmental factors and between study designs by batch effects across experiments than pooling all data.

In summary, the proposed general statistics S_Hom and S_Het are useful for detecting CP associations. In particular, S_Het is better for analyzing multiple different phenotypes because heterogeneity occurs frequently. These methods could easily be deployed in existing consortia collections of association study metadata to improve the chances of novel discoveries and provide more return from those investments, as we have demonstrated in the COGENT consortium. The software of S_Hom and S_Het can be freely downloaded from the author’s website.

Consortia

The members of the COGENT BP Consortium are Nora Franceschini, Ervin Fox, Zhaogong Zhang, Todd L. Edwards, Michael A. Nalls, Yun Ju Sung, Bamidele O. Tayo, Yan V. Sun, Omri Gottesman, Adebawole Adeyemo, Andrew D. Johnson, J. Hunter Young, Ken Rice, Qing Duan, Fang Chen, Yun Li, Hua Tang, Myriam Fornage, Keith L. Keene, Jeanette S. Andrews, Jennifer A. Smith, Jessica D. Faul, Zhang Guangfa, Wei Guo, Yu Liu, Sarah S. Murray, Solomon K. Musani, Sathanur Srinivasan, Digna R. Velez Edwards, Heming Wang, Lewis C. Becker, Pascal Bovet, Murielle Bochud, Ulrich Broeckel, Michel Burnier, Cara Carty, Wei-Min Chen, Guanjie Chen, Wei Chen, Jingzhong Ding, Albert W. Dreisbach, Michele K. Evans, Xiuqing Guo, Melissa E. Garcia, Rich Jensen, Margaux F. Keller, Guillaume Lettre, Vaneet Lotay, Lisa W. Martin, Alanna C. Morrison, Thomas H. Mosley, Adesola Ogunniyi, Walter Palmas, George Papanicolaou, Alan Penman, Joseph F. Polak, Paul M. Ridker, Babatunde Salako, Andrew B. Singleton, Daniel Shriner, Kent D. Taylor, Ramachandran Vasan, Kerri Wiggins, Scott M. Williams, Lisa R. Yanek, Wei Zhao, Alan B. Zonderman, Diane M. Becker, Gerald Berenson, Eric Boerwinkle, Erwin Bottinger, Mary Cushman, Charles Eaton, Gerardo Heiss, Joel N. Hirschhron, Virginia J. Howard, Matthew B. Lanktree, Kiang Liu, Yongmei Liu, Ruth Loos, Karen Margolis, Bruce M. Psaty, Nicholas J. Schork, David R. Weir, Charles N. Rotimi, Michele M. Sale, Tamara Harris, Sharon L.R. Kardia, Steven C. Hunt, Donna Arnett, Susan Redline, Richard S. Cooper, Neil Risch, D.C. Rao, Jerome I. Rotter, Aravinda Chakravarti, Alex P. Reiner, Daniel Levy, Brendan J. Keating, and Xiaofeng Zhu.

Web Resources

The URLs for data presented herein are as follows:

• CPASSOC software, http://hal.case.edu/zhu-web/

• GWAS Catalog, http://www.genome.gov/gwastudies/

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/