Coverage-based treatment planning to accommodate deformable organ variations in prostate cancer treatment

Abstract

Purpose:

To compare two coverage-based planning (CP) techniques with standard fixed margin-based planning (FM), considering the dosimetric impact of interfraction deformable organ motion exclusively for high-risk prostate treatments.

Methods:

Nineteen prostate cancer patients with 8–13 prostate CT images of each patient were used to model patient-specific interfraction deformable organ changes. The model was based on the principal component analysis (PCA) method and was used to predict the patient geometries for virtual treatment course simulation. For each patient, an IMRT plan using zero margin on target structures, prostate (CTV_prostate) and seminal vesicles (CTV_SV), were created, then evaluated by simulating 1000 30-fraction virtual treatment courses. Each fraction was prostate centroid aligned. Patients whose D₉₈ failed to achieve 95% coverage probability objective D_98,95 ≥ 78 Gy (CTV_prostate) or D_98,95 ≥ 66 Gy (CTV_SV) were replanned using planning techniques: (1) FM (PTV_prostate = CTV_prostate + 5 mm, PTV_SV = CTV_SV + 8 mm), (2) CP_OM which optimized uniform PTV margins for CTV_prostate and CTV_SV to meet the coverage probability objective, and (3) CP_COP which directly optimized coverage probability objectives for all structures of interest. These plans were intercompared by computing probabilistic metrics, including 5% and 95% percentile DVHs (pDVH) and TCP/NTCP distributions.

Results:

All patients were replanned using FM and two CP techniques. The selected margins used in FM failed to ensure target coverage for 8/19 patients. Twelve CP_OM plans and seven CP_COP plans were favored over the other plans by achieving desirable D_98,95 while sparing more normal tissues.

Conclusions:

Coverage-based treatment planning techniques can produce better plans than FM, while relative advantages of CP_OM and CP_COP are patient-specific.

1. INTRODUCTION

Geometric uncertainties (GUs) should be adequately considered during the treatment planning process of external beam radiation therapy. GUs, in the form of delineation uncertainties, setup errors, interfraction and intrafraction organ variations may prevent one from achieving the therapeutic intent of treatment by introducing deviations between the planned (intended) and the treatment geometry. For prostate cancer treatment, interfraction organ displacement and deformation are primarily due to differential bladder and rectal filling, which can vary significantly during the treatment course.^1–5

To account for GUs, conventional planning applies safety margins to the clinical target volumes (CTVs) to create surrogate planning target volumes (PTVs) for treatment planning.^6,7 An ideal PTV margin ensures CTV coverage while maximally sparing the surrounding dose-limiting organs at risk (OARs) (i.e., bladder and rectum). However, the PTV margin is not easily determined for organ deformation and motion. One reason is that the characteristics of organ deformable motions are complex. In contrast to rigid organ motion and setup errors that can be described by six parameters comprising of shifts and rotations, organ deformable motions are of a much higher dimensionality. Therefore, the commonly used margin recipes^8,9 derived for rigid motion are at best approximate when used to accommodate deformations. Another reason is that the dosimetric consequence of a margin may vary with factors such as patient and plan quality and conformity. Although PTV margins to account for prostate and seminal vesicle interfractional variations have been suggested,^10,11 they are population based and therefore should be used with caution for each patient.

As advanced techniques for target localization and plan adaptation to reduce GUs have not become clinical routine procedure (due in part to its complexity, and in part to the clinical time demands), an intermediate solution can be found in coverage-based treatment planning (CP) techniques. Such techniques utilize GU models to evaluate a quantity called coverage probability, which is the probability that a realized target or OAR dose metric D_v exceeds the dose of interest (Rx, tolerance or other dose) when treatment planning and delivery uncertainties are taken into account.¹² By evaluating and optimizing coverage probability-based objectives, CP optimization techniques optimize the beam-fluences to ensure that a prespecified percentage (e.g., 95%) of probable patient treatment courses will meet the plan dosimetric criteria.

Our research group has developed two CP techniques—optimized-margin planning (CP_OM)¹³ and coverage-optimized planning (CP_COP).¹⁴ CP_OM is an iterative approach which modifies PTV margins until predefined coverage criteria are satisfied, while CP_COP does away with the PTV and modifies dosimetric “margins” between CTV and treated volume (the volume enclosed by a critical isodose surface⁷) until the coverage criteria are satisfied. In the presence of (rigid-body) setup errors, both CP_OM and CP_COP showed advantages relative to conventional PTV-based planning for prostate cancer patients. Using CP_OM for translation setup errors following a Gaussian distribution with standard deviation (SD) of 2 mm for systematic and random errors, the total volume of normal tissue receiving dose higher than 65 Gy was reduced on average by 19.3% or about 48 cm³.¹³ For translation setup errors following a Gaussian distribution with systematic and random SD 3 mm, using CP_COP was more likely to achieve CTV prescribed dose when OAR dose was below the optimization limits.¹⁴ However, the clinical advantages due to using CP_OM or CP_COP to accommodate the deformable organ motions have not been studied.

To explore potential advantages of CP based optimization, a representative GU model for simulating deformable organ motion is required. Many mathematical models have been developed.^11,15–20 Among these models, principal component analysis (PCA) was found to be an efficient and powerful model.^19,21 PCA compresses large and unorganized deformation data (e.g., from observations) to a low-dimensional system of basis vectors. These vectors, also called eigenmodes, are ranked according to their contribution to the deformation. The residual errors of a patient-specific PCA model for prostate, bladder, and rectum were small, e.g., less than 2 mm when eigenmodes representing more than 86% overall variability were used.¹⁹ (For population based variability, additional dominate eigenmodes are required.²⁰) PCA models have been implemented to estimate geometric coverage probabilities²² and to evaluate the dosimetric consequence of virtual treatment courses²¹ for prostate patients. However, to date, the implementation of PCA models has not been utilized for coverage-based plan optimization.

In this work, the prostate treatment plans were created to exclusively account for the interfraction organ deformation and translation simulated by a patient-specific PCA model. The plans using fixed margin-based planning (FM), CP_COP, and COP_OM are intercompared to investigate the potential clinical benefit of CP techniques.

2. METHODS

2.A. Prostate plans

Prostate image sets provided by the Netherlands Cancer Institute were used in this study. The patients’ characteristics were described by Deurloo et al.,²³ while the images and image processing were described by Sharma et al.²⁴ In summary, the image sets provided were bony-anatomy aligned and included an initial planning fan-beam computed tomography (CT) and multiple repeat fan-beam CTs (rCT, N_rCT = 7–12) acquired throughout the 7–8 week course of radiotherapy. For each CT image, the structures including prostate, seminal vesicles, rectum, bladder, left femur, and right femur were delineated by a single physician at VCU. All patients were assumed to have high-risk prostate cancer for the purposes of this study. The target volumes, CTVs, were the prostate (CTV_prostate) and the seminal vesicles (CTV_SV). No associated lymph nodes were included. The remaining contoured structures (bladder, rectum, etc.) were regarded as OARs, while the left and right femurs and the small bowel were excluded since their dose limits are rarely violated due to being more distant from the CTVs than the bladder and rectum.

For each patient, the first CT image was selected as the reference image set for planning. All of the IMRT plans utilized seven coplanar beams in the patient’s transverse plane, with gantry angles 30°, 80°, 130°, 180° (posterior), 230°, 280°, and 330° with the isocenter at the prostate centroid.

Table I lists the in-house IMRT criteria protocols used for the technique that was dependent (FM or CP_OM) or independent (CP_COP) of the PTV margins, respectively. The prescription dose 78 Gy to CTV_prostate was planned assuming 30 treatment fractions. For CP_COP plans, 95% and 5% coverage value were selected for minimum or maximum probabilistic DVH (pDVH) criteria to achieve static dose–volume criteria (used for FM or CP_OM) for 95% of the treatment courses simulated. The norm_tissue_ring was an artificial structure extending from 7 to 30 mm from CTV_prostate and CTV_SV to force a steep dose drop-off. Exclusively for the implementation of CP_COP for some treatment planning system (TPS), CTV_neighborhood was required to set the initial beam fluence. Here, CTV_neighborhood was defined as a virtual target expansion extending 12 mm from the union volume of CTV_prostate and CTV_SV on all image sets. This structure did not play an active role during optimization due to the zero objective weight.

TABLE I.

Optimization criteria used for (a) CP_COP and (b) FM and CP_OM plans. Doses (D) are in gray (Gy). The first subscript is percentage volume, the second the coverage value. Criterion weights are shown in square brackets. PTV 1 = CTV_prostate + CTV_prostate PTV margin and PTV 2 = CTV_SV + CTV_SV PTV margin.

(a) Optimization criteria for CPCOP plans
CTVprostate	D98,95 ≥ 78 [100], D2,5 ≤ 81 [50]
CTVSV	D98,95 ≥ 66 [100]
Bladder	D70,5 ≤ 18, D50,5 ≤ 36, D30,5 ≤ 57, D20,5 ≤ 66,
	D14,5 ≤ 69, D9,5 ≤ 75, D2,5 ≤ 81 [10]
Rectum	D50,5 ≤ 36, D30,5 ≤ 51, D20,5 ≤ 66, D5,5 ≤ 69, D2,5 ≤ 75 [10]
Norm_tissue_ring	(static) D0 ≤ 60 [1]
CTV_neighborhood	(static) D25 ≥ 10 [0]
(b) Optimization criteria for FM and CPOM plans
PTV1	D98 ≥ 78 [100], D2 ≤ 81 [50]
PTV2	D98 ≥ 66 [100]
Bladder	D70 ≤ 18, D50 ≤ 36, D30 ≤ 57, D20 ≤ 66,
	D14 ≤ 69, D9 ≤ 75, D2 ≤ 81 [10]
Rectum	D50 ≤ 36, D30 ≤ 51, D20 ≤ 66, D5 ≤ 69, D2 ≤ 75 [10]
norm_tissue_ring	D0 ≤ 60 [1]

All optimizations were performed using the Pinnacle³ (Version 9.100) TPS (Philips Medical Systems, Fitchburg, WI), based on direct machine parameter optimization (DMPO). The optimizer was run for maximal 50 iterations, since the composite objective values converge quickly, with small improvements which increase plan complexity afterward. Dose grid resolution was 2 × 2 × 2 mm³ when performing plan evaluation/comparison and 3 × 3 × 3 mm³ for optimization. (See Sec. 2.C for details.)

2.B. Deformable motion models—PCA

The interfraction organ deformable motions were modeled by PCA on a patient-specific basis. The mathematics are similar to published surfaced based PCA models.^19,21,25 The interested reader is referred to the Appendix for the PCA implementation details.

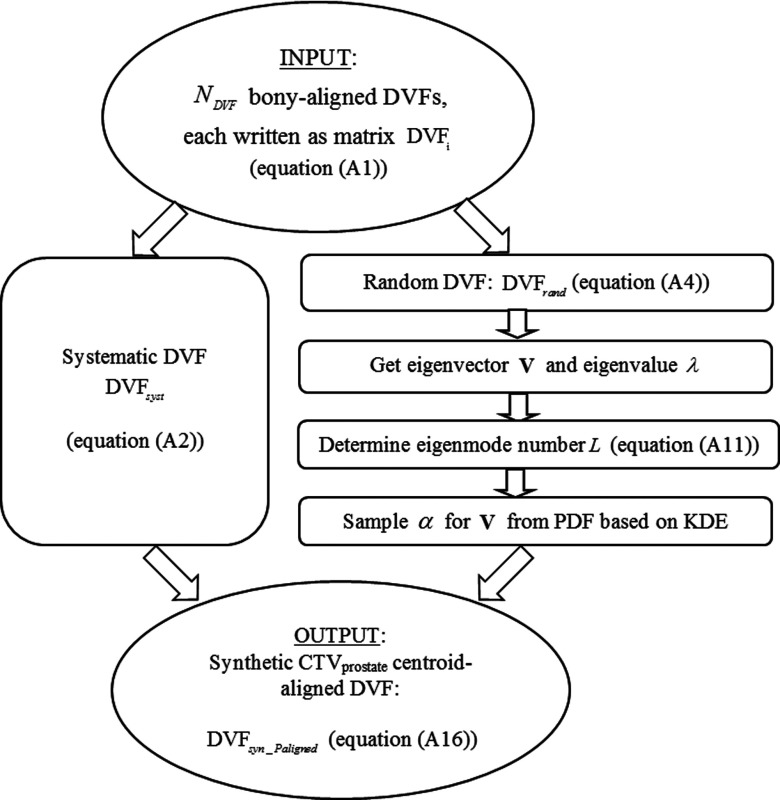
The PCA model was used to produce prostate centroid aligned synthetic DVFs $\left(\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{syn}\_\mathrm{Paligned}}\right)$ (Fig. 1). These DVFs were then used to map the reference prostate CTV, bladder, and rectum to plausible anatomically deformed ROIs for the virtual treatment fractions in the CP_OM/CP_COP optimization processes. Based on the anatomical deformation information and the algorithm described in Sec. 2.C, the ROI coverage was estimated and used to optimize dose distribution which met probabilistic criteria.

FIG. 1.

The flow chart for creating a patient-specific PCA model used in the treatment simulations.

2.C. Coverage estimation and coverage-based optimization

2.C.1. Coverage estimation—pDVH

One way to evaluate the effect of GUs on dose-based plan evaluation metrics is to use Monte Carlo to sample a synthetic patient anatomy then mimic dose delivery to that anatomy. By repeating the simulation n_frac = 30 times, a single treatment course is simulated, and plan evaluation metrics for that treatment course can be tallied. By repeating the treatment course simulations many (e.g., 1000) times, distributions of the plan evaluation metrics can be obtained. A major plan evaluation tool used in this study was the pDVH, which permits evaluation of coverage probability. A pDVH corresponding to coverage q is a virtual DVH created by connecting all D_v with coverage probability q. The steps to generate a pDVH for a target or CTV can be referred to Gordon et al.¹⁴ In this study, a pDVH is a result of “dynamic” DVHs which are different in each virtual treatment course due to the different DVFs sampled from PDFs of PCA model.

2.C.2. Planning technique—FM

FM is a PTV-based treatment planning technique based on the conventional margin-based planning method where predefined PTV margins are determined empirically. The fixed uniform PTV margins utilized by FM in this work were 5 mm for CTV_prostate and 8 mm for CTV_SV for all patients, according to a published work.¹¹

2.C.3. Planning technique — CP_COP

CP_COP optimizes the dose at prescribed coverage-based on the pDVH criteria, which operate on pDVH with possible variability considered. The basic mathematics can be found in the proof-of-concept work.¹⁴ CP_COP optimization is briefly described in the following paragraph.

As opposed to the conventional IMRT optimization that utilizes margin-based structures (i.e., PTV for CTV or PRV for OAR) to ensure coverage when the underlying ROI changes position and/or shape, CP_COP optimizes dose directly to the variable CTV/OAR. This requires adjusting fluence elements that can intersect the CTV/OAR at its varying positions (in the accelerator coordinate system), a volume call the ROI neighborhood. Similar to a PTV/PRV, the ROI neighborhood can be determined via CTV/OAR expansion or via direct knowledge of probable locations of the CTV/OAR based on simulation. The latter method was used in this work; 1000 virtual treatment courses simulations were performed and voxels covered by the “moving” CTV/OAR in any fraction of any virtual treatment course were included in the ROI neighborhood. For the planner using CP_COP, exact specification of the ROI neighborhood is not required. Undersizing the ROI neighborhood results in an inability to achieve CTV/OAR coverage which would be noticed and corrected for during planning. Oversizing the ROI neighborhood does not affect coverage but incrementally slows the optimization by the inclusion of noncontributing fluence elements in the optimization loop. To enhance conformity and efficiency, CP_COP utilizes voxel weighting factor ω_i for each ROI neighborhood voxel. As in the work of Gordon et al.,¹⁴ ω_i = 5⋅P_i was used here with P_i being the probability of the voxel i being covered by the moving ROI.

CP_COP optimizes ROI dose utilizing Newton’s method with pDVH-based objectives to minimize the sum of squared dose differences. For a minimum pDVH objective [criterion Pr[D_CRx ≥ D_Rx] ≥ q_Rx, D_CRx being the dose at the prescribed coverage probability q_Rx (e.g., 95%)] and D_Rx being the prescription dose), the objective function in this study was

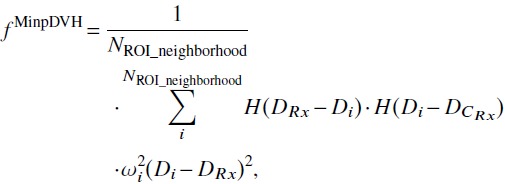(1)

where H was Heaviside function defined as

$${\displaystyle H\left(x\right)=\{\begin{array}{cc}1\hfill & (x>0)\hfill \\ 0\hfill & (x\le 0)\hfill \end{array}.}$$ (2)

The maximum pDVH objective [criterion Pr[D_CRx ≤ D_Rx] ≥ 1 − q_Rx], the objective function was

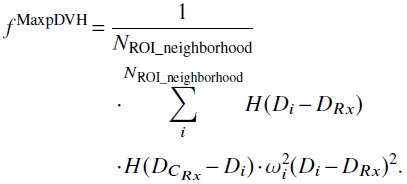(3)

CP_COP minimized the sum of a series of pDVH objectives to form the “optimized” dose using identical techniques as the dose–volume-based optimization described by Wu et al.²⁶

Here, 100 virtual treatment courses were simulated during the optimization to save computation time and memory, which increase with the number of virtual treatment courses. (For a 50-iteration optimization, the run time for COP on a 2.93 GHz Quad Core Processor Core i7-870 is 3–4 h.) 1000 treatment courses were used for postoptimization evaluations.

2.C.4. Planning technique — CP_OM

Based on the work of Gordon et al.,¹³ CP_OM used in this work started with 0 PTV margins for CTV_prostate and CTV_SV. If the CTV(s) failed to achieve the prescribed D_98,95, PTV margin(s) was(were) iteratively increased uniformly in 1 mm increments. In the outer loop of each iteration, the D_98,95 values were estimated based on the dosimetric simulation of 1000 virtual treatment courses with the PCA model incorporated. The iteration stopped when both CTVs achieved their D_98,95. CP_OM contrasted with CP_COP in that CP_OM used standard dose–volume objectives for OAR while CP_COP considered OAR coverage probability during optimization and generated dosimetric margins (effectively nonuniform PTV margins) surrounding the targets in place of uniform PTV margins. Overall, CP_OM was less complicated and placed more emphasis on CTV coverage than CP_COP.

2.D. Study decision flow

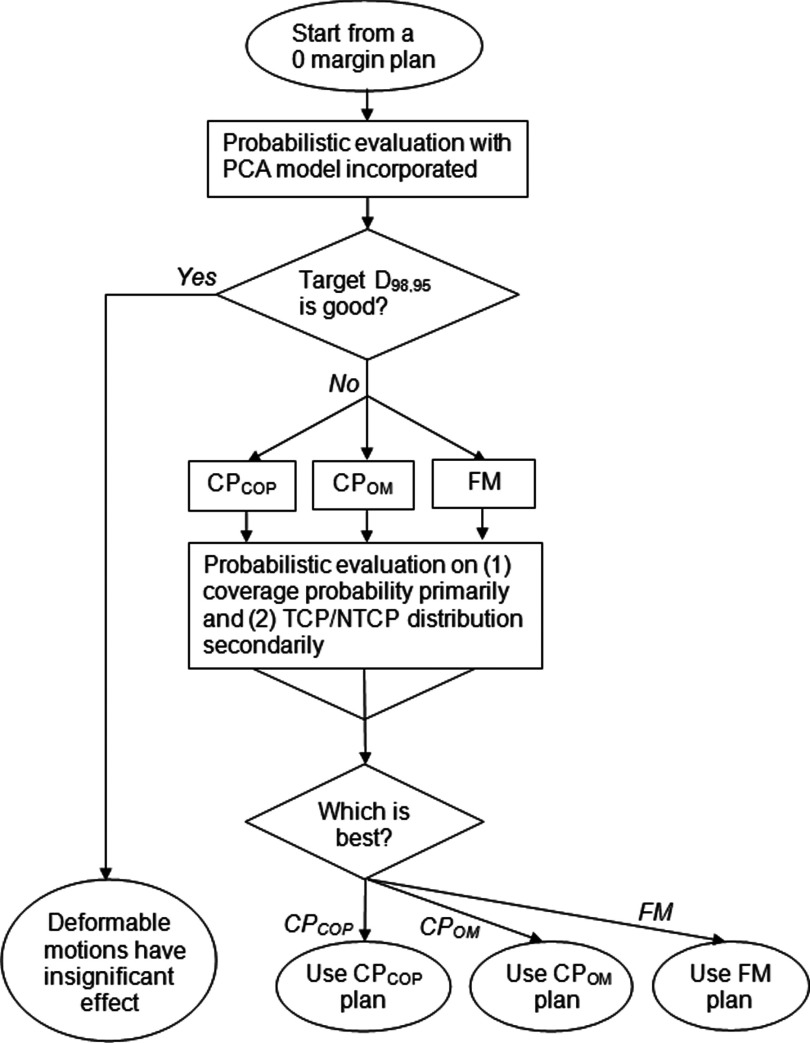
A treatment planning decision flow was designed as shown in Fig. 2. This decision flow existed to address two questions (1) Whether the dosimetric effect of GUs is insignificant and (2) how to determine which plan among the three FM, CP_OM, and CP_COP plans is preferred.

FIG. 2.

Decision flow to compare the CP_COP, CP_OM, and FM techniques when plan evaluation considers the effect of deformable organ motion. The decision criteria is the target coverage, with a secondary criteria based on TCP/NTCP/P+ values.

2.D.1. Dosimetric effect evaluation on zero-PTV-margin plans

First, the dosimetric effect of PCA modeled deformable organ motion was evaluated on a zero-PTV-margin IMRT plan with PTV 1 = CTV_prostate and PTV 2 = CTV_SV. 1000 virtual treatment courses (30 fractions per treatment course) were simulated with the PCA model to incorporate the GUs. The target dose–volume metric D₉₈ at a prescribed coverage probability of 95% (D_98,95) was computed for both CTV_prostate and CTV_SV. Denote D_98,95,Rx as the prescribed dose 78 Gy for CTV_prostate and 66 Gy for CTV_SV. If D_98,95 ≥ D_98,95,Rx for both CTV_prostate and CTV_SV, the dosimetric effect of deformable organ motions for this patient would have been regarded as insignificant since target coverage probability was resistant to anatomical variability. Otherwise, replanning the plan to further improve target coverage probability was required.

Two quantities were computed for all zero-PTV plans. One was the percentage dose degradation %ΔD_98,95

$${\displaystyle \%\Delta D_{\text{98,95}}=\{\begin{array}{cc}\frac{D_{\text{98,95},Rx}-D_{\text{98,95}}}{D_{\text{98,95},Rx}}\cdot 100\%\hfill & (D_{\text{98,95}}<D_{\text{98,95},Rx})\hfill \\ 0\hfill & \left(\text{Else}\right)\hfill \end{array}.}$$ (4)

The other was the percentage DVH spread %ΔDV H_98,5-95

$${\displaystyle \%\Delta {\mathrm{DV\; H}}_{\text{98,5-95}}=\frac{D_{\text{98,5}}-D_{\text{98,95}}}{(D_{\text{98,5}}+D_{\text{98,95}})/2}\cdot 100\%.}$$ (5)

%ΔDV H_98,5-95 showed how the possible DVHs in different virtual treatment courses scatter within the 90% confidence interval around mean DVH.

2.D.2. FM vs CP_OM vs CP_COP

When replanning was required, FM, CP_OM, and CP_COP were performed and the three plans were compared to determine which planning technique is preferred. The preference criteria were primarily target coverage probabilities corresponding to the optimization objectives. Additionally, the P+ (probability of complication free control) value was examined for a secondary comparison.

$${\displaystyle \mathrm{P}+=E\left[{\text{TCP}}_{\text{prostate}}\right]\cdot \left(\text{1}-E\left[{\text{NTCP}}_{\text{rectum}}\right]\right)\cdot \left(\text{1}-E\left[{\text{NTCP}}_{\text{bladder}}\right]\right),}$$ (6)

where the formulas and parameters of TCP and NTCP are listed in Table II. In our probabilistic framework, TCP and NTCP were independently evaluated on the base-CTV structures for each simulated treatment course. From the 1000 treatment course simulations, distributions of TCP and NTCP were evaluated. We believe that using the expectation values of TCP and NTCP had significant advantages with respect to TCP/NTCP evaluations on static geometries since our evaluation was for the actual tissue of interest, e.g., CTV instead of PTV, and it incorporated the effects of organ deformation and other uncertainties when modeled.

TABLE II.

A summary of TCP and NTCP models and parameters for CTV _prostate, bladder, and rectum used in this work. Note, conventionally TCP or NTCP values are calculated for a PTV or PRV volume. Here, TCP or NTCP are computed for the base CTV or OAR volumes during the coverage simulations, yielding distributions of the parameters.

TCP: Poisson model (Refs. 27–30)
Equation	$\begin{array}{c}\begin{array}{c}\text{TCP}=exp\left(-\frac{ln2}{N}\sum _{i}exp\left[2\frac{{\gamma }_{50}}{ln2}\left(1-\frac{{\mathrm{BED}}_i}{D_{50}}\right)\right]\right)\text{or}\hfill \\ =exp\left(-ln2\cdot exp\left[2\frac{{\gamma }_{50}}{ln2}\left(1-\frac{\text{gBEUD}}{D_{50}}\right)\right]\right)\hfill \end{array}\hfill \\ \text{where }{\mathrm{BED}}_i=D_i\cdot \left[1+\frac{D_i/n}{\left(\alpha /\beta \right)}\right]\text{ and gBEUD}={\left(\sum _i{\nu }_i\cdot {\mathrm{BED}}_i^a\right)}^{1/a}\hfill \end{array}$
Parameters	D50 (dose producing 50% tumor control), γ50 (slope parameter), a (EUD parameter), α/β (BED parameter)
CTVprostate (Ref. 31)	D50 = 67.5 Gy, γ50 = 2.2, a = 0.16, α/β = 3 Gy
NTCP: Lyman–Kutcher–Burman model (Refs. 32 and 33)
Equation	$\begin{array}{c}\text{NTCP}=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{t}duexp\left(-u^2/2\right)\hfill \\ \text{where }t=(\text{gBEUD}-T{D}_{50})\text{/}\left(mT{D}_{50}\right),\hfill \\ \text{gBEUD}={\left(\sum _i{\nu }_i\cdot {\mathrm{BED}}_i^a\right)}^{1/a}{\text{ and BED}}_i=D_i\cdot \left[1+\frac{D_i/n}{\left(\alpha /\beta \right)}\right]\hfill \end{array}$
Parameters	TD50 (the tolerance dose producing a 50% complication probability), m (slope parameter), a (gBEUD parameter), α/β (BED parameter)
Bladder (Refs. 34 and 35)	TD50 = 80 Gy, m = 0.11, a = 20, α/β = 5 Gy
Rectum (QUANTEC)	TD50 = 76.9 Gy, m = 0.13, a = 11.1, α/β = 5 Gy

3. RESULTS

3.A. Dosimetric effect evaluation on zero-PTV-margin plans

Even with CTV_prostate centroid aligned, none of the patients is immune to the degradation effect of target coverage due to deformable organ motions (Table III): 0/19 patients satisfy the D_98,95,Rx objective for both CTV_prostate and CTV_SV, as one or the other %ΔD_98,95 > 0%. The range of %ΔD_98,95 is 0.7%–10.5% for CTV_prostate and 0.0%–28.3% for CTV_SV, and the range of %ΔDV H_98,5-95 is 0.2%–2.3% for CTV_prostate and 1.4%–16.3% for CTV_SV. Though the dosimetric consequence of deformable motions differs from patient to patient, all 19 patients need PTV margins or CP_COP to further improve the target dose coverage.

TABLE III.

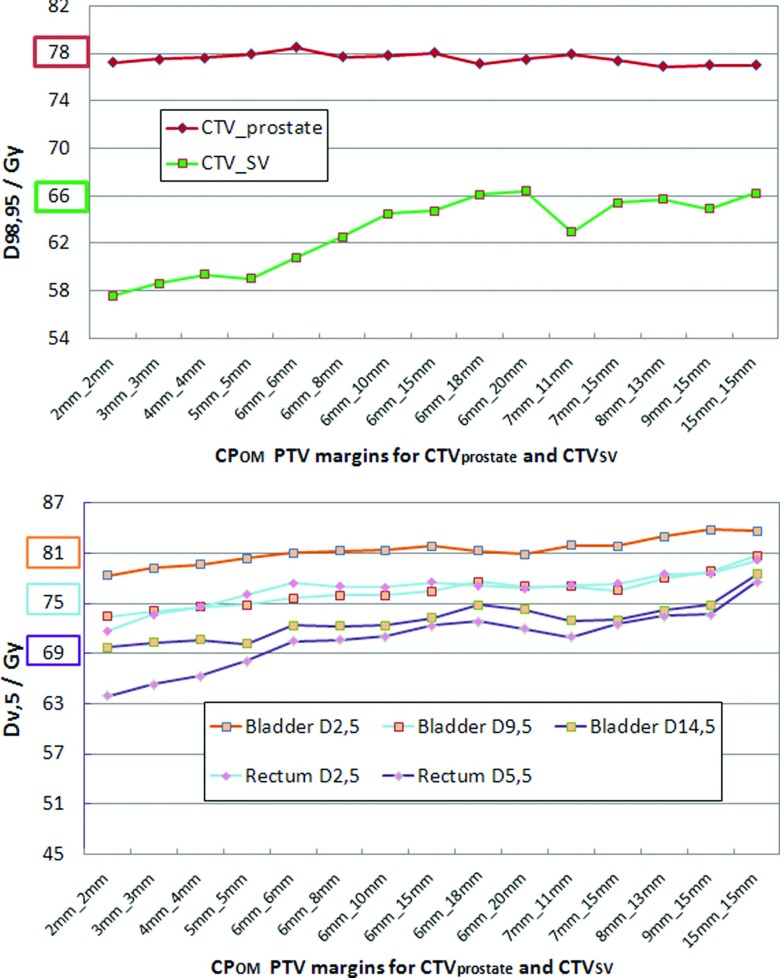
The percentage target dose degradation %ΔD_98,95 for CTV _prostate (P) and CTV _SV (S) for zero-PTV-margin plan, and the optimized PTV margins obtained by CP_OM technique across 19 patients.

ID	Zero-PTV-plan %ΔD98,95(%)	CPOM PTV(mm)
1	P: 4.9 S: 14.5	P: 2 S: 8
2	P: 5.8 S: 6.4	P: 10 S: 5
3	P: 5.3 S: 1.3	P: 5 S: 3
4	P: 7.7 S: 14.4	P: 5 S: 3
5	P: 1.3 S: 8.5	P: 2 S: 6
6	P: 0.8 S: 8.5	P: 1 S: 3
7	P: 2.2 S: 0.0	P: 2 S: 0
8	P: 1.7 S: 0.0	P: 4 S: 3
9	P: 2.9 S: 16.9	P: 6 S: 18
10	P: 11.1 S: 24.7	P: 7 S: 15
11	P: 9.5 S: 0.0	P: 9 S: 0
12	P: 7.5 S: 9.8	P: 9 S: 5
13	P: 2.7 S: 31.4	P: 5 S: 4
14	P: 0.8 S: 32.9	P: 4 S: 8
15	P: 0.8 S: 0.0	P: 1 S: 0
16	P: 2.4 S: 0.0	P: 2 S: 2
17	P: 3.1 S: 24.8	P: 3 S: 5
18	P: 2.6 S: 4.6	P: 4 S: 4
19	P: 0.7 S: 0.0	P: 2 S: 0

3.B. FM vs CP_OM vs CP_COP

Among the CP_COP, CP_OM, FM plans generated for each patient, either (12/19) CP_OM plans or (7/19) CP_COP plans were preferred (Table IV). The relative advantages between the three plans were patient-specific. The patient-specific clinical benefit of CP plans was significant for some patients. Relative to FM plans, 5/7 CP_COP plans and 3/12 CP_OM plans improved target D_98,95 value up to 5% of the prescribed dose, and 2/7 CP_COP and 9/12 CP_OM plans achieved better OAR sparing with P+ gain from 0.9%–22.8%. When CP_COP and CP_OM competed with each other, the advantage of the most preferred plan was either better target coverage or lower OAR dose. 3/7 CP_COP plans versus 10/12 CP_OM plans improved D_98,95 values up to 1.2% versus 9.8% of the prescribed dose. 4/7 CP_COP plans versus 2/12 CP_OM plans resulted in maximum 5.9% versus 2% P+ gain.

TABLE IV.

Patient study ID, the preferred planning technique and the most representative gain with respect to the other two plans in terms of target dose D_98,95 for CTV _prostate or CTV _SV, normal tissue coverage D_v,5 for bladder or rectum, and probability of complication free control P+. ID with */†/‡ denotes CP_COP/CP_OM/FM plan that fails to achieve target D_98,95.

ID	Best plan	Gain relative to the other plans
1*	CPOM	CPCOP (+0.8% CTVprostateD98,95)	FM (+6.5% P+)
2*†‡	CPOM	CPCOP (+4.0% CTVprostateD98,95)	FM (+1.3% CTVprostateD98,95)
3*	CPOM	CPCOP (+3.4% CTVprostateD98,95)	FM (+2.8% P+)
4*‡	CPOM	CPCOP (+7.3% CTVSVD98,95)	FM (+1.0% CTVprostateD98,95)
5*	CPOM	CPCOP (+7.2% CTVSVD98,95)	FM (+11.9% P+)
6*	CPOM	CPCOP (+1.0% CTVprostateD98,95)	FM (+21.5% P+)
7	CPCOP	CPOM (−3.2% Rectum, D2,5)	FM (+4.2% P+)
8*	CPOM	CPCOP (+9.8% CTVSVD98,95)	FM (+0.9% P+)
9*†‡	CPOM	CPCOP (+7.3% CTVSVD98,95)	FM (+5.0% CTVSVD98,95)
10*†‡	CPCOP	CPOM (+1.2% CTVSVD98,95)	FM (+5.5% CTVSVD98,95)
11‡	CPCOP	CPOM (+5.9% P+)	FM (+1.1% CTVprostateD98,95)
12†‡	CPCOP	CPOM (+0.8% CTVprostateD98,95)	FM (+2.4% CTVprostateD98,95)
13	CPOM	CPCOP (+2% P+)	FM (+3.1% P+)
14	CPOM	CPCOP (−3.1% Rectum, D2,5)	FM (+3.3% P+)
15*	CPOM	CPCOP (+8.8% D98,95)	FM (+22.8% P+)
16‡	CPCOP	CPOM (+1.7% P+)	FM (+1.0% CTVprostateD98,95)
17*	CPOM	CPCOP (+3.9% CTVSVD98,95)	FM (+9.5% P+)
18*†‡	CPCOP	CPOM (+0.6% CTVprostateD98,95)	FM (+0.8% CTVprostateD98,95)
19	CPCOP	CPOM (−0.6% Rectum D30,5)	FM (+6.4% P+)

When pDVHs and P+ gains were averaged across 19 patients, the advantages of CP_COP and CP_OM plans relative to FM somewhat canceled out on a population basis because some patients have target coverage improvement or where others have better OAR dose sparing. Still, the average P+ gain of CP_COP and CP_OM relative to FM was 1.1% and 3.1%, respectively.

4. DISCUSSION

Coverage probability is an important metric for the evaluation/optimization of plans under the influence of GUs. PTV/PRV margins are the primary method used in current clinics to account for errors and uncertainties in ROIs as these margins are intuitive, simple to implement, and have been extensively studied. For a typical (static) plan, evaluation/optimization is performed on a single image set and coverage is thought of in terms of isodose coverage of a PTV/PRV. Of note, it is ICRU defined treated volume,¹² not PTV/PRV, that dictates coverage. Unlike PTV/PRV margins that may be intended to ensure a prespecified coverage probability,⁵ coverage probability provides a probability estimate of achieving isodose coverage. Since computed coverage probabilities often differ considerably from the value implied by margin formulas for PTV-based the static plans,^12,31 coverage probability adds useful information that is missing from current clinical practice.

Acknowledging the challenges presented by daily organ deformations, many research groups have concentrated on developing time-of-treatment adaptive replanning to accommodate errors.^37–41 While adaptive replanning may become the standard, it will only do so if/when is benefits outweigh the drawbacks of the daily reimaging, daily replanning time, and added resources required compared with current practice or other competing methods.

The CP methods described in this paper describe one potential competing method. Like current margin-based approach, it designs treatment beams which can be delivered throughout a radiation therapy course (or subcourse if desired) avoiding the drawbacks of daily replanning. While CP methods may eventually be compared with daily replanning methods to justify replanning dosimetric advantages with respect to CP, the present study justifies CP for deformable organs with respect to the fixed margin approach. In this paper, the CP model is idealized since it presupposes a set of 7–12 patient-specific repeat CT image sets to generate the PCA model. Such number of sets would be unlikely, however, a reduced number of input images might suffice, nonionizing (MR) based image sets, or population based image sets might provide alternatives. Nonetheless, this idealized study is necessary to determine if pursuing these other options is worthwhile. The scope of this work is limited to the interactional deformable motions. Other uncertainties, including setup uncertainties target delineation, are covered in separate studies¹³ or future work.

Three planning techniques—CP_COP, CP_OM, and FM—were used to consider the ROI interfractional deformable motions which naturally occur through the treatment course while achieving the treatment intent. CP_COP directly optimizes the dose distribution and yields a dosimetric margin which accommodates modeled geometric uncertainties for CTV and OARs, while both CP_OM and FM utilize a surrogate volume PTV and ignores the effect of deformation on OARs during optimization. The PTV size for FM was empirically determined and for CP_OM was optimized based on target coverage probability. FM represents the conventional clinical method which is convenient but faces the fundamental problem of how to determine the optimal PTV margins tailored to each patient’s characteristics. CP_OM represents a simple form of coverage probability-based treatment planning to optimize patient-specific PTV margins. The optimized PTV margins are uniform, without being shaved for OARs.

As expected, when coverage probability is explicitly analyzed during plan optimization (i.e., CP_COP and CP_OM), the resultant treatment provides better coverage than the FM method. CP techniques show the potential clinical benefit in either target coverage probability or OAR sparing or both (Table IV). On a population based comparison, the advantages of CP techniques relative to FM are not pronounced due to the cancellation of gains in target coverage for some patients and gains in OAR sparing for the others. Overall, the benefit of using CP techniques is patient-specific and can be significant for certain cases.

Another benefit of the CP methods is that plan delivery complexity does not get increased. A simplistic surrogate of treatment plan complexity is the number of monitor units required to achieve the prescription dose.

Table V compares the monitor units per fraction for CP_COP, CP_OM, and FM techniques. Larger MUs typically indicate an increase in the complexity (number of segments) for the delivery. On average, CP_COP requires the fewest MUs, followed by CP_OM and FM. If the most deviant CP_OM plan (A5) is removed, then CP_OM requires on average the same number of MU as CP_COP.

TABLE V.

The monitor units per fraction for CP_COP plans and percentage deviation from CP_COP for the CP_OM and FM plans.

ID	CPCOP	CPOM	FM
1	483	−13	−8
2	448	+29	+20
3	636	−7	−1
4	531	−8	−3
5	489	0	+3
6	401	−6	+4
7	406	−5	+6
8	361	+10	+29
9	440	+70	+8
10	537	+5	−7
11	478	+33	+33
12	565	−5	+2
13	555	−10	+7
14	541	−10	−5
15	434	−8	+11
16	441	−5	+14
17	552	−3	+5
18	476	+6	+23
19	405	+1	+10
Average	483.1	+3	+7

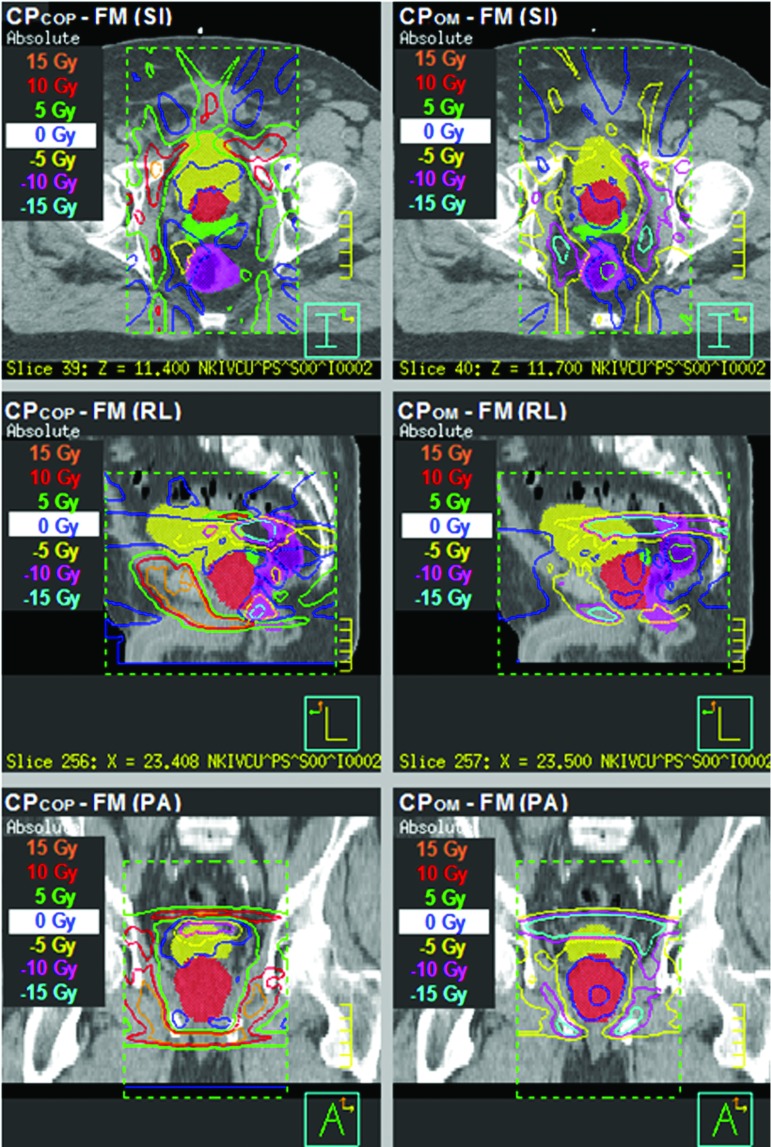
When it comes to the relative advantages of CP_OM and CP_COP, it also shows patient-specific characteristics. As implemented, the CP_OM method effectively yields a CTV coverage hard constraint: when the current PTV margins are regarded as too small, they are increased without considering the OAR criteria. In contrast, the flexibility of CP_COP yields dose distribution differences with respect to the CP_OM and FM margin-based plans. As Fig. 3 shows, CP_OM and FM plans differ little around the CTV_prostate volume as indicated by the 0 Gy isodose surface, while this is not the case for the difference between the CP_COP and FM plans. In this example, CP_COP tends to push dose to the non-OAR region adjacent to the target to ensure target coverage. Since CP_COP balances all coverage probabilities for CTVs and OARs that are associated with the optimization criteria, no hard constraint is placed on the CTV coverage. Consequently, CP_COP can be compromised to OAR sparing to ensure the composite objective value is minimized. Such compromises eliminated CP_COP from contention, when target coverage probability was the primary selection criteria for the preferred plan.

FIG. 3.

The simulated dose distribution differences between different plans, CP_COP minus FM (left column) and CP_OM minus FM (right column), in SI, RL, and PA slices for patient 19 for a single treatment course when deformable organ motion is considered. The ROIs displayed as colorwash are CTV _prostate (red), CTV _SV (green), bladder (yellow), and rectum (magenta). The dose distribution around CTV _prostate in CP_COP plan is quite different from that on CP_OM and FM plans.

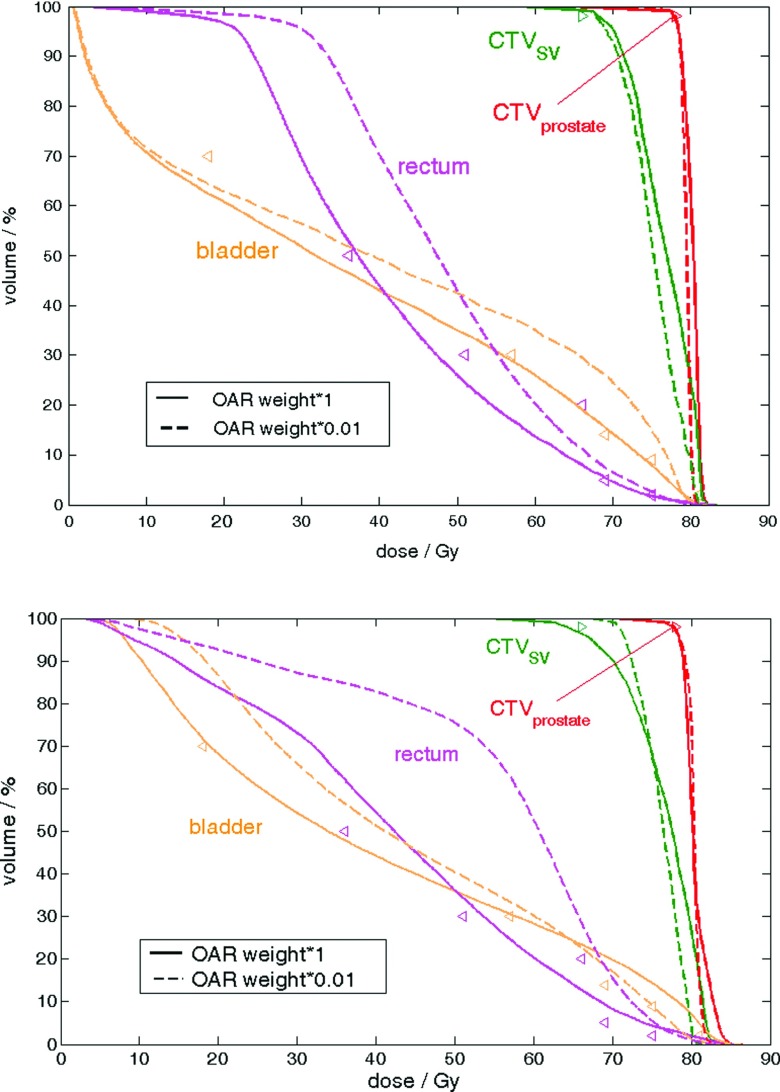
Future implementations to further improve CP technique could consider optimal objective function weights or inclusion of hard constraints. By using the objectives in Table I, Table VI shows that 11/19 CP_COP plans and 5/19 CP_OM plans (versus 8/19 FM plans) had nonzero %ΔD_98,95 for either CTV_prostate or CTV_SV and thus failed to meet the optimization criteria of target coverage probability D_98,95. As discussed, CP_COP is most likely to fail the prescribed D_98,95 mainly because of the selected objective weights of CTVs and OARs. The typical %ΔD_98,95 of a CP_COP plan was within 1%, although it could be up to 4.1% for CTV_prostate and 9.3% for CTV_SV. When the CP_COP plan achieved the prescribed D_98,95, it was most likely to be preferred among the three. As indicated in Fig. 4, preferred objective function weights for CP techniques may be patient and ROI specific. CP_OM failed for some patients when PTV margins were expanded to a very large size (Table III), which resulted in overlap volumes between larger PTV, bladder, and rectum.

TABLE VI.

Target percentage degraded dose %ΔD_98,95 (%) of CP_COP, CP_OM or FM plan for patients 1–19 when accommodating deformable motions.

	%ΔD98,95 of CTVprostate			%ΔD98,95 of CTVSV
ID	CPCOP	CPOM	FM	CPCOP	CPOM	FM
1	0.2	0.0	1.4	0.0	0.0	0.0
2	4.1	0.1	1.4	0.0	0.0	0.0
3	2.7	0.0	0.0	0.3	0.0	0.0
4	0.0	0.0	1.0	3.7	0.0	0.0
5	1.0	0.0	0.0	7.2	0.0	0.0
6	0.8	0.0	0.0	0.0	0.0	0.0
7	0.0	0.0	0.0	0.0	0.0	0.0
8	0.0	0.0	0.0	9.3	0.0	0.0
9	3.7	1.1	0.5	7.1	0.0	4.9
10	0.5	1.1	1.2	2.9	4.1	8.4
11	0.0	0.0	0.1	0.0	0.0	0.0
12	0.0	0.6	2.3	0.0	0.0	0.0
13	0.0	0.0	0.0	0.0	0.0	0.0
14	0.0	0.0	0.0	0.0	0.0	0.0
15	1.3	0.0	0.0	7.7	0.0	0.0
16	0.0	0.0	0.2	0.0	0.0	0.0
17	0.9	0.0	0.0	1.5	0.0	0.0
18	0.1	0.0	0.9	0.0	0.4	0.0
19	0.0	0.0	0.0	0.0	0.0	0.0

FIG. 4.

Examples of the CP_COP plans of two patients with ID 1 (upper) and 10 (lower) that use the original OAR objective weights (solid) (listed in Table I) versus reduced OAR objective weights with a factor 0.01 (dashed). The pDVHs are of 95% for CTV _prostate (red) and CTV _SV (green) and 5% for bladder (orange) and rectum (magenta). Reduced OAR objective weights for these two patient cases result in improved target coverage at the price of OAR doses above the treatment objectives.

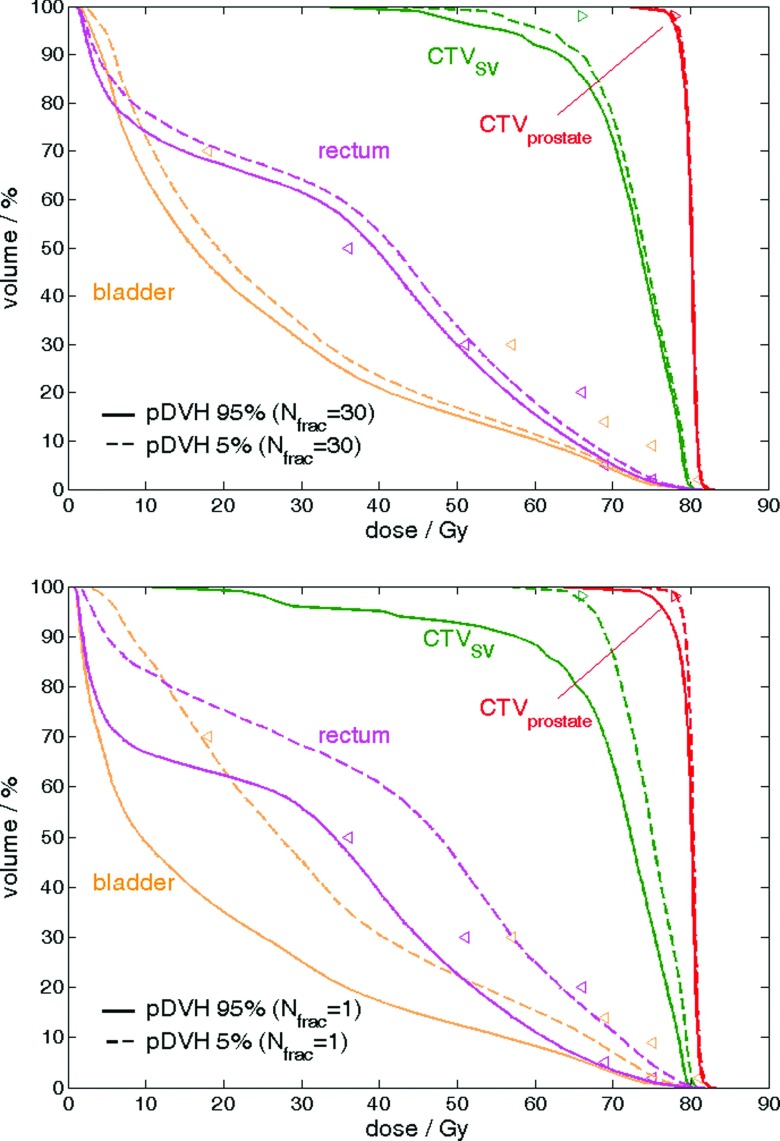
Figure 5 shows the tendency of the competing target and OAR doses at each prescribed coverage probability using different PTV margins. Due to this challenge, increasing uniform PTV margins was not the universal solution to ensure target coverage probability. Still, CP_OM reasonably expanded PTVs according to the target coverage probability for most patients and CP_OM was much less limited by the selections of objective weights of CTVs and OARs. Nonetheless, CTV coverage would have been achieved if OAR weights were reduced.

FIG. 5.

An example of the increasing competition between target and OAR criteria with increasing PTV margins during CP_OM optimization. The target prescribed dose or the OAR tolerance dose is highlighted in the same color as the achieved dose curve for each ROI criterion. On the abscissa, the values are given in the format Xmm_Ymm, where X is the CTV _prostate margin and Y is the CTV _SV margin.

To validate that 1000 simulations were sufficient for our coverage calculations, two patients were arbitrarily selected to determine the convergence of D_v,q using 10, 100, 200, and 500 virtual treatment courses relative to that using 1000. Denote D_{v,q_Ntx} the estimated D_v,q based on N_tx virtual treatment courses. For CTV_prostate and CTV_SV, D_{98,95_Ntx} relative to D_{98,95_1000} was $\le \left|\pm 0.2\right|\%$ when N_tx is 500. For OARs, the absolute value of the percentage difference remained within 1% (mostly <0.5%) in the high dose region (where v of D_v,q was small) and tended to be larger (1%–5%) in the low dose region (where v of D_v,q was large). The precision was tested by reproducing each D_{v,q_1000} for 7–10 times. The maximum absolute percentage difference among all repeated estimated values was 0.2% for CTV_prostate, 0.3% for CTV_SV, and 3.5% for all OARs. In general, D_v,q is more precise in high dose regions. As the low dose region was of less interest in terms of dose sparing and OAR toxicity, these test cases supported that coverage estimation using 1000 virtual treatment courses was adequate. Our finding agreed with study from Söhn et al.²¹ where 10 000 35-fraction treatment courses were simulated. We both showed that the effects of deformable motions for cumulative plan are smaller than those from a single fraction because hot spot and cold spots in moving voxels cancel out when fraction number is much larger than 1 (Fig. 6).

FIG. 6.

An example of pDVHs 95% (solid) and pDVHs 5% (dashed) evaluated on a patient treatment case with (upper) 30 fractions (i.e., N_frac = 30) and (lower) 1 fraction (i.e., N_frac = 1) for the CTV _prostate (red), CTV _SV (green), bladder (orange) and rectum (magenta) with optimization objectives (triangle markers). When N_frac ≫ 1, the per voxel dose variability reduces, decreasing the spread in the 95% and 5% pDVHs.

Although 1000 treatment courses were used for the coverage evaluation, we opted to simulate 100 courses during the optimization to reduce the overall computational burden. While this leads to more optimization iterations due to course-set to course-set statistical variations, trial-and-error testing revealed that 100 in-optimization treatment course simulations were sufficient to ensure convergence and provide a reasonable compromise/reduction in overall computation time, which is approximately proportional to the number of treatment course simulations times the number of optimization iterations. In any event, the final coverage evaluation utilized 1000 virtual treatment courses to iterations to ensure accurate evaluation of the final coverage.

5. CONCLUSION

For the high-risk prostate cancer patients treated with external beam radiation therapy, dosimetric variability caused by interfractional tissue deformation should be considered during treatment planning in order to ensure target coverage and organ sparing. Simulating such deformations via application of PCA model permits evaluation of probability of achieving coverage or avoidance. When these models are utilized within the plan optimization loop, e.g., CP_COP and CP_OM, improved target dose coverage or lower normal tissue toxicity is achieved compared with fixed PTV margin techniques.

APPENDIX: PRINCIPAL COMPONENT ANALYSIS FOR GENERATION OF 3D DISPLACEMENT VECTOR FIELDS

This section briefly describes the PCA model used to generate the synthetic displacement vector fields (DVFs) utilized to deform the reference planning ROIs to synthetic “per-fraction” ROIs for treatment simulations used to assess the ROI coverage probabilities.

The per-patient PCA model input data consisted of the set of DVFs that relate voxel locations on the reference planning image to point on the repeat FBCT images. The input DVFs were calculated by the deformable registration algorithm called small deformation inverse-consistent linear elastic (SICLE).⁴² The registration was based on the grayscale information as well as the contours for prostate, bladder, and rectum. Input DVFs were quality assured via visual inspection of contours plus dice coefficient relative to manual contours.

The PCA model workflow is illustrated in Fig. 1 and is described here for a single patient. Registrations utilizing the N_rCT rCTs yielded N_{DV F} DVFs. Prior to PCA input, each DVF was used to form a vector DVF_i ∈ R^3N_vox×1 (where $i=\left\{1,2,\dots ,N_{\mathrm{DV\; F}}\right\}$) with N_vox being the number of DVF voxel elements. R^3N_vox×1 indicates that the size of vector, expressed as a 3N_vox (rows) by 1 (columns) matrix

$${\displaystyle \mathbf{D}\mathbf{V}{\mathbf{F}}_i={\left(\begin{array}{cccccccccccc}\hfill x_{1,i}\hfill & \hfill x_{2,i}\hfill & \hfill \cdots \hfill & \hfill x_{N_{\mathrm{vox}},i}\hfill & \hfill y_{1,i}\hfill & \hfill y_{2,i}\hfill & \hfill \cdots \hfill & \hfill y_{N_{\mathrm{vox}},i}\hfill & \hfill z_{1,i}\hfill & \hfill z_{2,i}\hfill & \hfill \cdots \hfill & \hfill z_{N_{\mathrm{vox}},i}\hfill \end{array}\right)}^T,}$$ (A1)

where x, y, z were the displacement vector field components in the x, y, z directions for each DVF voxel and ( )^T denoted the transpose of the matrix. The systematic component DVF_syst ∈ R^3N_vox×1 from the DVF_i set related the patient’s average anatomy to the reference image set, and equals the mean of the N_{DV F} DVFs

$${\displaystyle \mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{syst}}=\frac{1}{N_{\mathrm{DV\; F}}}\sum _{i=1}^{N_{\mathrm{DVF}}}\mathbf{D}\mathbf{V}{\mathbf{F}}_i.}$$ (A2)

The residual per-image-set variation from DVF_syst can be cast as “random” components, DVF_rand,i ∈ R^3N_vox×1, where

$${\displaystyle \mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand},i}=\mathbf{D}\mathbf{V}{\mathbf{F}}_i-\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{syst}}.}$$ (A3)

DVF_rand,i is then composed into DVF_rand ∈ R^{3N_vox×N_DVF}, where each column corresponds with an DVF_rand,i.

$${\displaystyle \mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}=\left(\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand},1}\hspace{0.17em}\hspace{0.17em}\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand},2}\hspace{0.17em}\hspace{0.17em}\dots \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand},N_{\mathrm{DVF}}}\right).}$$ (A4)

PCA analysis was performed on DVF_rand.

For DVF_rand, the covariance matrix C ∈ R^{3N_vox×3N_vox} that generalized the notion of variance to dimensions 3N_vox × 3N_vox (Refs. 43 and 44) is

$${\displaystyle \mathbf{C}=\frac{1}{N_{\mathrm{DV\; F}}}\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}{\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}}^T,}$$ (A5)

where ( )⋅( )^T represented the outer product of the two matrices. The diagonalization of C yields a set of eigenvectors, V(l) ∈ R^3N_vox×1, and their associated eigenvalues, λ_l ∈ R^1×1. These eigenvectors and eigenvalues satisfy the following relation, CV = λV. In practice, the 3N_vox × 3N_vox covariance matrix is intractable. To reduce the computational burden, V and λ are calculated using an alternative method useful when N_{DV F} ≪ 3N_vox.⁴⁵ First, Eq. (A5) is substituted into the eigenvector equation

$${\displaystyle \frac{1}{N_{\mathrm{DV\; F}}}\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}{}^T\mathbf{V}=\lambda \mathbf{V}.}$$ (A6)

Multiplying by DVF_rand^T and defining U = DVF_rand^TV gives

$${\displaystyle \frac{1}{N_{\mathrm{DV\; F}}}\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}{}^T\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}\mathbf{U}=\lambda \mathbf{U}.}$$ (A7)

This permits U to be calculated as the eigenvectors of the smaller N_{DV F} × N_{DV F} matrix, DVF_rand^TDVF_rand. Multiplying both sides of the above equation by DVF_rand gives

$${\displaystyle \frac{1}{N_{\mathrm{DV\; F}}}\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}{}^T\left(\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}\mathbf{U}\right)=\lambda \left(\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}\mathbf{U}\right).}$$ (A8)

Thus, the eigenvectors for the full covariance matrix are determined by the relation

$${\displaystyle {\mathbf{V}}_i=\frac{1}{\sqrt{N_{\mathrm{DV\; F}}{\lambda }_i}}\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}{\mathbf{U}}_i,}$$ (A9)

where $1/\sqrt{N_{\mathrm{DV\; F}}{\lambda }_i}$ is a factor used to renormalize the computed eigenvectors. These eigenvectors, also called eigenmodes, represent pseudo-DVFs of correlated displacements of N_vox voxels. The eigenvectors were mutually independent vector fields and the maximum number of eigenmodes that existed was N_{DV F} − 1. Therefore, the whole eigenvector matrix was V ∈ R^{3N_vox×(N_DVF−1)}. To measure the fraction of overall random tissue motion variability represented by an eigenmode with index l, the relative eigenvalue ${\overline{\lambda }}_l$ was calculated as

$${\displaystyle {\overline{\lambda }}_l=100\%\cdot \frac{{\lambda }_l}{\sum _{i=1,2,\dots ,\underset{\mathrm{DVF}}{N}}{\lambda }_i}.}$$ (A10)

The larger the eigenvalue, the more dominating the eigenmode was due to capturing a larger percentage of the geometric variability in DVF_mat. The total percentage of geometric variability $\overline{\lambda }$ accounted for by the L most “principal” eigenmodes was

$${\displaystyle \overline{\lambda }=\sum _{i=1,2,\dots ,L}{\overline{\lambda }}_i.}$$ (A11)

To ensure that the set of synthetic DVFs represented at least 90% of the overall geometric variability, L was determined by $\overline{\lambda }\ge 90\%$ and consequently ranged from 4 to 7 for the 19 patients.

For each eigenvector, coefficients were found in a matrix Coeff ∈ R^{N_DVF×(N_DVF−1)}, which was the product of DVF_rand^T and eigenvector matrix V

$${\displaystyle \mathbf{Coeff}={\left(\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{rand}}\right)}^T\mathbf{V}=\left(\begin{array}{ccccc}\hfill c_{1,1}\hfill & \hfill \cdots \hfill & \hfill c_{l,1}\hfill & \hfill \cdots \hfill & \hfill c_{N_{\mathrm{DVF}-1},1}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \cdots \hfill & \hfill ⋰\hfill & \hfill ⋮\hfill \\ \hfill c_{1,i}\hfill & \hfill \cdots \hfill & \hfill c_{l,i}\hfill & \hfill \cdots \hfill & \hfill c_{N_{\mathrm{DVF}-1},i}\hfill \\ \hfill ⋮\hfill & \hfill ⋰\hfill & \hfill \cdots \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill c_{1,N_{\mathrm{DVF}}}\hfill & \hfill \cdots \hfill & \hfill c_{l,N_{\mathrm{DVF}}}\hfill & \hfill \cdots \hfill & \hfill c_{N_{\mathrm{DVF}-1},N_{\mathrm{DVF}}}\hfill \end{array}\right),}$$ (A12)

where i and l were the row and the column indexes of Coeff corresponding to DVF_rand(i) and $\mathbf{V}\left(l\right)$. Based on this finite data sample of eigenvector coefficients Coeff, a probability density function (PDF) for the lth eigenvector could be estimated by kernel density estimation (KDE).^46–49 For the lth eigenvector, the PDF P_l of random variable t was represented using a Gaussian kernel

$${\displaystyle P_l[a\le t\le b]=\frac{1}{N_{\mathrm{DV\; F}}\cdot {\sigma }_l\cdot \sqrt{2\pi }}\sum _{i=1}^{N_{\mathrm{DVF}}}{e}^{-{\left(t-c_{i,l}\right)}^2/2{\sigma }_l^2},}$$ (A13)

where c_i,l was the matrix Coeff element in the ith row and the lth column in Eq. (A12). For sampling purposes, the PDF is calculated over the symmetric range a to b, where these cutoff parameters were chosen to ensure that $P_l\left[a\right]\text{ and }{P}_l\left[b\right]<0.0001max\left[P_l\right]$. The Gaussian SD σ_l was determined using the rule of thumb equation.⁵⁰

$${\displaystyle {\sigma }_l=\frac{1.06}{{N_{\mathrm{DV\; F}}}^{0.2}}\sqrt{\frac{\sum _i^{N_{\mathrm{DVF}}}(c_{i,l}-\frac{1}{N_{\mathrm{DVF}}}\sum _i^{N_{\mathrm{DVF}}}{c_{i,l})}^2}{N_{\mathrm{DV\; F}}-1}}.}$$ (A14)

The eigenvectors create a new orthogonal basis for the input DVFs. Thus, without loss of generality, any DVF_rand,i can be represented as a linear combination of scalar expansion coefficients, c_l,i, and their associated eigenvectors, $\mathbf{V}\left(l\right)$. As the eigenvectors are uncorrelated, synthetic DVFs, DVF_syn ∈ R^3N_vox×1, can be created by sampling a set of expansion coefficients, α, from the PDFs calculated in Eq. (A13). The synthetic DVFs can then be calculated as

$${\displaystyle \mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{syn}}=\mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{syst}}+\sum _{l=1}^L{\alpha }_l\cdot \mathbf{V}\left(l\right).}$$ (A15)

In this work, rejection sampling was used to select α_l. This method of making samples of synthetic DVFs from PCA eigenvectors and statistical distributions of expansion coefficients was adapted from Murphy et al.⁴⁹

As current clinical practice uses soft tissue target alignment for treatments, the bony-anatomy aligned DVF_syn generated by the afore developed PCA model were translated to CTV_prostate centroid aligned DVF. Let the vector element of DVF_syn be represented by (x_syn,i, y_syn,i, z_syn,i), where i = 1, 2, …, N_vox and denote synthetic x_syn,P, y_syn,P, z_syn,P as displacement vector of CTV_prostate centroid. The synthetic DVF for CTV_prostate centroid-aligned anatomies DVF_{syn_Paligned} ∈ R^3N_vox×1 was

$${\displaystyle \mathbf{D}\mathbf{V}{\mathbf{F}}_{\mathrm{syn}\_\mathrm{Paligned}}=\left(\begin{array}{c}\hfill x_{\mathrm{syn},1}-x_{\mathrm{syn},P}\hfill \\ \hfill x_{\mathrm{syn},2}-x_{\mathrm{syn},P}\hfill \\ \hfill \cdots \hfill \\ \hfill \begin{array}{c}\hfill x_{\mathrm{syn},N_{\mathrm{vox}}}-x_{\mathrm{syn},P}\hfill \\ \hfill \begin{array}{c}\hfill y_{\mathrm{syn},1}-y_{\mathrm{syn},P}\hfill \\ \hfill y_{\mathrm{syn},2}-y_{\mathrm{syn},P}\hfill \\ \hfill \cdots \hfill \\ \hfill \begin{array}{c}\hfill y_{\mathrm{syn},N_{\mathrm{vox}}}-y_{\mathrm{syn},P}\hfill \\ \hfill \begin{array}{c}\hfill z_{\mathrm{syn},1}-z_{\mathrm{syn},P}\hfill \\ \hfill z_{\mathrm{syn},2}-z_{\mathrm{syn},P}\hfill \\ \hfill \cdots \hfill \\ \hfill z_{\mathrm{syn},N_{\mathrm{vox}}}-z_{\mathrm{syn},P}\hfill \end{array}\hfill \end{array}\hfill \end{array}\hfill \end{array}\hfill \end{array}\right).}$$ (A16)

The PCA model generated sets of DVF_{syn_Paligned} for use in the postplanning evaluation to judge/compare treatment plans and in the CP_OM/CP_COP optimization processes.

The PCA generated synthetic DVFs for this study were validated using several methods. Initially, statistical characteristics of several synthetic DVFs were compared with those of the input data sets. For large-scale validation, 1000 synthetic ROI sets were generated to permit comparison of distributions of synthetic ROI characteristics (centroid location, volume) with respect to those from the input image sets. For example, the distributions of synthetically derived and the manually derived ROI centroid locations were compared for any significant deviations (p < 0.05) using a two sample t-test, the Mann–Whitney U test, and the Kolmogorov–Smirnov test. No significant deviations were found between the two distributions in any direction. Additionally, visual inspection of several synthetic prostate, bladder, and rectum regions of interest (ROIs) to ensure they appeared realistic and similar to the ROIs contoured on the input images (Fig. 7).

FIG. 7.

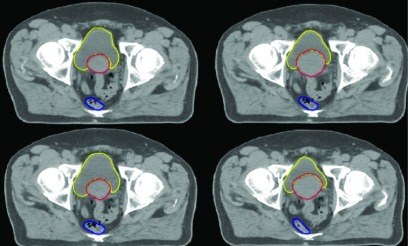
Four synthetically created PCA geometries for a single patient. Each image shows the same slice of a given patient at four synthetically sampled time points over the patient’s treatment course. For illustration purposes, the deformed contours are showed overlaid on the deformed CT images. In this work, only the deformed contours are incorporated into the methodology.

In terms of the number of PCA input image sets required, others have addressed the minimum number of input geometries to adequately model patient-individual dosimetric variability using PCA. Söhn et al.²¹ stated that 2–6 dominating eigenmodes⁵¹ are sufficient for modeling and mathematically 3–7 input geometries are required to obtain a proper estimation for these eigenmodes. A head and neck cancer study which used PCA modeling showed that dose estimation accuracy after first three weeks of treatment of cancer was within 1% for most of organs and that the geometric variations can be represented by 3–4 dominating eigenmodes.²⁵ Therefore, CP application with a limited set (e.g., 4–7 eigenmodes for ≥90% of variability in this work) is plausible.