Membrane Shape at the Edge of the Dynamin Helix Sets Location and Duration of the Fission Reaction

SUMMARY

The GTPase dynamin polymerizes into a helical coat that constricts membrane necks of endocytic pits to promote their fission. However, the dynamin mechanism is still debated because constriction is necessary but not sufficient for fission. Here, we show that fission occurs at the interface between the dynamin coat and the uncoated membrane. At this location, the considerable change in membrane curvature increases the local membrane elastic energy, reducing the energy barrier for fission. Fission kinetics depends on tension, bending rigidity, and the dynamin constriction torque. Indeed, we experimentally find that the fission rate depends on membrane tension in vitro and during endocytosis in vivo. By estimating the energy barrier from the increased elastic energy at the edge of dynamin and measuring the dynamin torque, we show that the mechanical energy spent on dynamin constriction can reduce the energy barrier for fission sufficiently to promote spontaneous fission.

INTRODUCTION

Membrane fission is an essential step in membrane traffic, as it separates membrane cargoes from donor compartments. It is the inverse reaction to fusion. In many of the various fusion events in cells, a single type of machinery, the SNAREs, mediate the collapse of membranes. The general principle of the SNAREs mechanism is that the energy spent in the assembly of the SNARE complex overcomes the energy barrier to fusion by generating a hemifusion intermediate, also called the “stalk intermediate” (Kozlovsky and Kozlov, 2002). The stalk intermediate is a structure where the cytosolic leaflets of the two membrane compartments are fused into one, whereas the lumenal leaflets are still separated. In the case of fission, different machineries mediate the separation of two compartments depending on the cellular context: dynamin during endocytosis; endosomal sorting complex in retrograde transport-III (ESCRT-III) in multivesicular body biogenesis, cytokinesis, and viral budding (Hurley and Hanson, 2010). Small GTPases (Sar1, Arf1) involved in the initiation of the coat proteins (COPs)-dependent Golgi trafficking have also been recently implicated in the fission reaction of the COPs (Fromme et al., 2007). However, in all these fission reactions, it is not known whether the different machineries mediate fission on the basis on the same principle, mostly because physical understanding of how fission is mediated is lacking. By analogy to fusion, it has been, however, suggested that they operate through a similar stalk intermediate (Kozlovsky and Kozlov, 2003). Here, we focused on the physics of membrane fission, taking the dynamin system as a model in which the biochemistry is arguably better characterized than in other systems.

Dynamin has been biochemically and genetically implicated in fission of endocytic vesicles (Ferguson and De Camilli, 2012). It is a GTPase that polymerizes into helical collars at the neck of clathrin-coated pits (CCPs). The helical structure of dynamin immediately suggested that fission could be driven by a constriction of the helix.

When assembled in absence of guanosine triphosphate (GTP), the nonconstricted dynamin helix surrounds a membrane tube with a radius, R_u, of 10 nm (Chen et al., 2004; Danino et al., 2004). Upon GTP hydrolysis, a conformational change of dynamin at the dimer and the polymer levels (Chappie et al., 2011; Faelber et al., 2011; Ford et al., 2011) constricts the membrane (Danino et al., 2004; Sweitzer and Hinshaw, 1998). Constriction correlates with a reduction of the helix radius, itself reflected by a reduction of the number of dimers per helix turn from 14 to 13 (Chappie et al., 2011) and torsion. This torsion of the entire helical polymer can be monitored by live imaging (Roux et al., 2006). Early models (Hinshaw and Schmid, 1995; Takei et al., 1995) proposed that constriction was sufficient to break the neck, as constriction would proceed until fission is fully completed. More recent data have modified our understanding of the possible role of constriction in dynamin-mediated membrane fission: (1) dynamin cryoelectron microscopy images and 3D reconstruction showed that the polymer can constrict down to a constriction radius, R_c, of 4–5 nm (Danino et al., 2004), filled with a tubular membrane (2 nm thick) that surrounds a water lumen (2–3 nm) (Chappie et al., 2011). These structural data support the idea that dynamin does not reach the hemifission state by constriction. (2) GTP-mediated constriction (Danino et al., 2004) and torsion (Roux et al., 2006) do not lead to fission unless the tube is both attached to the substrate (Danino et al., 2004) and subjected to longitudinal tension (Roux et al., 2006). These results showed that membrane constriction is not sufficient for fission and also suggested that mechanical parameters of the membrane (tension, bending rigidity) could play role in controlling fission.

Theory of membrane mechanics links the elastic energy, E_el, of the membrane to its shape via the Canham-Helfrich equation (Helfrich, 1973):

$$E_{el}=\sigma \Delta A+{\int }_A\frac{\kappa }{2}{J}^{2}dA.$$

The first term of this equation (σΔA) is the energy associated with membrane stretching, which depends on the membrane tension, σ, and the change in its surface area, ΔA. The second term is the energetic cost associated with membrane bending, a function of the local curvature, J (which characterizes the local shape of the membrane), multiplied by the membrane bending rigidity, κ, integrated over the whole membrane area, A. This rigidity depends on the lipid composition of the membrane. The Canham-Helfrich equation allows for calculating shapes and energies of lipid membranes in practically any conditions by measuring both membrane tension and rigidity.

As the dynamin helix constricts, it imposes a strong curvature on the membrane tube that it covers. This strong curvature has a high energetic cost. We thus reasoned that dynamin constriction could be significantly impeded by membrane elasticity, leading us to study how membrane mechanics influences the dynamin-mediated fission reaction.

In this study, we show that membrane fission is occurring at the frontier between the constricted dynamin coat and the bare membrane, a place where the important change in membrane curvature increases locally the elastic energy of the membrane. We further show that the energy barrier to fission is reduced by this local increase of membrane elastic energy, making fission spontaneously occur at the edge of dynamin. By setting rigidity (16 k_BT) and tension (from 10⁻⁵ to 5.10⁻⁴ N/m) and calculating the elastic energy difference between the unconstricted state (10 nm radius) of dynamin and the hemifission intermediate (3 nm radius), we estimate the energy barrier to fission to be of the order of 30–60 k_BT. By measuring the constriction strength, the torque of dynamin, we show that it is in the order of 700–1,000 pN nm, about 10 times larger than torques measured for other proteins. The huge value of the torque is, however, required to constrict the membrane to such extent. Moreover, we show that the mechanical energy spent by dynamin in constriction is sufficient to reduce the energy barrier to fission by the same amount evaluated from the elastic energy of the membrane. Our results support a mechanism by which dynamin constricts fast, within a few hundreds of milliseconds, forcing the membrane to reach a high elastic energy state at the edge of the dynamin coat. The increased elastic energy of the membrane then triggers spontaneous fission at the edge of dynamin, which takes a few seconds.

RESULTS

Fission Occurs at the Edge of the Dynamin Coat

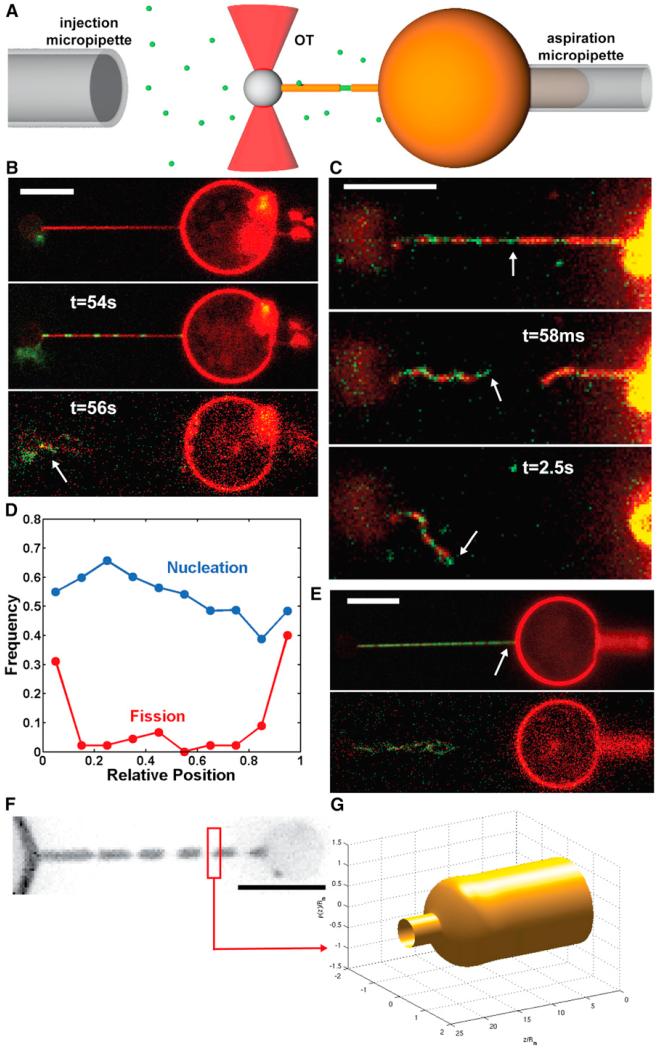
We adapted an in vitro assay (see Figure 1A) developed for the study of curvature-dependent lipid sorting (Sorre et al., 2009) and protein binding (Roux et al., 2010; Sorre et al., 2012). The assay is based on the generation of a membrane nanotube pulled out of a giant unilamellar vesicle (GUV) by means of optical tweezers. The membrane tension, σ, was set through aspiration of the GUV in a micropipette, allowing control over the dynamin-free tube radius, $r=\sqrt{\kappa ∕2\sigma }$. Using a second micropipette, we injected a mix of fluorescent Alexa-488 dynamin 1/nonfluorescent dynamin 1 in the vicinity of these nanotubes (see Experimental Procedures). In the absence of GTP, nucleation of dynamin seeds onto the nanotube, but no fission, was observed (Roux et al., 2010; data not shown). When GTP was added along with dynamin, small dynamin seeds formed along the tube, and membrane fission subsequently occurred (see Figure 1B; Movie S1). As previously described (Roux et al., 2006), the tube retracted rapidly following the first break, and no further break was observed. Using fast dual-color confocal imaging (see Extended Experimental Procedures), we observed that fission occurred at the edge of dynamin domain in 90% (N = 10) of the events (see Figures 1C and S1; Movie S2). Indeed, after fission, one extremity of the broken tube was covered with dynamin, whereas the other one was not (Figures 1C and S1; Movie S2). No fission was observed in the uncoated regions of the tube.

Figure 1. Localization of Fission Events at Dynamin-Membrane Edges.

(A) Schematic drawing of the experimental set-up. A micropipette (right) set the GUV’s tension. A membrane nanotube is extracted from the GUV via a microbead trapped in optical tweezers (red cones). A second micropipette (left) injects locally dynamin and GTP.

(B) Confocal pictures of a GUV labeled with BodipyTMR-PI(4,5)P₂ (red channel) and dynamin labeled with Alexa 488 (green channel); see also Movie S1. Top: Membrane nanotube before injection of dynamin + GTP. Middle: Nanotube partially coated with dynamin after injection of dynamin + GTP. Bottom: Fission 56 s after start of polymerization. Remaining tube is still attached to the bead (white arrow). Scale bars, 5 μm.

(C) Images from dual-color spinning disk confocal microscopy. Top: tube before fission. Middle: Same tube 58 ms after fission. Bottom: Same tube 2.5 s after fission. After fission, extremity of the left stump is covered with green dynamin, whereas the right stump is uncoated, showing that fission occurred at the edge between a seed of dynamin (white arrows) and the dynamin-free membrane nanotube (see also Figure S1 and Movie S2). Scale bars, 5 μm.

(D) Frequency of dynamin nucleation (blue) and fission (red) along the nanotube. Position is normalized so that 0 and 1 are, respectively, the bead boundary and the connection between the tube and the GUV. N = 44 tubes.

(E) Confocal pictures of a GUV and a dynamin-coated nanotube as shown in (B) (see also Movie S3). Nothing remaining of the tube is seen on the GUV, showing that fission occurred at the connection between the tube and the GUV (white arrow). Scale bars, 5 μm.

(F) Fluorescence image of a membrane tube constricted by dynamin in presence of GTP (TMRPE). Scale bars, 5 μm.

(G) Calculated shape a single dynamin-membrane edge by simulations.

We hypothesized that the considerable change of curvature from the highly constricted dynamin-coated part to the less curved bare tube could favor fission. We were thus prompted to look at the efficiency of fission at the connection between the tube and the GUV, where the change in curvature is even more dramatic. Indeed, most of the fission events occurred at the boundary between the tube and the GUV (38%) or at the boundary between the tube and the bead (36%) (N = 44; Figures 1D and 1E; Movie S3). It is worth noting that shapes of the membrane at both connections are similar, as the membrane-bead adhesion patch is much larger (several hundreds of nano-meters) than the size of the tube in this assay (Koster et al., 2005). Dynamin nucleation was homogeneous along the tube axis (Figure 1D, blue curve), indicating that this higher probability of fission was not due to preferential nucleation of dynamin at the bead, at the GUV, or on the parts of the nanotube adjacent to them but consistent with an influence of the local membrane shape (Figure 1F).

The Membrane Shape at the Dynamin-Membrane Edge Facilitates Fission

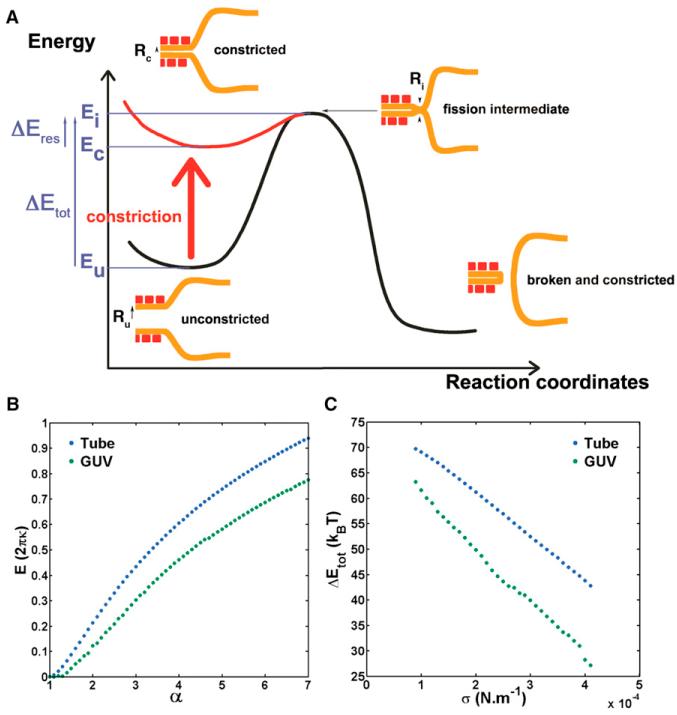
We then calculated the shape of the membrane at the edge of the constricted dynamin tube (hereinafter called the “dynamin-membrane edge”). By setting the constriction radius R_c, σ, and κ (see Extended Experimental Procedures) and numerically minimizing the elastic energy of the membrane, we can calculate the shape of the dynamin-membrane edge (Figures 1F and 1G). The funnel shape of the dynamin-membrane edge is associated with a local increase in elastic energy that can be estimated numerically (Figure 2B) (Shlomovitz et al., 2011). This elastic energy depends on the ratio α = R_m/R_c, where R_m is the radius of the bare tube, which is set by membrane tension and bending rigidity. Thus, the smaller R_c is (the more dynamin constricts), the higher the elastic energy of the dynamin-membrane edge is.

Figure 2. Energy Landscape of Dynamin-Mediated Fission.

(A) Mechanism and associated energy landscape for dynamin-mediated fission reaction. Intermediate state corresponds to hemifission, in agreement with experiments using lysolipids shown in Figure S2.

(B) Energy of the neck joining the bare membrane tube with the dynamin-coated tube (blue) and energy of the neck joining a GUV or bead to a dynamin-coated tube (green) as a function of α = R_m/R_c with R_m as the radius of the dynamin-free tube and R_c as the radius of the constricted dynamin-coated tube.

(C) Total energy barrier for fission within the lipid tube (blue) or in the GUV-dynamin or bead-dynamin edge (green) as a function of tension for κ = 16 k_BT and R_i = 3nm, R_u = 10 nm.

We reasoned that the local increase of elastic energy of the membrane edge could favor fission by reducing its energy barrier. Fission was proposed to occur wherever the membrane reaches a hemi-fission state, when the membrane radius shrinks below a threshold R_i ~3 nm (Kozlovsky and Kozlov, 2003), comparable to the membrane thickness (see fission intermediate in Figure 2A). The existence of such hemifission intermediate is supported by the experimental fact that fission is nonleaky (Bashkirov et al., 2008). Reaching an intermediate state with such a strongly curved membrane is a rare event and must thus be the rate-limiting step of membrane fission. We propose that, by constriction of dynamin, the elastic energy of the membrane increases most at the edge of the dynamin coat, thereby reaching the constricted state (Figure 2A). Then thermal fluctuations of the membrane edge would allow spontaneous fusion of the inner layer of the tube, reaching the hemifission state. Since the energy of the intermediate state E_i and of the unconstricted state E_u corresponds to the elastic energy of the membrane at the edge of dynamin, the full energy barrier is ΔE_tot = E_i − E_u (see Figure 2A).

We numerically estimated the magnitude of the energy barrier ΔE_tot in two cases: (1) for the membrane edge connected to the bead or GUV; and (2) for the membrane edge connected to the bare tube. For (1), ΔE_tot = 20–65 k_BT, and for (2), 35–70 k_BT (Figure 2C; k_BT is the thermal energy). These values are close to previous theoretical estimations for the fission energy barrier (Kozlovsky and Kozlov, 2003). The actual value of the barrier depends on membrane tension (see Figure 2C) and rigidity (data not shown). Also, as shown in Figure 2C, we predict that the energy barrier is smaller close to the bead or vesicle, thus accounting for a higher fission probability there (Figure 1D). We further estimated the probability to break close to the bead or GUV from the difference of these energy barriers (see Extended Experimental Procedures). Considering the range of tensions we have in our experiments (10⁻⁶ N/m–10⁻⁴ N/m), we found this probability to be between 70% and 95%, consistent with the above experimental value of 38 + 36 = 74%.

To further test the role of membrane elasticity in dynamin-mediated fission, we used our model to estimate the expected dependence of the average fission time, <t_f>, with membrane tension and bending rigidity. According to the model (see Figure 2A), after constriction, fission at the dynamin-membrane edge is spontaneous and the residual energy barrier after constriction, ΔE_res = E_i − E_c is, this way, small enough to be overcome by thermal fluctuations of the membrane (see Figure 2A). If after constriction, fission is thermally activated, <t_f>, should satisfy a simple Arrhenius equation, <t_f> = τe^ΔE_res/k_BT, where τ ~1 ns is the typical time scale of the membrane tube thermal fluctuations. By taking a linear approximation for the elastic energy of the edge with the curvature of the constricted dynamin tube (1/R_c), we find (see Extended Experimental Procedures):

$$\langle t_f\rangle \approx \tau \exp \left(b\frac{{\kappa }^{3∕2}}{\sqrt{\sigma }}/k_{B}T\right),$$ (Equation 1)

where b is a constant that depends on R_i and R_c; σ, membrane tension; and κ, membrane rigidity.

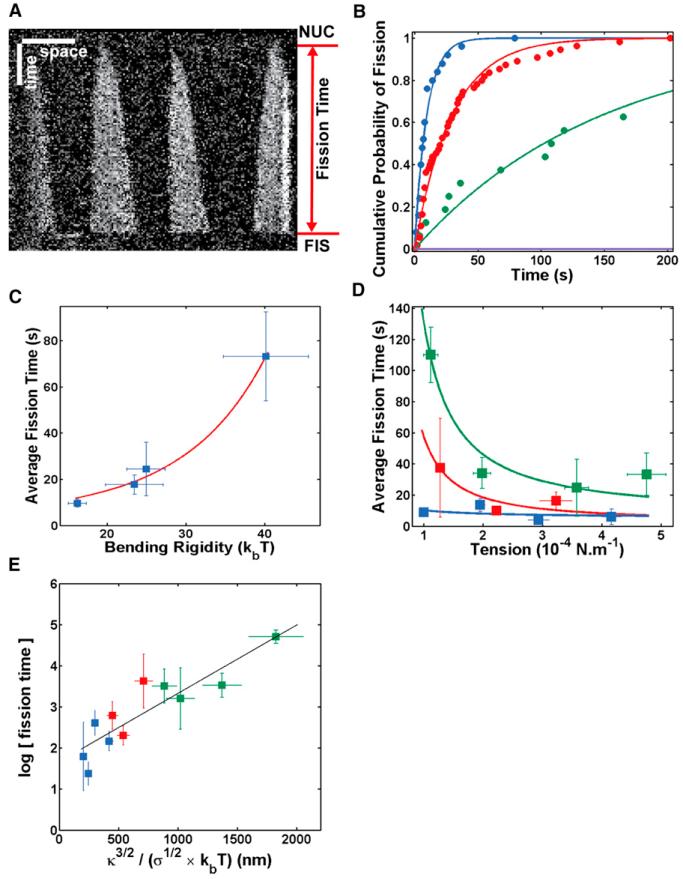
We experimentally validated Equation 1 by studying how long it takes for dynamin to break membrane tubes. As dynamin and GTP are coinjected, we defined the fission time t_f as the time elapsed between nucleation of dynamin seeds and fission (see kymograph in Figure 3A). At 150 μM GTP, a physiological concentration of GTP (Otero, 1990), the average fission time <t_f> was 9.6 ± 1.7 s, similar to the in vivo values (Taylor et al., 2011). The fission time decreased when the GTP concentration increases, with <t_f> at 1 μM GTP = 85.3 ± 8.7 s and <t_f> at 10 mM GTP = 6.2 ± 0.8 s (see Table S1). As a first test of our model, we verified that the fission times were exponentially distributed (Figure 3B; Table S1) as expected for a thermally activated, single-step process obeying Poisson statistics. We then verified that the dynamin-mediated fission reaction proceeds through a hemifission intermediate. Lysolipids, such as lysophosphatidylcholine (LPC), are known to inhibit fusion because their conical shape increases the hydrophobic mismatch in the stalk intermediate, increasing the energy barrier to fusion (Chernomordik and Kozlov, 2008). We found that 30% mol/mol LPC increased the average fission time to 48.8 ± 16 s, with 10% of the tubes not breaking after 300 s (see Figure S2). These results strongly support our assumption that dynamin-mediated membrane fission proceeds through a hemifission intermediate, similar to the stalk/hemifusion intermediate in fusion.

Figure 3. Kinetics of Dynamin Fission.

(A) Kymograph. Fluorescence of Alexa488-dynamin along a membrane tube as a function of time. Dynamin polymerizes from four initial nucleation seeds until fission occurs. Fission time is measured as the time elapsed between start of polymerization (NUC) and fission (FIS). Here, t_f = 168 s.

(B) Cumulative probability of fission at four different conditions: [GTP] = 500 μM (blue); [GTP] = 5 μM (red); [GTP] = 375 μM + [GTPγS] = 125 μM (green); and [GTP] = 250 μM + [GTPγS] = 250 μM (purple). Circles, experimental points. Line, exponential fit 1−exp(−t/τ). The fitted parameters, τ, for different GTP concentrations are listed in Table S1. Scale bars: horizontal, 5 μm; vertical, 30 s.

(C) Bending rigidity dependence of fission time. Blue squares and bars: experimental points, average + SEM. Red line: y = a*exp(bx^3/2). Different lipid compositions are used to obtain different bending rigidities; see Table S2.

(D) Tension dependence of fission time. Blue: κ = 16.2 ± 1.2 kT [EggPC+PI(4,5)P₂]. Red: κ = 25.0 ± 2.4kT [EggPC + Cholesterol + PI(4,5)P₂]. Green: κ = 44.8 ± 5.1kT [Sphingomyelin+PI(4,5)P₂]. Squares and bars: experimental points, average + SEM. Lines, y = a*exp(b/x^0.5).

(E) Relationship between the log of fission time and κ^3/2/σ^1/2. Same color code as in (D). Squares and bars: experimental points, average + SEM. As predicted by our model, we observed a linear dependence (black line), linear fit: y = a*x+b, a = 1.17 ± 0.42 10⁶, b = 0.59 ± 0.27, R² = 0.82.

We next tested the dependence of the fission time with membrane tension and rigidity (see Equation 1). In our in vitro assay, membrane tension can be tuned by changing the aspiration pressure in the micropipette, and rigidity can be tuned by changing the lipid composition (see Table S2; Extended Experimental Procedures). As expected, the fission time increased with membrane rigidity (Figure 3C), following exp(constant×κ^3/2) (see Equation 1). Dependence of the fission time with membrane tension compatible with the predicted relation in $\exp (constant∕\sqrt{\sigma })$ was also observed (Figure 3D). The observed dependences of the fission time with tension and rigidity are in good agreement with our model, but our model also states that they should be the dominant membrane parameters controlling the fission time. Following this statement, we expected the logarithm of <t_f> to have a linear dependence with ${\kappa }^{3∕2}∕\sqrt{\sigma }$ (see Equation 1), which was experimentally verified (Figure 3E). We concluded that the dependences of the fission time with membrane tension and rigidity further show that the mechanical determinants of the membrane shape control the kinetics of the dynamin fission reaction.

The Dynamin Torque Is Sufficient for Constriction

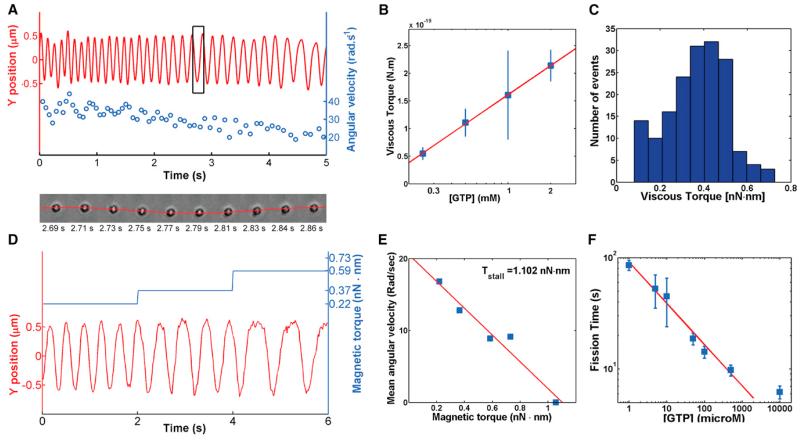
The mechanism proposed earlier for dynamin-mediated fission reaction is strongly dependent on the ability of dynamin to constrict. We thus wondered if the constriction strength of dynamin was sufficient to constrict such membrane necks. As dynamin undergoes torsion during constriction, it generates a torque (see Figures 4A and S3C; Movie S4). Thus, the constriction torque of dynamin must be strong enough to counteract membrane elasticity that widens the tube. In order to verify this, we measured the torque, Γ, exerted by dynamin during constriction by monitoring the position of beads of radius, r, attached to the dynamin coat. The beads rotated following GTP addition, allowing us to track the torsion of the dynamin coat (Morlot et al., 2010; Roux et al., 2006). Because of this fast motion, the beads incurred a viscous drag, which counteracted the torque generated by dynamin and limited the maximal angular speed. The viscous drag acting on a bead of radius r spinning around a linear axis is: Γ_visc = 14πηr³ω, where ω is the angular velocity of the bead and η is the viscosity of water. We used beads of 675 nm radius and measured an average angular speed of ω = 15.8 ± 5 rad/s at 2 mM GTP (Figure 4B), corresponding to an average torque of 214 ± 74 pN.nm. These beads are significantly slower than beads of 95–180 nm radii used in previous studies (~55 rad/s) (see Morlot et al., 2010; Roux et al., 2006) indicating that the viscous torque acting on the 675 nm beads is of the same order of the dynamin torque. Because the beads are rotating, the torque of dynamin is larger than the measured viscous torque. The highest value of the viscous torque (730 pN.nm; see Figure 4C) obtained for the fastest bead is thus a closer underestimate of the dynamin torque. Γ = 730 pN.nm is 20 times larger than the torque developed by proteins twisting DNA (10–20 pN.nm for the recombinase RecA) (Lipfert et al., 2010) or the rotational motor F1 ATPase, which usually generate torques of 40 pN.nm (Yasuda et al., 1998).

Figure 4. Torque Measurements.

(A) Top: Y-position trace (red) and corresponding angular velocity values (blue) of a bead rotating around a membrane tube induced through dynamin twisting upon GTP hydrolysis. Bottom: Sequence of 10 frames of the bead performing exactly one rotation corresponding to the black rectangle. See also Movie S4.

(B) Linear dependence of the viscous torque with the log of the GTP concentration. Blue squares and bars: experimental points, average + SEM. Red line: linear fit, y = a*x+b, a = 1.43 ± 1.00 10⁻¹⁹, b = 9.80 ± 3.70 10⁻²⁰, R² = 0.95.

(C) Histogram of viscous torques measured from the fastest bead, as shown in Movie S4.

(D) Position relative to the axis of the tube of a magnetic, 695-nm radius streptavidin-coated bead rotating after addition of 1 mM GTP, and under the magnetic torque (blue; see text for explanations) generated by a magnetic field. The bead slows down as magnetic torque increases; see also Figure S3.

(E) Velocity of a rotating bead as the function of the magnetic torque. Bead stops at 1.1 nN.nm. See also Movie S5.

(F) [GTP]-dependence of fission time. Blue squares and bars: experimental points, average + SEM. Red line: linear fit, y = a*x+b, a = −0.37 ± 0.07, b = 4.51 ± 0.27, R² = 0.98.

We measured the maximum torque of dynamin (stall torque Γ_s) by attaching magnetic beads to dynamin-coated tubules and blocking their rotation with a magnetic field. After calibration of the set-up (see Extended Experimental Procedures and Figures S3A, S3B, S3D, and S3E), magnetic fields were translated into the magnetic torque experienced by the bead in the magnetic field. We found that beads stopped to rotate when magnetic torques exceeded 1,300 pN.nm at 1 mM GTP. Rotational movement started again upon switching off the magnetic field (Figure S3F; Movie S5), confirming that abrupt stop was due to magnetic field. We observed that the angular velocity of the bead decreased linearly with increasing intensities of the magnetic field (Figures 4D and 4E). Linear fits (Figure 4E) gave an average value of the stall torque of dynamin of 1,100 ± 340 pN.nm.

From the free energy of a dynamin-constricted tube (see Extended Experimental Procedures), we calculated that R_c is related to the dynamin torque by R_c = R_u/(1 + (ΓR_u/2πκh)), where h = 13 nm is the dynamin pitch. According to this relation, constriction from R_u = 10 nm to R_c = 5 nm radius would require a torque of approximately 500 pN.nm. We concluded that the large value of the dynamin torque measured earlier was necessary and sufficient for constriction of membrane necks.

Dynamin Mechanical Work Reduces the Energy Barrier to Fission

The mechanical work of dynamin is partially spent in reducing the energy barrier to fission. If our model is valid, this fraction of the mechanical work reduces significantly the energy barrier. The residual barrier ΔE_res should be in the range of a few k_BT. Thus, we expect the dynamin work to be of the same order of magnitude as the full barrier ΔE_tot estimated from the elastic energy of the membrane (discussed earlier). Theoretically, the fraction of the dynamin work can be subtracted from the energy barrier (see Extended Experimental Procedures), with ΔE_res = ΔE_tot − cΓθ, where Γθ is the dynamin work (Figure S3C; also discussed later). The fission time expression is then:

$$\langle t_f\rangle \approx \tau \exp (\Delta E_{tot}-c\Gamma \theta ∕k_{B}T),$$ (Equation 2)

where c is a constant and θ is the angle by which the helix rotates for each GTP it hydrolyzes (Figure S3C). According to this definition, we can identify Γθ as the work performed by the helix per hydrolyzed GTP. According to Equation 2, for each amount Γθ of mechanical work performed per GTP, ΔE_tot is lowered by an amount cΓθ. Thus, c characterizes the efficiency with which mechanical work is used to lower the fission barrier. The work performed by dynamin upon the hydrolysis of one GTP is proportional to the difference in chemical potential between GTP and its hydrolysis products. Thus, for experimental concentrations of GTP, we expect:

$$\Gamma \theta =\xi k_{B}Tln\left(\right[GTP\left]\right)+constant,$$ (Equation 3)

where the dimensionless number ξ is the yield of the conversion of chemical energy into work. As a consequence, the product cξ characterizes the efficiency with which dynamin uses chemical energy to lower the barrier to fission. Inserting Equation 3 into Equation 2, we finally find:

$$ln(<{\mathrm{t}}_{\mathrm{f}}>)=\mathrm{c}\xi ln\left(\right[GTP\left]\right)+constant.$$ (Equation 4)

To validate this extended mechanochemical framework experimentally, we sought to verify the predicted GTP dependences and to characterize the efficiency cξ. We first showed (Figure 4B) that the torque Γ depended linearly on ln([GTP]), as expected from Equation 3. The slope allowed us to estimate ξ/θ = 34. Knowing the full constriction angle θ_full from structural data (Mears et al., 2007; 1/14 of a turn leads to θ_full = 2π/14 ≈ 0.45 rad), and assuming that ξ = 1, we could calculate the minimal number of hydrolyzed GTPs to reach full constriction N = θ_full/θ = 34×0.45 ≈ 15. We then measured the dependence of the fission time on GTP concentration, yielding very good agreement with Equation 4 (Figure 4F) for values of GTP concentration lower than 10 mM. The experimental verification of Equation 4 validates our picture of the role of GTP hydrolysis in lowering the energy barrier to fission through a modification of the membrane shape. It is interesting that the slope of this curve gave cξ = 0.37 ± 0.07, meaning that over a large range of GTP concentrations, the reduction of the fission energy barrier represents 37% of the energy available from GTP hydrolysis. Knowing the minimal number N of GTP required for a full constriction of dynamin, we estimated the minimal energy E_min spent by dynamin in reducing the energy barrier to fission: One GTP delivers ~20 k_BT; thus, E_min = Fraction of chemical energy×N×Energy of hydrolysis of one GTP = 37%×15×20k_BT ≈ 111k_BT. This value is of the same order of magnitude as the energy barrier ΔE_tot values (35–70 k_BT) estimated from the change in shape of the dynamin-membrane edge mediated by dynamin constriction. This simple calculation shows that dynamin through its constriction transfers enough energy to the membrane to significantly reduce the energy barrier to fission so that it becomes spontaneous at the dynamin-membrane edge.

Dynamin Reaction Kinetics Is Controlled by Membrane Tension In Vivo

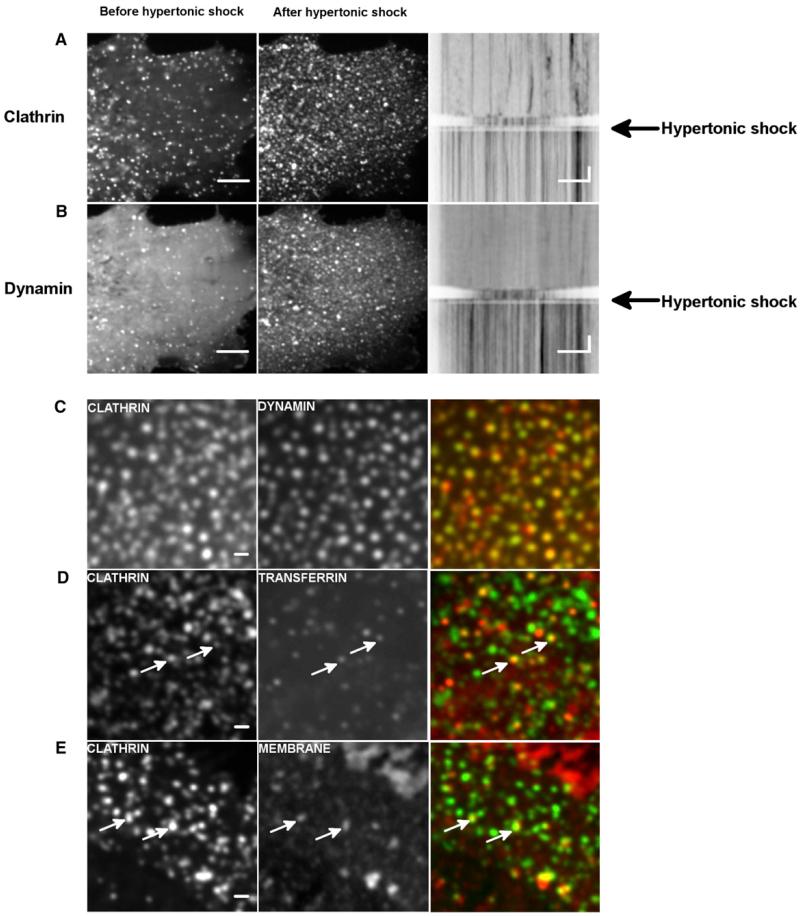
We next studied if the shape of the dynamin-membrane edge could control the kinetics of dynamin fission in vivo. We aimed at reducing membrane tension and tracked the effect on the dynamics of CCP formation. We exchanged quickly the culture medium of Cos7 cells to medium containing 0.45 M sucrose (Heuser and Anderson, 1989) and followed the dynamics of clathrin-GFP by confocal imaging. As previously described (Heuser and Anderson, 1989), the rapid turnover of clathrin-GFP dots at the plasma membrane in Cos7 cells stopped within seconds after the shock (Figure 5A; Movie S6). The number of clathrin-GFP dots increased after the shock. These clathrin-GFP structures seemed to stay attached to the plasma membrane, suggesting a block of the clathrin-coated pits at the fission level. Consistently, dynamin-GFP followed the same behavior: More dots were seen after the shock (Figure 5B; Movie S6), without turnover (see kymograph in Figure 5B). Moreover, the clathrin-RFP structures perfectly colocalized with dynamin-GFP dots after the shock (~85%; see Figure 5C), showing that clathrin structures were blocked at the stage of dynamin ring formation. As the dynamics of clathrin bud are altered by overexpression of endocytic proteins, we tested the effect of hypertonic shock on genome-edited SKML-2 cells, where clathrin-RFP and dynamin-GFP are expressed at the same level as that of endogenous proteins (Doyon et al., 2011). When hypertonic medium was applied to these cells, the number of clathrin/dynamin dots increased, and their dynamic exchange was blocked (data not shown). As in Cos7 cells, clathrin-RFP dots colocalized with dynamin-GFP dots (see Figure S4).

Figure 5. Block of Fission of CCPs by Hypertonic Shock.

(A) COS-7 cells transfected with mCTLA-mCherry before and after hypertonic shock; resulting kymograph that follows the time course before and after hypertonic shock.

(B) COS-7 cells transfected with DNM2-GFP before and after hypertonic shock; resulting kymograph that follows the time course before and after hypertonic shock. Scale bar, 5 μm; time scale, 5 s. see also Movie S6.

(C) Colocalization of mCTLA-mCherry (red) and DNM2-GFP (green) in COS-7 cells after hypertonic shock; see also Figure S4.

(D) Colocalization of mCTLA-GFP (green) and transferrin (red) in COS-7 cells after hypertonic shock.

(E) Colocalization of mCTLA-GFP (green) and plasma membrane (red) in COS-7 cells after hypertonic shock. Scale bar, 1 μm.

We next verified that the clathrin dots blocked at the fission step were fully assembled CCPs. They indeed partially colocalized with transferrin, showing that cargo were present in these structures (see Figure 5D). As well, the plasma membrane lipophilic dye MASK (Invitrogen) showed a slightly increased signal in clathrin structures, reflecting the curved membrane of the bud (see Figure 5E). Taken together, these results strongly support the idea that many of the clathrin-coated dots frozen at the plasma membrane are fully assembled CCPs, blocked at the assembled dynamin stage, unable to break the membrane. These in vivo results are consistent with our in vitro results: They show that a membrane tension decrease blocks dynamin-dependent endocytosis at the fission step, in a similar way than reduced membrane tension strongly delayed fission in vitro. Moreover, as previously reported (Boulant et al., 2011), we find that hypo-osmotic shock delays CCPs formation but does not alter dynamin dynamics in the first few minutes after the shock (data not shown).

DISCUSSION

In this study, we first showed that dynamin-mediated fission occurs at the edge of the dynamin coat. Consistently, in mitochondrial fission, breakage was often observed at the boundary between the DNM1 ring and the rest of the mitochondria (Bleazard et al., 1999). We then showed that fission was facilitated at the dynamin-membrane edge because of the local membrane elastic energy increase due to considerable change in curvature. We next showed that not only the location but also the kinetics of the reaction is set by the shape of the membrane connecting the constricted tube to the bare part of the membrane. The constriction torque of dynamin and membrane elasticity parameters such as tension and bending rigidity that control the membrane edge shape thus act directly on the kinetics of dynamin-mediated membrane fission. Moreover, we showed in this study that the calculation of the energy barrier estimated from the shape of the membrane (from which we can estimate the elastic energy of the membrane) is in the range of 50–70 k_BT and can be overcome by the mechanical work generated by dynamin during constriction (in the range of 100 k_BT). It is important to note that the contributions of the dynamin work, tension and rigidity to the kinetics of the fission reaction are different: Measured GTPase rate of dynamin in the assembled form (Praefcke and McMahon, 2004) suggests that the minimal amount of GTP required for full constriction is hydrolyzed within hundreds of milliseconds. Our previous study of the dynamics of dynamin constriction (Morlot et al., 2010) consistently showed that constriction should also happen within a few hundreds of milliseconds. As for nonlimiting GTP concentrations, fission takes a few seconds at least; our results are compatible with, first, (1) a fast constriction of dynamin, and then (2) a long delay to spontaneous fission of the constricted neck. Thus, at nonlimiting GTP concentrations (closer to in vivo situation), the kinetics of dynamin-membrane fission are expected to be primarily regulated by the elasticity of the membrane.

Indeed, we showed that, consistently with our in vitro results, clathrin-mediated endocytosis is blocked by reducing membrane tension in vivo. Also, in vivo (Taylor et al., 2011) and in vitro (this study and Bashkirov et al., 2008), typical fission times (a few seconds) are similar, with membrane tension values averaging 10⁻⁴ N/m, (for in vivo values, see Dai et al., 1997). Our finding that reduced membrane tension delays membrane fission is qualitatively similar to previous results showing the need of longitudinal tension for dynamin-mediated membrane fission (Roux et al., 2006). Consistently, when membrane tension is artificially kept low by using an excess of membrane reservoir, dynamin-mediated membrane fission takes several tens of seconds, close to a minute (Pucadyil and Schmid, 2008). Finally, we showed that increased membrane rigidity delays fission, which is consistent with previous findings where increased membrane rigidity inhibited fission (Bashkirov et al., 2008). These observations strengthen the idea that fission kinetics is controlled by elasticity of the membrane in vivo.

Recent studies (Bashkirov et al., 2008; Pucadyil and Schmid, 2008) have been undertaken to suggest that dynamin-mediated fission could be triggered by GTP-induced depolymerization instead of constriction. Our results showing that fission occurs at the edge of the dynamin coat indicate that it requires partial coating of the membrane, which can be achieved either by partial polymerization of a bare membrane, or partial depolymerization of a fully coated membrane. However, in our experiments, we never observed depolymerization of the dynamin coat before (see Figure 3A) or after (see Figure 1C; t = 2.5 s) fission. Because in our experiments the optical resolution limit is above the size of a dynamin turn, we cannot exclude depolymerization restricted to a few turns. In the hypothesis that fission is mediated through depolymerization, it was predicted that long coats would have a reduced fission efficiency (Pucadyil and Schmid, 2008), as they would require more time to be fully depolymerized. In our experiments, we saw no dependence of the fission time with length of single dynamin seeds, from 150 nm to 10 μm (see Figure S1B). Also, GTP energy was proposed to be spent in depolymerization rather than constriction (Bashkirov et al., 2008). The authors used conductance through dynamin-coated membrane tubes to measure their radii and found very small radii for assembled, nonconstricted dynamin (between 2 and 3 nm, 5–7 nm with membrane) when compared to the 10–11 nm radii found in other studies (Chen et al., 2004; Danino et al., 2004; Roux et al., 2010). When GTP was added, conductance increased before fission, suggesting disassembly. They concluded that GTP-induced depolymerization of dynamin could lead to spontaneous fission because of the narrow radius of assembled dynamin. This scenario becomes realistic for radii much below 10 nm, as tubules of 10 nm are stable. As the authors did not take into account the Debye length (Roux and Antonny, 2008), the screening distance of ionic charges (in the order of 1–2 nm), the conductance values of radii may not be accurate, which would explain discrepancy with other techniques (Chen et al., 2004; Danino et al., 2004; Roux et al., 2010; Sweitzer and Hinshaw, 1998; Takei et al., 1999). Thus, most probably, assembled dynamin makes tubules of 10 nm radius, which require further GTP-dependent constriction to be cut. In our present study, the good agreement between energetics of membrane constriction and dynamin torque work favors the hypothesis that GTP energy is primarily spent in constriction rather than in depolymerization.

In a broader perspective, the model presented here to explain the mechanism of dynamin function might show the important role of membrane elasticity for all fission reactions mediated by the constriction of a narrow membrane neck, as it is proposed for ESCRT-III-mediated fission (Fabrikant et al., 2009) and as it is the case in lipid phase separation (Roux et al., 2005). However, how constriction is performed and which energy source is used in other, dynamin-independent, fission reactions remains to be understood.

EXPERIMENTAL PROCEDURES

A full description of the methods is in the Extended Experimental Procedures.

Nanotube Pulling From GUV

GUVs were made by a modified protocol of the electroformation technique (Angelova et al., 1992; Roux et al., 2010). The aspiration of a GUV of radius R_GUV within a micropipette of radius R_pipette allowed to set membrane tension: σ = (1/2)R_pipetteΔP)/(1 – (R_pipette/R_GUV) (Evans and Rawicz, 1990).

A lipid nanotube was extruded from a micropipette-aspirated GUV containing 0.03% mol/mol of a biotinylated lipid (DSPE-PEG2000-Biotin, Avanti Polar Lipids, Alabaster, AL, USA) by moving away the pipette from an optically trapped, 3 μm diameter streptavidin-coated bead (Spherotec, Lake Forest, IL, USA) attached to the GUV prior to pulling. The fixed optical trap was custom-made and calibrated (see Extended Experimental Procedures; stiffness, k = 360 pN.μm⁻¹·W⁻¹). A mix of baculovirus purified human dynamin 1 (see Extended Experimental Procedures for purification details) and GTP (Roche Applied Science, Indianapolis, IN, USA) was injected in the vicinity of the lipid tube via a second micropipette. Two-color time-lapse acquisitions were performed with either a confocal microscopy (Eclipse C1 Nikon, Tokyo, Japan) or a spinning disk confocal (Intelligent Imaging Innovations, Denver, CO, USA).

Torque Measurement by Viscous Drag and Magnetic Field

Streptavidin beads (1.35 μm diameter streptavidin-coated, polystyrene beads, Spherotec, Lake Forest, Illinois, USA) are grafted onto biotinylated dynamin tubules formed from membrane sheets (see Extended Experimental Procedures) (Morlot et al., 2010; Roux et al., 2006). The beads rotate following GTP addition and resulting constriction of the dynamin coat (Morlot et al., 2010; Roux et al., 2006), experiencing a viscous torque Γ_v = 14πη(R + r)³ ω = ξω (Happel and Brenner, 1983), where η is the viscosity of the surrounding fluid, R is the radius of the bead, r is the radius of the tubule, and ω is the angular spinning velocity. Differential interference contrast (DIC) and computer-based live recording of the rotating beads with a GUPPY camera (Allied Vision Technologies, Stadtroda, Germany) allowed direct measure of the angular spinning velocity and estimation of the viscous torque from the aforementioned formula.

The stall torque, Γ_S, was measured by using magnetic beads (1.31 μm diameter streptavidin-coated, paramagnetic beads; Spherotec, Lake Forest, IL, USA), to which is applied an external torque via a variable electromagnetic field. This magnetic field was calibrated by two independent methods detailed in the Extended Experimental Procedures.

Cell Transfections, Plasma Membrane Staining, Transferrin Uptake, and Hypertonic Shock

COS-7 cells were transfected using FuGENE-6 (Roche Applied Science, Indianapolis, IN, USA) with dynamin 2 fused to green fluorescent protein (GFP) (kindly provided by P. De Camilli; Howard Hughes Medical Institute [HHMI], Yale University) or mouse clathrin-light-chain fused to mCherry or GFP (kindly provided by C. Merrifield, Cambridge University, and by P. De Camilli, HHMI, Yale University). Cells were imaged 18 to 24 hr posttransfection in Leibovitz medium (GIBCO, Life Technologies, Paisley, UK). While imaging, the medium was changed with a hypertonic solution of 0.25 M sucrose in Leibovitz medium. Cell membrane staining was achieved by incubating cells for 5 min at 37°C with deep red Cell Mask (Molecular Probes, Life Technologies, Paisley, UK) before imaging. For Transferrin uptake assays, cells were starved in serum-deprived Dulbecco’s modified Eagle’s medium M-F12 for 30 min on ice, then incubated with 5 μg/ml Alexa-fluor 594 Transferrin (Invitrogen, Grand Island, NY, USA) in hypertonic medium (0.25 M sucrose Leibovitz medium) for 3 min at RT. Cells were washed with hypertonic buffer before imaging.