Protein Denaturants at Aqueous–Hydrophobic Interfaces: Self-Consistent Correlation between Induced Interfacial Fluctuations and Denaturant Stability at the Interface

Abstract

The notion of direct interaction between denaturing cosolvent and protein residues has been proposed in dialogue relevant to molecular mechanisms of protein denaturation. Here we consider the correlation between free energetic stability and induced fluctuations of an aqueous–hydrophobic interface between a model hydrophobically associating protein, HFBII, and two common protein denaturants, guanidinium cation (Gdm⁺) and urea. We compute potentials of mean force along an order parameter that brings the solute molecule close to the known hydrophobic region of the protein. We assess potentials of mean force for different relative orientations between the protein and denaturant molecule. We find that in both cases of guanidinium cation and urea relative orientations of the denaturant molecule that are parallel to the local protein–water interface exhibit greater stability compared to edge-on or perpendicular orientations. This behavior has been observed for guanidinium/methylguanidinium cations at the liquid–vapor interface of water, and thus the present results further corroborate earlier findings. Further analysis of the induced fluctuations of the aqueous–hydrophobic interface upon approach of the denaturant molecule indicates that the parallel orientation, displaying a greater stability at the interface, also induces larger fluctuations of the interface compared to the perpendicular orientations. The correlation of interfacial stability and induced interface fluctuation is a recurring theme for interface-stable solutes at hydrophobic interfaces. Moreover, observed correlations between interface stability and induced fluctuations recapitulate connections to local hydration structure and patterns around solutes as evidenced by experiment (Cooper et al., J. Phys. Chem. A2014, 118, 5657.) and high-level ab initio/DFT calculations (Baer et al., Faraday Discuss2013, 160, 89).

I. Introduction

The pursuit for a global and self-consistent conceptual, mechanistic, and theoretical framework within which to discuss the denaturing properties and behaviors of cosolvents such as urea and guanidinium chloride (GdmCl) continues to garner a significant amount of scientific curiosity and effort.¹⁻⁸ The quest for a fundamental understanding of protein denaturation has a long and rich history, to which the reader is referred.⁹⁻²⁵ Based on recent experimental and molecular simulation studies, the notion of direct interactions of denaturants with proteins in solution has come to be accepted in consensus. Since common denaturants used in practical situations are needed in significantly high concentrations, i.e., 5 M urea for instance, the notion that there are no direct interactions between denaturant and protein becomes less justifiable.⁷ Within the context of direct interactions, one of two major mechanisms for denaturation involves the lessening of the hydrophobic effect as it relates to the formation of a compact “prefolded” ensemble of states where protein hydrophobic surface exposure to solvent is reduced in relation to the purely unfolded ensemble of states. The idea is that by associating with hydrophobic regions of the protein (specific residues, clusters of residues forming extended topographical “surfaces”, hydrophobic side chains, etc.), denaturant molecules can shield the hydrophobic surface area even in unfolded or extended configurations of the peptide/polymer. This chemical denaturation mechanism naturally involves direct interaction of the cosolvent molecule with regions of the protein surface. A particular aspect of this interaction deals with the precise nature of association geometries and the associated free energetics; specifically, molecules such as urea, and more so guanidinium cation (Gdm⁺), can present several predominant relative orientations to the protein surface through which the interaction is mediated. In general, it is proposed that a dominant interaction of urea with surface groups in protein simulations involves hydrogen bonding with polar side-chain functions,^26,27 while the unique hydration properties of the Gdm⁺²⁸ support alternative interaction modes involving stacking with side-chain planar and hydrophobic groups. However, we should note that the nature of the relative orientations would be dictated in part by the nature of solvation and hydrophobic effects as they pertain uniquely to each denaturant molecule. Understanding of the precise geometrical and associated free energetic properties of denaturant–protein interactions is important as a piece in a more complete understanding of the denaturation process from a molecular perspective. Previous studies have shown that cosolvents such as Gdm⁺ adopt orientations relative to “flat”, model hydrophobic surfaces that are planar. These hydrophobic surfaces include the aqueous liquid–vapor interface,^29,30 flat hydrophobic plate,^7,18 and hydrophobic polymer surface.²⁰ However, there is a lack of direct evidence for similar orientational behavior of Gdm⁺ upon approaching more complex aqueous protein interfaces. The inherent chemical and topographical heterogeneity of protein surface makes it difficult to find a qualitatively rigorous approach to evaluate the relative orientation between the surface of Gdm⁺ and the protein. To fill this gap, we apply molecular dynamics simulations investigating the association of Gdm⁺ cation with a specific protein with a relatively flat surface region consisting of hydrophobic residues. In the context of chemical denaturation via direct association, we ask here about the orientations that Gdm⁺ and urea adopt when interacting with hydrophobic regions of proteins. The combination of this analysis addresses ideas of direct interaction as well as hydrophobic effects as they pertain to the denaturation process. Furthermore, there is sentiment in the literature demonstrating the importance of solvent fluctuations and their relation to what is called the hydrophobic nature of solutes. For example, using molecular dynamics simulations, Godawat et al.³¹ found that water density near the surfaces of self-assembled monolayers (SAMs) with hydrophobic head groups (−CF₃, −CH₃) shows a poor distinction from that of SAMs with hydrophilic head groups (−OH, −CONH₂). However, differences arise when considering the fluctuations of water density near the two regions. Enhanced fluctuations reflected by the broad probability distributions of water number density are observed around hydrophobic surfaces compared with the bulk solution and hydrophilic surfaces.^32,33 Moreover, the enhanced density fluctuations around hydrophobic surfaces are further characterized by more compressible hydration shells and increased cavity formation,^34,35 indicating that the nature of hydration shells around hydrophobic surfaces is softer and more flickering than near hydrophilic ones. Since the long-ranged solute-induced perturbations of aqueous protein interfaces involve the coupling of local hydration shells of the solutes with distant hydration shells around protein surfaces, the natures of both would affect the extent of induced interfacial fluctuations. It would be interesting to compare the interface height fluctuations as Gdm⁺/urea approaches the hydrophobic/hydrophilic protein regions. We note that the interface height fluctuations we are pursuing here are conceptually different from the density fluctuations of refs (32, 33, 36, and 37), though both reflect the nature of hydration water around the protein surfaces. It is natural here to investigate the nature of induced fluctuations of the solvent at the protein–water interface via consideration of the fluctuations of the height of this interface (once defined in a well-controlled manner) upon approach of a denaturant molecule to a hydrophobic protein region as well as when the denaturant resides at very close separation to the protein–water interface.

The particular protein on which we are focusing in this study is hydrophobin-II (HFBII), a small protein expressed by filamentous fungi. The protein is known for its ability to form hydrophobic coatings on surfaces and self-assembles into monolayers on hydrophobic/hydrophilic interfaces such as the water/air interface.³⁸⁻⁴¹ These behaviors are mainly determined by the protein’s amphiphilicity. Acharya et al.⁴² mapped the effective hydrophobic regions and effective hydrophilic regions of HFBII by considering the density of small probe hydrophobic solutes around each region of the protein. They selected three regions with different hydrophobicity based on this and further monitored the density fluctuations in the vicinity of these regions. Their calculation shows that the largest density fluctuations occur around the most hydrophobic region whereas the least density fluctuations are detected around most hydrophilic region. This particular observation suggests hydrophobins as useful candidate proteins for comparing behaviors at hydrophobic and hydrophilic interfaces as denaturant molecules approach. We note that the purpose of this study is to demonstrate the specific denaturant’s stability and orientational preference around regions with different hydrophobicity of the protein with implication of the direct interaction as well as hydrophobic effects for the association between denaturant and the protein. The aim of this study does not focus on the denaturation process by these denaturants, so we use the totally fixed protein in the simulation along with quite low concentration of denaturants (1 M and an extreme case, single solute) compared with the significant high concentration (up to 5 M) in the actual denaturation experiments. We further emphasize that by using the single solute in this study, it is possible for us to systematically distinguish underlying characters of stability for different species (Gdm⁺ and urea) and orientational preference for different orientations (parallel and perpendicular relative to the regions of interest).

The paper is organized as follows. In section II we discuss the simulation protocols and computational details of the liquid–vapor interface and aqueous protein interfaces. Our results are presented in section III and are organized into four topics. We begin with discussion of potentials of mean force (PMFs) and interfacial fluctuations as single Gdm⁺/urea cross the aqueous liquid–vapor interface. We consider Gdm⁺/urea density distributions around the aqueous HFBII hydrophobic interface in 1.0 m solutions in the second part. We further investigate the PMFs and interfacial fluctuations as single Gdm⁺/urea approach this aqueous protein hydrophobic interface, demonstrating the resemblance between liquid–vapor interface and hydrophobic protein interface in terms of solute specific effect and orientational preferences. We finish this section by examining single Gdm⁺/urea approaching another region, which is considered a hydrophilic patch compared with the hydrophobic region we initially study. We address our conclusions and general discussion in section IV.

II. Method

A. Simulation Details

All the simulations in this study were performed with MD program NAMD 2.9b3,^43,44 using CHARMM22 all-atom force fields with CMAP backbone torsion correction term.⁴⁵ Simulations of single Gdm⁺/urea approaching the liquid–vapor interfaces were performed in the NVT ensemble. The simulation cell was rectangular with dimensions 40 Å × 40 Å × 150 Å, in which z is the direction normal to the liquid–vapor interface. The system contained one single Gdm⁺/urea and 1977 nonpolarizable TIP3P water model⁴⁶ water molecules. A rigid water geometry is enforced using SHAKE⁴⁷ constraints, and an integration time step of 1.0 fs was used. The temperature was kept constant at 300 K by applying the Langevin friction force scheme with a damping coefficient of 5 ps^–1. A switching distance of 10 Å, nonbonded real-space cutoff of 12 Å, and pair list generation distance of 14 Å were used for the van der Waals interactions, and the particle mesh Ewald (PME)⁴⁸ method was employed for the calculation of conditionally convergent electrostatic interactions. The grid size of PME in x-dimension is 40, in y-dimension is 40, and in z-dimension is 150 (as close to a 1 Å grid point separation as possible). In order to obtain the PMF for transferring single Gdm⁺/urea from bulk aqueous environment to the liquid–vapor interface, we define a collective variable, which is based on the Cartesian z-component of the separation between the water slab center of mass and single Gdm⁺/urea central carbon, describing this pseudochemical reaction path. To enhance sampling of the distribution of configurations where the collective variable holds a particular value, relevant restraint potentials were introduced on the collective variable in order to prevent it from moving outside of the desired range. In this case, we constructed 31 continuous “windows” with width 1.0 Å. In each window, central carbon of single Gdm⁺/urea was restrained to z-positions from 0 to 30 Å relative to the water slab center of mass using a harmonic potential U_restraint(z; z_relative,ref) = ¹/₂k(z – z_relative,ref)² with the force constant of 4 (kcal/mol)/Ų. To consider the orientational dependence of Gdm⁺ around interface, we further desired to compare the free energetics of single Gdm⁺/urea transferring from the bulk with two distinctive orientations: the planar ring of Gdm⁺/urea parallel to the liquid–vapor interface and perpendicular to the liquid–vapor interface. Here the orientations were defined based on identical definitions from previous publications^29,30 in which the angle θ between the vector normal to the molecular ring and the z-axis was computed. Gdm⁺/urea was considered as parallel (as shown in Figure 1A) and perpendicular (as shown in Figure 1B) to the liquid–vapor interface when θ = 0° and θ = 90°, respectively. We note that for the parallel orientation the normal vector of the molecular ring is along z-direction; for the perpendicular orientation, the normal vector of the molecular ring can either be along x or along y direction. Because of the homogeneous nature of liquid–vapor interface and the identical setup in x and y dimensions in the simulation, here we only need to consider one (when the normal vector is along y direction) of these two configurations in the perpendicular orientation case. In these two sets of simulations, initially, the parallel and perpendicular configurations of Gdm⁺/urea were selected as starting structures, and the orientations were maintained by restraining the directions of central carbon–nitrogen vectors. Based on the definition of orientations above, Gdm⁺ with parallel configuration has all three central carbon–nitrogen vectors in the plane of XY, with the magnitude along z-direction being zero. Therefore, harmonic potentials with force constant k = 1000 (kcal/mol)/Ų were applied to keep the magnitudes of z components of two of the three central carbon–nitrogen vectors as zero. With this restraint protocol, we can ensure the parallel orientation of single Gdm⁺ with respect to the liquid–vapor interface. For Gdm⁺ with perpendicular orientation, all three central carbon–nitrogen vectors are in the plane of XZ. To maintain this orientation, harmonic potentials with force constant k = 1000 (kcal/mol)/Ų were applied to restrain the magnitudes of y components of the carbon–nitrogen vectors as zero. These restraint protocols were also applied to single urea molecule by considering only the two central carbon–nitrogen vectors. Apart from the orientational restraints, identical choice of collective variable and setup of simulation windows were applied. The total sampling time for each window was 15 ns for all the simulations and properties were calculated from all but the initial 1 ns, which was treated as equilibration.

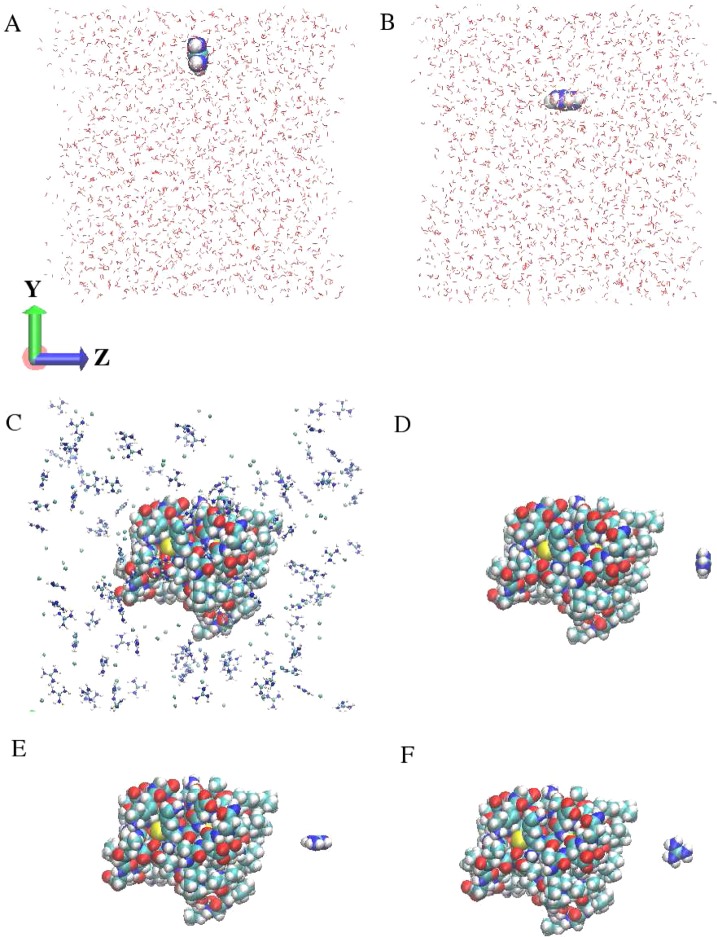
Figure 1.

(A) Representative snapshot of single Gdm⁺ with parallel orientation to the liquid–vapor interface. (B) Single Gdm⁺ with perpendicular orientation to the liquid–vapor interface. (C) HFBII protein in 1.0 m concentration of GdmCl aqueous solution. (D) Single Gdm⁺ with parallel orientation to the HFBII protein–solvent interface. (E) Single Gdm⁺ with perpendicular y orientation to the HFBII protein–solvent interface. (F) Single Gdm⁺ with perpendicular x orientation to the HFBII protein–solvent interface.

Simulations of HFBII in 1.0 m concentration of GdmCl/urea aqueous solutions were performed in the NPT ensemble using a cubic cell with a box size 60 Å × 60 Å × 60 Å. NPT ensemble was used to eliminate the liquid–vapor interfaces, so only the protein–water interfaces were considered in the system. The protein structure was based on the ultrahigh resolution structure of HFBII, with PDB code 2B97, and it was constructed using CHARMM-GUI.⁴⁹ Monomer of this HFBII protein, which is composed of 70 residues, was placed in the center of the box and fully solvated with 6481 water molecules, along with 116 pairs of GdmCl or 116 urea molecules. The initial structure of the protein was arranged in a way that its largest hydrophobic patch, consisting of amino acid residues Val 18, Leu 19, Leu 21, Ile 22, Val 24, Val 54, Ala 61, Leu 62, and Leu 63 (the three letters representing the amino acid types and the number representing the position of the amino acid in the primary sequence), was nearly perpendicular to the z direction (further verification is in Table S1 of the Supporting Information). The protein was rigidly fixed at the original configuration during the simulation while other system components were unrestrained. Temperature was maintained by Langevin bath at 300 K, and the pressure was kept constant by Langevin pressure control at 1 atm. A switching distance of 10 Å, nonbonded real-space cutoff of 12 Å, and pair list generation distance of 14 Å were used for the van der Waals interactions. For the grid size of PME setup, the values are changed to 60 in all dimensions, corresponding to the cubic simulation cell in this case. Six different replicates were applied for each system, and properties were computed based on at least 10 ns of production run for each replicate. A representative snapshot of the simulation system can be found in Figure 1C.

Furthermore, in order to illustrate the molecular details of orientation and free energetics of Gdm⁺/urea around protein interfaces, we simulated a system with single Gdm⁺/urea approaching the hydrophobic aqueous protein interface with different orientations. We use an identical protein starting structure as in the 1.0 m solution case, with the hydrophobic interface of the protein nearly perpendicular to the z direction. In this way, similar to the liquid–vapor interface case, the relative orientations between single solute and protein interface can be defined in a straightforward way: when the normal vector of Gdm⁺/urea ring is along z direction, the solute is considered to be parallel to the hydrophobic protein interface as shown in Figure 1D; when the normal vector is along y direction (Figure 1E) or x direction (Figure 1F), the solute is considered to be perpendicular to the hydrophobic protein interface. Because of the asymmetry of hydrophobic protein interface, differences arise between these two perpendicular configurations. For the convenience of discussion, we denote the orientations in Figures 1E and 1F as perpendicular y orientation and perpendicular x orientation, indicating that the normal vector is along y direction and x direction, respectively. Here, we note that although the hydrophobic protein patch is commonly considered as flat, it still has some curvature. Hence, strictly speaking, speaking of an actual parallel or perpendicular orientation of Gdm⁺ plane relative to the protein patch is not rigorous. However, in this work, we aimed to study the contrasting hydration properties and surface fluctuations induced by different orientations of Gdm⁺ (water-depleted flat faces versus the more strongly water-associated ring (edge-on) side of the cation) with respect to the hydrophobic patch of the protein. Therefore, in this convention, parallel orientation simply indicates that Gdm⁺ has more overlap with the protein patch in terms of their projections to the XY plane, relative to the perpendicular orientation. The whole protein was fixed during the simulation with center of mass located at (x = 0 Å, y = 0 Å, z = 0 Å). A fixed Cl^– (at x = 0 Å, y = 0 Å, z = −15 Å) was added as the counterion to neutralize the positive charge in the case of Gdm⁺. Similar to the liquid–vapor interface situation, for calculation of PMF, we use the Cartesian z component of the separation between the center of mass of protein and central carbon of single Gdm⁺/urea as the collective variable. Select configurations of single Gdm⁺/urea with parallel, perpendicular y, and perpendicular x orientation were used as starting structures with central carbon of the molecule located at x = 0 Å and y = 0 Å. X component and y component of the solute’s central carbon were restrained at this original position x = 0 Å and y = 0 Å during the simulation using NAMD’s “selectConstraints” infrastructure, with sufficiently large force constant k = 1000 (kcal/mol)/Ų. The orientations were maintained by restraining the directions of the central carbon–nitrogen vectors with the same protocol as liquid–vapor interface cases mentioned above. In this case, single Gdm⁺/urea will approach the specific spot on the patch (x = 0 Å and y = 0 Å) with particular orientation while still keeping some rotational degree of freedom by using the normal vector to the molecular ring as rotation axis. We just centered on one specific region on the patch due to the fact that the interface is heterogeneous, resulting in the differences of the extent of inherent interface fluctuations at various locations (to be discussed further below). For a meaningful discussion of the molecule-induced fluctuation (fluctuation in addition to the level inherent in pure water) as it approaches the hydrophobic interface, one representative spot with fixed position and unchanged inherent fluctuation had to be defined. For more discussion of the situations of the single solute with other restraint conditions (totally rigid solute or restrained in a specific sampling volume), the reader is referred to the Supporting Information, Section S1. In this case, along the positive z direction, 49 continuous “windows” with width 0.2 Å ranging from area around protein–solvent interfaces to bulk water region were constructed. The spans of the windows going from interfacial region to bulk region (in Å) were [15.4:15.6], [15.6:15.8], [15.8:16.0], ..., [24.4:24.6], [24.6:24.8], [24.8:25.0]. In each window, a harmonic restraint potential with force constant of 10 (kcal/mol)/Ų was applied. Other simulation conditions remain the same as that of the system of protein in 1 m concentration of GdmCl/urea aqueous solution. The first 2 ns was allowed for equilibration before a total of 20 ns production data was generated for each window.

For a complete understanding of the influence of the hydrophobicity of the protein patch on the orientational preference of Gdm⁺ solute, we considered another system in which single Gdm⁺ approaches a more hydrophilic protein region which consists of residues Asp 25, Cys 26, Lys 27, Thr 28, Ala 58, Asp 59, and Gln 60. The simulation conditions remained identical except that the protein was posed in a different way in the simulation cell with the selected hydrophilic interface almost perpendicular to the z direction. The window setup ranged from [14.0:14.2], [14.2:14.4], [14.4:14.6] .. to [24.4:24.6], [24.6:24.8], [24.8:25.0] for a total of 56 windows.

B. Instantaneous Protein Interface and Interface Fluctuations

We discuss the protocol for constructing the liquid–vapor interface and protein–solvent interface. It has been previously explored by Willard and Chandler⁵⁰ that one can construct a coarse-grained solvent density field from atomic coordinates in individual snapshots of an MD simulation. The interface related to the solvent is defined as a constant density surface for the coarse-grained field in space. Specifically, in this work, we are interested in the water–vapor interface and water–protein interface; we thus use the water oxygen atom as a reference point for constructing coarse-grained interfaces. The oxygen atom in most, including the present, force fields is sufficiently large that its size represents the majority of the size of the model molecule; thus, using only the water oxygen atom to construct the interfaces is a justifiable approximation. The water oxygen density field is constructed as follows: we set up series of spatial grid points and compute the corresponding coarse-grained densities at space-time point r, t, represented as ρ̅(r,t) by eq 1.

1

where r_i(t) is the “i”th water oxygen atom’s position in space. The summation over all water molecules’ density contributes to the coarse-grained density at a particular grid point. Each oxygen atom’s density contribution is coarse-grained via a Gaussian function in eq 2.

2

where r is the magnitude of r, ξ is taken as 3.0 Å, and d stands for dimensionality (3 in this case). The final d-dimensional density field will be constructed by acquiring each grid point’s density. The interface is determined as the (d – 1)-dimensional manifold with a constant value c. Differences arise when constructing the liquid–vapor interface and liquid–protein interface considering that the shape of the liquid–vapor interface is different than the protein–water interface. Thus, we select a Cartesian coordinate system to construct the liquid–vapor interface and spherical coordinate system for the protein–water interface. The liquid–vapor interface is constructed by connecting grid points where ρ(x,y,z) = ρ_bulk/2. This instantaneous surface is denoted as (h_t(x,y), at time t). We can average these instantaneous surfaces to obtain the mean surface ⟨h(x,y)⟩. Subtracting the mean values from the h_t(x,y), we obtain δh_t(x,y) as surface height and the height fluctuations ⟨δh²(x,y)⟩. For the protein–water interface, grid points in space are defined by (r,θ,ϕ) and each (θ, ϕ) coordinate set in the spherical system defines a radial vector. Points are defined to belong to the interface if ρ(r₀,θ,ϕ) = 0.6ρ_bulk. We use a different constant value c = 0.6ρ_bulk here compared with the liquid–vapor interface case because this choice results in a more unambiguous construction of a protein–solvent interface. We note that other parameters, ξ and d, remain the same. Correspondingly, instantaneous protein interface can be expressed as (h_t(θ,ϕ)), mean surface as ⟨h(θ,ϕ)⟩, surface height as δh_t(θ,ϕ), and height fluctuation as ⟨δh²(θ,ϕ)⟩.

III. Results and Discussion

A. Liquid–Vapor Interface

We first consider a single Gdm⁺/urea solute approaching the liquid–vapor interface. This analysis provides a reference context within which to discuss the results at a hydrophobic protein interface later. To first address solute orientational propensities as they vary along the order parameter, we compute orientationally resolved probability distribution profiles along the z-axis as a single Gdm⁺/urea approaches the liquid–vapor interface as shown in Figure 2A,C. Here, in a statistical manner, we consider the probability of the single solute at position z with orientation θ, which is defined based on the following eq 3:²⁹

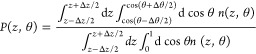3

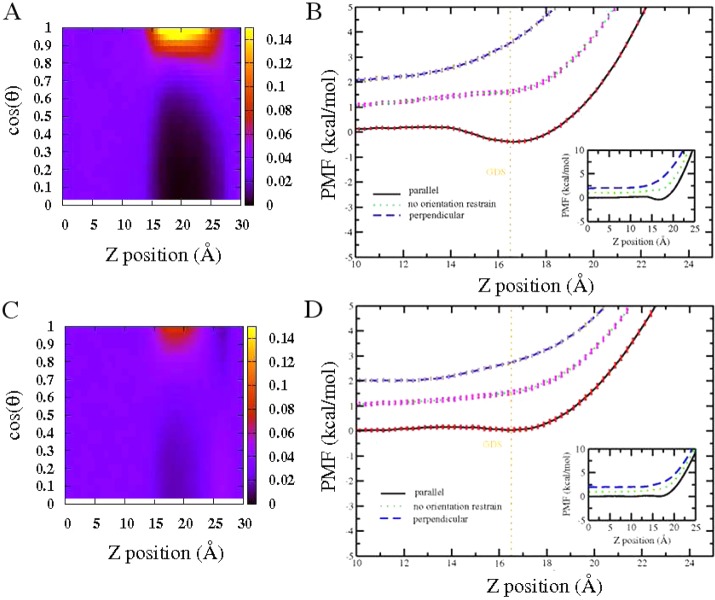
where n(z,θ) denotes the solute number count at position z with orientation θ. The numerator represents the number of solutes in a slab from z – Δz/2 to z + Δz/2, with select orientation within the range of cos(θ – Δθ/2) and cos(θ + Δθ/2). The denominator represents the total number of solutes in the slab region z – Δz/2 to z + Δz/2; this is used to normalize the probabilities in the relevant slab whose boundaries along the order parameter are z – Δz/2 to z + Δz/2. The limits cos(θ) = 1 and cos(θ) = 0 represent Gdm⁺ orientations that are parallel and perpendicular to the liquid–vapor interface, respectively. In bulk region with z < 13 Å, the probabilities of Gdm⁺/urea with different orientations are identical, indicating no orientational preference, while in the interfacial region (15 Å ≤ z ≤ 20 Å), single Gdm⁺ manifests a higher tendency to adopt the configuration that is parallel to the liquid–vapor interface. This observation is consistent with the result in our previous publication on an identical system using a polarizable force field (TIP4P-FQ)³⁰ and Wernersson et al.’s work using 1.1 and 5.3 m GdmCl solutions.²⁹ Single urea also displays a marginal orientational preference for a parallel configuration as well; urea’s propensity for the parallel orientation is lower than that of Gdm⁺ based on the lower intensity of the corresponding region in Figure 2C. We note that this higher probability of parallel orientation of single solute around interfacial region suggests a lower free energy of this configuration relative to the perpendicular. To further explore this difference, we consider potentials of mean force for single Gdm⁺/urea from bulk through liquid–vapor interface being restrained at particular orientations as shown in Figures 2B and 2D for Gdm⁺ and urea, respectively. In both panels, black lines represent conditional PMF profiles for single solute with parallel orientation; blue dashed lines represent conditional PMF profiles for single solute with perpendicular orientation. The orientation-averaged PMF profile (with no restraints on the orientation) is shown as a dotted green line. The weighted histogram analysis method (WHAM) was used for generating the final PMF in all cases.⁵¹ The standard error was estimated by using the block averaging method obtained from each consecutive 0.5 ns time block in the production run of each umbrella sampling window. This selection will ensure the block size was significantly larger than the correlation time in each window. The PMF is defined to be zero when the solute is in the bulk, which is determined by window z = 0 Å. To better compare the interface stability among different orientations, in the large graph of panels B and D, we emphasized the PMFs around the interfacial region while the entire PMF along the collective variable can be found in the inset. For single Gdm⁺, the parallel orientation shows a minimum of roughly −0.4 kcal/mol, with uncertainty about 0.1 kcal/mol, prior to the GDS at the separation of z = 16.5 Å, while the perpendicular orientation displays no surface stability at all. Overall, when there is no orientational restraint applied on the Gdm⁺, as shown by the green line, no surface stability is found near the interface. The PMF is less repulsive in the case with no orientational restraint compared to the perpendicular orientation scenario; this is consistent considering that it is an average result from the contributions of all possible configurations. The PMF for no orientational restraints (green dotted line) shows a slight shoulder around z = 16 Å, indicating the effect of the parallel orientations. However, since the stability of the parallel orientation is rather small, and configurations differing from the parallel geometry are associated with significantly higher free energies at the interface, the overall effect leads to a PMF displaying no apparent interfacially stable state. For single urea, the parallel orientation PMF shows a slight minimum of 0.04 ± 0.07 kcal/mol. Considering the uncertainty here, whether parallel orientation of urea shows surface stability or not is debatable. However, we notice that, in contrast to the perpendicular orientation, the parallel orientation is more free energetically favorable, although this trend is not as obvious as the case for Gdm⁺. All these PMF results are consistent with the probability distributions of orientations as discussed above. We note that this orientational preference of Gdm⁺ around liquid–vapor interface may be related to the hydration structure of Gdm⁺ as previously studied by Mason et al.^16,28 and Cooper et al.¹ The hydration around Gdm⁺ is anisotropic. In the molecular plane, the N–H group can serve as hydrogen bond donor, interacting with water molecules¹ as demonstrated in the gas phase, while above or below the planar face, it is inadequate to serve either as hydrogen bond donor or acceptor. Therefore, when single Gdm⁺ approaches the liquid–vapor interface with parallel orientation, it is easy for desolvation to occur, which is free energetically favorable. For the structurally analogous molecule urea, it still can serve as hydrogen bond donor above or below the planar face, so it is less facile for the parallel urea molecule to desolvate compared with that of Gdm⁺.⁵²

Figure 2.

(A) Orientationally resolved probability map of single Gdm⁺ around liquid–vapor interface. (B) PMF of single Gdm⁺ from bulk transporting through liquid–vapor interface with parallel orientation, perpendicular orientation, and no orientational restraint. (C) Orientationally resolved probability map of single urea around liquid–vapor interface. (D) PMF of single urea from bulk transporting through liquid–vapor interface with parallel orientation, perpendicular orientation, and no orientational restraint. For clarity, in (B) and (D), no orientational restraint profiles are shifted by 1 kcal/mol; perpendicular profiles are shifted by 2 kcal/mol. The GDS positions are denoted as orange dashed lines in (B) and (D).

Recent studies have demonstrated an interesting connection between liquid–vapor interfacial stability of chemical species and the extent to which the presence of these molecular species in the vicinity of the interface induces collective fluctuations of the interface in addition to the level inherent in pure water (absence of the solute) due to thermal motion; these studies have focused on monovalent inorganic ions as initial test systems.^30,53,54 Initially, it is found that the species demonstrating an interfacial stability (e.g., I^–) as demonstrated by free energy minima in the region of the GDS as evaluated via potentials of mean force, appear to enhance liquid–vapor interfacial fluctuations, while those that show no interfacial stability (e.g., Cl^–) induce no or lesser extent of fluctuations. The differences in induced interfacial fluctuations by two representative ions, Cl^– and I^–, has been attributed to these two types of ions presenting distinct hydration shell environments. The first solvation shell of I^– is more malleable than that of Cl^–. The nature of the solvent structure around I^– determines that it is more amenable to inducing fluctuations of the interface as a consequence of a greater disruption of the solvent structure on approach to the interface. Inspired by this, we consider that differences in induced interfacial fluctuations should arise as the parallel and perpendicular orientations of Gdm⁺ approach the liquid–vapor interface since these two configurations display distinct hydration shell environments with parallel orientation presenting a more malleable solvent environment and perpendicular orientation showing a more rigid hydration environment due to the more effective hydrogen bonding of water in the plane of the ring. The two orientations are associated with dramatically different free energetic profiles at the liquid–vapor interface. The surface height fluctuations were computed with the protocol of section II.B. The mean surface height and surface height fluctuation when single Gdm⁺ resides at the position of z = 14 Å is shown in Figures S1A and S1B of the Supporting Information. Both the mean surface profile and surface height fluctuation profile are radially symmetric, with the largest value at the position where the Gdm⁺ is just approaching the point (x = 0, y = 0). For convenience, we use this representative value ⟨δh²(x = 0, y = 0)⟩ to compare the magnitude of interface fluctuations when the solute is restrained at different z-positions, with the result shown in Figure 3. Fluctuation profiles for Gdm⁺ and urea with distinct orientations are presented in panels A and C, respectively. In the case of pure TIP3P water without the existence of solute, the inherent fluctuation for current system size is around 1.32 Ų. Using this value as a normalization factor, normalized fluctuation profiles were obtained, presented in panels B and D for Gdm⁺ and urea, respectively, which will display solute-induced contribution in a direct way. ⟨δh_L²⟩ > 1 indicates the surface height fluctuation is enhanced relative to pure water; with ⟨δh_L²⟩ < 1, it denoted that the surface height fluctuation is damped. In the Gdm⁺ case, the parallel orientation induces a large fluctuation, with the maximum normalized fluctuation value around 2.2 at the location of z = 14 Å, which is around 3 Å prior to the position of the free energy minimum. In stark contrast, no obvious enhancement of surface fluctuations is associated with perpendicular orientation. These trends are expected considering the distinct hydration structures for the parallel and perpendicular orientation of Gdm⁺. The nature of the malleable hydration shell around parallel orientation Gdm⁺ is similar to that of single, low charge density anions, like I^–. The solvent structure is more amenable to inducing larger fluctuations due to the fact that it is more easily disrupted as the solute approaches the interface. On the other hand, the perpendicular orientation of Gdm⁺ showing no interface stability is more like Cl^–, with more rigid solvation structure around the periphery of the ring due to the existence of hydrogen bonding. These results using a nonpolarizable force field are consistent with our previous work using the TIP4P-FQ polarizable force field,³⁰ indicating a force field independence of the fundamental, underlying physical origin of this correlative phenomenon. Previously, it has been pointed out the importance of considering polarizability in the ion-specific effect.^55,56 By neglecting the polarizability in the force field, larger anion I^– may not show significant surface stability, giving a poor distinction with respect to Cl^–. However, our results indicate that in the case of Gdm⁺ the orientational preference is pronounced enough even in the nonpolarizable force field. In light of this, in the following section for the discussion of Gdm⁺ around the protein surface, we use this nonpolarizable force field. We also notice that differences in induced fluctuations also exist in the case of urea with dissimilar orientations. For the parallel orientation, the largest induced normalized fluctuation value is around 1.85, which is still larger than the fluctuation from perpendicular orientation, 1.45. Interestingly, for the parallel orientation, the induced fluctuations from Gdm⁺ is larger than that from urea, corresponding to Gdm⁺’s greater free energetic stabilization; the perpendicular orientations show a reverse trend as the induced fluctuation from Gdm⁺ is smaller than that from urea, which correlates with the PMF trend that Gdm⁺ is more repulsive in this case. Again, the smaller differences in interfacial stabilization and induced fluctuation between parallel and perpendicular orientation is related to the spatial location of hydrogen bonding network, either below or above the planar face, leading to the closer solvation structure of the parallel oriented and perpendicular oriented urea. Overall, the differences in orientational preference around liquid–vapor interface, interfacial stability, and induced fluctuation between Gdm⁺ and urea may possibly be connected to the efficiency of these two solutes as denaturants via direct interactions with hydrophobic side chains and surface regions of proteins. For a further understanding of this, we attempt to extend this investigation from the ideally hydrophobic aqueous liquid–vapor interface to a somewhat more realistic and more complex aqueous protein hydrophobic interface.

Figure 3.

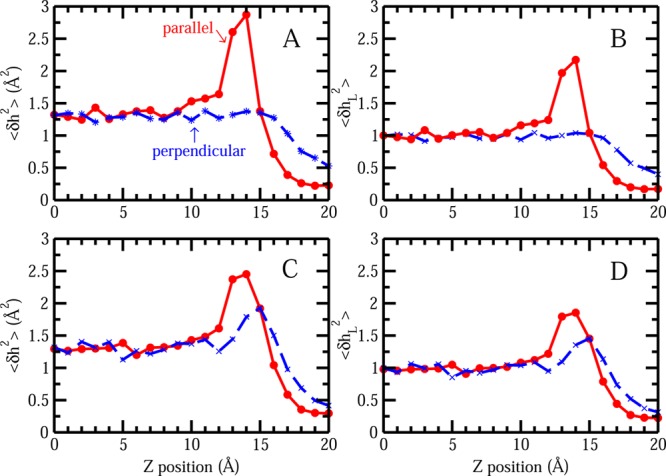
(A) Surface height fluctuation for liquid–vapor interface at (x = 0, y = 0) as a function of position of single Gdm⁺. (B) Normalized surface height fluctuation for liquid–vapor interface at (x = 0, y = 0) as a function of position of single Gdm⁺. (C) Surface height fluctuation for liquid–vapor interface at (x = 0, y = 0) as a function of position of single urea. (D) Normalized surface height fluctuation for liquid–vapor interface at (x = 0, y = 0) as a function of position of single urea.

B. Aqueous Protein Interface

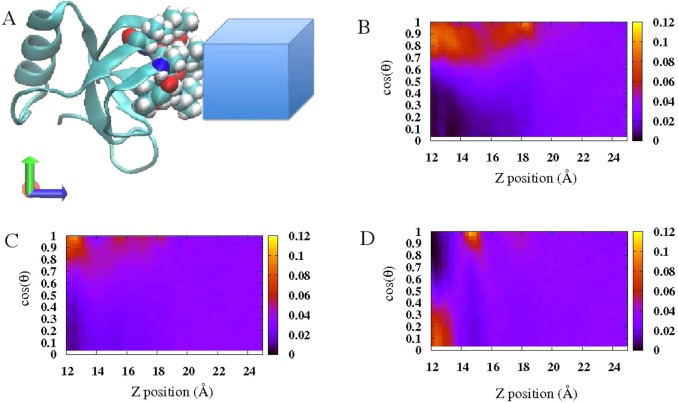
Before we consider the free energetics of single Gdm⁺/urea approaching the hydrophobic protein interfacial region, we provide a general overview of distributions of solute orientation relative to the hydrophobic protein patch. To probe this, generally, we define a sampling volume in the Cartesian space corresponding to the hydrophobic patch around the protein. This sampling volume is shown in Figure 4A, within the range of −8 Å ≤ x ≤ 8 Å, −8 Å ≤ y ≤ 8, and 12 Å ≤ z ≤ 25 Å, roughly including residues Val 18, Leu 19, Leu 21, Ile 22, Val 24, Val 54, Ala 61, Leu 62, and Leu 63. Orientationally resolved probability distribution of Gdm⁺ around this defined region is shown in Figure 4B. The probability at position z with orientation θ in this case is defined in the same way as that in liquid–vapor interface system in eq 3. Around the selected hydrophobic protein surface, Gdm⁺ displays a higher propensity for the parallel configuration. We note that this marked tendency has previously been noticed in proximity to hydrophobic surface. England et al.^7,18 found that Gdm⁺ accumulates in the vicinity of flat hydrophobic plate in a roughly parallel way. Godawat et al.²⁰ also mentioned the Gdm⁺ has a preference for parallel stacking with the hydrophobic polymer surface from the snapshots of their simulations. Here, using a simple approach, we defined the relative orientations between Gdm⁺ solute and hydrophobic protein surface and showed the orientational preference of Gdm⁺ around the hydrophobic patch of HFBII. Furthermore, we consider orientationally resolved probability distributions of urea in an identical probe volume in Figure 4C. Parallel oriented urea is also preferred compared with the perpendicular configuration around the hydrophobic protein surface. However, this trend is less intense in the case of urea compared with Gdm⁺, which is similar to the situation at the liquid–vapor interface. This is consistent with the previous report that urea, compared with Gdm⁺, displays more orientational diversity around hydrophobic plate-like surfaces.¹⁸ So far, we only concentrated on solute distributions around the hydrophobic region of the protein and attempted to connect this with the similar observation around the liquid–vapor interface, which is one model of an ideal hydrophobic interface. A complementary study would be focusing on another distinct region around the protein surface with different hydrophobicity. Therefore, we define another sampling volume corresponding to the hydrophilic patch of the protein (including residues Asp 25, Cys 26, Lys 27, Thr 28, Ala 58, Asp 59, and Gln 60) in Cartesian space within the range of −8 Å ≤ y ≤ 8 Å, −8 Å ≤ z ≤ 8, and 12 Å ≤ x ≤ 25 Å. The volume of this sampling region remains the same as that defined for the hydrophobic region, but the position of the probe region in Cartesian space is different. In Figure 4D is shown the orientationally resolved probability distribution for Gdm⁺ around this hydrophilic region. Overall, no preference for parallel oriented Gdm⁺ is observed in this case, although this preference can be detected in a small portion of the map with the separation of z = 14 Å. Compared to the orientationally resolved probability maps for Gdm⁺ around hydrophobic (panel B) and hydrophilic area (panel D), it is safe to claim that around more hydrophobic regions there is a stronger tendency for the parallel stacking of Gdm⁺ with protein surface, which is also been noticed in flat plate systems previously.¹⁷ We note that these general trends are robust as an identical patch with different sampling volume, as defined in the Supporting Information Figures S2 and S3, further verifying this orientational preference around hydrophobic/hydrophilic regions.

Figure 4.

(A) Representative of sampling volume for probing orientational resolved probability of solute around certain region of protein interface. (B) Orientational resolved probability distribution of Gdm⁺ around hydrophobic protein interface in 1.0 m GdmCl solution. (C) Orientational resolved probability distribution of urea around hydrophobic protein interface in 1.0 m urea solution. (D) Orientational resolved probability distribution of Gdm⁺ around hydrophilic protein interface in 1.0 m GdmCl solution.

The PMF profiles for single Gdm⁺/urea approaching the hydrophobic protein surface region are shown in Figure 5. Panel A shows the PMF of single Gdm⁺ with parallel orientation (solid red line), perpendicular y orientation (dotted green line), and perpendicular x orientation (dashed blue line) moving toward the hydrophobic patch region from the bulk, which is located at z = 25 Å in this case. The PMF profiles were generated by postprocessing umbrella sampling MD trajectories with WHAM, and the standard errors were estimated by using the block averaging method obtained from each consecutive 0.5 ns time block in the production run of each umbrella sampling window. The parallel configuration gives rise to a PMF minimum of −2.85 ± 0.04 kcal/mol as it nears the hydrophobic patch at a separation of z = 15.7 Å; a shallow second minimum can be observed at a separation of z = 19 Å. A free energetic barrier can be observed between these two minima, which may be related to the dramatic change of the number of water molecules within the first hydration shell of the solute as shown in Figure S4 of the Supporting Information. There is a shallow minimum with free energy −0.48 ± 0.04 kcal/mol around z = 17 Å for the perpendicular y orientation Gdm⁺, while for perpendicular x Gdm⁺, a monotonically repulsive trend was observed. This difference may be determined by the exact composition and local spatial arrangement of the residues on and near the hydrophobic patch as shown in Figures S5A and S5B of the Supporting Information. When Gdm⁺ with perpendicular x orientation approaches the patch, there is a repulsive interaction between NH groups of Gdm⁺ and side chains of residues Ile 22 and Leu 63 on the patch. More importantly, we notice that compared with PMFs for perpendicular oriented Gdm⁺ showing marginal or no stability, PMFs for parallel orientation Gdm⁺ are much more free energetically favorable. This further echoes the result shown in Figure 4B, indicating that Gdm⁺ prefers to associate with the hydrophobic protein patch with its more hydrophobic, easily desolvated, parallel orientation. This preference is explained by England et al.^7,18 as hydrophobicity-driven stacking interaction in their study using hydrophobic plate. Because of the inability of hydrogen bond formation between hydrophobic surface and water molecules, the hydrophobic surface has a stronger tendency to minimize the exposed area in the aqueous environment. This can be achieved by the face-on coating by Gdm⁺ of the surface, which is free energetically favorable. The observed stacking mode of self-association among Gdm^+16,21,57 can also be considered as hydrophobically driven interaction. Instead of association with large hydrophobic plate or protein surface, in this case, Gdm⁺ pairs with another Gdm⁺ by maximize the overlapping of their hydrophobic planar rings. We further verify this by considering the PMFs of single Gdm⁺ approaching another Gdm⁺ with different relative orientations. The details of this can be found in the Supporting Information, section S2. In Figure 5B, PMF profiles for urea with different orientations moving toward the identical hydrophobic patch are presented. Again, parallel oriented urea molecule shows the most free energy stability with a value around −2 kcal/mol compared with the two perpendicular orientations. However, comparing parallel urea association free energy around hydrophobic protein patch with that of parallel Gdm⁺, we find that it is less favorable, which is due to the lower hydrophobicity of urea’s planar surface as discussed earlier. These behaviors are consistent with the results from orientation distribution maps in Figure 4.

Figure 5.

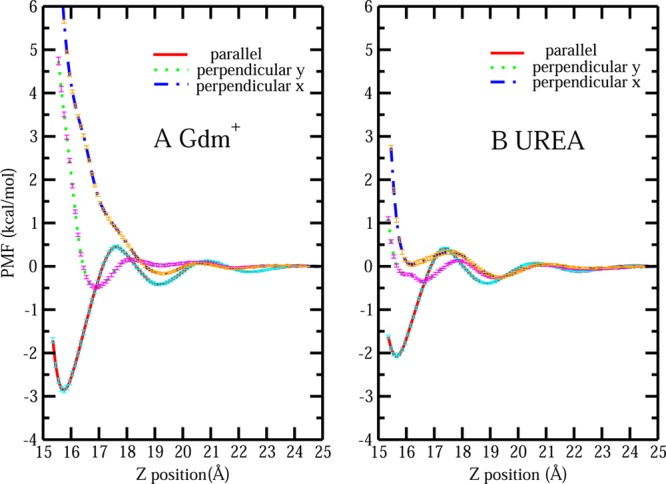
(A) PMF for single Gdm⁺ with parallel orientation, perpendicular y and perpendicular x orientation from bulk approaching the hydrophobic protein–solvent interface. (B) PMF for single urea with parallel orientation, perpendicular y, and perpendicular x orientation from bulk approaching the hydrophobic protein–solvent interface.

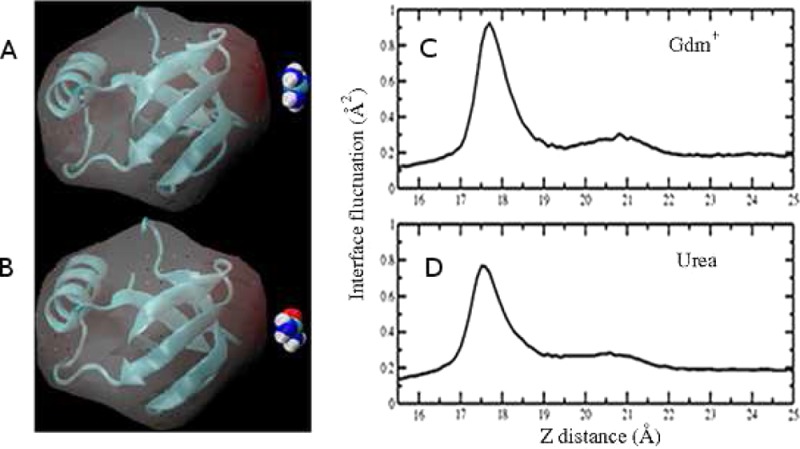
The stability of a single solute at the protein interface correlates with the induced interfacial fluctuations as the solute approaches. The protein–solvent interface was constructed based on the protocol mentioned in section II.B. A representative average protein–solvent interface is shown in Figure S1C, and the corresponding height fluctuation is shown in Figure S1D. Overall, the contour of the mean interface is reasonable considering that the shape of the protein is globular. The magnitude of interface fluctuations can be judged by the color scale in panel D, in which case a single Gdm⁺ is located at z = 18 Å right above the position x = 0, y = 0. We consider this point as a reference point since it displays the largest induced fluctuations compared with other regions on the protein surface as indicated by the bright ring in Figure S1D. To better illustrate the change in interface fluctuation magnitude as single Gdm⁺/urea approaches the patch, the induced fluctuation at this reference point, ⟨δh²(x = 0, y = 0)⟩, as a function of z position of the central carbon of the solute is plotted in Figure 6. In Figure 6A, at large separations of the single Gdm⁺ from the hydrophobic patch region, none of the configurations of Gdm⁺ show increased perturbation of the aqueous protein interface. The magnitude of undulations of the protein–solvent interface solely comes from the inherent, thermal fluctuation. As the restrained Gdm⁺ with distinct orientations approaches the hydrophobic patch, the induced fluctuation profiles exhibit striking differences. Parallel-oriented Gdm⁺ induces large fluctuations of the interface (0.95 Ų) at the separation of z = 18 Å, which is around 5 times that of the inherent interfacial fluctuation (0.19 Ų). In the case of perpendicular-orientated Gdm⁺, maxima in the fluctuation profiles can also be found at the same separation of z = 18 Å. However, the extent of the induced interfacial fluctuation is smaller compared with that of the parallel orientation, with perpendicular y giving a value of 0.4 Ų (2 times of inherent fluctuation) and perpendicular x giving a value of 0.35 Ų (1.8 times of inherent fluctuation). This is consistent with the trends at the liquid–vapor interface showing that interfacially stable parallel configurations of Gdm⁺ induce larger interfacial fluctuations than the perpendicular, less interface-stable orientations of Gdm⁺. As expected, parallel orientations urea induces a larger extent of fluctuation (around 0.75 Ų) than the perpendicular ones (around 0.45 Ų), corresponding to the greater free energy stability of the parallel configurations around the interface shown in Figure 5. Comparing the induced fluctuation values between parallel configurations of the two solutes, the more hydrophobic and more surface stable Gdm⁺ gives a higher level of enhanced fluctuation. These results support the argument that the more hydrophobic nature of the parallel-oriented Gdm⁺ makes the hydration shell weakly bound and less ordered, so that it has more tendency to break and couple with the hydration water in the vicinity of hydrophobic protein patch region, which will cause a large perturbation of the protein–solvent interface in addition to the level present in pure water. According to the previous studies,^53,54,58,59 this enhanced fluctuation represents an increase of interface entropy, which may contribute to differentially stabilizing configurations where the parallel orientation Gdm⁺ is closer to the interface compared to other configurations of the solute.

Figure 6.

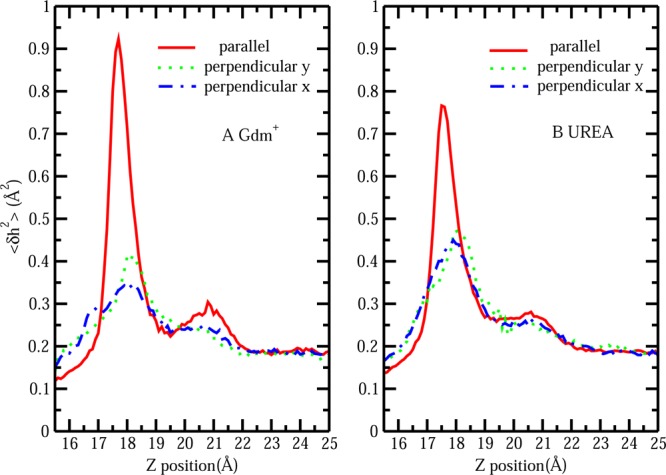
(A) Surface height fluctuation for hydrophobic protein interface at (x = 0, y = 0) as a function of restrain z position of single Gdm⁺ with parallel, perpendicular y, and perpendicular x orientation. (B) Surface height fluctuation for hydrophobic protein interface at (x = 0, y = 0) as a function of restrain z position of single urea with parallel, perpendicular y, and perpendicular x orientation.

To close this discussion about induced interfacial fluctuations, we address potential artifacts in our algorithm for computing interfacial fluctuations. One may ask whether the instantaneous coarse-grained interface we construct can artificially pass “through” the solute, thus giving rise to artificially large fluctuations. To explore this, we plot the difference Δ in the z-position of the central carbon of Gdm⁺ and the z-position of the interface (z_interface) as Gdm⁺ moves toward the protein patch along the z-axis. Here, the z-position of the interface is equal to the value of the surface height of the interface at the point (x = 0, y = 0, z_interface). Δ > 0 means the interface is between single Gdm⁺ and the protein patch; while Δ = 0 indicates that interface just passes through the Gdm⁺; Δ < 0 implies that the Gdm⁺ resides between the interface and the protein. We will show that even when all the z_interface values are distributed on one side of the solute with Δ value constantly being larger or smaller than zero, the distribution of z_interface is not necessarily small. This would suggest that the induced fluctuations are nonartifactual, and the higher fluctuation values are not due to the combination of three different scenarios (Δ > 0, = 0, and < 0). Figure 7 displays the values of Δ and the distributions of Δ as single Gdm⁺ is located at three representative positions: z = 16, 18, and 19.5 Å. Panels A and D correspond to the parallel configuration; panels B and E correspond to the perpendicular y configuration; panels C and F correspond to the perpendicular x configuration. At a separation of z = 18 Å, where the Gdm⁺ induces a large interfacial fluctuation, we observe that Δ is always larger than zero for all the three cases, indicating that the interfaces will always reside between the protein and the solute, so there is no artifact where the surface passes through the solute. The same applies to the situation that Gdm⁺ is located at z = 19.5 Å as indicated by the blue line. Although at the separation of z = 16 Å there are some Δ values less than zero, at this point the interfacial fluctuation is suppressed by the presence of the solute. This suggests further that enhanced fluctuations are not influenced by the interface fluctuating on both sides of the solute. Furthermore, at closer separations of Gdm⁺ and the protein–water interface, the meaning of the local interface becomes ambiguous perhaps, but this is not a serious issue as the major differences in interface effects occur well before the solute arrives at the interface. An additional point worth addressing is that at a separation of z = 18 Å we observe that the parallel configuration of Gdm⁺ exhibits a wider distribution of Δ values as shown in the panel D green line. This is consistent with the earlier result of Figure 6A that parallel orientations of Gdm⁺ induce larger fluctuations of hydrophobic protein–solvent interface compared to the perpendicular ones. In a recent study, Patel et al. discussed that water near hydrophobic surfaces can be described as being near a phase transition characterized by enhanced fluctuations in relevant order parameters.^60,61 The relevant order parameter is solvent density in their work, the distribution of which varies from unimodal (when two hydrophobic interfaces are far apart) to bimodal at separations where the volume between surfaces fluctuations between wet and dry states to unimodal once the intersolute space is completely dry (post-dewetting transition). In this work, as solutes approach the hydrophobic surface as a perturbation to the interfacial water, a different order parameter based on the interfacial height is considered. Ideally, this interfacial height should display the same signatures of bimodal distribution as the solute reside at the position that induces the largest surface fluctuation. From previous discussion, Δ is the difference between z_Gdm and z_interface. Since z_Gdm is almost constant (this is the fixed position of the solute), the distribution profiles of Δ and z_interface should be identical except the shift along the X-axis. We will just use the distribution of Δ in the following discussion. A fat tail in the distribution profile in Figure 7D is observed as the solute is located at a separation of z = 18 Å, which is near the position of largest fluctuation. Furthermore, the distribution profiles of Δ for Gdm⁺ with parallel orientation at the separation of z = 17.5 Å and z = 17.7 Å are shown in Figure 8A. Interestingly, at the exact separation where solute induces the largest fluctuation, z = 17.7 Å, a prominent bimodal distribution is observed, which is consistent with the view that at this position, there would be transitions between a “wet” and “dry” region between the solute and the protein–water interface. Figure 8B shows the log probability of Δ versus Δ, analogous to Figure 3C in Patel et al.⁶⁰ The present probability distributions for the interface position recapitulate the results of Patel et al. in a rather dramatic fashion. This further speaks to the notion that water near hydrophobic interfaces, even on the smaller scales of specific regions of biomolecules, is poised close to phase transitions, which upon perturbation by external potentials (in this case, a solute approaching the interface and perturbing the solvent density near the protein surface as a consequence of the nature of the solute’s hydration shell) undergoes a transition. This transition is now considered as an alternative signature of the hydrophobic effect.

Figure 7.

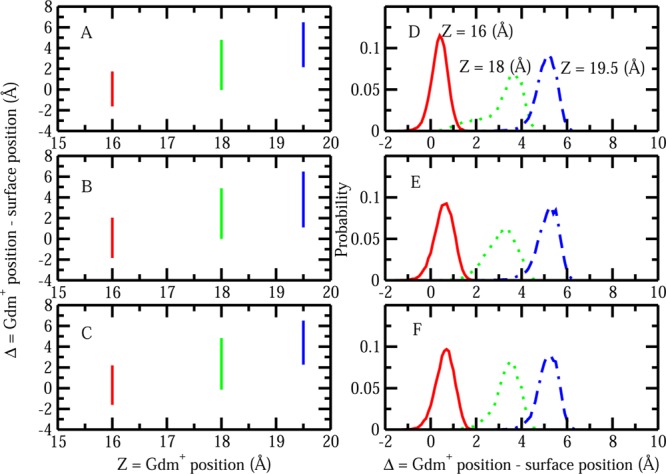
(A–C) Differences between single Gdm⁺ position and surface position (surface position is defined by the surface height at position x = 0, y = 0) Δ for Gdm⁺ with different restrained orientations locating at various positions: (A) parallel orientation, (B) perpendicular y orientation, and (C) perpendicular x orientation. (D–F) Probability distributions of Δ for Gdm⁺ with different restrained orientations locating at various positions: (D) parallel orientation, (E) perpendicular y orientation, and (F) perpendicular x orientation.

Figure 8.

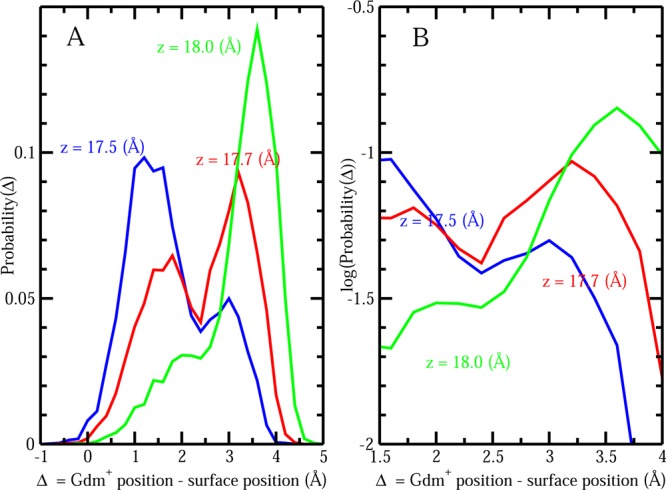
(A) Probability distributions of Δ for Gdm⁺ with parallel restrained orientation locating at various positions close to the peak of largest fluctuation. (B) Probability distributions (log scale) of Δ for Gdm⁺ with parallel restrained orientation locating at various positions close to the peak of largest fluctuation.

Finally, we consider PMFs of single Gdm⁺ approaching a hydrophilic region on the protein surface. Figure 9A shows the PMF profiles of a single Gdm⁺ approaching the hydrophilic protein patch with parallel orientation (red), perpendicular y orientation (green), and perpendicular x orientation (blue). A slight free energy stabilization is observed in all the cases, which may due to the electrostatic interaction between the −NH group of Gdm⁺ and side chain of hydrophilic residues (like Asp 25) on the patch as shown in Figure S5C of the Supporting Information. However, compared with the free energy of Gdm⁺ with most favorable parallel configuration approaching the hydrophobic protein region (−3 ± 0.15 kcal/mol), the free energetic advantages from Gdm⁺ with all three configurations approaching the hydrophilic patch are quite small (around −0.5 ± 0.15 kcal/mol). Furthermore, all three configurations show little to no difference in free energy, suggesting that the orientational preference of Gdm⁺ around certain types of surfaces is highly dependent on the effective hydrophobicity of the region, with significant orientational preference of Gdm⁺ occurring around the more hydrophobic surface regions. Furthermore, the induced interfacial fluctuation profiles of single Gdm⁺ with these distinct orientations approaching this hydrophilic region are shown in Figure 9B. Previously, we have reported that for the protein in pure water regions with different hydrophobicity will display dissimilar inherent interface height fluctuations.⁵⁹ The larger magnitude of fluctuations are related to the malleable nature of the water and facile cavity formation around hydrophobic patches.³² When Gdm⁺ is located far from the patch, in all three cases, an inherent fluctuation value of 0.07 Ų is detected, which is lower compared with the inherent fluctuation value around hydrophobic protein region 0.18 Ų. As Gdm⁺ moves closer to the hydrophilic interface, both parallel and perpendicular orientation have an inappreciable effect on hydrophilic interfacial fluctuations. Although parallel configuration may induce a little larger fluctuation compared with the perpendicular one, the difference is quite small, around 0.02 Ų. Such negligible differences in inducing fluctuations among these configurations corresponds to the marginal differences of free energies around hydrophilic interface.

Figure 9.

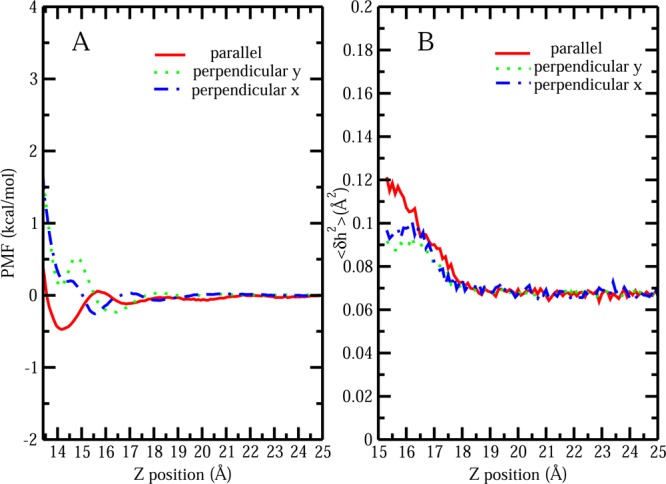
(A) PMF for single Gdm⁺ with parallel, perpendicular y, and perpendicular x orientation from bulk approaching the hydrophilic protein–solvent interface. (B) Surface height fluctuation for hydrophilic protein interface at (x = 0, y = 0) as a function of restrain z position of single Gdm⁺ with parallel, perpendicular y, and perpendicular x orientation.

IV. Summary and Conclusions

In this article, we continue to explore and demonstrate a connection between interfacial stability and induced interfacial fluctuations as interfacially stable solutes approach ostensibly hydrophobic aqueous–hydrophobe interfaces. The context in which we consider the present work is relevant for discussion of the nature of direct chemical interactions between typical chemical denaturants of proteins, Gdm⁺ and urea, specifically at hydrophobic regions of a model protein, HFBII. Our calculations of potentials of mean force indicate that Gdm⁺ and urea exhibit nontrivial stability at the aqueous–hydrophobe interface as indicated by Figure 5. Furthermore, we observe a richer subdivision of the contributions to the total free energy arising from two relative orientations of the solute that we have chosen to study: the parallel and perpendicular orientations as defined relative to the surface of the protein. Though the protein surface is not quite parallel to the axis chosen as our order parameter for calculations of potentials of mean force, the selected definitions, we feel, suffice for the current purposes. With respect to the orientation-free energy correlation, our calculations indicate that the orientations of both solutes in which the solute is parallel to the interface are associated with stronger free energy minima compared to configurations where the solutes approach in a perpendicular orientation. These two orientations appear to envelope the total free energy profiles (though we cannot say with certainty what contributions intermediate orientations would offer; however, we stress that in this study our aim is to demonstrate the self-consistency of the free energy profiles computed via the potentials of mean force with the orientation probability densities determined from free, solute-unrestrained MD simulations of the solutes in solution with the protein). Furthermore, we find that the correlative behavior between solute orientation and free energy stability (using the current force field combinations for water, solute, protein, and ions) mimics that observed at the aqueous liquid–vapor interface (Figures 2 and 4, probability distribution maps). Our results for both the protein–water interface and the pure liquid–vapor interface are in agreement with previous studies.^29,30

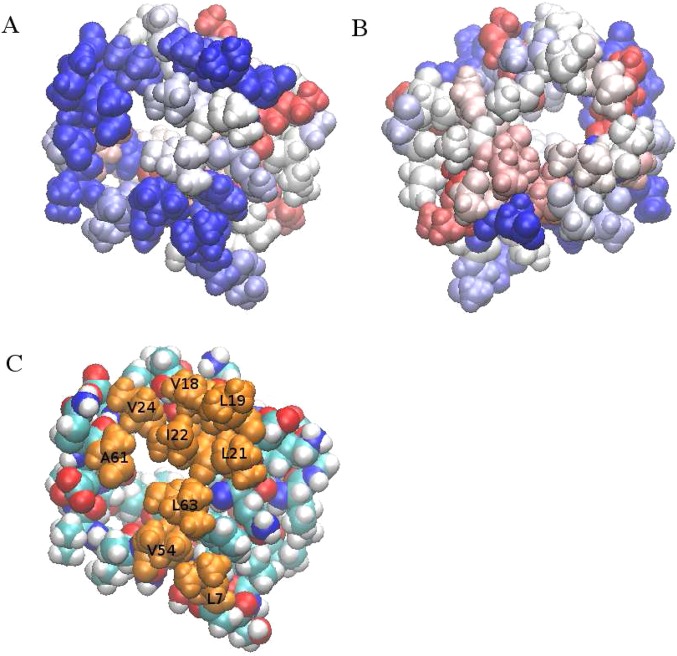
Recent simulations have highlighted the unique nature of hydrophobic interfaces as it relates to the fluctuations induced in solvent density vicinal to the interface (refer to Garde et al.’s work^31,62). Complementary studies have illuminated the fluctuations of aqueous–hydrophobe interfaces as simpler atomic species (monovalent ions) and slightly more complicated molecular species approach such interfaces. Both these approaches ostensibly define a further characteristic property associated with hydrophobic solutes (and perhaps the hydrophobic effect in general). The present calculations indicate that associated with interfacial stability of the chosen chemical denaturants is an induced fluctuation of the interface upon approach of the solute to the interface. We stress that the induced fluctuations of the interface formed between the hydrophobic region of the protein and solvent occur before the solute resides directly at the interface. This is an important detail, as it speaks to the somewhat long-ranged nature of the effects generated by certain solutes prior to any direct interaction being realized. That solutes can affect an interface from a distance is a subtle though non-negligible effect we suggest. Moreover, the present results suggest that denaturant orientations that are parallel to the interface (vis-à-vis, display interfacial stability) are the orientations that induce the largest fluctuations of the interface (and hence the solvent density). The relation between solute orientation and induced fluctuations is related to the nature of the solvation shells of the solute presented toward the interface upon approach of the solute. In the case of Gdm⁺ approaching the interface in a parallel orientation, the solvation shell presented is a more “malleable” one, where the solvent is more labile and free to rearrange. This leads to greater solvent density fluctuations and hence higher interfacial induced fluctuations. In the case of the perpendicular orientations of Gdm⁺ and urea, the tighter hydrogen bonding patterns of water (as demonstrated in previous studies¹) create a more rigid, well-defined solvation shell that is not easily disrupted. This translates to lower solvent density fluctuations and hence lower induced fluctuations (or even suppression of interfacial fluctuations). The present results are thus consistent with recent work and provides yet another example of the relation of hydrophobic effect, solvent fluctuations, and interfacial stability. This relationship appears to be common across a series of atomic and molecular species as well as encompassing charged, polar, and nonpolar characteristics of the solutes considered. These observations suggest that molecular ions, such as Gdm⁺, as well as polar molecules with heterogeneous charge distributions (at least in the context of empirical molecular mechanics force fields) inherently have built into them regions of high and low charge density. The dependence of local solvation structure on this heterogeneous (or asymmetric) charge density is to a large extent involved in determining the propensities of the modalities involved in specific association of molecules with specific types of interfaces. Observations based on classical simulations as well as recent DFT-based calculations² thus suggest an intriguing fundamental underlying theme. These ideas call for further study regarding specific details about the nature of the relationship between fluctuations, degree of solute hydrophobicity, solute solvation/hydration shell properties, and interfacial stability. Finally, Figure 10 shows the number density of Gdm⁺ molecules in the vicinity of the canonical hydrophobic region of HFBII as well as on the side opposite to this hydrophobic patch (the opposite side not being hydrophobic to any significant extent). Our analysis of simulation data from 1 M Gdm⁺ solutions with no restraints demonstrates a propensity for the Gdm⁺ to the hydrophobic region. This is consistent with the analyses presented in this work.

Figure 10.

(A) Gdm⁺ number density map around HFBII protein (hydrophobic side). Blue represents higher number density, while red represents lower number density. (B) Gdm⁺ number density map around HFBII protein (opposite side). (C) Representation of hydrophobic protein patch of HFBII with orange highlighting each hydrophobic residue on the patch.

Supporting Information Available

Discussion of aspects of mean surface height and surface height fluctuation of liquid–vapor and aqueous protein interface, orientational resolved probability distribution around hydrophobic patch region based on different sampling volume, coordinate water numbers profiles of Gdm⁺, PMF, and induced fluctuation profiles of Gdm⁺ with other restrain conditions. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States