Mathematical modeling of postmenopausal osteoporosis and its treatment by the anti-catabolic drug denosumab

Abstract

Denosumab, a fully human monoclonal antibody, has been approved for the treatment of postmenopausal osteoporosis. The therapeutic effect of denosumab rests on its ability to inhibit osteoclast differentiation. Here, we present a computational approach on the basis of coupling a pharmacokinetics model of denosumab with a pharmacodynamics model for quantifying the effect of denosumab on bone remodeling. The pharmacodynamics model comprises an integrated systems biology-continuum micromechanics approach, including a bone cell population model, considering the governing biochemical factors of bone remodeling (including the action of denosumab), and a multiscale micromechanics-based bone mechanics model, for implementing the mechanobiology of bone remodeling in our model. Numerical studies of postmenopausal osteoporosis show that denosumab suppresses osteoclast differentiation, thus strongly curtailing bone resorption. Simulation results also suggest that denosumab may trigger a short-term bone volume gain, which is, however, followed by constant or decreasing bone volume. This evolution is accompanied by a dramatic decrease of the bone turnover rate by more than one order of magnitude. The latter proposes dominant occurrence of secondary mineralization (which is not anymore impeded through cellular activity), leading to higher mineral concentration per bone volume. This explains the overall higher bone mineral density observed in denosumab-related clinical studies. Copyright © 2013 John Wiley & Sons, Ltd.

1 INTRODUCTION

Osteoporosis is a disease characterized by significant bone loss, leading to an increased risk of bone fracture. It is particularly common in postmenopausal women and the elderly. Often postmenopausal osteoporosis (PMO) is first apparent from a bone density scan, and for this reason it is sometimes called the “silent disease”, as there may be no noticeable symptoms associated with bone loss ¹. Once detected, various ways to limit further bone loss or induce bone gain have been tried clinically. These include dietary changes and exercise, and different drug treatments that influence the turnover of bone, including administration of bisphosphonates and parathyroid hormone (PTH) ^2–4.

Recently, Amgen ⁵ developed a monoclonal antibody named denosumab for the treatment of osteoporosis. Denosumab binds with high affinity and specificity to the molecule known as RANKL, the ligand of the receptor activator of nuclear factor kappa-B ⁶, which is essential for the development of active osteoclasts – osteoclasts are the cells responsible for bone resorption ⁷. Following the successful completion of more than 30 clinical trials involving a large number of patients ^8–12, denosumab is now available for the treatment of osteoporosis and is marketed for this purpose under the name Prolia ¹³, whereas denosumab is also marketed under the name Xgeva for the purpose of treating of bone cancer metastases.

Anticipating the progression of PMO and the effects of therapeutic agents (such as denosumab) on the basis of experimental observations alone is difficult (if not impossible), owing to complex interactions between the cells governing the bone physiology in health and disease. Hence, experiment-based drug design is a lengthy and expensive process. Given the continuously increasing capability of computer simulations, supporting and complementing the design of drug administration regimes by computational modeling has proven promising ^14–16. The gold standard of mathematical modeling of disease systems comprises coupling pharmacokinetic (PK) models (quantifying the “availability” of the drug at sites of interest) with pharmacodynamic (PD) models (quantifying the time-dependent effect of the drug on the overall physiological system). Most of previous PK/PD-type models relate, on a simplistic phenomenological basis, drug exposure to related levels of so-called biomarkers, which serve as indicators for drug effectiveness and safety ^17–19. While state-of-the-art approaches, see for example the works of Marathe et al. ²⁰, Pivonka et al. ²¹, or Peterson and Riggs ²², provide valuable qualitative insights on the effects of drug administration, two major shortcomings are evident in any of the state-of-the-art models we found in the literature:

1. The studied disease is usually driven through a constant change of certain parameters. However, as pointed out by Post et al. ¹⁹, it is essential to consider the experimentally observed time-dependence of the biological factors triggering progressive, chronic diseases such as PMO.

2. Bone remodeling is driven solely biochemically, without consideration of biomechanical feedback. It is, however, beyond any doubt ²³ that bone remodeling is regulated both biochemically and biomechanically.

In this paper, we aim at resolving these shortcomings by developing and integrating computational models in an attempt to better understand the mechanism(s) of the action of denosumab on remodeling events in bone. We also take into consideration the clinically observed increase in bone density following treatment with denosumab. Remarkably, this observation is a counterintuitive clinical outcome as preventing bone resorption (which is the functional principle of anti-catabolic drugs such as denosumab) does not, by itself, imply any bone gain. In particular, we aim at explaining how the binding of RANKL by denosumab may be related to the clinically observed increase in bone density.

For these purposes, we first develop a PK model, on the basis of the experimental data of Bekker et al. ⁸, that predicts the blood serum concentration of denosumab following subcutaneous administration (Section 2). We then link this PK model to a recently developed integrated systems biology-continuum micromechanics model of bone remodeling ²⁴. This model takes into account key features of the known physiology of bone remodeling, including the most significant biochemical and biomechanical regulatory mechanisms (Section 3.1). Here, the model of Scheiner et al. ²⁴ is extended: (i) to enable adequate simulation of the effects of PMO on bone remodeling (Section 3.2), and (ii) to also provide the pharmacodynamical effects of the exogenous drug denosumab (Section 3.3). We utilize our model then for simulation of PMO without administration of denosumab (Section 4.1), and we study the effects of single administration and multiple administrations of denosumab (Sections 4.2 and 4.3), and interpret the results through comparison with experimental data from biomarker measurements (Section 5.1) and from bone mineral density measurements (Section 5.2). After discussing the influence of the mechanical loading on the disease progress (Section 5.3), we round the paper off with concluding remarks (Section 6).

2 PHARMACOKINETICS OF DENOSUMAB

Denosumab is injected subcutaneously and over time is absorbed into the blood serum. Through blood circulation, denosumab may then reach surfaces of metabolizing bone. Mathematical description of the effect of denosumab requires formulation of a PK model taking into account the delay between drug administration and effectivity.

To this end, in line with Marathe et al. ²⁰, a two-compartment representation ²⁵ of the physiological system is chosen, with compartment I relating to the subcutaneous tissue, in which denosumab is present at mass concentration m_den,sub, and compartment II relating to the blood serum, in which denosumab is present at mass concentration m_den,ser, see Figure 1. The transfer of denosumab from the subcutaneous tissue to the blood serum is governed by absorption rate k_abs. We take into account that in the blood serum denosumab is subjected to degradation (also referred to as clearance) by both organs and enzymes. Degradation by organs is considered via degradation rate k_org, whereas degradation by enzymes is considered via degradation rate k_enz.

Figure 1.

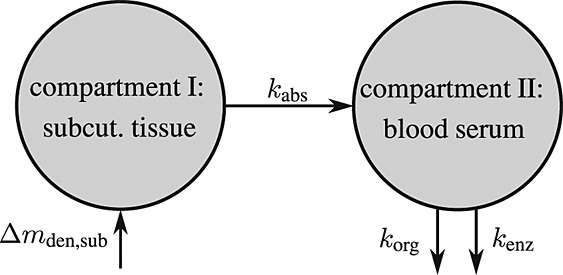
Pharmacokinetics model representation of denosumab: compartment I represents the subcutaneous tissue with denosumab being present at mass concentration m_den,sub, whereas compartment II represents the blood serum with denosumb being present at mass concentration m_den,ser; the compartment concentrations are governed by absorption rate k_abs, degradation rates k_org and k_enz, and the administered dose D_den (which is related to Δm_den,sub).

2.1 Governing equations for calculation of the denosumab concentrations

For development of a mathematical model describing the pharmacokinetics of denosumab, we assume that the absorption of denosumab from the subcutaneous tissue into the blood serum is linearly related to the actual mass (concentration) m_den,sub in the subcutaneous tissue. Accordingly,

1

Solution of Equation (1) requires consideration of an appropriate initial condition. In a single-dose administration regime, with denosumab administered at t = 0, t being the time variable, Δm_den,sub is the sudden increase of m_den,sub in the subcutaneous tissue due to the administered dose D_den, and prior to denosumab administration the concentration of denosumab in the subcutaneous tissue equals zero. Based on this initial condition, Equation (1) can be solved analytically, see Equation (A.1) in Appendix A.

In the blood serum, denosumab degradation occurs proportional to its actual concentration m_den,ser. However, experimental findings ²⁶ suggest that above a certain limit concentration, hereafter denoted as 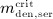, degradation is restricted. Following classical literature on enzyme kinetics ²⁷, we include in our PK model that this degradation restriction can be attributed to a limited degradation capacity of the involved enzymes. In mathematical terms, the serum concentration of denosumab is hence governed by

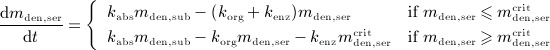2

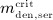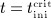Prior to administration of denosumab, at t = 0, the denosumab serum concentration equals zero, thus m_den,ser(t = 0) = 0. Due to absorption of denosumab from the subcutaneous tissue m_den,ser builds up over time, governed by Equation (2)₁, and arrives at limit concentration at . For 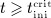the evolution of m_den,ser follows Equation (2)₂ (because 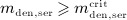). After reaching a dose-dependent peak concentration, m_den,ser decreases, because of the decreasing supply from the subcutaneous tissue, until it reaches again 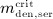at . 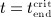For 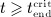the serum concentration is smaller than the limit concentration and hence again governed by Equation (2)₁. On the basis of these conditions, Equation (2) can be solved for m_den,ser, see Equations (A.2)–(A.4) in Appendix A.

Depending on the administration intervals and the delivered doses, a denosumab administration regime involving multiple administrations is characterized by a large number of possible initial and boundary conditions on the basis of which the Equations (1) and (2) have to be solved, see Appendix A.

2.2 Calibration of the absorption and degradation rates

Now, the PK model derived in Section 2.1 and Appendix A is calibrated through determination of parameters k_abs, k_org, and k_enz. For this purpose, we use the clinical data of Bekker et al. ⁸, who measured the temporal evolutions of the serum concentration for six different administration doses 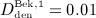 mg/kg,  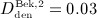mg/kg,  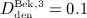mg/kg,  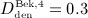mg/kg,  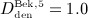mg/kg, and  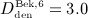mg/kg. A two-membered evolution algorithm ²⁸ is employed for determination of absorption and degradation rates, aiming at minimization of the relative error between computed and experimentally determined serum concentrations.

Dosing of denosumab occurs relative to the patient body mass. For conversion of the administered dose into a corresponding increase of m_den,sub, we consider an average subject body weight of 70 kg ²⁹, and a blood serum volume of 3 liters ³⁰, resulting in 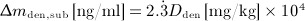. Because, for patient convenience, denosumab administration regimes preferably involve a small number of high-dose administrations rather than a large number of low-dose administrations, we consider only doses 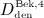, , 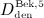and 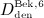for model calibration, to focus on practically relevant doses. Furthermore, the experimental data of Bekker et al. ⁸ show that above a serum concentration of ≈ 750 ng/ml, denosumab degradation kinetics are restricted, thus  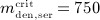ng/ml. On this basis, the implemented evolution algorithm yields k_abs = 1.8498 month ^− 1, k_org = 0.9500 month ^− 1, and k_enz = 0.9932 month ^− 1, see Figure 2 for a comparison of clinical data to PK model results.

Figure 2.

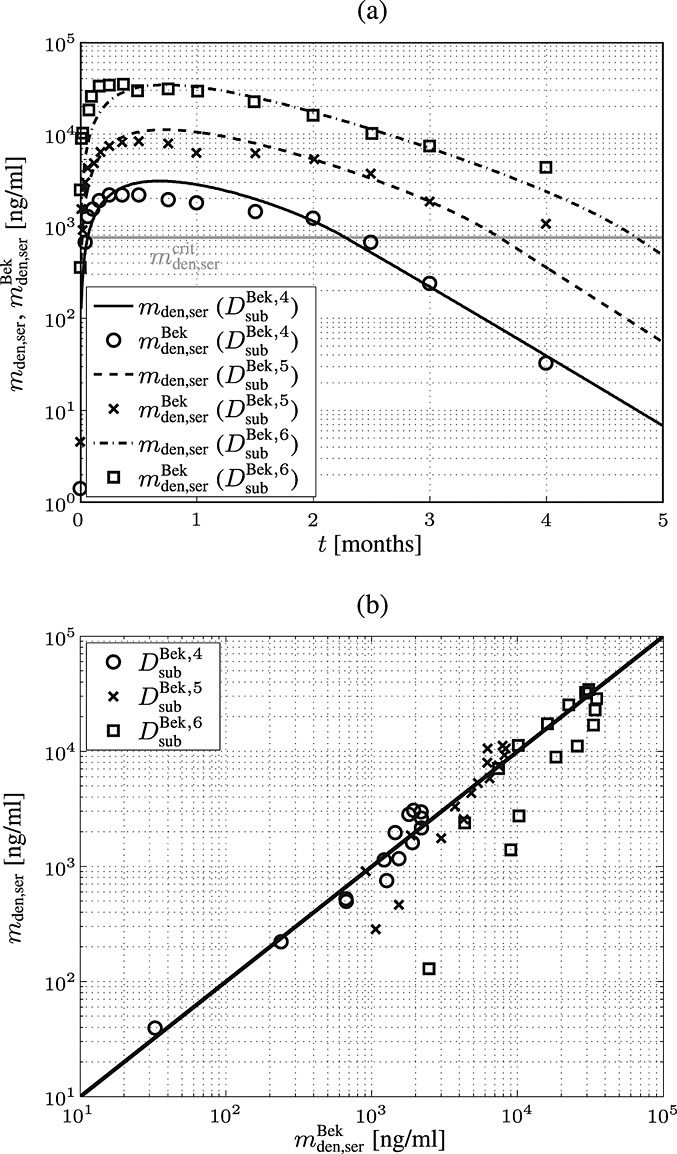
Calibration of the denosumab pharmacokinetics model against the clinical data of Bekker et al. ⁸: (a) comparison between temporal evolutions of model-predicted and measured serum concentrations, and (b) model-predicted versus measured serum concentrations; 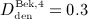 mg/kg,  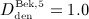mg/kg, and  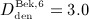mg/kg.

3 THEORETICAL BASIS FOR MODELING THE EFFECT OF DENOSUMAB ON REMODELING OF BONE SUBJECTED TO POSTMENOPAUSAL OSTEOPOROSIS

3.1 A bio-chemo-mechanically coupled mathematical model of bone remodeling

The main novelty presented in this paper, namely a mathematical model enabling simulation of the effect of denosumab on bone remodeling within a representative volume element of bone subjected to PMO, is centered around a recently developed model integrating bone cell population kinetics and multiscale bone mechanics ²⁴. For conciseness, we here present the model components as follows: While model extensions that are original contributions of this paper are presented at appropriate length, any model components borrowed from previous publications are only outlined briefly.

3.1.1 General remarks

The previously developed and here utilized integrated approach to computational simulation of bone remodeling ²⁴ is based on the notion of a representative volume element (RVE). Within an RVE of bone microstructure (with a characteristic length of 1 to 3 mm), bone remodeling, together with the underlying biochemistry and the mechanical environment, occurs (quasi-)homogeneously. Hence, spatial effects (such as transport processes and local variations of biochemical factors or mechanical properties) can be neglected.

3.1.2 Bone cell population kinetics

The biochemically and biomechanically guided evolutions of osteoblasts (the cells responsible for bone formation) and osteoclasts (the cells responsible for bone resorption) are mathematically modeled by means of a so-called bone cell population model (BCPM), the foundation of which was laid by Lemaire et al. ³¹, explicitly considering various distinct developmental stages of osteoblasts and osteoclasts. Namely, the model takes into account the populations of uncommitted osteoblast progenitor cells (abbreviated to OB_u), osteoblast precursor cells ( OB_p), active osteoblasts ( OB_a), osteoclast precursor cells ( OC_p), and active osteoclasts ( OC_a). The populations of these cell types are expressed in terms of respective molar concentrations C_i (describing the “amount” of the species per unit volume and being thus equivalent to corresponding average cell numbers). Progression of osteoblasts and osteoclasts along the chosen developmental stages ( OB_u → OB_p → OB_a and OC_p → OC_a) is implemented considering the (regulatory) mechanisms described in the following paragraphs, see Figure 3 and ^21,24,32, as well as references therein, for details on the mathematical implementation.

Figure 3.

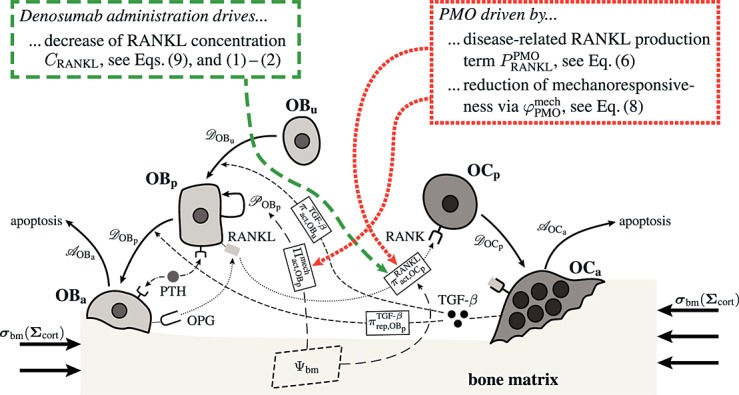
Graphical sketch, adapted from Pivonka et al. ³³, showing all mechanisms considered in the model presented in this paper, with novel contributions colored green and red: guidance of cell developments (OB_u → OB_p → OB_a and OC_p → OC_a) occurs biochemically (governed by TGF-β and the RANK-RANKL-OPG pathway, including the action of PTH) via related activator and repressor functions, π_act and π_rep, and biomechanically (the macroscopic loading Σ relates to microscopic loading σ_bm, causing microscopic deformations represented by the microscopic strain energy density Ψ_bm, the latter entering the bone cell population model); evolutions of the different cell developmental stages follows cell differentiation (considered through maximum differentiation rates 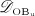, , and 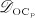), cell proliferation (considered through maximum proliferation rate 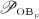), and cell apoptosis (considered through maximum apoptosis rates 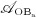and ); 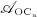the mechanisms based on which the effects of PMO and denosumab administration, respectively, are depicted in the red-colored box (dotted thick lines) and in the green-colored box (dashed thick lines), respectively; see Sections 3.2–3.4 for details on related model extensions.

The concentration of the OB_ps, 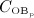, increases because of differentiation of OB_us (which are assumed to exhibit a constant concentration), governed by maximum differentiation rate 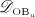and activated through binding of transforming growth factor β (TGF- β) to its receptors ^34,35, via activator function 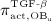; it further increases because of proliferation of OB_ps, governed by maximum proliferation rate 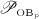and activated through increased mechanical loading ^36–39, by means of activator function 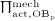, see Equation (7) and ²⁴ for details; and it decreases because of differentiation of OB_ps to OB_as, governed by maximum differentiation rate 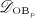and inhibited by binding of TGF- β to its receptors ^34,35, via repressor function :

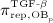3

The concentration of the OB_as, 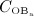increases because of differentiation of OB_ps, governed by maximum differentiation rate 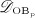and inhibited through binding of TGF- β to its receptors, via repressor function 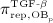; and it decreases because of apoptosis governed by constant apoptosis rate :

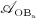4

The concentration of the OC_as, 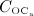increases because of differentiation of OC_ps (which are assumed to exhibit a constant concentration), governed by maximum differentiation rate 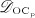and activated through binding of receptor activator nuclear factor kappa β (RANK) to its ligand, RANKL, via activator function 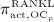; and it decreases because of apoptosis, governed by maximum apoptosis rate 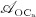and activated through binding of TGF- β to its receptors ⁴⁰, via activator function :

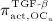5

Note that 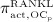, further specified in Section 3.3, also considers the influence of the parathyroid hormone (PTH) and osteoprotegerin (OPG) on binding of RANK to RANKL ⁶, as well as the reduction of RANKL production because of increasing mechanical loading ^41–44, see Equation (8) and ^24,32 for details.

Activator functions 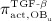, , 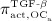and 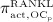, as well as repressor function 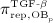are defined according to the concept of Hill functions ⁴⁵, governed by concentrations of the respective substances, namely TGF- β and the RANK-RANKL complex. The complete formulations of these functions, as well as respective derivations, are given in full detail in ^24,32.

3.1.3 Relation of bone cell populations to bone composition

The considered RVE of cortical bone is composed of extravascular bone matrix and vascular pore space. ¹ Importantly, we consider the quasi-instantaneous character of primary mineralization ^46–48 by having the modeled osteoblasts deposit directly mineralized solid bone matrix, thereby omitting consideration of the initially laid down unmineralized osteoid. For the mineralized bone matrix, we consider a constant, organ-dependent mineralization state, see Appendix B and ^24,49 for further details. The “amount” of the aforementioned components within the studied RVE, namely extravascular bone matrix and vascular pore space, is quantified by means of volume fractions: the volume fraction of extravascular bone matrix is defined as its volume within the RVE divided by the total volume of the RVE, f_bm = V_bm / V_RVE; the volume fraction of vascular pore space, f_vas, is defined analogously, f_vas = V_vas / V_RVE. A numerical value of f_bm = 1 thus expresses that the RVE consists solely of extravascular bone matrix, in turn implying f_vas = 0 (because f_bm + f_vas ≡ 1). Dealing with cortical bone only, the initial bone composition in all simulations presented in Section 4 is defined through 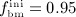. The change of volume fractions is governed by bone resorption and bone formation. To relate the bone cell concentrations 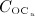and 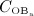, obtained from the BCPM, to corresponding changes of the bone constituent volume fractions, we define resorption rate k_res, quantifying how much bone is resorbed per concentration of active osteoclasts, and formation rate k_form, quantifying how much bone is formed per concentration of active osteoblasts:

6

Accordingly, 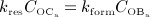represents equilibrated bone remodeling (with constant bone constituent volume fractions f_bm and f_vas), 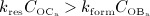represents a catabolic bone remodeling regime (where f_vas increases), while 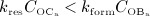represents an anabolic bone remodeling regime (where f_bm increases).

3.1.4 Mechanical regulation of bone remodeling

In line with Scheiner et al. ²⁴, we consider the strain energy density that is experienced by the extravascular bone matrix, Ψ_bm, as adequate mechanoregulatory quantity; in other words, the current magnitude of Ψ_bm dictates whether and to which extent addition or removal of bone is triggered by the mechanical loading. Estimation of Ψ_bm is accomplished by means of a continuum micromechanics-based ⁵⁰ multiscale bone mechanics model ⁴⁹: Based on the morphology of the RVE, on the intrinsic, experimentally accessible stiffnesses of the bone constituents (extravascular bone matrix and pore space), and on the corresponding volume fractions accessible through evaluation of the bone cell concentrations obtained from the BCPM, see Equation (6), the microscopic strain tensor of the extravascular bone matrix, Ψ_bm, is estimated. Ψ_bm follows then through 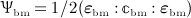, with 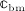denoting the microscopic stiffness tensor of the extravascular bone matrix (see Appendix B for the numerical values of the components of 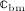), and “ :” denoting a mathematical operation called second-order tensor contraction. Note that 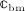relates Ψ_bm to the microscopic stress tensor σ_bm through a linear constitutive relation, .

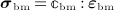Importantly, continuum micromechanics allows to “downscale” the stresses Σ_cort, acting upon the bone on the macroscale, to the related strain tensor Ψ_bm on the microscale. For the sake of simplicity, we prescribe, in all simulations presented in Section 4, a constant, uniaxial compression loading scenario, with Σ₃₃ = − 30 MPa. ² In our model, both mechanically governed activation of OB_p proliferation and mechanically governed production of RANKL are regulated by Ψ_bm ²⁴, establishing a feedback-type relation between bone biology and bone mechanics:

7

8

In Equation (7), 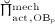denotes the value of 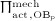related to “normal” mechanical loading, which, in turn, induces a corresponding SED 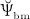, 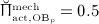; note that 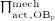governs the osteoblast precursor proliferation in Equation (3). The sensitivity of OB_p proliferation to increased mechanical loading can be adjusted by the so-called anabolic strength parameter λ. This parameter has been found to reasonably replicate mechanically stimulated bone gain if set to λ = 1.25 if 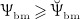, and λ = 0 if 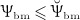²⁴. In Equation (8), 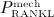denotes the production of RANKL because of decreased mechanical loading (compared with normal loading conditions). In our model, 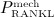co-governs the concentration of RANKL, see Equation (12) and below, this way modulating the differentiation of OC_p to OC_a. Inhibition parameter κ allows for adjustment of the sensitivity of RANKL production to a reduced mechanical loading. Setting κ = 10⁵ pM/day if 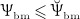and κ = 0 if 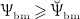has proven to give rise to reasonably simulated bone loss if subjected to disuse scenarios ²⁴.

3.2 Consideration of the effect of postmenopausal osteoporosis on bone remodeling

Experimental studies on the pathophysiology of PMO reveal that several mechanisms might occur simultaneously, together inducing the disease pattern known as PMO. Among several other potential pathogenic mechanisms, estrogen deficiency ³ has been widely accepted as the main cause of PMO ^51,52, resulting in increased osteoclast and osteoblast concentrations (and thus in an increased bone turnover) ⁵³. Relative to the cell concentrations in healthy (premenopausal) bone, the increase of 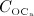is higher than the increase of 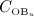that leads to (potentially) significant bone loss after onset of PMO. This initial phase of PMO is accompanied by an increased ratio of the RANKL concentration over the OPG concentration, compared with normal bone physiology ⁵⁴. After some time (some months up to a few years), the rate of bone loss decreases, and postmenopausal bone is subjected to long-lasting moderate bone loss thereafter.

Driving PMO biochemically can be achieved in different ways; see 21 for a related study. Estrogen and its role in bone remodeling is not considered explicitly in our model, so PMO cannot be simulated by feeding experimentally observed estrogen levels into the model. Instead, PMO is initiated by introducing disease-related increased production of RANKL, leading to increased osteoclast differentiation. In order to account for the moderate bone loss in the second phase of PMO, it is assumed that the excess production of RANKL reduces over time. In detail, we prescribe the following RANKL production regime for 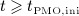, with t_PMO,ini being the point in time when PMO is initiated:

9

with 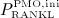as PMO-initiating excess production rate of RANKL, and with 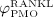as a reduction factor of 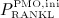, which we define as

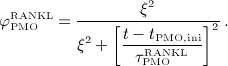10

Parameter ξ and the characteristic time of the RANKL production decrease, 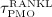, together determine the shape of the Lorentz-type function given by Equation (10). In our model, 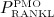co-governs the concentration of RANKL, see Equation (12) and below, this way modulating the differentiation of OC_ps to OC_as. Furthermore, in vivo data suggests that the decreasing mechanoresponsiveness of bone due to increased osteocyte apoptosis, another effect of estrogen deficiency, also plays a major role for the progression of PMO ^52,56. In order to incorporate this effect into our model we assume that, after onset of PMO at t = t_PMO,ini, the parameters governing the sensitivity of bone remodeling to a changing mechanical loading, κ and λ, see Equations (7) and (8), are decreased via reduction factor ,

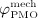11

with τ_PMO as the characteristic time of the PMO-related mechanoresponsiveness decrease of cortical bone. Hence, contrary to conventional PK/PD approaches, in our model the disease-governing parameters are not held constant, but are varied over time, following the pathophysiological trends reported in the literature ¹⁹.

The set of Equations (9)–(11) can be considered as a (semi-)phenomenological approach to the sum of processes that in reality contribute to initiation and maintenance of PMO. While such an approach is common practice for simulation of complex physiological systems, the model parameters introduced in this section cannot be measured or directly deduced from experimental data. Thus, for the time being, we are content with adjusting these parameters such that simulation results agree well with corresponding experimental data, as demonstrated in Section 4.1.

3.3 Incorporation of the action of denosumab

In our model, denosumab contributes to regulation of osteoclast differentiation via activator function 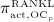. Denosumab competes with RANK (and OPG) as for binding to RANKL, meaning the higher the concentration of denosumab the lower the concentration of RANKL-RANK complexes, hence the lower the numerical value of 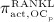and the lower the fraction of the osteoclast precursor population that differentiates into active osteoclasts. Adapting the approach of Pivonka et al. ³², the concentration of RANKL follows

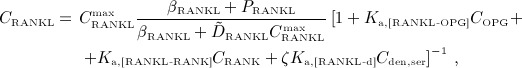12

where K_{a,[RANKL-OPG]}, K_{a,[RANKL-RANK]}, and K_a,[RANKL-d] are the equilibrium association binding constants for binding of OPG, RANK, and denosumab to RANKL, C_OPG, C_RANK, and C_den,ser are the molar concentrations of OPG, RANK, and denosumab, β_RANKL is the intrinsic RANKL production rate, P_RANKL is the RANKL dosage term, 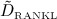is the constant degradation rate, and 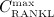is the maximum concentration of RANKL. The concentration of RANKL-RANK complexes is considered through

13

While the BCPM and respective concentrations of regulatory factors are formulated for a specific RVE of bone tissue, the concentration of denosumab is given in the blood serum. In Equation (12), the varying accessibility of denosumab to different RVEs of bone tissue is taken into account through accessibility factor ζ: ζ = 1 represents unrestricted access to denosumab, whereas ζ < 1 reflects access restrictions (for example because of low or uneven blood circulation). In the following, we only consider the case of uniform and sufficient blood circulation, ζ = 1. Finally, activator function 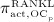is governed by ³²

14

with K_d,[RANKL-d] as the corresponding equilibrium dissociation binding constant. In the present model, the external production rate of RANKL, P_RANKL, is made up of two components: 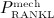(stemming from decreased mechanical loading), see Equation (8), and 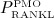(for simulation of postmenopausal osteoporosis, see Equation (9), .

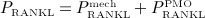3.4 Governing model parameters

The interaction of RANKL and denosumab is considered via the denosumab serum concentration m_den,ser, see Section 2, and the association binding constant K_a,[RANKL-d] which quantifies the affinity of denosumab-binding to human RANKL. Choice of the numerical value of K_a,[RANKL-d] is based on the in vitro experiments performed by Kostenuik et al. ⁵⁷. Solution equilibrium binding analysis revealed an equilibrium dissociation binding constant of K_d,[RANKL-d] ≈ 3 pM. The equilibrium association binding constant is defined as the inverse of the corresponding dissociation constant, K_a,[RANKL-d] = (K_d,[RANKL-d])^− 1 ≈ 0.33 pM ^− 1. Furthermore, the denosumab concentrations provided by the PK model are given in ng/mg, whereas the unit of the equilibrium association binding constant is pM ^− 1 = (10^− 12 mol/l)^− 1. Hence, PK model-derived mass concentrations m_den,ser have to be converted to the corresponding molar concentration C_den,ser. This conversion follows from fundamental principles of physical chemistry ⁵⁸: Given the molecular weight of denosumab, M_den = 147 kDa ⁵⁹, the molar concentration corresponding to a mass concentration of m_den,ser = 1 ng/ml is C_den,ser = 6.8027 pM.

Further model calibration has been thoroughly dealt with in ^21,24,32; the numerical values of the parameters that are explicitly mentioned in this paper are summarized in Appendix B.

4 NUMERICAL STUDIES

4.1 Simulation of postmenopausal osteoporosis without administration of denosumab

In this section, the model introduced in Section 3.2 is calibrated such that porosity evolutions observed clinically during PMO progression ⁶⁰ can be replicated, yielding 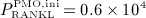 pM/d, ξ = 65,  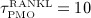d, and  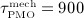d, compare Equations (9) and (10). Considering the such defined PMO-related RANKL-production and the decline of the mechanoresponsiveness of cortical bone, see Figure 4(a), yields corresponding evolutions of osteoclast and osteoblast concentrations, see Figure 4(b). The corresponding increase of the vascular porosity over time agrees well with physiologically observed porosity evolutions in osteoporotic bone ⁶⁰, see Figure 4(c).

Figure 4.

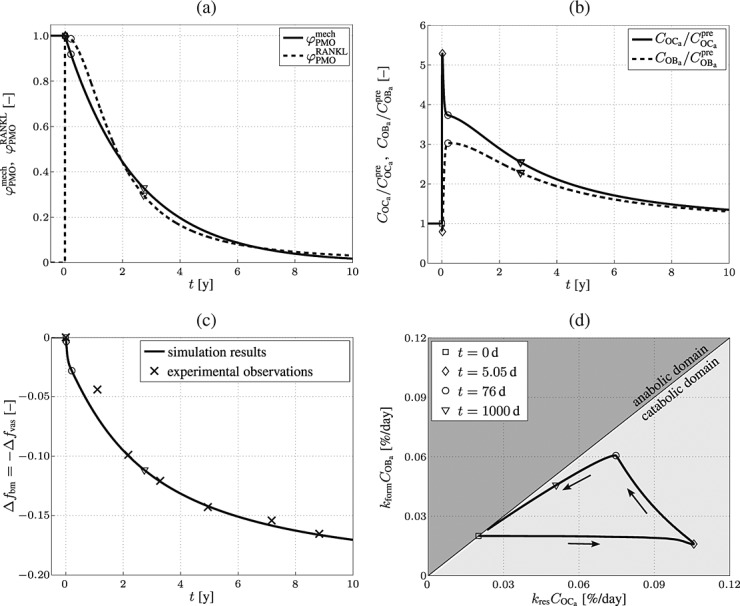
Simulation of postmenopausal osteoporosis (PMO) with disease initiation at t_PMO,ini = 0: (a) prescribed temporal evolutions of the reduction factor of the disease-related RANKL production rate, 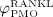, and of the mechanoresponsiveness reduction factor, 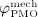, (b) model-predicted evolutions of the concentrations of active osteoclasts, 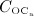, and active osteoblasts, 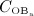, normalized with respect to the concentration before onset of PMO, 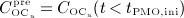and 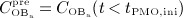, (c) the increase of the vascular porosity of osteoporotic cortical bone over time, Δf_vas(t), simulated by our model, compared with corresponding experimental results, and (d) the phase diagram comparing bone resorption versus bone formation responses associated to the simulated porosity increase of osteoporotic cortical bone; the arrows indicate path directions.

Alternatively, to elucidate the bone remodeling kinetics leading to such porosity evolution, the simulation results can be plotted in terms of a comparison of resorbed bone per time (bone resorption rate times concentration of active osteoclasts, 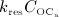) versus formed bone per time (bone formation rate times concentration of active osteoblasts, 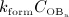), see Figure 4(d) – such graphical presentation is also referred to as “phase diagram”. A balanced bone turnover implies 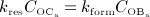, and related data points lie on the diagonal line in Figure 4(d). A catabolic bone remodeling regime, indicated as light grey-shaded area in Figure 4(c), is characterized by dominating bone resorption, thus 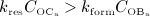, and corresponding data points lie below the diagonal line.

On the other hand, an anabolic regime, indicated as light dark-shaded area in Figure 4(d), is characterized by dominating bone formation, thus 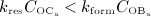, and corresponding data points lie above the diagonal line.

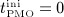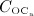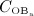Onset of PMO, at , leads to drastically increasing bone resorption, because of a significant, quasi-instantaneous increase of osteoclast differentiation, and thus implying an increased osteoclast concentration, see Figure 4(b). The maximum ratio of over (and thus the maximum rate of bone loss) is reached after 5.05 days, indicated by the diamond-shaped markers in Figure 4. Subsequently, osteoclast differentiation decreases because of decreased disease-related RANKL-production, see Figure 4(a), thus the path of the phase diagram moves towards the diagonal line, see Figure 4(d). Furthermore, TGF- β is released during bone resorption, which leads to up-regulation of osteoblast differentiation, indicated by the delayed increase of the osteoblast concentration after onset of PMO in Figure 4(b). Osteoblasts produce RANKL, thus an increased osteoblast concentration implies also increased RANKL production, which, in turn, leads to increased osteoclast differentiation and in further consequence to deceleration of the decrease of the osteoclast concentration because of decreasing PMO-related production of RANKL, see the circle-shaped markers in Figure 4(b). This deceleration provides the explanation for the kink observed in the phase diagram at 76 days, see Figure 4(d). This kink is followed by decreasing bone turnover, meaning that both bone resorption and bone formation slowly diminish. Thus, while still in the catabolic domain, bone remodeling converges to balanced bone resorption and formation, also indicated by the continuously flattening slope of the solid graph in Figure 4(c).

It should be noted that micromechanics-based stiffness homogenization does not only serve as an integral part for implementing mechanoregulation of bone remodeling in our model (as described in Section 3) but also allows for mathematical modeling-based tracking of the bone stiffness over time (not plotted in this paper), in terms of orthotropic Young's moduli E₁, E₂, and E₃, shear moduli G₁₂, G₁₃, and G₂₃, and Poisson's ratios ν₁₂, ν₁₃, and ν₂₃ as stiffness-defining material properties, see 24,61 for details. For example, after 10 years of progressing PMO, the vascular porosity is increased by 17.04%, see Figure 4(c), whereas Young's moduli are decreased by up to 33.55%, shear moduli are decreased by up to 34.64%, and Poisson's ratios are decreased by up to 16.43%. Hence, the effect of PMO on the mechanical integrity of bone can be significantly more severe than the underlying change of the bone composition – in order to simulate this effect, a sound multiscale model of bone mechanics, such as the one utilized in this paper, is essential.

4.2 Single-dose administration of denosumab

Now, we consider a regime of denosumab administration involving only one single administration, to thoroughly elucidate general characteristics of the model response. We prescribe that denosumab is injected 6 months ⁴ after initiation of PMO (at 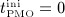), and we investigate three different administration doses,  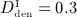mg/kg,  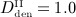mg/kg, and  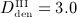mg/kg. Based on these input data, the model is evaluated in terms of bone cell concentrations, as well as in terms of corresponding phase diagrams and evolutions of the bone constituent volume fractions.

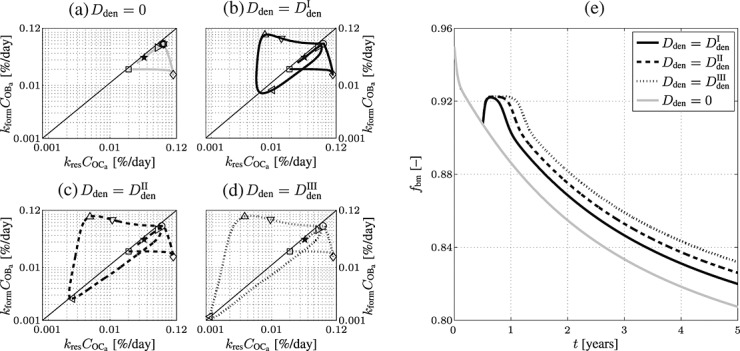
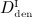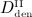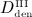For t < 6 months (prior to administration of denosumab), all graphs (representing doses , , and , as well as the zero dose) obviously coincide, see the paths between the square-shaped and the circle-shaped markers in Figures 5(a)–(d). For 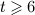months, the presence of denosumab entails inhibition of the differentiation of osteoclast precursor cells to active osteoclasts, consequently leading to fast decrease of 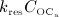, see the paths in Figures 5(b)–(d) after passing the circle-shaped markers. At the same time, a temporary increase of 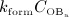is observed, leading to a short but steep increase of f_bm following denosumab administration, see Figure 5(e). This increase, indicated by the phase diagram paths crossing the balanced turnover-representing diagonal lines in Figures 5(b)–(d), stems from how the action of TGF- β is considered in our model. On the one hand, TGF- β inhibits differentiation of osteoblast precursor cells to active osteoblasts. Administration of denosumab leads to downregulation of the concentration of active osteoclasts, entailing a reduced release of TGF- β, and in further consequence an increase, due to reduced differentiation inhibition, of the concentration of active osteoblasts. Moreover, the presence of TGF- β is required for maintaining differentiation of osteoblast progenitor cells to osteoblast precursor cells. This means that reduction of the concentration of TGF- β leads to downregulation of the aforementioned differentiation process, and thus, with a certain time delay, to downregulation of the concentration of active osteoblasts, completing the “anabolic loops” observed in Figures 5(b)–(d).

Figure 5.

Simulation results obtained for administration regimes involving one administration of denosumab: (a)–(d) phase diagrams (in logarithmic scales) for the simulated doses, (a) D_den = 0, (b) 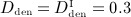mg/kg, (c) 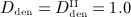mg/kg, and (d) 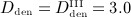mg/kg, with the temporal progress indicated by respective markers (days, ⋄…5 days, ○ …182.5 days, ▽ …185 days, △ …190 days, days, ▹…700 days, and days after onset of postmenopausal osteoporosis), and (e) the corresponding temporal evolutions of the volume fractions of the extravascular bone matrix, f_bm, as postmenopausal osteoporosis progresses.

Subsequent to the temporary dominance of 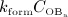over 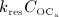, the action of denosumab comes to full effect, and the bone turnover is decreased to a very low level (as compared to the initial state), 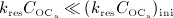and 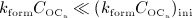, see the region around the leftwards-pointing triangles in Figures 5(b)–(d). Notably, the higher the dose of denosumab the lower the minimum bone turnover, and the longer the duration of low bone turnover, compare with the time characteristics of the phase diagrams depicted in Figures 5(b)–(d), and the corresponding evolutions of f_bm, see Figure 5(e). After clearance of denosumab, the paths of the dose-dependent bone turnover converge to the grey-colored path in Figure 5(a), representing PMO without administration of denosumab. In terms of the simulated evolutions of f_bm, this means that after the temporary bone gain “peak”, related to denosumab administration, subsequent evolutions of f_bm exhibit the same slope as the evolution of f_bm related to PMO only (with D_den = 0), see Figure 5(e).

The temporal evolutions of f_bm, depicted in Figure 5(e), reveal a prominent characteristic of the model. While the long-term evolution of the volume fraction of extravascular bone matrix is adequate – denosumab leads, as long as the internal degradation mechanisms described in Section 2 have not led to clearance of denosumab, to a delay of further porosity increase – the short-term response to drug administration does not quite resemble the experimentally and clinically observed trends. The previously described temporary dominance of osteoblast activity over osteoclast activity leads, according to the model, to a short period of very fast bone gain (Δf_bm = 0.0125 within Δt ≈ 20 days), see Figure 5(e). After this short period of significant bone gain, max (df_bm / dt) = 8.12 × 10^− 2 % day^− 1, the model predicts constant volume fractions, relating to the decrease of bone turnover to a very low level as shown in Figure 5(a), after which the effect of denosumab wears off, and the volume fraction of bone matrix decreases further (consequently the volume fraction of porosity increases), because of uninhibited progress of PMO. While increasing the dose of denosumab leads to lengthening of the volume fraction “plateau”, no dosing effect on the overall bone gain can be observed.

4.3 Multidose administration of denosumab

In order to assess the predictive capabilities of our model, Section 4.3 is devoted to simulation of denosumab administration regimes involving multiple administrations, as commonly investigated in experimental (in vivo) studies and in clinical practice. We present the results of simulations considering three different administered doses, 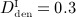 mg/kg,  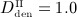mg/kg,  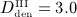mg/kg, and four different intervals between administrations,  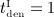month,  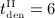months,  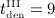months,  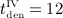months.

The simulation results are presented in terms of bone matrix volume fraction evolutions, see Figures 6(a) and (c), and corresponding phase diagrams, see Figures 6(b) and (d), to also shed light on the underlying bone turnover kinetics. Obviously, decreasing the administered dose leads to decreasing the anti-catabolic effect of denosumab because of shortened suppression of PMO-driven bone loss, see Figure 6(a). Intuitively, the same should be true for increasing the administration interval – this is for example observed when increasing the administration interval from 9 to 12 months. However, Figure 6(c) also shows that increasing the administration interval from 1 to 6 months results, for the administered dose of D_den = 1.0 mg/kg, in a slight increase in bone gain. On the one hand, this effect is caused by the considered mechanoregulatory mechanisms (see Section 3.1), or in other words by the attempt of bone to re-establish its original composition (for the investigated cortical bone related to f_bm = 0.95). On the other hand, administration regimes including multiple administrations of denosumab also exhibit the short period of fast bone gain discussed in Section 4.2, which can, if administered doses and administration intervals are specifically coordinated, as well create an anabolic bone remodeling response – the paths of the phase diagram related to such administration regimes remain, on average, in the anabolic domain for a longer stretch of time.

Figure 6.

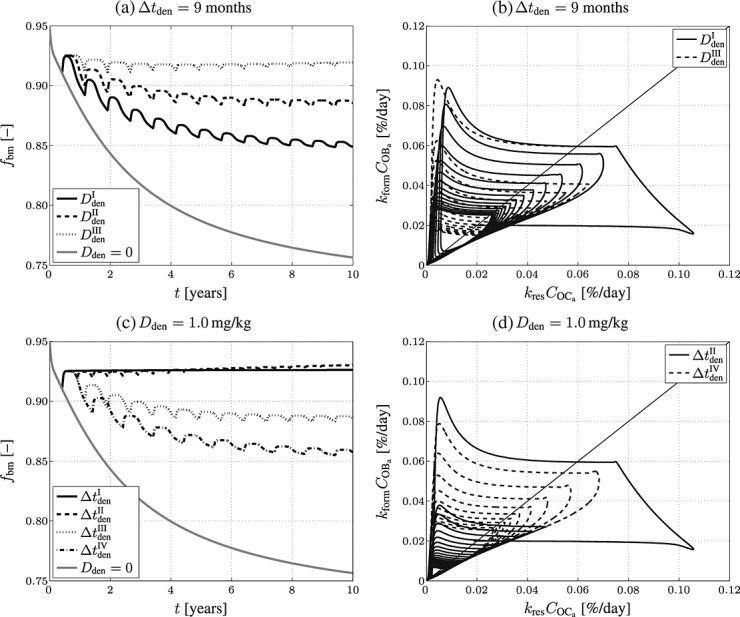
Simulation results obtained for administration regimes involving multiple administrations of denosumab: temporal evolutions of volume fractions of the extravascular bone matrix, f_bm, during progression of PMO (a) for different administered doses (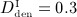 mg/kg,  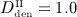mg/kg, and  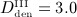mg/kg) and (c) different administration intervals ( 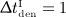month,  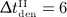months,  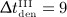months, and  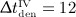months), as well as the corresponding phase diagrams (b) and (d), where each loop corresponds to one of the “hills” in (a) and (c), representing one administration interval; the paths depicted in (b) and (d) are directed counterclockwise.

For intervals 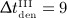 months and  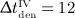months, the long-term influence is negligible due to the opposite effect (a short period of very fast bone loss) observed after clearance of denosumab. For interval 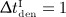month, the concentration of denosumab constantly remains at a sufficiently high level to maintain suppression of bone remodeling activities so the bone volume fraction remains constant. Increasing the interval of denosumab administration from 1 to 6 months, with the administered dose fixed at D_den = 1.0 mg/kg, results in a higher bone matrix volume fraction: 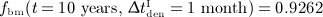, whereas 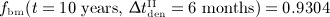. This trend is mainly caused by bone cell kinetics, a certain combination of bone remodeling parameters (characterizing for instance a specific patient), and denosumab administration parameters entail. Hence, our model allows to optimize administration intervals and doses to maximize bone gain after initiation of the administration regime. Clearly, careful tuning of administration interval and dose is the key to obtain such optimized administration regime, which underpins the potential benefit of supporting the design of drug administration regimes by means of computational modeling.

While we have performed a large number of simulations (not shown here) considering different combinations of administration doses and administration intervals, we have never observed any significant bone volume gain. We will further discuss the relevance of this observation with respect to experimental and clinical studies in Section 5.2.

5 DISCUSSION

5.1 Simulation results versus biomarker measurements

In physiological conditions, the direct effect of drug administration on bone remodeling at a particular bone site is hardly measurable. To nevertheless monitor the success of anti-catabolic drugs in the treatment of PMO, so-called bone turnover markers, also referred to as biomarkers, are commonly used in clinical practice ^53,62, measured in the urine or in the serum. The evolution of bone resorption is tracked on the basis of bone resorption markers, such as collagen type I cross-linked N-telopeptide (NTx), or collagen type I cross-linked C-telopeptide (CTx). Analogously, bone formation can be monitored by means of bone formation markers, such as osteocalcin (OC or BGLAP), bone-specific alkaline phosphatase (BALP or BSAP), or procollagen type I N-terminal propeptide (PINP). While bone turnover markers provide valuable information on the overall effect of drug administration on bone remodeling, inferring that bone remodeling is altered to the quantitatively same extent on specific sites seems inaccurate (the reason for this is discussed in the next paragraph). We will hence compare the model predictions with biomarker measurements in qualitative fashion only.

Lewiecki ²⁶ summarizes the biochemical effect of denosumab for different single-dose administrations. Compared with the results observed for placebo administration, the “reduction of NTx levels was observed to be dose-dependent, rapid, profound (up to 84%), sustained (for up to six months), and reversible with discontinuation”. The model-predicted evolutions of the concentration of active osteoclasts, serving as basis for computing the results depicted in Figure 5, fit reasonably well to these experimental observations. The only substantial difference is that after administration of denosumab the model-predicted concentration of active osteoclasts is reduced by more than 99% (in contrast to the reported reduction of NTx levels by up to 84% ²⁶). This difference can be explained by considering the involved observation scales. The computational results are based on an RVE in which the denosumab serum concentration is assumed to be uniform, thus denosumab is fully active throughout the RVE. In contrast, blood circulation and thus the distribution of denosumab is not uniform throughout the body, and clearly regions of low supply with denosumab do not contribute to the reduction of NTx as regions where the supply is higher. Taking this into consideration, the agreement between model predictions and experimental results is deemed satisfactory. ⁵

A qualitatively and quantitatively similar trend is observed for bone formation markers during a multiple denosumab administration regime. For example Eastell et al. ⁶³ observed a reduction of the PINP level of up to ≈ 90% and a reduction of the BALP level of up to ≈ 50%. Considering the importance of the actual observation scale of the results, as proposed in the previous paragraph, the model-predicted osteoblast concentration is assumed to be (qualitatively) consistent with experimental observations.

5.2 Simulation results versus bone mineral density measurements

Clearly, the most tangible effect of PMO is the related decrease of mechanical properties (such as stiffness and strength), leading to an increasing susceptibility to bone fractures. In clinical practice, the fracture risk is usually assessed by measuring the bone mineral density (BMD) by means of dual-energy X-ray absorptiometry on sites suspected or known to be subjected to PMO and comparing this value with the corresponding BMD in healthy bone, for example, via the so-called T-score ⁶⁴. Often, the success of anti-resorptive drugs, such as denosumab, in the treatment of osteoporosis is assessed by measuring the BMD evolution after drug administration. These measurements are then interpreted as follows: the higher the increase of the BMD the more potent the investigated drug. For example, after administration of denosumab the BMD has been reported to increase by up to 2 % in cortical bone and up to 9 % in trabecular bone (over a time span of typically 1 to 2 years), see for example 11,9,65–68. Mineral concentrations are not included into the present version of our mathematical model, so that a direct comparison of BMD increase with simulation results is out of reach for the moment. However, it is very instructive to compare the increase in BMD measured on denosumab-treated patients with the decreasing or constant bone volume predicted by our model in Figures 5 and 6.

By definition, denosumab (and in general anti-resorptive drugs) are intended to decrease the activity of osteoclasts. Our simulation results (see Section 4), as well as measurements of bone resorption markers ²⁶ confirm that denosumab indeed fulfills this intention. Simultaneously, because of communication between osteoclasts and osteoblasts, denosumab also entails significant decrease of the activity of osteoblasts – confirmation of this computationally observed behavior follows from measurements of bone formation markers ⁶³. Evidence is thus overwhelming that the increase of bone mineral density after administration of denosumab simply cannot arise from bone gain in the sense that osteoblasts lay down “new” osteoid. The only mechanism remaining that is able to cause the clinically observed BMD increase after administration of denosumab is increased bone tissue mineralization, triggered through denosumab. The following mechanism seems very probable. Denosumab suppresses the action of RANKL, which is itself promoting the dissolution actions by osteoclasts and osteocytes. In particular, the latter are responsible for keeping the tissue mineralization degree at some limit value ^69,70, that is, inhibiting purely chemically driven “anorganification” of bone tissue. Suppressed osteocytic dissolution action, however, would allow for progression of the so-called secondary mineralization process, and also increase the overall BMD, as evidenced in clinical studies ^71–78. Hence, our model gives valuable insight into the biological and chemical processes leading to denosumab-triggered BMD increase. For the sake of completeness, we remark that secondary mineralization-induced increase of bone tissue stiffness with respect to Equation (A.9) is not explicitly accounted for in the present approach, adding that, from a mechanical point of view, a rigorous multiscale approach translating mineralization degree to tissue stiffness is at hand ^79,70.

5.3 Influence of the mechanical loading on the disease progress

In the computational studies presented in this paper, we have considered a constant (that is time-invariant) uniaxial mechanical loading. It is perfectly clear that (i) such mechanical load case is a strong simplification of the “real” loading acting onto human bone (which is presumably always of three-dimensional nature, including nonzero shear components of the stress and strain tensors); and that (ii) mechanical loading varies (partly significantly) between different locations distributed across a human skeleton. In the context of the scope of this paper, the influence of a different load case is negligible as long as it is still time-invariant, and the resulting strain energy density is of comparable magnitude. This is because in our model, mechanical regulation is stimulated by changes of the strain energy density, irrespective of the exact shape of the related strain tensor. A temporarily changing mechanical loading, on the other hand, could potentially have a great influence on the disease progress (in terms of the resulting bone matrix volume fraction evolution); imposing such mechanical loading “histories” is, however, beyond the scope of this paper, which is restricted to mathematical modeling of PMO and its pharmaceutical intervention by means of the anti-resorptive drug denosumab. For a parametric study on the influence of the type of mechanical loading on the related bone remodeling behavior, see reference ²⁴.

Another important model aspect, related to the mechanical loading, is the sensitivity of the bone remodeling response to a changing (local) mechanical loading. In the simulations presented in this paper, the macroscopic mechanical loading is held constant at all times (as discussed in the previous paragraph). However, the disease-related increase of the vascular porosity (after the onset of PMO, see Figures 5 and 6) implies an increase of the strains experienced by the extravascular bone matrix, and thus an increase of the related strain energy density, which is the quantity that has been chosen as mechanoregulatory stimulus. An increase of the strain energy density, beyond the value that occurs if the studied piece of cortical bone is healthy, leads to an increase of OB_p proliferation, with the anabolic strength parameter λ as governing property, compare Equations (3) and (7). In the following, because of the apparent importance of parameter λ, we elucidate the sensitivity of the model predictions to variations of λ. In particular, we perform the simulations based on which Figure 6(a) has been created (that is a denosumab administration regime involving multiple administrations, with an administration interval of 9 months) for two alternative values of λ: λ_low = 0.125 (representing bone with low mechanoresponsiveness) and λ_high = 12.5 (representing bone with high mechanoresponsiveness). In Figure 7, the volume fraction of the extravascular bone matrix after 10 years of PMO progress is plotted, confirming the striking sensitivity of the model predictions to parameter λ.

Figure 7.

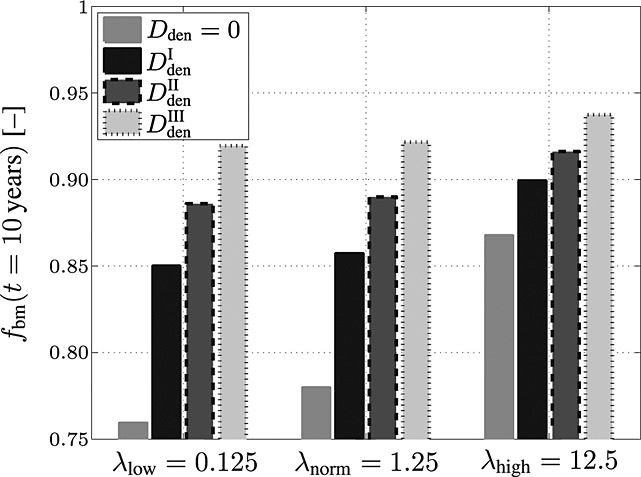
Study of the sensitivity of the model-predicted bone matrix volume fraction f_bm after 10 years of postmenopausal osteoporosis progress with respect to a varying anabolic strength parameter λ, computed for an administration regime involving multiple administrations of denosumab, with a constant administration interval Δt_den = 9 months and administered doses D_den = 0, 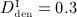mg/kg,  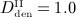mg/kg, and  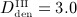mg/kg.

This parametric study also shows that the sensitivity of the model prediction to λ is indirectly proportional to the administered dose of denosumab: the higher the administered dose, the lower the sensitivity of the bone remodeling response to variations of λ. Thus, careful choice of the model parameters accounting for the mechanoresponsiveness of bone remodeling is crucial for the mathematical model presented here in order to replicate adequate predictions.

6 CONCLUSIONS

In this paper, an integrated model has been presented, allowing for simulation of the effects of postmenopausal osteoporosis on bone remodeling. For this purpose, a PK model of denosumab has been developed and coupled to a bone cell population model of bone remodeling, which itself communicates with a continuum micromechanics-based homogenization scheme of bone stiffness, in order to soundly take into account mechanobiological regulatory mechanisms of bone remodeling and corresponding changes of the bone stiffness.

The numerical studies presented in Sections 4 and 5 have shown that the new model proposed here allows for (qualitatively and quantitatively) reasonable simulation of osteoporotic scenarios, and of the pharmaceutical intervention through administering the anti-catabolic drug denosumab. In particular, the simulation results have given rise to the following specific conclusions:

1. In order to simulate PMO, the underlying mathematical model should be fed by temporally varying disease-triggering factors – in our model, PMO is driven, on the one hand, by disease-related RANKL production, see Equations (9) and (10), and, on the other hand, by disease-related reduction of the mechanoresponsiveness, see Equation (11). This way, not only the postmenopausal evolution of bone volume agrees well with corresponding clinical data, see Figure 4(c), but also the related bone turnover satisfyingly resembles the clinically and experimentally observed dynamics – a very high bone turnover in the initial phase of PMO is followed by a slow, long-lasting decrease converging to the normal, premenopausal bone turnover, see Figure 4(d).

2. Administration of denosumab entails, because of inhibition of osteoclast differentiation, down-regulation of both bone resorption and, with some time delay, bone formation to an ineffective level. One administration of denosumab has the following effects on the bone turnover: Initially, a short but significant phase of bone gain is observed, related to the time lag between drug-related inhibition of bone resorption and bone formation. Once bone formation is sufficiently down-regulated (approximately 5 to 10 days after denosumab administration, depending on the administered dose), the bone turnover reduces to a negligible level. Due to denosumab clearance, the bone turnover finally approaches the disease-related evolution, thus altogether denosumab administration causes a delayed progress of PMO. As expected, simulation results confirm that increasing the administered dose and/or decreasing the administration interval improves the anti-catabolic effect of denosumab, compare Figures 5(b)–(e).

3. The model predictions obtained through simulating denosumab administration regimes involving multiple administrations, see Section 4.3, agree, in qualitative terms, well with corresponding biomarker measurements.

4. One central component of the integrated model is the continuous estimation of the macroscopic bone stiffness by means of a continuum micromechanics-based homogenization scheme, appropriately taking into account the anisotropic mechanical behavior of bone. The such computed evolution of bone stiffness could serve as basis for assessing the risk of bone failure.

These findings highlight that the model proposed here could be a promising tool for computer simulation-based assessment of the effects of denosumab administration on osteoporotic bone. However, the results presented and discussed in Sections 4 and 5 also motivate to invest in explicit modeling of the secondary mineralization process and its linkage to RANKL and osteocytic action.

In addition to their important role for the mineralization process (as discussed previously), osteocytes are known to act as key players for sensing changes of the mechanical loading and for transducing these changes into corresponding biochemical events, leading to increase or decrease of the bone matrix volume fraction ^80,81,23,82. In the systems biology approach employed in this paper, osteocytes are not considered explicitly, which clearly constitutes a limitation of the model. Introduction of the population of osteocytes into our model, as demonstrated in alternative modeling approaches, see for example references 83–86, is thus deemed as promising model extension, in particular to bring the considered mechanoregulatory mechanisms closer to experimental evidence ^81,82,87,88. Furthermore, in future model extensions, we will aim at reduction of the number of model components to the necessary minimum; this will go along with reduction of the currently considerable number of model parameters, being another limitation of the model. These issues are topics of ongoing research.

APPENDIX A: ANALYTICAL SOLUTIONS OF THE PHARMACOKINETICS MODEL

A.1 Single-dose administration regimes

The analytical solution of differential equation (1), under consideration of initial condition m_den,sub(t = 0) = Δm_den,sub, see Section 2.1, reads

A.1

Note that Δm_den,sub is related to the administered dose D_den through consideration of an average patient body mass and serum volume, as discussed in Section 2.2. On the other hand, the solution of differential equations (2) is based on conditions m_den,ser(t = 0) = 0, 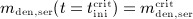, and 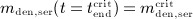. Solving Equations (2) for m_den,ser yields

A.2

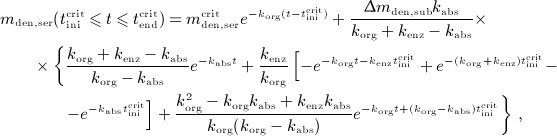A.3

and

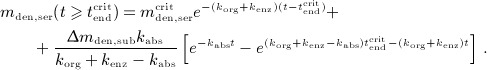A.4

Numerical evaluation of Equations (A.3) and (A.4) requires knowledge of time instants 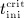and 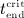. If the numerical value of 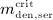is known, 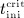and 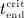are accessible implicitly via Equations (A.2) and (A.3): Equation (A.2), evaluated for 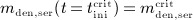, allows for determination of 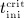, whereas Equation (A.3), evaluated for 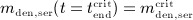, allows for determination of .

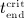A.2 Multidose administration regimes

We now want to derive analytical expressions describing the denosumab serum concentration over time for denosumab administration regimes involving multiple injections.

For this purpose, administration intervals and doses are assumed to be constant, and the corresponding initial conditions are periodic. ⁶ Because of this regularity, only two different scenarios have to be considered: at the end of the previous administration interval the denosumab serum concentration m_den,ser is (i) lower than the critical concentration 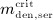, , 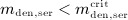and (ii) it is higher (or equal) 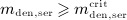, see Figure 8.

Figure 8.

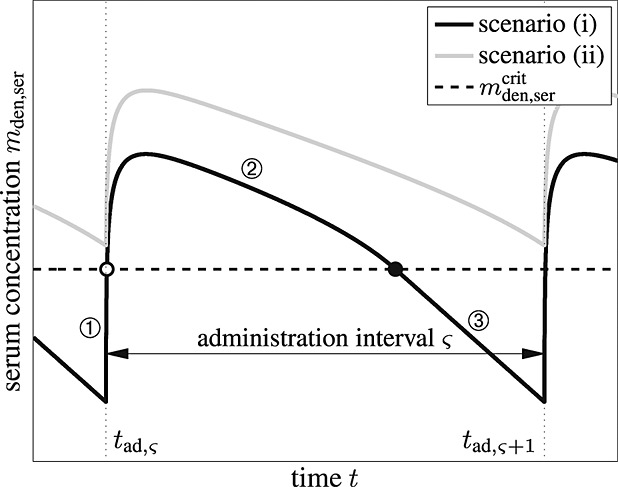
Two scenarios investigated for denosumab administration regimes involving multiple injections: in scenario (i), m_den,ser starts from a level below 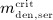in each administration interval ς, while in scenario (ii), m_den,ser remains higher than 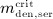at all times; within one administration interval scenario (i) comprises three domains ①, ②, and ③ based on whether m_den,ser is lower or higher than 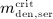(the transition between the domains is indicated by the white-faced circle-shaped marker, representing 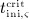and black-faced circle-shaped marker, representing 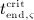), following Equations (A.5)–(A.7), whereas scenario (ii) follows Equation (A.8).

First, we investigate scenario (i). Denosumab is administered at the beginning of each administration interval ς, at t = t_ad,ς, with t_ad,1 = 0. The administered dose and thus Δm_den,sub are constant, and at the end of each interval the denosumab serum concentration has dropped to a level below the critical concentration, 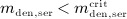. Consequently, each administration interval is characterized by domains of different enzyme kinetics, analogous to the single-administration regime elaborated in Sections 2.2 and A, which are delimited by the time instants at which the critical concentration is reache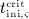d, and 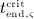, see also Figure A.1. The following notation is chosen for the different enzyme degradation regimes: 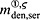denotes the denosumab serum concentration if 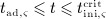, 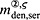denotes the denosumab serum concentration if 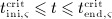, and 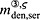denotes the denosumab serum concentration if 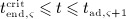. While 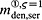, , 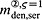and 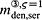are defined by Eqs.(A.2)–(A.4), 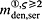, , 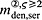and 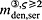follow as

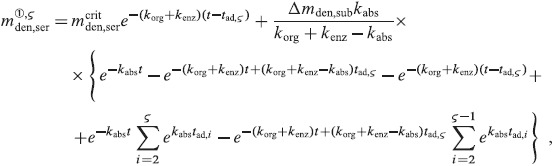A.5

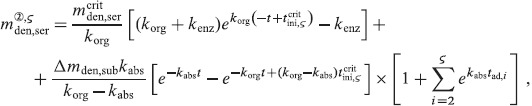A.6

and

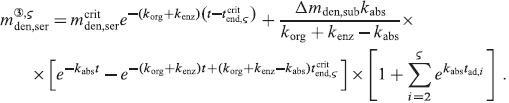A.7

In scenario (ii) the denosumab serum concentration remains, after exceeding 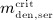at 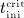in the first administration interval, above 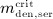at all times. Thus, distinction between different domains is, unlike scenario (i), not necessary, and only one analytic expression has to be derived. If 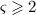, 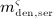reads as

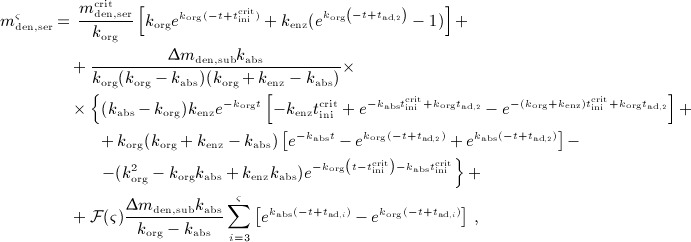A.8

where function 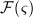is defined as 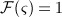if and 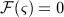otherwise.

APPENDIX B: MODEL PARAMETERS

In Table B.1, the model parameters of the integrated systems biology/micromechanical model, introduced in Section 3, that are explicitly mentioned in this paper, are summarized.

Table B.1.

Parameters of the integrated systems biology-micromechanical model, see also ²¹,³².

parameter	numerical value	unit
kres	2	(pMday)  − 1
	7 × 10 − 2	d  − 1
	1.6570 × 10 − 1	d  − 1
	2.1 × 100	d  − 1
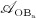	2.1107 × 10 − 1	d  − 1
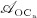	5.6487 × 10 − 4	d  − 1
Kd,[RANKL-d]	5.6797 × 100	pM
βRANKL	1.6842 × 102	pMd  − 1
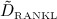	1.0132 × 101	d  − 1
Ka,[RANKL-RANK]	3.4118 × 10 − 2	pM  − 1
Ka,[RANKL-OPG]	1 × 10 − 3	pM  − 1
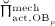	0.5	–
λ	1.25	–
κ	105	pM/day

The bone formation rate k_form is calibrated such that for the bone resorption rate, k_res, defined in Table 1, steady-state cell concentrations, 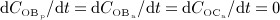, imply a balanced bone turnover; that is, f_vas = const. and f_bm = const.: 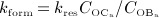. Calibration of the proliferation rate 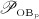is described in detail in ²⁴.

Furthermore, the stiffness tensor of the extravascular bone matrix, 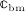, is defined in the line of Fritsch and Hellmich ⁷⁹; based on the ultrasonics tests by Ashman et al. ⁸⁹, conducted on human femurs, 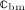reads in compressed notation ⁹⁰

A.9

APPENDIX C: NOMENCLATURE

Abbreviations:

BALP

bone-specific alkaline phosphatase

BCPM

bone cell population model

BMD

bone mineral density

CTx

collagen type I cross-linked C-telopeptide

DXA

dual-energy X-ray absorptiometry

NTx

collagen type I cross-linked N-telopeptide

OB_a

active osteoblasts

OB_p

osteoblast precursor cells

OB_u

uncommitted osteoblast progenitor cells

OC

osteocalcin

OC_a

active osteoclasts

OC_p

osteoclast precursor cells

OPG

osteoprotegerin

PD

pharmacodynamics

PINP

procollagen type I N-terminal propeptide

PK

pharmacokinetics

PMO

postmenopausal osteoporosis

PTH

parathyroid hormone

RANK

receptor of nuclear factor kappa-B

RANKL

ligand of RANK

RVE

representative volume element

SED

strain energy density

TGF- β

transforming growth factor beta

Latin symbols:

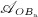
constant apoptosis rate of active osteoblasts

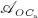
maximum apoptosis rate of active osteoclasts

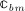
stiffness tensor of the extravascular bone matrix

C_den

molar concentration of denosumab

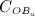
molar concentration of active osteoblasts

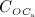
molar concentration of active osteoclasts

C_OPG

molar concentration of OPG

C_RANK

molar concentration of RANK

C_RANKL

molar concentration of RANKL

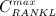
maximum molar concentration of RANKL

D_den

dose of denosumab administration

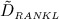
constant RANKL degradation rate

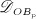
maximum differentiation rate of osteoblast precursor cells

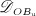
maximum differentiation rate of uncommitted osteoblast progenitor cells

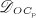
maximum differentiation rate of osteoclast precursor cells

E_i

Young's moduli of bone on the macroscopic observation scale, i = 1,2,3

f_bm

volume fraction of extravascular bone matrix

G_ij

shear moduli of bone on the macroscopic observation scale, ij = 12,23,13

k_abs

absorption rate

k_enz

degradation rate related to enzymes

k_form

bone formation rate

k_org

degradation rate related to organs

k_res

bone resorption rate

K_a,[RANKL-i]

equilibrium association binding constant for the binding of RANKL to substance i, i = denosumab, OPG, RANK

K_d,[RANKL-i]

equilibrium dissociation binding constant for the dissociation of substance i from RANKL, i = denosumab, RANK

m_den,ser

denosumab mass concentration in the blood serum

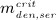
limit denosumab mass concentration in the blood serum

M_den

molecular weight of denosumab

Δm_den,sub

increase of denosumab mass concentration in the blood serum due to administration

m_den,sub

denosumab mass concentration in the subcutaneous tissue

P_RANKL

production rate of RANKL

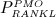
PMO-related production rate of RANKL

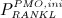
PMO-related production rate of RANKL directly after disease initiation

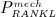
mechanical disuse-related production rate of RANKL

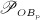
maximum proliferation rate of osteoblast precursor cells

t

time variable

t_PMO,ini

point in time when PMO is initiated

V_bm

volume of the extravascular bone matrix within a representative volume element

V_RVE

volume of the representative volume element

V_vas

volume of the vascular pore space within a representative volume element

Greek symbols:

β_RANKL

intrinsic RANKL production rate

Ψ_bm

microscopic strain tensor experienced by the extravascular bone matrix

ζ

denosumab accessibility factor

κ

RANKL production inhibition parameter

λ

anabolic strength parameter

ν_ij

Poisson's ratios of bone on the macroscopic observation scale, ij = 12,13,23

ξ

parameter introduced for definition of

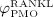
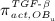
activator function for the differentiation of uncommitted osteoblast progenitor cells due to the action of TGF- β

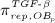
activator function for the differentiation of osteoblast precursor cells due to the action of TGF- β

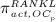
activator function for the differentiation of osteoclast precursor cells due to the action of RANKL

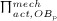
activator function for the proliferation of osteoblast precursor cells due to mechanical loading

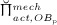
activator function for the proliferation of osteoblast precursor cells due to normal mechanical loading

σ_bm

microscopic stress tensor experienced by the extravascular bone matrix

ς

administration interval index in a multidose administration regime

Σ

macroscopic stress tensor

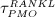
characteristic time of the RANKL production decrease

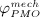
mechanoresponsiveness reduction factor

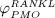
reduction factor

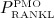
Ψ_bm

strain energy density experienced on the observation scale of extravascular bone matrix

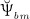
strain energy density experienced on the observation scale of extravascular bone matrix related to normal mechanical loading