Detecting Regular Sound Changes in Linguistics as Events of Concerted Evolution

Summary

Background

Concerted evolution is normally used to describe parallel changes at different sites in a genome, but it is also observed in languages where a specific phoneme changes to the same other phoneme in many words in the lexicon—a phenomenon known as regular sound change. We develop a general statistical model that can detect concerted changes in aligned sequence data and apply it to study regular sound changes in the Turkic language family.

Results

Linguistic evolution, unlike the genetic substitutional process, is dominated by events of concerted evolutionary change. Our model identified more than 70 historical events of regular sound change that occurred throughout the evolution of the Turkic language family, while simultaneously inferring a dated phylogenetic tree. Including regular sound changes yielded an approximately 4-fold improvement in the characterization of linguistic change over a simpler model of sporadic change, improved phylogenetic inference, and returned more reliable and plausible dates for events on the phylogenies. The historical timings of the concerted changes closely follow a Poisson process model, and the sound transition networks derived from our model mirror linguistic expectations.

Conclusions

We demonstrate that a model with no prior knowledge of complex concerted or regular changes can nevertheless infer the historical timings and genealogical placements of events of concerted change from the signals left in contemporary data. Our model can be applied wherever discrete elements—such as genes, words, cultural trends, technologies, or morphological traits—can change in parallel within an organism or other evolving group.

Graphical Abstract

Highlights

• •Linguistic evolution is dominated by events of concerted evolutionary change
• •Modeling concerted evolution improves phylogenetic inference and dating
• •Events of concerted change conform closely to a Poisson process
• •Our model can be applied to genes, languages, cultures, and technological change

Concerted evolution refers to the same evolutionary change occurring at different sites in a genome. It also occurs in languages when the same sound change occurs in different words. Hruschka et al. report a statistical model that can detect concerted changes and show how it substantially improves our understanding of how languages evolve.

Introduction

Concerted evolutionary change is widespread in genetic systems, being implicated in the genome-wide control of repetitive elements [1–3], the evolution of gene families [2], and homogenization of Y chromosome sequences [4, 5] and as a means by which asexual organisms might escape the debilitating consequences of Muller’s ratchet [3]. It might arise from several mechanisms, including homologous recombination, that allow certain favorable elements to spread or damaging elements to be neutralized.

Linguists have long recognized concerted change that affects copies of the same sound (or phoneme) appearing in different words as a central feature of linguistic evolution [6]. A well-known example is the ^∗p>f sound change in the Germanic languages wherein an older Indo-European p sound was replaced by an f sound, such as in ^∗pater>father, or ^∗pes, ^∗pedis>foot (linguistic convention is to use the “>” symbol to indicate a transition from one sound to another, and here the ^∗ symbol denotes a reconstructed ancestral form). These multiple instances of one phoneme changing to the same other phoneme yield regular sound correspondences between pairs or groups of languages. Linguists have proposed several explanations for the regularity of changes grounded in a number of basic processes, including speech production, perception, and cognition [7–9].

Can events of concerted change be detected statistically in sequence data, and do they improve the characterization of evolution and the inference of evolutionary histories? Although previous researchers working in a linguistic setting have used the concept of regular changes to build algorithms for automatically inferring cognacy, to our knowledge the model we report here is the first probabilistic description of concerted change. This places concerted evolution in a statistical setting that allows for formal hypothesis testing about the nature and rates of concerted changes. For example, the question of how many parallel changes are required to be recognized as an instance of concerted change is naturally dealt with in our model: the statistical signature of concerted or regular change is that the multiple parallel events are more probable if treated as a single coordinated change than as a collection of independent changes (Box 1).

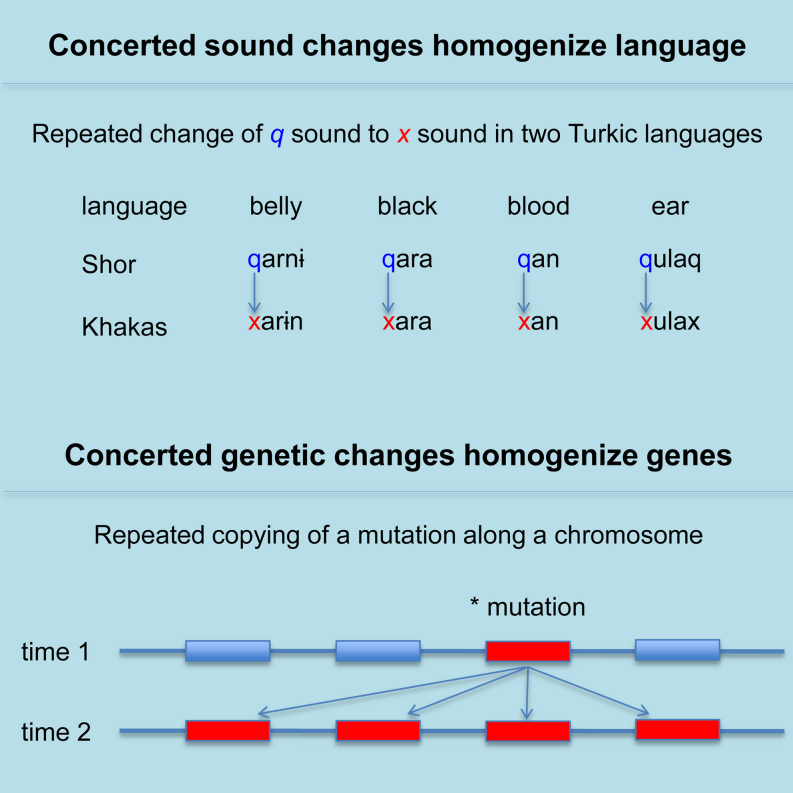
Box 1. The Anatomy of Concerted Change.

Four pairs of words from closely related Siberian languages—Shor and Khakas (Figure 2)—are shown below. In each case, the leading q in Shor corresponds to an x in Khakas (leading x and q shown in italics). In total, there are 35 aligned positions in our data where q appears in a Shor word, and in 34 of these, x occurs in the same position in Khakas. The one exception is the Khakas kirə- “to grow old,” which is qarɨ- in Shor.

Given the corresponding sounds in all other Turkic languages, the ancestral sound for these two sister languages is most likely q. This means that these x’s in Khakas arose following a Shor-Khakas split.

	“belly”	“black”	“blood”	“ear”
Shor	qarnɨ	qara	qan	qulaq
Khakas	xarɨn	xara	xan	xulax

A conventional sporadic change model would count the 34 transitions from q to x as 34 independent events. If the probability of a single sporadic change is denoted by $P_s\left(q\to x\right)$, then the probability of observing 34 independent q-to-x transitions is $P_s{\left(q\to x\right)}^{34}$.

By comparison, the model of concerted or regular change identifies these 34 events as a single instance of concerted change across the affected sites. If we denote the probability of a regular linguistic change from q to x by $P_r\left(q\to x\right)$, then as the number of events n increases, there will be a point at which $P_r\left(q\to x\right)>P_s{\left(q\to x\right)}^n$, and it will become statistically more probable to treat n events as a single instance of regular change. Not all instances of x and q will necessarily interchange between two languages, but if a sufficient number do, they are statistically more probable if treated as a single event of “regular” change.

In some cases, a change such as q to x will depend upon its context, that is, on other sounds in the word. A hypothetical example of context would be if leading q sounds in Shor words remained as q sounds in Khakas words when the leading q was followed by an e, but changed from q to x if followed by a or u vowels as above.

Currently, our model implements a general “context-free” description of concerted evolution applicable to a range of evolving systems, including genes and proteins. The theory can be extended to include context-dependent regularities (Discussion; Supplemental Experimental Procedures; [23]), but in this work we focus on the improvement that arises solely from unconditioned regularity of sound changes, and statistical methods for detecting such concerted evolution.

Usefully, the genetic and linguistic phenomena share fundamental properties relevant to their statistical characterization. Phonemes are the units of sound that make up words and distinguish one word from another, just as the four nucleotide bases (A, C, T, G) make up DNA gene sequences or the 20 amino acids make up protein sequences. The number of distinct sounds in a language varies greatly, but somewhere around 30–60 phonemes are commonly sufficient to describe the range of distinctive sounds in a language’s words [10]. Collections of words can therefore be thought of as providing phonemic “sequence information” that might be informative as to the history, rate, and patterns of concerted evolutionary change in language, and in a manner analogous to sequences of DNA.

Statistical Modeling of Concerted Evolution

We adopt a phylogenetic-statistical perspective that allows us to document events of concerted change that have occurred throughout the genealogical history of a linguistic or biological family, infer their historical patterning, and determine the rate and frequency with which they arise in nature [11, 12]. The statistical model we develop implements a fully probabilistic description of the sporadic or irregular and concerted or regular changes that characterize the temporal patterns of substitutions in strings of inherited information such as DNA or sound sequences as they evolve along the branches of the phylogenetic trees that record their evolutionary histories.

In a linguistic context, sporadic changes refer to the replacement, over some arbitrary interval of time, of one phoneme in one place by another and are analogous to single nucleotide or amino acid substitutions in gene sequences. Concerted or regular changes describe the parallel change of one discrete element such as a nucleotide, phoneme, or amino acid to the same other discrete element at many different sites (Box 1).

In contrast to genetic evolution, some historical linguists maintain that all sound changes are regular, with apparent irregularities arising from a number of processes working simultaneously, but others allow that sporadic effects also occur [13–15]. We will classify as irregular or sporadic all changes where there is not statistical evidence to support a concerted change. Some of these could be examples of rare regular changes, or of changes that occur in only a few phonetic contexts (Box 1).

We implement the model in a Bayesian Markov chain Monte Carlo (MCMC) approach (Experimental Procedures) that, when applied to a set of related sequences, simultaneously estimates posterior distributions describing the phylogenetic trees or genealogies, and the matrices that record the instantaneous rates of change from one phoneme (gene, amino acid) to another either at a single site (sporadic changes) or simultaneously at multiple sites (regular changes). The model places no constraints on the nature, rate, or temporal patterning of either sporadic or regular changes, starting instead with a set of uniform prior beliefs and then estimating all rates and patterns of change from the historical traces or imprints these changes have left in the contemporary data.

The sporadic change matrix is estimated as a single homogeneous process that applies throughout the tree. For protein sequence data, the model must estimate 380 distinct transition rates ([20 × 20] − 20) in the sporadic change matrix; for a phonetically transcribed data set of 62 distinct speech sounds, this number rises to 3,782 ([62 × 62] − 62). We therefore adopt a reversible-jump MCMC procedure that we have described elsewhere [16] to reduce the number of statistically distinct parameters. In comparison to the single sporadic matrix, the concerted or regular changes are discovered statistically on a branch-by-branch basis. The model proposes a separate sound change matrix and its position within the branch for each regular sound change that it identifies (Experimental Procedures).

This general approach, when applied to linguistic data, allows us to trace the temporal patterns of phonemic change among a set of related languages. Here we fit the model to lexical data corresponding to 225 etymological classes in 26 Turkic languages that were phonetically coded following the North American Phonetic Alphabet for 62 phonetic symbols [17]. Ideally, the analysis would be carried out on phonemically coded data, but most available data sets only provide a standardized orthography that occasionally distinguishes allophones. In practice, this means that the results for a specific language could depend upon whether its transcription data were consistently subphonemic or phonemic relative to other languages in the data set. To the extent that such allophonic differences are regular, our analyses will not be affected.

The phonetically coded data for each language were then multiply aligned by identifying cognate sites within each word (analogous to homologous gene-sequence alignment). This yielded a 26 languages × 1,120 sites matrix, where a site represents an aligned column of speech sounds.

Results

Fit of the Model to Transcribed Sound Data

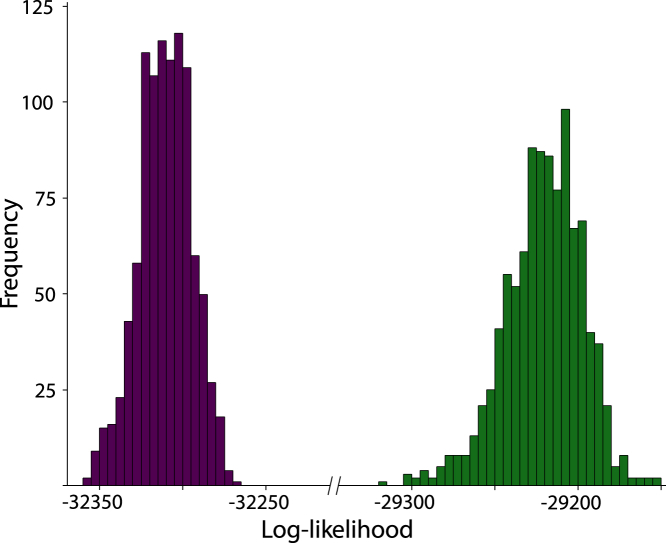
The sporadic-mutation-only model returns a mean log-likelihood in the Bayesian posterior distribution of phylogenetic trees of −32,303.9 ± 14.9 (mean ± SD), compared to −29,196.2 ± 15.1 for the model including regular and sporadic sound changes (hereafter the “regular model”), an improvement for the regular model of 3,108 log-units (Figure 1). The regular model’s improvement derives from its discovering an average of 74.27 ± 0.47 regular sound changes that have occurred in the phylogenetic history of the Turkic languages (mean ± SD in the posterior sample of trees; see Supplemental Experimental Procedures and Table S1 available online). A deviance information criterion test overwhelmingly favors the model of regular changes as a description of these data (ΔDIC = 3,739).

Figure 1.

Posterior Distributions of Log-Likelihoods from the Sporadic and Regular Change Models

Mean log-likelihoods: sporadic change model (purple) = −32,303.9 ± 15; regular change model (green) = −29,196.2 ± 15. Δlog-likelihood = 3,107, based on an average of 74.27 ± 0.47 parameters describing regular sound changes. Deviance information criterion test, ΔDIC = 3,739; values > 0 support regular model. Note: x axis is broken.

Regular Changes and the Phylogeny of Turkic Languages

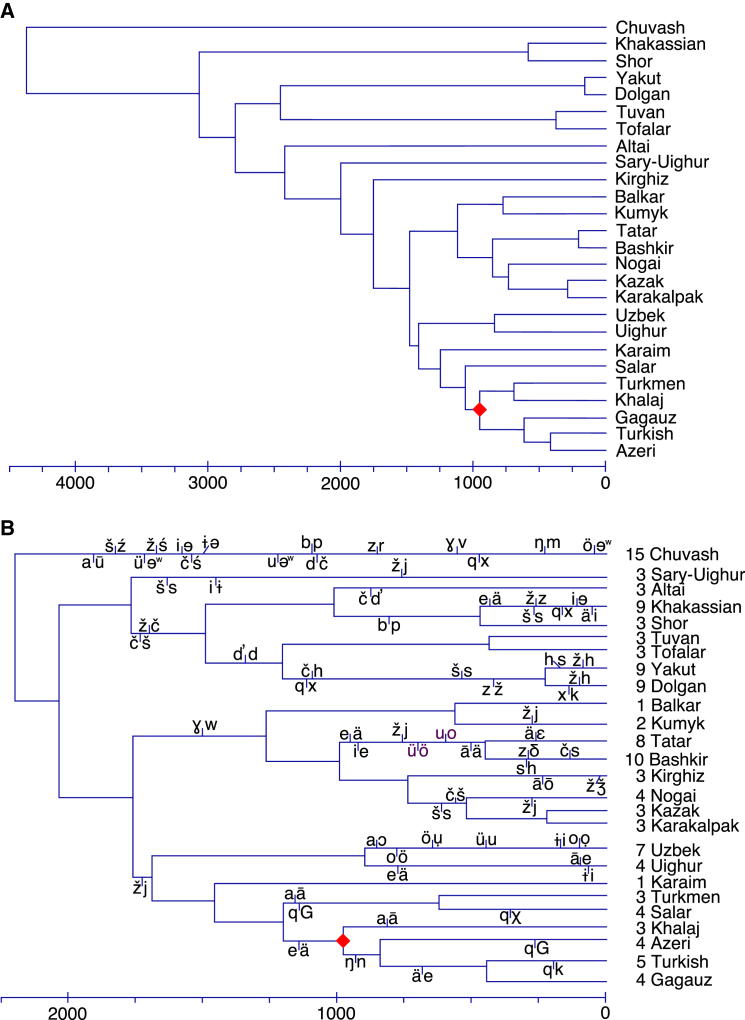
Events of regular sound change can provide strong signals preferring some phylogenetic placements over others and can improve the estimation of divergence times over the sporadic-change-only model, which will routinely overestimate the amount of independent change by assuming that each phonemic substitution is independent (Box 1). Both effects can be seen in Figure 2, where the model including regular changes (shown along branches) produces a different and better-supported consensus dated tree than that derived from the sporadic model, and one that conforms more closely to linguistic scholarship [17, 20].

Figure 2.

Phylogenetic Trees of the Turkic Language Family

Consensus topologies for the model allowing only sporadic changes (A) and the model allowing regular sound changes (B). Regular sound changes are indicated along the top and bottom of branches of the topology: events in black show directional changes from the beginning to ending phoneme; events shown in purple indicate two phonemes that have replaced each other. The model additionally estimates the position of each regular sound change along the branch. Mean estimated age of root between Chuvash and other Turkic languages: sporadic model (A) = 2408 BCE, with 95% credible intervals of 3993–1279 BCE; regular model (B) = 204 BCE, with 95% credible intervals of 605 BCE–81 CE. The posterior date of the calibration node (red dot; [18, 19]) is 1017 ± 20 CE.

The regular-change tree largely replicates the proposed major and minor divisions of the Turkic languages [20], inferring a distinct Siberian branch, which also includes Yellow Uighur, now located in China. In contrast, the sporadic-sound-change model describes the Siberian languages as successively diverging from a Turkic trunk. The regular-sound-change tree estimates a mean divergence time between the outgroup Chuvash and other Turkic languages of 204 BCE, with a 95% credible interval of 605 BCE to 81 CE. This compares to proposals from glottochronological analyses that suggest dates of 30 BCE to 0 CE [21] and 500 BCE to 50 CE from historical data [18, 21, 22]. The sporadic-sound-change model estimates the mean age of the tree to be more than two millennia older (2408 BCE, 95% CI = 3994–1279 BCE), because it wrongly assumes that the many occurrences of regular sound change along the outgroup Chuvash branch are multiple instances of independent phonological change.

The regular sound changes in Figure 2 include well-known linguistic processes affecting consonants, including voicing (e.g., q>G), devoicing (e.g., b>p), gliding (e.g., ž>j and ɣ>w), spirantization (e.g., q>χ, q>x), stopping (e.g., x>k), palatal fronting (e.g., š>s), debuccalization (e.g., s>h), deaffrication (e.g., č>š), and rhotacism (e.g., z>r). Regular changes affecting vowels include changes in height (e.g., ɨ>ə, i>e, u>o), backness (e.g., i>ə, i>ɨ, a>ɔ), and length (e.g., a>ā).

Most of these regular changes make a substantial contribution to the log-likelihood: the geometric mean improvement is 89.1 ± 72.1 log-units per event, measured as the improvement in log-likelihood when the effect is added conditional upon all the other regular sound changes being present. The three largest effects are the a>ɔ, ž>j, and q>k transitions, each of which contributes at least 275 log-units to the overall likelihood. Because these sounds are common in our data set, they make a large contribution to the likelihood when they are part of a regular sound change (Box 1).

The model also estimates the ordering of sound changes within a branch, in some cases allowing inferences to be made about “chaining” of sound changes. For instance, in the branch leading to Yakut, h>s appears before ž>h, indicating that h sounds at the beginning of the branch are more likely to be s by the end and that ž sounds later in the time period represented by that branch are more likely to be h by the end.

Typically, around 29 of the 50 branches of the phylogenetic trees in the posterior sample record at least one event of regular change, with an average of 1.49 ± 2.49 such events per branch, although this distribution is skewed (mode = 0, range = 0 to 15). Of the roughly 74 regular sound changes, 43.03 ± 0.17 involve changes between pairs of consonants, 31.22 ± 0.44 involve pairs of vowels, and 0.02 ± 0.14 occur between a vowel and a consonant (all means ± SD refer to the distribution over the posterior sample).

The same regular sound changes are frequently repeated in different parts of the tree such that 21 changes involve unique pairs of consonants, and 17 involve unique pairs of vowels (Table S1). Fewer than half (23 of 62) of all speech sounds produce a detectable regular sound change, and those that do tend to be more common (measured as a sound’s frequency of occurrence in the alignment, Spearman’s r_s = 0.54, p < 0.001), although this relationship might reflect the difficulty of inferring changes in rare sounds as being regular. The median number of regular sound changes does not differ between vowels and consonants (U test, p > 0.10), and vowels and consonants are equally likely to produce at least one event of regular change per sound (binomial test, p > 0.10).

Comparison of Inferred Regular Sound Changes to Historical Linguistic Inferences

Linguists have proposed regular sound changes affecting consonants and vowels in the Turkic language family based on historical linguistic studies of 23 of the 26 languages we report in Figure 2 (see also Table S2). A proposal takes the form of a putative proto- or ancestral sound changing to a different sound or set of sounds in a descendant language. For example, the ancestral u sound is proposed [17, 20] to have changed to o in Bashkir and Tatar, and to əʷ in Chuvash, but to have been retained as u in the other languages. In agreement with these proposals, the model of regular change finds a regular u>o sound change in the branch of the Turkic phylogeny that is ancestral to Bashkir and Tatar, and finds a regular o>əʷ event in the Chuvash branch (Figure 2).

For each of 634 proposed sound changes in the 23 languages (Figure 3; Table S2), we calculated the probabilities that the regular and sporadic change models assigned to the descendant sound, conditional upon the ancestral sound. Where more than one sound change is proposed to have occurred from the same ancestral sound, we summed the probabilities over all of the proposed descendant sounds, along with, in some cases, proposed partially retained ancestral sounds. We then calculated the ratio of the probability derived from the regular model to the probability of the sporadic change model as a measure of relative performance.

Figure 3.

Performance of the Model of Regular Change in Predicting Sound Changes

Colored (nongray) cells correspond to instances of regular sound change as proposed by linguists [17, 20] (see text and Table S2), ranging from ≥10× improvement by the regular change model (dark red) to cases in which the sporadic model outperformed the regular model (blue). Gray cells correspond to cases in which the ancestral phoneme has been retained (no phonological change has occurred). Geometric mean improvement across all colored cells (probability of regular model/probability of sporadic model) = 1.87 ± 2.98, range = 0.14 to 150.12; n = 371. Geometric mean improvement excluding cases of partial ancestral retention (white cells) = 3.71 ± 5.14, range = 0.14 to 150.12; n = 179. Leftmost columns: LA = ancestral phoneme derived from linguists’ proposals; MA = model-derived ancestral phoneme.

Red-tinted cells in Figure 3 denote instances where the regular change model improves on the sporadic model (ratio > 1 to 10) and generally correspond to cases in which the ancestral sound has been replaced by one or more different descendant sounds (Table S2). White cells correspond to ratios of approximately 1:1 and are typically cases in which ancestral sounds have been partially retained in the descendant languages. Blue-tinted cells record ratios < 1 where the regular model performs worse than the sporadic model.

Overall, the model of regular change approximately doubles the probability of correctly predicting the descendant sounds, as estimated using a geometric mean of the ratios to account for positive skew (geometric mean ratio = 1.87 ± 2.98, range = 0.14 to 150.12, n = 371 language X ancestral sound combinations), performing somewhat better for vowels (mean ratio = 3.38 ± 5.38, range = 0.47 to 150.12, n = 97) than for consonants (mean ratio = 1.52 ± 2.46, range = 0.14 to 39.72, n = 274). This difference in performance might merely be because vowels change more readily (faster) than consonants and so are more likely to show a change from the ancestral state.

These figures include instances in which the ancestral sound was partially retained, cases for which the regular model might not be expected to improve upon the sporadic model. For 179 of the proposals the ancestral sound is not retained, and for these, the model of regular change yields an approximately 4-fold geometric mean improvement (mean ratio 3.71 ± 5.14, range = 0.14 to 150.12) and is similar for vowels and consonants (vowels = 3.72 ± 5.40, consonants = 3.70 ± 4.90). A 4-fold improvement corresponds to the sporadic model assigning less than a 0.25 total probability to the proposed descendant sounds (mean = 0.16 ± 0.11).

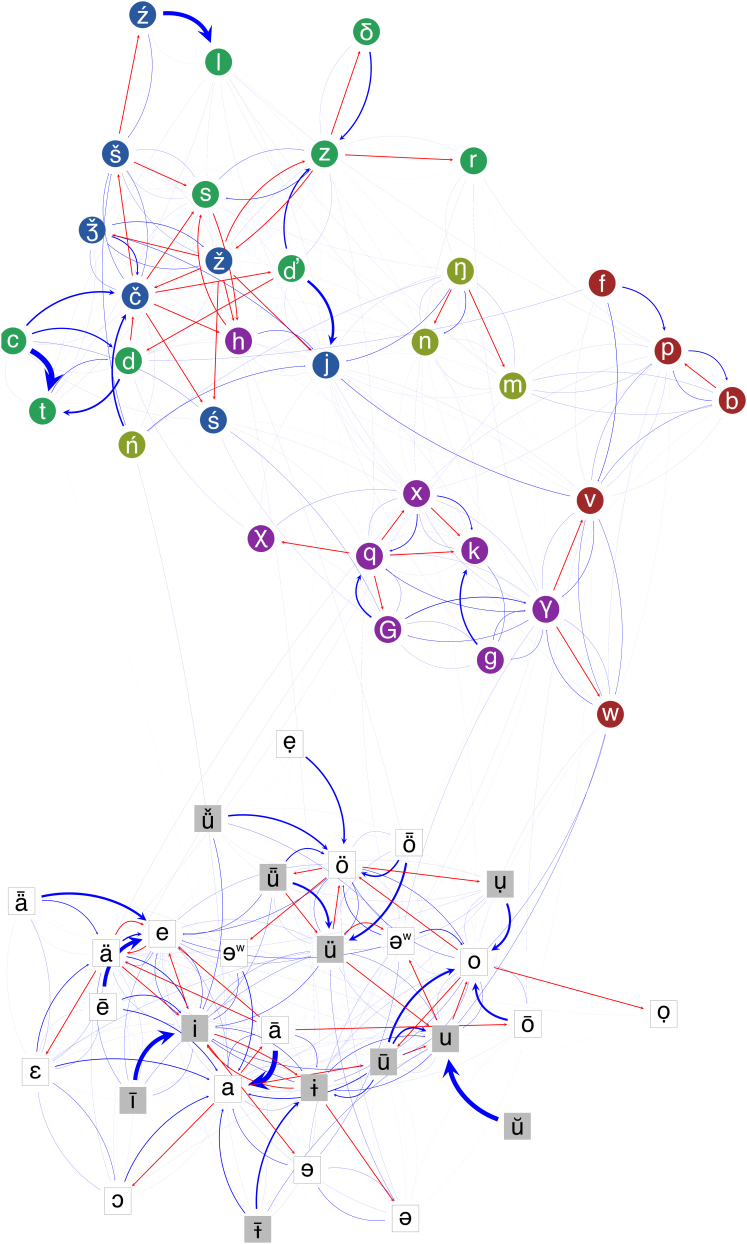
Regular Changes and Sound Transition Networks

The transition rate matrices that characterize the sporadic and regular sound changes define a network of connected phonemic substitutions or transitions that arise over time as words evolve at the level of their sounds (Figure 4). The network identifies the two major recognized [23] divisions of highly interconnected sound changes among pairs of consonants (mean transition rate/10³ years = 0.0061 ± 0.028) and among pairs of vowels (mean rate = 0.0091 ± 0.0373). Transitions between these two broad categories are rare, with a mean rate = 0.001 ± 0.003, corresponding to an approximately 0.2% chance of an ancestral consonant or vowel changing to the other category in 2,000 years. The network also finds the linguistically important bridge between consonantal and vowel changes through the high vowels (in particular through the semivowel or semiconsonant “w”).

Figure 4.

Sound Transition Networks Showing Regular and Sporadic Changes

Transitions among consonants (circles) and among vowels (squares) are frequent and regular (many connections) but are rare between them, save for those mediated by the semivowel w. Transitions are more frequent among sounds with similar places of articulation: consonants are coded as bilabials-labiodentals (red), nasal (light green), uvular-velar-glottal (purple), postalveolar-palatals (blue), and dental-alveolars (green); vowels divide into high (gray) and higher-mid to low (white) subsets. Blue lines denote sporadic transitions, with thicker lines denoting faster underlying rates. Red lines denote regular changes; arrows indicate the direction of change.

The regular sound changes (red lines in Figure 4) form a subset of the larger sound transition network, and sporadic and regular changes seem to obey the same rules. Consonantal changes group into subsets of articulation categories defined by the place and manner of vocal articulation. Sounds closer in speech production change to one another more readily than those further apart, highlighting a gradual or stepwise process of language change following “shortest routes,” similar to the phenomenon observed in protein evolution wherein amino acids are frequently replaced by amino acids with similar biochemical properties [24].

Thus, among the 43 regular consonant changes, 79% (n = 36) involved only a single change in one of the following: (1) voicing, (2) place of articulation (based on four categories: labial, dental/alveolar, postalveolar/palatal, and uvular/velar/glottal), or (3) manner of articulation (e.g., affricate to fricative), against a null expectation of 29% (χ² = 50.9, p < 0.0001). Among the 30 vowel transitions, 70% (n = 21) involved only a single change in one of the following: (1) front-central-back, (2) open-mid-closed, or (3) rounding, against a null expectation of vowel pairs of 45% (χ² = 7.5, p < 0.01) (Table S1).

The Contribution of Regular Changes to Phonemic Evolution

Regular sound changes emerge from our analyses as occupying a central role in sound evolution, consistent with the expectations of historical linguists [17, 20]. These regular sound changes accumulate approximately linearly in time, implying a constant rate of about 0.0026 regular sound changes per year (approximately one every 385 years) averaged over the tree (Figure 5A). The linear trend suggests that the model is not missing regular sound changes that occur deeper in the tree (i.e., older events) and supports a “uniformitarian” view—that this family of languages has been changing in the same ways throughout its history, an important assumption for statistical inference and ancestral reconstruction.

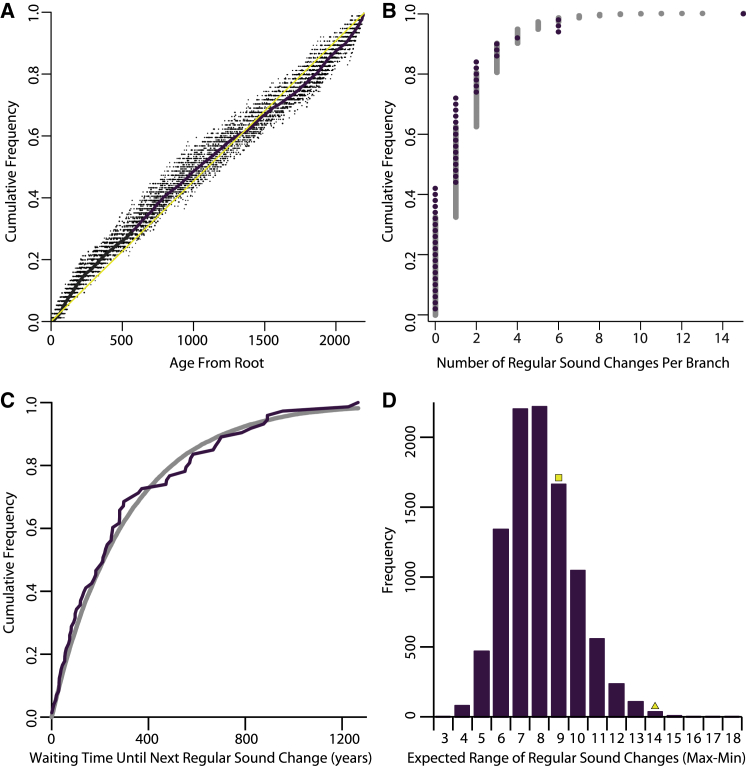
Figure 5.

Regular Sound Changes

(A) Approximately linear trend in the cumulative frequency of regular sound changes through time, indicating a constant rate of regular sound change of about 0.0026 events per branch per annum; trend is counts of regular change events per unit time in the tree, averaged across the posterior sample of trees. Purple line is the mean trend; yellow line is 1:1 trend.

(B) Expected Poisson (gray) and observed (purple) number of regular sound changes per branch. Expected values generated from a Poisson distribution with mean 0.0026 × t were calculated for each branch of the tree, where t is the length of the branch in years (generalized linear model test of deviation from Poisson expectation not significant: χ² = 16.95, df = 14, p > 0.26).

(C) Cumulative waiting times until the next regular sound change event (purple) and best-fit exponential distribution (gray). Exponential mean = 303 years; 95% confidence interval includes 385 years or 1/0.00262. The exponential provided the best fit when compared against gamma, Weibull, and log-normal cumulative densities.

(D) Expected range (max-min) of regular sound changes occurring in the histories of the 26 Turkic languages. Data were generated from 10,000 simulations of the Poisson expectation in each of the branches of the tree in Figure 2. Yellow triangle shows observed range (15–1); yellow square shows range adjusting for unique phonemes in Chuvash (see text).

The number of regular sound changes in a language’s history ranges from a low of 1 in Karaim and Balkar to a high of 15 in Chuvash (Figure 2B; the low count for Karaim might reflect phonetic transcription practices). The temptation is to interpret these as indicating different intrinsic rates, or perhaps different external pressures, for sound change, but large differences in the numbers of regular changes can arise among languages simply as a result of random fluctuations and shared phylogenetic histories. Thus, if events of regular change occur randomly at a constant rate (as in Figure 5A), then the number of such events per branch of the tree is expected to follow a Poisson distribution with mean rate given by 0.0026 × t, where t is the length of the branch in years.

Following expectations, the cumulative density of the observed number of events per branch (including branches with no regular sound changes) shows a close fit to the Poisson expectation (Figure 5B). The 21 branches in which no regular sound change occurred, along with those in which multiple events are inferred, can all be considered as samples from the same underlying stochastic process. A further characteristic of the Poisson process is that waiting times between successive events follow an exponential distribution. The distribution of waiting times between successive events of regular sound change on the phylogeny shows a striking fit to this expectation (Figure 5C).

The observed range of 14 in the number of regular sound changes per language is, however, wide, being expected to occur in approximately 0.68% of outcomes (Figure 5D). The outgroup, Chuvash, with 15 regular sound changes, might be unusual in having four phonemes that are unique among this group of languages. These four phonemes account for five of the regular sound changes in the branch leading to Chuvash. Removing these five, Chuvash with ten events yields a range (10–1) that now falls well within the Poisson expectation.

Discussion

Our analysis has shown how a model of concerted evolution can discover the timings and phylogenetic placements of multiple events of regular sound change, and without prior knowledge of the forms those regular changes might take. The events we find conform closely to linguistic expectations, and the model produces a description of the sound transition networks among the 62 speech sounds that captures the well-known patterns of sound change. Including regular sound changes also improves the reconstruction of the phylogenetic tree describing the languages’ evolutionary histories and returns more plausible and less variable dates. This confirms the importance that historical linguists have long attached to including regular sound changes into attempts to reconstruct protolanguages, identify borrowings, and infer the genealogical history of a set of related languages, including their probable dates of origin and subsequent divergences.

The close conformity of the timings of regular linguistic sound changes to a Poisson process model over the approximately 28,000 language-years of evolution represented by the branches of the Turkic tree is striking in revealing an underappreciated regularity in this otherwise complex process. It also provides a parsimonious explanation for why some languages experience so few and others so many regular sound events in their histories: these differences can in principal be explained as expected outcomes of a homogeneous random process, and hence there is no need to seek factors either internal or external to the languages in question to explain the variation among them, at least until the statistical expectation is violated.

That such a complex phenomenon could conform so closely to a homogeneous random process over such long time periods is surprising but finds an interpretation in statistical theory: where the potential causes of a discrete phenomenon (such as a regular sound change) are many, independent, and rare, and each one is individually capable of causing a regular change, the waiting times between successive events can be shown [25, 26] to follow an exponential distribution (as in Figure 5C), and events per unit time will follow a Poisson distribution. This interpretation, then, draws researchers’ attention to the “catalog” or list of potential cognitive, linguistic, and social causes of regular sound changes to explain their timings and frequencies throughout history. The excellent fit of the Poisson distribution indicates that this catalog has stayed roughly stable for the at least two millennia over which the Turkic family diverged.

Regular sound changes by their very nature make a disproportionate contribution to linguistic diversity. Regular sound changes might also help groups of language speakers create and then maintain a distinct identity [27, 28]. In this context, there are several reasons to believe that the 74 regular sound changes we have identified probably underestimate their true extent in these languages. For example, some regular changes might have decayed or been replaced by others over time, rare sound changes might not yet have been observed, and the relatively high rates of sporadic transition among vowels might also mean that some number of vowels affected by a regular change might have been masked by a later sporadic change.

In addition to these factors, in the form used here, our model provides a general “context-free” statistical description of concerted change that can be applied to any evolving hierarchical system of discrete elements. As a result, we might have missed some forms of regular sound change that depend upon multiphoneme combinations (Box 1). Many Turkic languages, for example, can exhibit a form of correlation of sounds within words known as vowel harmony, whereby vowels (and some consonants) in a word are homogenized into classes. In some Turkic languages, words can be harmonized according to whether the vowels and the uvular/velar consonants have “front” or “back” articulation [20]. For example, the plural suffix in Turkish can depend on the class of the word, such that the plural of horse is [at-lar] (using a back vowel) whereas the plural of cat is [kedi-ler] (using a front vowel).

A second and more general factor common in human languages is context, in which sound changes are influenced by where the sound occurs in a word, or by its proximity to other sounds [29]. Sounds can be lost within words in a manner equivalent to nucleotide deletions. Occasional metathesis, or reordering of sounds, is also observed. Finally, entire classes of phonemes often shift because of loss or gain of a phonemic feature like voicing, or when the change of one sound or phonemic distinction in a sound system may lead to cascades of other sound changes in the system, as has been postulated with the “Great Vowel Shift” in English [30]. These factors might prove valuable in understanding differences in the propensity of a given phonemic site to be affected by a regular change. There are methods for extending our theory to context-dependent regularities [29], and future work with our model will explore how they help to improve the statistical reconstruction of protowords.

Molecular biologists might recognize genetic analogs to the linguistic processes of context and harmony in some features of gene conversion. Thus, a recent study [3] of the rotifer (Adineta vaga) genome identified “abundant” evidence of gene conversion manifested in greater-than-expected similarity among alleles—in a sense, the presence of one allele “harmonizes” the other by making a particular form of the other more likely. Equally, concerted evolutionary changes can sweep through genomes, deactivating transposable elements [31]. Here, the presence of a particular string of nucleotides in a wider context of a transposable element appears to invite a deactivating change. A model such as we describe here could identify these instances of gene conversion statistically and on a genome-wide basis and, if applied to a group of related organisms, could provide a description of their extent and taxonomic distribution in nature. Identification of such events might also prove valuable for inferring and dating molecular trees.

We might expect concerted change to be a feature of evolving cultural systems where artifacts and institutions are hierarchically organized from a discrete set of repeatedly used building blocks (e.g., motifs, keystone technologies). Elements of style, dress, music, art, and technology might all be subject to forces that encourage a coordinated homogenization of these otherwise distinct building blocks, at least to some degree. Data sets here might not yet be as well developed as in genetics or linguistics, but the looming presence of “big data” [32] in the social sciences might allow a model such as we describe here to bring these phenomena to heel.

Experimental Procedures

Description of Transcribed Sound Data

We used lexical data corresponding to 225 etymological classes in 26 Turkic languages [17, 20] that were phonetically coded with 62 symbols following the North American Phonetic Alphabet [17]. The phonetically coded data for each language were then multiply aligned by identifying cognate sites within each word (analogous to homologous gene sequence alignment). Choosing the pairing of sounds that maximized a likelihood function based on the following model aligned sounds in cognate words from the same etymological class. Observed forms in each language are assumed to have descended from an ancestor by a combination of (1) language-wide regular sound changes and (2) word-specific sporadic sound changes. For alignment, languages are assumed to be independent except through their shared descent from the ancestor. The algorithm recursively estimates the alignments, sound inventories, regular sound changes, and sporadic sound changes that maximize the likelihood function derived from this model. This yielded a 26 languages × 1,120 sites matrix.

Statistical Model

The sporadic sound changes are modeled as a continuous-time Markov process, widely used in models of DNA or protein sequence evolution, where in place of the usual 4 × 4 or 20 × 20 matrices of nucleotide or amino acid transitions, we erect a 62 × 62 sound transition rate matrix, denoted Q_s (Supplemental Experimental Procedures). We estimate the elements of Q_s from the data employing a reversible-jump Markov chain Monte Carlo (RJ-MCMC) procedure described elsewhere [16] that allows the large number of potential parameters to be reduced to a potentially far smaller set of statistically distinct parameters, and without loss of statistical accuracy or prior knowledge on the part of investigators. We find that nine distinct rate classes, empirically estimated from the data, plus a category of rates estimated to be zero, are sufficient for the Turkic data.

Regular sound changes of the general form denoting the i^th sound changing to the j^th are modeled in a stochastic matrix Q_r that takes the form of an identity matrix with the i^th diagonal element interchanged with the off diagonal position (ji). Premultiplication of any stochastic matrix Q (e.g., that in $P\left(D|Q_s,t\right)$) by such a matrix is equivalent to adding all elements q_i1, q_i2,…q_ik to the corresponding values of q_j1, q_j2…q_jk and then zeroing out the q_i1, q_i2,…q_ik. We then use a different RJ-MCMC procedure to propose possible Q_r matrices in branches of the phylogenetic tree, thereby allowing regular changes to occur or not occur on a branch-specific basis. The model also estimates the position or timing of successive regular sound changes along a branch.

Phylogenetic Inference

We estimated time-dated phylogenetic trees by enforcing a variable-rates clock model that constrained all root-to-tip path lengths to have the same total time but allowed the average rates of sound evolution to vary throughout the tree. The variable-rate clock is modeled by applying a scalar multiplier to each branch of the tree that alters the rates in Q_s by some fixed amount. We assume these scalars are drawn from a log-normal prior distribution with μ = 1 and unknown σ² that we estimate from the data. We calibrated the trees against two points of reference: the current dates of dictionaries for each of the contemporary languages, and the Seljuk conquest of Baghdad (1055 CE), which is likely the latest date for divergence of Seljuk-derived languages (Turkish, Azeri, Gagauz) from other Oghuz languages (Turkmen), the earliest likely date being 985 CE [18, 19].

The parameters of the sound change model are estimated in a likelihood framework using Markov chain Monte Carlo methods [33] (Supplemental Experimental Procedures). Because the regular sound changes are directional, the likelihood depends upon the choice of a root in the tree. In practice, the likelihood is not able to determine the root with accuracy, and so most investigators root the tree using an outgroup. Here we use Chuvash. We ran many independent Markov chains to explore the model and then to infer the time-dated trees, allowing chains to run to stationarity following a burn-in of at least 10,000,000 iterations. Stationarity was assessed by enforcing a period of at least 10,000,000 iterations during which no average change in the likelihood occurred. Multiple independent runs were used to ensure convergence on a common consensus topology. The models were implemented in a modified version of BayesPhylogenies (http://www.evolution.reading.ac.uk/). In practice, to improve the rate of convergence of the Markov chains, we augmented the likelihood of the sound change model with that obtained from cognacy data for the same words, following methods described elsewhere [34, 35] (Supplemental Experimental Procedures).

Author Contributions

All authors contributed to modeling, computation, and analyses. M.P., T.B., and D.J.H. wrote the manuscript.