Reinforcement Learning of Two-Joint Virtual Arm Reaching in a Computer Model of Sensorimotor Cortex

Abstract

Neocortical mechanisms of learning sensorimotor control involve a complex series of interactions at multiple levels, from synaptic mechanisms to cellular dynamics to network connectomics. We developed a model of sensory and motor neocortex consisting of 704 spiking model neurons. Sensory and motor populations included excitatory cells and two types of interneurons. Neurons were interconnected with AMPA/NMDA and GABA_A synapses. We trained our model using spike-timing-dependent reinforcement learning to control a two-joint virtual arm to reach to a fixed target. For each of 125 trained networks, we used 200 training sessions, each involving 15 s reaches to the target from 16 starting positions. Learning altered network dynamics, with enhancements to neuronal synchrony and behaviorally relevant information flow between neurons. After learning, networks demonstrated retention of behaviorally relevant memories by using proprioceptive information to perform reach-to-target from multiple starting positions. Networks dynamically controlled which joint rotations to use to reach a target, depending on current arm position. Learning-dependent network reorganization was evident in both sensory and motor populations: learned synaptic weights showed target-specific patterning optimized for particular reach movements. Our model embodies an integrative hypothesis of sensorimotor cortical learning that could be used to interpret future electrophysiological data recorded in vivo from sensorimotor learning experiments. We used our model to make the following predictions: learning enhances synchrony in neuronal populations and behaviorally relevant information flow across neuronal populations, enhanced sensory processing aids task-relevant motor performance and the relative ease of a particular movement in vivo depends on the amount of sensory information required to complete the movement.

1 Introduction

Adaptive movements in response to stimuli sensed from the world are a vital biological function. Although arm reaching toward a target is a basic movement, the neocortical mechanisms allowing sensory information to be used in the generation of reaches are enormously complex and difficult to track (Shadmehr & Wise, 2005). Learning brings neuronal and physical dynamics together. In studies of birdsong, it has been demonstrated that reinforcement learning (RL) operates on random babbling (Sober & Brainard, 2009). In that setting, initially random movements initiated by motor neocortex may be rewarded or punished via an error signal affecting neuromodulatory control of plasticity via dopamine (Kubikova & Kostál, 2010). In primates, frontal cortex, including primary motor area M1, is innervated by dopaminergic projections from the ventral tegmental area (Luft & Schwarz, 2009; Molina-Luna et al., 2009; Hosp, Pekanovic, Rioult-Pedotti, & Luft, 2011), and recent neurophysiological evidence points to reward modulation of M1 activity (Marsh, Terigoppula, & Francis, 2011). It has been suggested that similar babble and RL mechanisms may play a role in limb target learning.

Many brain areas are involved in motor learning, likely including spinal cord, red nucleus, and thalamus, as well as the more well-characterized basal ganglia, cerebellum, and neocortex (Sanes, 2003). In addition to individual brain areas, connections between areas are likely vital (Graybiel, Aosaki, Flaherty, & Kimura, 1994; Hikosaka, Nakamura, Sakai, & Nakahara, 2002). Learning in these different areas will likely play different roles for different types of tasks and at different times in development. Neonates can perform directed reaching movements at birth and learn to reach a target within 15 weeks using proprioceptive and visual feedback (Berthier, Clifton, McCall, & Robin, 1999; von Hofsten, 1979). This process has been suggested to be primarily cortical (Berthier, 2011). Sensorimotor integration of reaching is learned through analysis of mismatches of perception and desired actions (Corbetta & Snapp-Childs, 2009). Similarly, adult learning of complex tasks, such as serving in tennis, uses the neocortical substrate at different stages of the learning process (Sanes, 2003).

Computational modeling of biologically realistic neuronal networks can aid in validating theories of motor learning and predicting how it occurs in vivo (Houk & Wise, 1995). Recently, learning models of spiking neurons using a goal-driven or reinforcement learning signal have been developed (Farries & Fairhall, 2007; Florian, 2007; Izhikevich, 2007; Potjans, Morrison, & Diesmann, 2009; Seung, 2003), many using spike-timing-dependent plasticity (Roberts & Bell, 2002; Rowan & Neymotin, 2013; Song, Miller, & Abbott, 2000; Neymotin, Kerr, Francis, & Lytton, 2011). Here, we present a simplified sensorimotor cortex network with an input sensory area (S1) that processes inputs from muscles, and an output area, representing primary motor cortex (M1), that projects to muscles of a virtual arm.

This letter extends our previous efforts to create a spiking neuronal model of cortical reinforcement learning of arm reaching (Chadderdon, Neymotin, Kerr, & Lytton, 2012). In Chadderdon et al., we demonstrated the feasibility of the dopamine system–inspired value-driven learning algorithm used in this letter in allowing a swiveling forearm segment controller to learn a mapping from proprioceptive state to flexion and extension motor commands needed to direct the virtual hand to the target: a task requiring only 1-degree-of-freedom motion. Here, we extend the scope of the task to 2-degrees of freedom, permitting the hand to explore a more complete virtual 2D work space. This is a more demanding and complex task because shoulder and elbow angle changes have the potential to interfere with each other in adjusting the hand-to-target error, and the proprioceptive-to-motor command mapping to be learned requires conjunction of the information of the two different joints. We also increased the number of synaptic connections that have active plasticity, which adds further challenges, as well as flexibility, for the learning method. In addition, we enhanced the robustness of the training and testing paradigm: we first trained the system, then turned off further learning, and only then quantified reach-to-target performance. Turning off further learning ensured that what was previously learned and the ongoing effects of the learning algorithm were isolated. Even with the added complexity of a 2D reaching task and the new testing paradigm, the model was able to learn the new reaching task. Analysis comparing naive and trained network dynamics showed a distinct increase of synchrony and task-relevant information flow, as measured by coefficient of variation and normalized transfer entropy, respectively. These results have predictive power and may allow better future understanding of electrophysiological data recorded in vivo from sensorimotor learning experiments.

2 Methods

2.1 System Overview

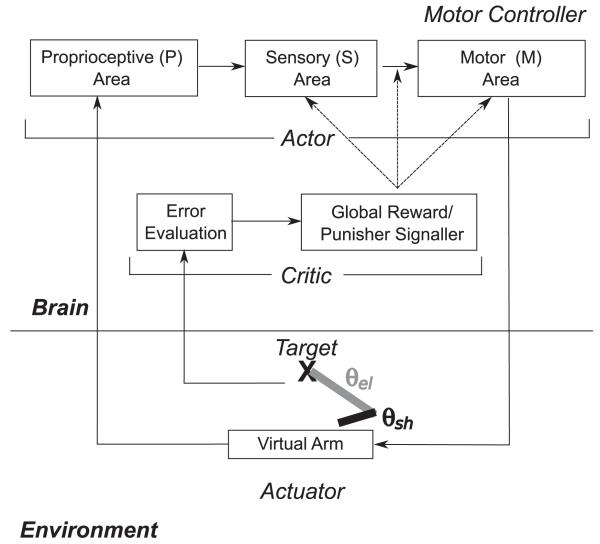
The entire closed-loop learning system architecture is shown in Figure 1. A brain and its interaction with an artificial environment were modeled, with the environment containing a virtual arm, which was a part of the simulated agent’s body, and a target object that the agent was supposed to reach for. The virtual arm possessed two segments (upper arm and forearm), which could be swiveled through two joints (shoulder and elbow) so that the arm and hand were able to move in a planar space. Each of the arm joints possessed a pair of flexor and extensor muscles for increasing or decreasing the angles, respectively, and that output a “stretch receptor” signal to the degree that the muscle was contracted.

Figure 1.

Overview of model. A virtual arm with joint angles θ_sh and θ_el (θ_sh: angle of upper arm with respect to x-axis; θ_el: angle of forearm with respect to upper arm) controlled by two pairs of flexor and extensor muscles, is trained to reach toward a target. A proprioceptive (P) sensory area translates muscle lengths into an arm configuration representation. Plasticity is present in excitatory-to-excitatory recurrent connections within the higher-order sensory (S) and the motor (M) areas, in feedforward and feedback excitatory to excitatory connections between the higher-order sensory and the motor areas, and in feedforward connections from excitatory to inhibitory cells within each area. Motor units drive the muscles to change the joint angle. The actor is trained by the critic, which evaluates error and provides a global reward or punishment signal.

An actor system consisting of proprioceptive sensory neurons (P), sensory cells (S), and motor cells (M) was used to control this system. The P cell receptive fields were tuned so that individual cells fired for a narrow range of particular “muscle stretches” for one of the four muscles. These P cells sent fixed random weights to the S cells, so that the S cells were capable of representing the conjunct of positions in both joints, though this feature was not optimally hardwired for these cells. The S cells then sent plastic weights to the M cells, which possessed a separate population of cells for each of the four muscles capable of stimulating contraction to the degree the corresponding subpopulations were active. Plasticity was present within the S and M unit populations and between them in both directions. This actor effectively performed a mapping between limb state, as measured by muscle stretch, and a set of commands for driving each muscle. The extensor population activity was subtracted from the flexor activity for a particular joint (shoulder, elbow) to yield a joint angle rotation command for the virtual arm.

It should be noted that the actor in this system was learning to make a blind reach for a single learned target (proprioceptive-to-motor-command mapping). The critic component of the system, however, possessed a means of calculating the visual difference between the hand’s location and the target (error evaluation) and determining from the last two viewed hand coordinates whether the hand was getting closer to or farther away from the target. Based on which was the case, the critic sent a global reward or punisher signal to the actor. Plastic synapses kept eligibility traces that allow credit or blame assignment. Rewards caused a global increase in the tagged weights, and punishers caused a decrease, effectively implementing Thorndike’s law of effect in the system (Thorndike, 1911); it allowed rewarded behaviors to be “stamped in” and punished behaviors to be “stamped out.”

As a result of this arrangement, although the actor did not possess vision, it was possible in theory for it to learn a mapping driving the hand toward a visual located target, provided that target was not moved after training. In an ideal learning case by this system, the limb configuration corresponding to the target’s location would learn to not move in either direction, but an overflexed arm would learn to extend and an overextended arm would learn to flex, so that the actor had learned an attractor for the remembered target stimulus. If the critic was not turned off before testing, the system effectively possessed vision and could in theory learn to adjust its responses even if the target was moved, although this was not tested.

An important component to the system in the actor was babbling noise that was injected into the M cells. An untrained system thus possessed some tendencies to move weakly in a random direction. The critic, then, was able to allow operant conditioning to shape the motor commands in the context of limb state.

The model was implemented in the NEURON 7.2 (Carnevale & Hines, 2006) simulator for Linux and is available on ModelDB (Peterson, Healy, Nadkarni, Miller, & Shepherd, 1996) (https://senselab.med.yale.edu/modeldb). We collected performance for a number of targets, random network wirings, and sets of injected babbling noise and ran both naive versions of the model for these and multi-epoch training sessions on a number of different starting positions of the arm. In addition to performance measures, we also compared the naive and trained models using measures of population firing synchrony and interpopulation information flow.

We next elaborate on the details of the model’s architecture. We first explain the environment (virtual arm and target) and then the actor portion of the model, including the P cells and the S and M cells (which constitute the primary spiking learning neuron portion of the model). Then we examine the critic and reinforcement learning algorithm in more detail, and, finally, the training and testing trial scheme we used and the measures we used for network population synchrony and information flow between network populations.

2.2 Environment: Virtual Arm and Target

The virtual arm consisted of two segments representing the upper arm (length 1) and forearm (length 2). There were two joint angles for the two joints (shoulder: θ_sh; elbow: θ_el) that were allowed to vary from fully extended (θ_sh: −45°; θ_el: 0°) to fully flexed (θ_sh: 135°; θ_el: 135°; large range of angles to more fully test learning). For each joint, an extensor and flexor muscle (lengths m_ext and m_flex) always reflected the current joint angle in the relationship as follows:

$$m_{ext}=\frac{(\theta -{\theta }_{\min })}{{\theta }_{\max }-{\theta }_{\min }},$$ (2.1)

$$m_{flex}=1-m_{ext}.$$ (2.2)

Arm position updates were provided at 50 ms intervals, based on extensor and flexor EM (excitatory cells in the motor area) spike counts integrated from a 50 ms window that began 50 ms prior to update time (50 ms network-to-muscle propagation delay). The angle change $\Delta \theta =\mathcal{S}pike{s}_{flexor}-\mathcal{S}pike{s}_{extensor}$ for each joint was the difference between the corresponding EM spike counts from flexor and extensor populations during the prior interval, with each spike difference translating to a 1° rotation. For simplicity, the arm model did not contain physical attributes, such as mass and inertia. P drive activity updated after an additional 25 ms delay, which represented peripheral and subcortical processing. Reinforcement occurred every 50 ms with calculation of hand-to-target error. The target remained stationary during the simulation.

2.3 Actor: Unit Types and Interconnectivity

The actor consisted of the proprioceptive sensory (P), higher-order sensory (S), and motor (M) populations described in Figure 1. Details of the cell models are described below. Input to the S cells was provided by 192 P cells, representing muscle lengths in four groups (two flexor- and extensor-associated groups for each joint).

The rest of the network consisted of both S (sensory) and M (motor) cell populations. The S population included 192 excitatory cells (ES cells), 44 fast-spiking interneurons (IS), and 20 low-threshold spiking interneurons (ILS); similarly, the M network had 192 EM, 44 IM, and 20 ILM cells. The EM population was divided into four 48-cell subpopulations dedicated to extension and flexion about each joint, projecting to the extensor and flexor muscles. The number of excitatory and inhibitory cells within an area was selected to keep 75% (192/256) of the neurons as excitatory, to approximate the ratios in neocortex.

Cells were connected probabilistically (fixed convergence; variable divergence) with connection densities and initial synaptic weights varying depending on pre- and postsynaptic cell types (see Table 1). Connection densities were within the range determined experimentally, which are approximately 1% to 100% depending on pre- and postsynaptic cell type (Thomson, West, Wang, & Bannister, 2002; Thomson & Bannister, 2003; Bannister, 2005). Initial synaptic weights were set to relatively low values so as to resemble activity in vivo, which typically requires several presynaptic inputs to arrive within a short time window in order to activate a postsynaptic neuron.

Table 1.

Connectivity Parameters.

Pre	Post	p	Conv	W	Pre	Post	p	Conv	W
P	ES	0.11250	22	15.0000	ES	ES	0.05625	11	* 1.3200
ES	IS	0.48375	93	* 1.9550	ES	ILS	0.57375	110	* 0.9775
ES	EM	0.09000	17	* 1.7600	IS	ES	0.49500	22	4.5000
IS	IS	0.69750	31	4.5000	IS	ILS	0.38250	17	4.5000
ILS	ES	0.39375	8	1.2450	ILS	IS	0.59625	12	2.2500
ILS	ILS	0.10125	2	4.5000	EM	ES	0.01913	4	* 0.4800
EM	EM	0.05625	11	* 1.1880	EM	IM	0.48375	93	* 1.9550
EM	ILM	0.57375	110	* 0.9775	IM	EM	0.49500	22	9.0000
IM	IM	0.69750	31	4.5000	IM	ILM	0.38250	17	4.5000
ILM	EM	0.39375	8	2.4900	ILM	IM	0.59625	12	2.2500
ILM	ILM	0.10125	2	4.5000

Notes: Area (Pre: presynaptic type; Post: postsynaptic type) interconnection probabilities (p), convergence (Conv), and starting weights (W). An asterisk next to W represents a plastic connection modified during learning. p is the probability of a connection being included among all possible connections between the two areas. Conv is the number of in puts each cell of type Post receives from type Pre. E cells used AMPA and NMDA synapses (NMDA, not displayed, had weights set at 10% of the colocalized AMPA synapse).

2.4 Actor: Proprioceptive Sensory (P) Cell Model

Proprioceptive sensory (P) cells (see Figure 1) were modeled using a standard, single compartment (diameter = 30 μm), parallel-conductance model with input current, to allow continuous mapping of muscle lengths to current injections provided to these cells. The rate of change of a P neuron’s voltage (V) was represented as $-C_m\frac{dV}{dt}=g_{pas}\ast V+i_{driv{e}^{\prime }}$, where C_m is the capacitive density (1 μF/cm) and i_drive was a current set according to muscle length. g_pas represents the leak conductance (0.001 nS), which was associated with a reversal potential of 0 mV. When a P neuron’s voltage passed threshold, the neuron emitted a spike and was set to a refractory state for 10 ms. Each P cell was tuned to produce bursting approaching 100 Hz (limited by refractory period) over a narrow range of adjacent, nonoverlapping muscle lengths, by setting the P cell’s i_drive variable to a heightened level. The i_drive variable of each P cell was updated when the arm moved (every 50 ms interval).

2.5 Actor: Primary Neuron Model (Sensory (S) and Motor (M) Cells)

Individual neurons in the higher-order sensory (S) and motor (M) areas were modeled as event-driven, rule-based dynamical units with many of the key features found in real neurons, including adaptation, bursting, depolarization blockade, and voltage-sensitive NMDA conductance (Lytton & Stewart, 2005, 2006; Lytton & Omurtag, 2007; Lytton, Neymotin, & Hines, 2008; Lytton, Omurtag, Neymotin, & Hines, 2008; Neymotin, Lee, Park, Fenton, & Lytton, 2011; Kerr et al., 2012, 2013). Event-driven processing provides a faster alternative to network integration. A presynaptic spike is an event that arrives after a delay at postsynaptic cells; this arrival is then a subsequent event that triggers further processing in the postsynaptic cells. Cells were parameterized as excitatory (E), fast-spiking inhibitory (I), and low-threshold-spiking inhibitory (IL; see Table 2).

Table 2.

Neuron Model Parameters.

Type	VRMP(mV)	Tn(mV)	Bn(mV)	τA(ms)	R	τR(ms)	H(mV)	τH(ms)
E	−65	−40	−25	5	0.75	8.0	1.0	400
I	−63	−40	−10	2.5	0.25	1.5	0.5	50
IL	−65	−47	−10	2.5	0.25	1.5	0.5	50

Notes: Parameters of the neuron model for each major population type. These parameters are based on previously published models of neocortex, which were culled from the experimental and modeling Literature (Kerr et al., 2012, 2013; Neymotin, Jacobs, Fenton, & Lytton, 2011; Neymotin, Kerr et al., 2011; Neymotin, Lee et al., 2011).

Each neuron had a membrane voltage state variable (V_m) with a baseline value determined by a resting membrane potential parameter (V_RMP, set at −65 mV for pyramidal neurons and low-threshold-spiking interneurons and at −63 mV for fast-spiking interneurons). This membrane voltage was updated by one of three events: synaptic input, threshold spike generation, and refractory period. These events are described briefly below; further detail can be found in the papers cited and code provided on ModelDB (Peterson et al., 1996; https://senselab.med.yale.edu/modeldb).

2.5.1. Synaptic Input

The response of the membrane voltage to synaptic input was modeled as an instantaneous rise and exponential decay: $V_n\left(t\right)=V_n\left(t_0\right)+w_s(1-V_n(t_0)∕E_i)e^{-\frac{t-t_0}{{\tau }_i}}$, where V_n is the membrane voltage of neuron n; t₀ is the synaptic event time (i.e., t - t₀ is the time since the event); w_s is the weight of synaptic connection s; E_i is the reversal potential of ion channel i, relative to resting membrane potential (where i = AMPA, NMDA, or GABA_A; E_AMPA = 65 mV, E_NMDA 90 mV, and E_GABA = −15 mV); and τ_i is the receptor time constant for ion channel i (where τ_AMPA = 20 ms; τ_NMDA = 300 ms; and τ_GABAA = 10 or 20 ms for somatic and dendritic GABA_A, respectively).

In addition to spikes generated by cells in the model, subthreshold Poisson-distributed spike inputs to each synapse of all units except the P and ES units were used to provide ongoing activity and babble (see Table 3). These Poisson stimuli also represented inputs from other neurons not explicitly simulated. Since the neuron model is a point-neuron model, each synapse represents the locus of convergent inputs from multiple neurons.

Table 3.

Noise Parameters.

Cell	Synapse	W	Rate
IS	GABAAsome	1.875	100
IS	AMPAdend	4.125	200
IS	GABAAdend	1.875	100
ILS	GABAAsoma	1.875	100
ILS	AMPAdend	3.000	200
ILS	GABAAdend	1.875	100
EM	GABAAsoma	1.875	100
EM	AMPAdend	3.938	200
EM	GABAAdend	1.875	100
IM	GABAAsoma	1.875	100
IM	AMPAdend	4.125	200
IM	GABAAdend	1.875	100
ILM	GABAAsoma	1.875	100
ILM	AMPAdend	3.000	200
ILM	GABAAdend	1.875	100

Notes: Noise stimulation to synapses of the different cell types. Weight (W) values are afferent weights. Rate values are average stimulation frequencies in Hz (inputs are Poisson distributed). This stimulation represents afferent inputs from multiple presynaptic cells, which are not explicitly simulated.

2.5.2 Action Potentials

A neuron fires an action potential at time t if V_n(t) > T_n(t) and V_n(t) < B_n, where V_n, T_n, and B_n are the membrane voltage, threshold voltage (−40 mV for pyramidal neurons and fast-spiking interneurons, −47 mV for low-threshold-spiking interneurons), and blockade voltage (−10 mV for interneurons and 25 mV for pyramidal neurons), respectively, for neuron n. Action potentials-arrive at target neurons at time t₂ = t₁ + τ_s, where t₁ is the time the first neuron fired and τ_s is the synaptic delay. τ_s values were selected from a uniform distribution ranging between 3 ms and 5 ms for dendritic AMPA, NMDA, and GABA_A synapses and were selected from a uniform distribution ranging between 1.8 ms to 2.2 ms for somatic GABA_A synapses. Synaptic weights were fixed between a given set of populations except for those involved in learning (described in section 2.1).

2.5.3. Refractory Period

After firing, a neuron cannot fire during the absolute refractory period, τ_A (2.5 ms for interneurons and 5 ms for pyramidal neurons). Firing is reduced during the relative refractory period by two effects: first, an increase in threshold potential, $T_n\left(t\right)=(1+R{e}^{-\frac{t-t_0}{{\tau }_R}})T_n\left(t_0\right)$, where R is the fractional increase in threshold voltage due to the relative refractory period (0.25 for interneurons and 0.75 for pyramidal neurons) and τ_R is its time constant (1.5 ms for interneurons and 8 ms for pyramidal neurons); and second, by hyperpolarization, $V_n\left(t\right)=V_n\left(t_0\right)-H{e}^{-\frac{t-t_0}{{\tau }_H}}$, where H is the amount of hyperpolarization (0.5 mV for interneurons and 1 mV for pyramidal neurons) and τ_H is its time constant (50 ms for interneurons and 400 ms for pyramidal neurons).

2.6 Critic: Reinforcement Learning Algorithm

The RL algorithm implemented Thorndike’s law of effect using global reward and punishment signals (Thorndike, 1911). The network is the actor. The plastic AMPA weights in Table 1 were trained to implement the learned sensorimotor mappings. The Critic, a global reinforcement signal, was driven by the first derivative of error between position and target during two successive time points (reward for decrease; punishment for increase), and therefore the reward and punishment signals were delivered at every movement generated by the network. As in Izhikevich (2007), we used a spike-timing-dependent rule to trigger eligibility traces to solve the credit assignment problem. The eligibility traces were binary, turning on for a synapse when a postsynaptic spike followed a presynaptic spike within a time window of 100 ms; eligibility ceased after 100 ms. When reward or punishment was delivered, eligibility-tagged synapses were potentiated (long-term potentiation LTP) or depressed (long-term depression LTD), correspondingly.

Synaptic weights w(t) were updated (for LTP/reward and LTD/punishment) utilizing weight scale factors, w_s:

$$w\left(t\right)=w_0\cdot w_s\left(t\right)$$

$$w_s(t+1)=w_s\left(t\right)+\Delta w_s$$

$$\Delta w_s=\{\begin{array}{cc}{w}_{inc}\cdot (1-w_s(t)∕w_s^{\max })\hfill & \text{for LTP reward},\hfill \\ -w_{inc}\cdot w_s\left(t\right)∕w_s^{\max }\hfill & \text{for LTD punisher}\hfill \end{array}\phantom{\}}$$

where $w_s^{\max }$ is maximum weight scale factor, w₀ is the initial synaptic weight, and w_inc is the weight scale increment. w_s was initialized to 1.0 for all synapses and varied between 0 and $w_s^{\max }\cdot w_s^{\max }$ was set to 6 and 2.5 times the synaptic weight of E → E and E → I baseline weights. w_inc was set to 25% of baseline synaptic weights.

2.7 Training and Testing Paradigm

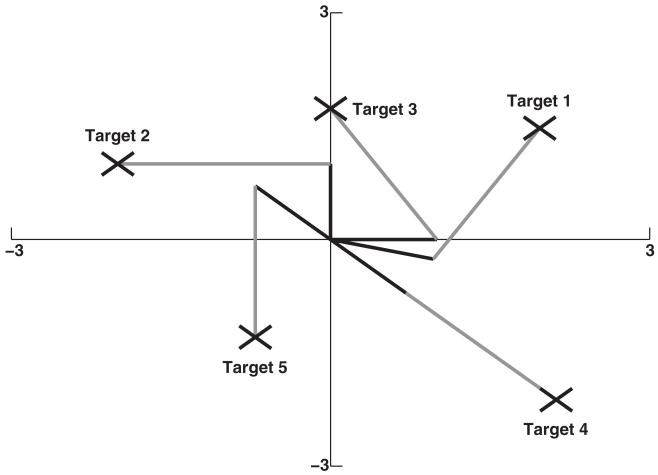
Networks were trained to reach the arm to a single target (targets shown in Figure 2). Training a network to reach to a single target consisted of 200 training sessions. Each training session consisted of allowing the network to perform 15 s of reaching, once from each of 16 sequential starting positions. The 16 starting positions were arranged from minimum to maximum angles for the two joints. We configured starting angles in this way to teach the network to control movement of the arm to the target from the entirety of positions in the 2D plane. Targets were chosen to allow thorough testing of reaching (both extrema and intermediate positions).

Figure 2.

Schematic of arm orientations at all five target locations. Each X symbol represents a target. The arm is drawn in an orientation that maintains its end point on each of the five targets. Targets were chosen to allow thorough testing of reaching (both extrema and intermediate positions).

After training, learning was turned off, and each network’s performance was assessed with the arm initialized from each of the 16 starting positions used for training. A reach was considered successful if the arm end point was moved to a position where the Cartesian error was ≤1. Overall learning performance for a target was calculated as the fraction of successful reach movements (Accuracy). A similar accuracy score was used for angular performance for each joint: when the angular error was ≤10 degrees, the reach for that given joint was a success.

2.8 Data Analysis

Data obtained from 400 naive trials (5 random network wirings, 5 random input seeds, 16 starting positions) were compared with 2000 trained trials (5 random network wirings, 5 random input seeds, 5 targets, 16 starting positions).

Synchrony between cells within different populations was measured using a normalized population coefficient of variation (CV_p Tiesinga & Sejnowski, 2004). CV_p makes use of the population’s interspike interval, defined for the temporally ordered set of spikes generated by neurons in the population as τ_v = t_v+1 - t_v, where t_i indicates the ith spike time. CV_p is then defined as $\frac{\sqrt{<{\tau }_v^2>-{<{\tau }_v>}^2}}{<{\tau }_v>}$, where p stands for population and <> denotes the average over all intervals. CV_p is normalized to be between 0 and 1 by subtracting 1 and dividing by $\sqrt{N}$. After the normalization, 0 indicates independent Poisson process synchrony, and 1 indicates maximum synchrony. Values that dip below 0 are set to 0 to allow calculating means.

We used normalized transfer entropy (nTE) between multiunit activity vectors (MUAs) of different populations before and after training as a measure of information flow (Gourevitch & Eggermont, 2007; Neymotin, Jacobs et al., 2011). MUA vectors were the time series formed by counting the number of spikes generated by a population in every 5 millisecond interval. nTE is a normalized version of transfer entropy, defined from probability distribution X1 to X2 as H(X2_future|X2_past) - H(X2_future|X2_past, X1_past). X2_future and X2_past represent the X2 probability distributions of future and past states, respectively, and H is the entropy of the given distribution. nTE from X1 to X2 is then defined as $\frac{T{E}_{X1\to X2}-<T{E}_{X{1}_{\text{shufed}}\to X2}>}{H(X{2}_{\text{future}}\mid X{2}_{\text{past}})}$. nTE removes bias from the estimate of transfer entropy by subtracting the average transfer entropy from X1 to X2 using a shuffled version of X1 denoted $<T{E}_{X{1}_{\text{shufed}}\to X2}>$ over several shuffles. It then divides the estimate by the entropy of H(X2_future|X2_past) to get a value between 0 and 1. nTE will be 0 when X1 transfers no information to X2 and 1 when X1 transfers maximal information to X2. For calculating nTE, we shuffled each presynaptic MUA vector 30 times. For more information on calculating nTE, see Neymotin, Jacobs et al. (2011).

For each network trained on a particular target, we calculated a per joint bias score, calculated as the difference between the sums of incoming excitatory weights to flexion and extension motor units. This bias measure was normalized to the range of −1 to 1, with −1 and 1 corresponding to extension and flexion biases, respectively.

3 Results

This study involved over 2000 15 s simulations of trained networks, using 5 different random wirings, 5 different input streams, 5 different targets, and 16 initial arm positions, as well as 400,000 15 s simulations run during training (5 random wirings, 5 input streams, 5 targets, 16 initial arm positions, 200 reaches from each position). The network learned to reach a 2-degree-of-freedom virtual arm from starting positions arrayed in a restricted subspace chosen around an oval (large set of θs with restricted r in polar coordinates). This choice provided curved solution trajectories, thereby avoiding the complex co-contractions of muscles associated with linear movements. Targets were set to test both extrema and intermediate positions. Simulations were run on Linux on a 2.27 GHz quad-core Intel XEON CPU. A 15 s simulation ran in 15 to 25 seconds, depending on the simulation type.

3.1 Learning Alters Network Dynamics

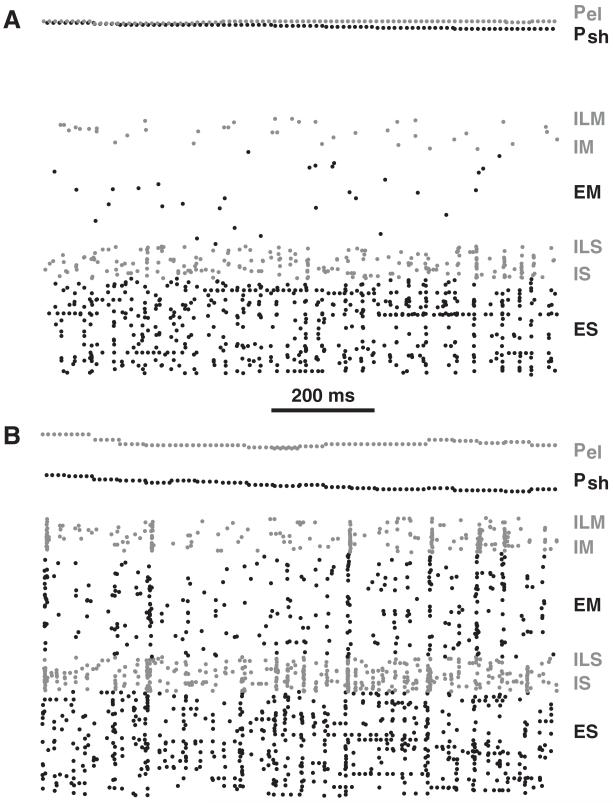
Prior to training, firing rates of units in the motor (M) area (EM,ILM,IM) were low with sparse firing produced by the stochastic inputs into the motor area (see Figure 3A and Table 4). This stochastic input was the source of motor babble, necessary to provide the variation that underlay motor learning. Before training, low variability of arm position kept proprioceptive sensory (P) cells at nearly constant low spiking rates (see Figure 3A). Due to strong fixed projections from P to higher-order sensory (S) populations, these low rates were able to maintain higher-order sensory cells at moderate levels of activity.

Figure 3.

Raster plot of network spiking. (A) Naive network. (B) Network after training. Gray (black) dots are spikes in inhibitory (excitatory) cells; ES, IS, ILS, EM, IM, ILM. (E, excitatory; I, inhibitory fast spiking; IL, inhibitory low-threshold spiking interneurons; S, higher-order sensory; M, motor; P_sh, proprioceptive sensory shoulder, gray; P_el proprioceptive sensory elbow, black).

Table 4.

Firing Rates.

Condition	P	ES	IS	ILS	EM	IM	ILM
Naive	0.98	3.36	5.60	3.36	0.17	0.53	0.41
Trained	1.01	3.37	8.42	4.87	1.74	4.32	2.45

Note: Average firing rates (Hz) for the different cell populations before (naive) and after training.

During training, plasticity was present at three sites: E→E recurrent connections in both S and M areas, bidirectional in E→E connections between S and M areas, and local E→I connections within S and M areas. As in our prior simulations, E→I learning was provided in order to avoid the runaway gain sometimes seen with excitatory loop learning, even in the presence of LTD (Neymotin, Kerr, et al., 2011). Excitatory weight gains between the different populations tended to increase three-fold: ES→ES: 3.2×, ES→EM: 3.1×, and EM→EM: 3.1×. However, synaptic weights did not saturate, remaining at intermediate values due to LTP and LTD co-occurring. By contrast, E→I projections increased only about 30%. The result of the overall increased excitation was an increase in firing rates in most cell types (see Table 4). However, ES rates were almost unchanged, although the inputs from P, which carried positional information, were now being used for control of reaching the arm to target (see below).

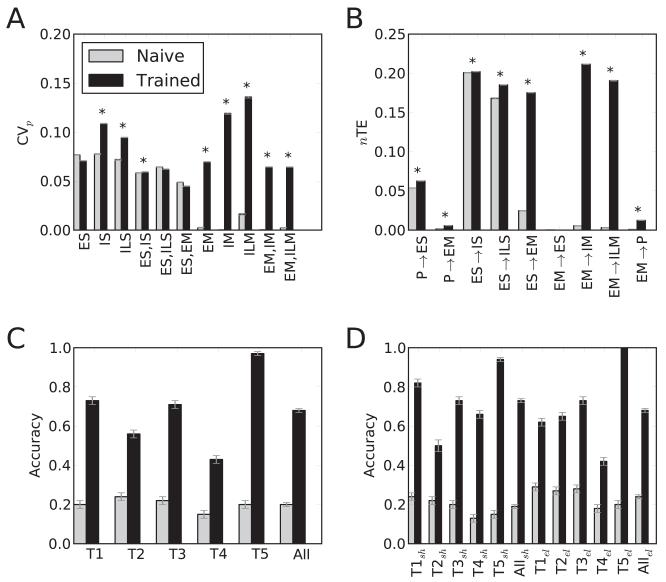
Synchrony between cells within the ES population was evident at baseline (vertical stripes in Figure 3A), with normalized population coefficient of variation (CV_p; Tiesinga & Sejnowski, 2004) showing nonzero synchrony, beyond independent Poisson process coincidence levels (0 on the CV_p scale of 0 to 1). Learning produced a significant increase in synchrony in several of the populations (see Figure 4A). Increase in synchrony was most evident in the M area, with significant increase in some S cell groups as well (see Figures 3B and 4A). This demonstrated the development of temporal structure manifested as synchrony, a correlate of the dynamical structure required to perform the task.

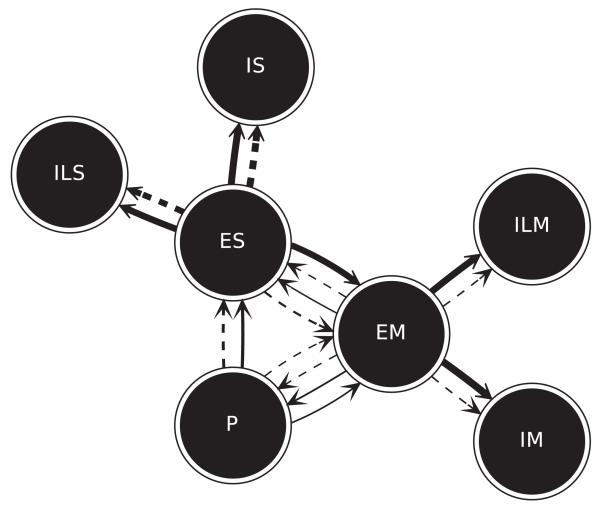
Figure 4.

Analysis across N = 2400 simulations with different randomizations, targets, starting positions. (A)Average population synchrony (CV_p). (SEMs not visible) Asterisks: significant increases; two-sided t-test, p < 0.01. (B) Average nTE. (SEMs not visible). Asterisks, significant increases; two-sided t-test, p < 0.01. (C) Successes (average hits ± SEM; all differences significant). (D) Angular hit scores (average ± SEM; all differences significant; sh, shoulder; el, elbow).

Normalized transfer entropy (nTE) between multiunit activity vectors (MUAs) demonstrated increased information flow between populations (see Figures 4B and 5). Although P→ES weights were fixed, there was a significant increase in nTE across these populations (0.0537 to 0.0625; SEMs ≤1%). This change demonstrated that network reorganization, due to changes in other projections onto the S area, allowed alteration of ES activity so as to better follow incoming proprioceptive information and improve performance. The large increase in nTE in the main feedforward pathway from ES→EM (0.0247 to 0.1752) reflected the presence of structure in proprioceptive information, which provided the ES populations the ability to select particular EM units to activate for the signaled movement. Increase in local-connectivity nTE from E→I within each region was consistent with tuning of network inhibition to suppress cells that would interfere with performance. This change suggested the emergence of lateral inhibitory feedback influences (the equivalent of a geometrical inhibitory surround). The projection from EM→P cells closed the loop. Increased nTE after learning (0.0008 to 0.0124) demonstrated that EM movement-related activity was then predictive of future proprioceptive states. This shift suggested how such a signal could also be utilized as efference copy.

Figure 5.

Average nTE before (dotted lines) and after (solid lines) learning. Each circle represents a population. Arrows represent direction of nTE. Thickness of lines indicates nTE magnitude (corresponding to bar magnitudes in Figure 4B).

3.2 Trained Networks Perform Reaching

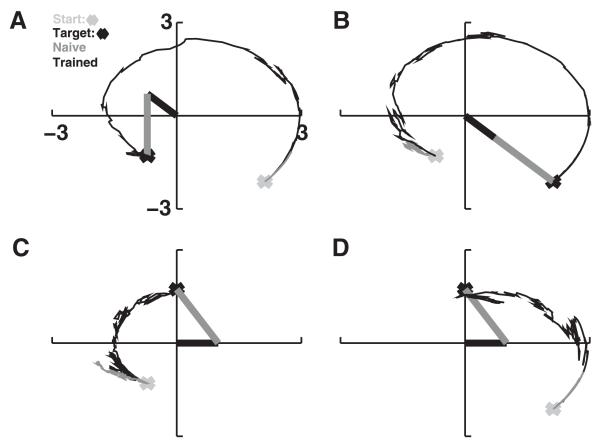
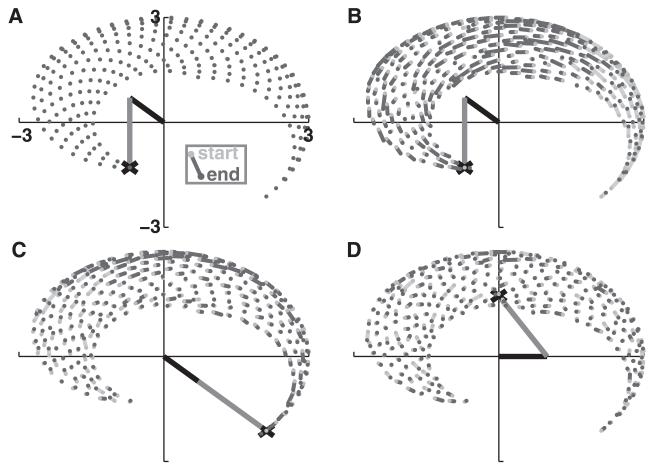
Individual networks were each trained to navigate toward a particular location (see Figure 6). Prior to training, the arm’s end point would move only slightly from its initial starting position (see Figure 6, gray traces). After training, with learning off, the network was able to move the arm from arbitrary starting positions to the trained target (see Figure 6, black traces). Generally the network moved the arm successfully to its target in a near-optimal trajectory. The ongoing noise in the system tended to reduce the smoothness of the motion and often caused the arm to deviate slightly from the target, once reached. Arm movements were successfully made to targets from one extreme to the other (extreme extension to extreme flexion in Figure 6A and the reverse in Figure 6B). A single network learned a single target but could reach this target from any starting point at either side of the target. In Figure 6C, the network moved the arm from maximum flexion toward the intermediately positioned target. The arm did not overshoot, demonstrating that the network was able to keep track of the end point position to determine which direction to move in. In Figure 6D, the same network directed the arm toward the target from an initial position of maximum extension. Here, a slight overshoot was seen, but the arm immediately moved back toward the target afterward.

Figure 6.

Sample model performance on four desired arm trajectories. Naive network trajectories in gray; trained in black. Arm is shown at target position (black: upper arm; gray: forearm). (A) Maximal flexion at both joints (T5). (B) Maximal extension (T4). (C, D) Intermediate target (T3) approached from opposite directions.

Across targets, training significantly improved performance compared to the naive networks with substantial variability, ranging from 0.43 to 0.97 success for trained networks and 0.15 to 0.24 for naive networks (see Figure 4C). Success was calculated for naive and trained networks from identical initial conditions (starting position and random inputs), where for each of the N = 2400 trials, a score of 1.0 indicated the hand had, during some time in the simulation, reached within a Cartesian distance of 1.0 from the target, and a score of 0.0 indicated this was not achieved. Networks were more readily trained for some targets, with maximum flexion being the easiest to reach and maximum extension being the most difficult. Training significantly improved performance for all targets (p < 1e-9, two-tailed t-test; see Figure 4C).

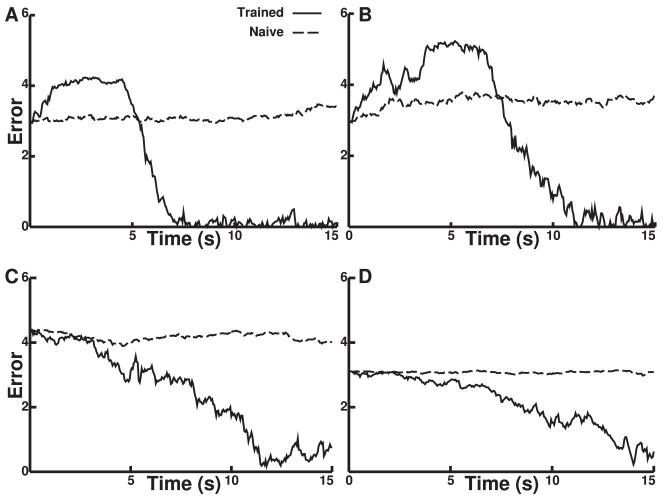
Trained networks reduced error (approached the target) over time (see Figure 7). The panels here correspond to those in Figure 6. In some cases, the initial movement of the trained network increased error; because hand location is constrained by rotation at the two joints provided, it must in some cases initially move away from the target in order to ultimately reach it. In these cases, movement begins to reduce error, after the arm passes through the vertical axis at about 5 s (e.g., sharp drop of error in Figure 7A). By contrast, when the target was centered, the error did not show this increase (see Figures 7C and 7D). In these cases, the arm oscillated more at the target, lacking the externally imposed constraint of the extremum as a counterbalance to attempted movement.

Figure 7.

Cartesian error versus time performance on four desired trajectories. The panels correspond to the trajectories over the 15 s simulations shown in the same Figure 6 panels.

Once the arm reached the target, error remained relatively low, with small oscillations caused by the ongoing noise or babble. Trained networks showed substantially greater reduction in overall error as a function of time. Pearson correlation between error and time values was significant (p < 0.05) and negative for the trained networks (average −0.31 ± 0.01) and showed significant difference (p < 0.05, two-tailed t-test) from the naive networks. Performance for individual targets varied, but all trained networks showed a trend toward decreasing error over time, as expected from the motion of the arm from its starting position toward the target.

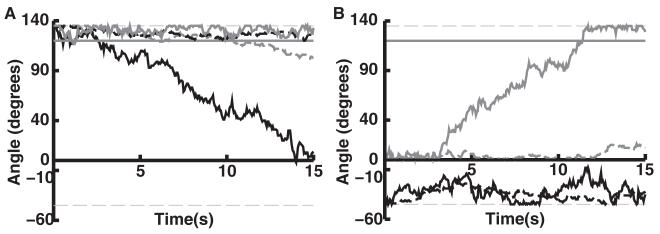
We examined trajectories of joint angles over time in individual reach trials (see Figures 8 and 4D). Trained networks were typically able to stabilize both joint positions within 10 degrees of target locations. After training and across targets, this occurred 73% and 68% of the time for shoulder and elbow angles, respectively, compared to only 19% and 24% for the naive networks (each of the N = 2400 scores used for calculating means in Figure 4D was set to 1.0 when, at some time during the simulation, the joint angle fell within 10 degrees of its target, and set to 0.0 when this did not occur). Depending on target, the accuracy of trained network performance ranged from 50% to 100% (see Figure 4D).

Figure 8.

Shoulder and elbow joint angle performance for two desired trajectories to the same target. (A, B) The same trajectories as in Figures 6C and 6D, both targeting T3. Shoulder (black) and elbow (gray) joint angles are shown over the course of the 15 second reach trial as controlled by a trained (solid lines) network and naive (broken lines) network to a particular target. Horizontal solid lines indicate the target angles in degrees (shoulder target at zero degrees). Thin horizontal gray lines indicate minimum and maximum angles.

Figures 8A and 8B correspond to the reaches depicted in Figures 6C and 6D. These reaches were accomplished by a single trained network, with the arm beginning at opposite sides of the target. In Figure 8A, the arm begins at maximum flexion. In this case, the majority of the reach is accomplished by rotation about the shoulder joint. Figure 8B shows movement to the intermediate target from maximum extension. Here, the majority of the movement is accomplished by rotation about the elbow joint. The network uses only minimal shoulder movements to bring the arm close to the target. These examples demonstrate that a single trained network can dynamically reconfigure which joint to use for a reach, depending on available proprioceptive information.

We evaluated reach performance as a function of training epoch (see Figure 9) for the three targets shown in Figure 6. Overall, training quickly reduced error below that of the naive networks. However, there was considerable variability in learning performance, depending on the target. The maximum flexion target showed fast learning, with the error dropping close to zero after the first training epoch (see Figure 9A). This is consistent with best overall performance (see Figure 4C, T5). The error for the maximum extension target tended to oscillate with high deviations, also consistent with the lower performance of reach movements toward the maximally extended target (see Figure 4C, T4). The intermediate target showed intermediate performance, with lower-amplitude oscillations in error. The oscillations in error were partially due to optimization of reach movements from specific starting positions, which could have a detrimental impact on reach performance from other starting positions. In addition, the babble noise was unmodulated as training progressed, which could lead to partial interference in learning.

Figure 9.

Average minimum Cartesian error (across 16 starting positions) as a function of training epoch. (A–C) Correspond to the average (over all starting positions) performance on the targets used in Figures 6A (T5), 6B (T4), 6C and 6D (T3), respectively. Performance at epoch 0 is the performance after the first training session.

By running a network for 15 s with both learning and muscle motions turned off and analyzing the direction that the EM units would have caused the arm to move in from a grid of 256 starting positions, we were able to extract motor command maps for four different cases of networks attempting to reach for a particular target (see Figure 10). Figure 10A shows an untrained network trying to reach for the most flexed target (T5); the motor commands at all of the starting positions are essentially insignificant, which is typical for all of the naive networks. After training, the vectors tended to point toward the target (see Figures 10B to 10D). Figure 10B shows a trained network reaching for, again, T5. Most of the vectors are colored dark grey, representing directional preferences that point toward the target. However, the light gray vectors in the bottom right quadrant of Figure 10B show movement preferences that actually increase error yet are nonetheless required for arm movement, based on rotational constraints at the joints. During training, the network would be punished for following these trajectories from these points, yet the overall training permits these movement preferences to be learned. Because the target is at extreme flexion, the overall tendency of the learning is to reinforce flexion and suppress extension. This permits global learning that is contrary to local cues. Similarly, Figure 10C shows a motor vector field pattern consistent with reinforced extension (T4).

Figure 10.

Movement command vectors (15 s of simulation from grid of 256 starting positions). Movement vectors are drawn from light to dark grey circles. Dark gray vectors (lines) point toward target (decreasing Cartesian hand-to-target error), and light gray point away (increasing error). Magnitude of each vector is scaled by 2X. (A) Movement commands generated by a naive network have no directional selectivity. (B) Maximum flexion and (C) maximum extension vectors tend to point toward the target. (D) Motor commands for intermediate target show directional selectivity toward the target from opposite direction, but have smaller magnitudes.

With the target at an intermediate position (see Figure 10D, T3), the vectors are not as clearly oriented and are of reduced magnitude. The reduced magnitude promoted more conservative movements, advantageous because positioning the arm over an intermediate target required balance: too much extension or flexion results in over- or undershooting the target. For the trained networks, average angular error reductions about each joint per movement command across targets and starting positions were −0.29° per move for shoulder and −0.15° for elbow (SEM ≤0.01°), demonstrating that the network tended to generate movements that would reduce error. The larger reduction in shoulder error is due to its larger role in positioning the end point of the arm, since the elbow position depends on the upper-arm position.

Flexion bias scores, representing difference between extension versus flexion weights at a joint from −1 to 1, showed the expected flexion bias at both joints (average ± SEM: 0.22 ± 0.01 and 0.27 ± 0.01 for shoulder and elbow, respectively) in the case of the maximum flexion target. However, the maximum extension target produced networks with flexion bias at the elbow (0.03 ± 0.02), with only slight extension bias at the shoulder joint (−0.12 ± 0.03). This corresponded to the lower hit score for the maximum extension target compared to maximum flexion target. The intermediate targets had extension bias at the shoulder (T1: −0.14 ± 0.02; T2: −0.01 ± 0.01; T3: −0.12 ± 0.01), with primarily flexion bias at the elbow (T1: 0.03 ± 0.02; T2: −0.02 ± 0.01; T3: 0.05 ± 0.01). Balancing bias at the two joints appeared to be a strategy to allow movement to occur readily in opposing directions so as to allow for target acquisition from different initial points.

4 Discussion

The results in this letter demonstrate the flexibility of the network architecture and learning algorithm developed in Chadderdon et al. (2012). Here we have extended the target tracking task to the more challenging problem of controlling two independent joints to perform the reach. ES cells contain random mappings from the proprioceptive P cells, which leads to individual ES cells forming conjunctive representations of configurations of both joints. The global reinforcement mechanism induces plasticity, which shapes the EM cell response to the current limb configuration represented in ES. The target is effectively represented implicitly (see below) by the visual set point, which the reinforcement algorithm uses to determine whether the network is rewarded or punished for the motor commands it issues in response to current limb configuration. Such a system effectively forms attractors for the target arm configuration by shaping the immediate response to particular points the arm is at in the trajectory. Figure 10 graphically shows the type of motor command map that implements these attractors. These attractors may function either when learning is turned off (as is done during testing in this paper) or left on, though continued learning may add some interference to the learned attractor. As a consequence of the attractor structure, only one target may be learned by the system at a time.

Additionally, although we did not actively test it under this task, we have previously demonstrated that this model is capable of unlearning old attractors and relearning new ones based on a shift of the reinforcement schedule (Chadderdon et al., 2012): a feature that adds great adaptive flexibility to the simulated agent’s reaction to its environment. Punishment “stamps out” no-longer-relevant attractors, and babbling in conjunction with reward is able to “stamp in” newer, desired attractors. Although we turn off learning before we test the performance of the model in this letter (in order to control for the possibility of new learning affecting performance), there is biologically plausibility in always leaving the learning algorithm on at some level (Sober & Brainard, 2009). This is easily accomplished, and in the future, we intend to adapt the level of babbling motor noise according to the degree to which the agent is being rewarded (more reward, less injected noise). When this is done, learning should become even more efficacious and leaving learning on less detrimental than is evidenced in Figure 9.

Learning produced alterations in network dynamics, including enhanced neuronal synchrony and enhanced information flow between neuronal populations. After learning, networks retained behaviorally relevant memories and utilized proprioceptive information to perform reaches to targets from multiple starting positions. Trained networks were able to dynamically control which degree-of-freedom (elbow versus shoulder) to use to reach a target, depending on current arm position. Learning-dependent dynamical reorganization was evident in sensory and motor populations, where synaptic weight patterning was produced through a balance of convergent excitatory weights onto motor populations projecting to extensors and flexors.

We make a number of specific, testable predictions from the model:

1. Balanced learning (changes in both E→E and E→I weights) is needed to produce selection of correct motor units while suppressing activation of incorrect motor units via selective inhibition. This is testable using selective pharmacological blockade or optogenetics.

2. Learning enhances synchrony in neuronal populations and enhances behaviorally relevant information flow across neuronal populations. This is testable with electrophysiological recording techniques (multiple areas or single units) and nTE. However, information flow (measured by nTE) can change across two populations due to dynamical factors in the absence of learning, or even direct synaptic connections, between these populations (e.g., EM→P in Figure 4). Thus, although nTEcan sometimes provide evidence of learning (Lungarella & Sporns, 2006), it must be interpreted cautiously.

3. Enhanced sensory processing works in tandem with motor alterations to improve task-relevant motor performance. This is testable in vivo by erasing memories from sensory areas (Pastalkova et al., 2006; Von Kraus, Sacktor, & Francis, 2010). Additionally, motor cortex erasure could be used to demonstrate that relearning is accelerated in the presence of the prior sensory learning. These predictions could also be tested further in our model.

4. Learning to a motion extremum is faster than learning to intermediate positions since motion limitations can be used, eliminating the need for learning balance across antagonist muscles (preliminary experiments confirm: P. Y. Chhatbar, personal communication). More generally, the relative ease of a particular movement in vivo depends on the amount of sensory information required to complete the movement. This is testable by kinesiology.

4.1 Environmentally Constrained Structure and Function

Functional connectomics seeks to explain dynamics and neural function as emergent from detailed neuronal circuit connectivity (Sporns, Tononi, & Kotter, 2005; Shepherd, 2004; Reid, 2012). Circuit changes have been correlated with brain diseases, such as epilepsy (Dyhrfjeld-Johnsen et al., 2007; Lytton, 2008) and autism (Qiu, Anderson, Levitt, & Shepherd, 2011). Our past modeling work has confirmed the importance of microcircuit structure on neural function, demonstrating that alterations in connectivity change both dynamics and information transmission in neuronal networks (Neymotin, Jacobs et al.,2011; Neymotin, Kerr et al., 2011; Neymotin, Lezarewicz et al., 2011; Neymotin, Lee et al., 2011).

The embedding of brains, and by extension neuronal networks, in a physical (or simulated) world has been hypothesized to be an essential part of learning, as seen as the evolution of network dynamics (Almassy, Edelman, & Sporns, 1998; Edelman, 2006; Krichmar & Edelman, 2005; Lungarella & Sporns, 2006; Webb, 2000). This theory maintains that the environment and brain influence each other as learning selects neuronal dynamics (selective hypothesis) (Edelman, 1987). In our work presented here, learning depended on the interaction with the rudimentary simulated environment: the virtual arm and target. This embodiment can now be used to make predictions for learning-related changes occurring during the perception-action-reward-cycle (Mahmoudi & Sanchez, 2011).

Embedding also provides a step toward using simulation to assess the functional importance of various dynamical measures commonly used on in vivo electrophysiological data. Here, we found that synchrony and nTE were both enhanced after learning. These measures have been suggested as a means for brains to coordinate activity and process information (Engel, Konig, Kreiter, Gray, & Singer, 1991; Lungarella & Sporns, 2006; Von der Malsburg & Schneider, 1986; Neymotin, Jacobs et al., 2011a; Uhlhaas & Singer, 2006). Our biomimetic brain model learned a function that can then be correlated with specific aspects of ensemble dynamics. The functional connectome can thus be dissected by looking at two steps: (1) the emergence of dynamics from connectivity (the dynamic connectome) and (2) the relation of function to aspects of dynamics (the functionome: the set of functions a network can perform as constrained by its dynamics and dynamical embedding within the environment).

4.2 Target Selection

Representation of both visual and somatosensory state information, including target information, is believed to be located in posterior parietal areas, and this information propagates to premotor and motor cortex (Shadmehr & Krakauer, 2008). These representations may be modulated by processes that select task-relevant information. Recent experiments have shown that premotor cortex activity is predictive of changes of mind that result in switching between targets midmovement (Afshar et al., 2011).

Our model selects the target implicitly using the Cartesian visual reference point that the reinforcement learning algorithm uses to determine whether the hand is moving closer (reward condition) or farther away (punishment condition) from the desired location. A part of the brain upstream of the dopamine cells signaling error might perform the error calculation and cue the correct valence of reinforcement (internal reinforcement source), or the environment itself might provide actual rewards or punishers based on the the agent’s choice (external source). In either case, the reinforcement schedule can implicitly select the target (Chadderdon et al., 2012). In future versions of the model, however, we may use a premotor cortex representation in order to allow mappings to be learned that map the conjunction of cued target representation and limb state to directive motor commands. Such a representation would presumably be cued by dorsal visual stream information propagating through posterior parietal cortex when the agent views a target in a particular location in the visual field. This would also allow the model to move beyond the current limitation of being able to retain a mapping to a single target at a given time.

Experiments have demonstrated that neuronal networks dynamically select between competing streams of information, depending on behavioral relevance (Kelemen & Fenton, 2010). This information selection is modulated by attention-like processes affecting neuronal dynamics and behavioral performance (Fenton et al., 2010). One dynamical mechanism implicated in attentional function is modulation of the level of oscillatory amplitude in the mu and alpha bands, elicited via top-down projections from higher- to lower-order brain areas (Mo, Schroeder, & Ding, 2011; Jones et al., 2010). We previously developed models of neocortex showing altered dynamics with attentional modulation (Neymotin, Lee et al., 2011). In these models, supragranular layers of neocortex received strengthened input as a stand-in for higher-order brain area activation. This had the effect of increasing 8 Hz to 12 Hz oscillation amplitude, while maintaining the peak oscillatory frequency location. We hypothesize that target information projecting from premotor- into supragranular layers of motor-cortex causes attentional modulation, allowing motor cortex to control movements to targets.

4.3 Learning Molecules

A major challenge in neuroscience will be to bridge the gap in understanding how activity at disparate scales is linked (De Schutter, 2008; Lytton, 2008; Le Novére, 2007). A phenomenon such as learning has important dynamics at different scales of granularity ranging from molecular up to network and behavioral levels. In this letter, we used a phenomenological learning rule that had a spike-timing dependence. This rule operated at the synaptic scale and was further modulated by more global neuromodulatory-like reinforcement signals. These global reinforcement signals bridged the gap from synaptic and molecular signaling to the behavioral level and were effective in eliciting desired behavioral responses from the sensorimotor network via the synaptic learning process.

Dopamine, a key signaling molecule in modulating learning, bridges the gap between behavioral, cognitive, and molecular levels (Evans et al., 2012). There is evidence that increased (decreased) dopamine concentration leads to synaptic LTP (LTD) via action of D1-family receptors (Reynolds & Wickens, 2002; Shen, Flajolet, Greengard, & Surmeier, 2008). Our model provides a link between global reinforcement, mediated via dopamine signals, and sensorimotor learning. In future work, we will explore a more detailed model of the dopaminergic reward pathway, with potential implications for modeling disorders such as schizophrenia and Parkinson’s disease (Frank, Seeberger, & O’Reilly, 2004; Cools, 2006; Frank & O’Reilly, 2006).