Abstract
Scientists and laymen alike have always been fascinated by the ability of lenses and mirrors to control light. Now, with the advent of metamaterials and their two-dimensional counterpart metasurfaces, such components can be miniaturized and designed with additional functionalities, holding promise for system integration. To demonstrate this potential, here ultrathin reflection metasurfaces (also called metamirrors) designed for focusing terahertz radiation into a single spot and four spaced spots are proposed and experimentally investigated at the frequency of 0.35 THz. Each metasurface is designed using a computer-generated spatial distribution of the reflection phase. The phase variation within 360 deg is achieved via a topological morphing of the metasurface pattern from metallic patches to U-shaped and split-ring resonator elements, whose spectral response is derived from full-wave electromagnetic simulations. The proposed approach demonstrates a high-performance solution for creating low-cost and lightweight beam-shaping and beam-focusing devices for the terahertz band.
The terahertz (THz) band of the electromagnetic spectrum is conveniently located between the microwaves and infrared regions allowing researchers to combine both optical and microwave techniques in THz instrumentation and to synthesize unique instrumental solutions1. Such a synthesis is proven to be very effective when planar metallized microstructures of subwavelength topology, commonly referred to as frequency selective surfaces or metasurfaces2, are used for manipulating amplitude, polarization and phase characteristics of microwaves3,4,5, quasi-optical THz6,7,8 and optical beams9,10,11,12 as well as acoustic waves13. In microwave and millimetre-wave engineering, control of the phase is essential in the technology of low-profile reflectarray antennas, whose conventional design implies exploiting a metasurface laying over a grounded-dielectric-slab with spatial-dependent reflection phase4,14,15. This reflection-type approach holds promise for THz beam-shaping and beam-focusing techniques as it allows creating purely flat, thin and lightweight reflectors capable of properly manipulating the wavefront through the control of the metasurface unit cell geometry. Due to relative simplicity in photolithographic fabrication, such kind of reflectors serve as an attractive alternative to the conventional diffractive optical elements (DOEs) based on cost-consuming structures with profiled surfaces16,17,18. In addition, working in reflection mode eliminates the Fresnel reflection loss and reduces the terahertz-material interaction. This lowers the overall insertion loss of the device compared to transmission metasurfaces.
In this paper we investigate the feasibility for effective focusing of terahertz waves using metasurface-inspired flat holographic reflectarrays (HRAs) (see Fig. 1), whose design is accomplished by using a combined approach involving: i) a computer-generated holography (CGH) method19,20,21 to synthesize an appropriate distribution of the reflection phase φHRA(x,y) over the holographic metasurface; ii) a full-wave-electromagnetic-analysis-based method to control the complex reflectance ρHRA(x,y) of the HRA at any local point (x,y) of its surface via proper morphing the metasurface unit cell geometry from metallic patches14,22 to U-shaped23 and split-ring resonator elements7,24,25 akin to surface wave inhomogeneous metalenses26. Given the anisotropy of the U-shaped and split-ring resonators, numerical investigation of the TM- and TE-polarization is done. We conclude that the TE-polarization scheme leads to a better overall performance due to its negligible cross polarization. We report experimentally two different metasurfaces designed for the reflective focusing of an incident TE-polarized Gaussian beam into a single spot and four spaced spots respectively, which were optimized for the operation frequency of 0.35 THz (free-space wavelength λ0 = 857 μm) chosen due to its positioning in the atmospheric-transmission window27. An overall efficiency ~ 80% is achieved in both cases, which outperforms that reported for transmission metasurfaces working at THz frequencies8.
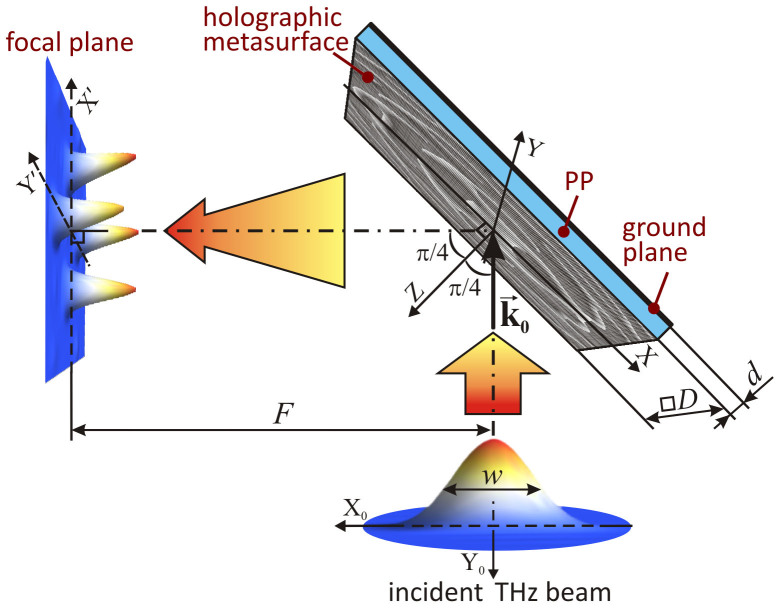
Figure 1. 90 deg-reflection schematic setup to focus a Gaussian terahertz beam by a metasurface.
k0 is the wave vector of the incident beam, having the following components in the (X, Y, Z) coordinate system: 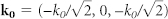 , where k0 = 2π /λ0. The plane (X, Y) is chosen to coincide with the outer interface of the metasurface.
, where k0 = 2π /λ0. The plane (X, Y) is chosen to coincide with the outer interface of the metasurface.
Design procedure and results
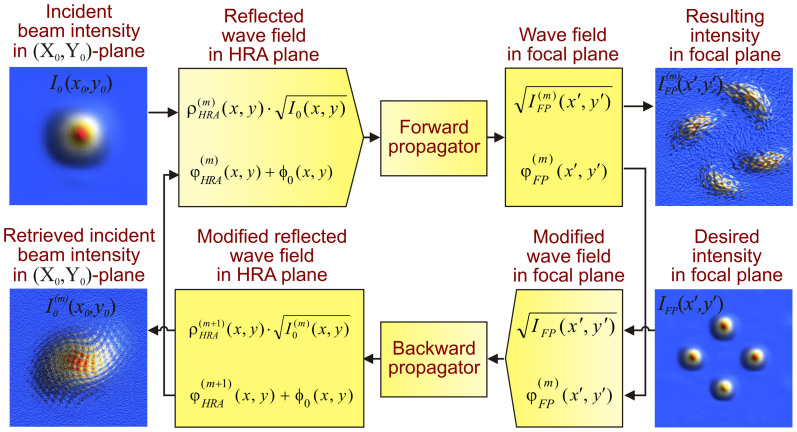
To attain the desired intensity distribution IFP(x′,y′) in the focal plane (X′, Y′) for the wavefront focused by the metasurface, the optimal surface distribution reflection phase φHRA(x,y) referred to the (X, Y) plane can be effectively calculated by using CGH phase retrieval methods originally developed for profiled DOEs. In this work, we employed the easy-to-code and robust iterative algorithm of Gerchberg-Saxton (GSA)19,20,21, following the workflow shown in Fig. 2. This algorithm, although more complex than alternatives such as the standard ray-tracing method, is applicable for any configuration and, in particular, provides more accurate results in non-paraxial configurations like the one here reported.
Figure 2. The workflow of the Gerchberg-Saxton iterative algorithm for retrieving surface distribution of the HRA reflection phase φHRA(x,y).
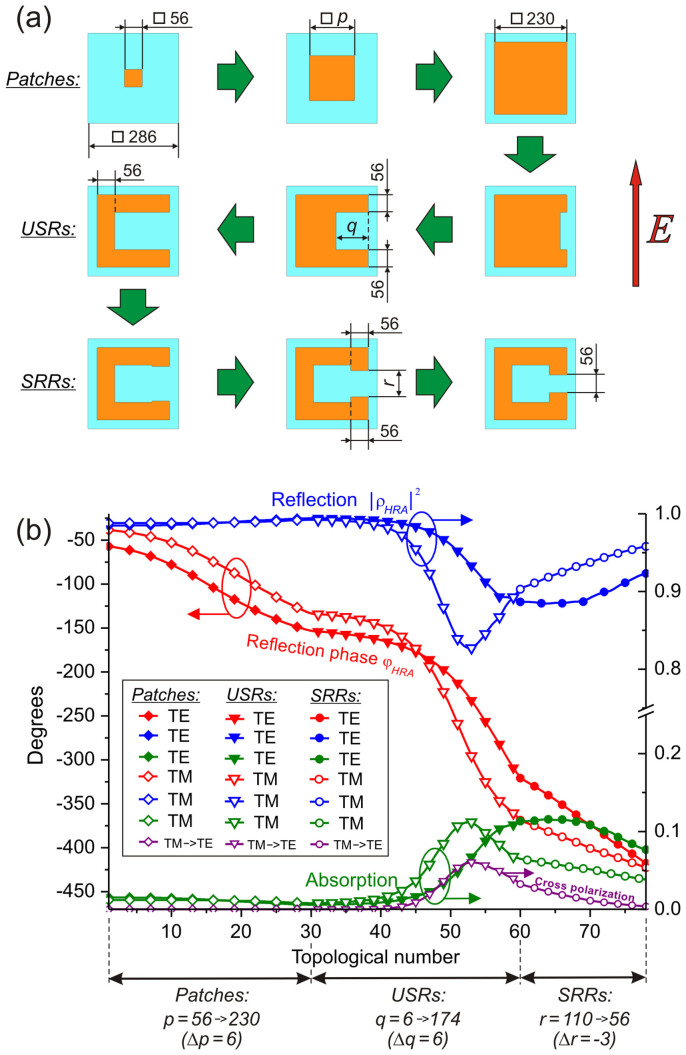
To cover the range of 360 deg variation of the reflection phase φHRA, which is necessary for accurate focusing, we continuously changed the metasurface unit cells geometry from square-shaped metallic patches14,22 to U-shaped resonators (USRs)23 and then to split-ring resonator elements (SRRs)7,24,25, as it is shown in Fig. 3(a). As a dielectric substrate, a polypropylene (PP) slab of thickness d = 190 μm (d ≅ λ0/4.5) was employed to minimize dielectric losses (tanΔ ≈ 0.001)28,29. To minimize Ohmic dissipation, 0.35 μm thick aluminum metallization was used both in the metasurface and ground plane layers. Due to a relatively low PP refractive index n (n ≅ 1.5), such topological morphing (“Patch-to-SRR”) enables to enhance subwalengthness of the unit cells compared to the patch-based RAs14,22 and, therefore, to decrease the phase errors when substituting the required local phase φHRA(x,y) by the one retrieved from simulations of the regularly patterned surfaces. Moreover, when using only a single layer metasurface, it allows us to overcome the key drawback of the patch-based structures – impossibility to overlap 360 deg for the reflection phase14,15. It should be also pointed out that the proposed metasurface based on “Patch-to-SRR” morphing is polarization-sensitive and supposed to be excited by the wave polarized transversely to USR and SRR gaps. Formally, a different morphology change involving for instance only isotropic unit cells could have been chosen at the expense of removing the polarization-dependence of the holographic metasurface. However, we found that “Patch-to-SRR” morphing enables to obtain smaller dimensions of the metasurface unit cells and, therefore, to enhance their subwalengthness, when the minimal feature size technologically allowable for the metasurface is fixed (56 μm in this work).
Figure 3. “Patch-to-SRR” morphing.
(a) “Patch-to-SRR” route for topological morphing of the metasurface pattern and (b) simulated performance of corresponding uniform-metasurface-based reflectarrays at the frequency of 0.35 THz. The exciting polarization is transverse to USR and SRR slots. The geometric parameters are given in micrometers. Metallization is shown in orange (dark).
Figure 3(b) illustrates variation of the absolute reflection phase φHRA and the reflection coefficient |ρHRA|2 induced by “Patch-to-SRR” topological morphing of the optimized metasurface pattern at the frequency of 0.35 THz simulated for the cases of TE- and TM-polarization. The morphing starts with a monotone increase of the patch width p from 56 to 230 μm (increment Δp = 6 μm). The largest patch then transforms to USR via forming a rectangular horizontal recess, varying q from 6 to 174 μm (increment Δq = 6 μm). Finally, USR turns into SRR by extending the metallic arms of the USR gap, so that the width r decreases from 110 to 56 μm (increment Δr = -3 μm). This three-step variation of the unit cell morphology is chosen to modify gradually the electromagnetic response such that the local periodicity approximation holds. For TE-polarization, such topological morphing leads to 360 deg variation of the reflection phase from the initial patch to the final SRR, see Fig. 3(a). For TM-polarization, the phase excursion is 384 deg.
A clear drawback of the TM case is the depolarization or cross-polarization (TM-to-TE conversion) under oblique incidence due to the intrinsic bianisotropy of the USR and SRR unit cells30. In Fig. 3(b) cross-polarization losses are clearly observed for USR and SRR cases, and are maximized for USR elements (6% in the worst case). On the other hand, under TE excitation cross-polarization due to bianisotropy does not appear30 and thus the level of TE-to-TM conversion does not exceed –60dB (10−6). Note that the cross-polarization losses decrease the TM-reflectivity down to 82.7% in contrast to 88.4% for the TE case. As for TE and TM absorption losses, whose values can be evaluated by the formulas 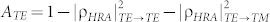 and
and 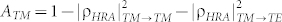 their maximal magnitudes reach ATE = 11.5% and ATM = 11.2% respectively (see Fig. 3(b)). The field analysis shows that absorption is attributed mainly to Ohmic dissipation in the metallization.
their maximal magnitudes reach ATE = 11.5% and ATM = 11.2% respectively (see Fig. 3(b)). The field analysis shows that absorption is attributed mainly to Ohmic dissipation in the metallization.
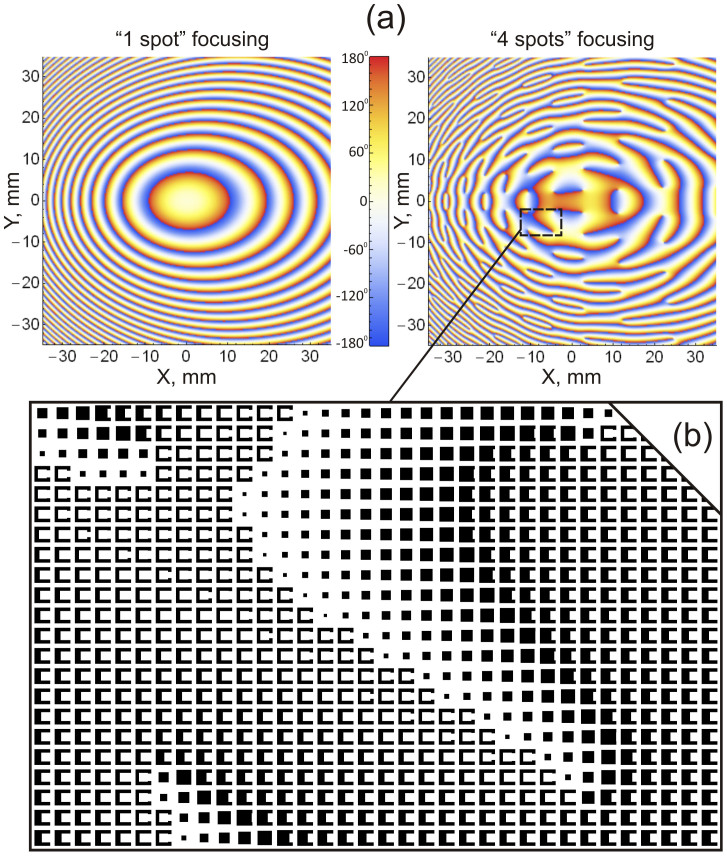
For the experimental confirmation of the proposed approach, the two kinds of metasurfaces designed were fabricated and experimentally investigated. In the first design an incident Gaussian beam is focused into a single spot (1-spot), whereas in the second it is divided into four spaced spots (4-spots) placed in the vertices of a symmetric cross with 12 mm axes. The metasurfaces were optimized for TE-polarized excitation to minimize cross-polarization losses. Figure 4(a) displays the GSA-computed distributions of the reflection phase φHRA(x,y) over the metasurfaces for a focal distance F = 60 mm. When realizing GSA, which typically converged after 20 iterations, the metasurface was spatially discretized into uniform pixels with dimensions 286 × 286 μm equal to the dimensions of the unit cells. This discretization step was used in the Fresnel-Kirchhoff surface integral computation and the phase was assumed to be constant within the pixel area. After computing the phase distribution φHRA(x,y), a photomask was generated with a MATLAB™ code by using the correspondence between the phase and the unit cell geometry represented in Fig. 3. This photomask was used for the fabrication of the metallic pattern via a photolithographic technique28,29. As only a relative phase shift between pixels makes sense, the phase of 180 deg was chosen to refer to the 1st number topology (“patch”, p = 56 μm), while the 78th topology (“SRR”, w = 56 μm) corresponded to the phase of −180 deg. Figure 4(b) shows a detail of the actual mask pattern corresponding to the 4-spots design.
Figure 4. Metasurface patterns.
(a) Distributions of the reflection phase over HRA surfaces for the cases of 90 deg reflective focusing into a single spot (left) and four spaced spots (right) computed for the focal distance of F = 60 mm and the operating frequency of 0.35 THz. (b) Fragment of the metasurface pattern for 4-spots HRA adapted to TE-polarized excitation. Metallized areas are shown by black.
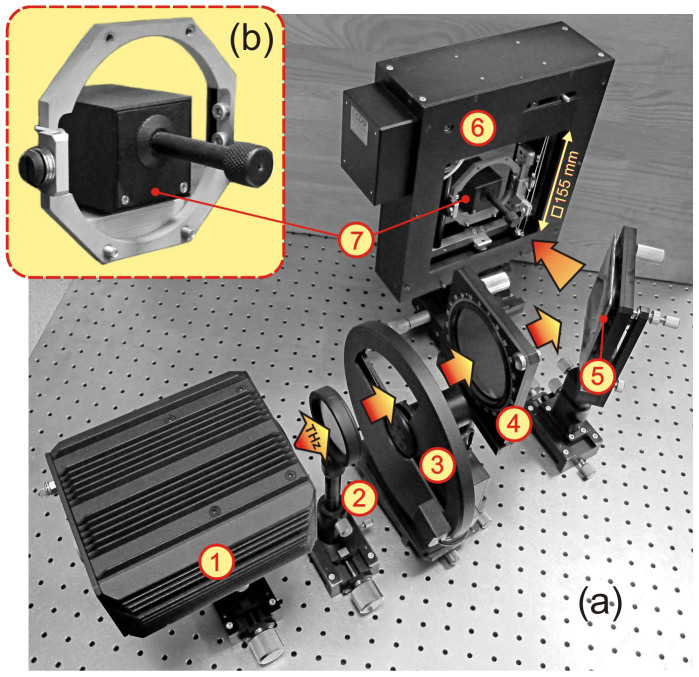
To evaluate the focusing performance, an experimental setup implemented with CDP System Corp. components32 and utilizing a quasi-optical BWO-spectroscopy technique33 was employed (Fig. 5). In this setup, the measurements were carried out with a polarization-insensitive pyroelectric sensor mounted on the tip of a metallic rod with length of 50 mm and outer diameter of 15 mm installed on a computer-controlled 2D raster scanner. The pyro-sensor was designed to have a receiving window diameter of 1.5 mm. The polarization of the BWO beam incident upon the metasurface was controlled with a wire grid polarizer.
Figure 5. Quasi-optical experimental setup.
(a) Photograph of the experimental setup used for measuring the focusing performance of the developed HRAs: (1) – THz BWO, (2) – beam forming lens, (3) – chopper, (4) – wire grid polarizer, (5) – HRA (fixed to the optical holder), (6) – 2D raster scanner, (7) – pyroelectric detector. (b) Magnified photo of the pyro-detector mounted on the carrying metallic frame.
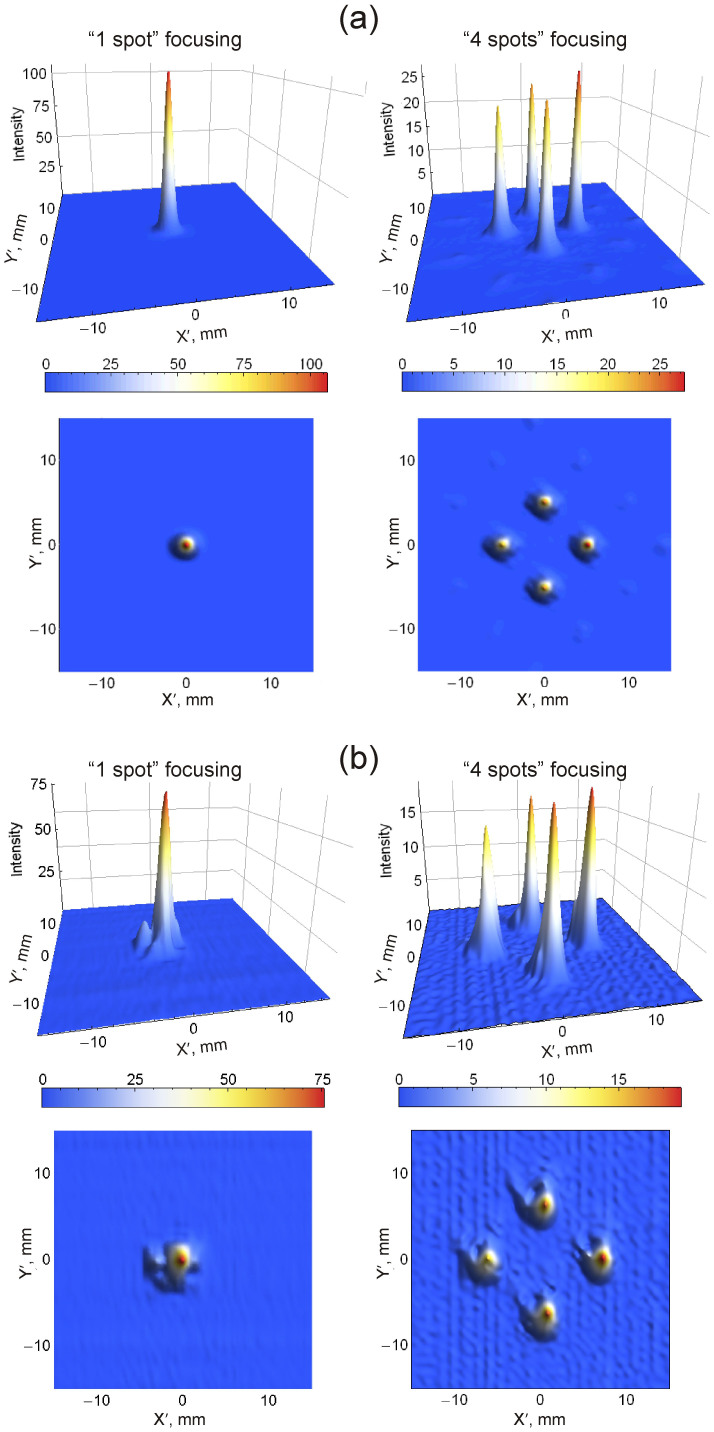
The theoretical and experimentally measured focusing characteristics for 1-spot and 4-spots designs are demonstrated in Fig. 6 where the intensity distributions IFP(x′,y′) in the focal plane (X′, Y′) are shown. The distributions are normalized to the intensity of the incident TE-polarized Gaussian beam. By inspection of Fig. 6, we conclude that there is good agreement between simulations and experimental data. The discrepancy is manifested as some reduction and broadening, as well as a slight deformation of the measured intensity peaks compared to the simulated ones. For instance, for the case of 1-spot, the theoretical intensity maximum is 106.5 and the spot has a round shape with the half-maximum diameter of 1.4 mm. In the experiment, the peak magnitude decreases down to 76.5 and the spot appears to be elongated along the Y′ axis having a quasi-elliptical shape with half-maximum dimensions of 1.9 × 2.5 mm. For the case of 4-spots focusing, the GSA computations converged to focal intensity profiles with unequal peak magnitudes distributed as 22.3 & 27.2 for the peaks located on the horizontal axis of the cross, and 24.6 & 23.8 for the peaks on the vertical axis. All simulated peaks are round-shaped with half-maximum diameter of 1.2 mm. It is noteworthy that the measurements of the 4-spots case showed qualitatively similar non-uniform peak distribution, also confirming the Y′-elongation phenomenon that also appears in the 1-spot case. The experimental magnitudes and dimensions of the 4-spots are shown in Table 1.
Figure 6. Focusing performance of the holographic metasurface.
Theoretical (a) and experimentally measured (b) intensity distributions in the focal plane (X′, Y′) obtained for 90° reflective focusing into a single spot (left) and four spots (right) at the frequency of 0.35 THz.
Table 1. Characteristics of the spots in the 4-spots experiment.
| Peak | ||||
|---|---|---|---|---|
| Left | Right | Bottom | Top | |
| Normalized intensity | 15.3 | 19.2 | 18.4 | 17.9 |
| Half-maximum dimensions (mm) | 2.5 × 3.4 | 2.7 × 3.5 | 2.3 × 3.4 | 2.5 × 3.4 |
Discussion of the results
Despite a possible distortion of the wave field intensity registered by a pyro-detector, the main reason to explain the effects of the magnitude reduction, spatial broadening and deformation of the focal peaks compared to the theoretical predictions is presumably related to phase errors. These arise inevitably when the correspondence between the phase and the unit cell geometry is established through the modeling of each metasurface as a spatially-uniform 2D array (see Fig. 3). However, in the practical realization each unit cell operates in nonuniform environment due to the gradual geometrical variation of the neighboring cells. This yields deviations from the theoretical phase values presented in Fig. 3. Such deviations can be noticeable in the pixels where the reflection phase φHRA(x,y) switches from 180 deg to −180 deg, i.e. where the topological pattern drastically changes: from patches of the first topological numbers to SRRs of the last ones (see “white-looking” areas faintly-filled with metal in Fig.4(b)). A correct evaluation of the mentioned phase errors lies beyond the scope of this paper; our goal herein is to demonstrate that, despite phase errors high-performance terahertz focusing devices, as proven by Fig. 6(b).
For practical applications, three additional important parameters of the focusing devices are usually analyzed: diffraction efficiency, spectral bandwidth, and, in case of utilizing polarization-dependent metasurfaces, sensitivity of focusing to variation of the incident polarization. In general, the DOE's diffraction efficiency (DE) is defined as the ratio of the power diffracted into a chosen diffraction order to the power of the incoming wave beam. For the case of 1-spot, the direct integration of the focal plane intensity distribution IFP (x′,y′) over the round area centered in the focal peak and diameter equal to three half-maximum diameters results in a DE equal to 93% and 80% for the theoretical and experimental cases, respectively. Similarly, the DE of 4-spots is 86% and 78% for the theoretical and experimental cases, respectively. These relatively high DE values are achieved thanks to using subwavelength pixels (λ0/g ≅ 3) that minimize the staircase variation step for the reflection phase φHRA(x,y) and lead to diminishing the spurious diffraction losses. This fact, makes the designed metasurfaces very attractive and promising for practical applications. Diffraction losses could be further reduced by increasing the λ0/g ratio so that the focal intensity profile is improved.
Regarding sensitivity of focusing to the incident polarization, both designs exhibit quite robust behavior: the magnitude of the foci decreases to half the maximum only when the exciting polarization changes at ± 40 deg relative to the optimal (TE) state. Additionally, our investigations show that, when properly designed for TM-polarized excitation, the metasurfaces keep all the main focusing characteristics obtained for TE-polarization, excluding the additional power losses, which are estimated on the level of 3–5% and are attributed to cross-polarization scattering.
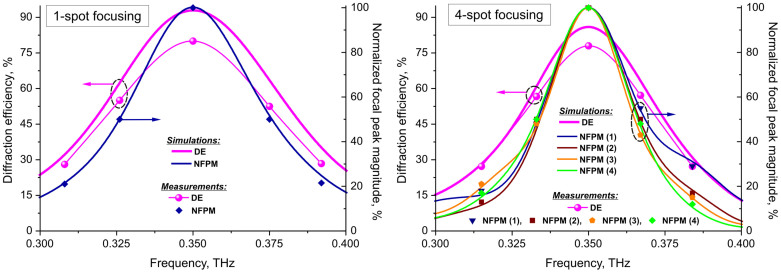
The spectral properties of the metasurfaces and, in particular, their operational frequency bandwidth (BW) are illustrated in Fig. 7 where the frequency dependences of the diffraction efficiency and the normalized focal peak magnitudes (NFPM) are shown. Referred to -3 dB level, DE-BW is evaluated as the frequency range where DE values are above half of their maxima. Relative to the frequency of 0.35 THz, both theoretical and experimentally measured DE-BW are estimated around 19% for 1-spot and 15% for 4-spots. Unlike DE, which is the area-integrated characteristics, NFPM is more sensitive to a frequency variation. Moreover, in the case of 4-spots each one of the peaks degrades slightly differently, resulting in some variation of the individual NFPM-BW (see Fig. 7 (right)). Referred to -3 dB decay relative to the peak magnitude, the theory and experiment yield the concordant values of NFPM-BW: 14% for 1-spot and on average 9.4% for 4-spots (it actually varies from 8.8% to 10% for different peaks).
Figure 7. Focusing performance of the holographic metasurfaces as a function of frequency.
Spectral behavior of the diffraction efficiency and focal peak magnitude normalized to its maximum when focusing into a single spot (left) and four spots (right). For 4-spots, the peaks from Fig. 6 (right) are numerated as follows: 1 - left, 2 - right, 3 - bottom, 4 - top.
Similar to reflectarrays4,14,15, the spectral performance of the holographic metasurfaces is limited by two factors: the bandwidth of the metasurface unit cells, and a differential spatial phase delay resulting from different path lengths from the focal spots to each point of the metasurface. To gain a deeper insight on the phase mismatching, we may consider two arbitrary metasurface points A and B having the reflection phases 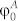 and
and  respectively, which are specified for the optimized frequency ν0 = 0.35 THz. Limiting our consideration to 1-spot focusing, the phase relation for ideal focusing can be formulated as
respectively, which are specified for the optimized frequency ν0 = 0.35 THz. Limiting our consideration to 1-spot focusing, the phase relation for ideal focusing can be formulated as 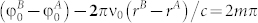 , where rA and rB are the distances between the focal point and the points A and B respectively, c is the speed of light in vacuum, and m is an integer. To make the focal plane intensity independent on frequency (implying a constant incident beam profile, for simplicity), we should impose the requirement to fulfill this relation at any other frequency ν where the A and B reflection phases are equal to φAand φB respectively: (φB-φA)-2πν(rB-rA)/c = 2mπ. These two relations can be reduced upon elimination of rA and rB to the next equation:
, where rA and rB are the distances between the focal point and the points A and B respectively, c is the speed of light in vacuum, and m is an integer. To make the focal plane intensity independent on frequency (implying a constant incident beam profile, for simplicity), we should impose the requirement to fulfill this relation at any other frequency ν where the A and B reflection phases are equal to φAand φB respectively: (φB-φA)-2πν(rB-rA)/c = 2mπ. These two relations can be reduced upon elimination of rA and rB to the next equation:
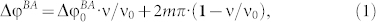 |
where ΔφBA = (φB-φA), 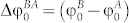 .
.
The first term on the right side of (1) describes the ideal frequency dispersion law for the metasurface unit cells necessary to compensate a phase shift between surface points when changing the frequency. However, such compensation will work for the whole surface only if all the partial waves arriving at the focal point from the metasurface have the relative phase shift modulus not exceeding 360°. This corresponds to the condition m = 0 and can be realized when the metasurface transverse size D is relatively small compared to the focal distance F (D
<(8λ0F)1/2). For the case D/F ≅ 1, the second term on the right side of (1) becomes non-zero and cannot be neglected. It introduces a supplementary non-compensable phase shift which increases when |m| grows and results in an extra narrowing of the bandwidth for the metasurfaces having a large number of the operating zones shifted in phase by 360° (see Fig. 4(a)). In this work, at least four of such zones should be taken into account as the metasurfaces are illuminated by the wave beam with the half-maximum diameter w ≅ 18 mm. To quantify both terms in equation (1) applied to the “Patch-to-SRR” morphing from Fig. 3 and, thus, to get information on the phase mismatch corresponding to the actual values of the metasurface bandwidth, we will consider the quantities ΔφBA and 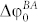 as the differences between the TE reflection phases of the 1st number topology (the patch of the smallest size) and the variable topological number X (X∈[1, 78]) determined at the specified frequencies: ΔφBA≡Δφ1vsX(ν) = φTopol1(ν)-φTopolX(ν),
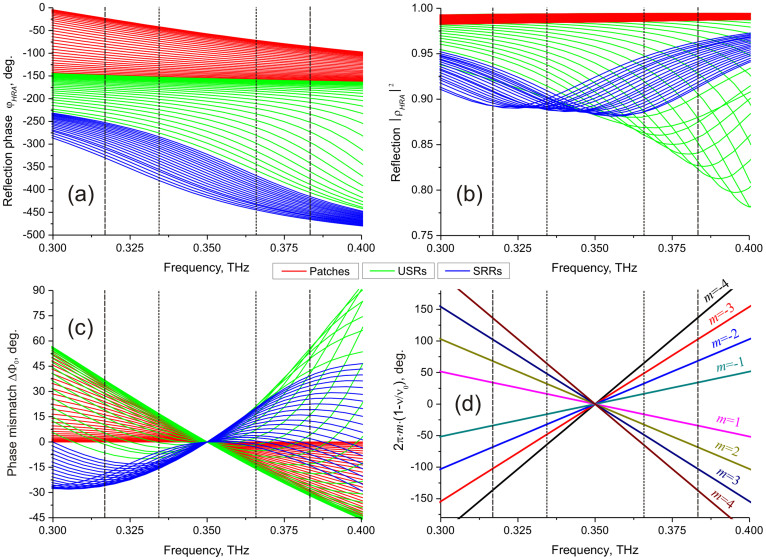
as the differences between the TE reflection phases of the 1st number topology (the patch of the smallest size) and the variable topological number X (X∈[1, 78]) determined at the specified frequencies: ΔφBA≡Δφ1vsX(ν) = φTopol1(ν)-φTopolX(ν), 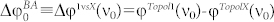 . Figures 8(a), (b) illustrate the frequency dispersion of the complex TE-reflectance for the full morphology set comprising 78 topological variants of the uniform-metasurface-based reflectarrays from Fig. 3 computed in the range of 0.3-0.4 THz. Introducing the phase mismatch function Δφm
. Figures 8(a), (b) illustrate the frequency dispersion of the complex TE-reflectance for the full morphology set comprising 78 topological variants of the uniform-metasurface-based reflectarrays from Fig. 3 computed in the range of 0.3-0.4 THz. Introducing the phase mismatch function Δφm
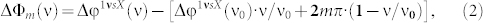 |
to describe a deviation of the actual phase shift Δφ1vsX(ν) between the two metasurface points having the local topological numbers 1 and X from the ideal phase shift specified by (1), we can further track out the spectral behavior of ΔΦm using the dispersion curves from Fig. 8(a). Fig. 8(c) demonstrates the numerical results for the case of m = 0, while Fig 8(d) represents the extra term 2mπ·(1-ν/ν0) for m ≠ 0. One can see a relatively rapid variation of the functions ΔΦ0 versus frequency which, in addition, behave differently for different topologies. The spread of ΔΦ0 magnitudes is summarized in Table 2 and provides information on the minimal, maximal, and mean values (uniformly averaged over all 78 topologies) referred to the boundary frequencies of the broadest and narrowest bands determined in this work: 19% (1-spot DE-BW) and 9% (4-spots NFPM-BW) bandwidths respectively. We deduce from Table 2 that a ΔΦ0 magnitude up to ~ 30–50° is allowable to realize DE with 19% bandwidth, while only ~ 15–20° are permissible for 9% of NFPM-BW. Note that such values of the phase mismatch are achieved when several zones with different m jointly work in our metasurfaces. For each zone with m ≠ 0, the phase mismatch is increased by an extra factor ∓180°·m·BW. The values of this extra factor for different m are summarized in Table 3. By decreasing the number of actually operating zones through reducing the D/F ratio, the bandwidth can be expanded.
Figure 8. Spectral properties of the uniform-metasurface-based reflectarrays.
(a) The reflection phase; (b) the reflection coefficient; (c) phase mismatch function ΔΦm for m = 0, and (d) extra factor 2mπ · (1-v/v0) for different m. TE polarization, 45° oblique incidence. The vertical lines delimit 19% (dash) and 9% (short dash) bandwidths.
Table 2. Calculated boundary and mean values for the phase mismatch function ΔΦ0.
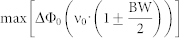 |
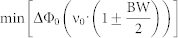 |
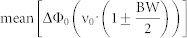 |
|
|---|---|---|---|
| BW = 0.19 | +55.4° | −31.8° | −3.8° |
| +36.9° | −26.0° | +11.1° | |
| BW = 0.09 | +21.2° | −15.8° | −2.2° |
| +17.0° | −15.9° | +3.8° |
Table 3. Calculated extra factor 2mπ·(1-ν/ν0) for different m.
| m = ±1 | m = ±2 | m = ±3 | m = ±4 | |
|---|---|---|---|---|
| BW = 0.19 | ∓34.2° | ∓68.4° | ∓102.6° | ∓136.8° |
| BW = 0.09 | ∓16.2° | ∓32.4° | ∓48.6° | ∓64.8° |
To conclude, in this work a new type of planar holographic metasurfaces (or reflectarrays) designed for simple and sophisticated focusing of THz radiation using “Patch-to-SRR” topological morphing of the metasurface pattern is proposed and experimentally investigated at the frequency of 0.35 THz. A TE-polarization scheme is chosen judiciously to reduce the cross-polarization losses that are susceptible to arise in anisotropic unit cells such as the USRs and SRRs. The experimental measurement confirms the theoretical predictions with a good degree of concordance and shows that the holographic metasurfaces enable to realize the operation bandwidth up to 20% in the non-paraxial configuration with F/D ≅ 1. The considered approach demonstrates the high-performance solution with the experimentally measured diffraction efficiency around 80% for creating purely flat, thin, light-weight and relatively inexpensive passive beam-shaping and beam-focusing devices for the THz band.
Methods
Gerchberg-Saxton iterative algorithm
For reflecting DOEs, here generically referred to as holographic reflectarrays (HRAs), GSA19,20,21 starts with computing the electric field amplitude distribution E0(x,y) for the wavefront in the HRA plane (X, Y) using the beam intensity distribution I0(x0,y0) given in the beam-waist plane (X0, Y0) (see Fig. 1, 2). The field amplitude E0(x,y) is related to the wave intensity I0(x,y) and phase ϕ0(x,y) as E0(x,y) = (8π I0(x,y)/c)1/2 · exp(jϕ0(x,y)), where c is the speed of light. For a Gaussian beam, the transition from I0(x0,y0) to I0(x,y) and ϕ0(x,y) is readily realized with the help of classical Gaussian optics formulas6. Knowing E0(x,y), the field reflected from the HRA at every surface point (x,y) is computed afterwards via multiplying E0(x,y) by the HRA's complex reflectance 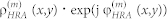 , where ρHRA(x,y) and φHRA(x,y) correspond to the reflection amplitude and phase respectively, while the superscript (m) indicates the iteration number. It is assumed that ρHRA(x,y) is a known function of φHRA(x,y), thus only the unknown distribution
, where ρHRA(x,y) and φHRA(x,y) correspond to the reflection amplitude and phase respectively, while the superscript (m) indicates the iteration number. It is assumed that ρHRA(x,y) is a known function of φHRA(x,y), thus only the unknown distribution 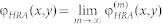 is to be determined via a GSA iterative procedure. For the first iteration (m = 1), the distribution
is to be determined via a GSA iterative procedure. For the first iteration (m = 1), the distribution 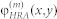 is chosen to be arbitrary (e.g. random).
is chosen to be arbitrary (e.g. random).
As soon as the distribution of the wave field reflected from the HRA is established for the iteration m, it is further used to figure out the wave field in the focal plane (X′, Y′) by applying a “forward propagator” operator, which is basically represented by the Fresnel-Kirchhoff integral31. The computed focal plane intensity distribution 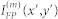 is compared afterwards with the desired intensity distribution IFP(x′,y′). If the maximal relative error
is compared afterwards with the desired intensity distribution IFP(x′,y′). If the maximal relative error 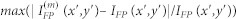 over the focal area exceeds the prescribed convergence limit or the maximally acceptable number of iterations is not achieved, the iterative process continues to the stage (m + 1). From this point, the computed focal plane field
over the focal area exceeds the prescribed convergence limit or the maximally acceptable number of iterations is not achieved, the iterative process continues to the stage (m + 1). From this point, the computed focal plane field 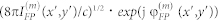 is modified by substituting
is modified by substituting 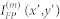 for IFP (x′,y′) and is further sent back to HRA. By applying the Fresnel-Kirchhoff integral to such backward propagation of the wavefront from the focal plane to HRA, one can calculate the modified field distribution in the HRA plane (X, Y) and therefore the modified HRA reflection phase
for IFP (x′,y′) and is further sent back to HRA. By applying the Fresnel-Kirchhoff integral to such backward propagation of the wavefront from the focal plane to HRA, one can calculate the modified field distribution in the HRA plane (X, Y) and therefore the modified HRA reflection phase 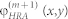 . The latter one is derived from the resulting surface phase distribution after subtracting the ϕ0 (x,y) factor originated from the incident Gaussian beam. The iterative loop closes when the distribution
. The latter one is derived from the resulting surface phase distribution after subtracting the ϕ0 (x,y) factor originated from the incident Gaussian beam. The iterative loop closes when the distribution 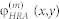 is replaced by
is replaced by 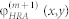 and the iterative procedure continues. The iterative process repeats until the computed focal plane intensity distribution maximally conforms to the desired distribution IFP (x′,y′). In this case, the incident beam intensity distribution retrieved on the “backward” branch of the iterative loop should fit the original distribution I0 (x0,y0), and the resulting phase function φHRA (x,y), i.e. the required “computer-generated hologram”, is obtained.
and the iterative procedure continues. The iterative process repeats until the computed focal plane intensity distribution maximally conforms to the desired distribution IFP (x′,y′). In this case, the incident beam intensity distribution retrieved on the “backward” branch of the iterative loop should fit the original distribution I0 (x0,y0), and the resulting phase function φHRA (x,y), i.e. the required “computer-generated hologram”, is obtained.
Full-wave simulation
As the direct full-wave modeling of oversized HRA composed of non-uniform unit cells requires enormous amount of computational resources, a good approximation is to assume local periodicity. That is, to reduce the problem to modeling uniform RAs differed in metasurface patterns and then to synthesize the output HRA using the correspondence between the RA's reflection phase and its metasurface unit cell geometry. In this work, 78 variants of regular RAs with different metasurface patterns, covering the full transformation cycle from Fig. 3(a), were numerically optimized in ASYS HFSS™ electromagnetic software to achieve the optimal performance for the output HRA excited by the electromagnetic wave polarized transversely to USR and SRR gaps. All RAs were modeled as infinite regular 2D arrays with identical x and y lattice constants g by exploiting the regime of Floquet ports and periodic boundary conditions applied to the RA unit cell. Due to fabrication limitations, the restriction of 56 μm for the minimal width of the metallized strips, as well as the inter-element spaces in metasurface patterns was imposed in the geometry optimization. As a result, for the PP slab 190 μm thick, the minimized unit cell dimensions g × g providing 360 deg of the reflection phase variation ΔφRA at the operation frequency of 0.35 THz and TE-polarized excitation were found to be 286 × 286 μm. Thus, the subwalengthness factor, defined as the ratio of the free space wavelength λ0 to the unit cell periodicity g, is evaluated as λ0/g ≅ 3.
Experimental setup
The experimental scheme for terahertz focusing by the HRA investigated in this work is shown in Figs. 1 and 5. The metasurface is lithographically patterned on a grounded dielectric slab and is illuminated by a Gaussian beam from a backward-wave oscillator (BWO) under an incidence angle of 45 deg. After reflection from the metasurface and a proper amplitude-phase transformation, the wavefront is focused afterwards on the focal plane, which was chosen to be positioned at the distance of F = 60 mm from the metasurface center, while its normal is oriented at 90 deg relative to the propagation direction of the incident beam (“90 deg-reflection scheme”). In our experiments, the metasurface is square with overall dimensions of D × D = 70 × 70 mm2, which are almost fourfold larger than the incident beam diameter w evaluated as 18 mm at half maximum of the beam intensity.
The measurements (see Fig. 6) were done with a pyroelectric detector mounted on the tip of a metallic rod with the outer diameter of 15 mm installed on a computer-controlled 2D raster scanner. The step of 2D raster scanning along both axes was 0.43 μm (i.e., 0.5λ0). The pyro-detector developed by CDP System Corp32 was implemented to have the receiving window diameter of 1.5 mm.
Author Contributions
S.K. conceived the idea and supervised the study. M.A.A. implemented the Gerchberg-Saxton iterative algorithm. S.K., M.A.A. and M.N.-C. contributed to the numerical results. S.K. fabricated the samples. S.K. and M.A.A. performed the experiment and data analysis. S.K., M.A.A., M.B. and M.N.-C. contributed to the discussion. S.K., M.A.A., M.B. and M.N.-C. wrote the paper.
Acknowledgments
In memoriam Prof. Mario Sorolla. This work was supported by the Ministry of Education and Science of the Russian Federation under the State Assignment Contract #3002 (implementation of the Gerchberg-Saxton iterative algorithm and experimental testing), the Russian Science Foundation under the Project 14-12-01037 (full-wave electromagnetic simulations), and the Spanish Government under contracts Consolider “Engineering Metamaterials” CSD2008-00066, and TEC2011-28664-C01. M. Beruete acknowledges funding by the Spanish Government under the research contract program Ramón y Cajal RYC-2011-08221. M. N.-C. was supported by Imperial College London through a Junior Research Fellowship.
References
- Yun-Shik L. Principles of Terahertz Science and Technology (Springer, New York, 2009). [Google Scholar]
- Holloway C. L. et al. An Overview of the Theory and Applications of Metasurfaces: The Two-Dimensional Equivalents of Metamaterials. IEEE Antennas Propag. Mag. 54, 10–35 (2012). [Google Scholar]
- Munk B. A. Frequency Selective Surfaces: Theory and Design (John Wiley & Sons, New York, 2000). [Google Scholar]
- Balanis C. A. Modern Antenna Handbook, Hoboken (John Wiley & Sons, NJ, 2008). [Google Scholar]
- Pfeiffer C. & Grbic A. Metamaterial Huygens' Surfaces: Tailoring Wave Fronts with Reflectionless Sheets. Appl. Phys. Lett. 110, 197401-1-5 (2013). [DOI] [PubMed] [Google Scholar]
- Goldsmith P. F. Quasioptical Systems: Gaussian Beam Quasioptical Propagation and Applications (IEEE Press, Piscataway, NJ, 1998). [Google Scholar]
- Aznabet M. et al. Polypropylene-substrate-based SRR-and CSRR-metasurfaces for submillimeter waves. Opt. Express 16, 18312–18319 (2008). [DOI] [PubMed] [Google Scholar]
- Hu D. et al. Ultrathin Terahertz Planar Elements. Adv. Opt. Mat. 1, 186–191 (2013). [Google Scholar]
- Aieta F. et al. Aberration-Free Ultrathin Flat Lenses and Axicons at Telecom Wavelengths Based on Plasmonic Metasurfaces. Nano Lett. 12, 4932–4936 (2012). [DOI] [PubMed] [Google Scholar]
- Ni X., Kildishev A. V. & Shalaev V. M. Metasurface holograms for visible light. Nature Comm. 4, 2807 (2013). [Google Scholar]
- Huang L. et al. Three-dimensional optical holography using a plasmonic metasurface. Nature Comm. 4, 2808 (2013). [Google Scholar]
- Salem M. A. & Caloz C. Manipulating light at distance by a metasurface using momentum transformation. Opt. Express 22, 14530–14543 (2014). [DOI] [PubMed] [Google Scholar]
- Zhao J., Li B., Chen Z. & Qiu C.-W. Manipulating Acoustic Wavefront by Inhomogeneous Impedance and Steerable Extraordinary Reflection. Sci. Rep. 3, 2537 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J. & Encinar J. A. Reflectarray Antennas (John Wiley & Sons, Hoboken, NJ, 2008). [Google Scholar]
- Shaker J., Reza Chaharmir M. & Ethier J. Reflectarray Antennas: Analysis, Design, Fabrication, and Measurement (Artech House, Boston., 2013). [Google Scholar]
- Vinokurov N. A. et al. Diffractive optical elements and quasioptical schemes for experiments on a high-power terahertz free-electron laser. Radiophys. Quant. Electron. 50, 803–812 (2007). [Google Scholar]
- Vedernikov V. M. et al. Diffractive Elements for a Free Electron Laser. Optoelectron. Instrum. Data Proc. 46, 365–375 (2010). [Google Scholar]
- Agafonov A. N. et al. Silicon diffractive optical elements for high-power monochromatic terahertz radiation. Optoelectron. Instrum. Data Proc. 49, 189–195 (2013). [Google Scholar]
- Gerchberg R. W. & Saxton W. O. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik 35, 237–242 (1972). [Google Scholar]
- Soifer V., Kotlyar V. & Doskolovich L. Iterative methods for diffractive optical elements computation (Taylor & Francis, London, 1997). [Google Scholar]
- Soifer V. A. Methods for Computer Design of Diffractive Optical Elements (John Wiley & Sons, New York, 2002). [Google Scholar]
- Pozar D. M. Wideband reflectarrays using artificial impedance surfaces. Electron. Lett. 43, 148–149 (2007). [Google Scholar]
- Luo L. et al. Broadband terahertz generation from metamaterials. Nature Comm. 5, 1–6 (2014). [DOI] [PubMed] [Google Scholar]
- Marqués R., Martín F. & Sorolla M. Metamaterials with Negative Parameters: Theory, Design, and Microwave Applications (Wiley, Hoboken, NJ, 2008). [Google Scholar]
- Padilla W. J., Taylor A. J., Highstrete C., Lee M. & Averitt R. D. Dynamical Electric and Magnetic Metamaterial Response at Terahertz Frequencies. Phys. Rev. Lett. 96, 107401-1-4 (2006). [DOI] [PubMed] [Google Scholar]
- Wan X., Jiang W. X., Ma H. F. & Jun Cui T. A broadband transformation-optics metasurface lens. Appl. Phys. Lett. 104, 151601-1-4 (2014). [Google Scholar]
- Yang Y., Mandehgar M. & Grischkowsky D. Broadband THz Pulse Transmission Through the Atmosphere. IEEE T. THz Sci, Tech. 1, 264–273 (2011). [Google Scholar]
- Kuznetsov S. A. et al. Regular and Anomalous Extraordinary Optical Transmission at the THz-gap. Opt. Express 17, 11730–11738 (2009). [DOI] [PubMed] [Google Scholar]
- Navarro-Cía M. et al. Route for bulk millimeter wave and terahertz metamaterial design. IEEE J. Quant. Electron. 47, 375–385 (2011). [Google Scholar]
- Beruete M., Sorolla M., Marqués R., Baena J. D. & Freire M. J. Resonance and cross-polarization effects in conventional and complementary split ring resonator periodic screens. Electromagnetics 26, 247–260 (2006). [Google Scholar]
- Born M. & Wolf E. Principles of Optics (Cambridge University Press, Cambridge, UK, 1999). [Google Scholar]
- CDP System Corporation, http://www.teraspectr.ru/ Date of access: 24/11/2014.
- Kozlov G. V. & Volkov V. V. [Coherent Source Submillimeter Wave Spectroscopy]. Millimeter and Submillimeter Wave Spectroscopy of Solids [Grüner, G. (ed.)] [51–109] (Springer-Verlag, Berlin, Heidelberg, 1998). [Google Scholar]