Helical buckling of actin inside filopodia generates traction

Significance

Filopodia are essential membrane protrusions that facilitate cellular sensing and interaction with the environment. The mechanical properties of filopodia are crucial for their ability to push and pull on external objects and are attributed to actin dynamics. We confirm the presence of F-actin inside extended filopodia and reveal a new mechanism by which actin can exert traction forces on external objects. This mechanism is mediated by rotation and helical buckling, which cause shortening and retraction of the actin shaft. By imaging of F-actin and simultaneous force spectroscopy, we reveal and detail how force propagates through this spiral actin structure and show how torsional twist of the actin shaft is translated into a traction force at the filopodial tip.

Abstract

Cells can interact with their surroundings via filopodia, which are membrane protrusions that extend beyond the cell body. Filopodia are essential during dynamic cellular processes like motility, invasion, and cell–cell communication. Filopodia contain cross-linked actin filaments, attached to the surrounding cell membrane via protein linkers such as integrins. These actin filaments are thought to play a pivotal role in force transduction, bending, and rotation. We investigated whether, and how, actin within filopodia is responsible for filopodia dynamics by conducting simultaneous force spectroscopy and confocal imaging of F-actin in membrane protrusions. The actin shaft was observed to periodically undergo helical coiling and rotational motion, which occurred simultaneously with retrograde movement of actin inside the filopodium. The cells were found to retract beads attached to the filopodial tip, and retraction was found to correlate with rotation and coiling of the actin shaft. These results suggest a previously unidentified mechanism by which a cell can use rotation of the filopodial actin shaft to induce coiling and hence axial shortening of the filopodial actin bundle.

Tubular membrane remodeling driven by the actin cytoskeleton plays a major role in both pathogenesis and in a healthy immune response. For instance, invadopodia, podosomes, and filopodia are crucial for invasion and migration of cells (1). Filopodia are thin (100 to 300 nm), tube-like, actin-rich structures that function as “antennae” or “tentacles” that cells use to probe and interact with their microenvironment (2–4). Such structures have been studied in vitro using model systems where the point-like 3D contacts with the extracellular matrix (ECM) have been mimicked by using optically trapped dielectric particles, functionalized with relevant ligands. These model systems allow for mechanical and visual control over filopodial dynamics and have significantly advanced the understanding of cellular mechanosensing (5).

Extraction of membrane tubes, using optical trapping, has been used to investigate mechanical properties of the membrane–cytoskeleton system (6–10), or membrane cholesterol content (11), and has revealed important insight into the mechanism that peripheral proteins use to shape membranes (12). Motivated by the pivotal role of F-actin in the mechanical behavior of filopodia and other cellular protrusions, special focus has been on revealing the presence of F-actin within extracted membrane tubes (1, 13–16). However, apart from a single study (9), fluorescent visualization of the F-actin was achieved by staining and fixation of the cells, and literature contains conflicting results regarding the presence or absence of actin in membrane tubes pulled from living cells (8, 11, 17).

Filopodia in living cells have the ability to rotate and bend by a so-far unknown mechanism (13, 18–20). For instance, filopodia have been reported to exhibit sharp kinks in neuronal cells (21–23) and macrophages (6). These filopodial kinks have been observed both for surface-attached filopodia (23) as well as for filopodia that were free to rotate in three dimensions (6, 19).

Other filaments such as DNA and bacterial flagella are common examples of structures that shorten and bend in response to torsional twist. Filopodia have previously been shown to have the ability to rotate by a mechanism that exists at their base (18, 19) and could have the ability to twist in presence of a frictional force. Rotation of the actin shaft results in friction with the surrounding filopodial membrane, and hence torsional energy can be transferred to the actin shaft. The myosin-Vb motor has been found to localize at the base of filopodia in neurite cells and to be critical for rotational movement of the filopodia; however, inhibition of myosin-Vc did not affect the rotation (19).

Here, we reveal how actin filaments can simultaneously rotate and helically bend within cellular membrane tubes obtained by elongation of preexisting filopodia by an optically trapped bead. Simultaneous force measurements and confocal visualization reveal how the actin transduces a force as it rotates and retracts. After ∼100 s, the force exerted by the filopodium starts to exhibit pulling events reflecting transient contact between the actin and the tip region of the filopodium, which is attached to the optically trapped bead. We show that helical bending and rotation of the actin shaft (defined as the visible part of the actin) occurs simultaneously with movement of actin coils inside filopodia, which can occur concomitantly with a traction force exerted at the tip. The velocity of the coils depends on their location along the tube, thus indicating that retrograde flow is not the only mechanism driving the motion. Our data, and accompanying calculations, show that the rotation of the actin shaft, and the resulting torsional twist energy accumulated in the actin shaft, can contribute to shortening and bending of the actin shaft in conjunction with a retrograde flow.

Results

Force and Actin Dynamics Are Correlated in Filopodia.

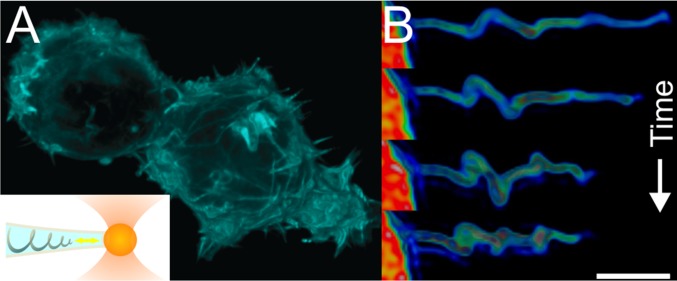
To investigate the dynamic behavior of the F-actin present in filopodia, we extended filopodia from living HEK293 cells that were transfected to express GFP-Utrophin, a reporter of F-actin (24) as schematically shown in the Inset of Fig. 1A. The cells were seeded 2–6 h before measurements and the phenotype of the cells was usually rounded as shown in a 3D reconstruction of the actin distribution from a confocal z stack of two cells in Fig. 1A. Freshly seeded round cells allowed us to pull filopodia at a greater height away from the coverslip due to their rounded shape. We elongated existing filopodia primarily to avoid interactions with other nearby filopodia that tend to grab onto the bead. With the high density of active filopodia (Fig. 1A), the chance of having neighboring filopodia interact with the trapped bead (d = 4.95 μm) was very high. Therefore, by extending the filopodial membrane to ∼10 μm, we could perform force spectroscopy over timescales of 5–20 min. The high density of filopodia together with the large size of the bead makes it unlikely that tubes were pulled from a flat membrane. In the following, “actin-labeled cells” refers to living cells that were expressing GFP-Utrophin (24). The actin shaft is assumed to consist of ∼10 actin filaments labeled by GFP-Utrophin, which has high affinity for F-actin. The number of filaments is not constant along the filopodium as the fluorescence intensity was measured to have a negative gradient along the filopodium toward the tip (SI Appendix, Fig. S1A). Cells labeled with another marker for F-actin, Lifeact-GFP (25), exhibited similar actin dynamics. We observed that actin gradually polymerized into the extended filopodium, as shown in SI Appendix, Figs. S2 and S3, with the highest concentration of actin being near the cell body. This gradient in intensity was observed for all tethers (n = 90). As a control, we show how a cytoplasmic dye diffuses into the tether during a few seconds that it took to complete the pulling, as shown in SI Appendix, Fig. S4.

Fig. 1.

Actin dynamics inside filopodia studied by simultaneous force spectroscopy and confocal microscopy. (A) HEK293 cells display a high density of short filopodia on their surface as visualized by fluorescently labeled F-actin (GFP-Utrophin). Inset shows schematics of the F-actin inside a filopodium held in place by an optically trapped bead (diameter = 4.95 μm) showing helical bending of the actin shaft. The yellow double arrow indicates the observed dynamic movement of the actin near the tip of the filopodium. (B) Deconvoluted 3D reconstruction of the fluorescently labeled F-actin (GFP-Utrophin) inside an extended filopodium. The images are taken at times t = 50.4, 84.0, 100.8, and 151.2 s after extension with an optically trapped bead. (Scale bar: 3 μm.)

The optical trap was integrated with a confocal microscope, thus enabling us to measure force curves and to simultaneously image the F-actin dynamics inside filopodia (see details on the setup in ref. 26). A filopodium was extended for 5–20 min while we simultaneously recorded the holding force and imaged the F-actin content. As shown in SI Appendix, Fig. S5A, and in agreement with literature (8, 11, 27), the force curves show the following characteristics of membrane tube extraction from cells, namely (i) an initial linear increase in the force, with slopes as given in SI Appendix, Fig. S5B, due to elastic deformation of the cytoskeleton; (ii) a sudden decrease in the force caused by the delamination of the membrane from the cellular cytoskeleton; and (iii) a subsequent plateau force, which remained constant for short extractions due to an excess of membrane area reservoir in the cell (28, 29). However, after an extended period, the force curves displayed the dynamics shown in SI Appendix, Figs. S5C and S6, with transient force jumps of ∼10 pN, which would be sufficient to deform ECM fibers (30). The force and actin dynamics were significantly suppressed after treating the cells with F-actin disrupting agents as shown in SI Appendix, Fig. S7.

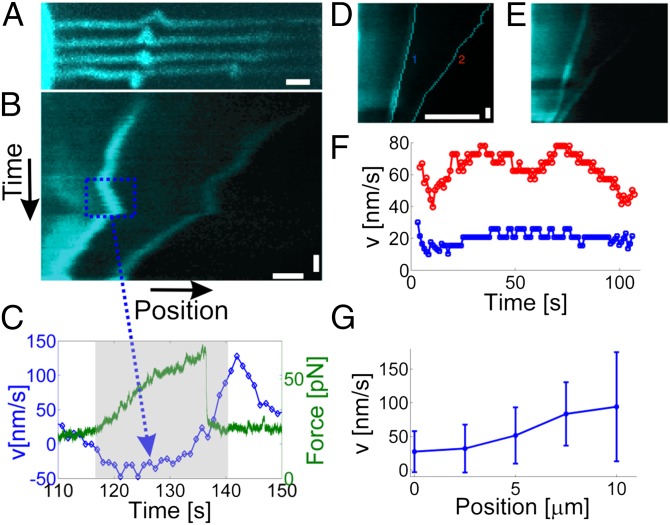
After a filopodium had been extracted and kept at a constant extension for minutes, retrograde flow of actin occurred together with 3D helical buckling and rotation of the actin shaft as shown schematically in the Inset of Fig. 1A and in Fig. 1B. Rotation was detected for 55 actin-containing filopodia out of 90, but the remaining 35 filopodia either appeared straight or had a fluorescent signal that was too low to determine possible rotation. Several localized coils could be observed on the same filopodium, which traveled toward the cell body as shown in Fig. 2 A and E. The actin shaft was initially observed to bend locally, followed by translation and rotation around its axis as shown in Fig. 2A (Movies S1 and S2). To quantify the shortening of the actin shaft, we calculated the velocity of the coils relative to the trapped bead by subtracting the displacement of the bead during force transduction from the sample reference frame. The velocity of the coils in Fig. 2A varies significantly over time as shown in the kymograph in Fig. 2B, and the direction of travel is occasionally observed to reverse and transiently move toward the trapped bead (blue boxed region in Fig. 2B). A change in the velocity of the coil was detected concomitantly with a displacement of the trapped bead as shown in Fig. 2C (n = 18) and hence could be directly related to a change in the force. This kind of correlation indicates that a tensile force can be transduced along the actin shaft in presence of a buckle. We show several of these velocity changes in the kymographs in SI Appendix, Fig. S8. A negative velocity (shaded area in Fig. 2C) leads to a smaller distance between the tip and the location of the coil. During this negative velocity regime the force on the trapped bead increased and reached a peak value, thus suggesting a force-generating mechanism originating from shortening of the actin shaft. Subsequently, we measured a sudden drop in the holding force (green curve in Fig. 2C), indicating a sudden release of tension within the actin shaft. Concomitantly with the drop in force, the velocity of the coils rapidly changed sign and the coils moved again toward the cell body (blue curve in Fig. 2C).

Fig. 2.

Quantification of the velocity of actin coils traveling toward the cell body. (A) Progressive bending and traveling of two coils. The four images show the same actin filament at four consecutive time points (t₁ = 75.9 s, t₂ = 91.5 s, t₃ = 93.6 s, and t₄ = 116.5 s). Notably, the leftmost coil initially points upward and gradually rotates ∼180°. (Scale bar: 1 μm.) See also Movie S2. (B) Kymograph of the coils in A showing the positions of the coils versus time. Importantly, the position of the coil is consistently quantified in the reference frame of the trapped bead. The blue dashed rectangle shows the occurrence of a reversal in the velocity of the coil relative to the trapped bead. (Scale bars: 1 μm and 10 s.) (C) Quantification of the coil velocity (blue) and the corresponding pulling force on the trapped bead (green). The gray shaded area denotes the approximate time interval during which the velocity becomes negative in B. (D and E) Examples of two coils located at different distances relative to the cell body and traveling at different velocities. The positions of the coils are shown in D; these were found as the maximum of the intensity gradient of the raw data shown in E. (Scale bars: 5 μm and 10 s.) (F) The velocities of the two coils in D; the blue curve is from the left coil, and the red is from the right coil. (G) Distribution of velocities from n = 40 coils as a function of distance from the cell body. Error bars denote ±1SD.

Coil Velocity Depends on Filopodial Location.

The kymographs for two helical coils at two different locations in the same filopodium are shown in Fig. 2 D and E. The velocities of the individual coils (Fig. 2F) differ markedly, although they are connected by an F-actin structure, thus indicating a mechanism that shortens the actin within the tube. The velocity distribution of 40 different coils confirms that a coil’s velocity depends on its location along the filopodium as shown in Fig. 2G. Actin is subjected to myosin-pulling activity at the cellular base, which causes retrograde flow (23). Our data indicate that this is not the only mechanism responsible for the motion of the coils: actin polymerization at the filopodial tip and depolymerization at the cell body would cause a linear translation of the helical coils traveling toward the cell body contrary to our observation of varying coil velocities.

Torsional Twist in the Actin Shaft Is Responsible for Helical Buckling.

The energy of the filopodial curved actin shaft confined within a membrane tube is described in SI Appendix, SI Text. Helical buckling in filopodia was predicted theoretically in refs. 31 and 32, but the presence of a trapping force, which is applied in our experiments, prevents buckling caused by axial compression of the membrane tension as explained in SI Appendix, SI Text and Fig. S9.

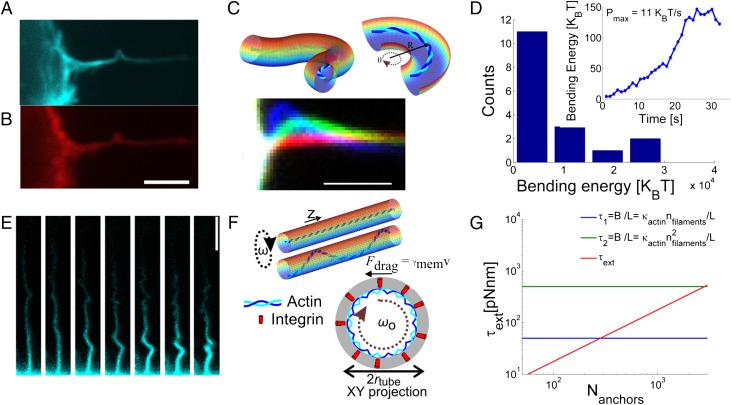
By integrating the curvature (first term in SI Appendix, Eq. S4) along the actin contour projected onto the image plane, we obtained the maximum bending energies of n = 17 actin shafts as summarized in a histogram in Fig. 3D. While calculating the bending energies in Fig. 3D, it was assumed that each filopodium contains 10 not cross-linked actin filaments, as in ref. 18, giving a total persistence length of l_p = Nl_actin = 150 μm. The bending energies span approximately an order of magnitude, which, most likely, reflects the fact that filopodia contain different numbers of actin filaments with varying degree of cross-linking by, e.g., fascin (9). By quantifying the actin intensity in the filopodia just before buckling, we show that the thickness of the actin bundle influences the curvature of the actin shaft. From the actin intensity, it is clear that the actin bundles are on average thicker near the cell body (see SI Appendix, Fig. S2A, and average intensities for 17 actin shafts in SI Appendix, Fig. S1A), and consequently these buckles have a larger extent and lower curvature than buckles further away from the cell body, as shown for 34 buckles in SI Appendix, Fig. S1B. The rate of work needed to bend the actin shaft shown in Fig. 3C, is plotted in the Inset of Fig. 3D, which shows the bending energy versus time. The maximum slope of P = 11 K_BT/s gives a number for the largest power dissipation for the bending shown in Fig. 3C.

Fig. 3.

Helical bending dynamics of actin filaments inside filopodia. (A and B) Bending of the F-actin (A) also induces a local bending of the membrane (labeled with DiD) as shown in B. (Scale bar: 3 μm.) (C) Plot of a tube, containing F-actin, which is bent into an arc of radius R. The overlay images below show progressive buckling of an actin bundle near the cell body. The colors represent three different relative time points at t_red = 0 s, t_green = 13 s, and t_blue = 30 s. (Scale bar: 2 μm.) (D) Histogram of the maximum bending energy calculated from n = 17 filopodia displaying different degrees of bending. The energy is calculated assuming a bundle of 10 parallel actin filaments. The Inset shows the progressive increase in curvature energy versus time for the single buckle shown in C. The highest power consumed to bend the actin bundle reaches 11 K_BT/s. (E) Example of a coiled actin structure inside a filopodium captured at different time points separated by 2 s. (Scale bar: 3 μm.) See also Movie S3. (F) Axial rotation of the actin within the membrane tube leads to friction between the membrane and the actin. Two initial scenarios depicting an actin filament within a membrane tube. In a filopodium, the actin will align along the inner membrane either as a straight rod (upper sketch) or a deformed shape, possibly a helix (lower sketch), within the tube. We model the actin–membrane linkages as connections between the actin and transmembrane integrins as shown by the XY projection of the membrane tube with an actin filament tracing a helix (with same radius as the tube) within the tube. The integrins (red cylinders) are dragged through the membrane by the rotating actin filament. (G) The total external torque on the actin shaft depends linearly on the number of anchors, N_anchors, connecting the actin with the membrane. Two critical buckling torques, τ_crit, are plotted by the horizontal lines; these correspond to an actin shaft consisting of 10 actin filaments that are cross-linked (green line) or not cross-linked (blue line).

During buckling of the actin shaft, the filopodial membrane tube will bend as well. Bending the membrane tube will counteract bending of the actin shaft. The energy needed to bend a cylindrical tube of radius $\hspace{0.17em}{r}_{\text{tube}}$ into an arc of radius R (Fig. 3 B and C) is given by (33):

$$F_{\text{tube}}\hspace{0.17em}=\frac{{\kappa }_{\text{mem}}}{2R^2}\pi r_{\text{tube}}L,$$ [1]

where the bending rigidity of the membrane has been measured to be ${\kappa }_{\text{mem}}$ = 6.6 × 10⁻²⁰ J for blebs pulled from fibroblasts (17). 1/R is the curvature of the tube in the θ direction as depicted in Fig. 3C. For a curved tube segment (similar to the one in Fig. 3A) with $r_{\text{tube}}=145$ nm, R = 1 μm, and a typical length of L_tube = 1 μm, we get F_tube = 3.8 K_BT. Although this number may vary somewhat depending on the above parameters, this calculation shows that the energy required to bend the membrane is much less than the energy needed to bend an actin bundle. Therefore, the energy needed to bend the filopodial membrane tube does not necessarily prevent buckling of the actin shaft but rather slightly increases the energy threshold for buckling.

In case of compressive buckling, we should detect a repulsive force, pointing away from the cell body, on the trapped particle. However, we always measured an attractive force during buckling or no force at all. The bending of the actin shaft occurred simultaneously with a tensile force on the filopodium and could even be correlated with an increase of the holding force (Fig. 2 B and C). A physical mechanism that could contribute to buckling and pulling, at the same time, is torsional energy accumulated within the actin shaft. This suggests that torsional twist is responsible for bending and shortening the actin shaft much like the helical bending resulting from twisting a rubber band at one end while keeping the other end fixed.

Torsional twist accumulated within the actin shaft can occur, provided that sufficient friction between the actin and the surrounding membrane tube is generated. The physical problem has some analogy to the twirling–whirling transition of an elastic rod that is rotated at one end in a viscous fluid (34). The friction in the current case arises from filopodia-associated membrane proteins like integrins (10, 35) that are being moved laterally within the membrane as depicted in Fig. 3F.

Here, we model each transmembrane integrin as a rod-like cylinder with radius R_prot spanning the membrane as depicted in Fig. 3F. During rotation of the actin shaft, each cylinder is moved through the viscous membrane, having viscosity ${\eta }_{\text{mem}}$ at a fixed speed of ω_o leading to a viscous drag force, F_drag, that can be assumed to locally act tangential to the membrane surface. The resulting torque due to the drag from a single anchoring rod is τ₁ = r_tube × F_drag, and from N anchors, we get τ_N =$N_{\text{anchors}}$ τ₁. In this approximation, we only consider the drag orthogonal to the tube axis.

The drag from a single cylinder moving at a constant speed through the membrane is as follows (36, 37):

$$F_{\mathrm{drag}}\mathrm{=}\frac{4\pi {\eta }_{\mathrm{mem}}L}{\ln \left(\frac{L}{2R_{\mathrm{prot}}}\right)\mathrm{+}{\alpha }_{\mathrm{\perp }}},$$ [2]

where ${\eta }_{\text{mem}}$ is the membrane viscosity, L is the length of the transmembrane cylinder, $R_{\text{prot}}$ is the radius of the protein, and ${\alpha }_{\mathrm{\perp }}=0.90$ is a correction factor for integrins in a membrane (SI Appendix, SI Text). The total external torque around the axis of the shaft therefore becomes ${\tau }_{\text{ext}}=r_{\text{tube}}{N}_{\text{anchors}}{F}_{\text{drag}}$. Using published values for $r_{\text{tube}}=145\hspace{0.17em}\text{nm}$ [for HEK293 cells (11)], ω_o = 1.2 radians/s (18), and ${\eta }_{\text{mem}}=250$ cp (38), we get the result plotted in Fig. 3G (red line).

A buckling instability for an elastic filament will occur when the torque exceeds the ratio between the bending modulus and the length of the filament, B/L (34). The bending modulus of a bundle of $n_{\text{filaments}}=10$ can be expressed as $B=n_{\text{filaments}}{\kappa }_{\text{actin}}$ for un–cross-linked actin filaments (horizontal blue line in Fig. 3G) and $B=\hspace{0.17em}{n}_{\mathrm{filaments}}^2{\kappa }_{\text{actin}}$ for tightly cross-linked actin filaments (horizontal green line in Fig. 3G), where ${\kappa }_{\text{actin}}$ is the bending modulus for a single actin filament (18). Assuming no filament cross-linking, then buckling will occur when 283 actin–membrane links exist and for a tightly cross-linked actin bundle buckling requires ∼2,800 actin–membrane links. Although the exact density of actin–membrane linkages is unknown in filopodia, it has been shown that the membrane of red blood cells has a density of 1,000/μm² linkages with the underlying skeleton (39), and with a total area of a filopodium of ∼10 μm² such a density would easily allow >1,000 filopodial actin–membrane anchors to exist.

Transduction of Force Is Propagated Through Actin.

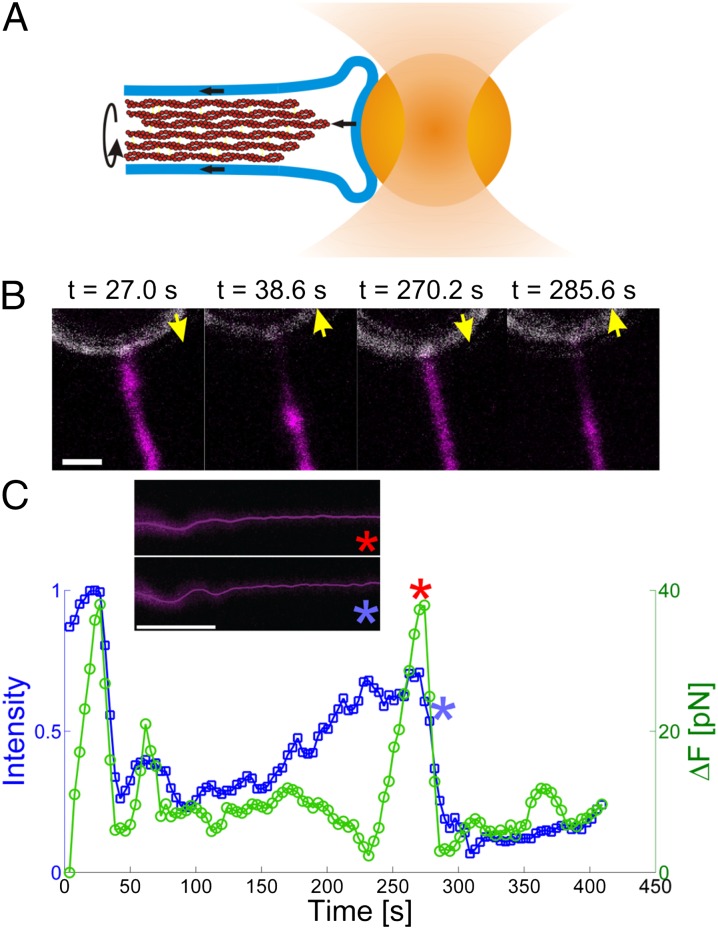
Bending of the actin filaments also occurred concomitantly with an increase in the measured holding force (Inset images in Fig. 4C). If the force exerted on the bead was propagated through the actin shaft from the cell body, it would mean that bending could be sustained in presence of longitudinal stress along the actin shaft, thus strongly supporting the idea that the bending and retraction stem from torsional twist in the actin. As shown in Fig. 4, the presence of a peak in the force exerted by the cell on the trapped bead correlates with the observation of Lifeact-GFP at the tip of the filopodium. When the actin appeared at the tip (Fig. 4 A and B, and squares in Fig. 4C), an increase in the force on the bead, directed toward the cell, was observed (as shown by the circles in Fig. 4C). Detachment of actin from the tip of the filopodium resulted in actin gliding toward the cell body, thus dissipating the tension built up in the actin filament. As this happened, the trapped bead moved back to its previous equilibrium position, as shown in Fig. 4C by the blue and red asterisks (see SI Appendix, Fig. S10, for two other examples). The strong correlation between the force and actin signal clearly suggests that the force exerted by the cell to retract the filopodial tip is transduced along the actin shaft. We note that, in many experiments, actin was not detectable at the tip and yet we measured transient forces that could be caused by poorly fluorescent-expressing cells and a limited detection efficiency of our system.

Fig. 4.

Force generation correlates with presence of actin at the tip of the filopodium. (A) Schematics of the attachment of the filopodium to the trapped bead. A small patch of membrane adheres to the bead substrate, thus allowing actin to bind to a fixed membrane at the tip. Binding of actin to the side walls of the tubular and fluid membrane results in a frictional dissipative force during rotation and directed flow of actin. (B) Images of the F-actin (magenta, labeled with Lifeact-GFP) at the tip of the filopodium overlaid with the reflection signal from the trapped bead (white). Correlation of successive detachment and reattachment of the actin to the bead with the forces exerted reveal a load-and-fail behavior of the actin filaments at the tip. Yellow arrows show the direction of movement of the optically trapped bead. See also Movie S4. (C) Quantification of the results shown in B. The blue curve shows the intensity of actin at the tip of the filopodium (see Movie S5 and SI Appendix, Fig. S11, for details). The green curve shows the change in the pulling force on the bead in the optical trap. The red and blue asterisks mark two time points; red, just before detachment of actin from the tip; blue, just after detachment of actin from the tip. The corresponding images (Inset) reveal that bending of the actin (shown by the solid line, which is the tracked skeleton of the actin shaft) is present both before and after release of tension.

Discussion

Our results strongly suggest that retrograde flow and a rotational mechanism are synergistically responsible for the observed bending and traction performed by filopodia. Retrograde flow occurs in filopodia (13, 40) and can be assisted by a pulling force arising from the frictional coupling mechanism within the cell body as described previously (9). Our experimental observations show that coils on the actin shaft move at different velocities depending on their proximity to the cell body. The data shown in Fig. 2 reveal a pulling mechanism within the actin shaft that is inconsistent with retrograde flow as being the only mechanism of force generation. If only retrograde flow was responsible for the movement, the actin shaft would be translated backward in a linear fashion and coils on the same actin shaft should have the same velocities irrespective on the location within the filopodium. Because myosin-II motors are typically not detected within narrow structures like filopodia (13), an internal acto-myosin contractile mechanism is unlikely to be a mechanism at play here. Moreover, the contractile motor myosin-II has previously been inhibited using blebbistatin without any significant effect on filopodial mechanics (6). However, the observation of bending, shortening, and rotation of the actin shaft indicates that rotation of the actin shaft accumulates torsional energy in the actin that can be released by helical bending. The combination of twist and axial load is more efficient in buckling the actin shaft than twist alone. However, in this work, we hold the membrane by an optical trap and therefore demonstrate that helical buckling can occur efficiently in absence of the axial load delivered by the membrane tension in free filopodia. To accumulate torsional energy within the actin shaft, an active rotation mechanism is required at one end and friction, or a fixed contact point with a substrate, is needed along the actin filaments. Actin-linked integrins and other filopodia-associated proteins containing an IBAR domain will create a density-dependent friction during rotation of the actin within the filopodium. Interestingly, it was shown recently that β3-integrins upconcentrated in filopodia of fibroblasts after ∼100 s (41), which corresponds well to the duration before we observe the onset of buckling. We confirmed that the filopodial actin contributes to the friction between the actin and the membrane by performing fast elongation of the filopodium (1 μm/s). In the presence of actin, the force increased by up to ∼40 pN (SI Appendix, Fig. S7A), which corresponds to a maximum viscosity of ∼20 pNs/μm. After disrupting actin (blue curve in SI Appendix, Fig. S7B), we measured a viscosity of ∼2 pNs/μm, which is closer to the values for tethers from pure membrane vesicles (26).

The rigidity of the actin shaft is highly dependent on the concentration and dynamic binding rates of fascin cross-linkers. Fascin is found in filopodia (40, 42) and cross-links actin filaments into stiff bundles. Interestingly, fascin has an off-rate of 1.2 s⁻¹ and can therefore allow slow deformation rates of bundled actin as shown in ref. 40. Another actin-binding protein, cofilin, can shorten actin filaments in filopodial bundles and has been associated with disassembly of retracting filopodia (43). Notably, cryoelectron tomography images of filopodia in Dictyostelium revealed that actin bundles do not consist of long parallel bundles but instead contain discontinuously bundled actin filaments (44). These biochemical cellular factors have the ability to change the mechanical requirements and significantly lower the buckling thresholds plotted in Fig. 3G.

The transient increase in force from retracting filopodia often displays a step-like behavior (SI Appendix, Fig. S12) resembling the pulling behavior of a molecular motor. Stepwise pulling forces have previously been reported for filopodia in macrophages after inhibition of myosin-II (6). According to ref. 19, the rotation of filopodia in neurites is driven by the spiral interactions between myosin-Va or -Vb and the actin filaments. Myosin-Va,b could therefore be involved in building up torsional energy in the actin shaft, eventually leading to coiling and shortening of the actin shaft. The power measured in the Inset of Fig. 3D of 11 K_BT/s can be provided by the hydrolysis of ∼0.5 ATP/s. This energy consumption corresponds to ∼50% of the work performed by one single myosin-V motor per step (45) but is most likely an underestimation due to dissipative loss in the friction between the actin and the membrane. Although the bending of the membrane tube requires additional energy, these calculations show that the collective action of a few myosin motors would be sufficient to generate the power needed to bend the actin shaft.

The surrounding membrane, which has a radius below the optical resolution, acts to stabilize the filament against buckling, as previously shown for microtubules within membrane vesicles, in a tension-dependent manner (46). The filopodia membranes in our experiments were indeed under tension as we showed by the rapid elongation and retraction of a calcein-filled filopodium in SI Appendix, Fig. S13. Rapid elongation of membrane tethers resulted in a transient increase in the membrane tension, which acted to reduce the radius of the filopodium as shown by the decrease in the calcein signal. Even when the trapped bead was moved toward the cell body with 1 μm/s, the membrane did not buckle. Instead, the membrane tube becomes slightly thicker due to a decrease in tension (SI Appendix, Fig. S13).

In ref. 4, it was shown that a force originating from retrograde flow in filopodia was transduced to a compliant substrate when dynamic linkers attached the actin to an external substrate. This so-called motor-clutch mechanism is consistent with our findings that the actin–bead contact, shown in Fig. 4, correlates with a traction force on the bead. The traction force on the bead has been proposed to originate from retrograde flow in filopodia (9, 40), but we suggest an additional force contribution originating from twist induced buckling that leads to shortening of the actin shaft. Interestingly, in ref. 23, a similar buckling and shortening of actin in filopodia was found in neuronal cells in conjunction with actin flow toward the cell body. However, no force was detected in ref. 23, and hence the mechanism behind the buckling could not be resolved.

Conclusion

Through simultaneous visualization of actin filaments in filopodia and measurements of the associated retraction force, we reveal a new mechanism for force generation by the actin shaft inside filopodia. This mechanism is based on the rotation and consequent helical coiling of the actin, which leads to shortening of the actin shaft by release of torsional energy. We consistently observed rotation, bending, and shortening of the actin within the filopodia. This behavior could not be explained by theoretical calculations of compressive buckling of the polymerizing actin against the filopodial tip. Helical coiling was even present when a tensional pulling force was transduced along the actin shaft, which suggests that torsional twist is involved in the actin-mediated force generation.

Methods

Cell Culture.

HEK293 cells (ATTC; CRL-1573), denoted as “HEK cells,” were cultured in DMEM [Gibco; supplemented with 9% (vol/vol) FBS, 1% PenStrep] in T25 or T75 tissue culture flasks (BD Falcon) at 37 °C in a 5% CO₂ incubator. They were passaged by washing with 4 mL of Dulbecco’s PBS (1×, [−] CaCl₂, [−] MgCl₂; Gibco), detaching with 0.5–0.7 mL of TrypLE Express (Gibco) and diluting with growth medium before they were seeded in new flasks. All cells used were in passages 2–22. Sample preparation and methods for labeling cellular actin and cytoplasm are described in detail in SI Appendix, SI Text. F-actin was disrupted using either 5 μM cytochalasin D or 1 μM latrunculin B (SI Appendix, SI Text).

Simultaneous Optical Tweezers and Confocal Laser-Scanning Measurements.

The setup is described in more detail in ref. 26. More details concerning the experimental setup and Matlab analysis (47) are provided in SI Appendix, SI Text.

Image Analysis.

Details concerning data and image analysis are provided in SI Appendix, SI Text.