Carbon-bearing iron phases and the carbon isotope composition of the deep Earth

Significance

Due to its bonding environments, carbon can make up numerous compounds with many other elements. However, the abundance and dynamics of carbon in the deep Earth remains uncertain due to its complex behavior during the primary accretion and differentiation of the Earth in its early history. The naturally occurring stable isotopes of carbon serve as a useful tracer to study the carbon cycle, both on the surface and in the deep Earth. Here, a new model is presented for understanding a first-order carbon cycle within the Earth, including the sources of the building blocks and core formation processes. Low carbon isotope compositions of carbonaceous materials from ancient rocks have to be used with a caution as biosignatures.

Abstract

The carbon budget and dynamics of the Earth’s interior, including the core, are currently very poorly understood. Diamond-bearing, mantle-derived rocks show a very well defined peak at δ¹³C ≈ −5 ± 3‰ with a very broad distribution to lower values (∼−40‰). The processes that have produced the wide δ¹³C distributions to the observed low δ¹³C values in the deep Earth have been extensively debated, but few viable models have been proposed. Here, we present a model for understanding carbon isotope distributions within the deep Earth, involving Fe−C phases (Fe carbides and C dissolved in Fe−Ni metal). Our theoretical calculations show that Fe and Si carbides can be significantly depleted in ¹³C relative to other C-bearing materials even at mantle temperatures. Thus, the redox freezing and melting cycles of lithosphere via subduction upwelling in the deep Earth that involve the Fe−C phases can readily produce diamond with the observed low δ¹³C values. The sharp contrast in the δ¹³C distributions of peridotitic and eclogitic diamonds may reflect differences in their carbon cycles, controlled by the evolution of geodynamical processes around 2.5–3 Ga. Our model also predicts that the core contains C with low δ¹³C values and that an average δ¹³C value of the bulk Earth could be much lower than ∼−5‰, consistent with those of chondrites and other planetary body. The heterogeneous and depleted δ¹³C values of the deep Earth have implications, not only for its accretion−differentiation history but also for carbon isotope biosignatures for early life on the Earth.

Major Earth-forming processes (accretion, magma ocean formation, Moon-forming giant impact, and core segregation) might have caused significant loss of the primordial volatiles, including carbon to space and the core. Our current estimate of a carbon budget in the mantle varies more than an order of magnitude (1−40 ×10²³ g of C), due to uncertainties in carbon concentrations and proportions of different mantle components (1, 2). Carbon in shallow oceanic mantle generally exists as dissolved CO₂ in melts or C−O−H fluids due to low carbon solubility in silicates (3). With increasing depth, various carbonates become the major C-bearing solid phases. Graphite and then diamond become main hosts for C at deeper depths. Recent experimental studies suggest that Earth's mantle as shallow as 150–250 km may be saturated with iron and the Fe–Ni metals (4). In the presence of Fe-rich metals, diamond can be converted to iron carbides (Fe₃C and Fe₇C₃) and dissolved C in Fe−Ni metals (5–7). The occurrence of cohenite, (Fe, Ni)₃C, has been well documented from iron meteorites, but only recently, several investigators reported rare terrestrial occurrences of Fe carbides (Fe₃C, Fe₂C, and Fe₂₃C₆) from kimberlite (8), from minerals of subcratonic lithosphere or possible lower-mantle origins (9, 10) and others (11). Thus, Fe carbides and Fe−Ni metals are increasingly recognized as potential C-bearing phases in the lower mantle and core. The occurrence of other carbides (SiC, WC, and Cr₃C₂) has also been verified. These carbide phases are formed under very reducing conditions at depths and possibly during adiabatic decompression such as eruption (12). Carbon also appears to substitute for oxygen in silicates under deep-Earth conditions (13).

Extensive investigations of various C-bearing phases from mantle-derived volcanic rocks and xenoliths (bulk carbons, C−O−H inclusions, carbonatite, and graphite−diamond) in the past decades (14–18) established a strong, primary mode of δ¹³C values at −5 ± 3‰. A blurred secondary mode of δ¹³C values also occurs at −10‰ to −20‰ in diamonds and other forms of carbon with the lowest observed δ¹³C values of −42‰ (17, 18). Several models have been put forward to explain these low δ¹³C values. Firstly, mantle carbon could have inherited isotopic heterogeneity of original Earth-building materials despite Earth’s early, violent history. Chondrites and other silicate planetary objects have varying δ¹³C values of the total carbon (organic matter, graphite, carbide) from −24‰ to +5‰ (2, 19). Secondly, the subduction of lithosphere with marine organic sediments has been widely advocated for the depleted δ¹³C values of eclogitic and other types of diamond. However, the lack of a carbon component representing the δ¹³C value of sedimentary carbonates (∼0‰) has been noticed (14, 20), which is far more abundant than organic matter in pelagic marine sediments (21). Nitrogen contents and δ¹⁵N values of eclogitic diamonds are also inconsistent with the hypothesis of the recycled organic matter (22). Thirdly, Rayleigh-type isotope fractionation processes at mantle conditions (>1,000 °C) have been proposed to explain the low δ¹³C values, including diamond deposition from C−O−H fluids, CO₂ degassing from carbonatite melts (16, 23, 24). However, only Rayleigh-type fractionation processes to near completion can produce very negative δ¹³C values, because of small (≤3‰) carbon isotope fractionation among C−O−H fluids, CaCO₃, and diamond under mantle conditions.

Very low δ¹³C values (−18‰ to −35‰) have been reported for SiC from several localities (25). Recently, Mikhail et al. (8) reported that diamond and coexisting iron carbide from Jagersfontein kimberlite, South Africa, have low δ¹³C values: −12.7‰ to −17.3‰ (diamond) and −18.6‰ to −25.2‰ (cohenite). An increasing number of the occurrences of carbides from the upper and lower mantles, associated with diamond with low δ¹³C values, points to a genetic relationship between these diamonds with low δ¹³C values and carbides. Thus, various carbides, particularly the Fe−C phases (dissolved C in Fe−Ni metals and Fe carbides), may play an important role in the deep carbon cycle, not only in terms of a carbon reservoir, but also in carbon isotope distributions in the deep Earth.

Results and Discussion

Here, we have calculated the reduced partition function ratios (β-factors) for carbon isotopes (¹³C/¹²C) of two key carbides, cementite (Fe₃C) and moissanite (SiC) (Materials and Methods). Our calculations of the ¹³C β-factors of cementite and silicon carbide can be expressed as

$$\mathrm{F}{\mathrm{e}}_3\mathrm{C}\text{:}{10}^3\ln \beta =4.514031\cdot x-0.02779097\cdot x^2+1.299374\cdot {10}^{-4}\cdot x^3$$ [1]

$$\mathrm{SiC}\text{:}{10}^3 \ln \beta =10.69719\cdot x-0.207930\cdot x^2+0.00370146\cdot x^3$$ [2]

where x = 10⁶/T². Then, an equilibrium fractionation factor between two substances A and B (α_A-B) can be expressed by

$${10}^3\ln {\alpha }_{A-B}={10}^3\ln {\beta }_A-{10}^3\ln {\beta }_B.$$ [3]

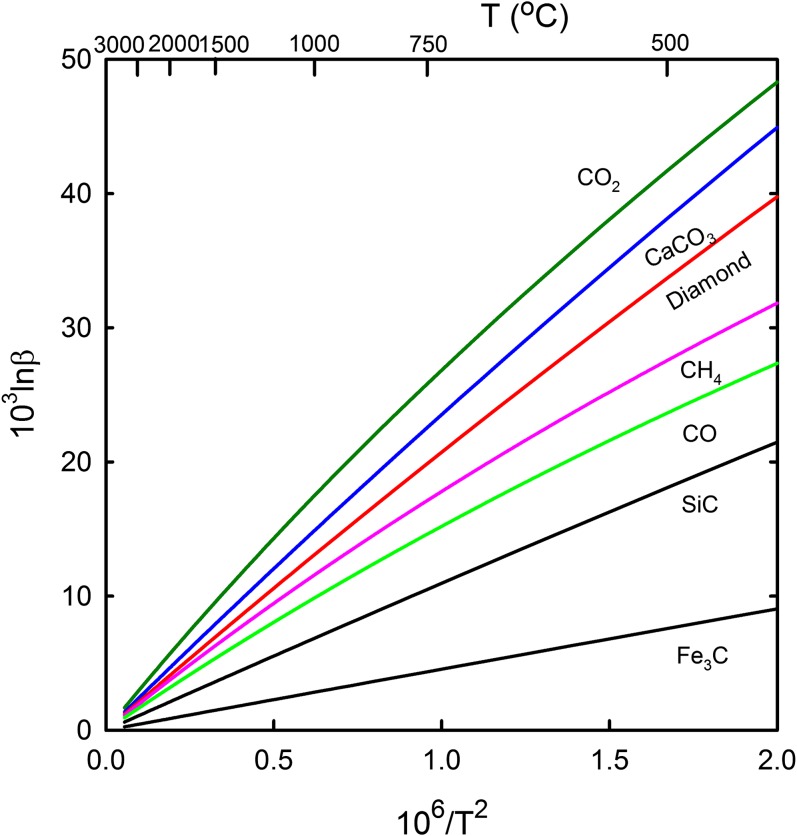
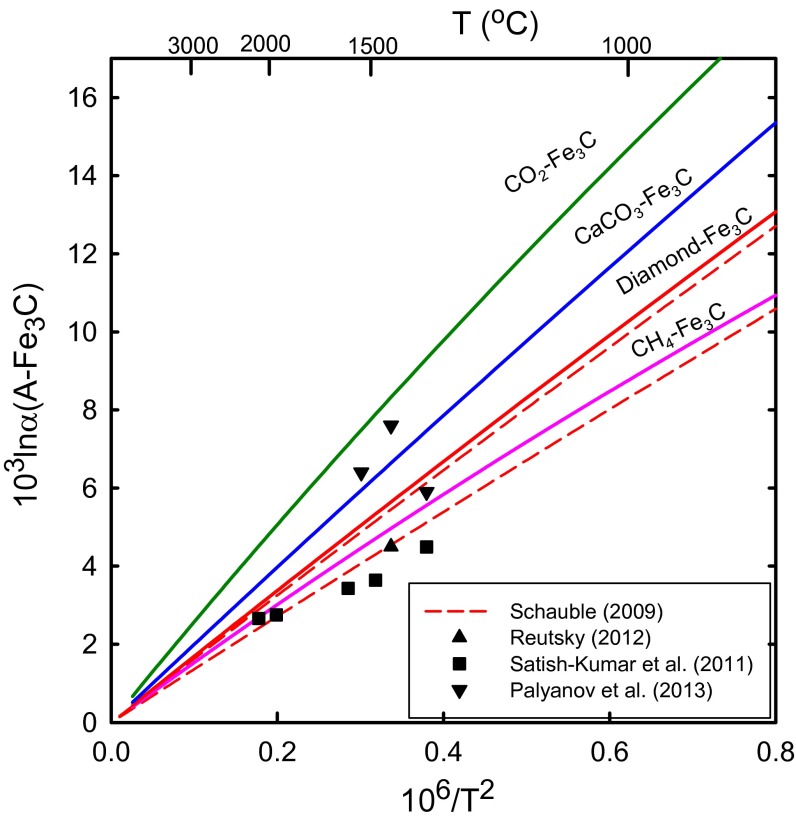
The ¹³C β-factors for the two carbides are smaller than those for any other carbon-bearing compounds ever reported in the literature, including methane and CO (Fig. 1). The effect of pressure on ¹³C/¹²C fractionation between Fe₃C and other mantle phases are not significant at mantle temperatures (26) (SI Text). Thus, δ¹³C values of Fe₃C are lower than any other C-bearing mantle phases (diamond, CO₂, CH₄, and CaCO₃) by 10–14‰ and 3–5‰ at 1,000 °C and 2,000 °C, respectively (Fig. 2). The δ¹³C values of SiC are also lower by 6–11‰ and 2–4‰ at 1,000 °C and 2,000 °C, respectively. The effect of polymorphic transitions of CaCO₃ (and CO₂) with increasing pressure is probably insignificant (27, 28), although not quantified yet. Our calculations for ¹³C β-factors of Fe₃C are very close to density functional theory calculations for Fe₃C and η-Fe₂C (29) (Fig. 2). Recent experimental results of ¹³C/¹²C isotope fractionation factors between graphite/diamond and Fe−C melts/Fe carbides at 1200–2100 °C and 2–15 GPa vary from 2.7‰ to 7.6‰ (30–32) (Fig. 2). It should be noticed that the attainment of isotope equilibrium has not been demonstrated in these experimental studies. Our calculations generally agree with the experimental data, especially at the high temperature (≥2,000 °C). It is likely that Fe₇C₃, a probable main phase in the lower mantle and the inner core, has β-factors similar to Fe₃C. Collectively, the theoretical and experimental studies clearly demonstrate significant depletion of ¹³C in various carbides (Fe carbides and SiC) and C dissolved in Fe−Ni metals at mantle temperatures.

Fig. 1.

Comparison of the ¹³C β-factors for carbides (SiC and Fe₃C) and other carbon-bearing compounds at high temperatures. Data sources: SiC, Fe₃C, CaCO₃ (this study), CO (60), CO₂ and diamond (61), and CH₄ (62).

Fig. 2.

Calculated equilibrium ¹³C/¹²C fractionation between mantle carbon phases (A) and Fe₃C, compared with experimental data. Two dashed red lines are density functional theory calculations for diamond−Fe₃C (above) and diamond−η−Fe₂C (below) fractionation (29−32).

Cohenite in iron meteorites is depleted in ¹³C by 11.5–12.5‰ relative to coexisting graphite (33–35). Carbon dissolved in taenite (Fe−Ni alloy) from several types of meteorites is also depleted in ¹³C relative to graphite (34, 36). Assuming ¹³C β-factors of cohenite are very similar to those of cementite, the graphite and cohenite equilibrated at 850–900 °C. Recently, Mikhail et al. (8) reported that the difference in the δ¹³C values between the diamond and coexisting iron carbide from Jagersfontein kimberlite, South Africa, averaged 7.2 ± 1.3‰. This isotope fractionation corresponds to a formation temperature of 1,250 °C ± 150 °C, which is within a typical range for the formation of subcontinental lithospheric diamonds (1,150 °C ± 100 °C). The δ¹³C values of terrestrial SiC have also been reported to range from −18‰ to −35‰, which are much lower than coexisting diamond or CaCO₃ (37, 38). Thus, the observed low δ¹³C values of carbide minerals are consistent with their low ¹³C β-factors relative to other C-bearing mantle minerals even at mantle temperatures.

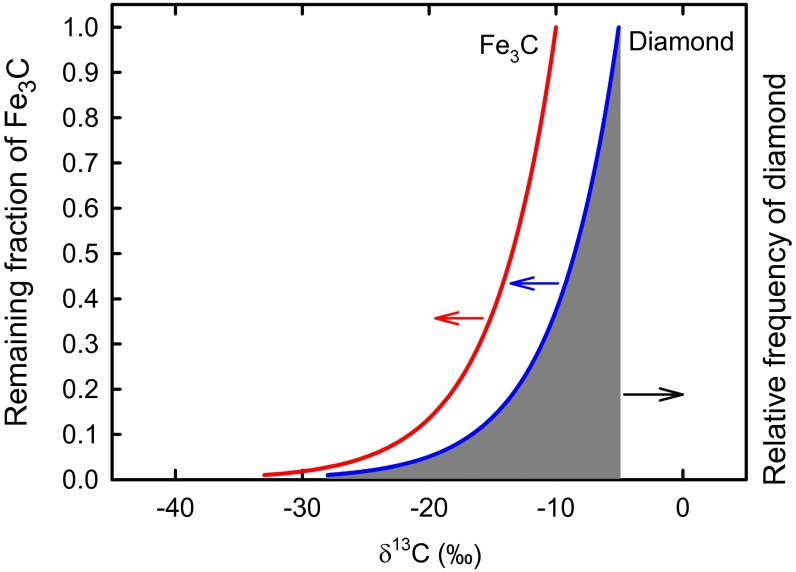
With increasing depth within the mantle, CO₂ and carbonates become unstable with respect to diamond at 120–200 km. In greater depths, the fO₂ further decreases to that of iron-wustite, and eventually (Fe, Ni) metal becomes stable at about 250 km and below (“redox freezing”) (39, 40). With typical concentrations of C in the oceanic mantle (20−300 ppm), all diamond is converted first to dissolved C in the Fe−Ni metal phase, and then to a discrete iron carbide phase (Fe₃C and Fe₇C₃) after carbon saturation, followed by diamond. A recent experimental study between Mg−Ca carbonate and metallic Fe at 1,000–1,650 °C and 6.5–7.5 GPa (30) demonstrated the formation of diamond and Fe₃C together with metastable graphite along the steep fO₂ gradient. Using the results of our theoretical calculations of ¹³C β-factors, we now can build a first-order model for δ¹³C distributions among these C-bearing mantle minerals (carbonate, diamond, and Fe₃C) during mantle−slab interactions within the deep Earth. When carbonate-rich lithosphere is subducted into the metal-saturated zone, mantle domains with the Fe−C phase form (collective term used here for C dissolved in Fe−Ni metal and various Fe carbides) with excess carbon as diamond. Because δ¹³C values of Fe₃C are lower by ∼5–6‰ than diamond at ∼250 km (∼1,400–1,600 °C for modern and Archean mantles), lithosphere with a typical δ¹³C of −5‰ that undergoes deep subduction would contain Fe₃C and diamond with δ¹³C of −11‰ to −5‰ and −5‰ to +1‰, respectively, depending on Fe₃C/diamond ratios. The subducted lithosphere may further penetrate deep into the transition zone and even into the upper part of the lower mantle. When the domains of subducted lithosphere with Fe−C phases (and diamond) become entrained into mantle upwelling, first reoxidation of the Fe−C phase to diamond, then diamond to carbonatite melts occurs (“redox melting”). The oxidation of the Fe−C to diamond/carbonate could occur below the metal saturation (250 km) to the 660-km discontinuity, corresponding to ∼1,400−1,600 °C (modern mantle) or to ∼1,600−1,900 °C (Archean mantle). Thus, equilibrium δ¹³C fractionation between diamond and Fe₃C ranges from ∼3.5‰ to ∼6‰. This oxidation process could occur by Rayleigh-type open-system fractionation, because C diffuses very rapidly in Fe−C phases, but very slowly in diamond (D ≈ 10⁻²³ m²/s to 10⁻²⁵ m²/s in the transition zone) (41), limiting the isotope exchange with the Fe−C phase. Thus, it is very likely that during oxidation of Fe−C to diamond, their δ¹³C values can become progressively lower from their starting values, reaching δ¹³C < −20‰ at low remaining fractions of carbide (f < 0.1) (Fig. 3). Further oxidation of the diamonds to carbonatite could slightly lower the δ¹³C value of remaining diamond (<∼1‰ at 1,400–1,500 °C). Thus, within the framework of the redox freezing and melting cycle, the Fe−C phases and diamond with δ¹³C values much lower than −5‰ can be readily produced (Fig. 3). It has been well documented that the bulk of diamond are metasomatic in origin, deposited from C-bearing fluids. It is very likely that the carbon cycle during the redox freezing and melting discussed above (CO₂/carbonates to diamond to Fe−C phases and reverse) is mediated by small amounts of C−O−H fluids [CO₂, CH₄ and possibly other hydrocarbons (42)] or carbonate melts. However, the δ¹³C distribution of diamond and Fe carbides discussed above and in Fig. 3 remain essentially the same.

Fig. 3.

Modeling of δ¹³C distribution during a Rayleigh-type redox melting of Fe₃C to diamond: red and blue lines (δ¹³C of Fe₃C and diamond, respectively, as a function of the remaining fraction of Fe₃C) and gray area (δ¹³C relative frequency of diamond produced by the oxidation of Fe₃C).

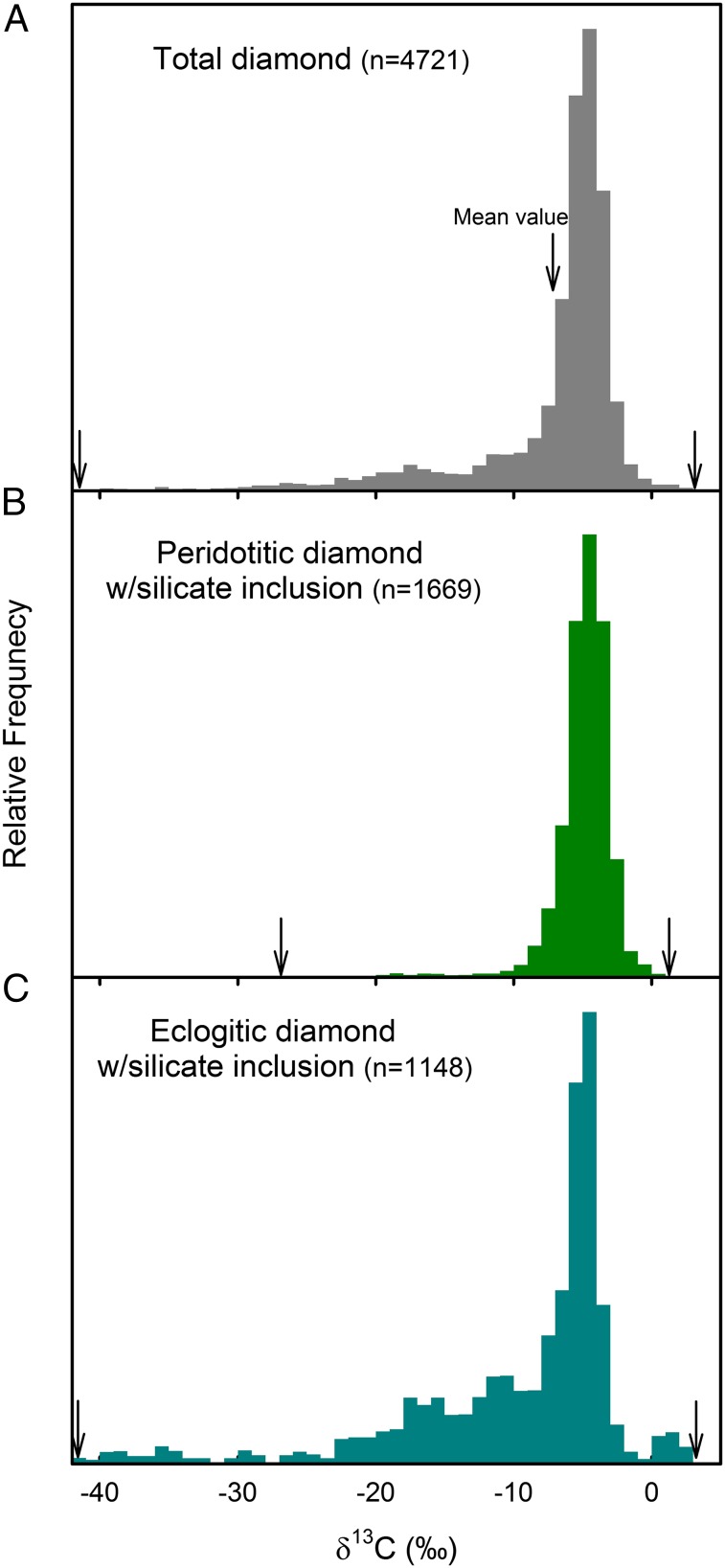
A comparison of results from our modeling for δ¹³C relative distribution of diamonds (gray area, Fig. 3) with the compiled δ¹³C distribution of natural diamonds (Fig. 4A) reveals similar semiexponential tailings to lower values, but a much stronger peak for the natural diamonds at δ¹³C = −5 ± 3‰ than our modeling. It is also well recognized that the δ¹³C distribution of eclogitic diamonds show a very pronounced tailing pattern to lower values than peridotitic diamonds (Fig. 4 B and C) despite the fact that the both types of diamonds are formed in the keel of subcontinental lithospheric mantle (SCLM) at similar temperature–pressure conditions (1,150 °C ± 100 °C and ∼5 GPa) (43). The appearance of eclogite may reflect the change in geodynamical processes from shallow subduction and delamination or “intraplate” lithospheric extension/mantle upwelling before ∼3 Ga to modern, large-scale plate tectonics with deep subduction of oceanic crust (44, 45). The Archaean oceanic crust was probably thicker and hotter than present-day oceanic crust, owing to higher heat flow and higher degrees of melting at midocean ridges. Thus, shallow subduction with flatter angles and recycling of oceanic crust were dominant. The period from 3 Ga to the end of the Archean (2.5 Ga) is increasingly viewed as a time of the onset of subduction-driven plate tectonics, the Wilson cycle. The oceanic crust became steadily thinner, and the whole crust could be subducted deep by the late Archaean. Subcretion of oceanic lithosphere to the base of continents resulted in deep SCLM with the core of old (>2.5–3 Ga) rheologically stiffer peridotitic nuclei and surrounding younger (<2.5–3 Ga) terranes of eclogitic compositions. In fact, compilations of the ages of diamond deposits (46, 47) show a general pattern that the majority of peridotitic diamonds formed in the Paleo to Neoarchean (2.7–3.5 Ga), while eclogitic diamonds have much younger ages (1−2.9 Ga).

Fig. 4.

The δ¹³C relative distributions of natural diamonds: (A) worldwide, (B) peridotitic with silicate inclusion, and (C) eclogitic with silicate inclusion. The arrows indicate the highest and lowest δ¹³C values of each group. A mean δ¹³C value of the worldwide diamond is −7.2‰. The data are from ref. 18.

Within this scenario of the tectonic evolution, the source of carbon for peridotitic diamonds before 2.5–3 Ga was largely restricted to the upperpart of the mantle (≤200 km), where major C-bearing materials included CO₂, carbonates, and diamond/graphite. After the onset of large-sale plate tectonics and deep subduction of oceanic crusts after 2.5–3 Ga, mantle rocks of eclogitic compositions started to form in the lower upper mantle and below (>250 km). The carbon cycle to this depth includes the Fe−C phases via the redox freezing and melting processes as discussed above. During the upwelling and subcretion of eclogitic domains, the Fe−C phases are either oxidized to diamond or mobilized as CH₄-bearing fluids, which are trapped and then oxidized to diamonds under SCLM keels. Thus, when subducted deep (>250 km), some of eclogitic diamond are produced via the net oxidation from the Fe−C phases to diamond, which induces large isotope fractionation as discussed above (Fig. 3). Peridotite components of lithosphere might have experienced the same redox freezing/melting, involving the Fe−C phases. In fact, peridotitic diamonds also show a wide δ¹³C distribution to lower values (−26.4‰ to +0.2‰), although much less pronounced relative to eclogitic diamonds (Fig. 4) (18). This sharp contrast in their δ¹³C distributions could be due to the change in their carbon cycles that was controlled by the evolution of global geodynamical processes: carbon from the upperpart of the mantle for old (>2.5–3 Ga) peridotite diamonds vs. carbon from deeply subducted lithosphere for young (<2.5–3 Ga) eclogitic diamonds. Diamonds from the transition zone and the lower mantle also show wide δ¹³C distributions to lower values (−24‰ to +5‰), which is generally consistent with the new model presented here that involves the deep carbon cycle via the redox freezing and melting. Porous, polycrystalline diamond (carbonado) and diamonds in ophiolites also have very low δ¹³C distributions: −32‰ to −5‰ (carbonado) and −28‰ to −18‰ (ophiolite). Their origins are still in debate, but they are undoubtedly formed under (local?) very reducing conditions as metal (Fe, Fe−Ni, Ni−Mn−Co) and carbides (SiC and Fe−C) occur along with the diamond. Diamond formation via these carbide phases is a likely process for producing the observed low δ¹³C values.

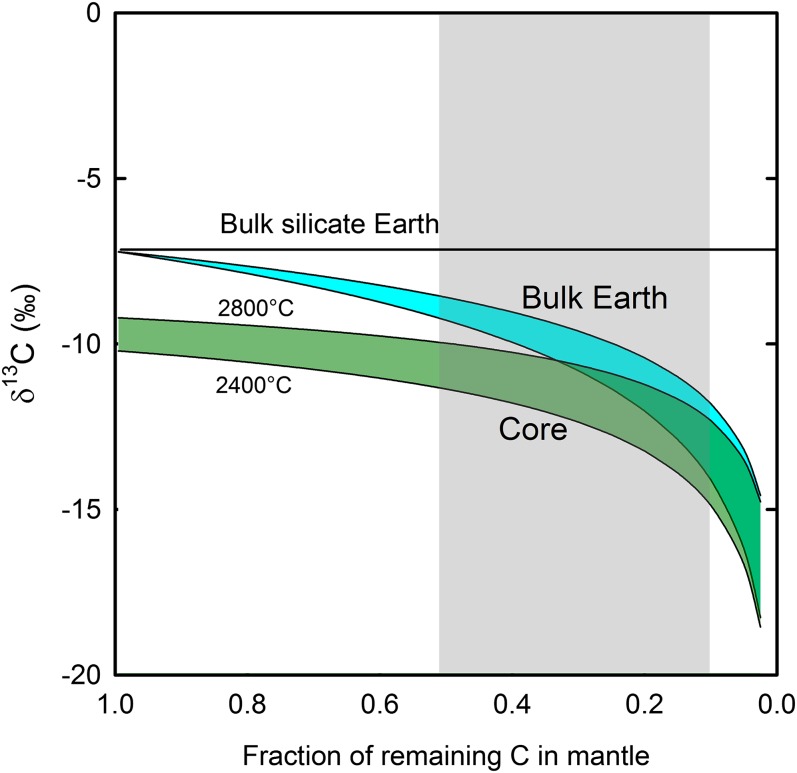
The proto-Earth likely experienced protracted (30–40 My) reequilibration between Fe metal and silicates during planetary accretion−growth, resulting in the core−mantle segregation. Carbon in the “magma ocean” was partitioned into iron droplets, which were then sequestered into the core via metal diapirs (48). An estimated total C content in the mantle varies widely (∼1–40 × 10²³ g of C) (1, 2). Assuming that δ¹³C values of diamonds collected worldwide (Fig. 4A) represent the mantle, the bulk silicate Earth has an average δ¹³C value of −7.2‰; carbonates and organic matter in the crust have much smaller reservoirs (∼10²¹ g of C) (21). Experimental studies on C solubility in Fe−C phases suggest that the core (mainly, liquid outer core) may contain 20–200 × 10²³ g of C (1, 19). Thus, our current knowledge suggests that the mantle may contain only 10–50% of C that was originally accreted from protoplanetary materials. Much of reequilibration between metallic cores of planetesimals and Earth’s silicate mantle took place in a deep magma ocean at temperatures as high as the solidus of the mantle (∼2,800 °C and >30 GPa) (48). If this carbon extraction from the silicate melts and metal−silicate reequilibration occurred in isotopic equilibrium at 2,400–2,800 °C, carbon in the Fe melts (assumed to have the same β-factors as Fe₃C) is depleted in ¹³C by 1.8–2.4‰ and 2.1–2.8‰ compared with diamond and CaCO₃ in magma ocean, respectively (Fig. 2). Under the deep magma ocean and heterogeneous accretion model (48), the core formation could be modeled by a Rayleigh-type fractional carbon segregation, rather than by a single-stage batch equilibrium process with the magma ocean. This scenario yields δ¹³C values of −15‰ to −10‰ for the core, and of −14‰ to −8.6‰ for the bulk Earth, depending on the degree of carbon extraction from the mantle to the core and the temperature (2,400−2,800 °C) (Fig. 5). No carbon addition (late veneer) is considered after the mantle−core segregation. These estimated δ¹³C values for the bulk Earth are moderately to significantly lower than the currently accepted mantle value (−5 ± 3‰). The range of δ¹³C values for the bulk Earth is in fact more consistent with those observed for chondrites and other meteorites (−24‰ to +5‰) (2, 49, 50). Recently, a conceptually similar, but qualitative model has been presented (48).

Fig. 5.

Modeling of δ¹³C values of the bulk Earth and the core as a function of (i) fraction of remaining C in the mantle during carbon sequestration to the core and (ii) temperature of Fe melt segregation from magma ocean. The δ¹³C of the bulk silicate Earth is assumed to be a mean δ¹³C value of the worldwide diamond (−7.2‰, Fig. 4A). The ¹³C/¹²C fractionation between CaCO₃ or diamond in magma ocean and Fe₃C in Fe-melt is 2–3‰ at 2,400–2,800 °C (Fig. 2). The fraction of remaining C in the mantle is estimated to be in the range 0.1–0.5 (gray area).

The carbon cycle involving carbides (SiC and Fe−C phases) has potentially significant implications for the study of early life on the Earth. Low δ¹³C values of carbonaceous materials (graphite) present in ancient rocks, particularly of Eoarchean (∼3.8 Ga) mineral associations from southern West Greenland, has been used as a proxy of ancient life (isotope biosignatures) (51). Several experimental studies in the past decade suggest that various abiotic reactions in the early atmosphere−oceans−crust could have produced hydrocarbons and other carbonaceous materials with such low δ¹³C values (52). Our calculations and modeling here show that carbide minerals and dissolved C in Fe−Ni produced even under deep-Earth conditions can have very low δ¹³C values (Figs. 2 and 3). Metamorphism of Eoarchean rocks in reducing environments could also have produced carbide minerals with low δ¹³C. SiC could also be produced by adiabatic decompression of volcanic eruption near the surface (12). These carbide phases might have later been oxidized to graphite. Thus, the “light carbon” of Hadean−Eoarchean rock record alone is not a viable biosignature. Abiogenic processes that can produce carbonaceous materials with low δ¹³C values, both near surface and in deep Earth, challenge our notion of carbon isotope biosignatures for early life on Earth and possibly other planets.

Materials and Methods

For a compound consisting of two elements such as cementite, the β-factor of one element can be calculated from the kinetic vibration energies of the entire compound and the other element (53–56):

$$\ln {\beta }_{{}^{13}\text{C}\text{/}{}^{12}\text{C}}=\left(\frac{K_{\text{total}}-3K_{\text{Fe}}}{RT}-\frac{3}{2}\right)\frac{\left(m_{{}^{13}\text{C}}-m_{{}^{12}\text{C}}\right)}{m_{{}^{12}\text{C}}{m}_{{}^{13}\text{C}}}{m}_{\text{C}}$$

where K_total and K_Fe are the kinetic energies of cementite and its iron sublattice, respectively. The $m_{{}^{12}C}$, $m_{{}^{13}C}$, and $m_C$ are the atomic masses of ¹²C, ¹³C, and carbon. The R and T are gas constant and temperature (K), respectively. The K_total and K_Fe were obtained, respectively, from the lattice contribution to the total heat capacity (57) and from ⁵⁷Fe partial density of state determined by means of nuclear resonant inelastic X-ray scattering experiments with synchrotron radiation (58) (see SI Text). To estimate ¹³C β-factors for silicon carbide (SiC), we used a cubic 3C modification of a rigid-ion lattice dynamic model, combining short-range central and noncentral interactions, and long-range Coulomb interactions (59). The ¹³C β-factors of SiC were then calculated from the modal β-factor value for a given vector, using six frequencies of Si¹²C and Si¹³C isotopologues and averaging over the number of the wave vectors (see SI Text):

$$\ln \beta =\frac{1}{N_k}{\displaystyle \sum _{i=1}^{N_k}{\displaystyle \sum _{j=1}^6\ln \left(\frac{u_{ij}^{\ast }\sinh (u_{ij}/2)}{u_{ij}\sinh (u_{ij}^{\ast }/2)}\right)}}$$

where $u=h\nu /k_{B}T$ is the dimensionless phonon frequency with ν the phonon frequencies, h is Planck’s constant, and k_B is the Boltzmann constant. The asterisk denotes Si¹³C isotopologue.