Precisely cyclic sand: Self-organization of periodically sheared frictional grains

Significance

Granular materials are used for a wide variety of technological applications in nearly every industry and also serve as an instructive prototype for far-from-equilibrium behavior. Although they have received considerable attention, there are few general guidelines describing how they collectively organize and yield under shear, especially in physically relevant frictional grains. Using simulations, we explore the response of granular packings to slow periodic shear, systematically varying both the friction and shear. We discover a previously unidentified state in which the otherwise chaotic motion gives way to a precisely repetitive limit cycle for each individual grain. Understanding how grains self-organize into stable, periodic limit cycle configurations in this unlikely system foretells new approaches to understand yielding and memory formation in disordered materials.

Abstract

The disordered static structure and chaotic dynamics of frictional granular matter has occupied scientists for centuries, yet there are few organizational principles or guiding rules for this highly hysteretic, dissipative material. We show that cyclic shear of a granular material leads to dynamic self-organization into several phases with different spatial and temporal order. Using numerical simulations, we present a phase diagram in strain–friction space that shows chaotic dispersion, crystal formation, vortex patterns, and most unusually a disordered phase in which each particle precisely retraces its unique path. However, the system is not reversible. Rather, the trajectory of each particle, and the entire frictional, many–degrees-of-freedom system, organizes itself into a limit cycle absorbing state. Of particular note is that fact that the cyclic states are spatially disordered, whereas the ordered states are chaotic.

Self-organization under periodic driving is a common feature in many disparate far-from-equilibrium systems (1–4). Recently, there has been substantial interest in self-organization in suspensions under slow, cyclic, low-Reynolds number shear (1, 5, 6). Non-Brownian suspensions were found to exhibit a phase transition from a dynamic fluctuating state to a reversible absorbing state depending on the shear amplitude and particle density. Here, there is a clear route to reversibility, because at low Reynolds numbers the equations of motion for the fluid are reversible, and irreversibility is only introduced through particle collisions or potential interactions. A similar cyclic behavior has been observed in periodically driven superconducting vortices (4), which interact via a nonlinear potential.

If one instead considers a pack of frictional grains, this picture changes dramatically and the conditions for reversibility/irreversibility and periodic motion remain poorly understood (7–9). Here, the equations of motion are not time-reversible and particles remain in contact with their neighbors at all times, interacting via hysteretic frictional forces instead of simple collisions. Although a priori the system is hysteretic and irreversible, it is still possible to exhibit correlations and self-organization. Indeed, experimental studies of grains under cyclic shear have found spontaneous crystallization (10, 11), dynamic heterogeneities (12), and subdiffusive caged motion (9, 13). Recent experiments on 2D frictional disks found limit cycles in the shear stress and pressure in shear-jammed packings (14), although the individual grain motion remains diffusive. However, experiments are limited to a narrow range of friction and one cannot easily vary this crucial parameter that determines the possible packing configurations (15) and the response of the granular system to applied shear. Although we do not find reversible states, we do find that, depending on the strain amplitude and grain friction, the granular system can organize itself and evolve into either spatially or temporally ordered phases, but surprisingly not both.

Results and Discussion

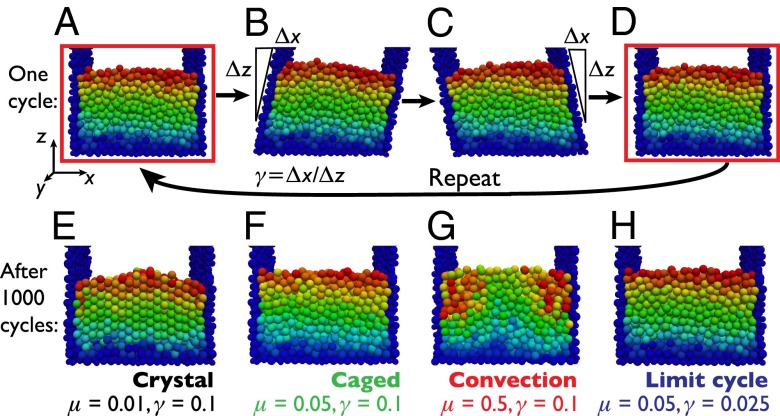
We perform 3D soft-sphere molecular-dynamics (MD) simulations of monodisperse grains with static friction using LAMMPS (16, 17). Unless otherwise noted, the simulations are performed using $N=\mathrm{2,000}$ grains with a linear spring–dashpot model for the contact forces. Dense initial packings are generated by pouring grains into the shear cell under gravity, randomly varying the initial grain positions during the chaotic pouring process to create an ensemble of initial configurations. For simulation details, see Materials and Methods. Fig. 1 A–D shows the shear cell and the progression of a single shear cycle. To shear the pack of grains, the two vertical walls are quasistatically rotated up to a maximum shear-strain $\gamma =\mathrm{\Delta }x/\mathrm{\Delta }z$ (Fig. 1B). The walls are then rotated back to vertical and continue in the opposite direction, reaching the same shear amplitude (Fig. 1C), and finally return to vertical to complete the shear cycle (Fig. 1D).

Fig. 1.

Grains under cyclic shear. A–D Illustrate a single shear cycle for $\gamma =0.2$ and $\mu =0.5$. E–H show the granular pack after 1,000 full shear cycles in the (E) Crystal, (F) Caged, (G) Convection, and (H) Limit Cycle phases. Particles are labeled with a fixed color set by their initial height in the container, running from blue at the bottom to red at the top. The side and bottom walls (dark blue particles) are made of polydisperse grains ranging in size from 0.65d to 1.2d. See SI Text for movies illustrating a single shear cycle (Movie S1) and each of the different phases: Crystal (Movies S2 and S3), Caged (Movie S4), Convection (Movie S5), and Limit Cycle (Movie S6).

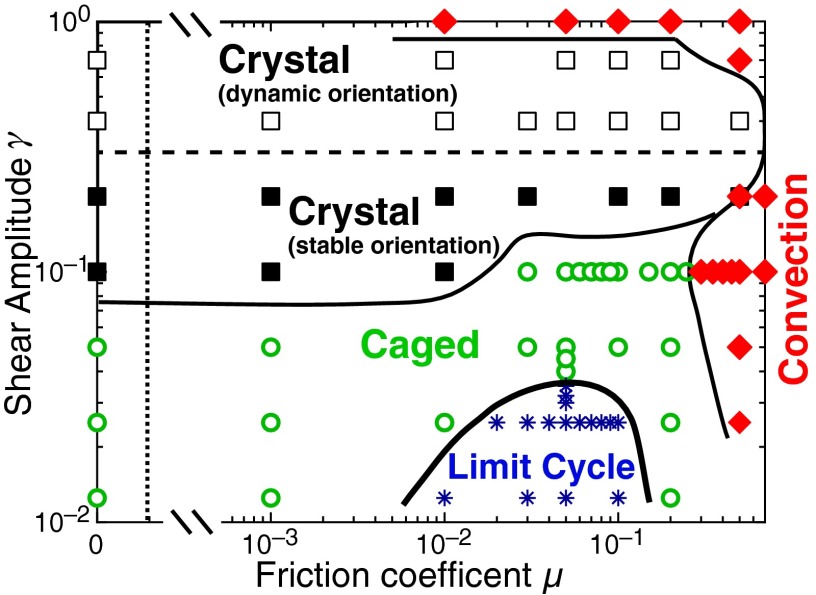
We shear the pack of grains for a variable number of shear cycles $n_{cyc}=100\to \mathrm{8,000}$ so that the cumulative shear is fixed ${\gamma }_T=4n_{cyc}\gamma =400$. Simulations are repeated with an ensemble of 5–20 randomized initial packings to examine the sensitivity to initial conditions, while single, longer runs up to ${\gamma }_T=800$ are performed to verify the long-time dynamics. After hundreds or thousands of cycles, the pack of grains can self-organize into a number of different phases depending on the shear amplitude γ and the friction coefficient μ (Fig. 2). Varying the shear amplitude $0.0125\le \gamma \le 1.0$ and the friction $0.00\le \mu \le 1.0$, we identify four distinct phases: a “Crystal” phase, where the grains order into dense-packed crystalline planes; a “Caged” phase, where the packing remains disordered and the grains exhibit subdiffusion motion; a “Convection” phase, where a persistent circulation develops and the grain motion is superdiffusive at long times; and a “Limit Cycle” phase, where the grains organize into configurations where all of the particles follow periodic trajectories from cycle to cycle, each particle retracing its path each cycle. Note that the crystalline phase is not a limit cycle phase and vice versa. The pronounced slips and shifts in the crystal planes from cycle to cycle (Movie S2) prevent the ordered grains from returning to their previous position, whereas the Limit Cycle phase remains spatially disordered.

Fig. 2.

Phase diagram of frictional grains under cyclic shear. Data points show the final state reached after a cumulative shear ${\gamma }_T=4n_{cyc}\gamma =400$ (i.e., $n_{cyc}=100$ for $\gamma =1.0$, $n_{cyc}=1,000$ for $\gamma =0.1$, and so on) for an ensemble of 5–20 simulations with identical μ and γ. The size of the ensemble M varied with γ, with $M=5$ for $\gamma \ge 0.4$, $M\ge 10$ for $0.4>\gamma \ge 0.05$, and $M=20$ for $\gamma <0.05$. Single realizations up to ${\gamma }_T=800$ were also performed for each point. Phase boundaries are sketched as a guide to the eye. The friction axis is broken (denoted by hatch marks and vertical dotted line) to include $\mu =0$ on the log scale.

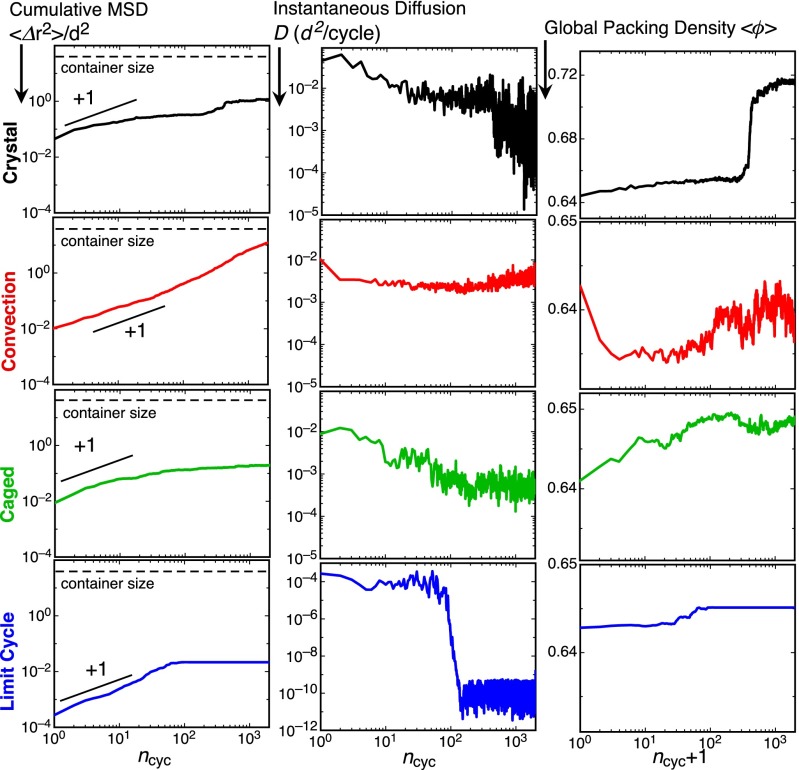
In Fig. 1 E–H, we show snapshots of the pack of grains after 1,000 shear cycles in each of the different phases, whereas in Fig. 3 we illustrate the evolution of the grain diffusion and packing density in each phase. Previous experimental studies of grains under cyclic shear have observed crystallization (11, 18), convection (19), and caged motion (9, 13). We briefly characterize these previously observed phases before turning our attention to the previously unidentified Limit Cycle phase.

Fig. 3.

Characterizing phases. Evolution of the cumulative MSD $\langle \mathrm{\Delta }{r}^2\rangle$, instantaneous diffusion D, and average packing density $\langle \varphi \rangle =V_{grain,tot}/V_{tot}$ as a function of the number of shear cycles $n_{cyc}$. The values of μ and γ for each phase are identical to the values used in Fig. 1. See the SI Text for ensemble averages of these same quantities.

Crystallization, shown in Fig. 1E, occurs with sufficiently large shear over a broad range of friction. The crystalline region nucleates in the bulk, differentiating the crystallization observed here from wall-induced crystallization (18), and in fact the irregular walls inhibit ordering along the sides and bottom even after the crystal has developed. At $\gamma =0.4$ and above, the shear distorts the orientation of the lattice planes, leading to a crystalline phase with a dynamic lattice orientation (Movie S3). The onset of crystallization is accompanied by an increase in the packing density $\langle \varphi \rangle$ from an initial packing density slightly above 0.64 to $\langle \varphi \rangle \approx 0.7$, above the range of $\langle \varphi \rangle$ expected in a random packing (20) and instead closer to the sphere close packing limit of $\varphi =\sqrt{\pi }/18\approx 0.74$.

Increasing either μ or γ leads to a phase where persistent convection develops, with grains on the top surface moving down along the walls and grains from the bottom upwelling in the center (Fig. 1G and Movie S5). This convection generally prevents crystallization, although at the phase boundary we observe coexistence where a dense crystalline region forms amid a sea of flowing grains (Movie S9). We use two measures to characterize the grain motion: the cumulative mean squared displacement (MSD) $\langle \mathrm{\Delta }{r}^2\left(n_{cyc}\right)\rangle =\langle {\left(\overrightarrow{r}\left(n_{cyc}\right)-\overrightarrow{r}\left(n_{cyc}=0\right)\right)}^2\rangle$ and the cycle-to-cycle displacement, or “instantaneous diffusion” $D\left(n_{cyc}\right)=\langle {\left(\overrightarrow{r}\left(n_{cyc}\right)-\overrightarrow{r}\left(n_{cyc}-1\right)\right)}^2\rangle$ (we use $\langle \cdots \rangle$ to denote averages over all grains, excluding those near boundaries, and a bar for ensemble averages). In the Convection phase, the instantaneous diffusion $D\approx$ constant at long times, whereas the cumulative MSD $\langle \mathrm{\Delta }{r}^2\rangle \propto n_{cyc}^{\beta }$ with $\beta \hspace{0.17em}\mathrm{\gtrsim }\hspace{0.17em}1$. This weakly superdiffusive behavior suggests that the grain dynamics are a combination of random, diffusive motion, and ballistic motion from the convective flow.

At lower shear amplitudes and over a wide range of friction, the pack of grains neither exhibits convection, nor does the pack crystalize. In this region of phase space, the motion is initially diffusive, with $\langle \mathrm{\Delta }{r}^2\rangle \propto n_{cyc}$. However, at longer times $\langle \mathrm{\Delta }{r}^2\rangle$ turns over and approaches a constant value much less than the container size. This indicates that the grains remain trapped in localized cages, unable to explore the full shear cell. Similarly, the instantaneous diffusion D slows down, and then levels off, while the packing density increases slightly then saturates. It is possible that these Caged states may be transient and would eventually absorbed by other phases if we could allow $n_{cyc}\to \infty$. However, we observe only a weak or nonexistent increase in the number of shear cycles needed to either crystallize or transition to a limit cycle as we approach the Crystal–Caged and Limit Cycle–Caged phase boundaries. Performing extralong simulations runs at points near these phase boundaries, we find that the phase diagram presented here does not strongly depend on our computation time (SI Text).

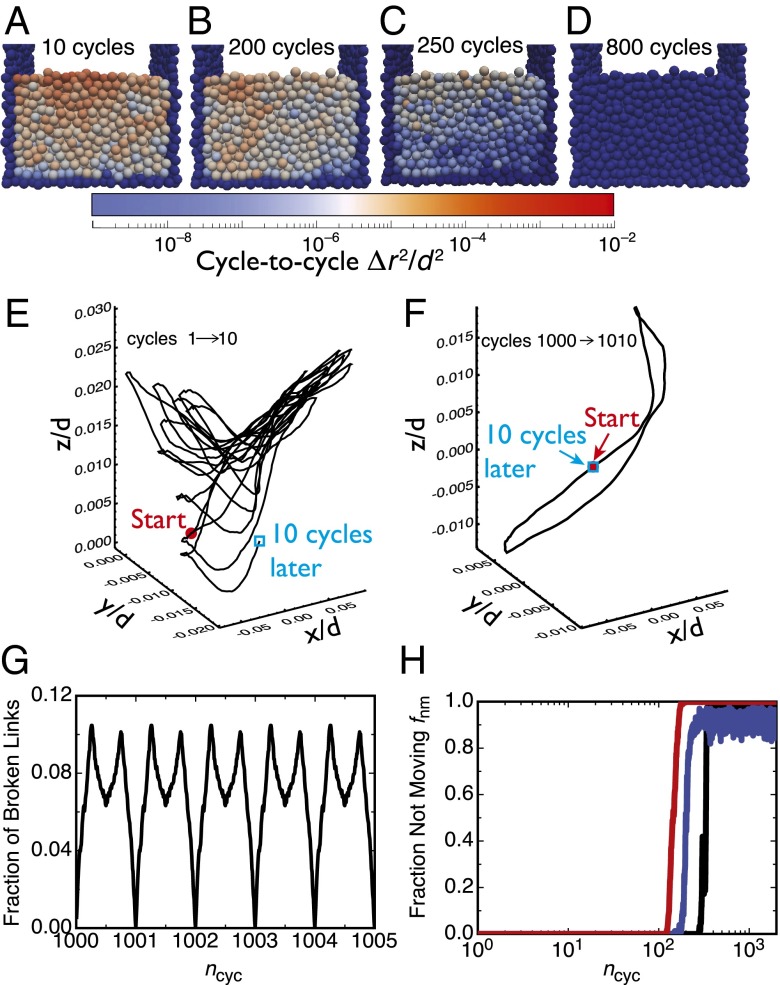
For small shear amplitudes and a range of small but nonzero friction, we find states where the system organizes itself in periodic limit cycles, with a significant fraction of the particles following their exact same trajectory from cycle to cycle. In this Limit Cycle phase, the cumulative MSD and packing density initially increase then saturate, as in the Caged phase. However, the instantaneous diffusion reveals a drastic change, dropping nearly five orders of magnitude in a relatively small number of cycles. Coloring the grains by their individual cycle-to-cycle displacements (Fig. 4 A–D), we find that nearly all of the grains return to the same position in the shear cell within a resolution of $\approx {10}^{-5}d$. In this Limit Cycle state, the grains retrace the same trajectory from cycle to cycle (Fig. 4F), although these trajectories are not reversible in the same way that particle motion in dilute suspensions at low Reynolds number is reversible. The grains only return to their initial positions at the completion of a full symmetric shear cycle, not just when the walls return to vertical at a half-cycle. Decreasing the shear amplitude or switching the shear direction breaks the limit cycle and grains resume diffusing until organizing into a new limit cycle.

Fig. 4.

Limit Cycle dynamics. (A–D) Strobed images with grains colored by their individual cycle-to-cycle displacements squared ${\left(\overrightarrow{r}\left(n_{cyc}\right)-\overrightarrow{r}\left(n_{cyc}-1\right)\right)}^2/d^2$. (see Movie S7) (E and F) Full (nonstrobed) trajectories of a single grain before (E) and after (F) the establishment of a limit cycle (also see Movie S8). (G) Fraction of broken links (21) relative to the contact network at the start of cycle 1,000. A–G correspond to a single realization with $\gamma =0.025$ and $\mu =0.05$. (H) $f_{nm}$ for three realizations with $\gamma =0.025$ and $\mu =0.05$.

Periodic limit cycles are only found at small shear amplitudes $\gamma \le 0.035$, suggesting minimal changes in the contact network during a shear cycle. However, we find this is not the case; during the cycle, over 10% of the contacts break and then reform by the completion of the cycle (Fig. 4G). This suggests much more subtle structural changes govern the onset and stability of these limit cycles. Just as the grains return to the same positions, both the normal and tangential contact forces return to the same values at the completion of a shear cycle in these limit cycle states. However, there is no immediate signature of the limit cycle onset in either the contact force distributions nor the number of contacts near yielding (SI Text). Note that our system exhibits microscopic periodicity in all degrees of freedom rather than the macroscopic periodicity of a few collectives degree of freedom, such as in the pressure and stress limit cycles recently observed in a 2D experimental system (14).

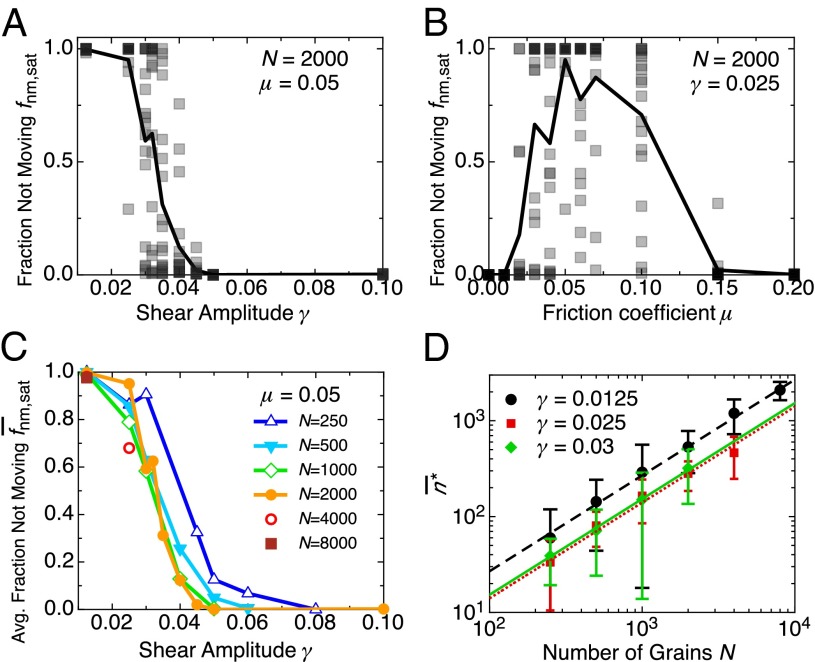
The exceptionally small cycle-to-cycle displacements in the Limit Cycle phase are still larger than our numerical precision of $\approx {10}^{-8}d$, although below $\approx {10}^{-4}d$ it becomes difficult to distinguish genuine displacements from nonphysical rattling motion due to rounding and truncation errors. We use the fraction of “not moving” grains $f_{nm}$, defined as the fraction of grains moving less than $\sqrt{{10}^{-9}{d}^2}=3.16\times {10}^{-5}d$ from one cycle to the next, as an order parameter to identify the onset of the Limit Cycle phase. $f_{nm}$ starts at zero as the particles initially diffuse around, and then rapidly increases and saturates at $f_{nm,sat}\approx 1$ when the particles organize into a limit cycle. However, the number of cycles needed to establish the limit cycle $n*$ and the fraction of the grains participating in exact limit cycle trajectories varies depending on the initial configurations (Fig. 4H). In the Limit Cycle phase, particularly near the phase boundaries, only a subset of the ensemble of simulations leads to a robust limit cycle with $f_{nm,sat}\approx 1$. Others still exhibit a sharp drop in D, but the cycle-to-cycle motion remains above our cutoff and $f_{nm,sat}<1$. In some cases, this motion reflects a higher-order periodicity, with grains returning to the same point only after multiple shear cycles, although in other cases the grain motion remains chaotic for the duration of the simulation (SI Text). However, the ensemble average smoothly increases from ${\overline{f}}_{nm,sat}\simeq 0$ in the Caged phase to ${\overline{f}}_{nm,sat}>0$ in the Limit Cycle phase as both μ and γ are varied (Fig. 5 A and B). For the phase boundaries in Fig. 2, we use the criteria ${\overline{f}}_{nm,sat}\ge 0.1$ to define the Limit Cycle phase.

Fig. 5.

Limit Cycle phase boundaries and onset. (A) $f_{nm,sat}$ vs. γ for $\mu =0.05$. (B) $f_{nm,sat}$ vs. μ for $\gamma =0.025$. (A and B) Squares: individual realizations. Solid line: ensemble average. (C) Ensemble averaged ${\overline{f}}_{nm,sat}$ vs. γ at $\mu =0.05$, varying the number of grains N. (D) Average number of shear cycles needed to establish a limit cycle $\overline{n}*$ vs. N for $\mu =0.05$. Lines show fits to $\overline{n}*=aN$ with (dashed line, $\gamma =0.0125$) $\gamma a=3.4\times {10}^{-3}\pm 5.6\times {10}^{-4}$, (dotted line, $\gamma =0.025$) $\gamma a=3.5\times {10}^{-3}\pm 6.9\times {10}^{-4}$, and (solid line, $\gamma =0.03$) $\gamma a=4.6\times {10}^{-3}\pm 1.4\times {10}^{-3}$. For ensemble averages, we used 20 realizations for $N\le \mathrm{2,000}$, 12 realizations for $N=\mathrm{4,000}$, and 5 realizations for $N=\mathrm{8,000}$. Error bars in D show the SD within an ensemble.

Although the detailed dynamics of individual realizations are sensitive to the initial configuration, this Limit Cycle phase is not sensitive to the simulation details. We observe limit cycles with flat walls and irregular walls, periodic and solid-wall y-boundaries, monodisperse and polydisperse grains, and linear and nonlinear (Hertzian) contact-force models (SI Text). To explore how the Limit Cycle phase depends on the system size, we vary the number of grains N from $N=250$ up to $N=\mathrm{8,000}$ at fixed $\mu =0.05$ and varying γ. For points deep in the Limit Cycle phase, the number of shear cycles needed to organize into a limit cycle $\overline{n}*$ increases with the number of grains as $\overline{n}*=aN$ (Fig. 5D). This scaling with system size reflects the global organization of the entire network of contacting grains in these limit cycle states. In contrast, the maximum shear amplitude for which limit cycles are observed varies little with N, suggesting that the boundaries for the Limit Cycle phase depend weakly on the system size (Fig. 5C).

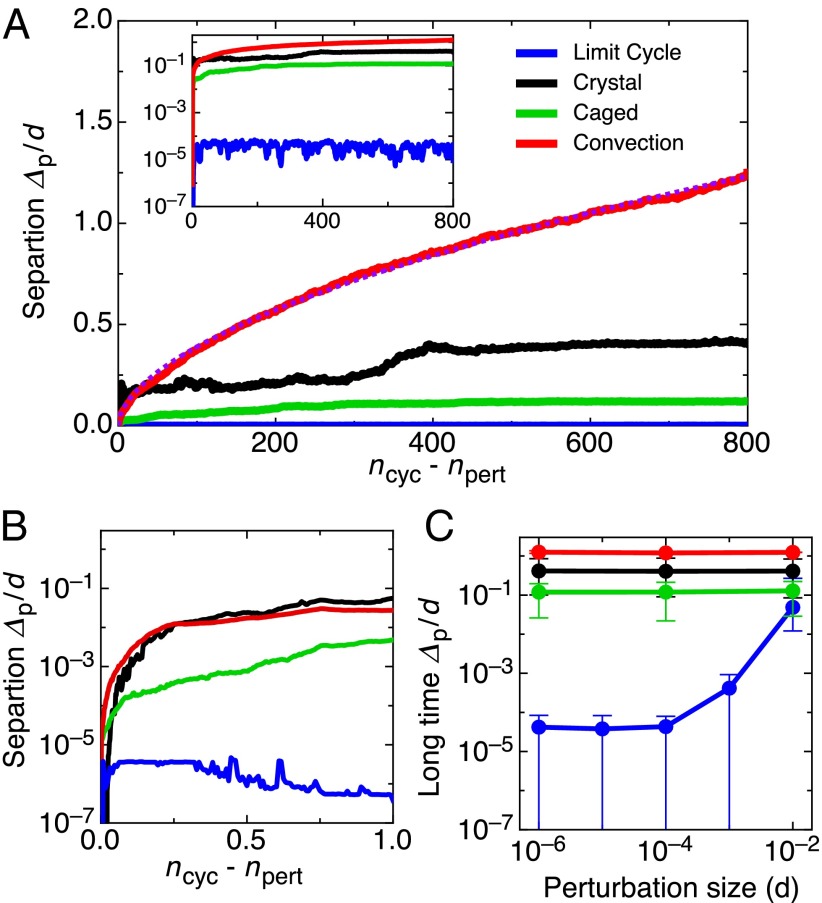
To further explore these Limit Cycle states, we examine how the dynamics respond to small perturbations. Following work on sheared suspensions (5, 22), we run pairs of identical simulations up to a cumulative shear of 100 to reach a steady state, and then perturb one of the copies by randomly displacing each grain a small distance drawn from a uniform distribution between $\left[-{\xi }_p,{\xi }_p\right]$. The simulations continue to run and we follow the evolution of the average separation between grain positions in the perturbed and unperturbed systems ${\mathrm{\Delta }}_p\equiv \sqrt{\langle {\left({\overrightarrow{r}}_{pert}-\overrightarrow{r}\right)}^2\rangle }$. Comparing ensemble averages of ${\mathrm{\Delta }}_p$ in each of the four phases (Fig. 6), we find that the Limit Cycle states stand out as remarkably stable against small perturbations. In the other three phases, after a perturbation with ${\xi }_p={10}^{-6}d$, ${\mathrm{\Delta }}_p$ increases four to five orders of magnitude over the course of a single shear cycle (Fig. 6B). Over the course of hundreds of shear cycles, the growth of ${\mathrm{\Delta }}_p$ slows, approaching a constant value $\approx 0.1d$ the Caged and Crystal phases while slowly increasing as ${\mathrm{\Delta }}_p\propto {\left(n_{cyc}-n_{pert}\right)}^{0.554}$ in the Convection phase (Fig. 6A). In the Limit Cycle phase, we do not see the rapid initial increase observed in the other phases, and over hundreds of shear cycles ${\mathrm{\Delta }}_p$ fluctuates around a constant value $\approx {10}^{-5}d$, orders of magnitude below the other phases. In the Caged, Crystal, and Convection phases, the long-time behavior of ${\mathrm{\Delta }}_p$ is independent of the perturbation size; however, in the Limit Cycle phase, the long-time separation begins to increase above ${\xi }_p={10}^{-4}d$ (Fig. 6C). This demonstrates that there is a finite range of stability for the limit cycle trajectories and that the difference in stability between the Limit Cycle and non-Limit Cycle states is evident in the short-time dynamics immediately following the perturbation.

Fig. 6.

Small perturbations. (A) Average separation ${\mathrm{\Delta }}_p/d$ between grain trajectories in perturbed and unperturbed systems in each of the different phases for ${\xi }_p={10}^{-6}d$. Values of μ and γ are the same as in Figs. 1 and 3. Dotted line: Fit to ${\mathrm{\Delta }}_p/d=A{\left(n_{cyc}-n_{pert}\right)}^{\beta }$ with $A=0.0304$ and $\beta =0.554$. Inset shows the same data on a log-linear axis. (B) Same data as in A, highlighting the separation during the first shear cycle following the perturbation. (C) Long-time separation evaluated at $n_{cyc}-n_{pert}=800$ vs. the perturbation size ${\xi }_p$. All data show an ensemble average of five realizations, each consisting of a perturbed and unperturbed copy. The system was sheared up to a cumulative shear of 100 to reach a steady state before perturbing the system.

Conclusions

These simulations reveal that a simple system of frictional grains under cyclic shear can give rise to a rich phase space of final states. In addition to mapping out boundaries in strain–friction space between different phases, previously observed in similar experiments, we have discovered a Limit Cycle phase, which could be experimentally realized in a sufficiently low-friction system. This phase differs substantially from the self-organized states typically encountered in driven far-from-equilibrium systems. The present system, with thousands of degrees of freedom, highly nonlinear and hysteretic equations of motion is a paradigm for chaotic behavior; therefore, it is surprising it exhibits a disordered absorbing state. The absorbing state dynamics found in non-Brownian suspensions at low Reynolds number are capable of encoding a rudimentary memory of the system’s driving history (23), yet in these systems noise is required to retain memories beyond a single shear amplitude. Recent simulations found that dense amorphous solids can retain multiple memories in a similar fashion, but without the need for added noise (24). It has been suggested that memory formation may be a generic feature in amorphous materials driven to a periodic absorbing state, although it remains to be explored how the hysteretic, frictional interactions alter or inhibit memory formation in these limit cycle states.

The limit cycle states found here correspond to fixed points in the dynamics that are uniquely stable to small perturbations. A better understanding of the connection between the mechanical structure of these configurations and this stability could open new avenues to understand yielding and flow in granular materials and other disordered materials. The unique ability of these limit cycle configurations to maintain their structure under repeated strain may also make relevant to the design of particulate-based self-healing materials (25) and soft robotic systems (26).

Materials and Methods

MD simulations of soft spheres with static friction are performed in 3D using LAMMPS (lammps.sandia.gov). Monodisperse grains are modeled as compressible spheres of diameter d that interact when in contact via a commonly used linear spring–dashpot model for the normal forces $F_n$ and a linear, history-dependent model for the tangential forces $F_t$:

$$F_n=k_n\delta +{\beta }_n\dot{\delta },$$ [1]

$$F_t=k_{t}u.$$ [2]

Here, δ is the overlap between contacting grains and u is the integrated tangential displacement, which accounts for sliding and rolling motion. Static friction is implemented by truncating the tangential force $F_t$ to satisfy the coulomb yield criteria $\left|F_t\right|<\mu \left|F_n\right|$, with μ as the static friction coefficient. See Table 1 for relevant simulation parameters. We verified that our results do not depend significantly on the choice of normal stiffness $k_n$, tangential stiffness $k_t$, or damping ${\beta }_n$ (which determines the restitution coefficient $e_n$).

Table 1.

Simulation parameters

Parameter	Value
Grain mass, m	$3.07\times {10}^{-3}\hspace{0.5em}\mathrm{kg}$
Grain diameter, d	0.0133 m
Gravitational acceleration, $\overrightarrow{g}$	$\left(-9.81\hspace{0.5em}\text{m}\mathrm{\cdot }{\text{s}}^{-2}\right)\widehat{z}$
Normal stiffness, $k_n$	$2.0\times {10}^{4}mg/d$
Normal damping, ${\beta }_n$	$12.4\times {10}^{4}m\sqrt{g/d}$
Restitution coefficient, $e_n$	0.5
Normal stiffness, $k_t$	$\frac{2}{7}{k}_n$
Time step, $\mathrm{\Delta }t$	$2.5\times {10}^{-5}$ s
Shear rate, $\dot{\gamma }$	0.03 s−1

The shear cell is $17d\times 11d$ in the $x\times y$ directions and periodic in y. It is typically filled with $N=2,000$ grains to roughly $11d$ in z. The top surface is open to allow the packing to dilate or compact, so the pressure in the pack of grains is set by the weight of the grains and varies with depth. The walls are made of polydisperse grains distributed between $0.65d$ and $1.2d$ and interact with the grains through the same force law as between pairs of grains in the pack. When varying the number of grains N, we adjusted the cell dimensions to maintain nearly the same aspect ratio for all values of N.

The sample is prepared by pouring in frictional particles under gravity and allowing them to settle with $\mu =0$ to generate a dense initial packing. We randomize the initial positions of the grains during this chaotic pouring process, where energetic grains violently bounce around the shear cell, to generate an ensemble of different initial configurations. The friction is reset to the desired value before initiating the shear, so that all simulations with different μ and γ start from the same set of initial packing configurations. Starting from a loose initial packing with finite friction does not affect the average long-time behavior. The shear rate $\dot{\gamma }$ is slow enough that the flow is “quasi-static,” meaning the ratio of the inertial timescale ($\sqrt{d^2\rho /P}$, where P is the pressure, d is the particle diameter, and ρ is the grain density) to the shear timescale $1/\dot{\gamma }$ is less than ${10}^{-3}$ throughout the system (27, 28). In this limit, the behavior of the grains is on average independent of the shear rate, which we verify by varying the shear rate over a factor of 8 (from 2 times faster to 4 times slower).

We compute the packing density using Voronoi tessellations to define a cell volume for each grain. The total volume $V_{tot}$ is the sum of the cell volumes, excluding cells touching walls or the top surface and $V_{grain,tot}=n_{cells}{v}_p$, where $n_{cells}$ is the number of cells and $v_p=\pi d^3/6$ is the volume of a single grain. The finite grain compressibility results in packing densities that are roughly ∼1% higher than in a similar packing of hard spheres. The global initial packing density varied little across the ensemble of initial configurations ${\overline{\varphi }}_0=0.643\pm 0.001$.