Mathematical models of electrical activity of the pancreatic β-cell: A physiological review

Abstract

Mathematical modeling of the electrical activity of the pancreatic β-cell has been extremely important for understanding the cellular mechanisms involved in glucose-stimulated insulin secretion. Several models have been proposed over the last 30 y, growing in complexity as experimental evidence of the cellular mechanisms involved has become available. Almost all the models have been developed based on experimental data from rodents. However, given the many important differences between species, models of human β-cells have recently been developed. This review summarizes how modeling of β-cells has evolved, highlighting the proposed physiological mechanisms underlying β-cell electrical activity.

Abbreviations

T2D

Type 2 Diabetes

GSIS

glucose-stimulated insulin secretion

Ca²⁺

calcium ions

ATP

adenosine triphosphate

ADP

adenosine diphosphate

K_ATP

ATP-sensitive K⁺ channels

[ATP]_i

cytosolic ATP

V_m

membrane potential

VDCC

voltage-dependent Ca²⁺ channels

[Ca²⁺]_i

intracellular calcium concentration

TRP

transient receptor potential

PMCA

plasma membrane Ca²⁺-ATPase

NCX

Na⁺/Ca²⁺ exchanger

ER

endoplasmic reticulum

SERCA

sarco-endoplasmic reticulum Ca²⁺-ATPase

IP₃R

inositol-1,4,5-trisphosphate receptors

RyR

ryanodine receptors

MCU

mitochondrial Ca²⁺ uniporter

mNCX

mitochondrial Na⁺/Ca²⁺ exchanger

[Ca²⁺]_m

mitochondrial calcium

K_Ca

Ca²⁺-dependent K⁺ channels

K_v

voltage-dependent K⁺ channels

CK

Chay-Keizer

CRAC

calcium release-activated current

[Na⁺]

Na⁺ concentration

DOM

dual oscillator model

HERG

human eter à-go-go related gene

TCA

trycarboxylic acid cycle

FBP

fructose-1,6-bisphosphate

PFK

phosphofructokinase

F6P

fructose-6-phosphate

cAMP

cyclic AMP

ROS

reactive oxygen species

GLUT

glucose transporter

Introduction

Insulin, synthesized and secreted by the pancreatic β-cells of the islets of Langerhans, is the only hormone responsible for lowering blood glucose levels. Under normal conditions, blood insulin is pulsatile both in humans and in rodents.^1,2 Interestingly, insulin oscillations are disrupted in patients with Type 2 Diabetes (T2D).³ It has been shown that single β-cells contribute to the oscillations of insulin at higher levels of organization,⁴ underscoring the importance of studying β-cell functioning at the cellular level.

In β-cells, glucose-stimulated insulin secretion (GSIS) is mediated by the increase of intracellular calcium concentration ([Ca²⁺]_i), driven by a well-established sequence of events (Fig. 1), beginning with the transport of glucose into the cell through the glucose transporters (GLUT), accelerating the metabolism and therefore the production of adenosine triphosphate (ATP) at the expense of adenosine diphosphate (ADP). This induces an increase in the ATP/ADP ratio, causing the closure of the ATP-sensitive K⁺ channels (K_ATP), and consequently, promoting the slow depolarization of the membrane potential (V_m) upon the threshold value at which the voltage-dependent Ca²⁺ channels (VDCCs) are activated, allowing the influx of calcium ions (Ca²⁺). It is the increase in [Ca²⁺]_i that finally promotes insulin secretion. This is the main pathway of GSIS, and it is referred to as the triggering or K_ATP-dependent pathway (Fig. 1). As a complement to the triggering pathway, GSIS is regulated by the amplifying pathway, also known as the K_ATP-independent pathway, which enhances the effects of [Ca²⁺]_i on the exocytotic machinery.^5–7

Figure 1.

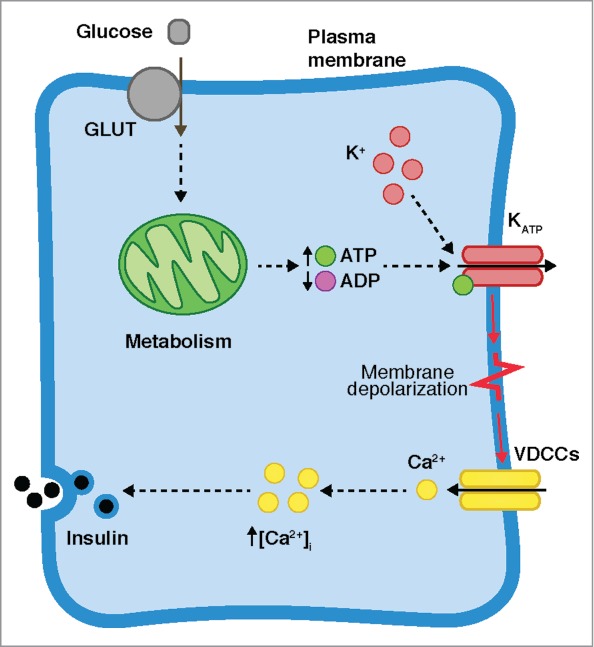
Glucose-stimulated insulin secretion (GSIS). After glucose is transported into the cell by the GLUT transporters, it is metabolized, potentiating the production of ATP and the closure of the ATP-sensitive K⁺ channels (K_ATP). The membrane is depolarized and voltage-dependent Ca²⁺ channels (VDCCs) are activated, allowing the influx of Ca²⁺. The increase of the intracellular Ca²⁺ concentration ([Ca²⁺]_i) stimulates Ca²⁺-dependent insulin secretion.

Alterations in β-cells are highly related to impaired fasting glucose and/or impaired glucose tolerance, which eventually progress to T2D,⁸ a disease characterized by insulin resistance and β-cell dysfunction. Several factors are known to impair the proper secretion of insulin at the cellular level. For example, mutations in ionic channels have been associated with a higher diabetes risk.^9–11 Moreover, it has also been demonstrated that defective β-cell sensitivity and impaired metabolism could result in hyperglycemia and eventually in T2D.^12,13

As a complement to experimental work, mathematical models of β-cells have been used to elucidate how the cellular mechanisms involved in GSIS interact, providing feasible explanations and hypotheses to experimental observations in β-cells. Models have grown in complexity as new experimental evidence has emerged: from the early minimal models that included a few ionic channels and a basic representation of Ca²⁺ handling and metabolism, to the current complex models that incorporate detailed representations of glycolysis and ATP production, and the recent appearance of models of human β-cells.

The aim of this work is to give a general overview of the progress in the field of β-cell modeling from a physiological perspective; thus, a detailed discussion about the mathematical aspects of the models is beyond the scope of this review. Interested readers are referred to other works on the subject.^14–16

This review is structured as follows. First, a brief introduction to the physiology of the pancreatic β-cells considered in mathematical models is presented. In the following section, we address the evolution of mathematical models of β-cells, including the most recent models developed specifically for human β-cells. Finally, we briefly discuss the applications and limitations of the mathematical models of the pancreatic β-cells.

General Overview of the Cellular Mechanisms Involved in the Electrical Activity of β-cells

Electrophysiology of the β-cell

The changes in membrane potential needed to allow the influx of Ca²⁺ through the VDCCs are generated through the concerted action of ionic transport mechanisms (ionic channels, pumps, and exchangers), which are regulated by ligands (e.g., Ca²⁺ or ATP) or by the V_m itself. Several ionic channels participate in the formation of the electrical activity pattern, including voltage-dependent Ca²⁺, Na⁺, and K⁺ channels and Ca²⁺-dependent K⁺ and Ca²⁺ channels.^17–20 Of special interest is the K_ATP channel, which links the changes in glucose metabolism to the electrical activity in β-cells.²¹ Nonselective cationic channels, like the transient receptor potential channels (TRP) have also been found in β-cells.^17,20 The detailed electrophysiological properties of ionic channels in β-cells can be found elsewhere.^17,18,20

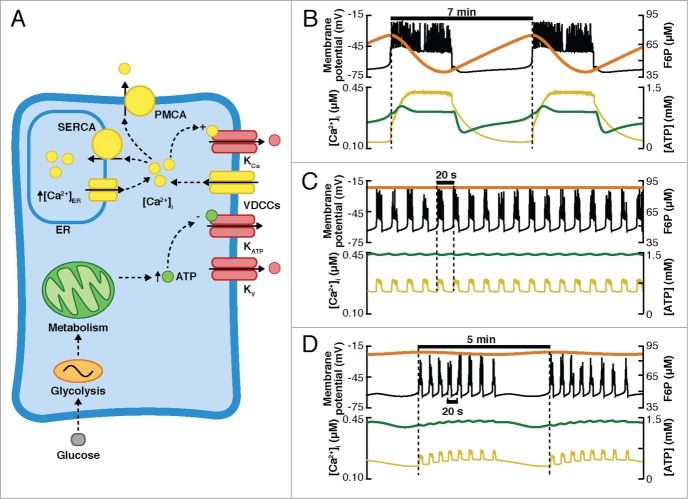
The expression of specific ionic channels differs between species,^22,23 which is reflected in the corresponding pattern of electrical activity (for recent reviews see refs. ^{10, 17, 20, 24}). In rodents, β-cells exhibit a characteristic electrical pattern, composed of slow oscillations in V_m, above which action potentials are superimposed.^17–19 This is known as bursts of action potentials, or bursting electrical activity. Heterogeneous bursting patterns have been reported in rodents,^25,26 which can be classified as “fast” (period of <60 s), “slow” (period from 1 to several minutes), and “mixed” or “compound” oscillations (fast oscillations superimposed on slow oscillations). Simulations of the distinct electrical patterns observed experimentally in rodent cells are shown in Fig. 2A (experimental recordings can be seen in Fig. 1 in ref. 25). On the other hand, in human β-cells, action potential firing is the most common electrical behavior, although bursting has been observed occasionally.^10,22,27,28 Simulations reproducing the electrical patterns observed in the human β-cell (see Figs. 1, 2 and 6 in ref. ²⁸ for the experimental recordings) are shown in Fig. 2B.

Figure 2.

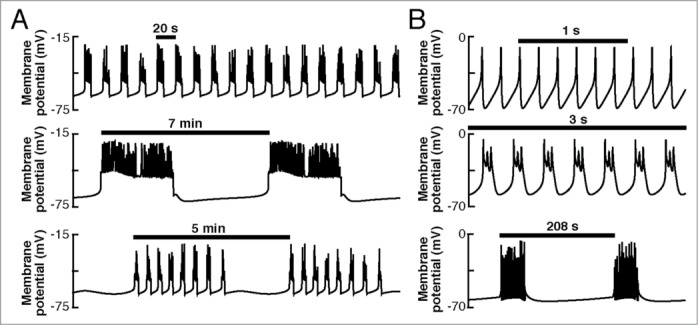
Electrical activity patterns in pancreatic β-cells. (A) Simulated fast (top), slow (middle), and compound (bottom) bursting behavior in rodent cells (simulations made with the Dual Oscillator Model¹²⁰). (B) Simulations of action potential firing (top), fast (middle), and slow (bottom) bursting in human cells (simulated with the model of the human β-cell of Riz et al.²⁸).

Calcium handling and metabolism

An increase in cytosolic Ca²⁺ concentration is used as a signal to control insulin exocytosis. It has been observed that [Ca²⁺]_i oscillates in synchrony with membrane potential^29–33 and that insulin exocytosis occurs when Ca²⁺ channels are active.^34–36 Several mechanisms are responsible for the oscillations of [Ca²⁺]_i. Calcium entry is mediated by the activity of voltage-gated Ca²⁺ channels, whereas Ca²⁺ is extruded from the β-cell mainly by the plasma membrane Ca²⁺-ATPase (PMCA)³⁷ and the Na⁺/Ca²⁺ exchanger (NCX).^38,39

Once in the intracellular space, [Ca²⁺]_i is regulated by internal stores, namely the endoplasmic reticulum (ER) and the mitochondria. The ER captures Ca²⁺ through the sarco-endoplasmic reticulum Ca²⁺-ATPase (SERCA) during the rise in [Ca²⁺]_i caused by the effects of depolarization on the VDCCs. This limits the amplitude of [Ca²⁺]_i oscillations. Upon membrane repolarization, Ca²⁺ is released from the ER, preventing an abrupt drop in [Ca²⁺]_i.^40,41 Efflux of Ca²⁺ from the ER through channels such as inositol-1,4,5-trisphosphate receptors (IP₃Rs) or ryanodine receptors (RyRs) is controlled by Ca²⁺ itself or by intracellular messengers (e.g., IP₃).^41–43 This enables the β-cells to respond to muscarinic agonists by releasing Ca²⁺ from the ER to the cytoplasm.⁴⁴ In addition, it has been shown that the ER is relevant for both the oscillations of [Ca²⁺]_i and the control of V_m.⁴⁵

On the other hand, mammalian mitochondria have a high capacity for Ca²⁺ uptake, although it is known that under resting conditions mitochondria do not play an important role as Ca²⁺ deposits as there is not a significant gradient between cytosolic and mitochondrial Ca²⁺ ([Ca²⁺]_m).^12,46 It has been proposed that mitochondria serve as a buffer of Ca²⁺ that limits the amplitude of the cytosolic Ca²⁺ transients.^47,48 A rise in [Ca²⁺]_i is relayed to the mitochondria where Ca²⁺ influx is mediated by the mitochondrial uniporter (MCU), which transports Ca²⁺ from the cytosol into the mitochondrial matrix. Ca²⁺ is then regulated by the mitochondrial Na⁺/Ca²⁺ exchanger (mNCX), responsible for Ca²⁺ efflux from the mitochondria.^49,50

Mitochondria and glucose metabolism play an extremely important role in the control of GSIS (extensively reviewed in refs. ^{12, 51–54}). In β-cells the first stage of metabolism is glycolysis, where glucose is metabolized to pyruvate by means of a complex cascade of enzymatic reactions. Pyruvate is then processed during the TCA (trycarboxylic acid) cycle, resulting in the electron carriers NADH and FADH₂, which are then used to generate a proton gradient across the mitochondrial membrane. The resulting proton flux through the ATP synthase finally drives the phosphorylation of ADP to ATP. ATP then regulates the activity of the K_ATP channels²¹ and drives several ATP-consuming processes of the cell, such as those involving Ca²⁺-ATPases (e.g., PMCA and SERCA),^38,45,55 and insulin exocytosis.⁵⁶ In spite of the higher demand for ATP due to the activation of the ATP-consuming processes, a net increase in the cytosolic ATP/ADP ratio has been observed.^49,57 This overcompensation can be explained by 2 factors: the greater availability of glucose to be metabolized in the first place and the subsequent effect of the increase of [Ca²⁺]_m in the oxidation of glucose,⁵² which is known to involve the activation of the mitochondrial dehydrogenases and other enzimes.^58–60 Consistent with this proposal, a biphasic behavior was observed in measurements of the ATP/ADP ratio and oxygen consumption.^49,57 In addition, it has been proposed that [Ca²⁺]_m also has a negative effect on ATP production by reducing the proton motive force,^48,61,62 although there is a large body of evidence that the overall effect of mitochondrial Ca²⁺ is to potentiate rather than to inhibit ATP production.^49,52,63 For example, it has been demonstrated that glucose oxidation is considerably reduced when Ca²⁺ influx is prevented.^64,65 In addition, recent studies^49,57 have demonstrated that increases of mitochondrial Ca²⁺ are required for normal changes in the ATP/ADP ratio to occur in response to glucose stimulation. Detailed models addressing the role of the main processes involved in energy metabolism in β-cells have been developed recently.^66,67 Besides the role of mitochondria in the triggering pathway of insulin secretion, it has been proposed that mitochondrial-derived metabolites are involved in the amplifying pathway of insulin secretion.^51,68 However, the role of mitochondria in this K_ATP-independent pathway is still poorly understood.

Insulin secretion is pulsatile with a period of several minutes.² Given that metabolic oscillations with a similar period have been observed,^{61,62,64,69–75} it has been proposed that they are involved in the generation of the pulsatile behavior of insulin secretion. For example, oscillations both in the cytosolic ATP ([ATP]_i) and ATP/ADP ratio have been linked to oscillatory changes in the conductance of the K_ATP channels.^69,70,72 In addition, oscillations in NAD(P)H,^64,73 O₂,⁷⁴ mitochondrial membrane potential,^61,62 and cAMP⁷⁵ have been reported. The origin of these oscillations is still matter of debate, though at least 2 hypotheses have been proposed. On the one hand, it has been suggested that metabolic oscillations are generated during glycolysis by the positive feedback of the product FBP onto the PFK activity.^76,77 On the other hand, other authors have proposed that the interplay between the production and consumption of ATP is responsible for the observed oscillations in [ATP]_i.^55,72,78 Interestingly, in a recent study, Tanaka et al.⁷⁹ failed to observe significant oscillations in cytosolic ATP in mouse islets during GSIS, in contrast to the oscillations of sub-membrane ATP reported by Li et al.⁵⁵

It is likely that mitochondrial dysfunction is involved in the onset of T2D and its related complications (reviewed in refs. ^80–82). For example, in islets from diabetic subjects it has been shown that mitochondria have an altered morphology.⁸³ In addition, reduced glucose oxidation, oxygen consumption and ATP production have been also reported.^83,84 Moreover, it has been proposed that alterations in the free radicals derived from metabolism (reactive oxygen species, ROS) could have negative effects on glucose oxidation.^51,63 It is thought that novel therapies to treat diabetes may involve pharmacologic agents targeting mitochondria whether to enhance mitochondrial function or to reduce negative effects of alterations in metabolism.⁸²

Mathematical Models of Pancreatic β-Cells

Models of β-cells have been proposed as a tool to explain how the cellular mechanisms involved in GSIS interact. Most of the cellular processes mentioned in the previous section have been included in models of β-cells. In this section, several models based on both mouse and human β-cells are described in terms of the physiological mechanisms involved. Model descriptions are accompanied with a schematic diagram of the corresponding physiological hypothesis. Simulations showing the behavior of key variables are also presented. Implementation of the models and simulations were performed in Mathematica 9.0 (Wolfram Research, Inc., Champaign, IL).

Models of rodent β-cells

Dean and Matthews^85,86 provided the first evidence of changes in the membrane potential of β-cells induced by glucose, consisting of fast bursting electrical activity. This fast pattern has been observed in isolated single mouse β-cells and isolated islets.^26,87,88 Several hypotheses have been proposed and analyzed theoretically in order to elucidate the cellular mechanisms responsible for the fast bursting behavior. In their pioneering model, Chay and Keizer⁸⁹ (CK model) were able to reproduce fast bursting electrical behavior (Fig. 3B, top panel). The CK model (Fig. 3A) includes Ca²⁺-dependent K⁺ channels (K_Ca) and voltage-dependent Ca²⁺ and K⁺ channels (VDCCs and K_v, respectively). Intracellular calcium handling was modeled in a minimal manner. As proposed by Atwater et al.,⁹⁰ the CK model uses the effects of [Ca²⁺]_i in the large conductance K_Ca channels as the mechanism to initiate or terminate the bursts of action potentials (Fig. 3B, bottom panel). During the active phase, sustained by K_v channels and VDCCs, [Ca²⁺]_i increases slowly, activating the K_Ca channels and leading to membrane repolarization. During the silent phase, Ca²⁺ entry through VDCCs is inhibited, resulting in a decrease in [Ca²⁺]_i due to the extrusion of Ca²⁺ from the cytosol. The K_Ca channels are then gradually closed, inducing depolarization of the membrane potential at which VDCCs and K_v are activated, initiating a new burst of action potentials. In this model, bursting depends entirely on one pacemaker variable ([Ca²⁺]_i). The hypothesis proposed by the CK model was discarded when [Ca²⁺]_i was measured in β-cells, revealing more rapid dynamics than predicted by the model.^29,30 Moreover, blocking K_Ca channels with charybdotoxin produced no significant effect on the electrical activity.⁹¹ Recently, Houamed et al.⁹² showed that the BK channels do contribute to the repolarization of the action potentials in mouse β-cells, without a relevant role in the duration of the active and silent phases of the bursting electrical pattern. In spite of the evidence against this hypothesis, practically all the existing models of β-cells are based on the minimal CK model. Subsequent models were able to generate fast bursting using the same mathematical principle as the CK model, only changing the identity of the slow pacemaker variable.

Figure 3.

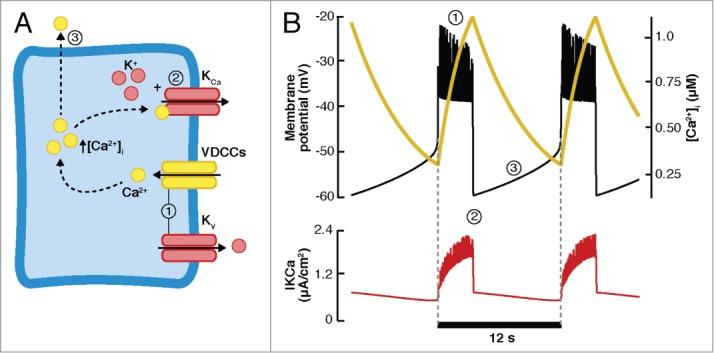
Minimal model of Chay and Keizer (CK model). A. Scheme of the CK model. The active phase (1) is sustained by the VDCCs and K_v channels, slowly increasing [Ca²⁺]_i. The K_Ca channels are activated, eventually repolarizing the membrane (2). During the silent phase (3), the VDCCs and K_v channels are closed and Ca²⁺ is extruded from the cell, inhibiting the activity of the K_Ca channels. The slow depolarization eventually activates the VDCCs and K_v channels, initiating a new burst. B. Fast bursting simulated with the CK model. Top: Membrane potential (black curve) and intracellular Ca²⁺ concentration ([Ca²⁺]_i, yellow curve). Bottom: Ca²⁺-dependent K⁺ (K_Ca) current.

Motivated by electrophysiological studies by Rorsman and Trube,⁹³ Chay et al.⁹⁴ replaced the K_Ca channels in the CK model with voltage-activated Ca²⁺-inactivated Ca²⁺ channels. In contrast to the CK model, in which the K_Ca channels are activated by an increase of [Ca²⁺]_i, in this proposal the Ca²⁺ channels are inactivated by the changes in [Ca²⁺]_i itself, allowing the K⁺ current to repolarize the membrane potential at the end of the burst of action potentials. Although it is well known that Ca²⁺ currents are extremely important for the electrical activity and insulin secretion both in mouse and human cells,^22,31,95 their role as a pacemaker variable lacks sufficient experimental support.²⁶

In 1984, K_ATP channels were identified in rodent β-cells,^96,97 emerging as a feasible link between metabolism and electrical activity. In short, the activity of the K_ATP channels is inhibited by ATP and stimulated by ADP. The K_ATP channels are extremely important for β-cells, being responsible for the resting membrane potential of β-cells. In addition, the closure of the K_ATP channels due to an increase of the cytosolic ATP allows inward currents carried by Na⁺ and/or Ca²⁺ to depolarize, thus triggering electrical activity.^10,21,97,98

Keizer and Magnus^99-101 and Smolen and Keizer¹⁰² introduced K_ATP channels to the models of β-cells in order to analyze the role of the cyclical changes in the ATP/ADP ratio in β-cell electrical activity. In general, these models follow the hypothesis (see Fig. 4) that stipulates that during the active phase of the electrical activity, the cytosolic ATP concentration decreases due to the inhibiting effects of Ca²⁺ on the production of ATP (i.e., increasing ADP). As a consequence, K_ATP channels are activated, repolarizing the membrane potential. Closure of VDCCs during the silent phase inhibits Ca²⁺ entry and its negative effects on ATP production, allowing [ATP]_i to increase, inhibiting K_ATP channels and initiating the slow depolarization to the threshold potential of activation of the VDCCs and K_v channels, once again initiating the active phase.

Figure 4.

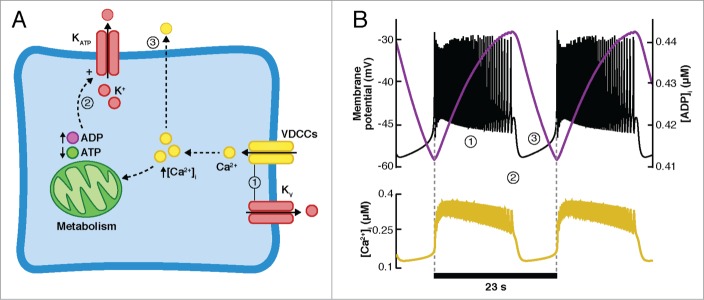
Oscillations in ATP regulate the conductance of the K_ATP channels. (A) During the active phase (1), sustained by the VDCC and the K_v channels, [Ca²⁺]_i increases, exerting a negative effect on the production of ATP, reflected in the increase in ADP and the corresponding decrease in the ATP/ADP ratio. The K_ATP channels are slowly opened, eventually repolarizing the membrane (2). During the silent phase, VDCCs are inhibited, and the influx of Ca²⁺ is ceased as Ca²⁺ is also extruded from the cell. As [Ca²⁺]_i decreases, the production of ATP is potentiated, closing the K_ATP channels and initiating slow depolarization (3). (B) Simulations with the model of Smolen-Keizer. Top: V_m (black curve) and [ADP]_i (purple curve). Bottom: the fast dynamics of [Ca²⁺]_i resembles the experimental observations.

The model of Keizer and Magnus⁹⁹ uses the changes in [ADP], following the slow oscillations in [Ca²⁺]_i as the pacemaker variable that triggers the transition between the active and silent phase of electrical activity by regulating the conductance of the K_ATP channels. One important drawback of this model is that, as in other models described above, the slow dynamics of [Ca²⁺]_i contradicts the fast dynamics observed experimentally.^29,30 However, Keizer and Magnus provided an equation for the K_ATP current that is still used in recent models. On the other hand, the Smolen-Keizer¹⁰² model (SK model) was able to reproduce the fast dynamics of [Ca²⁺]_i oscillations including an improved model of the Ca²⁺ currents. As can be seen in Figure 4B, where simulations performed with the SK model are shown, ADP concentration rises slowly during the active phase and [Ca²⁺]_i closely follows the dynamics of V_m. Assuming a constant nucleotide concentration, the latter means that ATP is declining during the active phase, thus activating the K_ATP channels and repolarizing the membrane potential. As mentioned above, these models assume a negative influence of Ca²⁺ in ATP production. Given the importance of metabolism on GSIS, Magnus and Keizer⁴⁸ developed a minimal model of β-cell mitochondrial Ca²⁺ handling, considering only the negative effects of Ca²⁺ in ATP production and neglecting the activation of the dehydrogenases by Ca²⁺. Later, they extended their model to include a more refined representation of glucose metabolism (including, for example, the activation of dehydrogenases) and combined it with a model of the electrical activity induced by glucose.^100,101 With this complex model, they explored the role of mitochondrial Ca²⁺-handling mechanisms during glucose-stimulated electrical activity.

There is experimental evidence of oscillations both in cytosolic ATP^55,72 and K_ATP channel conductance during glucose stimulation,¹⁰³ which supports this hypothesis. However, others have reported the persistence of electrical activity in β-cells that lack functional K_ATP channels,¹⁰⁴ possibly indicating that the modulation of K_ATP channel conductance by the ATP/ADP ratio is not the only pacemaker mechanism for bursting electrical activity. In addition, Ravier et al.¹⁰⁵ have suggested that K_ATP channels are not the only mechanism linking glucose metabolism with Ca²⁺-dependent insulin release via changes in membrane potential. The models based on the oscillations of the ATP/ADP ratio to produce bursting electrical activity by regulating the conductance of the K_ATP channels are unable to reproduce these observations, although it should be noted that the identity of the mechanism driving bursting electrical activity in K_ATP deficient β-cells is still unclear.

It has been proposed that ATP-consuming processes activated due to an increase of [Ca²⁺]_i (e.g., Ca²⁺-pumps) could be the origin of the observed oscillations in cytosolic ATP.^26,55,78,106 Recent ATP measurements in the sub-membrane compartment in β-cells suggest that Ca²⁺ extrusion mechanisms are responsible for the observed oscillations in ATP,⁵⁵ giving support to this proposal. Whether the changes in the conductance of the K_ATP channels are mediated by the influence (negative or positive) of Ca²⁺ in ATP production or by the interplay between ATP production and consumption is still a matter of debate. Other complex models that include a detailed description of glucose metabolism were developed later,^77,107,108 though based on the hypothesis of intrinsic glycolytic oscillations as the origin of the oscillatory behavior of β-cells (described below).

In contrast to the fast oscillations observed by Dean and Mathews,^85,86 Smith et al.¹⁰⁹ reported slow bursting activity with a periodicity of minutes. In order to explain the origin of the slow oscillations observed experimentally in single cells, clusters of β-cells, and isolated islets,^26,88,109 Bertram et al.¹¹⁰ and Chay et al.¹¹¹ included the endoplasmic reticulum (ER) as a second Ca²⁺ compartment in β-cell models (Fig. 5A). As observed experimentally, in these models, Ca²⁺ is transported into the ER by the SERCA pumps during the active phase of the electrical activity and is released during the silent phase, mainly through the IP₃ receptor channels and the ryanodine receptor channels.^41-43 One important aspect of these models is the presence of non-specific calcium release-activated currents (CRAC) in the β-cells. The main idea (depicted schematically in Fig. 5A) is that during the silent phase, Ca²⁺ is slowly released from the ER, preventing an abrupt drop of [Ca²⁺]_i (Figs. 5B and C, bottom panel). As [Ca²⁺]_i is extruded from the cell, the inactivation of the Ca²⁺-inactivating Ca²⁺ current is removed. Simultaneously, as the Ca²⁺ concentration in the ER ([Ca²⁺]_ER) declines, the CRAC current increases. Eventually, the combination of these 2 currents becomes large enough to initiate a new burst. Then, [Ca²⁺]_i is increased, driving the transport of Ca²⁺ into the ER, promoting inactivation of both the Ca²⁺ and CRAC currents. Finally, when these currents are sufficiently small, the active phase terminates. In terms of periodicity, models including [Ca²⁺]_ER as a second slow process were able to generate both fast and slow bursting (Figs. 5B and C), in contrast to models that depend on a single slow process (e.g., [Ca²⁺]_i in the CK model or [ADP] in the SK model), which only generated bursting with a periodicity of seconds (fast oscillations).^16,112 The period of the oscillations in models including the ER is determined by the release rate of Ca²⁺ from the ER. When the release rate is low, [Ca²⁺]_ER reaches a high level during the active phase, and because Ca²⁺ is released from the ER slowly, [Ca²⁺]_i stays elevated (thus making the Ca²⁺-dependent Ca²⁺ channels inactive), preventing the initiation of a new burst of action potentials. By including the ER, it was possible to simulate the effects of muscarinic agonists (e.g., acetylcholine) in the electrical activity of β-cells, which are known to mediate Ca²⁺ release from the ER.¹¹³

Figure 5.

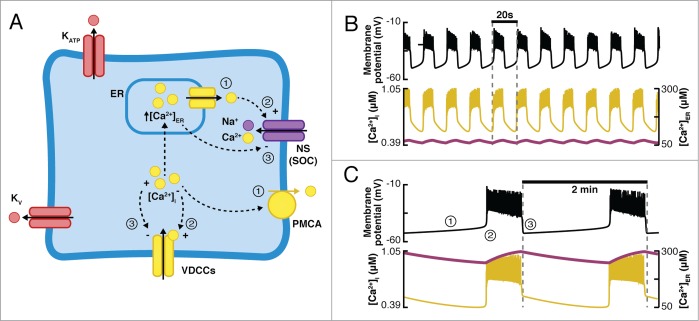
(A) Diagram of the models including ER as a second Ca²⁺ compartment and a non-specific calcium release-activated current (CRAC). During the silent phase (1), Ca²⁺ is released from the ER to the cytoplasm and is simultaneously extruded from the cell. This results in the activation of the CRAC current and the Ca²⁺-inactivated Ca²⁺ current, driving slow depolarization and initiation of a burst of action potentials (2). As [Ca²⁺]_i increases and Ca²⁺ is captured by the ER during the active phase, both the CRAC and the Ca²⁺-inactivating Ca²⁺ currents are inhibited, resulting in membrane repolarization (3). (B and C) Simulations using the model of Chay¹¹¹ including ER. Fast (B) and slow (C) bursting is produced by modifying the release rate of Ca²⁺ from the ER. In both cases, V_m (top, black curve), [Ca²⁺]_i, and [Ca²⁺]_ER (bottom, yellow and purple curves, respectively) are shown.

Other authors have proposed alternative mechanisms to explain the differences in the periodicity of bursting. Bertram et al.²⁵ developed a model based on the idea that the periodicity of bursting is determined by the interaction between a fast and a slow oscillatory variables. These models are capable of producing bursting with an intermediate period, distinct from the periods of the fast and slow variables. Because of this behavior, the models based on this principle are called phantom bursters. In addition, models using the phantom bursting mechanism can also produce fast and slow bursting, mediated entirely by fast and slow variables, respectively. Actually, the models described above that included the ER for the first time^110,111 are phantom bursters, though they were identified as such later (see ref. 16), after the appearance of phantom bursting proposal.²⁵ The identity of the fast and slow processes has been extensively investigated by means of mathematical models (see below).

With the discovery of a slow K_Ca current (TEA and charybdotoxine-insensitive) by Gopel et al.,¹¹⁴ the feedback of Ca²⁺ onto the K_Ca channels returned as a feasible candidate mechanism responsible for the periodicity of bursting activity. This was explored theoretically by Goforth et al.¹¹⁵ Simulations by Fridlyand et al.²⁶ support the idea that bursting with a periodicity of seconds could be driven by the Ca²⁺-dependent K⁺ current. However, this remains to be established experimentally.

Fridlyand et al.¹⁰⁶ proposed Na⁺ concentration ([Na⁺]) as an alternative slow mechanism (Fig. 6A). This model includes components that regulate the dynamics of Na⁺ in β-cells, namely the Na⁺/Ca²⁺ exchanger (NCX) and the Na⁺/K⁺ pump. They suggested that the increase of [Ca²⁺]_i during the active phase drives Na⁺ influx through the NCX exchanger, provoking a slow increase in [Na⁺]_i (Fig. 6B). This activates the Na⁺/K⁺ pump, carrying the net outward current responsible for burst repolarization. In the course of the silent phase, [Na⁺]_i decreases due to a reduction in the activity of the NCX exchanger, leading to the inhibition of the outward current generated by the Na⁺/K⁺ pump and membrane depolarization. Eventually, a new burst is initiated and the cycle is repeated. Other slow processes were also considered (i.e., ADP, IP₃, [Ca²⁺]_ER). This model was later extended in order to include more detailed models for the interactions between [Ca²⁺]_i, ATP/ADP, conductance of the K_ATP channels, and consumption of oxygen and glucose.¹¹⁶ It is important to note that in these models [Ca²⁺]_i shows a sawtooth like behavior that is followed by both [Na⁺]_i and the INa⁺/K⁺ current (see Fig. 6B). As mentioned before, experiments^29,30 have shown a more square shaped time course of [Ca²⁺]_i resembling the behavior of V_m. The model of Fridlyand et al.^106,116 is capable of generating square-shaped oscillations in [Ca²⁺]_i by modifying certain parameters (e.g., decreasing the rate of IP3 synthesis, see Fig. 3 in ref. 106) or by fixing other slow variables (e.g., [ATP]_i, [Na⁺]_i and [IP3]_i) to a constant value (see Fig. 6 in ref. 106). The role of [Na⁺]_i in β-cells has not been sufficiently studied. However, there is evidence of occasional oscillations of [Na⁺]_i in mouse β-cells, which can be associated with Ca²⁺ influx and the periodic activation of the NCX exchanger.¹¹⁷ To our knowledge, simultaneous measurements of V_m, [Ca²⁺]_i, and [Na⁺]_i in β-cells have not been performed, which could clarify the role of Na⁺ in GSIS. The framework of the models of Fridlyand et al.^106,116 was used by Cha et al.¹¹⁸ to analyze the contribution of the ionic channels involved in the GSIS in the distinct electric behaviors observed at different glucose levels. The authors concluded that the K_ATP channels mediate bursting at the physiological range of glucose. In addition, their simulations predicted that at higher glucose levels, the role of the K_ATP channels becomes practically negligible, as the electrogenic transport mechanisms (i.e. PMCA, NCX and Na⁺/K⁺ pump), together with a nonselective current, become more important for the regulation of bursting. Cha et al.¹¹⁹ further identified the fast ([ATP]_i or the inactivation gate of the Ca²⁺ current) and slow ([Na⁺]_i or [Ca²⁺]_ER) processes in their model as defined by the phantom bursting mechanism.

Figure 6.

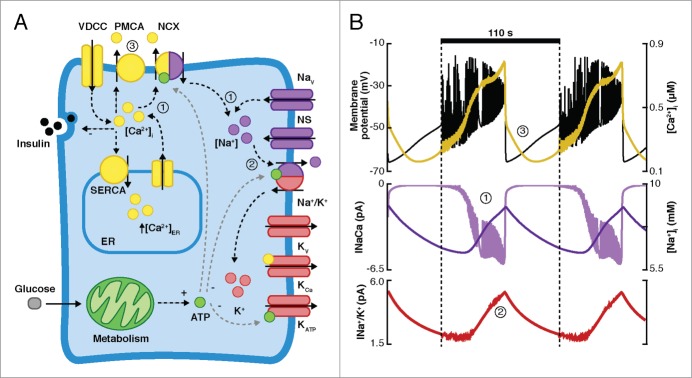
[Na⁺]_i as a pacemaker variable. (A) The model of Fridlyand et al.¹⁰⁶ is shown schematically. Entry of Ca²⁺ during the active phase activates the Na⁺/Ca²⁺ exchanger, inducing an increase of [Na⁺]_i (1). This promotes the activity of an outward current through the Na⁺/K⁺ pump, eventually repolarizing the membrane (2). In the silent phase, Ca²⁺ influx is inhibited, resulting in a reduction in both the activity of the NCX exchanger and the Na⁺/K⁺ pump, promoting slow depolarization (3). (B) Simulation of slow electrical activity. Top: V_m (black curve) and [Ca²⁺]_i (yellow curve). Middle: Current through the NCX exchanger (INaCa, light purple) and [Na⁺]_i (dark purple). Bottom: Current through the Na⁺/K⁺ pump (INa⁺/K⁺, red curve).

Bertram and Sherman¹⁶ proposed a model using the phantom bursting mechanism with 3 slow processes, [Ca²⁺]_i, [Ca²⁺]_ER, and ATP/ADP. Using a simple representation of these mechanisms, this model was able to reproduce several experimental findings, including the effects of acetylcholine and thapsigargin on electrical activity and the full range of periods of bursting. In a later model, called the Dual Oscillator Model (DOM, Fig. 7A), Bertram et al.¹²⁰ combined a model of glycolysis,⁷⁶ a model of mitochondrial metabolism,^100,101 and a model of electrical activity.¹²¹ The DOM model reproduces the full range of periods observed in bursting activity as well as the compound or mixed oscillations that are often observed (shown in Fig. 7D). In the DOM model, slow bursting is mediated by the glycolytic oscillations driving changes in the production of ATP and the conductance of the K_ATP channels (Fig. 7B). On the other hand, fast bursting depends entirely on the electrical component (Fig. 7C). Finally, compound bursting is driven by both the electrical and glycolytic components (Fig. 7D). In the DOM model, the glycolytic oscillations are mediated by the feedback of the product FBP onto the PFK reaction. Although this hypothesis has been questioned,^107,108 in recent years, some of the predictions of the DOM model have acquired experimental support. For example, oscillations in the membrane conductance of mouse β-cells were associated with changes in the conductance of K_ATP channels due to intrinsic metabolic oscillations and not because of oscillations produced by the effects of Ca²⁺ in the production of ATP.¹²² Moreover, direct experimental evidence of oscillations in the glycolytic pathway^123,124 have recently been presented. In addition, it is important to mention that the DOM model is the only model capable of reproducing other recent experimental observations. For instance, Merrins et al.¹²⁵ showed that in some cells, metabolic oscillations persisted in the absence of Ca²⁺ oscillations, while in the majority of cells the metabolic oscillations were abolished. In the latter case, it was possible to restore metabolic oscillations by a non-oscillating elevation of [Ca²⁺]_i (i.e by depolarizing with KCl). The DOM model reproduces these observations¹²⁵ given that Ca²⁺ oscillations are not needed by the model to produce metabolic oscillations. Moreover, based on their simulations with a reduced version of the DOM model, the authors have proposed that the distinct behaviors mentioned above could be mediated by different rates of the enzyme glucokinase among the cells.¹²⁶ In contrast, in other models (e.g., the models of Fridlyand et al.,^106,116 Keizer and Magnus⁹⁹ and Diederichs^107,108), metabolic oscillations are secondary to Ca²⁺ oscillations, thus membrane hyperpolarization (i.e., preventing Ca²⁺ influx) and a fixed [Ca²⁺]_i, mandatorily abolishes metabolic oscillations. It is worth noting that, as in the case of the models based on the cyclical changes in the conductance of the K_ATP channels as the mechanism underlying bursting electrical activity, the DOM model is not able to explain the origin of the oscillations in V_m and [Ca²⁺]_i observed in β-cells lacking functional K_ATP channels.^104,105

Figure 7.

Intrinsic metabolic oscillations (DOM model). (A) Diagram of the DOM model. The interactions between glycolytic, metabolic, and electrical components drive different electrical behaviors (simulations shown in B–D) depending on the regime of the glycolytic and electrical components. Glucose is metabolized by the glycolytic and metabolic components controlling the production of ATP, which mediate the changes in the conductance of the K_ATP channels, depolarization, and Ca²⁺ influx. The 3 compartments (glycolytic, electrical, and metabolic) are affected by the changes in [Ca²⁺]_i. (B) Slow bursting is produced entirely by oscillatory glycolysis. (C) Fast bursting produced by the electrical component. (D) The combination of glycolytic and electrical components produces compound bursting activity. (B–D) Top: V_m (black curve) and the state of glycolysis (represented by F6P, orange curve). Bottom: [Ca²⁺]_i (yellow curve) and [ATP]_i (green curve).

Other models of the rodent β-cell^127,128 have focused on the role of the ionic channels and transport mechanisms in the glucose induced electrical activity by including a more complete description of the electrophysiological properties of the cell. In fact, recent proposals^17,98 of the potential role of the different ionic currents in the electrical activity of the mouse β-cell involves the participation of several ionic transport mechanisms. In order to test the plausibility of this proposal by means of a computational model, an accurate and complete representation of all the mechanisms involved must be included.

Models of human β-cells

All the models described so far have been built based on rodent experimental data, assuming that these are a reasonable model for the human β-cell. However, it has been shown that there are several important differences between species at different levels, including, for example, the proportions and distribution of the different cells in the islets of Langerhans,^129,130 the glucose threshold at which insulin starts to be secreted,^131,132 the kinetics of insulin exocytosis,¹³³ and the ionic channels expressed and their role in electrical activity and insulin secretion.^10,20,22 Human β-cells have ATP-dependent K⁺ channels; T, L, and P/Q-type Ca²⁺ channels; voltage-gated Na⁺ channels; large and small conductance Ca²⁺-activated K⁺ channels (SK and BK respectively); inwardly rectifying and delayed rectifier K⁺ channels; HERG K⁺ channels; and transient receptor potential (TRP) channels.^10,22,24 Interestingly, in contrast to rodent cells, the most frequently observed electrical patterns in human β-cells consist of single action potential firing or fast bursting,^10,24,27 although slow bursting has been recently reported.²⁸

Based on these differences, mathematical models of human β-cells have recently been developed. Pedersen²⁷ built the first mathematical model based entirely on electrophysiological data from human β-cells.^{22,23,134,135} A limitation of this model is the absence of Ca²⁺ dynamics, metabolism, and SK channels, considering only the interaction between ionic channels. On the other hand, Fridlyand et al.²⁴ also proposed a model based on human data, but in contrast to Pedersen's model, their model included Ca²⁺ dynamics (although based on mouse experimental data), the SK current, and a minimal model of insulin secretion. Despite their limitations, several experimental observations can be reproduced using these models, like the firing of action potentials, fast bursting, and the effect of channel blockers in electrical activity.

Recently, Riz et al.²⁸ added the SK channels and Ca²⁺ dynamics to Pedersen's model of the human β-cell (Fig. 8A). Specifically, a cytosolic and a sub-membrane Ca²⁺ compartment were included. Besides the action potential firing (Fig. 8B) and fast bursting (Fig. 8C) produced by the sub-membrane Ca²⁺-feedback onto the SK channels (resembling the mechanism of the CK model), this model reproduced slow bursting activity (Fig. 2B and Fig. 8D) due to the addition of a slow glycolytic component that drives changes in ATP and the conductance of the K_ATP channels.

Figure 8.

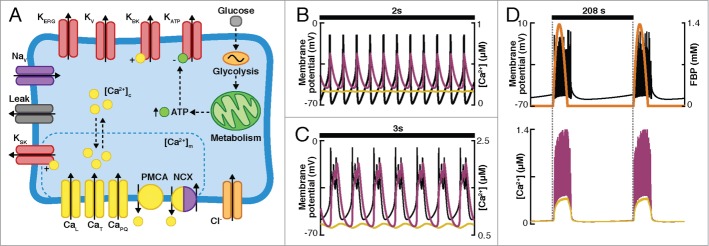
(A) Diagram of the mechanisms included in the model of Riz et al. of human β-cells.²⁸ Channels included in the model: ATP-dependent K⁺ channels (K_ATP), big and small conductance Ca²⁺-dependent K⁺ channels (K_BK and K_SK), voltage-dependent K⁺ channels (K_v), HERG-K⁺ channels (K_ERG), voltage-dependent Na⁺ channels (Na_v), L, T and P/Q-type Ca²⁺ channels (Ca_L, Ca_T, Ca_PQ, respectively), Cl⁻ channels (representing the current mediated by the neurotransmitter γ-aminobutiric acid, GABA). The Ca²⁺ dynamics included a cytoplasmic and a submembrane compartment and the plasma membrane Ca²⁺-ATPase (PMCA) and Na⁺/Ca²⁺ exchanger (NCX). (B–D) Simulations of V_m (black curve), submembrane Ca²⁺ (pink curve), intracellular Ca²⁺ (yellow curve), and glycolysis (FBP, orange curve) are shown. (B) Action potential firing. (C) Fast bursting. (D) Slow bursting.

It is evident that models of human β-cells are in an early stage compared to models of rodent β-cells. However, the former are likely to evolve rapidly and contribute to the understanding of the pathogenesis of T2D and other related diseases.

Discussion

Insulin-secreting β-cells have been intensively studied in the last decades, both experimentally and theoretically. In this review, we have described the main hypotheses behind the mathematical models of β-cells from a physiological viewpoint. It has been shown how models have evolved and grown in complexity as experimental evidence has emerged. Although models have contributed to a better understanding of the GSIS at the cellular level, there are still several open questions. One of the most important is to elucidate the origin of the heterogeneous oscillations observed in β-cells when exposed to stimulatory concentrations of glucose. This has been one of the main objectives of the models of β-cells. In a recent review, Fridlyand et al.²⁶ analyzed both the experiments and the mathematical models in order to identify possible cellular mechanisms behind these different behaviors. They concluded that a single mechanism is not capable of generating all the electrical behaviors, but that each of these behaviors could be driven by a different mechanism. In contrast, Bertram et al.^77,136 have proposed that different regimes of a single mechanism composed by the interacting glycolytic, electrical, and mitochondrial components (DOM model) can explain the variety of behaviors observed in β-cells from rodents. The latter proposal has received both indirect and direct evidence (as discussed above). In our opinion, given the experimental support it has acquired, the DOM model is currently the most comprehensive mathematical model in terms of both the experimental observations it can reproduce and the cellular mechanisms that it includes. Merrins et al.¹²³ have developed a technique to measure glycolytic oscillations, which opens the door to the possibility of testing the validity of the assumptions and predictions of the DOM model experimentally. In fact, using this novel technique, the authors presented convincing evidence that glycolytic oscillations are in phase with the mitochondrial redox potential,¹²³ which was also predicted by the DOM model.⁷⁷

Another important question is how the differences between rodent and human β-cells affect the secretion of insulin. As mentioned above, most of the models are based on experimental data from rodent β-cells, while models for human β-cells were only recently developed. Models of rodent β-cells have achieved a high level of complexity; to such an extent that detailed mathematical descriptions of glucose metabolism and Ca²⁺-handling have already been incorporated. On the other hand, mathematical models of human β-cells are still incomplete because of the lack of sufficient experimental data. In this regard, detailed measurements of intracellular ionic concentrations and metabolic variables would be extremely helpful to extend the current models and simulate the human β-cell more accurately. In spite of these limitations, significant and substantial progress has been made recently, by identifying the possible role of the ionic channels in the generation of action potentials firing and fast bursting,^24,27 and the possible participation of metabolism in slow bursting behavior.²⁸

In the beginning, mathematical models of the electrical activity of pancreatic β-cells were devoted to finding plausible explanations for experimental observations. However, interesting applications have been given to these models in order to use them in more realistic and complex scenarios. Some of the models have been extended to study the dynamics of insulin granule exocytosis. For example, Pedersen et al.¹³⁷ used a model of the electrical activity of the human β-cell²⁷ along with a compartmental description of Ca²⁺ dynamics and insulin exocytosis to evaluate the contribution of the different Ca²⁺ channels during exocytosis.

Models of β-cells have also been useful for investigating the importance of β-cell coupling in the islets of Langerhans, given that it has been proposed that in order to obtain proper insulin secretion in response to a glucose stimulus, the secretion of the β-cells must be synchronized (intra-islet synchronization). This has been tested theoretically, assuming there is electrical coupling between β-cells through gap junctions within the islets of Langerhans.^138,139 Similarly, mathematical models have been used to identify possible mechanisms for islet synchronization (inter-islet synchronization).^136,138 In a recent review, Han et al.¹⁴⁰ described how mathematical models have been used to study the effect of both β-cell interconnection through gap-junctions and paracrine interactions between islet cells.

Another of the aspects recently explored is the inclusion of models of β-cells in multiscale models. For example, Chew et al.¹⁴¹ coupled the Dual Oscillator Model to a model that describes the whole-body glucose regulation system during an oral glucose tolerance test. The aim of this model was to study the changes in the electrical pattern of β-cells due to real changes in blood glucose concentration, as opposed to the models of single β-cells, in which glucose is assumed to be in steady state. It would be interesting to adopt this multiscale approach using a model of human β-cells, such that differences between species are considered.

Given that β-cell dysfunction is implicated in the pathogenesis of T2D, it is likely that mathematical models of human β-cells will evolve rapidly as more experimental data become available. It is also expected that all this progress in the field of mathematical models of β-cells will contribute to the design of new therapies for treating diseases related to the glucose-insulin regulatory system, like T2D. For instance, it has been suggested that mathematical models of β-cells could establish the principles of design for engineered cells capable of sensing glucose and secreting insulin.^112,142

Considering the importance of the changes in [Ca²⁺]_i in GSIS, it is surprising that the spatial aspects have not been explicitly considered in the models of β-cells. We think that a necessary extension to the models is the inclusion of a more realistic description of the spatiotemporal distribution of [Ca²⁺]_i, such as its effects on the different cellular processes (e.g., regulation of ionic channels, metabolism, insulin exocytosis) occurring at different locations of the intracellular space are adequately simulated.

For several reasons, mathematical modeling is limited by unavoidable simplifications and assumptions at different levels. For example, when the CK model⁸⁹ appeared, detailed information about the cellular mechanisms involved in the electrical activity of the β-cell was lacking, which was reflected in the simplicity of the model. The same can be said about the model of the human β-cell of Pedersen,²⁷ given that the number of studies on human β-cells is scarce in comparison to those of rodent cells, perhaps because of the limited availability of human tissue. However, these minimal models have served as a starting point for further development. It is important to note that as more pieces of experimental evidence have emerged, models have been modified consequently. This can be seen for example in the evolution of the models of the different groups (e.g., Chay,^89,94,111 Fridlyand et al.^26,106,116 and Bertram et al.^16,25,77), that have been extended progressively.

Most of the models reviewed in this work have been built in order to reproduce specific experimental observations at the cellular level, aiming to propose plausible hypotheses that explain the origin of the phenomenon under study. This kind of models (often referred to as "whole cell models")¹⁴³ are constructed by combining individual models of each cellular process considered (e.g., ionic channels, Ca²⁺ handling, metabolism), hence simplifications and/or assumptions can be made in each of the individual models depending on the objective of the study. It can be said that the majority of the models attempt to capture the qualitative, rather than the quantitative aspects of the functioning of the β-cells. In our opinion, most of the simplifications and assumptions are understandable given the complexity of the system, as long as the implications of the resulting simulations, whether hypotheses or predictions, are bounded accordingly.

Funding

G. Félix-Martínez was supported by a graduate scholarship (No. 228853) from CONACYT (Mexican Council of Science and Technology).

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.