Modeling Functional Data With Spatially Heterogeneous Shape Characteristics

Summary

We propose a novel class of models for functional data exhibiting skewness or other shape characteristics that vary with spatial or temporal location. We use copulas so that the marginal distributions and the dependence structure can be modeled independently. Dependence is modeled with a Gaussian or t-copula, so that there is an underlying latent Gaussian process. We model the marginal distributions using the skew t family. The mean, variance, and shape parameters are modeled nonparametrically as functions of location. A computationally tractable inferential framework for estimating heterogeneous asymmetric or heavy-tailed marginal distributions is introduced. This framework provides a new set of tools for increasingly complex data collected in medical and public health studies. Our methods were motivated by and are illustrated with a state-of-the-art study of neuronal tracts in multiple sclerosis patients and healthy controls. Using the tools we have developed, we were able to find those locations along the tract most affected by the disease. However, our methods are general and highly relevant to many functional data sets. In addition to the application to one-dimensional tract profiles illustrated here, higher-dimensional extensions of the methodology could have direct applications to other biological data including functional and structural MRI.

1. Introduction

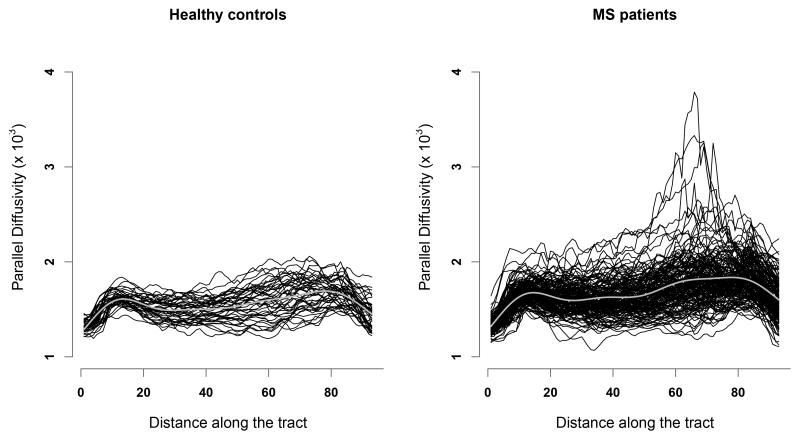
Most models used in functional data analysis (FDA) focus on modeling the mean and covariance functions. Although such models are often adequate, there are important cases where interest is focused on skewness or other shape characteristics. For example, the right panel of Figure 1 illustrates profiles of multiple sclerosis (MS) patients, recorded along the corpus callosum tract of the brain. The functions have skewed pointwise distributions, with the amount of skewness varying spatially. Modeling data with such characteristics represents the main focus and novelty of our work.

Figure 1.

Parallel diffusivity profiles within the corpus callosum tract in 162 MS patients (right panel) and 42 healthy controls subjects (left panel). Penalized spline estimates of the mean functions are shown as thick grey curves. Distance units are arbitrary.

In this paper, we develop models and inferential methods for the analysis of functional skewed data. Fundamentally different from the common method of moment-based approaches of modeling functional data (Di et al., 2009; Crainiceanu, Staicu, and Di, 2009; Staicu, Crainiceanu, and Carroll, 2010 etc.), our methods are based on pointwise distributional assumptions of the underlying stochastic process. The parametric assumptions are used to capture higher order moments of the pointwise distributions; in comparison the nonparametric approaches use only the first two moments. Specifically, our approach assumes that the pointwise distributions of the underlying stochastic process are in a parametric family with one or more shape parameters, for example, a skew normal or skew t family. The shape parameters, as well as the mean and variance, are modeled nonparametrically as function of location.

The third novel feature here is the use of copulas to model spatial dependence. We use Gaussian or t-copulas, since, unlike Archimedean copulas, they include correlation functions which are fundamental to FDA. The use of copulas allows a modular approach where the marginal distributions and dependencies can be modeled separately. In our model, the observed functions are transformations of an underlying latent Gaussian processes and, for a t-copula, a chi-squared random variable that induces tail dependence. Principal components analysis (PCA) and a Karhunen-Loève expansion can be applied to the latent Gaussian process, much as they would be applied if the observed data were Gaussian.

1.1 The diffusion tensor imaging study

The methodology described in this paper is motivated by a state-of-the-art diffusion tensor imaging (DTI) study that analyzes and compares white matter tracts in healthy individuals and MS patients. DTI is an in vivo magnetic resonance technique for imaging the white matter tracts in the brain by measuring the three-dimensional directions of water diffusion (Basser, et al. 1994, 2000). In the DTI study, we are interested in modeling DTI profiles, such as mean diffusivity and parallel diffusivity, along the corpus callosum, the major tract connecting the two cerebral hemispheres. Mean diffusivity is an orientation-independent measure of water movement within the tract, whereas parallel diffusivity estimates the component of that movement co-axial with the tract’s axon bundles.

Figure 1 displays parallel diffusivity profiles for healthy controls and MS patients. Parallel diffusivity is recorded at many locations along the tract, so that the tract profile can be viewed as a continuous curve sampled at a discrete set of points. Scientific interest includes comparing the means, quantiles, and correlation functions of the two samples; see Greven, et al. (2010) for more details on the scientific questions. At a quick look, the control and MS data seem to differ in a few ways, such as mean and variability along the tract, but perhaps even more so with respect to skewness. The MS subjects’ profiles exhibit more skewness compared to the controls, especially around locations 50–80 along the corpus callosum tract.

These data suggest that there is a need for methods that can accommodate strong temporally- or spatially-varying skewness and within-function correlation. The computational speed is essential, since FDA is faced with continuously larger and more complex data sets. Moreover, one needs inferential methods, for example, to test whether skewness differences between spatial locations, or between groups of subjects, are statistically significant. In addition to the application to one dimensional tract profiles illustrated here, higher-dimensional extensions of the methodology could have direct applications to other biological data including functional and structural MRI. In these applications, accurate modeling of the tails of distributions is a critical step in identifying abnormalities as well as limiting false positive results.

1.2 Current methods

A reasonable approach for the analysis of tractography data is functional data analysis (FDA)—see, for example, the excellent monographs of Ramsay and Silverman (2005), Ferraty and Vieu (2006), and Ramsay, Hooker, and Graves (2009). A fundamental idea in FDA is to decompose the space of curves into principal directions of variation by a Principal Component Analysis (PCA) of the raw data or smoothed curves. PCA provides a simple recipe for dimension reduction by including only eigenvalue–eigenvector pairs where the estimated eigenvalue is relatively large. However, PCA is a second-order methodology in that it uses only the mean and covariance functions, and the Karhunen-Loève expansion based on its eigen-decomposition assumes a joint Gaussian distribution (Yao, Müller, and Wang, 2005).

The focus of current FDA methods on mean and covariance functions ignores subtler differences in distributions that could be better characterized by quantiles. Quantiles, like means, have tremendous data compression potential and are easy to interpret, a sine-qua-non in the century of data. In simulation experiments, we have shown that the quantiles of asymmetric data are estimated with substantial bias if the Gaussian model typical of FDA is assumed; see Section 6 and Figure S2 of the supplemental materials.

The paper is organized as follows. Section 2 introduces functional processes with heterogeneous shape characteristics and describes the modeling methodology. Section 3 develops the estimation procedure and Section 4 discusses prediction. Section 5 contains an extensive simulation study. Section 6 presents a comparison of our methodology with alternatives. Applications to the tractography data are presented in Section 7. A brief discussion is given in Section 8.

2. Functional models with spatially-varying marginal distributions

Let $\left\{Y_i\right(t_{ij});t_{ij}\in \mathcal{T}\}$ with j = 1, …, m_i be the data for subject i, i = 1, …, N. We assume that Y_i is a random curve defined on domain $\mathcal{T}$ and sampled at a grid of points $\{t_{i1},\dots ,t_{i{m}_i}\}\in \mathcal{T}$; typically we take $\mathcal{T}=[0,1]$. Furthermore, suppose that

$$Y_i\left(t\right)=\mu \left(t\right)+\sigma \left(t\right)G^{-1}\left\{W_i\right(t);\alpha (t\left)\right\}$$ (1)

where μ(t) is the mean function, σ(t) is the standard deviation function, and W_i(t) is a latent process such that W_i(t) is uniformly (0, 1) distributed for each t. Here G(·; α) is a cumulative distribution function in a parametric family of distributions with zero mean, unit variance, and shape parameter vector α. For example, α can be the scalar shape parameter of the skew normal distribution (Azzalini, 1985) or the two-dimensional shape parameter vector of the skew t distribution due to Azzalini and Capitanio (2003) or a somewhat different skew t distribution of Fernandez and Steel (1998). Also, G⁻¹(·; α) denotes the usual inverse CDF. We assume that the shape parameter α(t) varies smoothly with t. To simplify notation, we sometimes use G_t:= G{·; α(t)}. Our main objectives are to estimate the population functions μ(t), σ(t), and α(t) and describe the dependence of the functional process.

We refer to model (1) as the quantile-induced functional model, because model (1) implies the following model for the pth quantile: Q_p(t) = μ(t)+σ(t)G_t⁻¹(p), 0 < p < 1. The advantage of representing the functional data using model (1) is that it allows the specification of the dependence of the random process Y_i through the latent process W_i. Since W_i(t) is uniformly distributed for each t, the joint distribution of {W_i(t_i1), …, W_i(t_imi)} is a copula, which we will model parametrically using Gaussian or t copulas.

An alternative to our methodology is to estimate the marginal distributions and the correlation structure separately. The marginal distributions could be estimated, for example, by quantile regression or by fitting univariate distribution at each time point by maximum likelihood or methods of moments. The correlation structure could be estimated by PCA. What is missing with this approach is a technique for combining the marginal distributions and the correlation structure into a probability model for the joint distribution of the data. Our copula methodology supplies this missing technique.

2.1 Population-level parameters

We model the mean function μ(t), variance function σ²(t), and the shape parameter functions α(t) using penalized splines, though other basis expansion approximations can be used. Because the variance is positive, we use log-splines to model σ²(t). Let $\mathbf{B}\left(t\right)={\left\{B_1\right(t),\dots ,B_q(t\left)\right\}}^T=\{1,t,\dots ,t^p,{(t-{\kappa }_1)}_{+}^p,\dots ,{(t-{\kappa }_K)}_{+}^p\}$ be a pth degree truncated power series spline basis with dimension q = 1 + p + K having fixed knots (κ₁, …, κ_K). Because the penalty prevents overfitting, the number of knots has very little effect on a penalized spline fit, provided the number of knots is sufficiently large to accommodate fine-level features in the data (Ruppert, 2002; Li and Ruppert 2008). However, an excess of knots will slow the computations. Therefore, in practice, we allow a different number of knots for μ, σ, and α, since some of these functions may require more knots than others. To keep notation simple, in our exposition we will use the same spline basis for each of these three functions. We write μ(t) = B(t)^Tβ_μ and log{σ²(t)} = B(t)^Tβ_σ, where the spline bases and coefficient vectors are q-dimensional. In some cases it is desirable to model, not α(t), but a suitable transformation of α(t), say h{α(t)}, where h{α(t)} applies a one-to-one transformation to each coordinate of α(t). For example, if any component of α(t) is positive we could log-transform that component. Our model for α(t) is α(t) = h⁻¹{B(t)^Tβ_α}. Here β_α is a q×dim{α(t)} matrix of parameters.

2.2 Functional dependence and copulas

A copula is a multivariate distribution function whose univariate marginal distributions are all uniform on (0,1). If X = (X₁, …, X_n) is a random vector and if F_i is the continuous marginal distribution of X_i, then the distribution of {F₁(X₁), …, F_n(X_n)} is called the copula of X. Copulas offer a convenient way of modeling multivariate observations because the modeling is broken into two independent parts: (1) modeling the dependencies through a copula; and (2) modeling the univariate marginal distributions (Sklar, 1959).

A Gaussian copula is the copula of some multivariate Gaussian distribution. The copula of a random vector is unchanged by strictly increasing transformations of its components, so a Gaussian copula is completely specified by a correlation matrix. If X has a Gaussian copula, this does not imply that X is Gaussian, only that X has the same copula as some Gaussian random vector. Stated differently, X has the same dependence structure as some multivariate normal random vector, but its marginal distributions need not be Gaussian. Similarly, a t-copula is the copula of some multivariate t-distribution and is specified by a correlation matrix and a scalar degrees of freedom parameter.

Gaussian copulas offer a convenient way to model multivariate dependencies, because these are determined by a familiar quantity, a correlation matrix. The limitation of the Gaussian copula concerns the tail dependence behavior. The coefficient of the tail dependence between a pair (X, Y) of random variables is ${\lim }_{p\to \infty }P\{Y>F_Y^{-1}(p)\mid X>F_X^{-1}(p\left)\right\}$, which is easily shown to be symmetric in X and Y. For a bivariate Gaussian pair, this coefficient is zero unless their correlation equals 1 (Embrechts, McNeil & Straumann, 2002). This means that under a Gaussian copula, the components behave in the extreme tails as if they were either independent, or perfectly correlated. In contrast, t-copulas exhibit tail dependence even in the case of zero-correlation; see McNeil, Frey, and Embrechts (2005). We found evidence of strong tail dependence in the DTI data; see Section 7.

3. Estimation Methodology

We use penalized maximum likelihood to estimate the mean, standard deviation and shape parameter functions, μ(t), σ(t) and α(t). Each of these functions contains a reasonably large number of parameters and the correlation matrix of the Gaussian or t-copula is also of sizable dimension. Because of the large number of parameters, simultaneous estimation of all parameters can take an excessive amount of computational time. To circumvent this problem, we have developed a more rapid multi-stage estimation procedure.

3.1 Mean, variance, and shape parameter functions

To speed computations, the estimates of μ(t), σ(t) and α(t) are obtained in two steps. In the first, the sample of curves is reduced to undersmoothed estimates of these three functions. In the second, these curve estimates are further smoothed by penalized splines.

Step 1: For simplicity, we start with the case where the functions are sampled on a common dense grid of points, so that t_ij = t_j for j = 1, …, m and all i. Initial estimates of the mean, variance and shape parameter functions are constructed as follows: for each fixed j, define μ_j = μ(t_j), σ_j = σ(t_j) and α_j = α(t_j). Then, the parametric estimates of μ_j, σ_j and α_j are obtained by maximizing the pointwise likelihood function

$${\ell }_j({\mu }_j,{\sigma }_j,{\alpha }_j)=\sum _{i=1}^n\log \left[g\right\{(Y_{ij}-{\mu }_j)∕{\sigma }_j;{\alpha }_j\left\}\right]-\log \left({\sigma }_j\right),$$ (2)

where g(x; α_j) = ∂G(x; α_j)/∂x is the density function corresponding to the distribution G_tj. For example, when G_t is in the skew normal or skew t family of distributions, the functions sn.mle or st.mle of the sn package for R (Azzalini, 2010) can compute these estimates.

Maximum likelihood estimation of α often requires some care. For example, if g is a skew normal density or a skew t density with known degrees of freedom, then the estimate of α (the skewness parameter) is infinite with positive probability for moderate sample sizes (Azzalini, 1985; Genton, 2004; Sartori, 2006). This instability problem is due to the choice of parameterization in that large changes in α lead to small changes in the density. It should be noted, however, that infinite values of α give valid densities, the half-normal (or half t) densities. The problem is that some estimation methods, for example, spline smoothing, have problems accommodating infinite values. A possible remedy for this problem is mentioned in “Alternative 1” below.

When the curves are sparsely sampled, another estimation method is needed. Note that the estimates of μ_j, σ_j and α_j in (2) are obtained by local polynomial estimating equations (Carroll, Ruppert, and Welsh, 1998), with degree zero polynomials and a bandwidth so small that only data exactly at t_j are used to estimate the functions at t_j. For sparse and irregularly spaced data, local estimating equations with larger bandwidths and higher polynomial degree can be used to compute estimates on a grid t₁, …, t_m, say. The estimates should be undersmoothed, since they will be smoothed further in Step 2. Suppose that the ith subject’s curve is observed at t_ij, j = 1, …, m_i. For estimation at t_k using Lth degree local polynomial estimation, define $\mu \left(t\right)={\Sigma }_{\ell =0}^L{\mu }_{\ell }{(t-t_k)}^{\ell }$, $\sigma \left(t\right)={\Sigma }_{\ell =0}^L{\sigma }_{\ell }{(t-t_k)}^{\ell }$, and ${\alpha }_q\left(t\right)={\Sigma }_{\ell =0}^L{\alpha }_{\ell ,q}{(t-t_k)}^{\ell }$ for the qth component function of α(t). Then estimating equation approach minimizes

$$\sum _{i=1}^n\sum _{j=1}^{m_i}\left[\log \right[g\left\{\right(Y_{ij}-\mu \left(t_{ij}\right))∕\sigma (t_{ij});\alpha (t_{ij}\left)\right\}]-\log \{\sigma \left(t_{ij}\right)\left\}\right]K_b\left\{\right(t_{ij}-t_k)∕b\}$$

over all coefficients in μ(t), σ(t), and α(t). The estimates of μ, σ, and α at t_k are μ₀, σ₀, and (α_0,1, … , α_0,Q), respectively, where Q is the dimension of α. Here K_b(·) is a kernel function and b is a bandwidth.

In summary, regardless of whether we have sparse or dense data, at the end of Step 1 we have undersmoothed estimates on a grid t₁, … , t_m. These estimates will be denoted by ${\tilde{\mu }}_j$, ${\tilde{\sigma }}_j$, and ${\tilde{\alpha }}_j$, j = 1, … ,m. Step 2 uses ${\tilde{\mu }}_j$ and ${\tilde{\sigma }}_j$ and, in Alternative 1, ${\tilde{\alpha }}_j$ is also used.

Step 2: The final estimates of μ(t), σ(t) and α(t) are constructed by smoothing the Step 1 estimates using penalized splines. The mean parameter β_μ, where μ(t) = B(t)^Tβ_μ, is estimated by minimizing the penalty criterion $P{L}_{\mu }\left({\beta }_{\mu }\right)={\Sigma }_{j=1}^m{({\tilde{\mu }}_j-{\mathbf{B}}_j^T{\beta }_{\mu })}^2+{\lambda }_{\mu }{\Omega }_{\mu }\left({\beta }_{\mu }\right)$, where ${\Omega }_{\mu }\left({\beta }_{\mu }\right)={\beta }_{\mu }^T{\mathbf{D}}_{\mu }{\beta }_{\mu }$, B_j = B(t_j), and D_μ is a q×q = diag(0, … , 0, 1 … , 1) (p+1 zeros followed by K ones) penalty matrix. This choice of penalty matrix shrinks the pth degree spline towards a pth degree polynomial, since the polynomial coefficients are not penalized. Only the truncated power functions, which give the deviation of the spline from a polynomial, are penalized. The penalty matrices D_σ and D_α used below have the same form as D_μ; see Ruppert et al. (2003) for a discussion of penalty matrices. In a similar way ${\widehat{\beta }}_{\sigma }$ is obtained by minimizing $P{L}_{\sigma }\left({\beta }_{\sigma }\right)={\Sigma }_{j=1}^m{\left\{2\log \right({\tilde{\sigma }}_j)-{\mathbf{B}}_j^T{\beta }_{\sigma }\}}^2+{\lambda }_{\sigma }{\Omega }_{\sigma }\left({\beta }_{\sigma }\right)$ for ${\Omega }_{\sigma }\left({\beta }_{\sigma }\right)={\beta }_{\sigma }^T{\mathbf{D}}_{\sigma }{\beta }_{\sigma }$.

For the shape function parameters, we propose a penalized marginal likelihood criterion where the mean and variance functions parameters are fixed at estimates (see also Sartori, 2006). More specifically, let ${\widehat{Y}}_{ij}=\{Y_{ij}-\widehat{\mu }(t_{ij}\left)\right\}∕\widehat{\sigma }\left(t_{ij}\right)$ be the standardized observations, using the estimates of the mean $\widehat{\mu }(\cdot )$ and variance functions $\widehat{\sigma }(\cdot )$ obtained above. Define the penalized marginal likelihood function:

$$P{L}_{\alpha }\left({\beta }_{\alpha }\right)=-2\sum _{i=1}^n\sum _{j=1}^m\left\{{\ell }_{ij}({\beta }_{\alpha };{\widehat{Y}}_{ij})\right\}+{\lambda }_{\alpha }{\Omega }_{\alpha }\left({\beta }_{\alpha }\right),$$

where ${\ell }_{ij}({\beta }_{\alpha };{\widehat{Y}}_{ij})=\log \left[g\left\{{\widehat{Y}}_{ij};h^{-1}\left({\mathbf{B}}_j^T{\beta }_{\alpha }\right)\right\}\right]$ is, up to an additive constant, the log-likelihood function corresponding to the distribution of ${\widehat{Y}}_i\left(t_{ij}\right)$. We use ${\Omega }_{\alpha }\left({\beta }_{\alpha }\right)={\beta }_{\alpha }^T{\mathbf{D}}_{\alpha }{\beta }_{\alpha }$ as the roughness penalty, where D_α is the roughness penalty matrix. The shape parameter β_α is obtained as the minimizer of the penalized criterion PL_α(β_α).

For the mean and variance estimation, we selected the smoothing parameters λ_μ and λ_σ using the restricted maximum likelihood estimation (REML) (Wood, 2006). For the shape parameter function estimation λ_α we used using the corrected AIC criterion (Ruppert et al., 2003); other choices, such as CSV or AIC can be used. The function optim of the stats package for R with the BFGS algorithm can be used for optimization. Let $\widehat{\mu }\left(t\right)=\mathbf{B}{\left(t\right)}^T{\widehat{\beta }}_{\mu }$, $\widehat{\sigma }\left(t\right)=\exp \{\mathbf{B}{\left(t\right)}^T{\widehat{\beta }}_{\sigma }∕2\}$ and $\widehat{\alpha }\left(t\right)={\mathbf{h}}^{-1}\left\{\mathbf{B}{\left(t\right)}^T{\widehat{\beta }}_{\alpha }\right\}$ be the estimated mean, standard deviation and shape parameter functions respectively.

Alternative 1

One fast alternative is to estimate the shape parameter functions using the same approach as for the mean and variance function. To handle infinite values of α_j, we model transformed parameters h(α_j) instead. For example, if G(·; α), −∞ ≤ α ≤ ∞, is the skew normal distribution, then an appropriate transformation is h(·) = log[Φ(·/s)/{1 − Φ(·/s)}, the normal CDF with standard deviation s, which maps [−∞, ∞] to [0, 1]; the choice s = 5 was used in our simulation study and worked satisfactorily. This transformation eliminates the infinite values that cause problems. The shape parameter β_α minimizes the penalized criterion $P{L}_{\alpha }\left({\beta }_{\alpha }\right)={\Sigma }_{j=1}^m{\left\{h\right({\tilde{\alpha }}_j)-{\mathbf{B}}_j^T{\beta }_{\alpha }\}}^2+\lambda {\beta }_{\alpha }^T{\mathbf{D}}_{\alpha }{\beta }_{\alpha }$, with λ and D_α defined as above. While this approach is extremely fast, it estimates the shape parameter function with higher variability.

Alternative 2

The estimation method described in this section estimates μ(t), σ(t) and α(t) without accounting for the dependence of the process. One way to incorporate the functional dependence is via a penalized full likelihood approach. We briefly outline this idea. Let C(; Ω) be a copula distribution and c(·; Ω) the corresponding copula density, where Ω is the vector of copula parameters. It follows that the log-likelihood of the full model can be written as:

$$\ell ({\beta }_{\mu },{\beta }_{\sigma },{\beta }_{\alpha },\Omega )=\sum _{i=1}^N\sum _{j=1}^m{\ell }_{ij}({\beta }_{\mu },{\beta }_{\sigma },{\beta }_{\alpha };Y_{ij})+\sum _{i=1}^N\log \left[c_{{\mathbf{t}}_{\mathbf{i}}}\right\{F_{Y,t_{i1}}\left(Y_{i1}\right),\dots ,F_{Y,t_{im}}\left(Y_{im}\right);\Omega \left\}\right],$$ (3)

where t_i = (t_i1, …, t_im), Y_ij=Y_i(t_ij), ${\ell }_{ij}({\beta }_{\mu },{\beta }_{\sigma },{\beta }_{\alpha };Y_{ij})=\log \left[g\right\{(Y_{ij}-{\mathbf{B}}_{ij}^T{\beta }_{\mu })∕\exp ({\mathbf{B}}_{ij}^T{\beta }_{\sigma }∕2);{\mathbf{h}}^{-1}\left({\mathbf{B}}_{ij}^T{\beta }_{\alpha }\right)\left\}\right]-{\mathbf{B}}_{ij}^T{\beta }_{\sigma }∕2$ is the penalized log-likelihood function of Y_ij and $F_{Y,t_{ij}}\left(Y_{ij}\right)=G\left\{\right(Y_{ij}-{\mathbf{B}}_{ij}^T{\beta }_{\mu })∕\exp ({\mathbf{B}}_{ij}^T{\beta }_{\sigma }∕2);{\mathbf{h}}^{-1}({\mathbf{B}}_{ij}^T{\beta }_{\alpha }\left)\right\}$. Here B_ij = B(t_ij) for all i and j. To avoid undersmoothing of the population-level functions, which may be caused by large-dimensional function bases, a penalized criterion will be used. The mean, variance and shape parameter functions parameters β_μ, β_σ and β_α are chosen to minimize the penalized pseudo log-likelihood $PL({\beta }_{\mu },{\beta }_{\sigma },{\beta }_{\alpha },\widehat{\Omega })=-2N^{-1}\ell ({\beta }_{\mu },{\beta }_{\sigma },{\beta }_{\alpha },\widehat{\Omega })+{\lambda }_{\mu }{\Omega }_{\mu }\left({\beta }_{\mu }\right)+{\lambda }_{\sigma }{\Omega }_{\sigma }\left({\beta }_{\sigma }\right)+{\lambda }_{\alpha }{\Omega }_{\alpha }\left({\beta }_{\alpha }\right)$, where $\widehat{\Omega }$ is a consistent non parametric estimate of the copula parameter Ω and Ω_μ, Ω_σ and Ω_α are roughness penalties. Estimation of Ω, that does not depend on parameters β’s, is discussed in Section 3.2.

Minimization of PL(β_μ, β_σ, β_α, $\widehat{\Omega }$) does not have a closed-form solution. To avoid the challenging numerical optimization problem, we use a three-step iterative algorithm. Denote by ${\beta }_{\mu }^{\left(k\right)}$, ${\beta }_{\sigma }^{\left(k\right)}$, ${\beta }_{\alpha }^{\left(k\right)}$ the current estimates of the mean parameters, variance parameters and shape parameters respectively. More specifically, in the first step the mean parameters β_μ are updated by ${\beta }_{\mu }^{(k+1)}=argmi{n}_{{\beta }_{\mu }}\{-2N^{-1}\ell ({\beta }_{\mu },{\beta }_{\sigma }^{\left(k\right)},{\beta }_{\alpha }^{\left(k\right)},\widehat{\Omega })+{\lambda }_{\mu }{\Omega }_{\mu }({\beta }_{\mu }\left)\right\}$. In the second step the variance parameters β_σ are updated by ${\beta }_{\sigma }^{(k+1)}=argmi{n}_{{\beta }_{\sigma }}\{-2N^{-1}\ell ({\beta }_{\mu }^{\left(k\right)},{\beta }_{\sigma },{\beta }_{\alpha }^{\left(k\right)},\widehat{\Omega })+{\lambda }_{\sigma }{\Omega }_{\sigma }({\beta }_{\sigma }\left)\right\}$. Finally, in the third step the shape parameters β_α are updated by ${\beta }_{\alpha }^{(k+1)}=argmi{n}_{{\beta }_{\alpha }}\{-2N^{-1}\ell ({\beta }_{\mu }^{\left(k\right)},{\beta }_{\sigma }^{\left(k\right)},{\beta }_{\alpha },\widehat{\Omega })+{\lambda }_{\alpha }{\Omega }_{\alpha }({\beta }_{\alpha }\left)\right\}$. At each step the corresponding smoothing parameter is chosen using the corrected AIC criterion (Ruppert et al., 2003). These three steps are then iterated until convergence; estimates under independence can be used as initial estimates of mean, variance and shape parameters.

Our experience from simulation studies is that, provided that the copula parameters are estimated accurately, Alternative 2 estimates of the population functions μ(·), σ(·), and α(·) are not very different from the estimates that use the working independence assumption with regards to the bias and variability. However the computational cost of Alternative 2 is considerably higher.

3.2 Calibrating copulas

The approach for estimating the copula parameters depends on the type of copula used. A Gaussian copula requires only estimation of the correlation matrix of the underlying Gaussian distribution. A t-copula requires estimation of a correlation matrix and a degree of freedom parameter. First, we describe estimation of the correlation matrix, which is similar for the two copula families, and then describe estimation of the degree of freedom parameter.

If a Gaussian copula is assumed, then the copula correlation is precisely the Pearson correlation of the Gaussian process

$$Z_i\left(t\right)={\Phi }^{-1}\left(G\right[\left\{Y_i\right(t)-\mu (t\left)\right\}∕\sigma \left(t\right);\alpha \left(t\right)\left]\right).$$ (4)

This process has standard normal marginal distributions, so K(s, t) = cov{Z_i(s), Z_i(t)} is both the process covariance and correlation function, and thus it is the latent copula correlation function. One straightforward way to estimate K(·, ·) is to use method of moment estimators of the covariance function corresponding to the approximately Gaussian processes obtained by replacing the population functions by their estimates, ${\widehat{Z}}_i\left(t_{ij}\right)={\Phi }^{-1}\left(G\right[\left\{Y_i\right(t_{ij})-\widehat{\mu }(t_{ij}\left)\right\}∕\widehat{\sigma }\left(t_{ij}\right);\widehat{\alpha }\left(t_{ij}\right)\left]\right)$. We model ${\widehat{Z}}_i\left(t\right)$ as the sum of two independent components: a finite basis expansion process, say ${\tilde{Z}}_i\left(t\right)$ with covariance function $\tilde{G}(s,t)$, and a white noise process with variance ${\sigma }_{∊}^{2}1(t=s)$. By a finite basis expansion process, we mean a Karhunen-Loéve expansion truncated at a finite, and generally small, number of eigenvectors (Di et al., 2009).

Let $\widehat{G}(t,s)$ be the method of moment estimator of $\mathrm{cov}\left\{{\widehat{Z}}_i\right(s),{\widehat{Z}}_i(t\left)\right\}$. Let $\tilde{G}(s,t)=\widehat{G}(s,t)$ for s ≠ t; for s = t, $\tilde{G}(t,t)$ is estimated using a bivariate thin-plate spline smoother applied to $\widehat{G}(t,s)$ for t ≠ s. This approach to estimation of the diagonal elements removes the “nugget effect” due to the white noise term, and was proposed by Staniswalis and Lee (1998). Because ${\tilde{Z}}_i$ is modeled by a finite basis expansion process, it makes sense to use a reduced rank approximation of the covariance of ${\tilde{Z}}_i$. We estimate ${\sigma }_{∊}^2$ by ${\widehat{\sigma }}_{∊}^2={\int }_0^1\left\{\widehat{G}\right(t,t)-\tilde{G}(t,t\left)\right\}$; if this estimate is not positive, then it is replaced by a small positive number. Assume that the reduced rank approximation of $\tilde{G}$ is ΨΛ_LΨ^T, where Λ_L is diagonal matrix of dimension L < m and Ψ is an m × L matrix with orthogonal columns. Here L is a finite truncation, determined by say the percentage of explained variance (Di et al., 2009). The correlation matrix of the copula density is the correlation matrix corresponding to the covariance matrix $\tilde{\mathbf{G}}+{\widehat{\sigma }}_{∊}^2{\mathbf{I}}_m$. Because ${\widehat{\sigma }}_{∊}^2>0$, this correlation matrix is guaranteed to be positive definite.

The estimates of the correlation matrix just described use the estimates of the population mean, variance, and shape functions, and will be degraded by errors in the estimation of these functions. As an alternative, the sample Kendall’s tau matrix can be used to estimate the latent correlation matrix K (McNeil, et al., 2005, Section 5.3.2). Estimation of the correlation matrix using Kendall’s tau is easiest when t_ij = t_j for all i, which is the case we will discuss. The sample Kendall’s tau is invariant to increasing transformations, so that using the data Y_i(t_j), or the transformed ${\widehat{Z}}_i\left(t_j\right)$ gives the same result. Using (5.32) of McNeil, et al. (2005), let ${\widehat{\rho }}_{\tau }(t_j,t_{j^{\prime }})$ be the sample Kendall’s tau between {Y₁(t_j), … , Y_N(t_j)} and {Y₁(t_j′), … , Y_N(t_j′)} and define $\widehat{G}(t_j,t_{j^{\prime }})=\sin \left\{\pi {\widehat{\rho }}_{\tau }\right(t_j,t_{j^{\prime }})∕2\}$. Then, the estimation of K proceeds as above.

In our extensive simulation study, the two methods of estimating the copula correlation matrix performed almost identically. When the data are sparse and t_ij = t_j for all i does not hold, then one can estimate the correlation matrix using the techniques in Yao et al. (2005). A full investigation of the sparse case is beyond the scope of this paper.

Suppose now that a t-copula is assumed. Consider the transformed random functions $Z_i^{\ast }\left(t\right)=T_{\nu }^{-1}\left(G\right[\left\{Y_i\right(t)-\mu (t\left)\right\}∕\sigma \left(t\right);\alpha \left(t\right)\left]\right)$, where T_ν is the t-CDF with ν degrees of freedom; these curves are distributed according to a t-process with ν degrees of freedom. One easy way to understand the t-process is through the following explicit construction. Let $\left\{Z_i\right(t):t\in \mathcal{T}\}$ be a Gaussian process with mean 0 and covariance function K(s, t) = cov{Z_i(s),Z_i(t)} such that K(t, t) = 1, so that K(t, t) is also the correlation function. Write $Z_i^{\ast }\left(t\right)=Z_i\left(t\right)∕\sqrt{{\chi }_{\nu ,i}^2∕\nu }$, where ${\chi }_{\nu ,i}^2$ is a chi-squared random variable with ν degrees of freedom and independent of Z_i. If ν > 2, then the covariance function of $Z_i^{\ast }$ is $K_Z^{\ast }(s,t)=\nu ∕(\nu -2)K(s,t)$ and so its correlation function is K(s, t). If ν ≤ 2, then $Z_i^{\ast }$ has infinite second moments, so it does not have a covariance or a correlation function. However, K(·, ·) can still be regarded as an “association function” of $Z_i^{\ast }$ and it is the correlation function of Z_i.

Calibrating the t-copula requires estimation of both correlation matrix K and degrees of freedom parameter ν. Estimation of K using Kendall’s tau is as for Gaussian copulas. To estimate ν, we use a “pseudo-likelihood” method. Pseudo-likelihood means estimating certain parameters by maximizing the likelihood with all other parameters fixed at estimates (Gong and Samaniego, 1981). Denote by $\widehat{\mathbf{K}}$ the estimate of the latent correlation matrix. Let ${\widehat{F}}_j$ be the empirical distribution function of {Y_i(t_j) : i = 1, … ,N} except that the denominator is N + 1, and not N. Let ${\widehat{W}}_{ij}={\widehat{F}}_j\left\{Y_i\right(t_j\left)\right\}=R_{ij}∕(N+1)$, where R_ij is the rank of Y_i(t_j) among {Y_i(t_j) : i = 1, … ,N}, where j = 1, … m. The “full pseudo-likelihood” method for estimation of ν is to fit the t-copula to the ${\widehat{W}}_{ij}$ with K fixed at the estimate $\widehat{\mathbf{K}}$.

4. Predicting response trajectories

Our methodology allows prediction of the trajectory Y for a subject from irregular measurements by prediction of the latent process W. Let ${\widehat{W}}_i\left(t\right)$ be the predicted latent process at a new time point t and corresponding to the ith subject; the predicted response at time point t is determined as

$${\widehat{Y}}_i\left(t\right)=\widehat{\mu }\left(t\right)+\widehat{\sigma }\left(t\right)G^{-1}\left\{{\widehat{W}}_i\right(t);\widehat{\alpha }(t\left)\right\}.$$ (5)

The prediction of the trajectory of the latent process differs according to the copula model assumed, and is detailed next.

Gaussian copulas

Consider first the case where the dependence is modeled with a Gaussian copula. Using (4) it follows that prediction of W_i is equivalent to prediction of Zi(t) = Φ⁻¹{W_i(t)}, or in fact of the de-noised Z_i. This is now easy, since under our model assumptions, Z_i(t) can be expressed using Karhunen-Loéve expansion as $Z_i\left(t\right)={\Sigma }_{\ell \ge 1}{\psi }_{\ell }\left(t\right){\lambda }_{\ell }^{1∕2}{\xi }_{i\ell }+{∊}_i\left(t\right)$, where {ψ_ℓ : ℓ ≥ 1} forms an orthogonal basis in the space of squared integrable functions, ξ_iℓ are uncorrelated, have mean zero and variance equal to one. Also ε_i(t) is assumed to have mean zero, variance ${\sigma }_{∊}^2$ for all t and be independent from the ξ’s.

Estimates of the covariance function of Z_i’s are obtained using the method of moments along with smoothing; see Section 3.2. Furthermore, estimates of the functional principal components (FPC) ψℓ’s, of the eigenvalues λ_ℓ’s and the noise variance are obtained by using Mercer’s theorem of the covariance function of the de-noised curves. It follows that prediction of the trajectory {Z_i(t) : t} reduces to prediction of the functional principal components (FPC) scores, ξ_iℓ. For this step we use Gaussian assumptions, that ξ_iℓ and ε_i(t) are jointly Gaussian. The best linear prediction of the FPC scores for the ith subject, given the data from that individual is the usual conditional expectation, which is found to be ${\tilde{\xi }}_{i\ell }=E[{\xi }_{i\ell }\mid {\mathit{Z}}_i]={\lambda }_{\ell }^{1∕2}{\psi }_{i\ell }^T{\Sigma }_{{\mathit{Z}}_i}^{-1}{Z}_i$. Here Z_i = {Z_i(t_i1), … ,Z_i(t_imi)}^T is the transformed data for the ith individual, ψ_iℓ = {ψ_ℓ(t_i1), … , ψ_ℓ(t_imi)}^T , and Σ_Zi is the m_i×m_i matrix of the covariance of Z_i with the (j, j′)th entry equal to ${\left({\Sigma }_{{\mathit{Z}}_i}\right)}_{j{j}^{\prime }}={\Sigma }_{\ell =1}^L{\lambda }_{\ell }{\psi }_{\ell }\left(t_{ij}\right){\psi }_{\ell }\left(t_{i{j}^{\prime }}\right)+{\sigma }_{∊}^{2}1(t_{ij}=t_{i{j}^{\prime }})$.

Then the prediction of the de-noised transformed trajectory Z_i(t) for the ith subject is ${\widehat{Z}}_i^L\left(t\right)={\Sigma }_{\ell =1}^L{\widehat{\psi }}_{\ell }\left(t\right){\widehat{\lambda }}_{\ell }^{1∕2}{\widehat{\xi }}_{i\ell }$, by using the first L eigenfunctions, where ${\widehat{\psi }}_{\ell }$’s and ${\widehat{\lambda }}_{\ell }$’s are the estimated FPC eigenfunctions and eigenvalues respectively and $\widehat{\xi }$’s are the estimated FPC scores. Here L is a finite truncation, determined by say the percentage of explained variance (Di et al., 2009). It follows that the prediction of W_i(t) is ${\widehat{W}}_i^L\left(t\right)=\Phi \left\{{\widehat{Z}}_i^L\right(t\left)\right\}$.

t-copulas

We consider the case of t-copula model and assume that the degree of freedom parameter, ν, is larger than 2. Now we need to work with $Z_i^{\ast }\left(t\right)$ which require transformation of the data using T_ν distribution, instead of Z_i(t) which uses the standard normal transformation. Notice that $Z_i^{\ast }\left(t\right)={\Sigma }_{\ell \ge 1}{\lambda }_{\ell }^{1∕2}{\psi }_{\ell }\left(t\right){\xi }_{i\ell }^{\ast }+{∊}_i^{\ast }\left(t\right)$, where ${\xi }_{i\ell }^{\ast }={\xi }_{i\ell }∕\sqrt{{\chi }_{\nu ,i}^2∕\nu }$, ${∊}_i{\left(t\right)}^{\ast }={∊}_i\left(t\right)∕\sqrt{{\chi }_{\nu ,i}^2∕\nu }$ and λ_ℓ’s and ψ_ℓ defined as before. Although the Gaussian assumptions no longer hold in this case, there is empirical evidence (Yao et al., 2005) that the above formula of ${\tilde{\xi }}_{i\ell }$ still provides the best linear prediction of the FPC scores, ${\xi }_{i\ell }^{\ast }$, given the transformed information for the ith subject. There are a few modifications to be made: 1) the new variance of the noise is $\nu ∕(\nu -2){\sigma }_{∊}^2$ and the new variance of the scores is ν/(ν − 2). The prediction for the de-noised transformed trajectory $Z_i^{\ast }\left(t\right)$ for the ith subject is then ${\widehat{Z}}_i^{\ast L}\left(t\right)={\Sigma }_{\ell =1}^L{\widehat{\psi }}_{\ell }\left(t\right){\widehat{\lambda }}_{\ell }^{1∕2}{\widehat{\xi }}_{i\ell }^{\ast }$ thus the prediction of W_i(t) is ${\widehat{W}}_i^L\left(t\right)=T_{\widehat{\nu }}\left\{{\widehat{Z}}_i^{\ast L}\right(t\left)\right\}$, where $\widehat{\nu }$ is the estimated degrees of freedom of the t-copula.

Prediction can be done with standard functional PCA tools; Section 5.2 contains the prediction errors obtained using conditional expectation directly (Di et al., 2009) and they are similar to the ones obtained by our method. However, our method also estimates the pointwise quantile functions, which is essential for prediction intervals. The pointwise quantile functions estimated using FPCA are based on a normality assumption of the scores and can fail terribly, as discussed in Section 6 and illustrated in the Supplementary material. Prediction methods currently do not exist for quantile regression because dependence is not modeled. However, it is possible to combine quantile regression for modeling the marginal distributions with our copula methodology for modeling dependence, as mentioned at the end of Section 6. For these reasons we view our modeling approach as a unifying approach for both prediction and quantile estimation.

5. Simulation studies

We conducted an extensive simulation study to assess the performance of the estimation procedures described in Section 3. For each of the combinations of mean, standard deviation, shape parameter, and covariance function described below, 100 data sets, each consisting of N = 200 random trajectories, were generated from model (1). Each curve was sampled on a grid of equi-spaced timepoints {t_ij : j = 1, … , 80} in [0, 1], where i = 1, … ,N. The simulated processes use W_i(t) = F_X,t{X_i(t)}, where X_i’s are a sample of mean-zero Gaussian curves and F_X,t(·) is the CDF of X_i(t) for all 0 ≤ t ≤ 1.

We set X_i(t) = Z_i(t) + ε_i(t), where the ε_i(t) are independent N(0, σ² = 0.10). Two main covariance structures of the underlying process Z_i are considered:

I. Finite basis expansion. We assume Z_i’s are a sample of random curves with mean 0 and covariance function K_Z(s, t) = cov{Z_i(t),Z_i(s)}. The covariance function has the expansion $K_Z(s,t)={\Sigma }_{\ell =1}^L{\lambda }_{\ell }{\psi }_{\ell }\left(s\right){\psi }_{\ell }\left(t\right)$ in terms of eigenfunctions ψ_ℓ’s and eigenvalues λ_ℓ’s. In the simulations, L = 3 and there were two cases:

1. ${\psi }_1\left(t\right)=\sqrt{2}\sin \left(2\pi t\right)$, ${\psi }_2\left(t\right)=\sqrt{2}\cos \left(4\pi t\right)$ and ${\psi }_3\left(t\right)=\sqrt{2}\sin \left(4\pi t\right)$; or

2. ${\psi }_1\left(t\right)=\sqrt{3}(2t^2-1)$, ${\psi }_2\left(t\right)=\sqrt{5}(6t^2-6t+1)$ and ${\psi }_3\left(t\right)=\sqrt{7}(20t^3-30t^2+12t-1)$,

   where 0 ≤ t ≤ 1. We chose λ_ℓ = (1/2)^ℓ−1 for ℓ = 1, 2, 3.

II. Matern covariance structure. We let Z_i be Gaussian process with mean zero, variance equal to 2, and Matérn auto-correlation function

$$\rho (\Delta ;\varphi ,\kappa )=\frac{1}{2^{1-\kappa }\Gamma \left(\kappa \right)}{\left(\frac{2{\kappa }^{1∕2}\Delta }{\varphi }\right)}^{\kappa }{K}_{\kappa }\left(\frac{2{\kappa }^{1∕2}\Delta }{\varphi }\right)$$ (6)

with (i) range φ = 0.07 and order κ = 1; and (ii) with range φ = 0.14 and order κ = 1. Here K_κ is the modified Bessel function of order κ.

We set G_t to be the standardized skew normal distribution with shape parameter α(t), which is implemented in the sn package of R. The standardization is such that the resulting distribution has mean 0 and variance 1. We consider all the possible combinations from the following scenarios:

1. mean function: (a) μ(t) = 6; and (b) μ(t) = −2.2t⁵ + 3t³ − 1.2t + 0.7;

2. variance function: (a) σ²(t) = exp(−5); and (b) σ²(t) = {2.2t⁵ −3t³ + 1.2t + 0.3}/ exp(4);

3. shape parameter function: (a) α(t) = 0; (b) α(t) = −21(t ≤ 0.5) + 41(t > 0.5); (c) α(t) = 5t² − 19t + 5; and (d) α(t) = −10 sin(2πt), for t ∈ [0, 1].

5.1 Model estimation performance

For the estimation of the mean and variance functions, the smoothing parameters were selected using REML implemented in the R package mgcv (Wood, 2006). For the estimation of the shape parameter functions, we used cubic regression splines with 5 knots, with the smoothing parameter selected by the corrected AIC criterion. We used a Gaussian copula to model dependence. For bivariate smoothing of the covariance function, tensor product penalized cubic regression splines with 10 knots per dimension were used, and REML estimation was used for the selection of the smoothing parameter (Wood, 2006).

The supplementary material (Figure S1) includes an illustration of a data set generated from covariance structure (IIii), mean function (1b), variance function (2b), and shape function (3d) along with the estimates of the mean, log-variance and shape parameter functions from 100 simulated data sets. The estimates of all population-level functions show nearly no bias and various degrees of smoothness. In particular, the log-variance estimates are somewhat undersmoothed, which is what is expected in the case of smoothing positively correlated data with a working independence assumption (Altman, 1990; Hart, 1991). Nonetheless, the undersmoothing does not degrade the MSE by much, as will be seen soon. In Table 1, we report estimates of the square root of the integrated mean squared error (IMSE), the integrated squared bias (ISBIAS), and the integrated variance (IVAR). For example, for $\widehat{\mu }\left(t\right)$, these quantities are defined as: $\mathrm{IMSE}={\int }_0^{1}E\left[{\left\{\widehat{\mu }\right(t)-\mu (t\left)\right\}}^2\right]dt$, $\mathrm{IVAR}={\int }_0^1\mathrm{Var}\left\{\widehat{\mu }\right(t\left)\right\}dt$ and $\mathrm{ISBIAS}={\int }_0^{1}E\left[{\left\{\widehat{\mu }\right(t)-\mu (t\left)\right\}}^2\right]dt$. Here $E\left\{\widehat{\mu }\right(t\left)\right\}$ and $\mathrm{Var}\left\{\widehat{\mu }\right(t\left)\right\}$ denote the sample mean and sample variance of $\widehat{\mu }\left(t\right)$, for 0 ≤ t ≤ 1. The results confirm our previous observations: the mean function estimator has very small IMSE, irrespective of the covariance structure. The somewhat larger IMSE of the log-variance function estimator is caused by its larger variability. For the shape parameter function estimator both the bias and the variability cause a larger IMSE. In general, estimation of the mean, log-variance and shape functions is not affected by the structure of the dependence of the latent process in cases where the latent process exhibits stronger dependence. As expected, when the latent process has very weak dependence, such as in scenario (II i), better estimates are obtained for all the population functions.

Table 1.

Estimates of the squared root of ISBIAS, the root of IVAR and the root of IMSE for the estimates of the mean function (1b), the log-variance function (2b), the shape parameter function (3d) when the latent process is specified as in (Ii) and (Iii) or in (IIi) and (IIii).

Latent Covariance	Population Level Functions	$\sqrt{ISBIAS}(\times {10}^2)$	$\sqrt{IVAR}(\times {10}^2)$	$\sqrt{IMSE}(\times {10}^2)$
(I i)	Mean	0.27	0.68	0.72
(I ii)		0.27	0.70	0.75
(II i)		0.27	0.55	0.61
(II ii)		0.27	0.63	0.69
(I i)	Log-variance	1.71	10.06	10.16
(I ii)		1.45	10.45	10.50
(II i)		1.69	7.58	7.73
(II ii)		1.68	9.51	9.61
(I i)	Shape	67.35	111.36	129.67
(I ii)		66.44	112.39	130.07
(II i)		61.30	57.72	84.00
(II ii)		65.54	71.76	96.25

Figure 2 illustrates the performance of our methodology with respect to capturing the true dependence of the functional process. Figure 2 displays the estimates of the first three eigenfunctions and eigenvalues of the copula correlation matrix in 100 simulated data sets from scenario (Ii). The true eigenfunctions and eigenvalues correspond to the correlation function derived from the model specified by the covariance structure (Ii); these eigenfunctions/eigenvalues are different from the ones defining the covariance functions. The copula correlation was estimated using Kendall’s tau; however, similar performance was noted when the sample Pearson correlation of the transformed curves was used.

Figure 2.

Estimated eigenfunctions (gray lines, top panels) and eigenvalues (bottom panels) and their corresponding true eigenfunctions (black lines) / eigenvalues (dotted line) derived from the true model, when the model uses mean function (1b), variance function (2b), shape function (3d), and covariance structure (Ii).

5.2 Prediction performance

We investigate the mean prediction error, in order to assess the performance of our prediction approach. Consider first a Gaussian copula and let ${\tilde{Z}}_i\left(t\right)={\Phi }^{-1}\left[{\widehat{F}}_t\right\{Y_i\left(t\right)\left\}\right]$, where ${\widehat{F}}_t$ is an estimate of the pointwise distribution of Y_i(t); notice that ${\widehat{F}}_t$ can be obtained using estimates of the mean, standard deviation and shape parameter functions, or by using the pointwise empirical distribution function. Also let ${\widehat{Z}}_i\left(t\right)$ be the predicted trajectory by the approach in Section 4. Then the prediction error is determined as $IPE={\int }_{\mathcal{T}}E\left[{\left\{\widehat{Y}\right(t)-\tilde{Y}(t\left)\right\}}^2\right]dt$. If {t_i1, … , t_imi} is the set of points at which the ith curve is observed for i = 1, … , n, then the IPE can be estimated by $\widehat{IPE}={\Sigma }_{i=1}^N{\Sigma }_{j=1}^{m_i}{\left\{Y_i\right(t_{ij})-{\widehat{Y}}_i(t_{ij}\left)\right\}}^2∕\left(N{m}_i\right)$, where ${\widehat{Y}}_i\left(t\right)$ is determined using (5). Table 3 reports the estimated squared root IPE using 100 simulated data sets from a few scenarios (IPE_o), and when F_t is estimated using the empirical CDF. In addition it presents the average squared root IPE for the trajectory of a new subject, which is observed either on the first half of the set of the sampling points (IPE_new1), or at randomly selected time points (IPE_new2). More specifically, let {t₁, … , t_m} be the sampling points in our data, and $\left[Y^{\ast }\right(t):t\in \{t_1^{\ast },\dots ,t_k^{\ast }\left\}\right]$ be the observed data corresponding to a new subject, where k < m. Our methodology allows to predict the trajectory for this new subject for the sampling points at which it has not been observed; Table 3 gives the estimate of the average squared root of IPE, calculated as $IP{E}_{new}={\Sigma }_{j=k+1}^m{\left\{{\widehat{Y}}^{\ast }\right(t_j^{\ast })-Y^{\ast }(t_j^{\ast }\left)\right\}}^2∕(m-k)$, where $\{t_{k+1}^{\ast },\dots ,t_m^{\ast }\}$ is the set of time points at which the subject has not been observed. For example IPE_new1 uses $t_j^{\ast }=t_j$ for j = 1, … , k, while for IPE_new2 we select $t_1^{\ast }$ < … < $t_k^{\ast }$ randomly from {t₁, … , t_m}; in both scenarios k = 41. In all the cases, the estimates of the mean, variance and shape parameter functions are obtained using the approach described in Section 3; for the shape parameter function Alternative 1 was used.

Table 3.

Estimates of the squared root of IPE using the observed data (IPE_o) and corresponding to two trajectories: one that is observed on the first 41 of the sampling design points (IPE_newl) and one that is observed at 41 random time points (IPE_new2). In parenthesis are displayed, the counterparts using common functional PCA tools (Di et al., 2009). The scenarios use skew normal distribution with the mean (1b), the log-variance (2b), the shape parameter (3d) and covariance structures (I i)-(II ii). The correct copula model is used in the estimation.

Latent Cov		Gaussian copula			t - copula with 4 d.f.
	$\sqrt{IP{E}_o}$	$\sqrt{IP{E}_{new1}}$	$\sqrt{IP{E}_{new2}}$	$\sqrt{IP{E}_0}$	$\sqrt{IP{E}_{new1}}$	$\sqrt{IP{E}_{new2}}$
(I i)	0.025 (0.025)	0.029 (0.036)	0.025 (0.027)	0.020 (0.020)	0.023 (0.025)	0.020 (0.020)
(I ii)	0.029 (0.029)	0.030 (0.037)	0.028 (0.029)	0.023 (0.023)	0.023 (0.028)	0.022 (0.023)
(II i)	0.056 (0.055)	0.125 (0.122)	0.075 (0.077)	0.045 (0.044)	0.094 (0.096)	0.056 (0.059)
(II ii)	0.038 (0.038)	0.139 (0.125)	0.049 (0.052)	0.031 (0.030)	0.096 (0.099)	0.037 (0.040)

It appears that the latent covariance structure has a slight effect on the performance of the prediction, especially in the case of forecasting the trajectory of a new subject. For both Gaussian and t-copulas, the prediction performance corresponding to the observed data, IPE_o, is very good for designs (I i) and (I ii); but somewhat poorer when the latent correlation has a shorter range, such as in designs (II i) and (II ii). We notice similar performance for the prediction of a new trajectory, although this varies further with the design of the time points at which the new subject is observed. The the accuracy of the prediction is very close to the one based on the observed data, when the new subject is observed at 41 randomly selected time points (fourth and seventh column of Table 3), than when it is observed at the first 41 time points (third and sixth column of Table 3). Overall, our prediction approach has good performance, which in addition is very close to the accuracy using common functional PCA tools (Di et al., 2009), as illustrated by Table 3.

6. Comparison between quantile regression and a Karhunen-Loéve expansion

One main advantage of our model is that it both estimates the pointwise quantile functions and provides a Karhunen-Loéve expansion to model dependencies. We are not aware of any competing methodology with this feature. Nonetheless, nonparametric quantile regression and a KL might be considered as alternatives to our methodology, so a comparison with them is in order. For fixed p ∈ (0, 1), our estimated quantile function is ${\widehat{Q}}_p\left(t\right)=\widehat{\mu }\left(t\right)+\widehat{\sigma }\left(t\right)G^{-1}\{p;\widehat{\alpha }(t\left)\right\}$. Table 2 gives the estimates of the IMSE and ISBIAS of ${\widehat{Q}}_p\left(t\right)$ for p = 1%, 10% and 50%, for one particular scenario. These results are compared to quantile regression estimates using constrained linear splines with an AIC chosen roughness penalty, implemented by the R package cobs of Ng and Maechler (2007). Our method outperforms cobs with respect to ISBIAS, IVAR, and IMSE, especially for more extreme quantile levels. Of course, the modeling of dependence by the KL expansion is an advantage of our methodology over quantile regression, because the KL expansion provide a probability model for the data generating mechanism, which facilitates prediction (Section 4) and allows model-based bootstrapping. However, non-parametric regression quantile estimation is a good competitor with respect to marginal quantile estimation. For an additional comparison, in Figure S2 of the supplementary material, we plot for one scenario the quantile functions estimated with our method, the cobs software, and the KL expansion which assumes that the scores are normally distributed. As expected, the quantile functions with the latter method are badly biased when asymmetry exists in the data. Moreover, although the KL expansion can model correlation, because of its Gaussian assumption, the KL expansion cannot accommodate tail dependence.

Table 2. Estimates of the squared root of ISBIAS, the root of IVAR and the root of IMSE for the estimates of the quantile functions of levels 1%, 2%, 5%, 10% and 50%, for the case when the true mean function is (1b), the log-variance function is (2b), the shape parameter function is (3d) and the latent process is specified by (Ii).

Method	Quantile level	$\sqrt{ISBIAS}(\times {10}^2)$	$\sqrt{IVAR}(\times {10}^2)$	$\sqrt{IMSE}(\times {10}^2)$
Model based	1%	0.46	1.58	1.64
COBS		1.40	1.95	2.39
Model based	2%	0.40	1.40	1.45
COBS		1.12	1.45	1.83
Model based	5%	0.33	1.17	1.21
COBS		0.71	1.18	1.37
Model based	10%	0.30	0.99	1.03
COBS		0.41	1.04	1.11
Model based	50%	0.31	0.65	0.72
COBS		0.39	0.77	0.85

Our methodology uses a parametric model for the marginal distributions, and we have focused on the skew normal and skew t families, with only 3, respectively, 4 parameters. In situations where the marginal distributions are not well approximated by either of these models, one could use a more highly parameterized model, such as normal mixture models. Alternatively, one could use quantile regression regression to estimate the marginal distributions in combination with our copula approach to modeling dependence.

7. Application: DTI tractography

We apply our proposed method to a study of the diffusion characteristics of white matter tracts in patients with multiple sclerosis (MS) and healthy controls. White matter tracts consist of axons that convey information between parts of the brain. These axons are covered with myelin, a white fatty coating. The myelin sheath helps the nerve transmit signals at a very fast rate. Myelin damage, as seen in MS and other demyelinating diseases, impairs axonal conduction and can be associated with axonal degeneration. Inflammatory demyelination and axon damage in the corpus callosum tract are prominent features of MS and may partially account for impaired performance on complex tasks (Ozturk et al., 2010).

DTI reveals microscopic details about the architecture of the white matter tracts by measuring the three-dimensional directions of water diffusion in the brain (Basser et al. 1994, 2000). Our study uses measurements of the parallel diffusivity within the corpus callosum for 162 MS patients and 42 healthy controls. Goldsmith et al. (2010) used parallel diffusivity within left intracranial cortico-spinal tracts to classify subjects as MS cases or controls. Figure 1 displays tract profiles sampled at 93 locations in MS patients and controls.

A quick inspection of Figure 1 suggests that the controls and MS patients have somewhat similar means but different variability and asymmetry across tract location. We assumed that at each tract location, the parallel diffusivity for each group has a skew t distribution with constant, but unknown, degrees of freedom and location-specific skewness. The degrees of freedom parameter (ν) was estimated through maximum likelihood under a working independence assumption. This approach yields $\widehat{\nu }=6.79$ for the MS group and $\widehat{\nu }=16482.29$ for the control group. Because $\widehat{\nu }$ of the control group is very large, and since the skew t distribution reduces to skew normal when ν = ∞, we used the skew normal for this group.

The estimated mean, variance and skewness functions in the healthy volunteer and MS groups, along with confidence intervals of the corresponding difference functions, are included in the supplementary material, Figure S3. The results indicate slightly larger mean of parallel diffusivity for cases than for controls. Furthermore, using 90% bootstrap confidence intervals (based on 1000 resamples) they depict significantly higher variability and considerably larger third-moment skewness coefficient functions for the parallel diffusivity in the MS group than in the control group. For the control group, the skewness function depends solely on the shape parameter that governs a skew normal distribution; while it depends on both the degrees of freedom and the shape parameters for the MS group. Figure S3 shows that the skewness function in the MS sample of parallel diffusivity is significantly larger than the skewness function in the control sample for locations 30-85 along the corpus callosum tract.

Figure 3 illustrates the comparison between the quantile functions of the parallel diffusivity profiles corresponding to the two groups at the quantile levels 1%, 50%, 95% and 99%. The lower quantile functions seem comparable for the two groups: this is expected when the mean functions are close to each other and the variance functions are small, which is our case. The higher level quantiles are indicative of the differences between the two groups in both the shape parameter and the variance. Figure 3 (bottom panel) shows the 90% pointwise confidence intervals of the estimated difference between the quantile functions of the two groups: the quantile functions for the MS group are significantly larger than the corresponding ones for the control group for probabilities of 50% and higher.

Figure 3.

Estimated quantiles of the parallel diffusivity profiles within the corpus callosum tracts of the MS patients and controls. Top panel: Estimated quantiles functions for the MS group (black lines) and the control group (grey lines). Bottom panel: Estimated difference between the quantiles of the MS and control groups (solid lines) with 90% pointwise confidence intervals (dashed lines) from 1000 bootstrap replicates.

We first used Gaussian copulas, with group specific parameters, to model the dependencies in the parallel diffusivity profiles. Figure 4 shows the estimated eigenfunctions and eigenvalues of the correlation matrices for the MS patients and control groups. The similarity between these estimates in the two groups is remarkable. It suggests that to compare these groups of curves, models with common correlation functions can be used in future analyses. At the same time, it indicates that the difference in the distributions of the parallel diffusivity profiles in the MS group and controls can be summarized solely by the marginal distributions. In particular one could use the pointwise quantile functions obtained in the control group to identify most unusual parallel diffusivity in the MS group. Furthermore, because the mean and the variance are significantly larger in the MS group than in the control group irrespective of the tract location, one can use the pointwise skewness to identify the most interesting parts of the tract.

Figure 4.

Estimated eigenfunctions of the latent Gaussian copula correlation functions in the MS (black) and control (grey) groups. Percentages of explained variance are given in parenthesis corresponding to MS and healthy subjects.

In addition, t-copulas were fit to the MS and control groups. The correlation matrices, estimated by the Kendall’s tau approach in Section 3.2, are very similar to the Gaussian copula correlation matrices. The maximum likelihood estimates of copula degrees of freedom were 3.30 for the control group and 4.88 for the MS group. (These estimates should not be confused with the estimates of ν for the marginal skew t distributions.) Such small values of the copula degrees of freedom parameter imply substantial tail dependence. The tail dependence would have been missed if Gaussian models had been used, since there is no tail dependence in a multivariate normal distribution, except in the case of perfect correlation. The tail dependence also seems apparent in the data, for example in Figure 1 where individual curves that are extreme at one tract location tend to be extreme at other locations. This behavior would not occur if the data had a multivariate Gaussian distribution, even with high correlation, unless the correlation were perfect.

Our findings are consistent with previous studies of diffusivity. These have shown that acute axonal injury at first decreases parallel diffusivity, but, as the tissue repairs, parallel diffusivity normalizes and then increases above normal. This is likely due to increased overall diffusivity and is probably not specific for a particular kind of tissue injury, e.g., not specific to MS. Another possibility is that the researchers have overestimated parallel diffusivity, because as the tract atrophies, one get contributions from adjacent cerebrospinal fluid (where diffusivity is high). However, the investigators have tried to minimize this effect, and it not considered to be a major problem. The main contributions of this new method to the understanding of MS are (1) identification of the most severely affected cases; and (2) identification of the interesting parts of the tract.

8. Conclusion

This paper introduces a model for functional data that exhibit non-Gaussian characteristics such as skewness, heavy tails, and tail dependence. Our model includes a Karhunen-Loève expansion for a latent, but estimable, Gaussian process that induces dependencies. Our approach is based on copula methodology and combines elements of parametric and nonparametric modeling. However, robustness of our methodology to the choice of the parametric families of marginal and copula distributions and goodness-of-fit testing of these families remain open problems.