Abstract
Substantial longitudinal relations between children's early mathematics achievement and their much later mathematics achievement are firmly established. These findings are seemingly at odds with studies showing that early educational interventions have diminishing effects on children's mathematics achievement across time. We hypothesized that individual differences in children's later mathematical knowledge are more an indicator of stable, underlying characteristics related to mathematics learning throughout development than of direct effects of early mathematical competency on later mathematical competency. We tested this hypothesis in two longitudinal data sets, by simultaneously modeling effects of latent traits (stable characteristics that influence learning across time) and states (e.g., prior knowledge) on children's mathematics achievement over time. Latent trait effects on children's mathematical development were substantially larger than state effects. Approximately 60% of the variance in trait mathematics achievement was accounted for by commonly used control variables, such as working memory, but residual trait effects remained larger than state effects. Implications for research and practice are discussed.
Keywords: mathematics achievement, cognitive development, state-trait models, education, intelligence
Mathematics achievement during schooling is a strong predictor of labor-market earnings (Murnane, Willett, & Levy, 1995; Ritchie & Bates, 2013). In addition, researchers consistently find that children's early mathematics achievement predicts their later mathematics achievement (e.g., Duncan et al., 2007). These findings have led many people to conclude that early intervention is likely to result in significant long-term gains in children's mathematics achievement and subsequent life outcomes. Indeed, the U.S. government spends at least as much on early-childhood programs as on educating disadvantaged students in kindergarten through Grade 12 (Whitehurst, 2014).
The efficiency of these early intervention programs depends on whether raising children's school-entry mathematical skills will better enable them to acquire more difficult mathematical skills later on. Consistent with this possibility are findings that in children's mathematical development, later knowledge often builds on earlier knowledge. For example, to solve a fraction addition problem, children must be able to accurately multiply and add whole numbers; children who make frequent errors in whole-number arithmetic make frequent errors on fraction arithmetic problems (Siegler & Pyke, 2013). Transfer of learning likely also contributes to longitudinal stability in children's mathematics achievement. For example, knowledge of mathematical concepts facilitates the learning of mathematical procedures, and vice versa (Rittle-Johnson & Siegler, 1998; Schneider, Rittle-Johnson, & Star, 2011).
Indeed, several studies have found that children's early mathematics knowledge is a robust predictor of their later mathematics achievement (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004; Bailey, Siegler, & Geary, 2014; Duncan et al., 2007; Geary, Hoard, Nugent, & Bailey, 2013; Jordan, Kaplan, Ramineni, & Locuniak, 2009; Siegler et al., 2012; Watts, Duncan, Siegler, & Davis-Kean, in press). This longitudinal stability holds after adjusting for domain- general cognitive abilities, such as IQ and working memory, reading and language skills, and socioeconomic status (SES). Further, the amount of time between measurements of early and later mathematics achievement is not clearly related to the strength of the association between them (Watts et al., in press); in fact, some evidence suggests that the strength of this relation increases over time (Claessens & Engel, 2013).
To the extent that this observed longitudinal stability in children's mathematics achievement predicts the likely effects of interventions, interventions that lead to short-term gains in children's mathematics achievement should show effects of at least the same magnitude persisting into the long term. However, studies of the effectiveness of early educational interventions suggest otherwise. Research on both general educational interventions (e.g., Campbell & Ramey, 1994; Puma, Bell, Cook, & Heid, 2010) and mathematics-specific interventions (Clements, Sarama, Spitler, Lange, & Wolfe, 2011; Clements, Sarama, Wolfe, & Spitler, 2013) has revealed that short-term test-score gains have diminishing effects on children's mathematics achievement across time. A comprehensive review of early-childhood education programs showed substantially decreasing effects with increasing time since the intervention (Leak et al., 2010). Therefore, despite a substantial literature indicating that individual differences in mathematics achievement are stable from school entry to school completion, early interventions targeting children's mathematics achievement show diminishing returns and do not consistently boost their much later mathematics outcomes. What can account for this apparent discrepancy?
We hypothesize that individual differences in children's later mathematical knowledge are more likely an indicator of unmeasured, stable characteristics related to mathematics learning throughout development (e.g., domain-general cognitive abilities, motivation) than of a direct effect of their early mathematical competency on their later mathematical competency. This hypothesis is supported by two findings from studies of children's mathematical development.
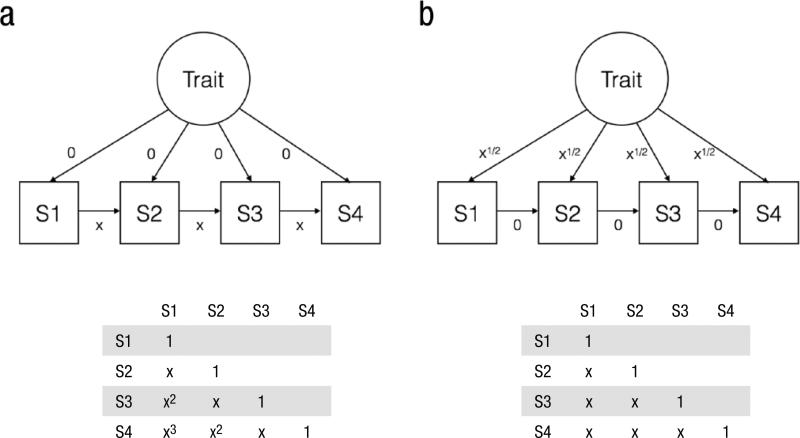
First, previous research has found a consistent relation between early and later measurements of mathematics achievement, regardless of the amount of time between measurements. If mathematical development is a purely autoregressive process, in which earlier knowledge alone directly influences later learning (Fig. 1a), the correlation between measures of mathematics achievement at different time points should decay exponentially as the time between the measures increases and the causal connection between these time points becomes increasingly indirect. If, at the other extreme, individual differences arise independently of previous mathematical knowledge (Fig. 1b), the correlation between mathematics achievement in one year and mathematics achievement in another year should be completely independent of the time gap between those years. The truth probably lies somewhere in the middle, because it is likely that both traits (stable characteristics that contribute to achievement) and previous knowledge contribute to children's mathematical development. However, the findings that the temporal distance between measurements of mathematics achievement is not clearly related to the strength of the association between those measurements are more consistent with the latter pattern.
Fig. 1.
Illustration of (a) state-only and (b) trait-only models of mathematics achievement and the correlation matrices they predict. Each model describes the relationships among latent trait mathematics achievement and measures of state mathematics achievement (S) at four time points (1–4). Although both models predict correlations of x between mathematics achievement at consecutive time points, they make differing predictions about the correlations between mathematics achievement at nonconsecutive time points. According to the purely autoregressive, state model, these correlations will decay exponentially with increasing distance in time between measurements, whereas according to the pure trait model, these correlations will be stable regardless of the distance in time between measurements.
Second, studies have also found relations between mathematics achievement and a large number of traits, which are unlikely to be fully controlled in longitudinal studies of mathematics achievement. A skeptic might argue that stable underlying traits are not likely to account for strong longitudinal relations in children's mathematics achievement because children's mathematics achievement shows rank-order longitudinal stability even after adjustments are made for IQ, working memory, and SES. Indeed, it is uncontroversial that these traits affect children's learning. For example, a large prospective study found that intelligence at age 11 accounted for 59% of the variance in mathematics achievement at age 16 (Deary, Strand, Smith, & Fernandes, 2007). However, the large set of traits that have been implicated in mathematics learning includes attention (Zentall, 2007), processing speed (Mazzocco & Grimm, 2013), several subfacets of working memory (Szücs, Devine, Soltesz, Nobes, & Gabriel, 2014), beliefs and expectancies (Meece, Wigfield, & Eccles, 1990), and motivation (Murayama, Pekrun, Lichtenfeld, & vom Hofe, 2013). The length of this list is problematic: No longitudinal study of children's mathematics achievement that we are aware of has assessed all of these traits, and therefore every such study has been confounded by unmeasured traits that may affect children's mathematics achievement across development. Consequently, reported findings may overestimate the potential effects of early interventions on much later mathematics achievement. The current study was designed to estimate the relative influences of stable traits and previous state knowledge (i.e., autoregressive effects) on children's mathematical development.
Method
We addressed the problem of confounds by using the state-trait modeling approach (Steyer, 1987) to analyze two longitudinal data sets. That is, we partitioned the variance in mathematics achievement throughout development into trait effects (i.e., effects of factors that influence an individual's mathematics achievement similarly across development) and state effects (i.e., effects of individual differences in mathematics achievement on subsequent mathematics achievement). Thus, mathematics achievement at a given time point was modeled as influenced by (a) a traitlike factor, (b) mathematics achievement at the immediately preceding measurement occasion (the state effect), and (c) unique sources of variation (e.g., measurement error; Jackson, Sher, & Wood, 2000). In our models, trait mathematics achievement was a set of factors that had a stable influence on mathematics achievement throughout development. State effects, in contrast, represented occasion-specific effects on children's mathematics achievement (e.g., the influences of specific teachers), effects of specific types of mathematics knowledge on the development of other knowledge, and a number of other factors.
We hypothesized that latent trait effects would contribute significantly to the longitudinal stability in children's mathematics achievement. We also hypothesized that most of the trait variance would be accounted for by domain-general cognitive abilities, reading achievement, and SES. However, because these variables do not account for all traits contributing to children's mathematics achievement, we also hypothesized that latent trait effects would continue to contribute to estimates of longitudinal relations between early and later mathematics knowledge even after we adjusted for these other variables.
Short-term data set
The participants in this data set were the 292 children who completed the first-grade assessments in a longitudinal study of mathematical development (Geary, 2010; Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007). Appendix A of the Supplemental Material available online provides additional information on this sample, including details about their SES.
Mathematics achievement
Participants’ mathematics achievement in first, second, third, and fourth grades was assessed using the number of correct answers on the Numerical Operations subtest of the Wechsler Individual Achievement Test II–Abbreviated (Wechsler, 2001). In this age range, the items involve number discrimination, rote counting, number production, basic addition and subtraction, and multidigit addition and subtraction; there are also some multiplication and division problems to be solved with paper and pencil. This test has been shown to be reliable in all four of these age groups (split-half reliabilities, calculated using the Spearman-Brown formula, were .85, .81, .91, and .88 for ages 6, 7, 8, and 9, respectively; Wechsler, 2001).
Reading achievement
First graders’ reading achievement was assessed using the number of correct answers on the Word Reading subtest of the Wechsler Individual Achievement Test II–Abbreviated (Wechsler, 2001). This subtest requires reading single words aloud.
Working memory
Central executive functioning in first grade was assessed by the number of correct answers on the Listening Recall, Counting Recall, and Backward Digit Recall subtests of the Working Memory Test Battery for Children (Pickering & Gathercole, 2001). This measure was reliable in the current sample (Cronbach's α = .77).
Intelligence
The Vocabulary and Matrix Reasoning subtests of the Wechsler Abbreviated Scale of Intelligence were administered and used to estimate Full Scale IQ in first grade (Wechsler, 1999).
SES
Data on parental education and household income were obtained through a survey completed by the participants’ parents.
Long-term data set
Data for our long-term models of mathematics achievement were drawn from the National Institute of Child Health and Human Development (NICHD) Study of Early Childcare and Youth Development (SECCYD). Participants were recruited at birth from 10 geographically diverse sites in both urban and rural areas and were followed through adolescence. We employed a subsample (n = 1,124) of participants who had at least one valid mathematics achievement score. Sampling procedures for the SECCYD study have been well documented (see Duncan & Gibson, 2000; NICHD Early Child Care Research Network, 2002). We present descriptive information about the participants in Appendix B of the Supplemental Material.
Mathematics achievement
The Woodcock-Johnson–Revised (WJ-R) Applied Problems subtest (Woodcock, McGrew, & Mather, 2001) was administered in Grades 1, 3, and 5 and at age 15. The Applied Problems subtest is a widely used measure of mathematics achievement (e.g., Siegler et al., 2012), and it is used to assess understanding of a broad range of mathematical procedures and concepts. In the current study, we used the standard score, which was age-normed to national standards (M = 100, SD = 15). This test was reliable in all four age groups of this sample (Cronbach's α = .83, .81, .82, and .87 for Grades 1, 3, and 5 and age 15, respectively).
Reading achievement
We used first-grade scores on the WJ-R Letter Word Identification subtest to measure early reading achievement. As with mathematics achievement, we used the standard score, which reflects students’ ability to correctly identify letters and simple words.
Working memory
The WJ-R Memory for Sentences subtest, which requires repeating sentences and phrases presented by a tape player, is a commonly used measure of working memory (e.g., Duncan et al., 2007). We used nationally normed standardized scores on this subtest for our measure of working memory.
Executive functioning
During first grade, children were administered the Tower of Hanoi puzzle, which assesses problem-solving and planning abilities. We used the efficacy score, which is derived from the number of trials the participant takes to complete each task (see Borys, Spita, & Dorans, 1982).
SES
Family income was measured via parental report six times from when the children were 1 month old to when they were in first grade. This information was transformed to an income-to-needs ratio at each time point, and we calculated the average ratio for each child. Mothers reported their level of completed education during interviews when the children were 1 month old.
Analyses
For each data set, we estimated a state-trait model with a latent trait and four state factors; each of the state factors was related to the corresponding mathematics measure via a path set to the square root of the reliability for that measure (to account for measurement error). We also estimated for each data set a model in which we regressed the latent trait on domain-general cognitive abilities (working memory, IQ or executive functioning), reading achievement (a measure of reading ability and proxy for general academic ability), and SES (household income, parental education). Thus, we estimated a total of four models.
We constrained the trait variance to be 1 and the paths from latent trait mathematics achievement to state mathematics achievement at the second, third, and fourth time points to be equivalent within each model. We freely estimated the path from latent trait mathematics achievement to state mathematics achievement at the first time point because it was the only time point that did not control for previous mathematics achievement. This practice is common in latent variable analyses (Little, Slegers, & Card, 2006). In the long-term data set, the latter constraint led to inflated standard errors for some of the paths, so we constrained the first, third, and fourth time points to be equivalent in each model for this data set. For the long-term data set, all latent variables and controls were regressed on site before being entered in the models. This practice is common in analyses using these data (Duncan et al., 2007; Watts et al., in press), as site characteristics have been shown to vary widely in this sample.
Results
Table 1 presents the correlation matrices for the short-term and long-term data sets. The correlations in both data sets approximate a pattern predicted by a trait model more closely than a pattern predicted by a purely autoregressive, state model. The average correlations for mathematics achievement measured at consecutive time points were .67 and .74 in the short-term and long-term data sets, respectively. Given these observations, an autoregressive process would predict estimates near .72 (.49) and .73 (.34) for correlations between mathematics achievement two and three time points apart, respectively. In contrast, a trait model would predict correlations close to .7 regardless of the lag between measurements. In the short-term data set, the correlations between mathematics achievement two time points apart averaged .58, and the correlation between Time 1 and Time 4 mathematics achievement was .51. In the long-term data set, the correlations between mathematics achievement two time points apart averaged .70, and the correlation between Time 1 and Time 4 mathematics achievement was .66, despite a lag of approximately 8 years between these time points. These correlations suggest substantial trait effects in both cases, but also provide some evidence of state effects.
Table 1.
Correlation Matrices for the Short-Term and Long-Term Data Sets
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1. State math achievement: Time 1 | .72 | .72 | .66 | .53 | .27 | .58 | .33 | .36 | |
| 2. State math achievement: Time 2 | .61 | .76 | .67 | .50 | .26 | .56 | .28 | .34 | |
| 3. State math achievement: Time 3 | .49 | .69 | .74 | .51 | .27 | .52 | .33 | .39 | |
| 4. State math achievement: Time 4 | .51 | .67 | .72 | .49 | .22 | .44 | .32 | .40 | |
| 5. Working memory | .41 | .53 | .58 | .59 | .19 | .45 | .30 | .33 | |
| 6. IQ/executive functioninga | .36 | .51 | .46 | .49 | .44 | .18 | .16 | .15 | |
| 7. Reading achievement | .44 | .49 | .55 | .55 | .55 | .51 | .23 | .28 | |
| 8. Household income | .23 | .30 | .28 | .33 | .22 | .37 | .36 | .55 | |
| 9. Parental education | .20 | .29 | .37 | .39 | .38 | .37 | .35 | .58 |
Note: Correlations in the short-term data set are below the diagonal; correlations in the long-term data set are above the diagonal. All correlations are significant, p < .03 (p < .001 for correlations in boldface).
Our second measure of domain-general ability was IQ in the short-term data set and executive functioning in the long-term data set.
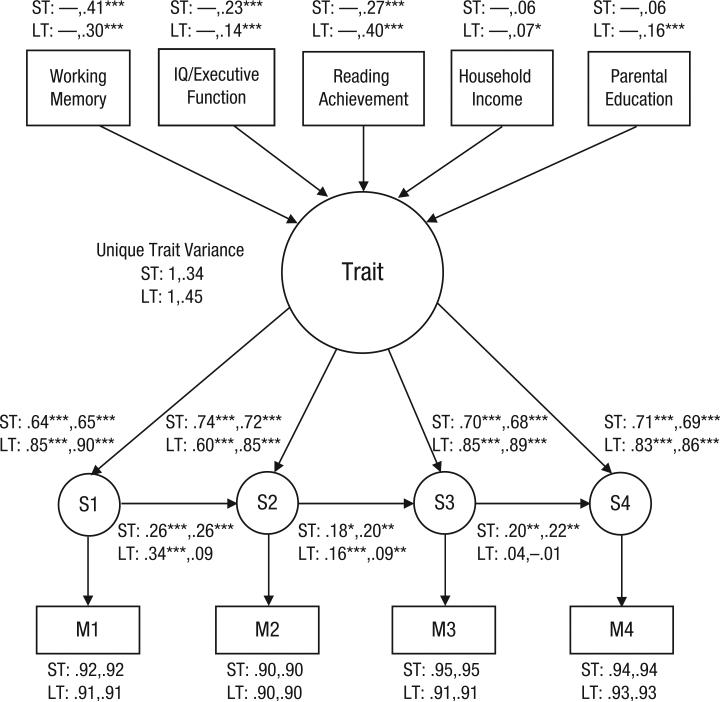
Figure 2 presents the state-trait models for the short-and long-term data sets before and after regressing the latent trait on domain-general abilities, reading achievement, and SES. We evaluated model fit using recommendations from Kline (2005). Specifically, we considered fit to be good if the comparative fit index (CFI) was at least .90 and the root-mean-square error of approximation (RMSEA), which measures fit adjusting for sample size, was less than .08, and preferably less than .05.
Fig. 2.
State-trait models for the short-term data set (ST) and the long-term data set (LT). For each data set, the first coefficient is from the model before the latent trait was regressed on domain-general abilities (working memory in both ST and LT; IQ in ST and executive functioning in LT), reading achievement, and socioeconomic status (household income and parental education), and the second coefficient is from the model after the latent trait was regressed on these variables. All coefficients are standardized. S1, S2, S3, and S4 = state mathematics achievement at the first, second, third, and fourth time points, respectively; M1, M2, M3, and M4 = measured mathematics achievement at these time points. Asterisks indicate coefficients that are significant (*p < .05, **p < .01, ***p < .005). The numbers at the bottom of the figure are the square roots of test reliabilities of each test at each time point; these values were used to adjust the state values for measurement error. Correlations between domain-general cognitive abilities, reading achievement, and SES are not shown, nor are the effects of site dummy variables on all manifest and latent variables in the long-term data set.
State-trait models for the short-term data set
The state-trait model fit the short-term data well both before and after we regressed the latent trait on domain-general abilities, reading achievement, and SES—before: χ2(1) = 0.65, p = .42, RMSEA = .00, CFI = 1.00; after: χ 2(6) = 19.89, p = .23; RMSEA = .03; CFI = .995. Before adjustment for domain-general cognitive abilities, reading achievement, and SES (see Fig. 2, first coefficient for each path), both state and trait effects were significant in all cases, but trait effects (range: .64–.74) were larger than state effects (range: .18–.26). For example, the proportion of variance in Time 2 mathematics achievement that was explained by direct trait effects was .55 (trait loading × trait variance × trait loading, or .74 × 1 × .74). In contrast, the proportion of variance in Time 2 mathematics achievement that was explained by Time 1 state mathematics achievement (including the indirect effect of the latent trait via Time 1 state mathematics achievement) was .07 (state effect2, or .262).
The ratio of the percentage of variance in Time 2 mathematics achievement accounted for by direct trait versus state factors (55:7) was striking. However, it is uncontroversial that traits affect children's mathematics achievement. Indeed, this is why researchers often adjust for some combination of domain-general cognitive abilities, reading achievement, and SES in longitudinal studies of children's mathematics achievement. Together, these variables accounted for 66% of the variance in trait mathematics achievement in the short-term data set. A more interesting question is whether trait effects vanished after adjustment for these variables? In the model adjusting for domain-general cognitive abilities, reading achievement, and SES (see Fig. 2, second coefficient for each path), .07 of the variance in Time 2 mathematics achievement was again explained by Time 1 mathematics achievement (the state effect); the direct trait effect was reduced, but at .18 (.72 × .34 × .72) was still more than twice the size of the state effect.
State-trait models for the long-term data set
The state-trait model fit the long-term data well both before and after we regressed the latent trait on domain-general abilities, reading achievement, and SES—before: χ2(1) = 4.48, p = .03, RMSEA = .056, CFI = .999; after: χ2(16) = 108.22, p < .001; RMSEA = .072, CFI = .975. As in the short-term data set, trait effects were substantially larger than state effects. The final state path was not statistically significant in either model for the long-term data set, but we note that the time between the third and fourth time points, 4 years, was the longest in either data set.
In the long-term data set, before the adjustments for domain-general abilities, reading achievement, and SES, the proportion of variance in Time 2 mathematics achievement that was explained by direct trait effects was .36 (.60 × 1 × .60), and the proportion of variance accounted for by state effects (including the indirect effect of the latent trait via Time 1 state mathematics achievement) was .12 (.34 × .34). Domain-general cognitive abilities, reading achievement, and SES together accounted for 55% of the variance in trait mathematics achievement. As in the short-term data set, adjusting for these variables (see Fig. 2, second coefficient for each path) reduced the proportion of variance in Time 2 mathematics achievement that was directly accounted for by the latent trait (.85 × .45 × .85, or .33), but this was still substantially larger than the amount of variance accounted for by state Time 1 mathematics achievement (.09 × .09, or .01).
Discussion
Results were quite similar across the two data sets, and were consistent with our predictions. Latent trait effects accounted for most of the longitudinal stability in children's mathematics achievement and were largely explained by measured domain-general cognitive abilities, reading achievement, and SES (and especially by working memory and reading achievement—see Fig. 2). However, as predicted, latent trait effects continued to be larger than state effects even after adjustment for these variables. This indicates that failing to consider other stable characteristics (e.g., motivation and external environmental effects, such as school effects) could substantially bias estimates produced by multiple regression models.
This study unites two discrepant lines of research: a large body of work indicating high levels of longitudinal stability of individual differences in children's mathematics achievement and studies showing diminishing effects of early mathematics interventions over time. The latter studies fail to adequately adjust for trait effects on mathematics achievement, and reported results consequently overestimate the likely effects of early interventions on much-later mathematics achievement outcomes. It is possible that trait mathematics achievement includes some early mathematical skills or skills, such as basic arithmetic skill, that contribute to performance on a wide range of mathematics tests, but this remains to be determined.
On the one hand, individual differences on some measures of basic arithmetic achievement (e.g., retrieval accuracy for simple arithmetic facts) tend to converge (Ackerman, 2007; but do not disappear, as we discuss in the next paragraph) and show weaker relations with relatively stable traits (e.g., domain-general cognitive abilities) as children progress in their mathematical development (Bailey, Littlefield, & Geary, 2012). These findings are inconsistent with the argument that trait mathematics achievement includes these basic mathematics skills. Further, it is unlikely that any particular set of factual knowledge can account for much of the trait variance we observed in children's mathematics achievement. This is because of the heterogeneity in the mathematical knowledge underlying variance in mathematics achievement from Grade 1 (the first time point in the long-term data set) to age 15 (the fourth time point in the long-term data set). For example, the 95th percentile of mathematics achievement at the first-grade time point corresponded to a raw score of 32, whereas a raw score of 33 on the same test corresponded to the 5th percentile of mathematics achievement at age 15. Therefore, the sets of problems on which children vary most are probably almost completely distinct at these two times.
On the other hand, individual differences in some basic skills (e.g., speed and accuracy of fact retrieval) persist even into adulthood (e.g., Geary & Widaman, 1992) and likely contribute to individual differences in performance in more complex mathematical domains. These observations are consistent with the argument that these basic skills may be included in the construct of trait mathematics achievement. However, a different pattern is found with general mathematics achievement, a more complex domain in which individual differences grow during development (Ackerman, 2007; Aunola et al., 2004; Geary et al., 2009) and remain substantially related to trait-level cognitive abilities (Table 1; Deary et al., 2007). The amount of observed variance in mathematics achievement accounted for by latent trait effects in our models is consistent with previous estimates of the effects of these cognitive abilities on mathematics achievement (Cowan & Powell, 2013; Deary et al., 2007), and the state-trait model fit both data sets well despite the constraint that trait loadings were constrained to be equivalent for three of the four time points. Therefore, if trait mathematics achievement includes specific types of mathematical skills, individual differences in mathematical knowledge would have to affect mathematics achievement similarly throughout development. Whether this is the case, and if so, what basic mathematics skills have these effects remain to be determined.
Implications for research
Findings from many longitudinal studies of children's mathematics achievement can be reinterpreted in light of these findings. Latent trait effects are likely confounds in studies of longitudinal stability in children's mathematics achievement and in studies of the numerical, mathematical, and domain-general skills that predict changes in children's mathematics achievement over time. Even studies that control for previous mathematics achievement (i.e., using an autoregressor) do not fully control for the traits that consistently affect children's mathematics achievement across development. However, interpretations of descriptive studies of the cognitive profiles of children with high and low mathematics achievement, or children at risk for low achievement, are not changed by the current study, and such studies remain useful for identifying children at risk for persistently low mathematics achievement.
The current study raises an important question: What traits account for the remaining variance in trait mathematics achievement? If it is possible to account for a very high proportion of the variance in trait mathematics achievement with a set of control variables, future longitudinal studies that include these variables can avoid confounds. Regardless, a simpler solution may be to include mathematics achievement data at enough time points to enable a state-trait analysis. The state-trait approach has a further advantage in that it can be used in currently existing longitudinal data sets to test hypotheses previously tested using the more traditional multiple regression approach. In addition to replicating the current findings, future research can address new questions raised by the state-trait framework, including whether early interventions affect state or trait mathematics achievement, whether state or trait mathematics achievement affects important life outcomes, and whether different types of key mathematical knowledge are related to mathematics achievement at the state or trait level. A final option for testing the direct effects of early mathematics knowledge on later mathematics achievement is the randomized controlled-trial design, which remains the gold standard for testing causal hypotheses.
Implications for practice
A practical implication of the current study is that early interventions that narrowly target skill acquisition for children with significant early mathematical deficits are likely insufficient to substantially alter their long-run achievement trajectories. That said, we believe these interventions are important and necessary. Several early interventions are known to quickly and effectively boost children's early numerical knowledge (e.g., Siegler, 2009), and a more intensive early mathematics intervention has shown benefits remaining at impressive levels 3 years later (Clements et al., 2011; Clements et al., 2013). Moreover, the alternatives to early intervention are not clearly more desirable. The state-trait model predicts that later mathematics intervention will produce larger endof-schooling gains in mathematics achievement for every standard-deviation gain in mathematics achievement that is immediately produced by the intervention. However, raising later mathematics achievement by 1 standard deviation is likely much more difficult than boosting earlier mathematics achievement by 1 standard deviation, as children are asked to master an increasingly large and complex set of knowledge as they get older.
Further, it is unclear at this point whether interventions also affect latent trait mathematics achievement. If so, the state-trait approach indicates the need to simultaneously target competencies that contribute to trait mathematics achievement above and beyond IQ, working memory, and the SES measures used here. For example, if the variance in trait mathematics achievement is related in part to motivation, perhaps promoting early numerical competence and motivation would increase trait mathematics achievement and later mathematical achievement on top of boosting state mathematics achievement. Consistent with this possibility is the finding that a successful early intervention with long-term effects on mathematics achievement also increased students’ motivation (Schweinhart et al., 2005). Interventions that change beliefs about the importance of effort for mathematics learning may also contribute to trait effects and boost long-term mathematics achievement (Blackwell, Trzesniewski, & Dweck, 2007). In other words, our results point to the need for multifaceted interventions that improve facets of trait mathematics achievement that can be most efficiently manipulated (perhaps motivational factors and beliefs), as well as successive interventions that target specific deficits in content knowledge throughout children's mathematical development. Finally, the current study addressed only individual differences in children's mathematical development. We emphasize that it is important to raise the mean level mathematics performance throughout development for all children.
Supplementary Material
Acknowledgments
We thank Mary Hoard, Lara Nugent, Linda Coutts, Chip Sharp, Jennifer Byrd-Craven, Chatty Numtee, Amanda Shocklee, Sara Ensenberger, Kendra Andersen Cerveny, Rebecca Hale, Patrick Maloney, Ashley Stickney, Nick Geary, Mary Lemp, Cy Nadler, Mike Coutts, Katherine Waller, Rehab Mojid, Jasmine Tilghman, Caitlin Cole, Leah Thomas, Erin Twellman, Patricia Hoard, Jonathan Thacker, Alex Wilkerson, Stacey Jones, James Dent, Erin Willoughby, Kelly Regan, Kristy Kuntz, Rachel Christensen, Jenni Hoffman, Stephen Cobb, and Deborah Vandell for help on various aspects of the project. We thank Jonathan Wai, Mimi Engel, Bob Siegler, Greg Duncan, Amy Claessens, Doug Clements, Pamela Davis-Kean, Katerina Schenke, Arena Chang, Tutrang Nguyen, and two anonymous reviewers for their comments on earlier drafts of this manuscript.
Funding This research was supported by the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD; Grants R01 HD38283 and R37 HD045914), the NICHD-supported Irvine Network on Interventions in Development (Grant HD065704 P01), and the University of Michigan's National Science Foundation–supported Center for the Analysis of Pathways From Childhood to Adulthood (Grant 0322356).
Footnotes
Declaration of Conflicting Interests The authors declared that they had no conflicts of interest with respect to their authorship or the publication of this article.
Supplemental Material Additional supporting information can be found at http://pss.sagepub.com/content/by/supplemental-data
Author Contributions D. H. Bailey and T. W. Watts developed the study concept. Testing and data collection were overseen by D. C. Geary. A. K. Littlefield oversaw and performed the data analysis, with help from D. H. Bailey and T. W. Watts. All authors contributed to writing the manuscript, and all authors approved the final version of the manuscript for submission.
References
- Ackerman PL. New developments in understanding skilled performance. Current Directions in Psychological Science. 2007;16:235–239. doi: 10.1111/j.1467-8721.2007.00487.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aunola K, Leskinen E, Lerkkanen M-L, Nurmi J-E. Developmental dynamics of math performance from preschool to Grade 2. Journal of Educational Psychology. 2004;96:699–713. [Google Scholar]
- Bailey DH, Littlefield A, Geary DC. The co-development of skill at and preference for use of retrieval-based processes for solving addition problems: Individual and sex differences from first to sixth grade. Journal of Experimental Child Psychology. 2012;113:78–92. doi: 10.1016/j.jecp.2012.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey DH, Siegler RS, Geary DC. Early predictors of middle school fraction knowledge. Developmental Science. 2014 doi: 10.1111/desc.12155. Advance online publication. doi:10.1111/desc.12155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackwell LS, Trzesniewski KH, Dweck CS. Implicit theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Development. 2007;78:246–263. doi: 10.1111/j.1467-8624.2007.00995.x. [DOI] [PubMed] [Google Scholar]
- Borys SV, Spitz HH, Dorans BA. Tower of Hanoi performance of retarded young adults and nonretarded children as a function of solution length and goal state. Journal of Experimental Child Psychology. 1982;33:87–110. doi: 10.1016/0022-0965(82)90008-x. [DOI] [PubMed] [Google Scholar]
- Campbell FA, Ramey CT. Effects of early intervention on intellectual and academic achievement: A follow-up study of children from low-income families. Child Development. 1994;65:684–698. [PubMed] [Google Scholar]
- Claessens A, Engel M. How important is where you start? Early mathematics knowledge and later school success. Teachers College Record. 2013;115(6):1–29. [Google Scholar]
- Clements DH, Sarama J, Spitler ME, Lange AA, Wolfe CB. Mathematics learned by young children in an intervention based on learning trajectories: A large-scale cluster randomized trial. Journal for Research in Mathematics Education. 2011;42:127–166. [Google Scholar]
- Clements DH, Sarama J, Wolfe CB, Spitler ME. Longitudinal evaluation of a scale-up model for teaching mathematics with trajectories and technologies: Persistence of effects in the third year. American Educational Research Journal. 2013;50:812–850. [Google Scholar]
- Cowan R, Powell D. The contributions of domain-general and numerical factors to third-grade arithmetic skills and mathematical learning disability. Journal of Educational Psychology. 2013;106:214–229. doi: 10.1037/a0034097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deary IJ, Strand S, Smith P, Fernandes C. Intelligence and educational achievement. Intelligence. 2007;35:13–21. [Google Scholar]
- Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, Japel C. School readiness and later achievement. Developmental Psychology. 2007;43:1428–1446. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Duncan GJ, Gibson C. Selection and attrition in the NICHD childcare study's analyses of the impacts of childcare quality on child outcomes. 2000 Retrieved from http://www.gse.uci.edu/person/duncan_g/docs/Duncan_Gibson_NICHD_childcare_quality_review_2000.pdf.
- Geary DC. Missouri longitudinal study of mathematical development and disability. British Journal of Educational Psychology Monograph Series II. 2010;7:31–49. [Google Scholar]
- Geary DC, Bailey DH, Littlefield A, Wood P, Hoard MK, Nugent L. First-grade predictors of mathematical learning disability: A latent class trajectory analysis. Cognitive Development. 2009;24:411–429. doi: 10.1016/j.cogdev.2009.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;78:1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Nugent L, Bailey DH. Adolescents’ functional numeracy is predicted by their school entry number system knowledge. PLoS ONE. 2013;8(1) doi: 10.1371/journal.pone.0054651. Article e54651. Retrieved from http://www.plosone.org/article/info%3Adoi%2F10.1371%2Fjournal.pone.0054651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Widaman KF. Numerical cognition: On the convergence of componential and psychometric models. Intelligence. 1992;16:47–80. [Google Scholar]
- Jackson KM, Sher KJ, Wood PK. Prospective analysis of comorbidity: Tobacco and alcohol use disorders. Journal of Abnormal Psychology. 2000;109:679–694. doi: 10.1037//0021-843x.109.4.679. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Kaplan D, Ramineni C, Locuniak MN. Early math matters: Kindergarten number competence and later mathematics outcomes. Developmental Psychology. 2009;45:850–867. doi: 10.1037/a0014939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kline RB. Principles and practice of structural equation modeling. 2nd ed. Guilford Press; New York, NY: 2005. [Google Scholar]
- Leak J, Duncan GJ, Li W, Magnuson K, Schindler H, Yoshikawa H. Is timing everything? How early childhood education program impacts vary by starting age, program duration and time since the end of the program.. Paper presented at the Fall Conference of the Association for Public Policy Analysis and Management; Boston, MA. 2010, November. [Google Scholar]
- Little TD, Slegers DW, Card NA. A non-arbitrary method of identifying and scaling latent variables in SEM and MACS models. Structural Equation Modeling. 2006;13:59–72. [Google Scholar]
- Mazzocco MMM, Grimm KJ. Growth in rapid automatized naming from grades K to 8 in children with math or reading disabilities. Journal of Learning Disabilities. 2013;46:517–533. doi: 10.1177/0022219413477475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meece JL, Wigfield A, Eccles JS. Predictors of math anxiety and its consequences for young adolescents’ course enrollment intentions and performances in mathematics. Journal of Educational Psychology. 1990;82:60–70. [Google Scholar]
- Murayama K, Pekrun R, Lichtenfeld S, vom Hofe R. Predicting long-term growth in students’ mathematics achievement: The unique contributions of motivation and cognitive strategies. Child Development. 2013;84:1475–1490. doi: 10.1111/cdev.12036. [DOI] [PubMed] [Google Scholar]
- Murnane RJ, Willett JB, Levy F. The growing importance of cognitive skills in wage determination. The Review of Economics and Statistics. 1995;77:251–266. [Google Scholar]
- NICHD Early Child Care Research Network Early child care and children's development prior to school entry: Results from the NICHD Study of Early Child Care. American Educational Research Journal. 2002;39:133–164. [Google Scholar]
- Pickering S, Gathercole S. Working Memory Test Battery for Children (WMTB-C) manual. Psychological Corp.; London, England: 2001. [Google Scholar]
- Puma M, Bell S, Cook R, Heid C. Head Start Impact Study: Final report. U.S. Department of Health and Human Services, Administration for Children and Families; Washington, DC: 2010. [Google Scholar]
- Ritchie SJ, Bates TC. Enduring links from childhood mathematics and reading achievement to adult socioeconomic status. Psychological Science. 2013;24:1301–1308. doi: 10.1177/0956797612466268. [DOI] [PubMed] [Google Scholar]
- Rittle-Johnson B, Siegler RS. The relation between conceptual and procedural knowledge in learning mathematics: A review. In: Donlan C, editor. The development of mathematical skills. Psychology Press; East Sussex, England: 1998. pp. 75–110. [Google Scholar]
- Schneider M, Rittle-Johnson B, Star JR. Relations between conceptual knowledge, procedural knowledge, and procedural flexibility in two samples differing in prior knowledge. Developmental Psychology. 2011;47:1525–1538. doi: 10.1037/a0024997. [DOI] [PubMed] [Google Scholar]
- Schweinhart LJ, Montie J, Xiang Z, Barnett WS, Belfield CR, Nores M. Lifetime effects: The High/Scope Perry Preschool study through age 40 (Monographs of the High/Scope Educational Research Foundation No. 14) High/Scope Press; Ypsilanti, MI: 2005. [Google Scholar]
- Siegler RS. Improving the numerical understanding of children from low-income families. Child Development Perspectives. 2009;3:118–124. [Google Scholar]
- Siegler RS, Duncan GJ, Davis-Kean PE, Duckworth K, Claessens A, Engel M, Chen M. Early predictors of high school mathematics achievement. Psychological Science. 2012;23:691–697. doi: 10.1177/0956797612440101. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Pyke AA. Developmental and individual differences in understanding of fractions. Developmental Psychology. 2013;49:1994–2004. doi: 10.1037/a0031200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steyer R. Konsistenz und Spezifitaet: Definition zweier zentraler Begriffe der Differentiellen Psychologie und ein einfaches Modell zu ihrer Identifikation [Consistency and specificity: Definition of two central concepts of differential psychology and a simple model for their identification]. Zeitschrift für Differentielle und Diagnostische Psychologie. 1987;8:245–258. [Google Scholar]
- Szücs D, Devine A, Soltesz F, Nobes A, Gabriel F. Cognitive components of a mathematical processing network in 9-year-old children. Developmental Science. 2014;17:506–524. doi: 10.1111/desc.12144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts TW, Duncan GJ, Siegler RS, Davis-Kean PE. What's past is prologue: Relations between early mathematics knowledge and high school achievement. Educational Researcher. doi: 10.3102/0013189X14553660. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. Psychological Corp.; San Antonio, TX: 1999. [Google Scholar]
- Wechsler D. Wechsler Individual Achievement Test II–Abbreviated. Psychological Corp.; San Antonio, TX: 2001. [Google Scholar]
- Whitehurst GJ. Whitehurst testimony on early childhood education to the House Committee on Education and the Workforce [Web log post] 2014 Feb 5; Retrieved from http://www.brookings.edu/blogs/brown-center-chalkboard/posts/2014/02/05-congressional-testimony-preschool-whitehurst.
- Woodcock RW, McGrew KS, Mather N. Woodcock-Johnson Tests of Achievement. Riverside; Itasca, IL: 2001. [Google Scholar]
- Zentall SS. Math performance of students with ADHD: Cognitive and behavioral contributors and interventions. In: Berch DB, Mazzocco MMM, editors. Why is math so hard for some children? The nature and origins of mathematical learning difficulties and disabilities. Paul H. Brookes; Baltimore, MD: 2007. pp. 219–243. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.