Abstract
Accurate analysis of scalp-recorded electrical activity requires the identification of electrode locations in 3D space. For example, source analysis of EEG/ERP (electroencephalogram, EEG; event-related-potentials, ERP) with realistic head models requires the identification of electrode locations on the head model derived from structural MRI recordings. Electrode systems must cover the entire scalp in sufficient density to discriminate EEG activity on the scalp and to complete accurate source analysis. The current study compares techniques for averaging electrode locations from 86 participants with the 128 channel “Geodesic Sensor Net” (GSN; EGI, Inc.), 38 participants with the 128 channel “Hydrocel Geodesic Sensor Net” (HGSN; EGI, Inc.), and 174 participants with the 81 channels in the 10-10 configurations. A point-set registration between the participants and an average MRI template resulted in an average configuration showing small standard errors, which could be transformed back accurately into the participants’ original electrode space. Average electrode locations are available for the GSN (86 participants), Hydrocel-GSN (38 participants), and 10-10 and 10-5 systems (174 participants)
Introduction
Scalp-recorded electrical activity with the electroencephalogram (EEG) or event-related potentials (ERP) can be applied to human neuroimaging to understand the relation between brain activity and behavior. ERP neuroimaging techniques primarily utilize electrical source analysis to infer cortical sources of the activity from scalp recorded electrical activity. A multi-modal strategy for cortical source analysis combines EEG/ERP with structural (anatomical) MRI to create realistic head models for the source analysis. Among other requirements, realistic head modeling requires accurate co-registration of electrode positions on the scalp with the MRI volumes from which the realistic head is determined (Darvas, Ermer, Mosher, & Leahy, 2006; Fonov, Evans, Botteron, McKinstry, & Collins, 2011).
The challenges to co-registration include identification of the electrode locations in one space, registration between the electrode-based space and the MRI space, and correct placement of the electrodes on the MRI volume. The current study developed averages for participants of a 128-channel electrode system (Geodesic Sensor Net: GSN; Johnson et al., 2001; Tucker, 1993; Tucker, Liotti, Russell, & Posner, 1994; and Hydrocel Geodesic Sensor Net: HGSN) and procedures for their use with structural MRI. The procedures tested registration methods for translating electrode locations to and from electrode averages. The methods would assist (1) researchers who have access to structural MRIs and EEG localization systems but measured them at different times and would like to choose the best co-registration technique; (2) researchers who can measure the placements of electrodes in 3D space with magnetic, radiofrequency, or imaging techniques, but have no access to individual structural MRIs; (3) researchers who have access to individual structural MRIs, but no system to localize EEG sensors; and (4) researchers who do not have access to structural MRIs nor EEG localization systems.
Accurate placement of electrodes on MRI volumes is necessary for realistic head modeling in electrical source analysis, with sensor misallocation (in space) resulting in comparable source misallocation (Wang & Gotman, 2001). Electrical source analysis hypothesizes electrical current sources inside the head that generate the electrical potential recorded on the scalp via the EEG (Hallez et al., 2007; Michel et al., 2004). EEG activity, recorded on the scalp, may be used to infer the location and strength of the sources with methods such as current density reconstruction (Plummer, 2011) and equivalent current dipole analysis (Scherg, 1990). Source analysis methods use a head model that describes the bone, scalp, brain tissue, and CSF inside the head and their relative conductivity. In theoretical comparisons, models with realistic descriptions of the head's interior perform more accurately than spherical models (Vatta, Meneghini, Esposito, Mininel, & Di Saller, 2010). Empirical data support the theoretical models (Darvas et al., 2006). The electrode locations, head model, and source locations are combined to develop a forward model that quantifies how current sources generate the electrical activity on the scalp. When the other aspects of the models are inaccurately measured, the effects of spatial measurement errors in electrode placement become cumulative (Wang & Gotman, 2001).
The traditional method for measuring electrode positions is to use head-based fiducial locations for both electrode placement on participant(s) and identification of locations in the MRI (see Tamraz & Comair, 2006 for a description of reference planes suitable for MRI). Fiducials are relatively easy to identify on the anterior regions of the skull using external landmarks, but are more difficult to identify on the posterior regions of the skull. There are significant individual differences in the size and shape of landmarks, and some critical landmarks are positioned on regions of the skull that change substantially throughout puberty. Even with technical skill in the identification of such landmarks, identification errors of sensor locations can occur at the magnitude of one centimeter or more (Jurcak, Okamoto, Singh, & Dan, 2005).
The 10-20 system (Jasper, 1958) defined 19 electrodes, which is insufficient to discriminate electrical activity on the scalp (Srinivasan, Tucker, & Murias, 1998) or doing electrical source analysis in adult populations (Michel et al., 2004); and at least 128 electrodes may be necessary for electrical source analysis in infant populations (Grieve, Emerson, Isler, & Stark, 2004). The principles of the 10-20 system can be extended to a 10-10 system of 74 (or 81) electrode placement locations (Chatrian, Lettich, & Nelson, 1985; Chatrian, Lettich, & Nelson, 1988; Jurcak, Tsuzuki, & Dan, 2007) and a 10-5 system of more than 300 electrode locations (Darvas et al., 2006; Jurcak et al., 2007; Oostenveld & Praamstra, 2001; see 10-10 placements in Jurcak et al., 2007).
Some EEG recording systems contain electrode locations that are not defined by the 10-20 system, but instead use a “cap” or “sensor net” with electrodes configured in different locations. A recent advance in EEG measurement is the construction of electrode placement systems that do not require the extensive manual measurements required for individual electrode placement. These include caps with electrodes sewn in a predetermined location such as the Electrocap (e.g., putative 10-10 locations measured on the cap; ElectroCap International, Inc. [Eaton, OH]) or other electrode locations such as the 128 channel Biosemi (Biosemi B.V. [Amsterdam, Netherlands]). The “geodesic sensor net” or “GSN” (EGI, Inc. [Eugene, OR]; Tucker, 1993; Tucker et al., 1994) has become a popular electrode placement system. More recently, a new model of the GSN system has smaller electrode pedestals and differs in placement from the GSN net (the ‘Hydrocel GSN’, or HGSN).
The GSN is a set of electrodes on small pedestals connected by flexible filaments between electrode pedestals. The GSN orients placement of the net on the head with external head fiducials (vertex, nasion, left and right preauricular), and the flexible filament connectors guide the placement of other electrodes. Presumably, cap and sensor-net systems provide reliable placements of the electrodes within a subject, and their ease of use is a great benefit (e.g., infant populations (Johnson et al., 2001; Reynolds & Richards, 2009).
Neither the cap systems nor the sensor net systems place the electrodes in analytically known locations on the scalp; some type of external measurement is necessary to quantify electrode locations on a 3D volume. A typical procedure for measuring electrode space with these systems is to use a device to locate the electrodes in 3D space on the participant head, e.g., using radio frequency locator to digitize the electrode positions relative to a known sensor location (e.g., Polhemus Fasttrack digitizer) or pictures around the head in 3D space (Geodesic Photogrammetry System, EGI, Inc.; Russel, Eriksen, Poolman, & Tucker, 2005). Localizer systems provide a set of electrode positions in an arbitrarily defined space. Common fiducial locations in the electrode space and the MRI volume space are used to co-register electrodes in MRI volume space.
Current Study
The current study had two primary goals. The first goal was to create average electrode montages for the GSN and HGSN 128-channel electrode sensor nets. In order to accomplish this goal the sensor array would need to be accurately measured in 3D space, the sensor array would need to contain points that could be co-registered to external landmarks on an individual's scalp. The landmarks assessed during collection of sensor array data would also need to be identifiable on an individual's MRI so that the datasets could be coregistered. Once the criteria for identification and coregistration were met, a process for creating an optimal average electrode array in combination with a coregisterd optimally averaged MRI would need to be developed.
Standardized montages for the GSN and HGSN electrodes are available, however the averages were derived from a small number of participants (N = 19), by identifying locations with the Polhemous Fasttrack digitizer, rotating the electrodes to a common orientation, and then using simple averaging of electrode positions across participants (Luu & Ferree, 2000; Luu & Ferree, 2005; see electrode placement map in either reference).
We have 86 participants with GSN electrode placement locations and 38 participants with HGSN electrode placement locations obtained with an external measurement device (Geodesic Photogrammetry System) for whom we also have structural 3.0T MRIs. Thus we have the known locations of the electrodes for each participant on individually recorded MRIs. We used an average MRI based on young adults (20-24 years; Sanchez, Richards, & Almli, 2012) as the basis for averaged electrode configurations for both the GSN and the HGSN electrodes. We compared simple averaging of electrode locations to methods that co-register the participant head to the average MRI template and transform the individual electrodes before averaging. We show that using simple rotated / untransformed electrode locations for an average electrode map does not fare well compared to methods which first co-register the individual participant locations and an average MRI template. We also have 174 participants for whom we have structural 3.0T MRIs. We used external scalp fiducial locations on the structural MRI to quantitatively determine the 10-10 ‘virtual electrodes’ (Jurcak et al., 2005, 2007) for each MRI. We also constructed a virtual 10-10 electrode placement map for the average MRI template (cf. Darvas et al., 2006; Fuchs et al., 2002; Jurcak et al., 2005). The techniques were applied also to the ICBM-152 template, or MNI-152 template, which a MRI volume that has become the standard stereotaxic space for neuroimaging. At least two studies examined its applicability as an average MRI with electrode placement maps for electrical source analysis (Darvas et al., 2006; Fuchs et al., 2002). The current techniques (co-registration; averaging) and montages (GSN, HGSN, 10-10 montages) were also applied to the ICBM-152.
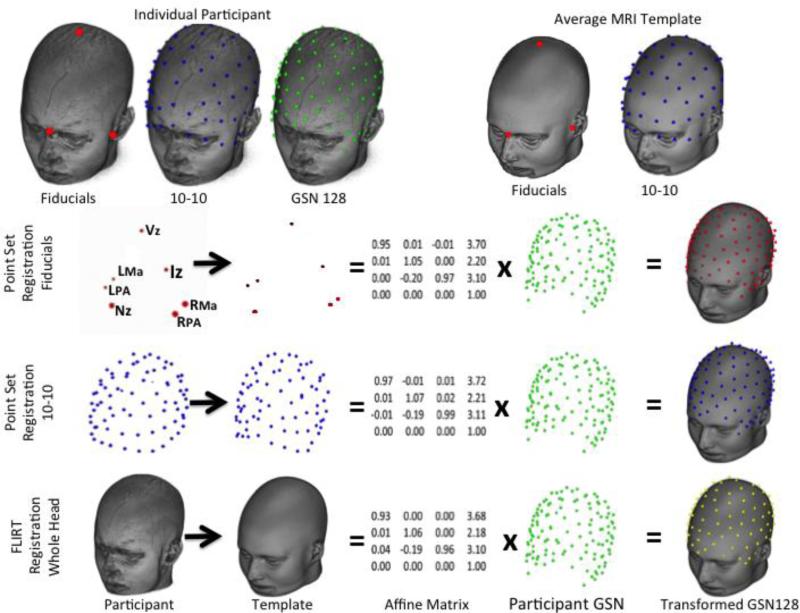
The second goal of the study was to test registration procedures for transforming the average electrodes to individual participant space. For situations in which the average electrode locations and average MRI may be applied to electrical source analysis, it is necessary to transform the average electrode positions and MRI to the individual participants. We used point-set registration methods (Myronenko, Song, & Carreira-Perpinan, 2007; Myronenko & Song, 2010) to register known fiducial locations on the participant and average head (Fuchs et al., 2002), and whole-head registration methods (Jenkinson & Smith, 2001) to register the whole-head T1W of the participant to the whole-head average T1W (Jurcak et al., 2005). Figure 1 illustrates the concepts underpinning point-set and whole-head registration techniques. The accuracy of these techniques was quantified by comparing the average electrodes transformed into the participant space with the actual electrode locations of the participants. The second goal allows the designation of procedures for the use of these average electrodes and average MRI in situations where either electrode locations are unknown or participant MRIs are unavailable.
Figure 1.
Differences in point set and whole head registration techniques. The first row shows the original locations for the participant (fiducials, 10-10 electrodes, GSN electrodes) and average MRI template (fiducials, 10-10). The second through fourth rows show the registration between the comparable locations for the participant and template, which generate an affine matrix, multiplied by the GSN 128 locations, to produce the transformed electrodes in the space of the average MRI template. (Fiducial marks: Nz = Nasion, Vz = Vertex, Iz=Inion, LPA=Left Preauricular point, RPA = Right Preauricular point, LMa = Left Mastoid, and RMz = Right Mastoid.
Methods
Participants
The participants came from studies at the University of South Carolina McCausland Center for Brain Imaging (USC-MCBI). All volunteers were recruited from university participant pool and were healthy adults (N= 174; 111 F, 4 unknown; age range 18.5 to 39 years). The majority of the participants were from ages 18.5 through 24 (68%). We kept track of racial / ethnic identity (137 Caucasion, 20 African-American, 9 Asian, 8 unknown), weight, and other demographic variables. This study was approved by the Institutional Review Board for the Use of Human Subjects at the University of South Carolina and informed consent was obtained from each participant.
MRI Data Acquisition
The MRI data were collected on a Siemens Medical Systems 3T Trio with an overall duration of about 15 min. A 3D T1-weighted “MPRAGE” RF-spoiled rapid flash scan in the sagittal plane and a T2/PD-weighted multi-slice axial 2D dual Fast Turbo spin-echo scan in the axial plane were collected. The USC-MCBI T1 scans had 1 mm1 resolution and sufficient FoV to cover from the top of the head down to the neck. The USC-MCBI (3T) files were read from DICOMM files to compressed NIFTI format (http://nifti.nimh.nih.gov/).
Average MRI Template
The average MRI template was derived from 108 MRIs of individuals aged 20-24 years old (see Sanchez et al., 2012). The iterative process began with a tentative MRI average. The original individual MRI volumes were then registered to this tentative volume and transformed in size and orientation with non-linear registration (using ANTS, “Advanced Normalization Tools”; (Avants et al., 2008) into the tentative average space. A new average was constructed from the transformed MRI files. The new average then became the next reference template for the registrations. The procedure iterated until the difference between successive averages was minimized.
ICBM-152 Head Template
The ICBM-152 T1W average template was derived from 152 high-resolution 3D MRIs that were registered and transformed to the original MRI-305 template (ICBM-152 defined in Mazziotta et al., 2001; MNI-305 in Collins, Neelin, Peters, & Evans, 1994; Evans, Brown, Kelly, & Peters, 1994; Joshi, Davis, Jomier, & Gerig, 2004). The ICBM-152 template is distributed as the MNI-152 T1W volume with neuroimaging processing programs (e.g., FSL, Smith et al., 2004; SPM, (Penny, Friston, Ashburner, Keibel, & Nichols, 2007) and programs that do electrical cortical source analysis (BESA, Besa GmbH, www.besa.de; CURRY, Neuroscan Inc., www.neuroscan.com/curry.cfm; MRViewer and EMSE, Source Signal, Inc., www.sourcesignal.com). The ICBM-152 head does not extend in the inferior axial direction far enough to contain the GSN or HGSN electrodes, so a modified ICBM-152 head was created that added lower face and neck from the average sample MRI.
MRI Head Measurements
We measured a series of external scalp locations (fiducials) in each individual's T1W MRI volume and in the two average MRI templates. The measures include: the following. The anterior commissure (AC) and posterior commissure (PC) in the brain; and the nasion (Nz), inion (Iz), left and right preauricular location (LPA, RPA), left and right mastoid (LMA, RMA), and vertex (Vz) on the scalp. The Nz, LPA, RPA, and Iz were defined by procedures in Jurcak et al. (2007). The LMA and RMA were defined in the MRI on the same axial plane as the preauricular fiducial on the same side, and on the scalp immediately behind the ear. The Vz was defined as the point whose coronal location was in the center of the left and right ears, sagittal location centered over the longitudinal fissure, and axial location on the top of the scalp. We also identified these external scalp fiducials on the average 20-24 years MRI template and the ICBM-152 template.
The location of the AC in the MRI volume was identified in meter coordinates. Each fiducial location was computed as the offset of the location from the AC. Thus the AC was the origin point for the electrodes in this system (cf. Talairach & Tournoux, 1988).
Electrode Configurations
10-10 Electrode Map
Each individual had a 10-10 electrode map computed on the MRI; this also was done on the average MRI template and the ICBM-152 template (see Table 1, Individual Participant Electrodes and Locations; Average MRI Template Electrodes and Locations). The 10-10 electrode configuration was calculated analytically on individual MRI volumes for each participant (“virtual electrodes”, Jurcak et al., 2005) following the 10-10 system described by Jurcak et al. (2007). The “Unambiguously Illustrated” procedure identifies reference curves on the MRI in the axial plane from RPA to Nz to LPA, from RPA to Iz to LPA; in the sagittal plane from Nz to Vz to Iz; and in the coronal plane from LPA to Vz to RPA. The Cz is defined as the intersection of the sagittal and coronal reference curves at 50% of the distance between the Nz-Vz-Iz reference curve and the LPA-Vz-RPA reference curve. The z electrodes (AFz, Fz, CFz, Cz, CPz, Pz, POz, Oz) were identified on the 10% intervals on the sagittal reference curve. The axial plane defined by the LPA-Nz-RPA and LPA-Iz-RPA reference curves were used to identify the 9/10 electrodes in 10% intervals (e.g., Fp1 and Fp2; AF9, AF10); 10% superior from this plane to Cz defines an axial plane used to identify the 7/8 electrodes in 10% intervals (e.g., F7, FC7, C7); and coronal reference curves from the 7/8 to the z locations are used to define the AC, F, FC, C, CP, P, and PO electrodes for the 1/2, 3/4, and 5/6 electrodes. We calculated a total of 81 electrodes with this procedure. We also calculated positions equally located between each adjacent pair of the 10-10 electrodes. This simulates the 10-5 system and resulted in 358 scalp locations (cf. Darvas et al., 2006; Jurcak et al., 2007; Oostenveld & Praamstra, 2001). An analytic 10-10 electrode montage and simulated 10-5 electrode montage were calculated on the average MRI template and the ICBM-152 (cf. Fuchs et al., 2002; Darvas et al., 2006; Jurcak et al., 2005).
Table 1.
Registrations and Transformations Applied to Electrode Positions and Locations
| Individual Participant Electrodes and Locations | ||
|---|---|---|
| Fiducials | External scalp locations | Identified on MRI with masks and locations |
| 10-10 (N=174) | International 10-10 | Virtual electrodes calculated for 81 locations |
| 10-5 (N=174) | Simulated 10-5 | Virtual electrodes derived from 10-10 inter-electrode locations |
| GSN128 (N=86) | EGI GSN | GPS, EGI positioning, fit on individual MRI |
| HGSN128 (N=86) | EGI HGSN | GPS, EGI positioning, fit on individual MRI |
| Simulated 470 (N=86) | Simulated HGSN | Simulated electrodes derived from HGSN 128 inter-electrode locations |
| Average MRI Templates Electrodes and Locations | ||
|---|---|---|
| Analytic Averages | ||
| Name | External scalp locations | Identified on MRI with masks and locations |
| 10-10 (N=174) | International 10-10 | Virtual electrode positions calculated for 81 locations |
| 10-5 (N=174) | Simulated 10-5 | Virtual electrode positions derived from 10-10 inter-electrode locations |
| Averages from Transformed Individual Data | ||
|---|---|---|
| Name | Data to be Transformed | Transformation Description |
| CPD-Fiducials-Rigid | Fiducials | CPD rigid registration (6 dof) |
| CPD-Fiducials-Affine | Fiducials | CPD full affine registration (12 dof) |
| CPD-TenTen-Rigid | 10-10 Locations | CPD rigid registration (6 dof) |
| CPD-TenTen-Affine | 10-10 Locations | CPD full affine registration (12 dof) |
| FLIRT-Head-Rigid | whole-head MRI | FLIRT rigid registration (6 dof) |
| FLIRT-Head-Affine | whole head MRI | FLIRT full affine registration (12 dof) |
| Untransformed | Participant electrodes | No registration or transformation |
| Inverse Transformations from Average MRI Template to Participant | ||
|---|---|---|
| Name | Data to be transformed | Transformation Description |
| CPD-Fiducials-Affine | Fiducials | CPD full affine registration (12 dof) |
| CPD-TenTen-Affine | Fiducials | CPD full affine registration (12 dof) |
| FLIRT-Head-Affine | Fiducials | CPD full affine registration (12 dof) |
| Untransformed | Average electrodes | No registration or transformation |
| CPD-Electrodes-Affine | GSN or HGSN positions | CPD affine registration between all locations on average MRI template and participant |
| CPD-Partial-Affine | GSN or HGSN positions | CPD affine registration between selected locations on average MRI template and participant |
GSN and HGSN Individual Electrode Map
Individual electrode maps were created with the GSN and HGSN montages (see Table 1, Individual Participant Electrodes and Locations). Eighty-six of the 174 participants were fitted with an EGI “Geodesic Sensor Net” (GSN); and thirty-eight of the 174 participants were fitted with a HGSN. Participants sat within the dome of the Geodesic Photogrammetry System while images were simultaneously acquired from eleven uniquely angled cameras. In combination, the images created a complete map of each participant's head. We discarded 7 additional participants whose GSN/Photogrammetry positions did not fit precisely on the scalp, and 2 additional participants whose HGSN/Photogrammetry positions did not fit on the scalp.
The Geodesic Photogrammetry System software package (Russel et al., 2005) was used to calculate electrode locations for the GSN and HGSN. We manually marked 11 cardinal sensors (each cardinal sensor is visible in three camera views), which serve as the foundation for overall electrode registration. The program uses triangulation of these points with the known positions from the camera system to label each location.
The output from the GPS program is a set of electrode locations referenced to a spatial system. We co-registered the GPS locations to the MRI in the following manner. We used 12 locations defined on the MRI with the 10-10 electrode placements and corresponding location in the Photogrammetry system output that are exactly on these positions (4 electrodes) or approximate these positions (6 locations). For example, the Nz, LPA, RPA, and Cz from the MRI locations correspond exactly to Photogrammetry-defined electrode locations. The MRI head positions of the inion and the FC1, FC2, CP1, CP2, and CPz correspond approximately to Photogrammetry-defined electrode positions. The MRI space and the Photogrammetry locations were co-registered with point-set registration. The point-set registration registers location points in one space to location points in a second space. The CPD procedure, “Coherent Point Drift” (CPD version 2; Myronenko et al., 2007; Myronenko & Song, 2010), based on the MATLAB computer program, registers two sets of points using a coherent point drift algorithm. We obtained a 6 degree of freedom (dof) rigid affine transformation (3 translation, 3 rotation) between the 12 locations defined on the MRI and the 12 locations defined by the Photogrammetry, and transformed the original 128 GSN or HGSN electrodes from the Photogrammetry coordinate space into the MRI coordinate space. This resulted in a set of electrode locations that were oriented correctly on the MRI. The placement of the electrodes on the MRI was visually examined by plotting the electrode locations on a MRI volume and viewing this with the MRICron or MRICroGL program (Rorden, 2012a, 2012b). We discarded 7 additional participants whose GSN/Photogrammetry positions did not fit precisely on the scalp, and 2 additional participants whose HGSN/Photogrammetry positions did not fit on the scalp. We also constructed a simulated 470-electrode configuration by using inter-electrode locations from the HGSN 128 map (Table 1, Individual Participant Electrodes and Locations).
Registration of Individual Participant Space to the MRI templates
The individual participant space was co-registered to the average MRI template using point-set registration or whole-head registration (Table 1 and Figure 1). Four of the procedures used the CPD program which registered a set of points on the participant MRI to the analogous set of points on the average MRI template. Two procedures used the external scalp fiducial points (Table 1, CPD-Fiducials-Affine, CPD-Fiducials-Rigid). Seven points on the individual MRI volume (Nz, Iz, LPA, RPA, LMA, RMA, Cz) from each participant were registered to the same points of the average MRI template (cf. Fuchs et al., 2002; using Nz, LPA, RPA) using the CPD procedure. We obtained a 6 degree of freedom rigid affine registration (3 translation, 3 rotation, “CDP-Fiducials-Rigid”) and a 12 degree of freedom affine registration (3 translation, 3 rotation, 3 scaling, 3 shear; “CPD-Fiducials-Affine”) with this method.
Two procedures used the entire 10-10 locations computed on the individual participants and on the average MRI template (Table 1, CPD-TenTen). This was done with a rigid and a full affine registration. Two procedures used a whole-head registration (Table 1, FLIRT-Head; Figure 1, last row). The FSL FLIRT, “FMRIB's Linear Image Registration Tool” (Jenkinson & Smith, 2001) was used to register the whole-head of the individual and average MRI template (cf. Jurcak et al., 2005, using SPM). The six registration methods (CPD-Fiducials-Affine, CPD-TenTen-Affine, FLIRT-Head-Affine, CPD-Fiducials-Rigid, CPD-TenTen-Rigid, FLIRT-Head-Rigid) each result in a registration matrix that can be applied to a three-dimensional point in one space to transform the point to a new space.
Average Electrode Maps
We created electrode maps from the individual participants’ electrodes using the six registrations, as well as an electrode map from untransformed participant electrode locations (Table 1, Averages from Transformed Individual Data). The individual participant electrode locations (GSN, HGSN) were transformed into the template MRI headspace by the transformation matrix from the co-registration. The transformed locations from individuals were averaged to construct the six average electrode maps. We also used the untransformed participant electrode configurations to construct a separate averaged electrode map. The resulting electrode maps were fitted to the MRI template(s) by moving the electrodes to the nearest location on the scalp on a line extending from the center of the head to the average electrode. This fitted the average electrode map on the scalp of the MRI template. The registration / transformation averages were completed for the average MRI template and the ICBM-152 template.
Testing the Transformation of the Average Electrode Maps to Individual Participants
After constructing the average electrode maps, and testing them for consistency with the projected individual electrode maps, we determined that the CPD-TenTen-Affine average had the smallest residual squared variance, and adopted this as our test average. We then compared methods for transforming the average electrodes back into the participant space. This was done in order to recommend methods for using these electrode maps. We compared the difference between the inverse-transformed-average maps and the actual participant locations. The three affine registration methods (Table 1, Inverse Transformations from Average MRI Template to Participant) and the untransformed average were used.
We did two additional registrations between the individuals and the averages. One used the full set of GSN (or HGSN) electrodes from the individuals and MRI templates, using CPD full affine registration (CPD-Electrodes; Table 1, Inverse Transformations from Average MRI Template to Participant). This was done to get a ‘baseline’ reference for the limits of the linear registrations. Second, we used a partial set of electrodes from the GSN (or HGSN) from the individual and MRI templates (CPD-Partial; Table 1, Inverse Transformations from Average MRI Template to Participant). The CPD-Partial was done with the idea that some labs without full MRIs could have positioning systems that result in a reduced set of electrode positions. In addition, many electrode identification systems require a time intensive process with the electrodes in place on the participant. As the number of electrodes increase, identification of each sensor position becomes unrealistic.
Finally, we also compared some CPD-registration methods with varying numbers of fiducials in the registration. These included a set of locations with 5 fiducials (front and side, Nz, LPA, RPA, LMA, RMA), 6 fiducials including Iz (front, side, rear; Nz, LPA, RPA, LMA, RMA, Iz); 6 fiducials including Vz (front, side, top; Nz, LPA, RPA, LMA, RMA, Vz), and seven fiducials (Nz, LPA, RPA, LMA, RMA, Iz, Vz). These were analogous to the registration used with the full set of external fiducials. The registration with only the Nz and side fiducials is similar to that done with the Nz, LPA and RPA (e.g., Fuchs et al., 2002).
Results
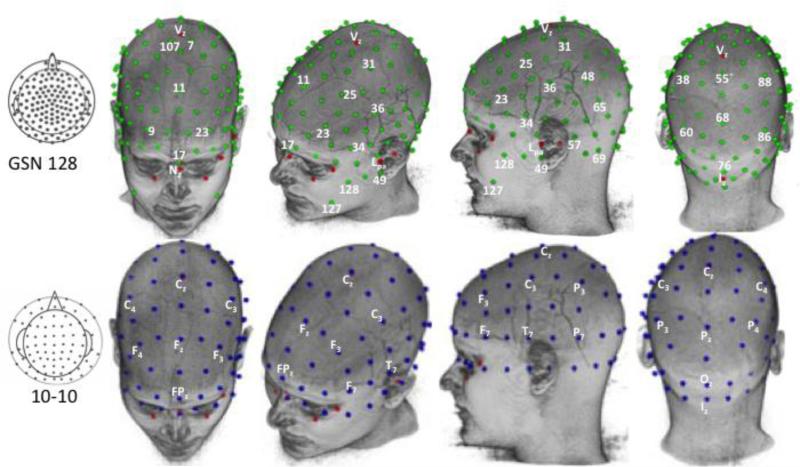
The first step in our procedure was to perform the Photogrammetry procedure to produce GSN and HGSN electrode configurations for each participant, and calculate the 10-10 positions. Figure 2 (top row) shows the result of this placement for one participant's GSN electrodes. The electrode placement for this participant fitted snugly on the MRI across the entire scalp without adjustment. Some of the participants’ Photogrammetry GPS locations did not have the same volume as the MRI. These participants had the electrodes adjusted so that they fitted on the scalp. An examination of each sensor's distance from the origin revealed that cardinal points differed in distance from the origin (relative to their nearest neighbors) less than non-cardinal points. This pattern appeared to be related to the acquisition methodology of the photogrammetry unit. Figure 2 (second row) shows the 10-10 electrode map on this MRI. The 10-10 locations are located on the surface of the scalp with the computational procedure, so no adjustments were necessary. The HGSN electrode configuration was done for the 38 participants for whom we had HGSN Photogrammetry data.
Figure 2.
Electrodes displayed on the MRI head of a single participant. The GSN 128 electrodes were calculated with the Photogrammetry system. The 10-10 electrodes were calculated based on the fiducials and analytic placements on the MRI. Selected electrodes are labeled on both types of electrode nets. We have used the L/R orientation of the figure to display the electrodes, though the MRI pictures have a reversed orientation.
Individual Participant to Sample Average
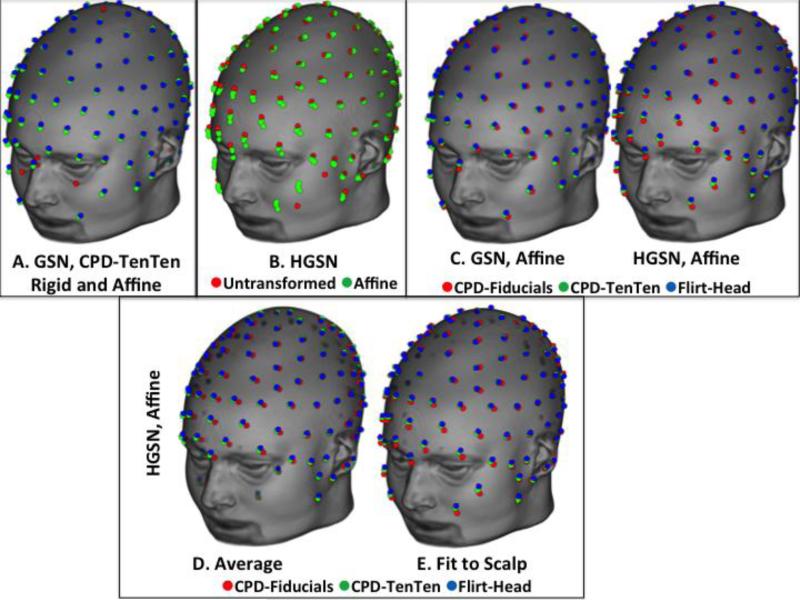
Individual electrode placement configurations were transformed into the average space via one of seven transformation matrices (CPD-Fiducials-Affine, CPD-Fiducials-Rigid, CPD-TenTen-Affine, CPD-TenTen-Rigid, FLIRT-Head-Affine, FLIRT-Head-Rigid, Untransformed). The transformed values were then averaged across participants. Figure 3 shows some of the transformations on the average MRI template. Figure 3A shows the CPD-TenTen-Rigid and CPD-TenTen-Affine for the GSN electrode configuration; there were only slight differences in the average from the affine and rigid procedures.
Figure 3.
Comparison of averaging methods. There was a difference between rigid and affine registrations Panel A); between the transformed participant averages and the untransformed participant average (Panel B). The CPD-Fiducials-Affine, CPD-TenTen-Affine, and FLIRT-Head-Affine results are displayed for the GSN and HGSN configurations (Panel C). The bottom figures show the CPD-Fiducial-Affine transformation method resulted in a smaller volume configuration than the other two transformation methods before the fit to the head (Panel D) and was different after (Panel E).
Figure 3B shows the similarity of the averages made from the transformed-affine procedures (CPD-TenTen, CPD-Fiducials, and FLIRT-Head- Affine) with the average from Untransformed locations. There were noticeable differences between the average from the untransformed participant data and the averages from the transformed data. Finally, Figure 3C shows the GSN and HGSN net configurations, respectively, for the averages from the three affine transformations.
The effect of the fit to scalp for the averages may be seen in Figure 3 (bottom row, panels D and E). Figure 3D shows the HGSN configuration averages from the average of the electrodes, and the right figure shows the same HGSN configurations fit to the scalp of the average MRI. Both figures show the difference between the CPD-Fiducial-Affine average and the two other affine averages. The average based on the fiducials transformation had a smaller volume than the average head and showed a larger difference when the electrodes were fitted to the scalp of the average MRI template, whereas the original average of the CPD-Electrodes-Affine and FLIRT-Head-Affine fit closely on the scalp without the additional scalp-fit procedure. This likely occurred because the latter two procedures use locations distributed over the whole-head, whereas the fiducial locations are on the fiducial points of the sphere for the scalp (i.e., front and rear, left and right, and top).
Consistency of Transformations for Average Electrode Maps
The consistency of the transformations for the average electrode maps was examined. This was done by calculating the distance of each electrode position of the average MRI map to the electrode position of the individual participant maps. This was done on the average before fitting the electrodes to the scalp of the MRI template. This serves as a measure of variability of the estimated mean location.
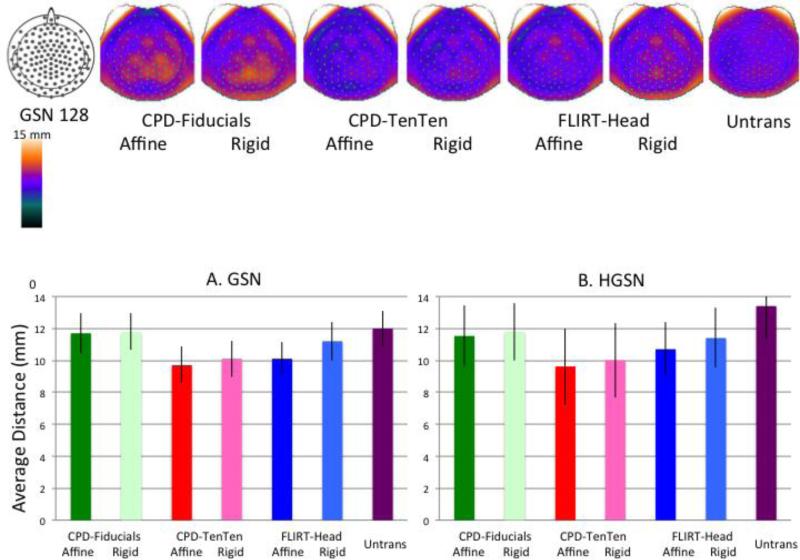
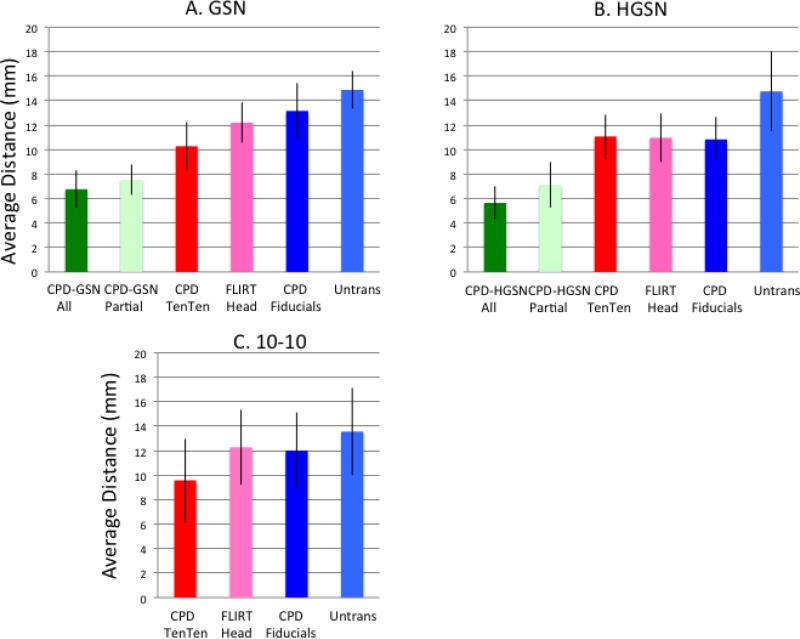
The RMS difference between the average location for an electrode, and the forward-transformed locations that made up the average was calculated. Figure 4 (top row) shows this value separately for each electrode by plotting the value on a topographical electrode map (using EMSE 5.5 software). The CPD-Fiducials, both Rigid and Affine transformations, showed the largest distances around the superior central part of the head. The smallest values occurred for the CPD-TenTen transformations. Figure 4A (left bar chart) show the average distance of the transformation methods averaged across electrodes for the GSN configuration. The two CPD-TenTen transformations had the smallest average distance, followed by the FLIRT-Head-Affine, FLIRT-Head-Rigid, the two CPD-Fiducials methods, and the Untransformed electrodes. This same pattern occurred for the HGSN electrodes (Figure 4B).
Figure 4.
Topographical maps for the GSN electrodes showing the average distance between the locations of the forward-transformed participant and average electrode. The topographical maps represent this variability at different electrodes across subject. The bar graphs show the average difference (with STD error bars) of the location distance averaged across subjects for the six transformation methods and the untransformed average, separately for the GSN (A) and HGSN (B) electrode averages.
An ANOVA with average type nested within participants resulted in a significant difference among the averaging types on this variability measure for the GSN electrodes, F (6, 779) = 4.21, p < .001. Individual post hoc comparisons confirmed the mean differences, where the two CPD-TenTen methods were not significant different from each other, but were smaller than the two CPD-Fiducials transformations. A comparison of the three affine and the three rigid methods found that the distance measure was significantly smaller for the affine methods. Similar ANOVA results were found with the HGSN configuration.
Electrode Map Template Availability
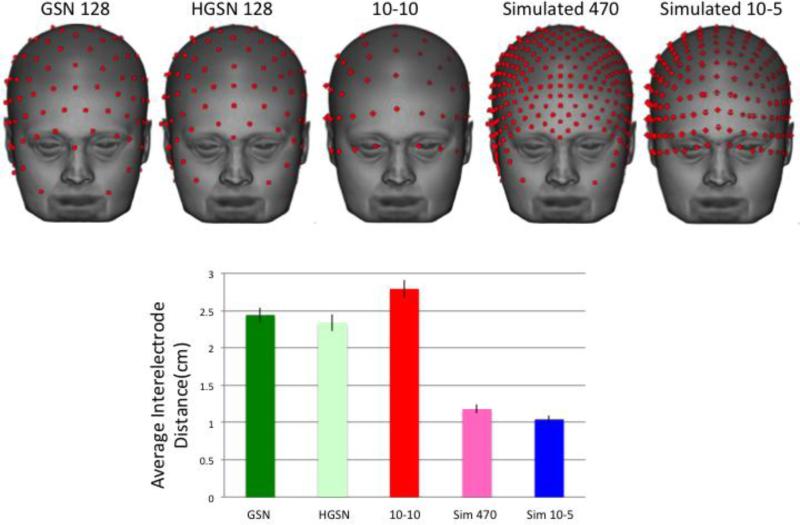
Figure 5 shows the GSN and HGSN electrode map templates on the average MRI template. Figure 5 also shows the analytic 10-10 positions on this head. Figure 6 shows the electrode map templates, compared with a simulated 10-5 and simulated 470-electrode configurations. We computed the inter-electrode distance for each electrode as the distance of that electrode location from its closest electrode. Figure 6 shows the average inter-electrode distance, summed over all electrodes and all individual participants. This was largest for the 10-10 electrode map, approximately equal for the two EGI configurations, and less than 50% of this size for the simulated high-density configurations.
Figure 5.
Final average electrodes displayed on the average MRI template.
Figure 6.
Average electrode maps for the simulated 470 and simulated 10-5 electrode configurations, and interelectrode distance for the closest electrode averaged across the electrode locations, separately for the five electrode configurations.
The electrode templates are available for use by other investigators (http://jerlab.psych.sc.edu/neurodevelopmentalmridatabase). The available data are: the fiducial markers for the average MRI head; lists of electrode locations for the seven averaging procedure for the GSN and HGSN electrodes (CPD-TenTen-Affine, CPD-TenTen-Rigid, CPD-Fiducials-Affine, CPD-Fiducials-Rigid, FLIRT-Head-Affine, FLIRT-Head-Rigid, Untransformed), and the virtual 10-10 electrode locations. We also include the simulated 10-5 positions and the simulated 470 positions for the CPD-TenTen-Affine electrode average. The electrodes are presented as lists of electrode numbers and locations (GSN, HGSN) or electrode names and locations (10-10, fiducial locations). We also include comparable data (fiducials, electrodes) for the ICBM-152 head. The template volumes are in compressed NIFTI format (http://nifti.nimh.nih.gov/). The data are on a file server that may be accessed with the Secure Shell (SSH) file transfer protocols (SCP or SFTP). Instructions for access are given online (http://jerlab.psych.sc.edu/neurodevelopmentalmridatabase). Interested users should contact John E. Richards (richards-john@sc.edu).
Average Template to Participant
Based on the analyses in the previous section, we chose the average derived from the CPD-TenTen-Affine transformation for testing. Recall that this transformation uses all the 10-10 locations defined on the individual MRI and the 10-10 locations defined on the average MRI template with CPD registration. This resulted in the most consistent projections from the individual participants to the average MRI template, i.e., smallest distribution of individual's electrode positions around the average electrode positions. We therefore adopted this CPD-TenTen-Affine for the tests in this section, though acknowledge that the other transformation methods would likely produce similar results.
The average electrode map was transformed with inverse registration matrices into the participant MRI space and the inverse transformed map for each participant was compared to that participant's actual electrodes. For the GSN electrodes we had enough participants to do a split-half procedure in which we re-estimated the average electrode map on one-half of the data, and tested the projections on the rest of the data. Additionally, for the GSN and HGSN electrodes, we calculated the CPD registration with full affine 12--dof rotations using the average electrodes and the participant electrodes (CPD-Electrodes-Affine) or a partial set near the fiducials (CPD-Partial-Affine). The comparison of the inverse transformed average map to the participant's actual electrodes tested the efficacy of the CPD with full electrode information, and should be a baseline for the linear affine registration method.
For the 10-10 locations, the electrode configuration from the average MRI template is based on the virtual electrode quantification on the average MRI template, so the projection from the average MRI template to each participant will test the methods for projecting the 10-10 electrodes to a new participant that does not have a MRI upon which to calculate the virtual 10-10 positions. We tested the complete 10-10 electrode locations (CPD-10-10-Affine), whole-head FLIRT registration (FLIRT-Head-Affine), the CPD of the fiducials, and an untransformed average electrode configuration.
The distance between transformed and actual electrodes was calculated, and a mean value for that location error was computed across electrodes for each subject. Figure 7 shows the mean location error for the CPD-TenTen-Affine average with the six inverse transformations and the untransformed average. An ANOVA for the GSN and HGSN electrodes with method-type as a repeated measure factor resulted in significant one-way effect for both the GSN and the HGSN configurations (F (5,342) = 11.98, p < .0001 for GSN and F (5, 284) = 17.33, p < .0001 for HGSN). The location error was significantly different for the transformations using the actual electrodes (CPD-GSN-All, CPD-GSN-Partial) and the transformations using the 10-10, fiducials, or whole-head (CPD-TenTen, FLIRT-Head, CPD-Fiducials). All six transformation methods resulted in less location errors between the transformed electrodes and the participant electrodes than did the untransformed average.
Figure 7.
Average distance between the inverse-projected average configurations and the original participant electrode locations. This is shown separately for the five transformation methods and the untransformed average for the GSN (A) and HGSN (B) configurations, and the three transformation methods and untransformed average for the 10-10 electrodes (C).
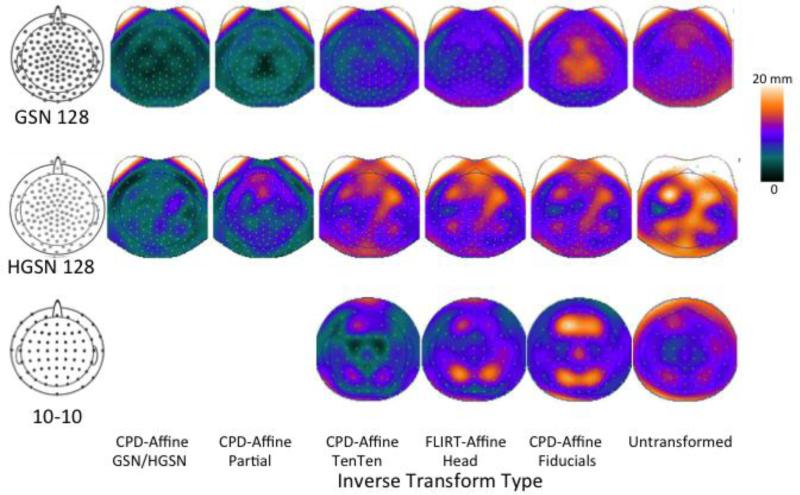
Figure 8 shows the location differences for the six inverse projections for the GSN and HGSN electrode configurations on a topographical map. The most notable finding was that the transformation with fiducials (CPD-Fiducials-Affine for GSN) and untransformed comparison showed the most differences near the vertex of the head. The comparison of the analytical average 10-10, and the participant 10-10 maps, is also shown in Figures 7 and 8. The CPD-TenTen-Affine transformation, which uses the actual electrodes on the participant and average, is the ‘baseline’ for how well the averaging procedure works with the actual electrodes. Both the FLIRT-Head and CPD-Fiducials did not fit as well as the actual electrodes; both were only minimally better fits than the untransformed average.
Figure 8.
Topographical maps representing the average location differences shown in Figure 7, but for the different electrode locations across the head. The GSN and HGSN has two additional methods involving registration between actual GSN/HGSN electrode locations on the participant and average; this is represented for the 10-10 electrodes by the CPD-10-10-Affine registration.
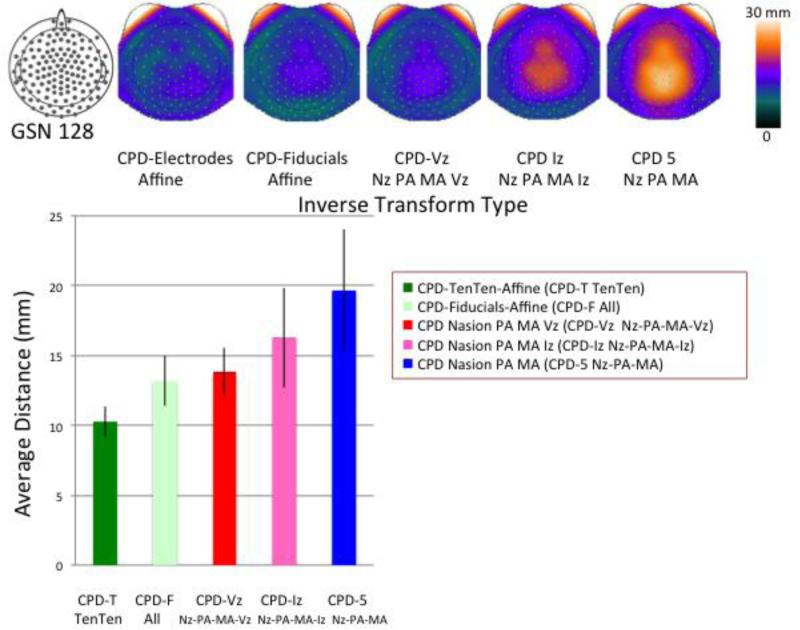
The CPD-TenTen average was transformed with the registrations based on the limited sets of fiducials (front, sides; front, sides, rear; front, sides, top) and transformed to the participants’ electrode space. Figure 9 (bar chart) shows the mean location difference for these limited fiducial registrations along with the CPD-TenTen transformations (from Figure 5). The procedure using only front and side fiducials produced a poor fit between the inverse transformed average electrodes and the participants’ electrodes (far right bar). Similarly, the registration with the Iz added was significantly poorer than the full fiducial fit (CPD-Fiducials) or registration with the 10-10 electrodes (CPD-TenTen). Adding the Vz to the front and side fiducials was not as good as the full fiducial registration, but was much closer.
Figure 9.
Topographical maps for the GSN electrodes showing the average location differences across the head for the CPD inverse transformation for various fiducial combinations. The bar graph shows the average location difference for the transformations. Note the large standard error and location difference for the CPD registrations without the Vz (two right topographical maps and two right bars).
Discussion
The results of the study may be summarized in terms of the two goals of the study. First, average electrode montages were computed for the GSN, Hydrocel GSN, 10-10, and 10-5 electrode systems using electrodes and an average MRI from 86 participants who had identified electrode location and individual structural MRIs. The point-set registration of the individual participant 10-10 locations with the average MRI template's 10-10 locations resulted in transformed electrodes that produced the lowest standard error of the location estimate for the average electrodes. This fit was superior to either untransformed averages, or those based on point-set registrations between external fiducial locations measured on the participant and average MRI, or whole-head linear affine registration. Second, the electrode averages were transformed back into participant space with several methods. This included the inverse registration from the forward registrations used to construct the averages, the entire set of average and participant electrodes, or limited sets of external fiducials. The inverse transformations based on the forward methods using the whole head (CPD-Ten-Ten, Flirt-Head) worked equally well in the fit of the inverse transformed average to the actual participant electrodes. A limited set of fiducials, particularly the elimination of the vertex fiducial, resulted in poorer fit between the inverse transformed average and the participants’ electrodes. The co-registration of average and participant electrodes resulted in the best fit. The electrode averaging based on the average MRI template worked well, with even closer fits between the inverse transformed average and participant electrodes.
The success of the CPD-TenTen point-set registration between the participant and average MRI template in the construction of the averages is likely based on the 10-10 locations providing a good scalp coverage and whole head shape. The registration estimates the four factors of the affine transformation matrix (translation, rotation, scale, skew). The CPD-TenTen's apparent advantage over the fiducial-based and whole-head registration methods may be due to more complete coverage of the external scalp with the MRI volumes than with the fiducials points. Complete coverage of the scalp resulted in the forward transformed participant electrodes to be in similar locations in the average MRI space, and low variability in the locations. This average set performed well when transforming the electrodes from the average space to the participant space for either the 10-10 point-set registration and the whole-head linear FLIRT registration (Figures 7, 8). The superior fit of the point-set CPD estimation using the entire electrode set likely is due to the increased coverage of the entire head with the electrodes. Whole-head registration for electrode-MRI affine co-registration has been reported in the literature (Jurcak et al, 2005), but has not been compared with point-set registration tools.
The poor fit of the average electrodes to actual electrodes transformed by the point-set fiducial registration without the vertex electrode is notable in this study. Large variability in the fit likely occurs because the scaling between the coronal (Nz to LPA-RPA) and sagittal (LPA to RPA) dimensions for the two volumes is handled well by the reduced set, but the scaling in the axial dimension cannot be determined without the vertex. The registration without the vertex fiducial resulted in errors occurring primarily in the superior axial electrode locations. A prior study advocating the use of an average realistic head model based on the ICBM-152 head used only nasion, left and right preauricular points in the registration, and coronal and axial scaling (Fuchs et al., 2002). Registration using this limited set of fiducials is not recommended for this work. Similarly, some computer software for electrical source analysis offers registration of electrodes to an average head with three-fiducial methods (e.g., CURRY; MRViewer and EMSE). Registration problems are likely with simple three-point registrations; both computer programs offer added scalp points that may be used as fiducial locations. The current results suggest that the vertex is critical for this work. The accuracy of the 10-10 point-set registration is similar to adding a set of scalp points both in the two spaces to be co-registered, so might be recommended for these computer programs.
It is important in some circumstances to use appropriate average MRI volumes. It is likely that special populations, particularly infants and children, will have neural anatomical differences from any adult MRI template and that age-appropriate MRI templates can be used for realistic models for infant participants (Reynolds & Richards, 2009; Richards, 2010; Sanchez, Richards, & Almli, 2012). For example, average MRI templates for children and adolescents recently have become available (Fonov et al., 2011; Sanchez et al., 2011; Sanchez et al., 2012) and templates for infants are available (Sanchez et al., 2011). These templates may be used for the realistic head model for BEM, FEM, or FDM electrical source methods. These types of realistic models are currently available for infants from 3 to 12 months, and children / adolescents from 6 through 18 years (Sanchez et al., 2012). Another important aspect of this research is the implications for errors in electrode position at specific locations on the head. The specific templates offered in this paper demonstrate that error in electrode positioning is not specific across the head, and differs based on the average template to which one applies the methods. Researchers who choose to use the templates will be aware of their weaknesses, and researchers who choose to develop their own templates can use the methods proposed in this manuscript to test error in individual electrode positions.
The methods of our study are not limited to the 128-channel recording systems (EGI's GSN, HGSN), nor simply to EGI's electrode systems. EGI has sensor net systems with other numbers of channels (e.g., 64, 256) that have positions that can not be derived from the 128-channel locations. Similarly, other electrode recording configurations (e.g., Electrocap, putative 10-10 locations measured on the cap; ElectroCap International, Inc. [Eaton, OH]; Biosemi, 128 channel electrode system, Biosemi B.V. [Amsterdam, Netherlands]) have electrode configurations that cannot be derived from the 10-10 system nor from the EGI locations. These configurations can be evaluated similar to our evaluation of the EGI 128-channel systems. Some kind of measurement device (e.g, Polhemius digitizer; or Geodesic Photogrammetry System, EGI) would be necessary to gather electrode locations, and participants would also need to have structural MRI recordings to do the co-registration between the measured electrode locations and the MRI.
We offer practical recommendations for four scenarios in which EEG is recorded: (1) researchers who have access to structural MRIs and EEG localization systems and would like to choose the best co-registration technique; (2) researchers who can measure the placements of electrodes in 3D space with magnetic, radiofrequency, or imaging techniques, but have no access to individual structural MRIs; (3) researchers who have access to individual structural MRIs, but no system to localize EEG sensors; and (4) researchers who do not have access to structural MRIs nor EEG localization systems.
First, (1) researchers who have access to structural MRIs and electrode localization systems have the data to choose the optimal approach for co-registering MRIs and electrode locations. The known electrode locations could come from the analytic definitions provided by the 10-10 system or by 3D measurement of electrode locations. Our results showed that a partial set of electrode locations worked nearly as well as having the entire electrode map (Figures 7, 8); thus it may be circumspect to identify a reduced set of locations with the electrode localization system and use the point-set registration methods used in this paper. The structural MRIs are used to develop realistic head models for that specific participant. There are differences between using this type of individualized method and average templates (Darvas et al., 2006) that leads to the inference that individual methods are optimal for electrical source analysis and some clinical or population (e.g., infants) rationales necessitate this approach. The current set of average electrodes and average MRI (average MRI template) could provide a common normalization standard even when individual models are used for the electrical source analysis. In this situation the entire electrode set would provide the best registration between the participant MRI and average MRI template, followed by a partial electrode set, then the 10-10 or whole-head registration (Figures 7, 8).
The next recommendations are for studies with known locations of electrodes, or individual participant MRIs, but not both. A common situation for EEG research occurs when (2) researchers, who can measure the placements of electrodes in 3D space with magnetic, radiofrequency, or imaging techniques have no access to individual structural MRIs. If the electrode locations are known, the full set of electrodes can be registered to the average electrode locations with point-set methods (Darvas et al., 2006 for similar registration method). The resulting registration matrix may then be used with the average MRI to transform the MRI into the participant space, or the participant into the MRI space, and realistic head models based on the average MRI can be individually co-registered with the participant electrodes. There is a clear advantage of realistic head models from an average template over spherical head models when a structural MRI is unavailable (Darvas et al., 2006). The existence of average templates and realistic head models based on infant and child participants (Sanchez, Richards, & Almli, 2011) also would be beneficial to studies of pediatric EEG recording.
In the latter situation, (3) researchers have access to individual structural MRIs, but no system to localize EEG sensors. The point-set registration based on the 10-10 virtual electrodes provided the best translation of the GSN and HGSN electrodes from the average MRI template to the individual participant MRI. However, whole-head affine registration between the participant structural MRI and the average MRI may be used to generate registration matrices that may be applied to the average electrodes to provide putative electrode locations in the participant space. These may be further aided by simple measurement of fiducial locations on the participant head, or photographs showing where specific electrodes fit. Systems doing simultaneous recording of EEG and MRI (EEG/fMRI) often do not have a measurement device to determine the precise location of the recording electrodes.
Researchers using 10-10 electrode locations and who have access to a structural MRI should use the virtual-electrode method. The level of accuracy of translation from the virtual 10-10 locations of the average MRI template to the individual result in an average error of 10+ mm when using whole-head registration or fiducial-based point-set registration (Figure 7, 8). The 10-10 virtual electrode generation is not complex and should provide the most reliable measurement of this electrode system when the structural MRI is known. Note that using a completely untransformed virtual 10-10 configuration from an average MRI template resulted in much greater average errors (~15 mm), almost half the interelectrode distance (Figures 6, 7).
Finally, (4) researchers who do not have access to structural MRIs nor EEG localization systems may find this work useful. External fiducial locations can be measured with calipers (linear distance) and tape measure (circumference). A set of 3D fiducial locations can be determined from such measurement (Fuchs et al., 2002)2. Some conditions may be extremely impractical for structural MRI; infant participants, special populations. The point-set registration between external fiducials measured on the participant and the same locations on the average MRI could be used to translate both the electrodes and MRI into the participant headspace (Fuchs et al., 2002). We expect that this procedure will result in electrical source models that are an improvement over standard spherical models (Darvas et al., 2006) and may also be important when age-appropriate head models are used (Reynolds & Richards, 2009).
The next step will be to examine how co-registration between electrode placement maps and MRI models impact the accuracy of source estimation. Simulations suggest that the influence of electrode position on source localization is mediated by the signal to noise ratio (Wang & Gotman, 2001). Several variables impact SNR including: Recording quality, ongoing EEG, the technique used to extract the signal from the, and anatomical variability. Signal extraction techniques such as such as ICA, which significantly decrease the ratio of signal to noise, increase the impact of electrode misallocation on source localization for superficial and deep sources (Wang & Gotman, 2001). Our study does not directly assess the influence of electrode mislocation on cortical source model accuracy. However, source analysis using models with realistic descriptions of the head's interior perform more accurately than spherical models (Vatta, Meneghini, Esposito, Mininel, & Di Saller, 2010). Empirical data support the theoretical models (Darvas et al., 2006). An important part of a realistic source model is the placement of the electrode locations accurately with respect to the realistic head model. Our study is a step towards providing accurate electrode placement methods for individual and average head models and should enhance the accuracy of source analysis.
Acknowledgments
This work was supported by the NIH grant to JER, R37 HD18942, and by the USAMERA grant to JMCV, W81XWH-06-1-0272.
Footnotes
The ANOVAs were done with the SAS GLM analysis program. The averaging type for this analysis was nested in the participants, and the appropriate error term was estimated with explicit testing routines. For the post hoc comparisons, the Tukey LSD method was used, with the error term for the analysis coming from the MS error term for the omnibus averaging type test.
We have developed measurement and calculation procedures for determining in subject space the locations of Nz, Iz, Vz, LPA, RPA, LMA, and RMA based on external head measurements. A circumference of the head is measured on the Nz-Iz horizontal plane, the vertical planes are defined as being perpendicular to the Nz-Iz horizontal plane, with the left-right plane's circumference measured from the LPA to the RPA with the vertex point as laying at 50% of this circumference and the anterior-posterior circumference measured as the circumference from the Nz to the Iz through the Vz. The Cz is defined as 50% of the circumference on the anterior-posterior plane. In addition to the circumferences, we measure the diameter from the Nz to the Iz, and the LPA and the RPA. The origin is defined as a point at the intersection of the three planes, and all fiducials can be defined in relation to these points.
References
- Avants B, Duda J, Kim J, Zhang H, Pluta J, Gee J, Whyte J. Multivariate analysis of structural and diffusion imaging in traumatic brain injury. Acad Radiol. 2008;15:1360–1375. doi: 10.1016/j.acra.2008.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatrian GE, Lettich E, Nelson PL. Modified nomenclature for the “10%” electrode system. Journal of Clinical Neurophysiology : Official Publication of the American Electroencephalographic Society. 1988;5:183–186. [PubMed] [Google Scholar]
- Chatrian G, Lettich E, Nelson P. Ten percent electrode system for topographic studies of spontaneous and evoked EEG activity. American Journal of EEG Technology. 1985;25:83–92. [Google Scholar]
- Collins D, Neelin P, Peters T, Evans A. Automatic 3D intersubject registration of MR volumetric data in standardized talairach space. Journal of Computer Assisted Tomography. 1994;18:192–205. [PubMed] [Google Scholar]
- Darvas R, Ermer J, Mosher J, Leahy R. Generic head models for atlas-based EEG source analysis. Human Brain Mapping. 2006;27:129–143. doi: 10.1002/hbm.20171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans AC, Brown E, Kelly RL, Peters T. 3D statistical neuroanatomical models from 305 MRI volumes. IEEE; Piscataway, NJ: 1994. [Google Scholar]
- Fonov V, Evans A, Botteron KA, McKinstry R, Collins D. Unbiased average age-appropriate atlases for pediatric studies. Neuroimage. 2011;54:313–327. doi: 10.1016/j.neuroimage.2010.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs M, Drenckhahn R, Wischmann H, Wagner M. An improved boundary element method for realistic volume-conduction modeling. IEEE Transactions on Biomedical Engineering. 1998;45:980–997. doi: 10.1109/10.704867. [DOI] [PubMed] [Google Scholar]
- Fuchs M, Kastner J, Wagner M, Hawes S, Ebersole J. A standardized boundary element method volume conductor model. Clinical Neurophysiology. 2002;45:980–997. doi: 10.1016/s1388-2457(02)00030-5. [DOI] [PubMed] [Google Scholar]
- Grabner G, Janke A, Budge M, Smith D, Pruessner J, Collins D. Symmetric atlasing and model based segmentation: An application to the hippocampus in older adults. In: Larsen R, Niesen M, J. S., editors. MICCAI. Springer-Verlag; Berlin: 2006. pp. 58–66. [DOI] [PubMed] [Google Scholar]
- Grieve P, Emerson R, Isler J, Stark R. Quantitative analysis of spatial sampling error in the infant and adult electroencephalogram. Neuroimage. 2004;21:1260–1275. doi: 10.1016/j.neuroimage.2003.11.028. [DOI] [PubMed] [Google Scholar]
- Hallez H, Vanrumste B, Grech R, Muscat J, De Clercq W, Vergult A, Lemahieu I. Review on solving the forward problem in EEG source analysis. Journal of Neuroengineering and Rehabilitation. 2007;4:46–78. doi: 10.1186/1743-0003-4-46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jasper H. The ten-twenty electrode system of the International Federation. Electroencephalography and Clinical Neurophysiology. 1958;10:371–375. [PubMed] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Medical Image Analysis. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Johnson M, de Haan M, Oliver A, Smith W, Hatzakis H, Tucker L, Csibra G. Recording and analyzing high-density event-related potentials with infants using the Geodesic Sensor Net. Developmental Neuropsychology. 2001;19:295–323. doi: 10.1207/S15326942DN1903_4. [DOI] [PubMed] [Google Scholar]
- Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic construction for computational anatomy. NeuroImage. 2004;23:s151–s160. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]
- Jurcak V, Okamoto M, Singh A, Dan I. Virtual 10-20 measurement of MRI images for inter-model linking of transcranial and tomographic neuroimaging methods. NeuroImage. 2005;26:1184–1192. doi: 10.1016/j.neuroimage.2005.03.021. [DOI] [PubMed] [Google Scholar]
- Jurcak V, Tsuzuki D, Dan I. 10/20, 10/10, and 10/5 systems revisted: Their validity as relative head surface based positioning systems. NeuroImage. 2007;34:1600–1611. doi: 10.1016/j.neuroimage.2006.09.024. [DOI] [PubMed] [Google Scholar]
- Luu P, Ferree T. Determination of the Geodesic Sensor Nets’ electrode positions and their 10-10 international equivalents. Technical Note, Electrical Geodesics, Inc; Eugene, OR.: 2000. [Google Scholar]
- Luu P, Ferree T. Determination of the Hydrocel Geodesic Sensor Nets’ average electrode positions and their 10-10 international equivalents. Technical Note: Electrical Geodesics, Inc; Eugene, OR.: 2005. [Google Scholar]
- Mazziotta J, Toga A, Evans A, Fox PL, Zilles K, Simpson G, Kabani N. A probabilistic atlas and reference system for the human brain. Philosophical Transaction of the Royal Society of London: B. Biological Sciences. 2001;356:1293–1322. doi: 10.1098/rstb.2001.0915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michel C, Murray M, Lantz G, Gonzalez S, Spinelli L, Grave de Peralta R. EEG source imaging. Clinical Neurophysiology. 2004;115:2195–2222. doi: 10.1016/j.clinph.2004.06.001. [DOI] [PubMed] [Google Scholar]
- Myronenko A, Song X. Point Set Registration: Coherent Point Drift. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2010;32:2262–2275. doi: 10.1109/TPAMI.2010.46. [DOI] [PubMed] [Google Scholar]
- Myronenko A, Song X, Carreira-Perpinan M. Advances in Neural Information Processing Systems -- Proceedings of the 2006 Conference. Vol. 19. MIT Press; Vancouver: 2007. Non-rigid point set registration: Coherent point drift. pp. 1009–1016. [Google Scholar]
- Oostenveld R, Praamstra P. The five percent electrode system for high resolution EEG and ERP measurements. Clinical Neurophysiology. 2001;112:713–719. doi: 10.1016/s1388-2457(00)00527-7. [DOI] [PubMed] [Google Scholar]
- Penny W, Friston K, Ashburner J, Keibel S, Nichols J. Statistical Parametric Mapping: The analysis of functional brain images. Academic Press; New York: 2007. [Google Scholar]
- Pivik R, Broughton R, Coppola R, Davidson R, Fox N, Newer M. Guidelines for the recording and quantitative analysis of electroencephalographic activity in research contexts. Psychophysiology. 1993;30:547–588. doi: 10.1111/j.1469-8986.1993.tb02081.x. [DOI] [PubMed] [Google Scholar]
- Plummer C. EEG source analysis - time for a common language. Journal of Clinical Neurophysiology. 2011;28:76. doi: 10.1097/WNP.0b013e3182051374. [DOI] [PubMed] [Google Scholar]
- Reynolds G, Richards J. Cortical source localization of infant cognition. Developmental Neuropsychology. 2009;3:312–329. doi: 10.1080/87565640902801890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richards J. Attention in the brain in early infancy. In: Johnson S, editor. Neoconstructivism: The New Science of Cognitive Development. Oxford University Press; New York: 2010. pp. 3–31. [Google Scholar]
- Rorden C. MRIcroGL. 2012a Feb; Retrieved from McCausland Center: http://www.mccauslandcenter.sc.edu/mricrogl/
- Rorden C. MRICron. 2012b Retrieved from McCausland Center: http://www.mccauslandcenter.sc.edu/mricro/mricron/
- Russell G, Eriksen K, Poolman PL, Tucker D. Geodesic photogrammetry for localizing sensor positions in dense arrays. Clinical Neurophysiology. 2005;116:1130–1140. doi: 10.1016/j.clinph.2004.12.022. [DOI] [PubMed] [Google Scholar]
- Sanchez C, Richards J, Almli C. Neurodevelopmental MRI brain templates for children from 2 weeks to 4 years of age. Developmental Psychobiology. 2011:1–15. doi: 10.1002/dev.20579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez C, Richards J, Almli C. Age-specific MRI templates for pediatric neuroimaging. Developmental NeuroPsychology. 2012;37(5):379–399. doi: 10.1080/87565641.2012.688900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scherg M. Fundamentals of dipoles source potential. In: Grandon F, Hoke M, Romani G, editors. Auditory evoked magnetic fields and potentials. Vol. 6. Karger; Basel: 1990. pp. 40–69. [Google Scholar]
- Smith S, Jenkinson M, M.N., W., Beckmann C, Behrens T, Johansen-Berg H, Matthews P. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23:208–219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Srinivasan R, Tucker D, Murias M. Estimating the spatial nyquist of the Nyquist of the human EEG. Behavioral Research Methods, Instruments, & Computers. 1998;30:8–19. [Google Scholar]
- Talairach J, Tournoux P. Co-planar stereotaxic atlas of the human brain. Thieme Medical Publishers; New York: 1988. [Google Scholar]
- Tamraz J, Comair Y. Atlas of regional anatomy of the brain using MRI with functional correlations. Springer-Verlag; Berlin: 2006. [Google Scholar]
- Tucker D. Spatial sampling of head electrical fields: The geodesic sensor net. Electroencephalography and Clinical Neurophysiology. 1993;87:154–163. doi: 10.1016/0013-4694(93)90121-b. [DOI] [PubMed] [Google Scholar]
- Tucker D, Liotti M, Russell G, Posner M. Spatiotemporal analysis of brain electrical fields. Human Brain Mapping. 1994;1:134–152. [Google Scholar]
- Vatta F, Meneghini F, Esposito F, Mininel S, Di Saller F. Realistic and spherical head modeling for EEG forward problem solution: A comparative . Computational Intelligence and Neuroscience. 2010 doi: 10.1155/2010/972060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Gotman J. The influence of electrode location errors on EEG dipole source localization with a realistic head model. Clinical Neurophysiology. 2001;112:1777–1780. doi: 10.1016/s1388-2457(01)00594-6. [DOI] [PubMed] [Google Scholar]