fMRI and EEG Predictors of Dynamic Decision Parameters during Human Reinforcement Learning

Abstract

What are the neural dynamics of choice processes during reinforcement learning? Two largely separate literatures have examined dynamics of reinforcement learning (RL) as a function of experience but assuming a static choice process, or conversely, the dynamics of choice processes in decision making but based on static decision values. Here we show that human choice processes during RL are well described by a drift diffusion model (DDM) of decision making in which the learned trial-by-trial reward values are sequentially sampled, with a choice made when the value signal crosses a decision threshold. Moreover, simultaneous fMRI and EEG recordings revealed that this decision threshold is not fixed across trials but varies as a function of activity in the subthalamic nucleus (STN) and is further modulated by trial-by-trial measures of decision conflict and activity in the dorsomedial frontal cortex (pre-SMA BOLD and mediofrontal theta in EEG). These findings provide converging multimodal evidence for a model in which decision threshold in reward-based tasks is adjusted as a function of communication from pre-SMA to STN when choices differ subtly in reward values, allowing more time to choose the statistically more rewarding option.

Introduction

The neural mechanisms of simple forms of reinforcement learning (RL) and decision making (DM) have been well studied over the last decades. Computational models formalize these processes and allow one to quantitatively account for a large number of observations with relatively few parameters. In the case of RL, models account for sequences of choices across several trials with changing state action-outcome contingencies (Samejima et al., 2005; Pessiglione et al., 2006; Frank et al., 2007a). DM models on the other hand address choices in which the evidence for one option or the other is typically stationary across trials, but can predict not only choice proportions but also the full response time distributions for each choice and condition (Ratcliff and McKoon, 2008). These models assume that individuals accumulate evidence in support of each decision option across time, and that a choice is executed when the evidence for one option reaches a critical decision threshold. A few recent studies have applied DM models to reward-based decisions, where the rate of evidence accumulation for one option over the other was proportional to the relative differences in reward values of those options (Krajbich et al., 2010; Cavanagh et al., 2011; Ratcliff and Frank, 2012; Cavanagh and Frank, 2014).

At the neural level, the relative values among different options needed to accumulate evidence is reflected by activity in the VMPFC (Hare et al., 2011; Lim et al., 2011) and striatum (Jocham et al., 2011). Moreover, scalp EEG, intracranial recordings, and brain stimulation evidence indicates that the dorsal mediofrontal cortex communicates with the STN to modulate the decision threshold, particularly under conditions of choice conflict (Frank et al., 2007b; Cavanagh et al., 2011; Zaghloul et al., 2012; Green et al., 2013; Zavala et al., 2014). These results accord with computational models in which the STN raises the decision threshold by making it more difficult for striatal reward representations to gain control over behavior (Ratcliff and Frank, 2012; Wiecki and Frank, 2013). However, different methodologies have been used across the above studies, and it is unclear how EEG measures relate to fMRI. For example, the relevant theta-band EEG signals implicated in conflict modulation of decision threshold have been recorded over mid-frontal electrodes, but their posited source in dorsomedial frontal cortex has not been directly shown. Moreover, while DM models provide a richer description of the underlying choice process (by accounting for not only choice but entire RT distributions of those choices), they have not been applied to cases in which reward values change with experience (i.e., during reinforcement learning). Here we address both of these lacunae by administering a reinforcement learning task using simultaneous fMRI and EEG measurements. We estimate DM parameters allowing for reward values to change with experience, and assess whether decision threshold is modulated on a trial-to-trial basis as a function of choice conflict, mediofrontal theta, and BOLD signals from mediofrontal cortex and STN.

Materials and Methods

Subjects.

Eighteen people participated in the experiment for payment. All subjects gave informed consent. Data from three subjects were discarded because of residual cardioballistic artifact in the EEG data, determined by comparing mid-frontal EEG signals well studied in previous literature (error-related negativity and theta power enhancement) to previously reported data. Subjects were eliminated if the artifact was clearly present in those data (and note that this signal is observed during feedback outcome, and is thus independent of the data we analyze during the choice period in this study). The SyncBox was not working for at least two of these three subjects, which resulted in poor MRI artifact and cardioballistic artifact.

Of the 15 subjects analyzed, there were 9 male and 6 female subjects ranging from 18 to 28 years old. All subjects were right-handed, with normal or corrected-to-normal vision, were native English speakers, and were screened for the use of psychiatric and neurological medications and conditions, as well as for contraindications for MRI.

Stimuli.

Stimuli consisted of three pictures of easily nameable objects (elephant, sunglasses, and a tomato) presented 40 times each. All pictures were presented on a black background.

Procedure.

The task design was taken from Haruno and Kawato (2006). Subjects viewed the three pictures 120 times (40 times each). For each picture, subjects had to select a response and learn which was more likely to be correct. Reward probabilities differed for each picture, where the statistically correct response was rewarded on 85% of trials for one picture, and the other response would be rewarded on the remaining 15% of trials. The contingencies for the other pictures were 75:25 and 65:35, thereby inducing varying levels of reward probability/value difference.

Trials included a variable duration (500–3500 ms) green fixation (+) followed by a picture. Each picture was presented for 1000 ms. Participant responses were made using an MRI-safe button box during scanning. Using their index and pinky finger of their right hand, subjects made a left or right button response. Responses made after display offset were counted as nonresponse trials. Following their response, subjects were given visual feedback indicating whether their decision was “Correct” (positive) or “Incorrect” (negative). Feedback was presented for 500 ms.

We determined that the number of trials was sufficient because we have found that 20–30 trials per condition is sufficient for EEG and fMRI in prior work, fitting with convention and prior estimates of adequate signal-to-noise ratio (Luck, 2005), and we were able to replicate previous mid-frontal theta results despite the need for artifact removal in combination with fMRI. Moreover, the hierarchical Bayesian parameter estimation technique we used for the drift diffusion model (DDM) is particularly suitable for increasing statistical strength when trial counts are low by capitalizing on the extent to which different subjects are similar to each other. We have previously shown that DDM parameters, including those regressing effects of trial-to-trial variations of brain activity on decision parameters, are reliably estimated with hierarchical DDM (HDDM) for these trial counts, whereas other methods are noisier (Wiecki et al., 2013).

The order of trials and duration of jittered intertrial intervals within a block were determined by optimizing the efficiency of the design matrix to permit estimation of the event-related MRI response (Dale, 1999). Picture and response mappings paired with each reward probability condition were counterbalanced across subjects. Counterbalancing was such that each picture and left or right correct response was assigned (with equal probability across subjects) to the 65, 75, and 85% conditions. For example, for one subject, the elephant picture might be assigned to the 85% condition and the left response was correct, but this same picture would be assigned to a different reward probability and/or correct button press for another subject.

fMRI recording and preprocessing.

Whole-brain images were collected with a Siemens 3 T TIM Trio MRI system equipped with a 12-channel head coil. A high-resolution T1-weighted 3D multi-echo MPRAGE image was collected for anatomical visualization. fMRI data were acquired in one run of 130 volume acquisitions using a gradient-echo, echo planar pulse sequence (TR = 2 s, TE = 28 ms, 33 axial slices, 3 × 3 × 3 mm, flip angle = 90). Padding around the head was used to restrict motion. Stimuli were projected onto a rear projection screen and made visible to the participant via an angled mirror attached to the head coil.

fMRI was preprocessed using SPM8 (Wellcome Department of Cognitive Neurology, London). Data quality was first inspected for movement and artifacts. Functional data were corrected for slice acquisition timing by resampling slices to match the first slice, motion-corrected across all runs; functional and structural images were normalized to MNI stereotaxic space using a 12 parameter affine transformation along with a nonlinear transformation using a cosine basis set, and spatially smoothed with an 8 mm full-width at half-maximum isotropic Gaussian kernel.

Extracting single-trial ROI BOLD activity.

In this study, we aimed to test the putative roles of the pre-SMA, STN, and caudate in the regulation of decision parameters in reinforcement learning. As such we chose a priori ROIs but allowed the boundaries of these to be constrained by the univariate activity. To relate RL-DDM parameters to brain activity, ROIs were defined and estimates of their hemodynamic response were obtained. Definitions of the ROIs were unbiased with respect to subsequent hypothesis tests and model fitting. The STN was defined using a probability map from Forstmann et al. (2012). All voxels with nonzero probability were used, resulting in a small mask around STN. The compiled map from several studies can be found at http://www.nitrc.org/projects/atag. The pre-SMA cortex was defined based on univariate activity to stimulus onset, which yielded activations quite close to that described in the literature related to conflict-induced slowing (Aron et al., 2007). From each ROI, a mean time course was extracted using the MarsBaR toolbox (Brett et al., 2002), and then linearly detrended. The hemodynamic response function (HRF) used for the GLM was derived from a finite impulse response (FIR) model of each ROI. Beginning with pre-SMA, defined from activity during stimulus onset, we observed a peak at around TR = 2 (4 s). Since the ROI was defined based on stimulus onset, it was neutral with respect to our conditions of interest. Thus, there is little risk of circularity in using this peak timing information to test correlations with theta, etc. We then used the same peak measures for other ROIs (STN and caudate). This information was used in two ways. (1) ROI analysis: The data extracted for DDM model fitting (STN, caudate, and pre-SMA) was the percentage signal change 2 TRs after stimulus onset for that ROI's spatially averaged time course. (2) Whole-brain analysis: In the whole-brain GLMs, we used the canonical function (mixture of gamma functions) but with parameterization (i.e., a peak of 4 s) informed by the FIR models.

EEG recording and preprocessing.

EEG was recorded using a 64-channel MRI-compatible Brain Vision system with a SyncBox (Brain Products). EEG was recorded continuously with hardware filters set from 1 to 250 Hz, a sampling rate of 5000 Hz, and an on-line Cz reference. The SyncBox synchronizes the clock output of the MR scanner with the EEG acquisition, which improves removal of MR gradient artifact from the EEG signal. ECG was recorded with an electrode on the lower left back for cardioballistic artifact removal. Individual sensors were adjusted until impedances were <25 kΩ. Before further processing, MRI gradient artifact and cardioballistic artifact were removed using the average artifact subtraction method (Allen et al., 2000, 1998) implemented in the Brain Vision Analyzer (Brain Products). MR gradient artifact was removed using a moving average window of 15 intervals followed by downsampling to 250 Hz, and then epoched around the cues (−1000 to 2000 ms). Cardioballistic artifact was removed by first detecting R-peaks in the ECG channel followed by a moving average window of 21 artifacts. Following MR gradient and cardioballistic artifact removal, EEG was further preprocessed using EEGLAB (Delorme and Makeig, 2004). EEG data were selected from the onset to the offset of the scanner run. Individual channels were replaced on a trial-by-trial basis with a spherical spline algorithm (Srinivasan et al., 1996). EEG was measured with respect to a vertex reference (Cz). Independent component analysis was used to remove residual MR and cardioballistic artifact, eye-blink, and eye-movement artifact.

The EEG time course was transformed to current source density (CSD; Kayser and Tenke, 2006). CSD computes the second spatial derivative of voltage between nearby electrode sites, acting as a reference-free spatial filter. The CSD transformation highlights local electrical activities at the expense of diminishing the representation of distal activities (volume conduction). The diminishment of volume conduction effects by CSD transformation may reveal subtle local dynamics. Single-trial EEG power was computed using the Hilbert transform on this CSD data filtered in the theta frequency band from 4 to 8 Hz, for channel FCz. Each sample in the EEG time course was z-scored and outliers (z > 4.5) were replaced with the average EEG power. A small number of trials (4%) were removed due to unusable EEG.

Time-frequency calculations were computed using custom-written MATLAB routines (Cavanagh et al., 2013). For condition-specific activities, time-frequency measures were computed by multiplying the fast FFT power spectrum of single-trial EEG data with the FFT power spectrum of a set of complex Morlet wavelets (defined as a Gaussian-windowed complex sine wave: e^i2πtfe^−t2/2xσ2 where t is time, f is frequency (which increased from 1 to 50 Hz in 50 logarithmically spaced steps), and it defines the width (or “cycles”) of each frequency band, set according to 4/(2πf), and taking the inverse FFT. The end result of this process is identical to time-domain signal convolution, and it resulted in estimates of instantaneous power (the magnitude of the analytic signal), defined as Z[t] (power time series: p(t) = real[z(t)]² + imag[z(t)]²). Each epoch was then cut in length (−500 to +1000 ms). Power was normalized by conversion to a dB scale (10 * log10[power(t)/power(baseline)]), allowing a direct comparison of effects across frequency bands. The baseline for each frequency consisted of the average power from 300 to 200 ms before the onset of the cues.

The stimulus-locked theta-band power burst over mid-frontal sites (4–8 Hz, 300–750 ms) was a priori hypothesized to be the ROI involved in conflict and control.

Psychophysiological interaction methods.

Psychophysiological interaction (PPI) analysis usually refers to a method in which one explores how a psychological variable (such as conflict) modulates the coactivity of two brain regions as assessed by BOLD. Here we extend this analysis method to include EEG as another physiological indicator to determine which brain region as assessed by BOLD shows increased activity as a function of EEG frontal theta and decision conflict. This would allow us to determine whether there are putative downstream areas that respond to frontal theta signals when conflict increases. Previous electrophysiological studies have shown that mid-frontal theta is granger causal of STN theta during decision conflict (Zavala et al., 2014); this PPI allows us to test for evidence of a similar modulation of STN BOLD during reinforcement conflict. PPI analyses included the following regressors: conflict (stimulus boxcar*conflict, where conflict is considered high as value differences between choice options are small; conflict = −|value_diff|) regressor with a duration of.5 s, EEG theta power regressor, and an interaction regressor (conflict*theta power). All three regressors were convolved with an empirically derived HRF in pre-SMA area (peak 4 s) and the theta regressors were downsampled to the TR sampling rate (0.5 Hz). Six additional head-movement regressors were modeled as nuisance regressors. Regressors were created and convolved with HRF at 125 Hz sampling rate. Subject-specific effects for all conditions were estimated using a fixed-effect model, with low-frequency signal treated as confounds. Participant effects were then submitted to a second-level group analysis, treating participant as a random effect, using a one-sample t test against a contrast value of zero at each voxel.

DDM.

The DDM simulates two alternative forced choices as a noisy process of evidence accumulation through time, where sensory information arrives and the agent determines, based on task instructions and internal factors such as memory and valuation, whether this information provides evidence for one choice option or another. Evidence can vary from time point to time point based on noise in the stimulus or noise in neural representation, or in attention to different options and their attributes. The rate of accumulation is determined by the drift rate parameter v, which is affected by the quality of the stimulus information: higher drift rates are related to faster and more accurate choices. A choice is executed once evidence crosses a critical decision threshold a, also a free parameter related to response caution: higher decision thresholds are associated with slower but more accurate choices. A nondecision time parameter (t), capturing time taken to process perceptual stimuli before evidence accumulation and the time taken to execute a motor response after a choice is made, is also estimated from these data.

Here we tested whether the DDM provides a good model of choices and RT distributions during a reinforcement learning task in which the evidence for one choice option over another evolves with learning through trials. We further tested two critical assumptions. First, that in this setting, the drift rate is proportional to the (evolving) value difference between the two choice options, as posited to be mediated by striatal activity. Second, that the decision threshold can be adjusted as a function of choice conflict, and that this threshold adjustment is related to communication from dorsomedial frontal cortex to the STN.

We used hierarchical Bayesian estimation of DDM parameters, which optimizes the tradeoff between random and fixed-effect models of individual differences, such that fits to individual subjects are constrained by the group distribution, but can vary from this distribution to the extent that their data are sufficiently diagnostic (Wiecki et al., 2013). This procedure produces more accurate DDM parameter estimates for both individuals and groups than other methods, which assume that all individuals are completely different (or that they are all the same), particularly given low trial numbers. It is also particularly effective when one wants to estimate decision parameters that are allowed to vary from one trial to the next as a function of trial-to-trial variance in physiological and neural signals (i.e., via regressions within the hierarchical model). Estimation of the HDDM was performed using recently developed software (Wiecki et al., 2013). Bayesian estimation allowed quantification of parameter estimates and uncertainty in the form of the posterior distribution. Markov chain Monte Carlo sampling methods were used to accurately approximate the posterior distributions of the estimated parameters. Each DDM parameter for each subject and condition was modeled to be distributed according to a normal (for real valued parameters), or a Gamma (for positive valued parameters), centered around the group mean with group variance. Prior distributions for each parameter were informed by a collection of 23 studies reporting best-fitting DDM parameters recovered on a range of decision-making tasks (Matzke and Wagenmakers, 2009; Wiecki et al., 2013). Ten thousand samples were drawn from the posterior to obtain smooth parameter estimates.

To test our hypotheses relating neural activity to model parameters, we estimated regression coefficients within the same hierarchical generative model as that used to estimate the parameters themselves (Fig. 3). That is, we estimated posterior distributions not only for basic model parameters, but the degree to which these parameters are altered by variations in psychophysiological neural measures (EEG theta power, STN, caudate, and pre-SMA BOLD activity). In these regressions the coefficient weights the slope of parameter (drift rate v, threshold a) by the value of the neural measure (and its interactions with value/conflict) on that trial, with an intercept, for example: a(t) = β₀ + β₁STN(t) + β₂theta(t) + β₃STN(t) * theta(t). The regression across trials allows us to infer the degree to which threshold changes with neural activity; for example, if frontal theta is related to increased threshold, one would observe that as frontal theta increases, responses are likely to have a slower, more skewed RT distribution and have a higher probability of choice of the optimal response. This would be captured by a positive regression coefficient for theta onto decision threshold. It would not be captured by drift rate (which would require slower RTs to be accompanied by lower accuracies on average), or nondecision time (which predicts a constant shift of the RT distribution rather than skewing, and no effect on accuracy).

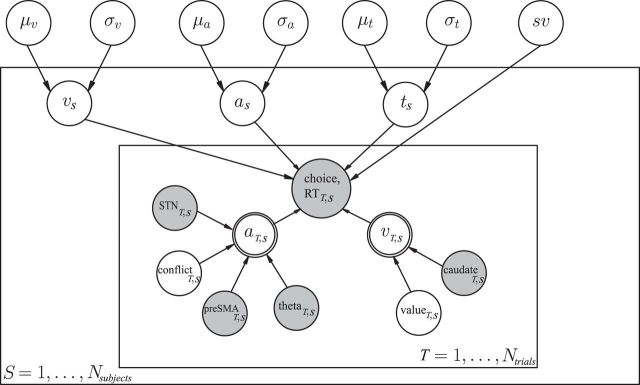
Figure 3.

Graphical model showing hierarchical estimation of RL-DDM with trial-wise neural regressors. Round nodes represent continuous random variables, and double- bordered nodes represent deterministic variables, defined in terms of other variables. Shaded nodes represent observed data, including trial-wise behavioral data (accuracy, RT) and neural measures (fMRI and EEG). Open nodes represent unobserved latent parameters. Overall subject-wise parameters are estimated from individuals drawn from a group distribution with inferred mean μ and variance σ. Trial-wise variations of decision threshold a and drift rate v (residuals from the subject-wise values) are determined by neural measures and latent RL value difference/conflict. Plates denote that multiple random variables share the same parents and children (e.g., each subject-wise threshold parameter a_S shares the same parents that define the group distribution). The outer plate is over subjects S while the inner plate is over trials T. Inferred relationships of trial-wise regressors were estimated as fixed effect across the group, as regularization and to prevent parameter explosion. sv = SD of drift rate across trials; t = time for encoding and response execution (“nondecision time”).

To address potential collinearity among model parameters (especially given noisy neural data affecting trial-wise parameters), we only estimated the group level posterior for all of the regression coefficients, which further regularizes parameter estimates, rather than assuming separate regression coefficients for each subject and neural variable, which would substantially increase the number of parameters/nodes in the model (Cavanagh et al., 2011, 2014). Moreover, Bayesian parameter estimation inherently deals with collinearity in the sense that it estimates not only the most likely parameter values, but the uncertainty about these parameters, and it does so jointly across all parameters. Thus any collinearity in model parameters leads to wider uncertainty (for example, in a given sample it might assign a high/low value to one parameter and a high/low value to another, and the reverse in a different sample). The marginal distributions of each posterior are thus more uncertain as a result, and any significant finding (where the vast majority of the distribution differs from zero) is found despite this collinearity issue (Kruschke, 2011). Further, we iteratively added in modulators to test whether successive additions of these modulators improved model fit. We confirmed with model comparison that fits are better when the frontal and STN modulators were used to affect threshold than when they are used to affect drift.

Bayesian hypothesis testing was performed by analyzing the probability mass of the parameter region in question (estimated by the number of samples drawn from the posterior that fall in this region; for example, percentage of posterior samples greater than zero). Statistical analysis was performed on the group mean posteriors. The Deviance Information Criterion (DIC) was used for model comparison, where lower DIC values favor models with the highest likelihood and least degrees of freedom. While alternative methods exist for assessing model fit, DIC is widely used for model comparison of hierarchical models (Spiegelhalter et al., 2002), a setting in which Bayes factors are not easily estimated (Wagenmakers et al., 2010), and other measures (e.g., Akaike Information Criterion and Bayesian Information Criterion) are not appropriate.

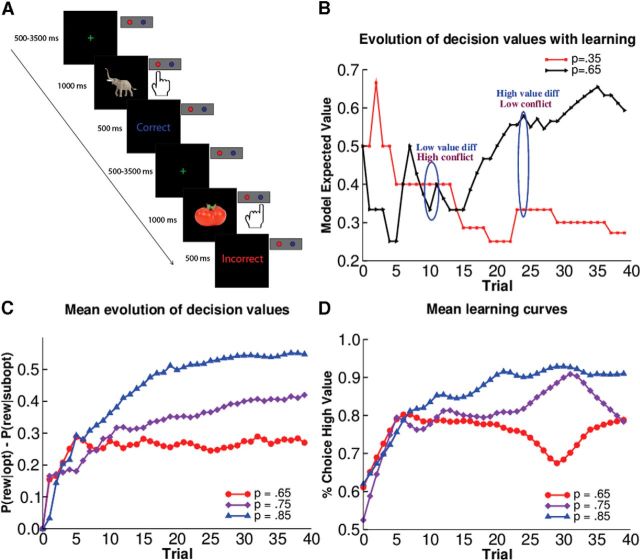
We quantified choice conflict as the absolute value of the difference in expected values between each of the options on each trial, with smaller differences signifying greater degree of conflict. The expected values were updated as a function of each reinforcement outcome using Bayes' rule, such that the expected values represent the veridical expectations based on an ideal observer (Fig. 1B,C). (Similar results were obtained using Q-values from a reinforcement learning model, but this requires an additional free parameter to estimate the learning rate, whereas the learning rate of the Bayesian observer depends only on the estimation uncertainty about the reinforcement value, and hence the number of outcomes observed thus far; Doll et al., 2009, 2011.)

Figure 1.

Probabilistic reinforcement learning task. A, Task/trial structure. Participants learned to select one of two motor responses for three different stimuli with different reward contingencies (85:15, 75:25, and 65:35% reward probabilities). B, Evolution of model-estimated action values as a function of experience, from an example subject and condition (p(r|a) = 0.35 and 0.65). The difference in values at each point in time was used as a regressor onto the drift rate in the DDM. Conflict is high on trials in which the values of the two choice options is similar. C, Mean evolution of the difference in model-estimated action values for each condition across all subjects, based on each subject's choice and reinforcement history. D, Mean behavioral learning curves in these conditions across subjects.

We first verified the basic assumptions of the model without including neural data. Specifically, we tested whether choices and response times could be captured by the DDM in which the drift rate and/or threshold varies as a function of the relative differences in expected values between each option (while also allowing for overall trial-to-trial variability in drift, estimated with parameter sv; Ratcliff and McKoon, 2008). After evaluating the results of best-fitting models (see Results), we subsequently tested whether trial-to-trial variability in neural measures from EEG and fMRI in regions of interest (pre-SMA, caudate, and STN from fMRI; mid-frontal theta from EEG) influence decision parameters (see Fig. 3 for graphical model). We quantified choice conflict as the difference in expected values between each of the options on each trial, with smaller differences signifying greater degree of conflict (Fig. 1B). We tested whether threshold was modulated not only by decision conflict, but by trial-to-trial variations in mediofrontal theta power from EEG, STN BOLD, and their interactions:

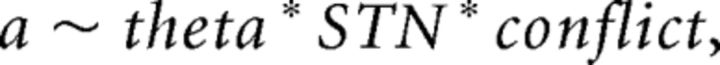including each individual component of the interaction as well as the three-way term. We further tested whether threshold was modulated by pre-SMA activity and conflict, and whether value effects on drift rate were modulated by caudate. The right caudate was used in this analysis because it provided a better behavioral fit to the data than the left caudate (DIC of 78 vs 81), and caudate was chosen because of its a priori role in reinforcement learning and because it was bilaterally activated at stimulus onset along with pre-SMA.

To account for outliers generated by processes other than the DDM (e.g., lapses in attention) we estimated a mixture model where 5% of trials are assumed to be distributed according to a uniform distribution as opposed to the DDM likelihood. This is helpful for recovering true generative parameters in the presence of such outliers (Wiecki et al., 2013). Ten thousand samples were drawn to generate smooth posterior distributions.

Behavior characterization and model fit.

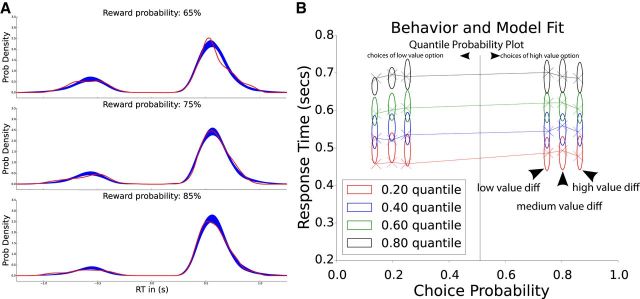
Application of the DDM to an RL task implies that the model should capture not only the evolution of choice probabilities with value but also the corresponding RT distributions. We first plot the overall RT distributions for each reward probability across the whole group, separately for each reward probability (Fig. 2A). This plot shows that the RL-DDM model captures choice proportions and RT distributions simultaneously, including the observations that choice proportions are more consistent, and RT distributions have smaller tails, with increasing reward probabilities. To be more precise, we also used a common tool for characterizing correspondence between behavior and DDM predictions, called the quantile-probability plot (Ratcliff and McKoon, 2008). This plot displays behavioral data in terms of both choice proportions (on the x-axis) and RT distributions (quantiles; on the y-axis), for various task conditions. Each task condition is displayed twice: once for choices of the more rewarding “optimal” option, and once for choices of the less rewarding “suboptimal” option. While the x-coordinate for these are redundant (p(opt) = 1 − p(subopt)), the RT distributions could potentially differ. A critical test of a DDM model is thus that it can capture the full set of choice probabilities and RT distributions for each of the task conditions. Although we used model fit statistics to select the best-fitting model, the best-fitting model could potentially not reproduce the key behavioral patterns it is intended to capture. We thus performed a posterior predictive check in which we generated data from the posterior distributions of model parameters, and plotted them alongside the behavioral data.

Figure 2.

Choice proportions and RT distributions are captured by RL-DDM. A, Behavioral RT distributions across the group are shown for each reward condition (red, smoothed with kernel density estimation), together with posterior predictive simulations from the RL-DDM (blue). Distributions to the right correspond to choices of the high-valued option and those to the left represent choices of the low-valued option. The relative area under each distribution defines the choice proportions (i.e., greater area to the right than left indicates higher proportion choices of the more rewarding action). Accuracy is worse, and tails of the distribution are longer, with lower reward probability. B, Model fit to behavior can be more precisely viewed using a quantile-probability plot, showing choices and quantiles of RT distributions. Choice probability is plotted along the x-axis separately for choices involving low, medium, and high differences in values (tertiles of value differences assessed by the RL model). Values on the x-axis >0.5 indicate proportion of choices of the high-valued option, and those <0.5 indicate choice proportions of the low-valued option, each with their corresponding RT quantiles on the y-axis. For example, when value differences were medium, subjects chose the high-valued option ∼80% of the time, and the first RT quantile of that choice occurred at ∼475 ms. Empirical behavioral choices/RT quantiles are marked as X and simulated RTs from the posterior predictive of the RL-DDM as ellipses (capturing uncertainty). Quantiles are computed for each subject separately and then averaged to yield group quantiles. Ellipse widths represent SD of the posterior predictive distribution from the model and indicate estimation uncertainty.

Note that for this plot, rather than showing the three categorical 65, 75, and 85% stimulus conditions (which describe the asymptotic reward values), we allow the model to be sensitive to the actual trial-by-trial reward value differences as assessed by the RL model. Thus we plot performance separately for tertiles of value differences (low, medium, and high) taken from each subjects' actual sequence of choices and outcomes, so that e.g., a trial for a subject in the 75:25 condition might get classified as “high value” rather than “medium value” if that subject happened to get a large sequence of rewards for the high-valued option in that condition.

Results

Participants learned the reward contingencies across 120 trials, with increasing consistency of selecting the more rewarded option for higher reward probabilities (Figs. 1D, 2A,B). We fit choice behavior with a DDM model in which the rate of evidence accumulation was modeled to be proportional to relative difference in reward values, as updated on a trial-by-trial basis as a function of experience (Fig. 1B). We used hierarchical Bayesian estimation of DDM parameters using HDDM, which optimizes the tradeoff between random and fixed-effect models of individual differences, such that fits to individual subjects are constrained by the group distribution, but can vary from this distribution to the extent that their data are sufficiently diagnostic (Wiecki et al., 2013). This method is particularly useful for estimating the impact of moderating variables (such as reward value differences, brain activity, and their interactions) on model parameters given a limited number of trials for each subject.

The model fits better when both drift rate and threshold varied as a function of value differences (DIC = 81) compared with just threshold (DIC = 219) or just drift rate (DIC = 142.6). Moreover, allowing the drift rate to vary parametrically with differences in expected value—involving a single parameter that scales the impact of value on drift rate to explain all of the data across trials and conditions—improved fit compared with a model in which we simply estimate three separate drift rates for each condition (65, 75, and 85% contingencies; DIC = 183.6). This finding confirms that dynamically adjusting drift rates by dynamically varying reward values improves model fit. (See below for parameter estimates further supporting this assertion.) The same conclusion was found with respect to threshold adjustment, in terms of model selection (DIC = 108 for a model in which threshold only varied as a function of condition instead of dynamic changes in value conflict), and the resulting regression coefficient. While there was a significant positive association between value difference and threshold, this effect was approximately five times smaller than that on drift. Below we describe how the threshold effect is modulated by neural indices related to conflict. Thus in sum, the best-fitting model allowed both threshold and drift rate to change dynamically; allowing either one to change only by categorical stimulus condition reduced the fit.

To evaluate whether choices and RT distributions are consistent with that expected by the DDM, we generated posterior predictive simulations, showing expected RT distributions and choice proportions based on fitted model parameters as a function of differences in reward values among options (Fig. 2). The RL-DDM model captures the finding of relative increases in choices for high-valued options as value differences increase, and also captures the relative differences in RT distributions for these conditions, including both RT distributions for choices of the more rewarding optimal response and those of the less rewarding suboptimal response. To further probe the combination of choice proportions and RTs, we generated a quantile-probability plot (Fig. 2B), showing the model predictions for choice proportions and RTs based on value differences. For example, in the “medium value difference” condition, participants chose the high-value option ∼80% of the time; the RT quantiles at which they made these choices are plotted with Xs in the middle vertical cluster on the right side of the graph. For the remaining 20% of trials, they chose the low-value option (on the left side), with corresponding RT quantiles. The ellipses show the predicted quantiles and choice probabilities for the model in DDM for each of these conditions. The higher choice consistency for higher valued options can be seen by the fact that choice probabilities are higher (further to the right) on the plot as value differences increase. In sum, these posterior predictive plots confirmed that the DDM provided a reasonable fit to behavioral choices (proportion of choices of high-value vs low-value option) and, simultaneously, the RT distributions for those choices.

Next, we tested the hypothesis that drift and threshold parameters would be modulated by neural data from EEG and fMRI in the regions of interest (Fig. 3). These models allow us to estimate the regression coefficients in HDDM models to determine the relationship between across-trial variations in psychophysiological neural measures from predefined ROIs (mid-frontal EEG theta power, STN, caudate, and pre-SMA BOLD activity) and model parameters (drift rate and decision threshold). In these regressions the coefficient weights the slope of parameter (drift rate and threshold) by the value of the neural measure (and its interactions with value/conflict) on that specific trial (Figs. 3, 4). Model fit established that the model including pre-SMA*conflict and STN*theta*conflict (DIC = 77.8) as modulators of decision threshold fit better than models that included only one of these terms (DIC = 80 and 79).

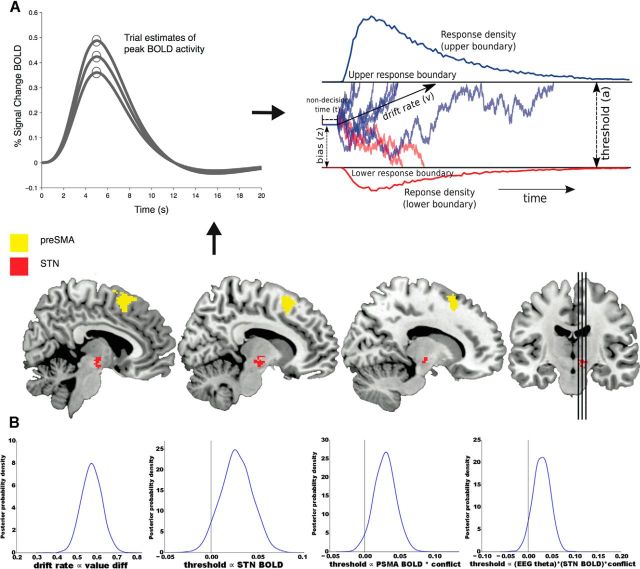
Figure 4.

Combining fMRI and EEG to estimate DM parameters. A, Trial-to-trial peak estimates of the BOLD signal from pre-SMA and STN ROIs (depicted on sagittal slices) along with trial-to-trial theta power estimates from mid-frontal EEG, were entered in as regressors to DDM parameters. The upper response boundary represents choices of the high-valued option, whereas the lower response boundary represents choices of the suboptimal option. Decision threshold reflects the distance between the boundaries, and the drift rate (speed of evidence accumulation) is proportional to the value difference between options. B, Posterior distributions on model parameter estimates, showing estimated regression coefficients whereby drift rate was found to be proportional to value differences and decision threshold proportional to various markers of neural activity and their interaction with decision conflict. Peak values of each distribution represent the best estimates of each parameter, and the width of the distribution represents its uncertainty. Drift rate was significantly related to the (dynamically varying across trials) value difference between each option (posterior distribution shifted far to the right of zero). Decision threshold was significantly related to STN BOLD; the interaction between pre-SMA BOLD and conflict; and the three-way interaction between mid-frontal theta power, STN BOLD, and conflict.

As noted earlier, model fits confirmed that behavioral data were better accounted for when drift rate varies according to learned trial-wise reward dynamics, compared with a model in which a single drift rate is estimated (or separate drifts per reward condition). Indeed, as expected, the regression coefficient estimating the effect of reward value differences on drift rate was positive, with the entire posterior distribution of this regression coefficient shifted far from zero (Fig. 4B, left). Prominent theories of reinforcement learning predict the degree to which differences in expected value drive choice is related to striatal activity. There was moderate evidence that the degree to which value difference impacted drift rate was modulated by variance in right caudate activity (92.5% of posterior >0), and model fits to behavior were improved by including this caudate activity (see Materials and Methods).

Next we evaluated the primary hypothesis: whether the decision threshold is modulated by decision conflict (where here conflict is stronger as the values are closer together). More specifically, we tested whether the degree to which this occurs is related to activity in the mediofrontal cortex (using both fMRI and EEG) and downstream STN (fMRI only). We found that the decision threshold was influenced by both neural modalities, as evidenced by model fits and parameter estimates. Specifically, trial-to-trial modulations of STN BOLD signal were parametrically related to larger decision thresholds (96% of posterior different from zero; Fig. 4B). This effect was further modulated by trial-to-trial variations in mediofrontal theta EEG activity, particularly as decision conflict rises (theta*conflict*STN interaction, 95% of posterior different from zero). (See Fig. 5 for the average theta power increases over mid-frontal electrodes across trials during the decision process.) Finally, there was also an interaction between conflict and pre-SMA BOLD activity on decision threshold (98% of posterior >0). Other interactions were nonsignificant.

Figure 5.

EEG and fMRI correlates of decision conflict. A, Mid-frontal theta power from EEG locked to stimulus onset, showing a strong increase in theta power across all subjects and trials. B, Trial-to-trial correlation between mid-frontal theta power from EEG and BOLD activity, showing strongest correlation in the SMA. Activation shown is thresholded at p < 0.001 uncorrected with a clustering extent of 120 voxels (corrected p value of p < 0.046 FWE). C, PPI identifies brain regions that preferentially respond as both mPFC theta and conflict rise, showing an isolated cluster of subcortical voxels overlapping with STN mask.

The above findings indicate that the decision threshold during learning is directly modulated by STN activity, but that influences of dorsomedial PFC (from fMRI and EEG) activity on threshold are dependent on conflict. To explore the relationship between EEG and fMRI measures, a whole-brain analysis confirmed that increases in mediofrontal theta were associated with increases in SMA activity (Fig. 5A,B), with significant voxels in a region just posterior to the pre-SMA (cluster corrected, 120 voxels, p = 0.04; p < 0.001 uncorrected). This finding implies that pre-SMA BOLD activity and mediofrontal theta share common underlying neural networks related to choice, supporting the finding that both measures are related to decision threshold adjustment as a function of conflict.

Finally, while the above analysis relied on ROI extractions to test our hypothesis that dorsomedial PFC interacts with STN to adjust decision threshold as a function of conflict, we also investigated this hypothesis across the whole brain. Specifically, we performed a PPI to investigate areas of the brain that would respond parametrically as a function of the interaction of mediofrontal theta and decision conflict. This whole-brain analysis revealed an isolated cluster of voxels that strongly overlapped with the a priori defined STN mask (Fig. 5C). Thus the PPI confirms that the STN responds to a greater degree when mid-frontal theta and conflict rise together. This finding converges with the previously reported three-way interaction in the DDM: while STN activity was directly related to decision threshold, this behavioral effect was also modulated by conflict and mid-frontal theta.

Discussion

Our findings contribute to a richer description of choice processes during reinforcement learning. The combined RL-DDM model accounts simultaneously for the incremental changes in choice probability as a function of learning (as do typical RL models), and the response time distributions of those choices (as do typical DM models). Moreover, our analysis suggests that single-trial EEG and fMRI signals can be used to investigate neural mechanisms of model parameters. In particular, we showed that coactivity between dorsomedial PFC and the STN is related to dynamic adjustment of decision threshold as a function of conflict in reinforcement values. This finding converges with a recent report showing that mid-frontal theta power is granger causal of STN theta during traditional conflict tasks (Zavala et al., 2014). The simultaneous fMRI and EEG method allowed us to investigate the potential neural source of the mid-frontal theta signals that have previously been attributed to cognitive control and threshold adjustment (Cavanagh et al., 2011, 2013), with the pre-SMA emerging as the likely generator. Together with neural modeling of the impact of frontal cortical conflict signals on the STN via the hyperdirect pathway (Frank, 2006; Wiecki and Frank, 2013), and granger causality findings showing frontal modulation of STN theta during conflict (Zavala et al., 2014), our evidence supports the notion that the mechanism for implementing such cognitive control is dependent on downstream STN activity. Indeed, these findings are to our knowledge the first direct evidence that trial-to-trial variation in STN activity relates to variance in decision thresholds, a conjecture that is based on computational modeling (Frank, 2006; Ratcliff and Frank, 2012) thus far supported by empirical studies showing that disruption of normal STN function (by deep brain stimulation) reverses the impact of frontal theta and leads to reduced thresholds (Cavanagh et al., 2011; Green et al., 2013).

The DDM is the most popular version of a more general class of sequential sampling models and provides a good account of response time distributions in this task, much like it does for perceptual decision-making tasks in which noisy sensory evidence needs to be integrated across time. While reinforcement values also need to be integrated across trials, it is natural to ask why evidence would need to be accumulated within a trial in this case: Could the learner simply retrieve a single integrated value estimate of each action in a single step? There are multiple potential resolutions to this issue. First, multilevel modeling exercises show that the DDM also provides a good description of RT distribution for reward-based decisions made by a dynamic neural network of corticostriatal circuitry (Ratcliff and Frank, 2012). In that case, the premotor cortex first generates candidate actions, but with noise leading to fluctuations across time in the degree to which each action is available for execution, and with the downstream striatum reflecting the momentary action values proportional to their cortical availability (“attention”) during that instant. This scheme leads to accumulation of striatal value signals across time with variable rates across trials, until one of the actions is gated by striato-thalamo-cortical activity. Our analysis provides limited evidence for this notion in that the degree to which drift rate was modulated by the difference between choice option values was marginally related to striatal (caudate) activity. Similarly, a recent study provided evidence that the degree of value accumulation (drift rate) in this type of task is related to the proportion of attention (visual fixation time) on each option, whereas the threshold is related to conflict-induced changes in pupil diameter, also thought to reflect downstream consequences of mid-frontal theta (Cavanagh et al., 2014).

Alternatively, it is possible that during learning, participants do not represent a single integrated value for each decision option, but instead repeatedly draw samples from individual past experiences, and compute the average value based on this sample (Erev and Barron, 2005; Stewart et al., 2006). Such a scheme accounts for seemingly suboptimal behavior such as probability matching in various choice situations. This framework is natural to consider from the DDM in that each previous memory sample would add or subtract evidence for that option depending on whether the sample retrieved was a gain or a loss, and the decision threshold would then dictate the number of samples needed to be drawn before committing to a choice.

Our study has various limitations. One possibility is that the neural measures we assess are related to value signals rather than conflict. Indeed, for the purposes of this study, conflict is defined by absolute differences in reinforcement value, i.e., we are studying the conflict between RL values and how they affect decision parameters. Moreover we can rule out a general effect of RL value instead of value difference, because (1) the average value of each stimulus pair on each trial is always the same (e.g., the mean of 0.85 and 0.15 is 0.5, similarly for other pairs) and (2) some studies show neural signals coding the value of the chosen action specifically (Jocham et al., 2011). This would correlate with value difference when the optimal action is chosen but would anticorrelate with it when the low-value option is chosen. We found that value difference drives decision variables (drift and threshold), i.e., that they affect the choice process itself, and these parameters are only discernable across both choices of high- and low-value options.

Next, although the methods allowed us to establish a link between pre-SMA BOLD activity and mid-frontal theta power, the conclusion that pre-SMA is the generator of mid-frontal theta is moderated by two caveats. First, our model assumes that changes in theta power are linearly related to changes in BOLD. But, such a linear relationship is by no means established, and some evidence supports differences in BOLD coupling across oscillatory frequencies (Niessing et al., 2005; Goense and Logothetis, 2008). Second, despite much evidence for mid-frontal generator of theta power, (for review, see Cavanagh and Frank, 2014; Cavanagh and Shackman, 2014), and other evidence implicating pre-SMA specifically in representation of conflict (Ullsperger and von Cramon, 2001; Isoda and Hikosaka, 2007; Usami, 2013), our correlational results cannot establish a causal link between these signals. Thus, it is conceivable that activation in pre-SMA could reflect local changes in neural activity that are simple correlates of theta generated elsewhere. Indeed, given growing evidence for cross-frequency coupling (Voytek et al., 2013), it is possible that pre-SMA BOLD reflects power changes in the gamma band, which is nested under theta. In this context, we note that the area most significantly related to EEG (mid-frontal theta) in a whole-brain analysis was SMA proper, whereas BOLD signal related to threshold adjustment as a function of conflict arose from the adjacent pre-SMA ROI (selected based on prior literature). Though this might reflect more complex cascading effects as described above, a strong functional distinction between SMA/pre-SMA cannot be drawn from these data.

Third, it should be noted that the exact location of the STN within each participant cannot be determined without higher resolution imaging than was used here. Thus, though our use of the probability map from Forstmann et al. (2012) gives us an acceptable degree of confidence that each participant's STN lies within our STN mask at the group level, it is possible, due to the resolution and smoothing, that signal outside of the STN was included, as well.

At a computational level, although we investigated here the neural correlates of decision threshold adjustment as a function of reinforcement conflict, it is not always clear that one would want to increase the threshold with conflict. Indeed, in the extreme case where there is no evidence for one option over the other—either they have the same known values, or they are both completely unknown—it would be maladaptive to have a large decision threshold. In such cases an “urgency signal” may be recruited to reduce the threshold with time (Cisek et al., 2009). Although this is typically considered an active process, which builds up to reduce the threshold, it can also be implemented by dissipation of an active process that raises the threshold. Indeed, in neural circuit models, while STN activity rises initially to raise thresholds, this activity subsides with time leading to a collapsing decision threshold (Ratcliff and Frank, 2012; Wiecki and Frank, 2013). Future work is needed to assess the degree to which collapsing thresholds can account for choice data during learning, and to address the form of a dynamic threshold model that is adaptive for different levels of conflict, to optimize the cost/benefit tradeoff.