Abstract
Over 90 years ago, anatomists noted the cortex is thinner in sulci than gyri, suggesting that development may occur on a fine scale driven by local topology. However, studies of brain development in youth have focused on describing how cortical thickness varies over large-scale functional and anatomic regions. How the relationship between thickness and local sulcal topology arises in development is still not well understood. Here, we investigated the spatial relationships between cortical thickness, folding, and underlying white matter organization to elucidate the influence of local topology on human brain development. Our approach included using both T1-weighted imaging and diffusion tensor imaging (DTI) in a cross-sectional sample of 932 youths ages 8–21 studied as part of the Philadelphia Neurodevelopmental Cohort. Principal components analysis revealed separable development-related processes of regionally specific nonlinear cortical thickening (from ages 8–14) and widespread linear cortical thinning that have dissociable relationships with cortical topology. Whereas cortical thinning was most prominent in the depths of the sulci, early cortical thickening was present on the gyri. Furthermore, decline in mean diffusivity calculated from DTI in underlying white matter was correlated with cortical thinning, suggesting that cortical thinning is spatially associated with white matter development. Spatial permutation tests were used to assess the significance of these relationships. Together, these data demonstrate that cortical remodeling during youth occurs on a local topological scale and is associated with changes in white matter beneath the cortical surface.
Keywords: cortex, cortical thickness, development, diffusion imaging, MRI, white matter
Introduction
The human cortex is among the most highly folded of all species, allowing a massive expansion of surface area (Van Essen, 1997; Zilles et al., 2013). Importantly, the cortex undergoes a protracted course of postnatal development during childhood and young adulthood, with cortical thinning occurring after ages 8–10 (Giedd et al., 1999; Sowell et al., 2004; Raznahan et al., 2011). This may result from white matter expansion that occurs because of ongoing myelination, resulting in a change in tissue classification (Paus et al., 2001; Paus, 2005; Alemán-Gómez et al., 2013); thinning may also occur as a result of a reduction in synaptic density (Huttenlocher and Dabholkar, 1997). Prior research documents substantial regional heterogeneity in cortical maturation and emphasizes correspondence with large-scale functional neuroanatomy (Sowell et al., 2004; Shaw et al., 2008). However, cortical development may also occur on a finer scale that is based on topological patterns of cortical folding. Almost 90 years ago, von Economo (1925) noted that cortical thickness “is reduced by about 50 per cent in passing from the crown of a gyrus, where it is thickest, to the floor of the furrow.” This relationship was confirmed in contemporary studies in adults using structural MRI (Fischl and Dale, 2000). However, it remains unknown how developmental changes in thickness are related to topological location on the cortical sheet. Describing how such local variations in cortical development occur is fundamental to understanding both normal and abnormal brain development, as differences in cortical thickness and folding patterns are widely documented in neuropsychiatric disorders (White et al., 2003; Shaw et al., 2012).
Two recent studies investigated developmental changes in patterns of cortical folding and described a process of cortical flattening whereby sulci become both wider and shallower (Alemán-Gómez et al., 2013; Klein et al., 2014). Such a process may be attributed to white matter expansion, but few investigations have directly examined the relationship between developmental changes in cortical thickness, underlying white matter, and surface topology. This is likely caused by three factors. First, the most common unit of analysis has been functional, atlas-based, or lobar subdivisions, which ignore topological patterns and average across gyri and sulci. Second, to increase statistical power, smaller studies often use large smoothing kernels that inevitably blur data across finer-scale gyral and sulcal boundaries. Finally, as measures of thickness and topology are both nonindependent and spatially autocorrelated, traditional statistical techniques are inadequate for hypothesis testing.
Here we investigate how age-related changes in cortical thickness and underlying white matter diffusivity are linked to local cortical topology in a large sample of youth imaged as part of the Philadelphia Neurodevelopmental Cohort (PNC). Our analysis includes a novel application of permutation-based statistical techniques adapted from microscopy research (Dunn et al., 2011). As described below, results provide evidence for dissociable patterns of cortical development based on local topology that are associated with changes in underlying white matter.
Materials and Methods
Subjects.
Subjects included 932 youths (504 female) ages 8–21 (mean, 14.8 years; SD, 3.6) of mixed race (405 white; 405 black; 122 other) who completed neuroimaging as part of the PNC. As described previously (Satterthwaite et al., 2014a), the PNC is a collaboration between the Brain Behavior Laboratory at the University of Pennsylvania (Penn) and the Center for Applied Genomics at the Children's Hospital of Philadelphia (CHOP). The Institutional Review Boards of both Penn and CHOP approved all study procedures. Of the initial 1445 subjects who completed imaging as part of this study, 332 subjects were excluded because of a history that suggested potential abnormalities in brain development. Specifically, subjects were excluded because of a history of medical problems that may affect the brain (n = 166), a history of inpatient psychiatric hospitalization (n = 51), or current use of a potentially psychotropic medication (n = 165). An additional 239 subjects were excluded as part of image quality assurance (QA) procedures (see below), yielding the 932 subjects included in the present analysis. Many subjects were excluded because of multiple criteria.
Image acquisition.
All data were collected on the same 3T Siemens TIM Trio whole-body scanner. Acquisition details are as described previously (Satterthwaite et al., 2014a). Briefly, a magnetization-prepared, rapid acquisition gradient-echo (MPRAGE) T1-weighted structural image was acquired, using the following parameters: TR, 1810 ms; TE, 3.51 ms; FOV, 180 × 240 mm; matrix, 256 × 192; 160 slices; TI, 1100 ms; flip angle, 9°; effective voxel resolution, 0.9 × 0.9 × 1 mm. Diffusion tensor imaging (DTI) used a four-lobed diffusion encoding gradient scheme combined with a 90 × 180 × 180 spin-echo sequence designed to minimize eddy-current artifacts (Reese et al., 2003), using the following parameters: FOV, 240 × 240 mm; matrix, 128 × 128 × 70; 64 diffusion-weighted directions; b = 1000 s/mm2; seven scans with b = 0 s/mm2; voxel resolution, 1.875 × 1.875 × 2.
Image processing.
Cortical reconstruction of the T1 image was performed for all subjects using FreeSurfer version 5.0.0 (Fischl, 2012). The FreeSurfer processing pipeline includes registration to a template, intensity normalization, gray and white matter segmentation, and tessellation of the gray matter/CSF and white/gray matter boundaries (Dale et al., 1999); cortical surfaces are inflated and normalized to a template via a spherical registration. Cortical thickness is measured as the shortest distance between the pial and the white matter tessellated surfaces (Dale et al., 1999). For sulcal depth, regions that move outward during inflation are positive and represent the depths of sulci, and regions that move inward are negative and represent the height of gyri (Fischl et al., 1999).
FMRIB Software Library's (FSL) Diffusion Toolkit was used to correct head motion and eddy-current effects, calculate the diffusion tensor, identify the eigenvalues of the tensor (λ1, λ2, λ3), and estimate mean diffusivity (MD; Smith et al., 2007). DTI was available in a subset of 740 subjects (415 female; 326 White; 320 Black; 94 other) ages 8–21 (mean, 15.34 years; SD, 3.28). Subjects' MD images were registered to the MPRAGE using boundary-based registration (Greve and Fischl, 2009). To examine the organization of white matter underlying the cortex, MD estimates were sampled from a depth of half of the cortical thickness beneath the gray/white junction. A depth proportional to the thickness was implemented as a way to account for changes in head size and cortical thickness that occur in this age range. MD describes the degree of unconstrained diffusion of water in all directions for a given volume (Jones et al., 2013). We chose to examine MD (instead of fractional anisotropy) as MD has the advantage of being a valid measurement in distal white matter underneath the cortical surface (Pierpaoli et al., 1996).
As part of group-level analyses, all cortical measures were resampled to the fsaverage5 atlas, which is composed of 10,241 vertices per hemisphere. A 10 mm FWHM surface-based smoothing kernel was applied before principal components analysis and mass-univariate models. However, for average sulcal depth, average MD, and the age correlation maps of these measures used in spatial correlation analyses, no smoothing was used to reduce autocorrelation among surface measurements that limits the ability to examine the fine topological scale.
Reconstruction quality assurance.
To maintain high-quality data despite the large sample size, a rigorous quality assurance process was performed. In this process, nine measures were evaluated for outlying values in excess of 2 SDs from the mean and flagged for detailed review if that threshold was met on any measure. These included five global measurements of mean cortical thickness, total surface area, cortical and subcortical gray matter volumes, and white matter volume. In addition, the number of outliers in mean thickness for all regions of the Desikan–Killiany atlas was calculated. Subjects were flagged for further review if they had high numbers (+2 SDs) of regional outliers. The same procedure was used for differences in laterality defined as . The last two measures used to evaluate image quality were the mean of the contrast-to-noise ratio of gray/white matter and gray matter/CSF as well as white matter signal-to-noise ratio in the unprocessed image. Flagged subjects were evaluated manually for inclusion or exclusion; no manual edits were performed. As part of this process, 315 images were flagged, and 239 subjects were excluded from analysis because of reconstruction errors.
DTI quality assurance.
All diffusion tensor imaging underwent a two-stage process of quality assurance. First, scan parameters (e.g., TR, number of directions) were validated, and only individuals with identical parameters were included. Second, manual QA was performed on all subjects completing DTI (n = 1285); images were categorized as “poor,” “good,” or “excellent” by a trained rater blind to age and gender. The trained rater evaluated each individual diffusion-weighted image (DWI; 64 images per subject) for all subjects. Poor scans included images with obvious motion and artifact on >20% of the individual DWIs. Good scans included images with little artifact, and no more than 10% of individual DWIs could be affected. Excellent scans were free of any visible artifact. All scans of poor quality were excluded from analysis. We are currently in the process of developing automatic QA procedures based on this manual QA (D. R. Roalf, M. A. Elliott, M. Quarmley, S. N. Vandekar, K. Ruparel, K. Prabhakaran, C. T. Jackson, R. Verma, H. Hakonarson, R. C. Gur, and R. E. Gur, unpublished observations).
Mass-univariate linear and nonlinear effects of age.
We examined linear effects of age-related changes on thickness and MD using mass-univariate regression analyses. However, as previous work has demonstrated nonlinear developmental effects (Giedd et al., 1999; Gogtay et al., 2004; Giedd and Rapoport, 2010), we additionally tested for the presence of nonlinear effects of age using penalized splines within a generalized additive model (GAM; Wood, 2011; R Core Team, 2012; Satterthwaite et al., 2014b). In this case, a GAM was fit at each vertex to test for the presence of a nonlinear relationship above and beyond the presence of any linear relationship. The parameter estimates for the nonlinear effects were fit as random effects and tested using simulation-based likelihood ratio tests with 500,000 simulations (Scheipl et al., 2008; Wood, 2011; R Core Team, 2012). In each analysis, sex, race, and intracranial volume were included as covariates. Intracranial volume was included to ensure that any observed age-related effects were not simply attributable to a global change in head size.
Principal components analysis.
Principal components analysis (PCA) was used to provide a concise multivariate summary of observed mass-univariate effects, thus facilitating subsequent analyses of the relationship to sulcal depth. PCA is a multivariate dimension reduction method that rotates the observed data to a lower dimensional, orthogonal basis that maximizes the amount of variance explained in the data (Jolliffe, 2005). For each component, PCA yields a principal score for each subject and a principal loading for every vertex. Before performing PCA, the effects age, sex, and intracranial volume were removed, and the data were normalized. PCA was performed using the svd function in R (R Core Team, 2012). A GAM was used to model the relationship between each component's principal scores and age. To estimate confidence intervals for the fitted trajectories of the GAMs, we repeated the entire PCA and GAM fitting procedure in 5000 bootstrap samples. For each bootstrap, a sample of 932 subjects was selected with replacement. A PCA was then performed in the new sample as described above. The principal scores for the new sample were then fit in a GAM with age as the independent variable, and the fitted trajectory was extracted and stored. Ninety-five percent confidence intervals were estimated by taking the 2.5 and 97.5% quantiles of the bootstrapped fitted values.
Relationships between cortical measures.
Characterizing relationships across the surface of the cortex presents two methodological issues that are not usually considered in neuroimaging. The first is that the spatial autocorrelation of each measure across the cortical surface makes estimating the true degrees of freedom for conventional hypothesis tests difficult and potentially inaccurate, as observations are not independent. The second is that the number of observations can be increased or decreased arbitrarily through resampling the surface. Thus, any negligible correlation between cortical measures across vertices could be rendered statistically significant by resampling the surface to a progressively larger number of vertices.
In microscopy, the null distribution from spatially correlated measures is estimated from “pairs of images that are out of registration with one another” (Dunn et al., 2011). This approach allows for estimation of the null distribution in the case where there is an indefinite number of points on the surface and spatial autocorrelation is present. Here, Spearman's correlation coefficient was calculated for each pair of cortical measures, considering the 20,482 vertices on the cortical surface as observations. After projecting each measure onto a sphere, permutation analyses were run by randomly rotating one of the spheres so the surfaces were not physiologically aligned and computing Spearman's correlation to estimate the null distribution.
Details of spatial permutation testing.
In each permutation, one point from each sphere was randomly selected, and one sphere was rotated so the two points are aligned. After this initial rotation, vertices that are approximately parallel to the axis of rotation have moved very little, so a second rotation is applied. For the second rotation, a neighbor of each of the two vertices selected above was randomly chosen, and the sphere was rotated around the vertices that were aligned in the first rotation (Fig. 1). Because of the configuration of vertices on the sphere, after rotation there are vertices in the rotated data that are not perfectly aligned with the original data. Inverse distance weighting (IDW) was used to interpolate the position of the values on the rotated surface to match the location of points in the original rotated data. IDW is a multivariate interpolation technique frequently used with spatial data (Shepard, 1968; Franke, 1982). Various formulations of inverse distance weighting have been developed (Franke, 1982); for simplicity and ease of computation, we implemented the original formulation described by Shepard (1968) using the nearest six vertices. Thus, the formula to estimate the value vr(x) of the rotated data at a point xϵℝ3 on the surface of the original data is as follows:
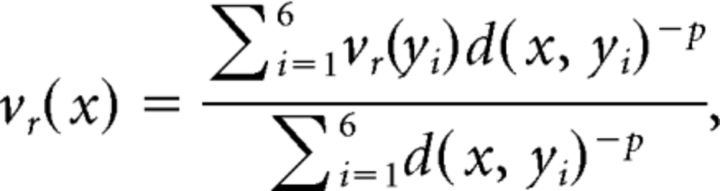 |
where vr(yi) is the value of the data at vertex location yi in the rotated data; d is a distance metric; and, typically, p = 2 (Franke, 1982). We implemented the metric d(x1, x2) = to measure the geodesic distance between points across the surface of the unit sphere. This is to ensure that nearest points are only found across the surface of the sphere, rather than measuring Euclidian distances through the sphere. After interpolation, Spearman's correlation coefficient was computed, and the process was repeated over 10,000 random permutations to estimate the null distribution.
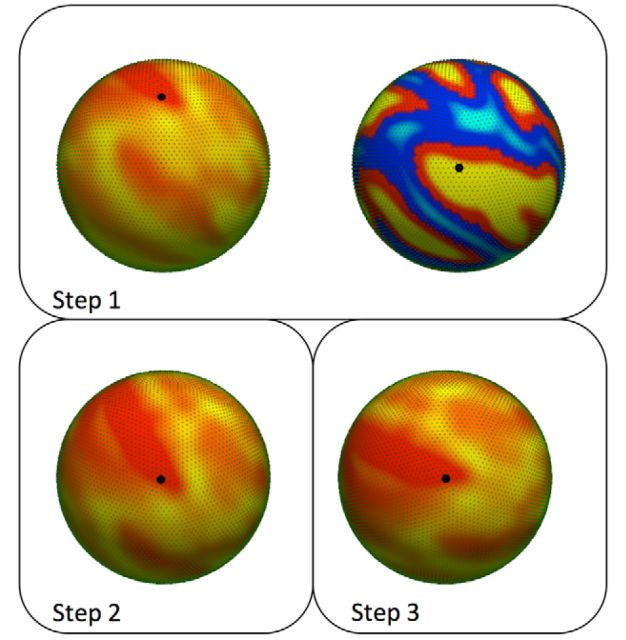
Figure 1.
A schematic of how surfaces are rotated for spatial permutation tests. First, a random vertex is selected on the surface of each sphere (Step 1). Next, one of the surfaces is rotated so the vertices on each sphere are aligned (Step 2). After the first rotation, the sphere is then rotated again about the randomly selected vertex (Step 3). After rotation, points are then interpolated to the original space, and Spearman's correlation is computed. This process is repeated 10,000 times to generate a null distribution.
Results
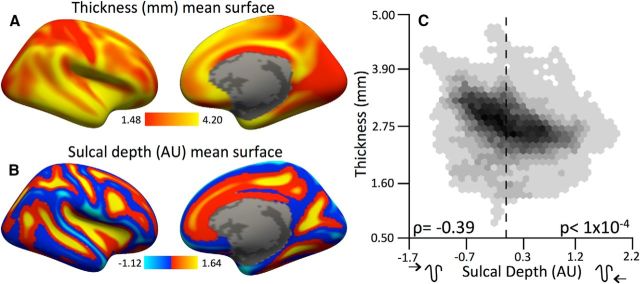
Mean cortical maps were created to summarize the spatial characteristics of cortical thickness and sulcal depth (Fig. 2A, Table 1). This analysis corroborated the observation that cortical thickness is inversely related to sulcal depth (Fig. 2B; ρ = −0.35, false-discovery rate (FDR) corrected p ≤ 0.0001).
Figure 2.
Cortical thickness is related to sulcal depth spatially across the cortex. A, B, Right-hemisphere mean maps for cortical thickness (A) and sulcal depth (B). C, Hexagonal bin plots of the relationships between cortical thickness and sulcal depth across the right and left hemispheres. Thickness declines linearly with sulcal depth, indicating that vertices deeper in sulci are, on average, less thick. Zero is marked by the dashed line. ρ is the Spearman's correlation; p values are FDR corrected across all spatial correlations with a maximum threshold of pFDR = 0.05.
Table 1.
Summary of investigation objectives, methods used, and associated figures
| Objective | Analysis method | Figure number |
|---|---|---|
| Describe spatial relationship between thickness and sulcal depth | Spatial correlation and permutation test | 2 |
| Describe linear age-related effects of thickness | Mass-univariate linear model | 3 |
| Describe nonlinear age-related effects of thickness | Mass-univariate generalized additive model | 4 |
| Summarize development of cortical thickness with multivariate model | Principal components analysis | 5, 6 |
| Describe spatial relationship between age-related change in cortical thickness and sulcal depth | Spatial correlation and permutation test | 7 |
| Describe spatial relationship between MD and sulcal depth | Spatial correlation and permutation test | 8 |
| Describe linear age-related effects of MD | Mass-univariate linear model | 8 |
| Describe spatial relationship between age-related changes in MD and sulcal depth | Spatial correlation and permutation test | 8 |
| Describe spatial relationship between age-related changes in MD and cortical and thickness | Conjunction overlay, spatial correlation, and permutation test | 8 |
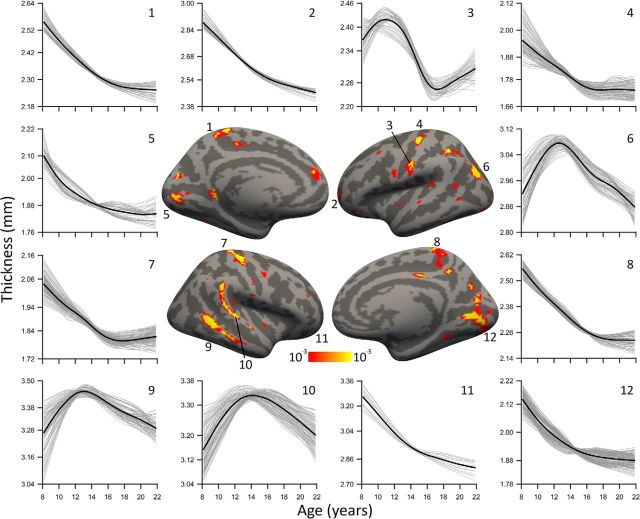
To estimate characteristic development of cortical thickness, we used a combination of linear and nonlinear GAM mass-univariate analyses. As expected, analyses demonstrated a robust linear decline in cortical thickness with age (Fig. 3). Additionally, nonlinear effects were detected by the GAM over and above linear effects across the cortex (Fig. 4). Several nonlinear trajectories in gyral cortex were characterized by an inverted U shape.
Figure 3.
Linear effects of age in cortical thickness. Blue represents decreases with age, and red/yellow represents increases with age. Linear declines of cortical thickness with age were widespread and most robust in dorsolateral prefrontal cortex, frontal pole, superior parietal lobe, precuneus, lingual gyrus, and superior temporal sulcus. Results are first masked with an FDR thresholded at pFDR = 0.05 in each hemisphere.
Figure 4.
Significant nonlinear age trajectories fitted with penalized splines with a GAM. Thin gray lines are vertex trajectories, and the thicker black line is the pointwise mean trajectory of the cluster. Clusters in the left visual cortex and the superior and inferior temporal gyri exhibited quadratic developmental trajectories (6, 9, 10). Peaks in these clusters occurred at ages 12.7, 13.1, and 14.2, respectively. Clusters in visual cortex (5, 12), central gyrus (4, 7), bilateral frontal pole (2, 11), and paracentral gyrus (1, 8) showed nonlinear trajectories that were characterized by faster thinning at younger ages with a reduced slope or flattening at later ages. Surface results are first masked with an FDR threshold at pFDR = 0.05 in each hemisphere and displayed with a minimum uncorrected threshold of p = 10−3.
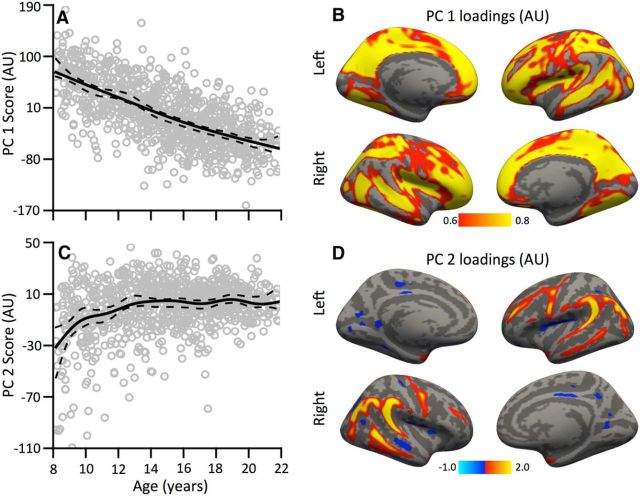
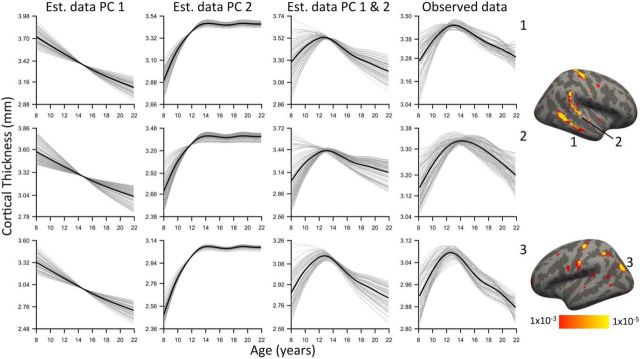
We used PCA to summarize linear and nonlinear effects of cortical thickness within a multivariate framework. Notably, the first two principal scores were highly age related: the first component was associated with a linear thinning of the cortex, whereas the second component demonstrated an early nonlinear increase in thickness between ages 8 and 14 (Fig. 5). The first two components, respectively, explained 15.1 and 2.3% of variance; the third component was unrelated to age and explained <2% variance. Therefore, only the first two components were considered. Vertices with large loadings on the first component (indicating a linear decline in thickness) were strongest in the depths of cortical sulci. In contrast, vertices with large positive principal loadings on the second component (indicating a nonlinear early increase in thickness) were disproportionally located on cortical gyri. Notably, each vertex on the cortex has loadings for both components; the summation of the first two components closely reproduced the observed nonlinear trajectories described by the spline fit of the GAM (Fig. 6).
Figure 5.
Principal component analysis reveals dissociable patterns of cortical development. A, Scores of the first component show a linear decline with age across subjects. B, The associated principal loadings for this component are shown, with greater loading in cortical sulci. C, D, In contrast, the second component shows a nonlinear increase until age 14 (C), with the highest loadings present on cortical gyri (D). In A and C, solid lines are fitted trajectories, and dashed lines are pointwise 95% confidence intervals from 5000 bootstrapped samples.
Figure 6.
Linear combinations of PCA components recreate observed nonlinear developmental effects. Results are plotted within clusters showing significant nonlinearity in the mass-univariate GAM analysis. The first two columns are the estimated cortical thickness trajectories using the first principal component (PC1) and second principal component (PC2). The third column is the pattern of development as estimated by the linear summation of the first two components. The fourth column is the observed data. Correspondence between observed nonlinearities and PCA components suggests that “inverted U” patterns of development may be the result of two distinct processes that were separated by the PCA. Thin gray lines are vertex trajectories, and thicker black lines are mean trajectories as fit by a penalized spline within a GAM.
Because examination of the spatial distribution of age-related effects suggested a relationship to cortical topology, we quantitatively tested how such linear and nonlinear developmental changes summarized by the PCA were related to sulcal depth. We performed spatial permutation tests of the correlation between component loadings and sulcal depth. This analysis revealed that loadings of the first principal component had a positive relationship with sulcal depth (Fig. 7A; ρ = +0.32, pFDR ≤ 0.0001), indicating that cortex in the depths of the sulci show the strongest linear decline in cortical thickness with age. In contrast, loadings of the second principal component had a robust negative relationship to sulcal depth (Fig. 7B; ρ = −0.60, pFDR ≤ 0.0001), indicating that increases in cortical thickness occurred most strongly within gyral cortex. These results provide evidence for dissociable patterns of early nonlinear cortical expansion and protracted linear cortical thinning that are differentially related to local surface topology.
Figure 7.
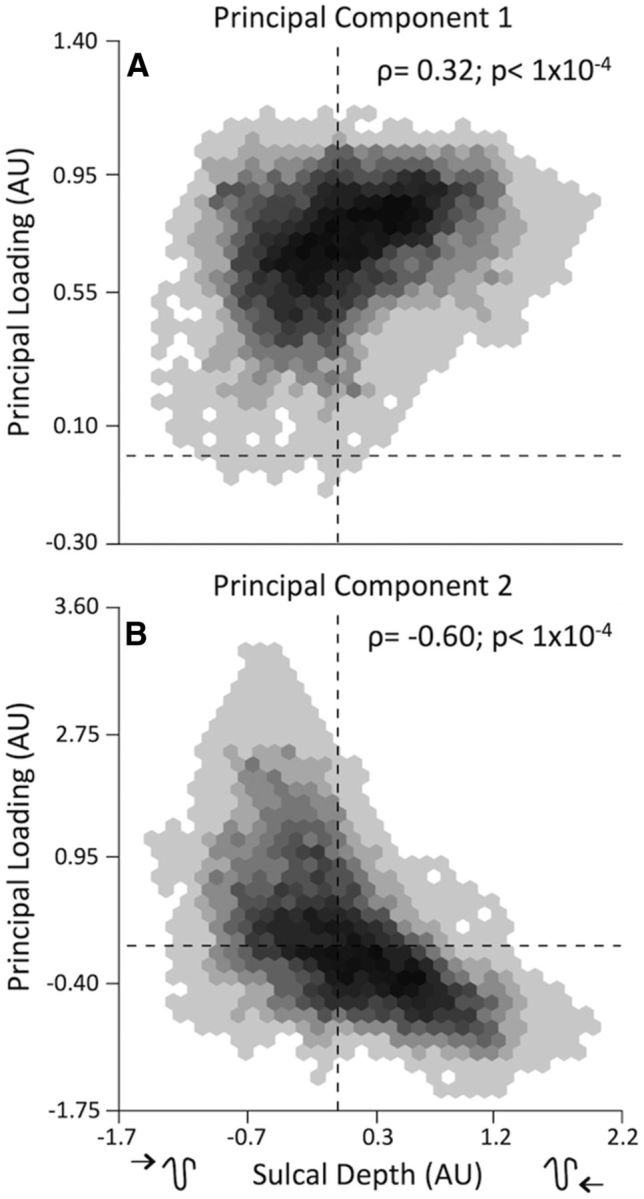
Dissociable developmental trajectories of cortical thickness are inversely related to sulcal depth. A, The first component shows a positive correlation of the principal loadings with sucal depth, indicating that regions deepest in the sulci (positive on x-axis) have greater thinning with age. B, In contrast, the second component has a negative correlation with sulcal depth, indicating that regions on gyri (negative on x-axis) have the strongest effects associated with the nonlinear trajectory of the second component. Note that negative loadings on the principal component represent an inverse of the associated relationship. Zero is marked by dashed lines. ρ is Spearman's correlation; p values are FDR corrected across all spatial correlations with a maximum threshold of pFDR = 0.05.
Based on prior work suggesting a relationship between age-related cortical thinning and white matter development, we examined the topological relationship between age-related changes in subcortical white matter and cortical thickness (Tamnes et al., 2010; Alemán-Gómez et al., 2013). Specifically, we expected that white matter would show the most developmental increase in organization below sulcal pits where the greatest thinning occurs. We found that MD was inversely related to sulcal depth spatially (Fig. 8A,B; ρ = −0.54, pFDR ≤ 0.0001); i.e., higher diffusion was found in gyri than sulci, indicating that the white matter below the surface of sulci is more restrictive to water movement. Age-related differences in MD were negative, widespread, (Fig. 8C), and occurred most strongly in sulci (Fig. 8D; ρ = −0.38, pFDR ≤ 0.0001). Moreover, linear cortical thinning was related to the decline in MD in underlying white matter (Fig. 8E; ρ = 0.31, pFDR ≤ 0.0001). Critically, both linear cortical thinning and decreasing subcortical white matter MD occurred most in the depths of the sulci (Fig. 8F). These results are consistent with a process of white matter expansion that differentially contributes to loss of cortical thickness in the sulci.
Figure 8.
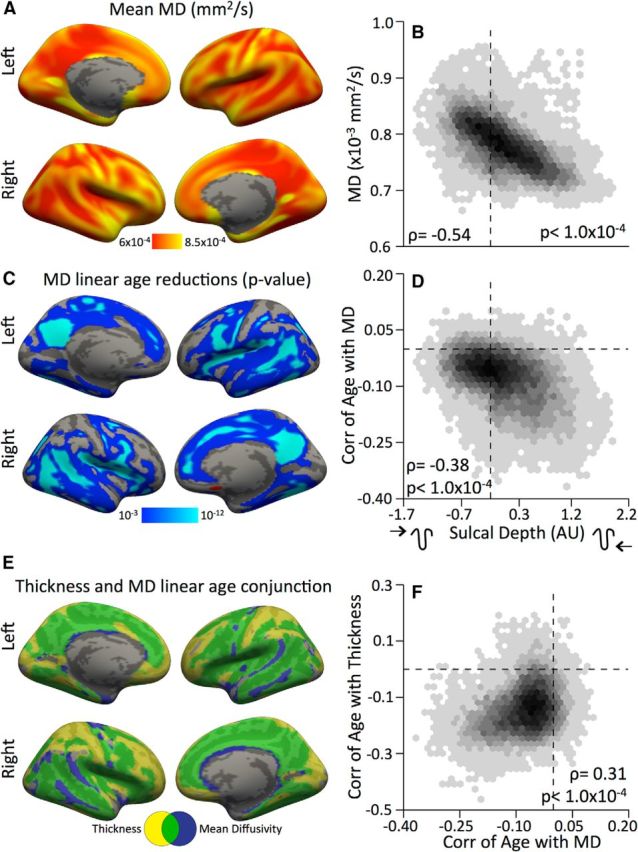
Changes in underlying white matter are related to thinning of sulcal cortex. A, B, Average MD across subjects (A) closely follows patterns of cortical topology (B). C, D, Age-related declines in MD also followed sulcal topology with regions in the sulci showing the strongest linear decline with age. E, Significant age-related reductions in cortical thickness and MD were spatially related and appear to occur most in sulcal regions. Yellow and blue represent significant age-related decreases in thickness and MD, respectively; green represents the overlap. F, Age-related changes in thickness and MD are spatially positively correlated. Zero is marked by dashed lines. All statistical maps are first masked with a threshold pFDR = 0.05 in each hemisphere. To maintain a consistent threshold across images, after FDR thresholding, all images are displayed with a minimum uncorrected threshold of p = 10−3.
Discussion
The striking relationship between cortical thickness and folding was noted 90 years ago by von Economo (1925) and other early anatomists (Thompson, 1900). Here, we provide evidence that this relationship undergoes dynamic maturation in youth and involves two dissociable patterns. Specifically, we demonstrate linear cortical thinning occurs principally in sulci, whereas early nonlinear cortical thickening occurs principally in gyri. Furthermore, data from DTI suggests that cortical thinning in the sulci is associated with increased organization of the underlying white matter. Together, these results demonstrate that the complex process of cortical maturation in youth occurs on a fine scale governed in part by local cortical topology.
Cortical thickness is related to sulcal depth in youth
Over 80 years after the initial discovery that the human cortex is thicker on the crowns of gyri than the depths of the sulci, Fischl and Dale (2000) confirmed this relationship in adults using structural MRI. Here we demonstrate that this relationship is present during youth. Animal and postmortem tissue research has postulated that the relationship between cortical thickness and sulcal depth arises as the cortex gyrifies during prenatal and early postnatal development (Kriegstein et al., 2006; Miller et al., 2012). During this process, the developing gyral cortex expands more rapidly than sulcal cortex, producing a common pattern of gyrification across individuals (Xu et al., 2010; Nie et al., 2011; Ronan et al., 2014). This model is supported by research showing that the tangential migration of subclasses of neurons from the subventricular zone along radial glia (Kolasinski et al., 2013) occurs robustly beneath sites that become gyral cortex (Britanova et al., 2006; Kriegstein et al., 2006; Reillo et al., 2011). Our results are consistent with such developmental accounts, whereby increased thickness in gyri relative to sulci may be related to greater neuronal proliferation, yielding a relative abundance of gray matter. As discussed below, our findings also show that such topological variation in cortical thickness continues to evolve through childhood, adolescence, and early adulthood.
Dissociable patterns of cortical development are related to cortical topology
In addition to early developmental processes that give rise to gyrification, the human cortex undergoes protracted development through young adulthood (Huttenlocher and Dabholkar, 1997; Levitt, 2003), characterized principally by a decline in cortical gray matter and an increase in white matter volume. However, a wealth of neuroimaging studies have demonstrated that this net decline in cortical gray matter volume and thickness has substantial regional variation (Salat et al., 2004). Specifically, late-peaking, inverted-U-shaped trajectories have been found in higher-order frontal, parietal, and temporal association cortex in gray matter volume (Giedd et al., 1999; Gogtay et al., 2004; Lenroot et al., 2007; Giedd and Rapoport, 2010; Raznahan et al., 2011) and thickness (Shaw et al., 2008; Raznahan et al., 2011). We demonstrate that in addition to such large-scale regional differences in development, variation in cortical remodeling occurs on a finer scale.
Critically, our results suggest that two dissociable processes occur in cortical development that vary by topological locations. The first process is a linear decrease in cortical thickness that occurs across most of the cortex throughout youth. Notably, this process has prominent variability and is most robust in the depths of the sulci. In contrast, the second more spatially localized process shows early nonlinear thickening that occurs between ages 8 and 14 principally within gyral temporal, parietal, and frontal cortex. In tandem, these two processes produce increasing divergence between the thickness of gyral and sulcal cortex with age.
These results may contribute to previous findings of developmental changes in cortical gyrification, which has been shown to decline in development (Raznahan et al., 2011; Klein et al., 2014). This decline is associated with reduced surface area as sulci become wider and shallower (Alemán-Gómez et al., 2013). Our data may be consistent with this account, to the degree that preferential myelination of white matter occurs in sulci, expanding them outward and reducing overall depth (Alemán-Gómez et al., 2013).
Cortical thinning in sulci is associated with changes in underlying white matter organization
The presence of such dissociable processes of cortical development suggests divergent neurobiological mechanisms. Investigators attribute cortical thinning to myelination extending into the cortex (Sowell et al., 2004; Lenroot et al., 2007) and also to expanding white matter volume stretching the cortex over a greater area (Seldon, 2005). Here results from DTI show that diffusivity tends to be lower in white matter underlying sulcal cortex. Importantly, changes in diffusivity are spatially correlated with cortical thinning, which is also maximal in sulci. When considered jointly, this suggests that rapid cortical thinning occurring in sulcal cortex is likely caused by ongoing myelination into cortical gray matter (Beaulieu, 2002; Sowell et al., 2004; Lenroot et al., 2007; Feldman et al., 2010; Nie et al., 2011; Taki et al., 2013). The observed results are consistent with results from recent studies of gray matter myelin mapping using T1/T2 MRI, which showed that thin sulcal cortex has higher myelin content (Glasser and Van Essen, 2011). In addition, Grydeland et al. (2013) showed that T1/T2 myelin ratios follow inverse lifespan trajectories to MD measures. Future research could examine the relationship of such findings with cortical topology.
It should be noted that there are exceptions to the relationship of development-related changes in thickness and diffusivity: marked age-related differences in thickness occur in frontal and parietal cortex without the same decline in diffusivity of the underlying white matter. Intriguingly, these regions are also the last to myelinate in development (Miller et al., 2012; Buckner and Krienen, 2013), and in vivo myelin-mapping techniques have also shown that higher-order cortex is less heavily myelinated. This suggests that a different process may be driving cortical thinning in these brain areas. Although further investigation is warranted, thinning in such regions may be attributable to global hemispheric inflation of white matter (Paus, 2010), which stretches the entire cortical sheet over greater areas (Seldon, 2005). It is also possible that thinning in these regions may be attributable in part to synaptic pruning or reductions in neuropil (Huttenlocher and Dabholkar, 1997).
Cortical thickening may be caused by ongoing growth
Compared with the potential mechanisms of cortical thinning, accounts of neurodevelopmental processes that may be driving the thickening of gyral cortex are less clear. Prior studies that have observed developmental increases in cortical thickness have speculatively associated such results with a second wave of synaptogenesis or increases in neuropil (Giedd et al., 1999). Research shows increases in gray matter are associated with synaptic development in neonates (Huttenlocher and Dabholkar, 1997; Gilmore et al., 2007); possibly, a similar process is active here.
As suggested by Sowell et al. (2004), the observed cortical thickening may be tied to the large improvements in cognitive capability that occurs during the critical developmental epoch spanning adolescence (Brown et al., 2005; Casey et al., 2005; Gur et al., 2012). The potential functional relevance of gyral thickening is supported by research demonstrating that cellular cytoarchitecture aligns well with macroscopic cortical topology (Fischl et al., 2008).
Limitations, conclusions, and future directions
Certain limitations of this study should be noted. Although this study benefitted from a large sample, it is cross-sectional. Longitudinal designs are necessary to track developmental trajectories in detail (Kraemer et al., 2000). Our adaptation of techniques derived from microscopy research allowed us to relate topology and thickness on a vertex-wise basis across the entire cortex. However, the spatial resolution of structural MRI in the current study was limited to ∼0.81 mm3 voxels. Future investigations using higher-resolution T1 MRI and higher-resolution multishell diffusion sequences may permit a more detailed assessment of topological relationships (O'Donnell and Westin, 2011; Scherrer et al., 2013).
These limitations notwithstanding, the present results indicate that age-associated differences in cortical thickness reflect two dissociable developmental processes that are anatomically distinct in their relationship to cortical folding. These effects likely relate to separate neurodevelopmental events, with white matter organization and expansion driving the thinning of sulcal cortex and synaptogenesis or increases in neuropil causing thickening in gyral cortex. The results show that the cortex continues to dynamically remodel within topological constraints through childhood, adolescence, and young adulthood.
In addition to providing information critical for understanding normal development of the human brain, these findings may have clinical relevance for diverse neuropsychiatric conditions that are associated with abnormal patterns of cortical change, including attention deficit hyperactivity disorder (Shaw et al., 2012), schizophrenia (Thompson et al., 2001; Steen et al., 2006; Csernansky et al., 2008; Voineskos et al., 2010), and Williams syndrome (Kippenhan et al., 2005; Meda et al., 2012). Understanding how abnormal development occurs on a local topological scale may provide new insights into describing the pathogenesis of neurodevelopmental disorders.
Footnotes
This work was supported by National Institute of Mental Health RC2 Grants MH089983 and MH089924. Support for developing statistical analyses (to S.N.V., R.T.S., and T.D.S.) was provided by a seed grant from the Center for Biomedical Computing and Image Analysis at the University of Pennsylvania. T.D.S. was supported by Grant K23MH098130 from the National Institute of Mental Health and the Marc Rapport Family Investigator grant through the Brain and Behavior Foundation. R.T.S. was supported by Grant R01NS085211 from the National Institute of Neurological Disorders and Stroke. D.R.R. was supported by Grant K01MH102609 from the National Institute of Mental Health. D.H.W. was supported by Grant R01MH101111 from the National Institute of Mental Health and the Sidney R. Baer, Jr. Foundation through the Brain and Behavior Foundation. S.N.V. was supported by Grant T32MH065218-11 from the National Institute of Mental Health. We thank Madhura Ingalhalikar and Alex Smith for assistance with data processing. We also thank the acquisition and recruitment team: Jeff Valdez, Raphael Gerraty, Marisa Riley, Jack Keefe, Elliott Yodh, and Rosetta Chiavacci. We thank Chad Jackson for data management. We thank Scott Troyan for assistance with figures. We sincerely thank Fabian Scheipl for help on hypothesis testing in general additive models. We thank Aaron Alexander-Bloch and Phil Reiss for advice on implementation of the general additive model.
The authors declare no competing financial interests.
References
- Alemán-Gómez Y, Janssen J, Schnack H, Balaban E, Pina-Camacho L, Alfaro-Almagro F, Castro-Fornieles J, Otero S, Baeza I, Moreno D, Bargalló N, Parellada M, Arango C, Desco M. The human cerebral cortex flattens during adolescence. J Neurosci. 2013;33:15004–15010. doi: 10.1523/JNEUROSCI.1459-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaulieu C. The basis of anisotropic water diffusion in the nervous system–a technical review. NMR Biomed. 2002;15:435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- Britanova O, Alifragis P, Junek S, Jones K, Gruss P, Tarabykin V. A novel mode of tangential migration of cortical projection neurons. Dev Biol. 2006;298:299–311. doi: 10.1016/j.ydbio.2006.06.040. [DOI] [PubMed] [Google Scholar]
- Brown TT, Lugar HM, Coalson RS, Miezin FM, Petersen SE, Schlaggar BL. Developmental changes in human cerebral functional organization for word generation. Cereb Cortex. 2005;15:275–290. doi: 10.1093/cercor/bhh129. [DOI] [PubMed] [Google Scholar]
- Buckner RL, Krienen FM. The evolution of distributed association networks in the human brain. Trends Cogn Sci. 2013;17:648–665. doi: 10.1016/j.tics.2013.09.017. [DOI] [PubMed] [Google Scholar]
- Casey BJ, Galvan A, Hare TA. Changes in cerebral functional organization during cognitive development. Curr Opin Neurobiol. 2005;15:239–244. doi: 10.1016/j.conb.2005.03.012. [DOI] [PubMed] [Google Scholar]
- Csernansky JG, Gillespie SK, Dierker DL, Anticevic A, Wang L, Barch DM, Van Essen DC. Symmetric abnormalities in sulcal patterning in schizophrenia. Neuroimage. 2008;43:440–446. doi: 10.1016/j.neuroimage.2008.07.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis: I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Dunn KW, Kamocka MM, McDonald JH. A practical guide to evaluating colocalization in biological microscopy. Am J Physiol Cell Physiol. 2011;300:C723–C742. doi: 10.1152/ajpcell.00462.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman HM, Yeatman JD, Lee ES, Barde LH, Gaman-Bean S. Diffusion tensor imaging: a review for pediatric researchers and clinicians. J Dev Behav Pediatr. 2010;31:346–356. doi: 10.1097/DBP.0b013e3181dcaa8b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B. FreeSurfer. Neuroimage. 2012;62:774–781. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci U S A. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis: II: inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fischl B, Rajendran N, Busa E, Augustinack J, Hinds O, Yeo BT, Mohlberg H, Amunts K, Zilles K. Cortical folding patterns and predicting cytoarchitecture. Cereb Cortex. 2008;18:1973–1980. doi: 10.1093/cercor/bhm225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke R. Scattered data interpolation: tests of some methods. Math Comput. 1982;38:181–200. doi: 10.1090/S0025-5718-1982-0637296-4. [DOI] [Google Scholar]
- Giedd JN, Rapoport JL. Structural MRI of pediatric brain development: what have we learned and where are we going? Neuron. 2010;67:728–734. doi: 10.1016/j.neuron.2010.08.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giedd JN, Blumenthal J, Jeffries NO, Castellanos FX, Liu H, Zijdenbos A, Paus T, Evans AC, Rapoport JL. Brain development during childhood and adolescence: a longitudinal MRI study. Nat Neurosci. 1999;2:861–863. doi: 10.1038/13158. [DOI] [PubMed] [Google Scholar]
- Gilmore JH, Lin W, Prastawa MW, Looney CB, Vetsa YS, Knickmeyer RC, Evans DD, Smith JK, Hamer RM, Lieberman JA, Gerig G. Regional gray matter growth, sexual dimorphism, and cerebral asymmetry in the neonatal brain. J Neurosci. 2007;27:1255–1260. doi: 10.1523/JNEUROSCI.3339-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Van Essen DC. Mapping human cortical areas in vivo based on myelin content as revealed by T1- and T2-weighted MRI. J Neurosci. 2011;31:11597–11616. doi: 10.1523/JNEUROSCI.2180-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gogtay N, Giedd JN, Lusk L, Hayashi KM, Greenstein D, Vaituzis AC, Nugent TF, 3rd, Herman DH, Clasen LS, Toga AW, Rapoport JL, Thompson PM. Dynamic mapping of human cortical development during childhood through early adulthood. Proc Natl Acad Sci U S A. 2004;101:8174–8179. doi: 10.1073/pnas.0402680101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greve DN, Fischl B. Accurate and robust brain image alignment using boundary-based registration. Neuroimage. 2009;48:63–72. doi: 10.1016/j.neuroimage.2009.06.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grydeland H, Walhovd KB, Tamnes CK, Westlye LT, Fjell AM. Intracortical myelin links with performance variability across the human lifespan: results from T1- and T2-weighted MRI myelin mapping and diffusion tensor imaging. J Neurosci. 2013;33:18618–18630. doi: 10.1523/JNEUROSCI.2811-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gur RC, Richard J, Calkins ME, Chiavacci R, Hansen JA, Bilker WB, Loughead J, Connolly JJ, Qiu H, Mentch FD, Abou-Sleiman PM, Hakonarson H, Gur RE. Age group and sex differences in performance on a computerized neurocognitive battery in children age 8–21. Neuropsychology. 2012;26:251–265. doi: 10.1037/a0026712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huttenlocher PR, Dabholkar AS. Regional differences in synaptogenesis in human cerebral cortex. J Comp Neurol. 1997;387:167–178. doi: 10.1002/(SICI)1096-9861(19971020)387:2<167::AID-CNE1>3.0.CO%3B2-Z. [DOI] [PubMed] [Google Scholar]
- Jolliffe I. Principal component analysis. Wiley Online Library. 2005 doi: 10.1002/0470013192.bsa501. [DOI] [Google Scholar]
- Jones DK, Knösche TR, Turner R. White matter integrity, fiber count, and other fallacies: the do's and don'ts of diffusion MRI. Neuroimage. 2013;73:239–254. doi: 10.1016/j.neuroimage.2012.06.081. [DOI] [PubMed] [Google Scholar]
- Kippenhan JS, Olsen RK, Mervis CB, Morris CA, Kohn P, Meyer-Lindenberg A, Berman KF. Genetic contributions to human gyrification: sulcal morphometry in Williams syndrome. J Neurosci. 2005;25:7840–7846. doi: 10.1523/JNEUROSCI.1722-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein D, Rotarska-Jagiela A, Genc E, Sritharan S, Mohr H, Roux F, Han CE, Kaiser M, Singer W, Uhlhaas PJ. Adolescent brain maturation and cortical folding: evidence for reductions in gyrification. PLoS One. 2014;9:e84914. doi: 10.1371/journal.pone.0084914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolasinski J, Takahashi E, Stevens AA, Benner T, Fischl B, Zöllei L, Grant PE. Radial and tangential neuronal migration pathways in the human fetal brain: anatomically distinct patterns of diffusion MRI coherence. Neuroimage. 2013;79:412–422. doi: 10.1016/j.neuroimage.2013.04.125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraemer HC, Yesavage JA, Taylor JL, Kupfer D. How can we learn about developmental processes from cross-sectional studies, or can we? Am J Psychiatry. 2000;157:163–171. doi: 10.1176/appi.ajp.157.2.163. [DOI] [PubMed] [Google Scholar]
- Kriegstein A, Noctor S, Martínez-Cerdeño V. Patterns of neural stem and progenitor cell division may underlie evolutionary cortical expansion. Nat Rev Neurosci. 2006;7:883–890. doi: 10.1038/nrn2008. [DOI] [PubMed] [Google Scholar]
- Lenroot RK, Gogtay N, Greenstein DK, Wells EM, Wallace GL, Clasen LS, Blumenthal JD, Lerch J, Zijdenbos AP, Evans AC, Thompson PM, Giedd JN. Sexual dimorphism of brain developmental trajectories during childhood and adolescence. Neuroimage. 2007;36:1065–1073. doi: 10.1016/j.neuroimage.2007.03.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt P. Structural and functional maturation of the developing primate brain. J Pediatr. 2003;143:S35–S45. doi: 10.1067/S0022-3476(03)00400-1. [DOI] [PubMed] [Google Scholar]
- Meda SA, Pryweller JR, Thornton-Wells TA. Regional brain differences in cortical thickness, surface area and subcortical volume in individuals with Williams syndrome. PLoS One. 2012;7:e31913. doi: 10.1371/journal.pone.0031913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller DJ, Duka T, Stimpson CD, Schapiro SJ, Baze WB, McArthur MJ, Fobbs AJ, Sousa AM, Šestan N, Wildman DE, Lipovich L, Kuzawa CW, Hof PR, Sherwood CC. Prolonged myelination in human neocortical evolution. Proc Natl Acad Sci U S A. 2012;109:16480–16485. doi: 10.1073/pnas.1117943109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nie J, Guo L, Li K, Wang Y, Chen G, Li L, Chen H, Deng F, Jiang X, Zhang T, Huang L, Faraco C, Zhang D, Guo C, Yap PT, Hu X, Li G, Lv J, Yuan Y, Zhu D, et al. Axonal fiber terminations concentrate on gyri. Cereb Cortex. 2011;22:2831–2839. doi: 10.1093/cercor/bhr361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Donnell LJ, Westin CF. An introduction to diffusion tensor image analysis. Neurosurg Clin N Am. 2011;22:185–196. viii. doi: 10.1016/j.nec.2010.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paus T. Mapping brain maturation and cognitive development during adolescence. Trends Cogn Sci. 2005;9:60–68. doi: 10.1016/j.tics.2004.12.008. [DOI] [PubMed] [Google Scholar]
- Paus T. Growth of white matter in the adolescent brain: myelin or axon? Brain Cogn. 2010;72:26–35. doi: 10.1016/j.bandc.2009.06.002. [DOI] [PubMed] [Google Scholar]
- Paus T, Collins DL, Evans AC, Leonard G, Pike B, Zijdenbos A. Maturation of white matter in the human brain: a review of magnetic resonance studies. Brain Res Bull. 2001;54:255–266. doi: 10.1016/S0361-9230(00)00434-2. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G. Diffusion tensor MR imaging of the human brain. Radiology. 1996;201:637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
- Raznahan A, Shaw P, Lalonde F, Stockman M, Wallace GL, Greenstein D, Clasen L, Gogtay N, Giedd JN. How does your cortex grow? J Neurosci. 2011;31:7174–7177. doi: 10.1523/JNEUROSCI.0054-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing; 2012. Available at: http://www.R-project.org/ [Google Scholar]
- Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med. 2003;49:177–182. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
- Reillo I, de Juan Romero C, García-Cabezas MÁ, Borrell V. A role for intermediate radial glia in the tangential expansion of the mammalian. Cereb Cortex. 2011;21:1674–1694. doi: 10.1093/cercor/bhq238. [DOI] [PubMed] [Google Scholar]
- Ronan L, Voets N, Rua C, Alexander-Bloch A, Hough M, Mackay C, Crow TJ, James A, Giedd JN, Fletcher PC. Differential tangential expansion as a mechanism for cortical gyrification. Cereb Cortex. 2014;24:2219–2228. doi: 10.1093/cercor/bht082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salat DH, Buckner RL, Snyder AZ, Greve DN, Desikan RS, Busa E, Morris JC, Dale AM, Fischl B. Thinning of the cerebral cortex in aging. Cereb Cortex. 2004;14:721–730. doi: 10.1093/cercor/bhh032. [DOI] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Ruparel K, Loughead J, Prabhakaran K, Calkins ME, Hopson R, Jackson C, Keefe J, Riley M, Mentch FD, Sleiman P, Verma R, Davatzikos C, Hakonarson H, Gur RC, Gur RE. Neuroimaging of the Philadelphia Neurodevelopmental Cohort. Neuroimage. 2014a;86:544–553. doi: 10.1016/j.neuroimage.2013.07.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Shinohara RT, Wolf DH, Hopson RD, Elliott MA, Vandekar SN, Ruparel K, Calkins ME, Roalf DR, Gennatas ED, Jackson C, Erus G, Prabhakaran K, Davatzikos C, Detre JA, Hakonarson H, Gur RC, Gur RE. Impact of puberty on the evolution of cerebral perfusion during adolescence. Proc Natl Acad Sci U S A. 2014b;111:8643–8648. doi: 10.1073/pnas.1400178111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheipl F, Greven S, Küchenhoff H. Size and power of tests for a zero random effect variance or polynomial regression in additive and linear mixed models. Comput Stat Data Anal. 2008;52:3283–3299. doi: 10.1016/j.csda.2007.10.022. [DOI] [Google Scholar]
- Scherrer B, Schwartzman A, Taquet M, Prabhu SP, Sahin M, Akhondi-Asl A, Warfield SK. Characterizing the distribution of anisotropic micro-structural environments with diffusion-weighted imaging (DIAMOND) Med Image Comput Comput Assist Interv. 2013;16:518–526. doi: 10.1007/978-3-642-40760-4_65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seldon HL. Does brain white matter growth expand the cortex like a balloon? Hypothesis and consequences. Laterality. 2005;10:81–95. doi: 10.1080/13576500342000310. [DOI] [PubMed] [Google Scholar]
- Shaw P, Kabani NJ, Lerch JP, Eckstrand K, Lenroot R, Gogtay N, Greenstein D, Clasen L, Evans A, Rapoport JL, Giedd JN, Wise SP. Neurodevelopmental trajectories of the human cerebral cortex. J Neurosci. 2008;28:3586–3594. doi: 10.1523/JNEUROSCI.5309-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw P, Malek M, Watson B, Sharp W, Evans A, Greenstein D. Development of cortical surface area and gyrification in attention-deficit/hyperactivity disorder. Biol Psychiatry. 2012;72:191–197. doi: 10.1016/j.biopsych.2012.01.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepard D. A two-dimensional interpolation function for irregularly-spaced data. Proceedings of the 1968 23rd ACM National Conference; New York: ACM; 1968. pp. 517–524. [DOI] [Google Scholar]
- Smith SM, Johansen-Berg H, Jenkinson M, Rueckert D, Nichols TE, Miller KL, Robson MD, Jones DK, Klein JC, Bartsch AJ, Behrens TE. Acquisition and voxelwise analysis of multi-subject diffusion data with Tract-Based Spatial Statistics. Nat Protoc. 2007;2:499–503. doi: 10.1038/nprot.2007.45. [DOI] [PubMed] [Google Scholar]
- Sowell ER, Thompson PM, Leonard CM, Welcome SE, Kan E, Toga AW. Longitudinal mapping of cortical thickness and brain growth in normal children. J Neurosci. 2004;24:8223–8231. doi: 10.1523/JNEUROSCI.1798-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steen RG, Mull C, McClure R, Hamer RM, Lieberman JA. Brain volume in first-episode schizophrenia: systematic review and meta-analysis of magnetic resonance imaging studies. Br J Psychiatry. 2006;188:510–518. doi: 10.1192/bjp.188.6.510. [DOI] [PubMed] [Google Scholar]
- Taki Y, Thyreau B, Hashizume H, Sassa Y, Takeuchi H, Wu K, Kotozaki Y, Nouchi R, Asano M, Asano K, Fukuda H, Kawashima R. Linear and curvilinear correlations of brain white matter volume, fractional anisotropy, and mean diffusivity with age using voxel-based and region-of-interest analyses in 246 healthy children. Hum Brain Mapp. 2013;34:1842–1856. doi: 10.1002/hbm.22027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamnes CK, Østby Y, Fjell AM, Westlye LT, Due-Tønnessen P, Walhovd KB. Brain maturation in adolescence and young adulthood: regional age-related changes in cortical thickness and white matter volume and microstructure. Cereb Cortex. 2010;20:534–548. doi: 10.1093/cercor/bhp118. [DOI] [PubMed] [Google Scholar]
- Thompson HB. A brief summary of the researches of theodore kaes on the medullation of the intra-cortical fibers of man at different ages. J Comp Neurol. 1900;10:358–374. doi: 10.1002/cne.910100306. [DOI] [Google Scholar]
- Thompson PM, Vidal C, Giedd JN, Gochman P, Blumenthal J, Nicolson R, Toga AW, Rapoport JL. Mapping adolescent brain change reveals dynamic wave of accelerated gray matter loss in very early-onset schizophrenia. Proc Natl Acad Sci U S A. 2001;98:11650–11655. doi: 10.1073/pnas.201243998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385:313–318. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]
- Voineskos AN, Lobaugh NJ, Bouix S, Rajji TK, Miranda D, Kennedy JL, Mulsant BH, Pollock BG, Shenton ME. Diffusion tensor tractography findings in schizophrenia across the adult lifespan. Brain. 2010;133:1494–1504. doi: 10.1093/brain/awq040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Economo C. The cytoarchitectonics of the human cerebral cortex. London: Oxford UP; 1925. (English translation by S Parker in 1929) [Google Scholar]
- White T, Andreasen NC, Nopoulos P, Magnotta V. Gyrification abnormalities in childhood- and adolescent-onset schizophrenia. Biol Psychiatry. 2003;54:418–426. doi: 10.1016/S0006-3223(03)00065-9. [DOI] [PubMed] [Google Scholar]
- Wood SN. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J R Stat Soc Ser B Stat Methodol. 2011;73:3–36. doi: 10.1111/j.1467-9868.2010.00749.x. [DOI] [Google Scholar]
- Xu G, Knutsen AK, Dikranian K, Kroenke CD, Bayly PV, Taber LA. Axons pull on the brain, but tension does not drive cortical folding. J Biomech Eng. 2010;132 doi: 10.1115/1.4001683. 071013-1–071013-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zilles K, Palomero-Gallagher N, Amunts K. Development of cortical folding during evolution and ontogeny. Trends Neurosci. 2013;36:275–284. doi: 10.1016/j.tins.2013.01.006. [DOI] [PubMed] [Google Scholar]