Longitudinal Dynamic Analyses of Depression and Academic Achievement in the Hawaiian High Schools Health Survey using Contemporary Latent Variable Change Models

Abstract

The scientific literature consistently supports a negative relationship between adolescent depression and educational achievement, but we are certainly less sure on the causal determinants for this robust association. In this paper we present multivariate data from a longitudinal cohort-sequential study of high school students in Hawai‘i (following McArdle, 2009; McArdle, Johnson, Hishinuma, Miyamoto, & Andrade, 2001). We first describe the full set of data on academic achievements and self-reported depression. We then carry out and present a progression of analyses in an effort to determine the accuracy, size, and direction of the dynamic relationships among depression and academic achievement, including gender and ethnic group differences. We apply three recently available forms of longitudinal data analysis: (1) Dealing with Incomplete Data -- We apply these methods to cohort-sequential data with relatively large blocks of data which are incomplete for a variety of reasons (Little & Rubin, 1987; McArdle & Hamagami, 1992). (2) Ordinal Measurement Models (Muthén & Muthén, 2006) -- We use a variety of statistical and psychometric measurement models, including ordinal measurement models to help clarify the strongest patterns of influence. (3) Dynamic Structural Equation Models (DSEMs; McArdle, 2009). We found the DSEM approach taken here was viable for a large amount of data, the assumption of an invariant metric over time was reasonable for ordinal estimates, and there were very few group differences in dynamic systems. We conclude that our dynamic evidence suggests that depression affects academic achievement, and not the other way around. We further discuss the methodological implications of the study.

Introduction

Many important studies in psychology deal with the relationships among some forms of psychopathology connected with real-life outcomes. Questions about the likely sequence of effects are often a fundamental aspect of developmental research (e.g., Ferrer & McArdle, 2010; McArdle, 2009; Flaherty, 2008). In cross cultural research questions raised about cultural differences in beliefs about normal and clinical psychological behaviors have led some researchers to conclude that both measurement and treatment should be culture specific (Higgenbothman & Marsella, 1988; Werner & Smith, 2001). However, other researchers using different analytic approaches seem to have come to notably different conclusions (e.g., regarding measurement, Beals, Manson, Keane, & Dick, 1991; Johnson, Danko, Andrade, & Markoff, 1997). A key question raised from such analyses is how much of the resulting differences is due to the people themselves, and how much of these differences are due to the methods of data analysis used. We consider whether different results can come from different forms of analysis.

In this paper we present multivariate data from a longitudinal cohort-sequential study of high school students in Hawai’i (see McArdle, 2009, McArdle, Johnson et al., 2001). We first describe the full set of data on academic achievements and self-reported depression. We then carry out and present a progression of analyses in an effort to determine the accuracy, size, and direction of the gender and ethnic group differences in the dynamic relationships among depression and academic achievements. We apply three recently available forms of longitudinal data analysis: (1) Dealing with Incomplete Data -- We apply these methods to cohort-sequential data with relatively large blocks of data which are incomplete for a variety of reasons (Little & Rubin, 1987; McArdle & Hamagami, 1992). (2) Ordinal Measurement Models (Muthén & Muthén, 2006; Hamagami, 1998) -- We use a variety of statistical and psychometric measurement models, including ordinal measurement models to help clarify the strongest patterns of influence. (3) Dynamic Structural Equation Models (DSEMs; McArdle, 2009) -- The DSEMs are used here to provide a formal assessment of the possible directionality of effects from observational data, and we include group differences in dynamic systems. After the full set of dynamic analyses is presented we conclude that our dynamic evidence suggests that depression affects academic achievement, and not the other way around.

Prior Research on Depression and Academic Achievement

Despite the enormous amount of research that has been conducted on educational achievement, only a small proportion of this research body has investigated the association between academic achievement in the form of academic achievements in school and individual psychological adjustment such as depressive symptoms. A parallel publication to the present study is by Hishinuma, Chang, McArdle and Hamagami (in press). Their Table 1 is an overview of previously published research, and this summary suggests prior research has found significant but small, negative associations between indicators of academic achievement, such as high school grade point average (GPA), and depressive symptoms. It seems that when the GPA range was not restricted and the depressive symptom measure was not combined with anxiety, the correlation between GPA and depressive symptoms ranged from −.16 to −.36 (see their Table 1), with only a few exceptions. This negative relationship between GPA and depressive symptoms was further confirmed by other studies. For example, Juvonen, Nishina, and Graham (2000), utilizing structural equation modeling (SEM) and a middle school sample, found evidence for perceived peer harassment leading to psychological distress (i.e., depressive symptoms as measured by the Children’s Depression Inventory, self-worth), which in turn leading to poor school adjustment (i.e., actual GPA, number of classroom hours missed during semester of data collection). This suggested that depressive symptoms occurred before lowered GPAs, although this study was not longitudinal in nature.

Table 1.

Summary of Available Data in the Hawaiian High Schools Health Survey (HHSHS) Collection Waves by Year, High School, and Grade Level (N = 7,317; D=12,284 Surveys Completed)

		School Year
		1	2	3	4	5
High School	Grade Level	1991-92	1992-93	1993-94	1994-95	1995-96	Total
1	9th	103	70	100			273
	10th	88	82	76			246
	11th	75	70	84			229
	12th	75	47	66	71		259
	Incomplete*	0	0	1			1
2	9th	119	110	118			347
	10th	94	69	100			263
	11th	85	56	79			220
	12th	71	37	54	23		185
	Incomplete*	0	0	3			3
3	9th	354	364	290			1,008
	10th	315	335	326			976
	11th	293	319	297			909
	12th	318	304	298	296		1,216
	Incomplete*	0	2	3	1		6
4	9th		417	385			802
	10th		388	371			759
	11th		329	312	327		968
	12th		229	275	294	310	1,108
	Incomplete*		1	4	4		9
5	9th		265	288			553
	10th		243	244			487
	11th		251	220	221		692
	12th		172	185	194	205	756
	Incomplete*		4	3	2		9
Total		1,990	4,164	4,182	1,433	515	12,284

^*Students who did not provide their grade level within the survey.

In attempting to determine any causal relationships between GPA (school achievement) and depressive symptoms (psychological adjustment), it is likely that longitudinal studies will be needed (see Duncan, 1975; Flaherty, 2008; McArdle, 2009). For example, Lehtinen, Raikkonen, Heinonen, Raitakari, and Keltikangas-Jarvinen (2006) assessed parents of Finnish students when the students were 9, 12, and 15 years of age, and then assessed the students when they were 21–36 years of age. The researchers found an overall negative association between GPA and later depressive symptoms, but no consistent relationship across age and gender. In particular, 12- and 15-year old girls’ lower GPA predicted depressive symptoms 12 and 17 years later. Despite GPA was thought to be the predictor of the depressive symptoms, the following conclusion was drawn: “The current findings, thus, suggest that depressive outcomes have a detrimental effect on success at school rather than vice versa: presumably, failure to cope with challenges at school could lead to different kinds of vicious circles, in which case deterioration of school performance would serve as a risk factor for adult depressive outcomes …” (p. 289).

A variety of other relevant studies are reviewed by Hishinuma et al. (in press). In general, only two studies could be identified that included both GPA and depressive symptoms in a longitudinal design that involved examining trajectories. Repetto and colleagues (2004) surveyed African American high school students from the 9^th grade with GPAs of 3.0 or lower, at-risk for high school dropout, and not diagnosed with emotional impairment or developmental disability. Depressive symptoms (six items from the Brief Symptom Inventory) and GPA (8^th to 10^th grades) were utilized; however, the analyses did not include incomplete data. The students were clustered in four groups based on their longitudinal depressive symptoms: (1) consistently high; (2) consistently low; (3) decreasing; and (4) increasing. Using multivariate analysis of variance (MANOVA), students who were consistently high in depressive symptoms were more likely to be female, have anxiety and stress, and have lower self-esteem and GPA. In independent work, Johnson and colleagues (2006) examined academic achievement trajectories in adolescences in the Minnesota Twin Family Study. Although data on a composite measure of “grades” were collected across multiple years, the depression indicator was collected only in Year 1 and was not significantly associated with the measure of academic achievement.

The issues surrounding the scaling of variables have generated a great deal of prior research on these kinds of measures. Scales of achievement have been developed which have interval properties (e.g., the Woodcock-Johnson scales, the American College Testing [ACT], etc.; see McArdle & Woodcock, 1998), but easy-to-obtain scales such as GPA, have engendered lots of criticism. “In college, for example, instructors grade students on an ordinal scale, A, B, C, D, F, and the registrars assign to these grades the numbers 4, 3, 2, 1, 0 respectively, in order to compute the ‘grade point average.’ Clearly such assignments are arbitrary …” (Duncan, 1975, p. 159).

Similarly, the use of the 20-item scale of the Center for Epidemiologic Studies-Depression (CESD, Radloff, 1977) was critiqued soon after it started to be used (Devins & Orme, 1985). Although group comparisons on the CESD scale have been around for a long time (e.g., Gatz & Hurwitz, 1990), the more recent work of Cole, Kawachi, Maller, and Berkman (2000) pointed out significant item bias between African American and White American responses to the CESD items (also see Yang & Jones, 2007). In our own prior work (McArdle, Johnson et al., 2001) we summarize the previous factor analytic work on the depressive symptom scales and find evidence for at least 3 or 4 measurable factors in the CESD (also see Beals et al., 1991). In this prior work, we also show how a simple form of rescaling of the CESD can lead to a simple and direct interpretation of resulting score as “the number of days of depression symptoms reported per week” (WCESD).

On a theoretical note, we are aware that the GPA and CESD scores have substantially different norms of reference. That is, the CESD is based on the same set of items measured on the same rating scale, so it is possible to examine both systematic growth and rapid changes in a common scale. However, GPA is not an ability score with a free range; instead, GPA is a score which is relative to a grade norm—that is, even if an individual presents a constant GPA across Grades 9–12, they are likely to be growing in the ability underlying the academic performance. In this way, GPA is much like an IQ (i.e., mental age / chronological age) score rather than a raw test score (i.e., mental age), and this limits our interpretations of growth and change that can emerge from the analysis of GPA trajectories.

Based on the overall literature, the past research on this topic seems limited in several respects:

1. The sample sizes are relatively small.

2. The samples have not involved large samples of Asian American and Pacific Islander adolescents.

3. The literature shows little consideration of longitudinal data on GPA and depressive symptoms.

4. The literature shows little consideration of the issues of incomplete data in analyses (e.g., Repetto et al., 2004) and in SEM (Juvonen et al., 2000).

5. There is little consideration given to the measurement or scaling of the key outcome variables as part of data analysis, even though it is known that scaling of measurements is critical to understanding lead-lag relationships.

6. More recent SEM analyses have been presented using more contemporary growth and trajectory modeling (e.g., Hong, Veach, & Lawrenz, 2005; Johnson et al., 2006; Juvonen et al., 2000; Lehtinen et al., 2006; Repetto et al., 2004; Shahar et al., 2006).

The approach taken here attempts to combine and overcome problems of all six types. The models used here are all based on incomplete longitudinal data, and the DSEM analysis approach has been used in several recent studies (see Ferrer & McArdle, 2010; Gerstorf et al., 2009; McArdle, 2009). In examples related to this specific problem, McArdle and Hamagami (2001) examined longitudinal data from the National Longitudinal Study of Youth (NLSY) and concluded that reading ability was a precursor to anti-social behavior. In a more extensive study using the NLSY, Grimm (2007) studied academic achievement and depression, and he concluded that academic achievement preceded the development of depression. These researchers all emphasize that people using the same data could come to different dynamic conclusions using different multivariate models. Therefore, we examine a few alternatives based on different forms of measurement models here.

The Hawaiian High Schools Health Survey (HHSHS) Study

A wide variety of psychosocial problems are being studied by the National Center on Indigenous Hawaiian Behavioral Health (NCIHBH), including the relationships between psychological health and culture. Data from a variety of sources indicate that persons of aboriginal Hawaiian ancestry are more “at risk for psychological problems” than residents of Hawai‘i of other ethnic backgrounds (e.g., Andrade et al., 2006; Danko, Johnson, Nagoshi, Yuen, Gidley, & Ahn, 1988; Werner & Smith, 2001; Yuen, Nahulu, Hishinuma, & Miyamoto, 2000). The aim of the HHSHS study was to assess the adjustment of a large community-based sample of adolescents of Hawaiian ancestry as well as a comparison sample of adolescents from other ancestral groups. The longitudinal approach used in prior work in the Hawaiian islands (Werner & Smith, 2001) partly inspired this cohort-sequential data collection design. The study further investigated the importance of demographic variation and measures of identification with the Native Hawaiian culture with indices of adjustment.

The NCIHBH has already conducted studies involving self-reported GPA and adjustment, utilizing a primarily Asian American and Pacific Islander high school sample. A statistically significant and negative relationship of −.18 (p < .05) was found between self-reported GPA and of the CESD (Hishinuma, Foster et al., 2001; Hishinuma et al., 2006). This negative association remained significant even when controlling for other demographic variables (i.e., ethnicity, gender, grade level, main wage earners’ educational attainment, main wage earners’ employment status) and academic measures (i.e., actual cumulative GPA, absolute difference between self-reported GPA and cumulative GPA).

This negative relationship found among GPA and CESD scores was particularly salient for children and adolescents of ethnic minority ancestry (Hishinuma, Foster et al., 2001; Hishinuma et al., 2006). Given the general finding of lower educational achievement being associated with poorer psychological adjustment (e.g., Hishinuma, Foster et al., 2001), and given the differential academic achievement among racial and ethnic groups (e.g., African Americans with lower high school GPAs than Caucasians; Caucasians with lower high school GPAs than Asian-Pacific Islanders), this area of study is critical in understanding the well-being of ethnic minorities. In the context of the present study, Native Hawaiian adolescents tend to have lower levels of achievement than non-Hawaiians in Hawai‘i (e.g., Hishinuma, Foster et al., 2001; Hishinuma, Johnson et al., 2001; Hishinuma et al., 2006).

Dynamic Modeling with Incomplete Data

The previous HHSHS analyses described the use of a multiple imputation (MI) procedure for handling incomplete data (McArdle, Johnson et al., 2001). This approach is reasonable for data missing within or over time, and it can be used when the incompleteness is due to attrition and other factors and the lack of data are considered missing at random (MAR; after Little & Rubin, 1987). The same assumptions underlie analyses based on any latent variable SEM which included “all the data”—not simply the complete cases (e.g., Horn & McArdle, 1980; McArdle, 1996). We expect non-random attrition, but our goal is to include all the longitudinal and cross-sectional data to provide the best estimate of the parameters of change as if everyone had continued to participate (Diggle, Liang, & Zeger, 1994; Little, 1995; McArdle & Anderson, 1990; McArdle & Bell, 2000; McArdle & Hamagami, 1991; McArdle, Prescott, Hamagami, & Horn, 1998). In computational terms, the available information for any participant on any data point (i.e., any variable at any occasion) is used to build up maximum likelihood estimates (MLEs) that optimize the model parameters with respect to any available data.

Another aspect of the methods used here is the investigation of a measurement model for each key outcome variable. In the case of GPAs, the scores are first treated in the typical way, as an interval scale, but due to its more uniform distribution an effort is made to consider this more realistically as an ordinal scale. Likewise, the CESD measurement of depressive symptoms is considered to be multi-factorial, so only some items are selected, and then due to the resulting skewness, models with both interval scaling and ordinal scaling are considered here. In addition, the requirement of invariance of measurement over high school grades is considered for each outcome separately in latent curve models, and then together in the dynamic systems models. These final dynamic models are compared over groups defined by gender and ethnicity.

Method

Participants

In previous analyses, we selected data from any student who participated in the HHSHS in 1993 and 1994 (N>5,000; e.g., McArdle, Johnson et al., 2001). The analyses presented here are based on survey data obtained from high school students in Hawai‘i who participated in at least one of five waves of measurement (1992–1996; see Andrade et al., 1994, 2006). In this longitudinal-cohort study, a large sample (N=7,317) of high school students were surveyed on a variety of well-known psychometric instruments designed to indicate different aspects of psychological health. These data reflect a large but generally non-representative epidemiological sample of high school students; namely, in this study we intentionally selected primarily Hawaiian communities in Grades 9–12 from three of Hawai‘i’s major islands.

For the purposes of those analyses, we classified all students into one of four broad groups. Hawaiian versus non-Hawaiian ancestry was based on questions about the parents’ ethnic background. Students whose parents had any Hawaiian ancestry were classified as “Hawaiian” and all others were classified as “non-native Hawaiians.” A second grouping was based on the students’ self-reported gender (as Male or Female). These two groupings led to four student groups: (1) Native Hawaiian Females (N=1,733), (2) Native Hawaiian Males (N=1,456), (3) Non-native Hawaiian Females (N=973), and (4) Non-native Hawaiian Males (N=881). Additional information about these four groups can be found in other more detailed reports (see Andrade et al., 1994, 2006). The same HHSHS data collection is used here, but now we use all the longitudinal data available at any wave of measurement.

Procedures

Parents and students were given written notification of the nature and purpose of the research study prior to administration, with the opportunity for parents to decline their youths’ participation. Students who provided their assent were administered the survey in their homerooms by their teachers. The majority of the surveys were completed by the students within 30–45 minutes. Based on the existing enrollments, approximately 60% of the students were surveyed. Separate analyses indicated that a higher proportion of males were not surveyed. In addition, those who were not surveyed had more absences, suspensions, and conduct infractions, and had lower actual GPAs (Andrade et al., 2006). All procedures were approved by the University of Hawai‘i’s Institutional Review Board.

Patterns of Available Longitudinal Data

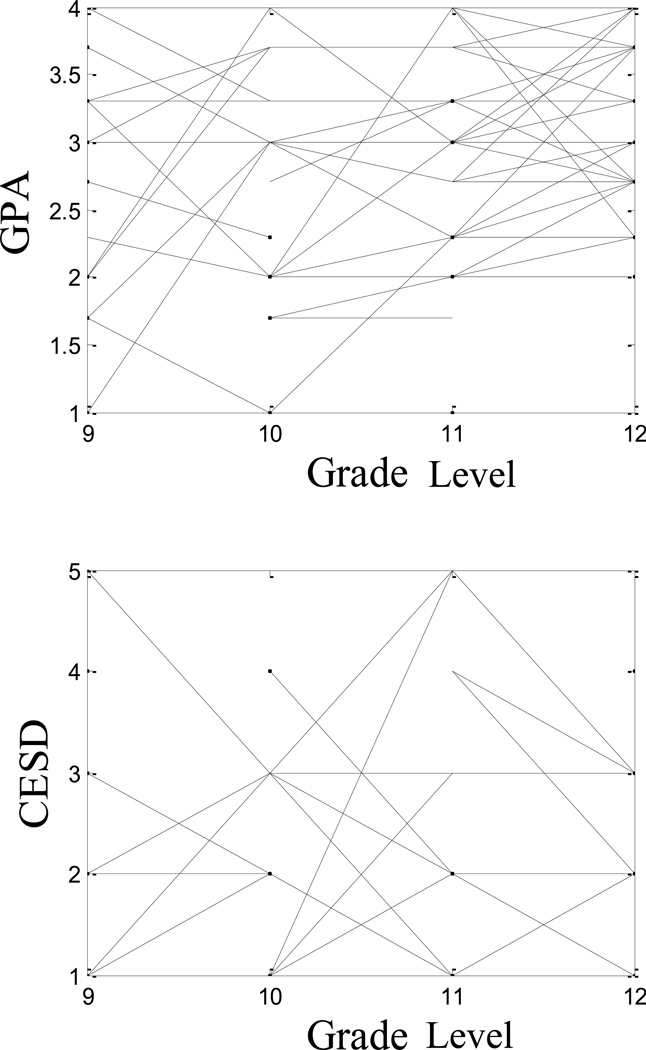
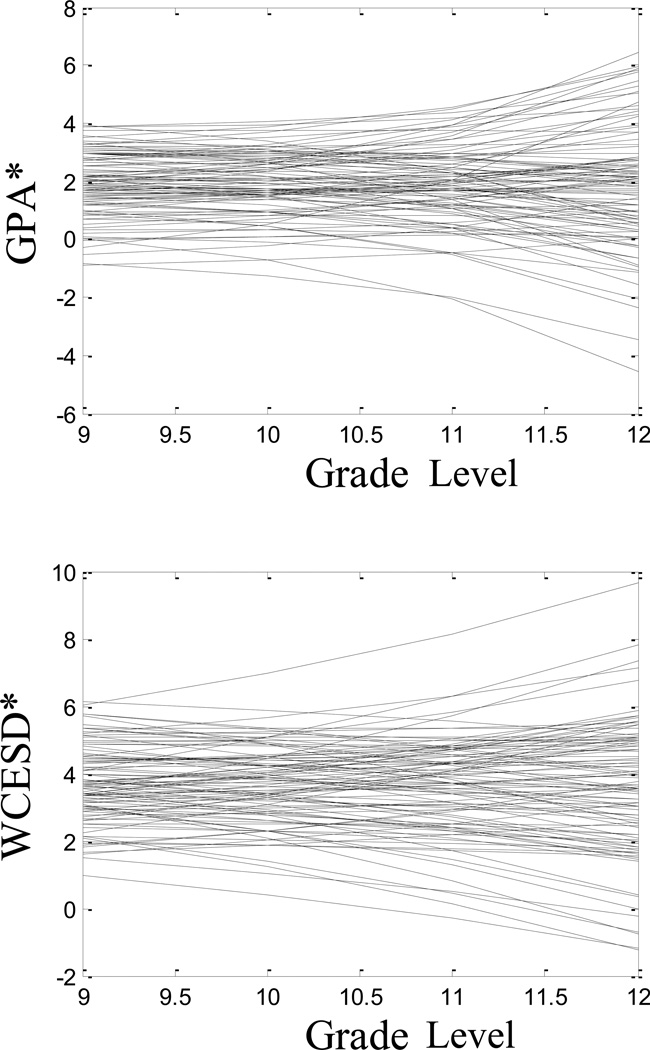
This investigation entailed a cross-sequential (i.e., cross-sectional and longitudinal) design whereby students from two to five high schools (located on three of the Hawaiian Islands) were surveyed across a five-year period (school years 1991-92 to 1995-96). The initial plan was to over-sample Native Hawaiian adolescents by surveying students from three high schools (High Schools 1–3) that had a large proportion of youths of Native Hawaiian ancestry. Table 1 provides a description of the patterns of responses at the individual level (see also Andrade et al., 2006) and Figure 1 is a plot of a small sample of trajectories from this larger longitudinal database. Figure 1a is a plot of the trajectories of the GPAs of 30 randomly selected individuals, and Figure 1b is a plot of the same 30 people on their CESD scores. Complex patterns of fluctuation are evident and the connection among these trajectories is not obvious.

Figure 1.

Observed longitudinal trajectories on the two key indicators variable for a random subset of n=30 persons. Figure 1a: Observed longitudinal trajectories for GPA; Figure 1b: Observed longitudinal trajectories for WCESD.

The HHSHS data used here are based on a complex sampling strategy highlighted in Table 1. This survey was conducted for the first three years of the study (1991-92 to 1993-94 school years) and for all high school grade levels (9^th−12^th). During Year 1 (1991-92), the decision was made to also survey in Year 2 (1992-93) students from two other high schools (High Schools 4–5) that would allow for more meaningful comparisons with non-Hawaiian adolescent cohort groups. As with High Schools 1–3, students from High Schools 4–5 were surveyed for all high school grade levels (9^th−12^th) in Years 2–3 (1992-93 & 1993-94). In order to obtain complete longitudinal data across all four grade levels for the 9^th graders who were surveyed in Year 1 (1991-92) for High Schools 1–3, and for the 9^th graders who were surveyed in Year 2 (1992-93) for High Schools 4–5, the decision was made to: (a) in Year 4 (1994-95) survey the 12^th graders from High Schools 1–3, and (b) in Year 4 (1994-95), survey 11^th and 12^th graders from High Schools 4–5, and in Year 5 (1995-96) survey 12^th graders from High Schools 4–5.

Among students who were in the 9^th grade, 3,644 (50.3%) never had an opportunity to take the survey, 2,938 (40.6%) took the survey, and 660 (9.1%) had the opportunity to take the survey, but did not for whatever reason (e.g., parent declined, student declined, student moved to another school). Seventy-five participants were not included in the previous count due to anomalies such as repeating a grade level. For the 10^th grade: 3,286 (45.4%), 2,707 (37.4%), 1,249 (17.3%), respectively; for the 11^th grade: 2,685 (37.1%), 2,984 (41.2%), 1,573 (21.7%), respectively; and for 12^th grade: 1,822 (25.2%), 3,498 (48.3%), 1,922 (26.5%) respectively.

This series of data collection decisions and methods resulted in the project starting during the 1991-92 school year, ending during the 1995-96 school year, and variably surveying 9^th−12^th graders across five high schools at different points in time. A total of 7,317 students were surveyed resulting in 12,284 completed questionnaires. We note that the potential for a lack of convergence of these data (McArdle & Hamagami, 1991) is considered in all analyses.

Measures

Self-reported Grade Point Average (GPA)

This variable was operationally defined by a single survey question, “On the average, what were your grades on your last report card?” with 10 response choices offered. This measurement of academic achievement demonstrated high concurrent validity with actual cumulative GPA in a sub-study of the same persons (r=.76; Hishinuma, Johnson et al., 2001) and construct validity with adjustment indicators, arrests/serious trouble with the law, and substance use (Hishinuma, Foster et al., 2001; Hishinuma et al., 2006).

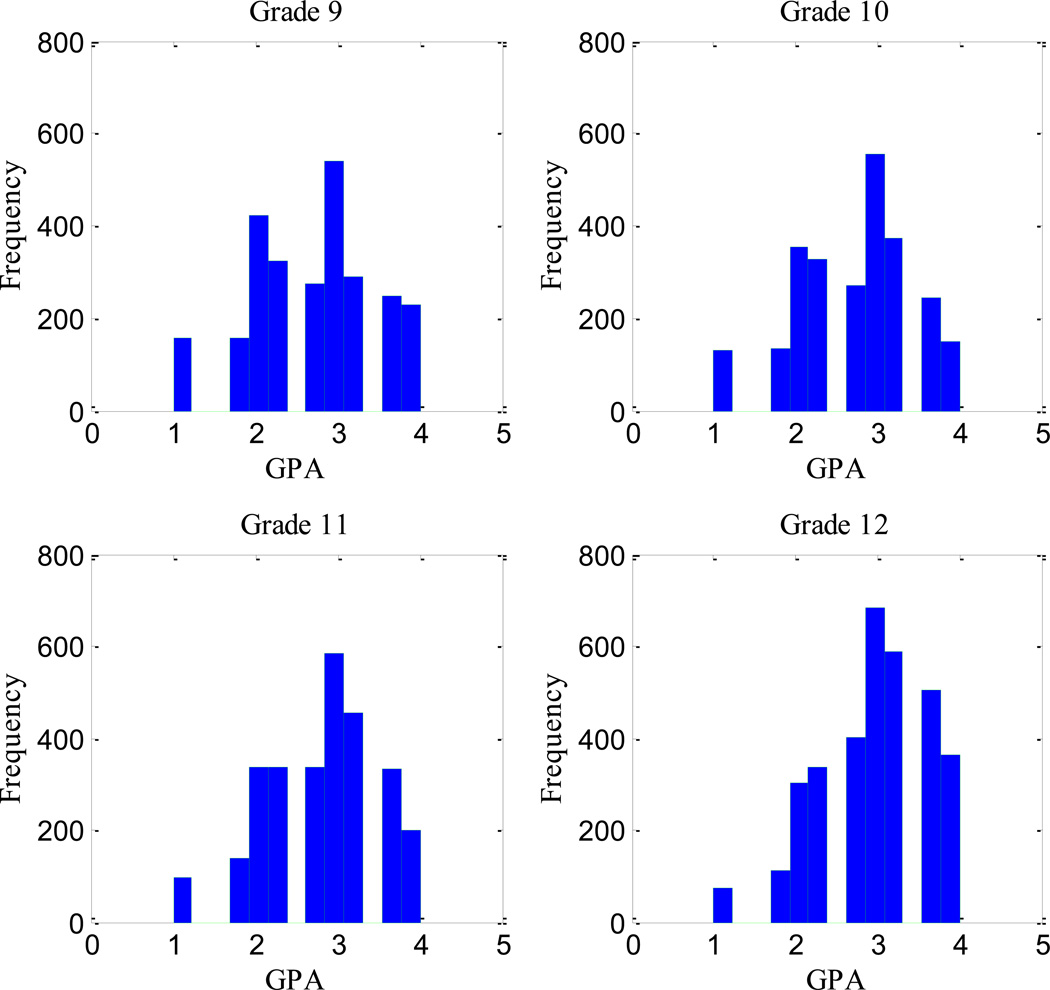
In subsequent calculations, we reconstructed this GPA variable using numerical values (in parentheses): A (4.0), A- (3.7), B+ (3.3), B (3.0), B- (2.7), C+ (2.3), C (2.0), C- (1.7), “D or less” (1.0), or “Don’t know” (converted to a missing score). Table 2a gives the percent of persons responding to each of these categories, and here we find a wide spread of responses at each year, with the highest proportion (>20%) of students suggesting they had a C+ average each year. As can be seen in Table 2a, we also found lower proportions of A averages and greater proportion of D averages over successive grades. We note that any selection due to flunking out of high school due to low GPA is not specifically indicated in these data (except perhaps by the earlier GPAs). Figure 2 includes histograms describing these GPA data at each grade.

Table 2.

Summary of Estimated Categorical Data Percentages (for sample sizes, see Table 1)

2a: Observed Grade Point Average Category Percentages
Category	Interpretation	Grade 9	Grade 10	Grade 11	Grade 12
1	A (4.0)	5.9	5.1	3.4	2.2
2	A- (3.7)	6.0	5.3	4.9	3.4
3	B+ (3.3)	16.0	14.0	12.0	9.0
4	B (3.0)	12.2	12.9	12.0	10.1
5	B- (2.7)	10.4	10.7	11.9	11.9
6.	C+ (2.3)	20.4	21.8	20.7	20.3
7	C (2.0)	11.0	14.7	16.2	17.4
8	C- (1.7)	9.4	9.6	11.8	15.0
9	D or less (1.0)	8.7	5.9	7.1	10.8

b: Observed Weekly CESD Category Percentages (Rounded Weekly Ratings of 13 Items)
Category	Interpretation	Grade 9	Grade 10	Grade 11	Grade 12
1	0–1 Days	64.2	67.2	66.9	68.6
2	1–2 Days	21.3	18.7	20.3	19.9
3	2–3 Days	8.1	8.0	7.5	6.9
4	3–4 Days	4.1	4.1	3.6	3.3
5	4–5 Days	1.8	1.8	1.4	1.1
6	5–7 Days	0.4	0.2	0.3	0.2

Figure 2.

Observed within-grade-level distributions of Grade Point Average (GPA) for all persons (N>7,000).

Self-Reported Depression

In one section of the 30–45 minute survey all students were asked to rate their depressive symptoms using the well-known Center for Epidemiological Studies-Depression (CESD) inventory (see Radloff, 1977; Zimmerman & Coryell, 1994). In the standard scoring system, the 20 CESD items are scored on a 0 to 3 scale and these scores are summed over the 20 items to form a CESD total score ranging from 0 to 60 (see Santor & Coyne, 1997). As mentioned earlier, a practical scoring system for the CESD was created and used in our earlier work (in McArdle, Johnson et al., 2001), and we expand upon this process here. The typical CESD item responses are based on “the number of days per week,” with four response categories: (1) Rarely or none of the time (<1 day), (2) Some or a little of the time (1–2 days), (3) Occasionally or a moderate amount of the time (3–4 days), and (4) Most or all of the time (5–7 days). It is possible to simply treat this as a 1–4 scale. As an alternative, it is also possible to alter the scale points to more directly reflect the average number of days per week for each symptom (so 1=0.5 days, 2=1.5 days, 3=2.5 days, and 4=6 days).

The unidimensionality of the CESD items has been questioned in prior research (Beals, Manson, Keane, & Dick, 1991; Dick, Beals, Keane, & Manson, 1994; Radloff, 1977). In our own work on this topic (McArdle, Johnson et al., 2001), we found more than one common factor were needed to account for all interrelationships among the CESD items. In these analyses, the first common factor was indicated by the most items (13) and these items reflected the basic construct of depression. Therefore, we considered only these 13 items here. To simplify the overall scaling, but retain the individual differences across time in these scores, we first (1) altered all items to be in the metric of days per week, then (2) averaged over the responses to the unidimensional items (13 out of 20), and finally (3) rounded the resulting averages into 6 reasonably sized categories of days per week (average days per week = 0–1, 1–2, 2–3, 3–4, 4–5, and 5–7). Incomplete data were not placed in any specific category.

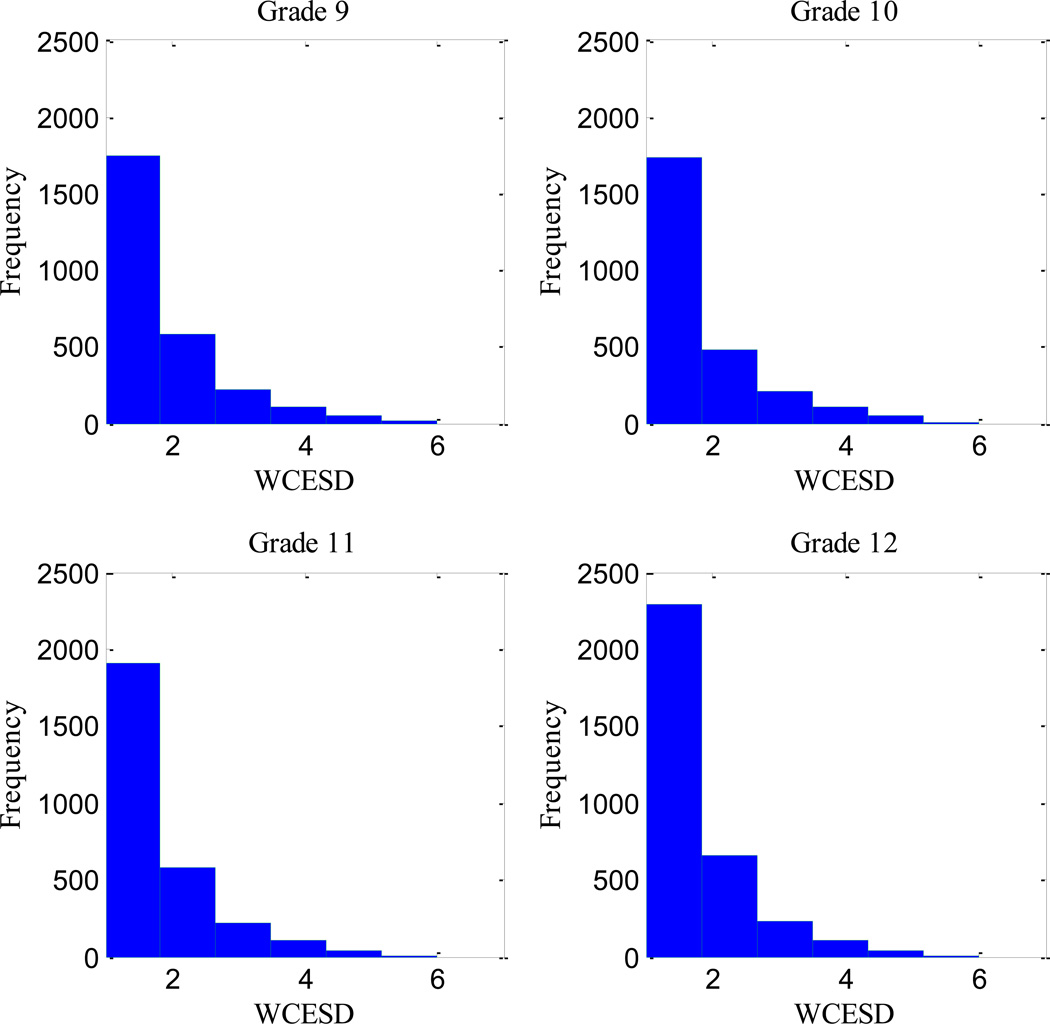
Table 2b gives the percentage of persons responding to each of these rounded six categories, and it is clear that the scale is highly skewed. The first category (0–1 days) includes over 64% of the responses, while the last category (5–7 days) includes less than 0.5% of responses within any year. Figure 3 includes histograms describing these WCESD data at each grade level. This skew seems rather severe, but a likely reflection of the construct of depressive symptoms (i.e., with no positive scores); therefore, we try to examine this variable with this statistical issue in mind.

Figure 3.

Observed within-grade-level distributions for Weighted Center for Epidemiologic Studies-Depression (WCESD) for all persons (N>7,000).

Modeling with Incomplete Data

Incomplete data techniques are now available in many current computer programs (e.g., SAS PROC MIXED; Littell, Milliken, Stroup, Wolfinger, & Schabenberger, 2006; Verbeke, Molenberghs, Krickeberg, & Fienberg, 2000), and we use Mplus 5.0 (Muthén & Muthén, 2006; see Ferrer, Hamagami, & McArdle, 2004). The Mplus program seems advantageous because it also allows us to deal with (a) survey sampling weights, (b) categorical measurement models, (c) multilevel models, and (d) a random-slopes approach to latent curve models (but see Ghisletta & McArdle, in press). The goodness-of-fit of each model presented here will be assessed using classical statistical principles relying on the model likelihood (f_MLE) and change in fit (χ²). In most models to follow, we use the MAR convergence assumption to deal with incomplete longitudinal records, and we discuss these assumptions later (e.g., Cnaan, Laird, & Slasor, 1997; Little, 1995).

These statistical models are also used to address group differences about the CESD and GPA at several different levels, and comparative statistical results are presented in the next four sections. Due to our relatively large sample size (N=7,317), only estimated coefficients whose 99% confidence boundary does not include zero are considered accurate estimates of effects. While this is precisely equivalent to stating an effect is not significant (at the α <.01 test level), this emphasis on the accuracy of estimates is more consistent with our overall modeling strategy. The overall goodness-of-fit of these models can also be examined in several ways (see Bollen & Long, 1993). However, most current SEM analyses rely on comparing observed and expected values based on a non-central chi-square (χ²) distribution (paralleling the F-distribution of ANOVA). Due to the relatively large sample size (N>7,000), we also examine statistical differences between models using the Browne and Cudeck (1993) Root Mean Square Error of Approximation (RMSEA, ε_a) and we calculate the “probability of close fit” to indicate a model with a discrepancy ε_a < .05. Our main goal is to use these empirical analyses to separate (a) which models seem consistent with the data and should be useful in future research, from (b) models which seem inconsistent with the data and should be dropped from further work.

Dealing with Non-Normal Outcomes

The evaluation of models for change over time is conceptually based on longitudinal analyses of multiple trajectories (e.g., McArdle, 2009). There is a long history of embedding categorical concepts within repeated measures longitudinal data (e.g., Hamagami, 1998; Koch, Landis, Freeman, Freeman, & Lehnen, 1977; Muthén, 1984). These approaches can clarify the results if we have either (a) categorical outcomes which are not ordinal, or (b) if the order categories are not equal in the interval between scale points. There are many techniques that can be used to deal with non-normally distributed outcomes and we will not be exhaustive here.

One classic way to deal with non-normal outcomes is to use score transformations, but these will not help here due to the extreme limits of some of our outcomes (e.g., Table 2b). Instead, we first use standard SEM approaches for estimating growth and change under the assumption of an interval scaling of the outcomes (as in McArdle, Johnson et al., 2001). This is not often based on MLE-MAR assumptions, but it is possible. In a parallel set of analyses we consider the same longitudinal data but we expand the model to include a set of ordinal thresholds (τsee Hamagami, 1998) and we highlight any differences in the substantive results for the same data.

To carry out calculations for the ordinal approach, we rely on the approach created by Muthén (for LISCOMP software; see Muthén & Satorra, 1995). In this approach, the first step is to use MLE-MAR to estimate the empirical distance between each entry of a categorical variable. Since we have 9 possible ratings of GPA at each occasion, we can estimate 8 thresholds describing the difference between these categories. Since we have only 6 possible categories of Weekly CESD, we estimate 5 thresholds to describe the difference among these categories. In the second step, we assume the underlying latent variables are normally distributed (with mean 0 and variance 1) and we estimate the correlations among latent variables using polychoric procedures. Finally, in a third step, a consistent estimator of the asymptotic covariance matrix of the latent correlations is based on a Weighted Least Squares Mean (WLSM) Adjusted estimator. Additional model assumptions based on the structure of the thresholds (i.e., invariant over time) or the model correlations (following a latent curve hypothesis) are added and the comparative goodness of fit is obtained. If needed, formal tests of the difference between models are made more accurate by using kurtosis adjustments (scaling correction factors; see Browne, 1984; Satorra & Bentler, 1994). In any case, each of these steps is now fairly easy to implement with contemporary software such as Mplus (Muthén & Muthén, 2006).

Methods for Univariate Dynamic SEM Analyses

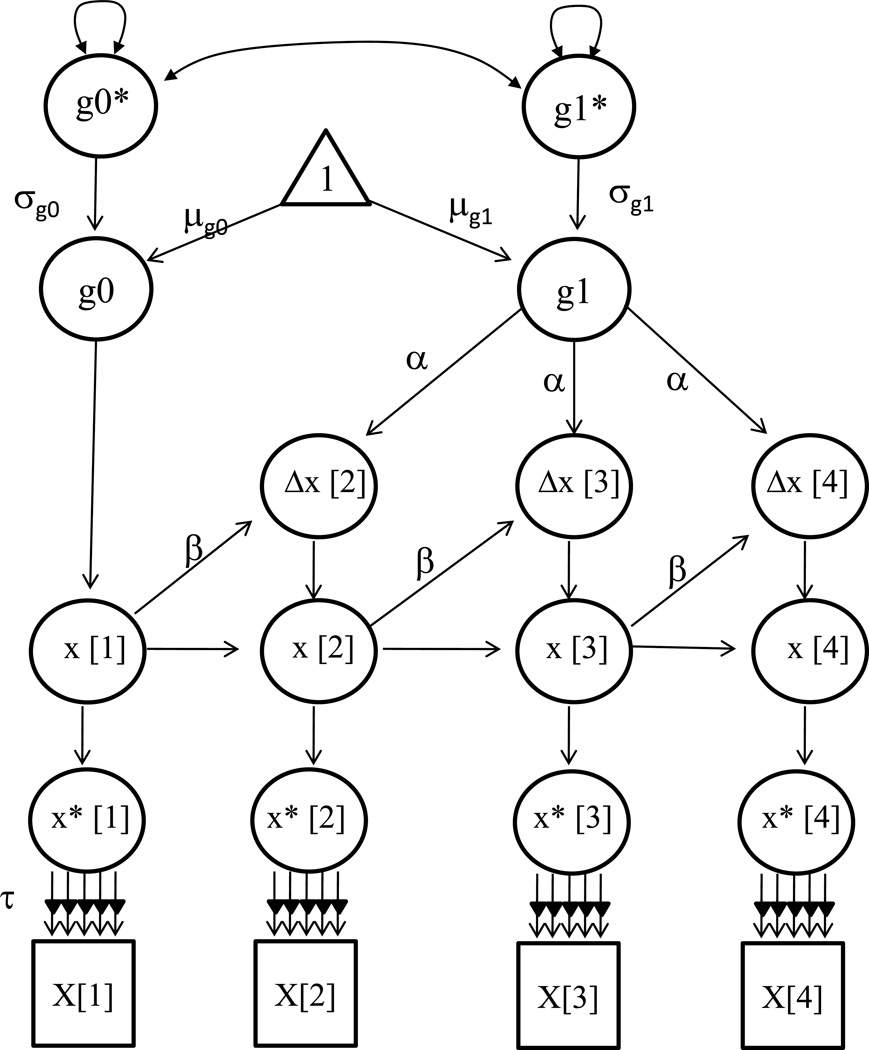
All analyses presented will be based on longitudinal structural equation models (e.g., McArdle & Nesselroade, 2003, in press; Singer & Willett, 2003). To be clear, we will emphasize the representation of trajectories over time and the dynamic interpretations of model parameters (see McArdle, 2009; McArdle & Hamagami, 2004). In recent research, we have found it most flexible to represent the classical growth and change models based on multiple latent change scores (see Figure 4; McArdle, 2009). These models are practically useful because they encompass the popular latent growth models and autoregressive time series models. In addition, because they are formed in a different way, they easily extend to multivariate forms (to follow).

Figure 4.

A univariate dual change score model to examine trajectories on grade level changes for each indicator (X). The model includes an estimate for intercept (g₀), mean intercept (µ₀), and mean slope (µ₁). Notes: The α represents constant changes and defines the form of the slope factor g₁ (i.e., a=1 is linear change). The β represents the size of the proportional auto-regressive changes. A correlation between the intercept and slope (ρ₀₁) is allowed, and the error variance (ψ²) is assumed to be constant at each grade level.

More formally, we first assume we have observed scores X[t] and X[t-1] measured over a defined interval of time (Δt), but we assume the latent variables (g[t]) are defined over an equal interval of time (Δt=1). This definition of an equal interval latent time scale is non-trivial because it allows us to eliminate Δt from the rest of the equations. This allows us to use latent scores g[t] and g[t-1], residual scores u[t] representing measurement error, and latent change scores Δg[t]. Even though this change Δg[t] is a theoretical score, and not simply a fixed linear combination, we can now write a structural model for any latent change trajectory. This simple algebraic device allows us to generally define the trajectory equation based on a summation (Σ _{i=1, t}) or accumulation of the latent changes (Δg[t]) up to time t.

These latent change score models allow a family of fairly complex nonlinear trajectory equations (e.g., non-homogeneous equations). These trajectories can be described by writing the implied basis coefficients (A_j[t]) as the linear accumulation of first differences for each variable (ΣΔg[j], j=0 to t). Of course, this accumulation can be created from any well-defined change model, and therefore, the procedure is quite flexible (e.g., see Ghisletta & McArdle, in press).

On a practical note, these latent change score structural expectations are automatically generated using any standard SEM software (e.g., R, LISREL, Mplus, Mx, etc.). That is, we do not directly define the basis (A[t]) coefficients of a trajectory equation, but we directly define changes as an accumulation of the first differences among latent variables. These dynamic models permit new features of the factor analytic assessment of the previous models (e.g., Ferrer & McArdle, 2004; McArdle & Hamagami, 2003, 2004).

Methods for Bivariate Dynamic SEM Analyses

A bivariate dynamic model can be used to relate the latent scores from one variable to another over time (see Figure 5). More formally, we first assume we have observed both sets of scores Y[t] and X[t] measured over a defined interval of time (Δt), but we assume the latent variables are defined over an equal interval of time (Δt=1). This is most useful when we start to examine time-dependent inter-relationships among multiple growth processes. In general, we write an expansion of our previous latent difference scores logic as the bivariate dynamic change score model. In this model, the g₁ and h₁ are the latent slope score which is constant over time, and the changes are based on additive parameters (α_y and α_x), multiplicative parameters (β_y and β_x), and coupling parameters (γ_yx and γ_xy). The coupling parameter (γ_yx) represents the time-dependent effect of latent x[t] on y[t], and the other coupling parameter (γ_xy) represents the time-dependent effect of latent y[t] on x[t]_. When there are multiple measured variables within each occasion, additional unique covariances within occasions (u_y[t] u_x[t]) are identifiable as well.

Figure 5.

A bivariate biometric dual change score model trajectories over grade level changes in two measured variables (Y and X). Notes: Error variance (ψ²) is assumed to be constant at each grade level within each factor; α_y and α_x represent constant change related to the slope factors y_s and x_s; β_y and β_x represent proportional change in Y and X; and cross-trait coupling is indicated by γ_yx and γ_xy. The model includes estimates for intercepts (y₀ and x₀), mean intercepts (µ_y0 and µ_x0), and mean slopes (µ_y1 and µ_x1). Other parameters are used to generate the decomposition of the correlation between the intercept and slope for X and Y.

Results

Initial Statistical Description Including Thresholds

An initial description of some relevant summary statistics appears in Table 3 and Table 4. Here we include estimated thresholds, means, deviations, and correlations estimated using the most typical incomplete data algorithms (MLE-MAR in Mplus 5.0; Muthén & Muthén, 2006; program scripts available on our website). One thing to note is that the interval score estimates presented here do not have any correction for non-normality, while the ordinal score estimates have been corrected.

Table 3.

Estimated Thresholds, Means, and Standard Deviations from the Hawaiian High Schools Health Survey for Grade Point Averages (GPAs) and the Center for Epidemiologic Studies-Depression (CESD) Scale

a Estimated (maximum likelihood estimate [MLE]) of ordinal thresholds for GPA (invariant over all for four grade levels)
Estimated Thresholds	τ1	τ2	τ3	τ4	τ5	τ6	τ7	τ8
GPA units	1.0 to 1.7	1.7 to 2.0	2.0 to 2.3	2.3 to 2.7	2.7 to 3.0	3.0 to 3.3	3.3 to 3.7	3.7 to 4.0
MLE GPA*	−2.14	−1.60	−0.86	−.039	0.01	0.71	1.31	2.03
Ratio of Distances	=0	1.80	2.47	2.05	0.13	2.33	1.50	3.43

b Estimated (MLE) ordinal thresholds for CESD (invariant over all for four grade levels)
Estimated Thresholds	τ1	τ2	τ3	τ4	τ5
WCESD (days)	0–1 to 1–2	1–2 to 2–3	2–3 to 3–4	3–4 to 4–5	4–5 to 5–7
MLE WCESD*	0.53	1.48	2.14	2.85	3.78
Ratio of Distances	=0	0.95	0.66	0.71	0.46

c Estimated means (MLE) and standard deviations (SDs) for four grade levels
Parameters & Fit	9th Grade	10th Grade	11th Grade	12th Grade
Estimated Means
GPA (GPA*)	2.69 (=0)	2.72 (0.31)	2.78 (0.19)	2.95 (0.47)
WCESD (WCESD*)	1.48 (=0)	1.44 (−0.09)	1.44 (−0.08)	1.38 (−0.13)
Estimated SDs
GPA (GPA*)	.792 (=1)	.749 (.670)	.732 (.625)	.712 (.642)
WCESD (WCESD*)	1.02 (=1)	1.01 (1.060)	.976 (.919)	.929 (.800)

Note:

^*indicates ordinal version of interval scale; see sample sizes in Table 1).

Table 4.

Estimated Pearson Product Moment (or Tetrachoric) Correlations from Hawaiian High Schools Health Survey for Grade Point Averages (GPAs) and the Center for Epidemiologic Studies-Depression (CESD) Scale

a Correlations of Interval GPA Over Time (and Ordinal GPA*)
Correlations	GPA[9]	GPA[10]	GPA[11]	GPA[12]
GPA[9]	1.00 (1.00)
GPA[10]	.590 (.610)	1.00 (1.00)
GPA[11]	.561 (.568)	.601 (.618)	1.00 (1.00)
GPA[12]	.494 (.524)	.476 (.513)	.587 (.609)	1.00 (1.00)

b Correlations of Interval WCESD Over Time (and Ordinal WCESD*)
Correlations	WCESD[9]	WCESD[10]	WCESD[11]	WCESD[12]
WCESD[9]	1.00 (1.00)
WCESD[10]	.472 (.550)	1.00 (1.00)
WCESD[11]	.452 (.482)	.503 (.539)	1.00 (1.00)
WCESD[12]	.458 (.509)	.453 (.511)	.520 (.563)	1.00 (1.00)

c Correlations of Interval GPA with Interval WCESD (and Ordinal GPA* with WCESD*)
Correlations	GPA[9]	GPA[10]	GPA[11]	GPA[12]
WCESD[9]	−.130 (−.154)	−.086 (−.085)	−.063 (−.037)	−.122 (−.082)
WCESD[10]	−.095 (−.077)	−.148 (−.162)	−.082 (−.152)	−.059 (−.076)
WCESD[11]	−.098 (−.109)	−.120 (−.149)	−.135 (−.141)	−.080 (−.117)
WCESD[12]	−.096 (−.223)	−.094 (−.174)	−.083 (−.148)	−.122 (−.156)

Note:

^*indicates ordinal version of interval scale; see sample sizes in Table 1.

Table 3 presents the estimated thresholds for GPA (now termed GPA*) and the WCESD (now termed WCESD*). There were obtained using the SEM software Mplus 5.0 under the constraint that these thresholds represented differences among the response categories, and that they were the same (i.e., invariant MLE) at each of the four grades. We note that this simplification of parameters is not a necessary feature of the data, and the scale could change from one grade to the next, but this is a prerequisite for all models to follow, and therefore, we present it first.

Table 3a shows the estimated thresholds for GPAs from category D to C- (i.e., 1.0 to 1.7) has a value of τ₁=−2.14. Because this was estimated in a normal probability, or probit metric, this value indicates the location on a normal curve for people above and below this GPA point (i.e., approximately 2% below, and 98% above). The next estimated value of τ₁=−1.60 suggests a slightly larger number of people are likely to respond between 1.7 and 2.0. The vector of eight thresholds T=[ −2.1, −1.6, −0.9, −.00, +0.0, +0.7, +1.3, +2.0] is seen to increase ordinally, even though this was not restricted (i.e., it was simply categorical). The nonlinear nature of these changes in responses can be seen from the difficulty of shifting between responses formed here as a ratio of the estimated differences to the observed differences (as in McArdle & Epstein, 1987). These differences would be constant if the scaling was equal interval, but these are Δ=[=0, 1.8, 2.5, 2.1, 0.1, 2.3, 1.5, 3.4], and this indicates the apparent difficulty of moving between the response categories not being equal to the stated distance. For this reason, linear relations within and among variables are likely to be much better represented by an ordinal scale of GPA*.

Table 3b shows the estimated thresholds for the WCESD for the category based on 0 to 1 days with a value of τ₁=0.53. Again, because this was estimated in a probit metric, this value indicates the location on a normal curve for people above and below this GPA point (i.e., approximately 52% below and 48% above). The next estimated value of τ₁=+1.48 suggests a slightly smaller number of people are likely to respond between 1 and 2 days. The vector of five thresholds T= [ +0.5, +1.5, +2.1, +2.9, +3.8] is seen to increase in an ordered progression, even though this was not restricted (i.e., it was simply categorical). The simple ratio of the estimated differences to the observed differences would be constant if the scaling was equal interval, but these are Δ=[=0, 1.0, 0.7, 0.7, 0.5]. Therefore, these findings reflect the difficulty of moving between the response categories not being equal. Thus, we expect that linear relations within and among variables are likely to be much better represented by this kind of an ordinal scale of WCESD*.

Table 3c is a listing of the means and deviations over four grade levels that would result from an interval or ordinal scaling of the two variables. These estimates are all based on MLE-MAR, so they utilize all available longitudinal data (see Table 1). GPA in an interval scale has easy-to-understand means, which seem to increase over grade levels 9^th, 10^th, 11^th and 12^th from 2.69, 2.72, 2.78, to 2.95. Once again, high school dropouts have been included in these calculations, but only to the degree that we had other measured information (i.e., 9^th grade GPA). The estimates for the ordinal scaling of the GPA are slightly different suggesting the GPA* goes from 0 (fixed for identification purposes) to 0.3 to 0.2 to 0.5, but the gain is neither linear nor as large. The estimated standard deviations are reduced in the GPA* metrics, and the changes are more complex for the WCESD* metrics.

Table 4 is a listing of the estimated Pearson correlations over four grade levels that would result from an interval scale (using invariant means and deviations). The correlations in parentheses are polychoric estimates of relationships based on ordinal scaling of the variables (using invariant thresholds). Each of these estimates is based on MLE-MAR, and therefore, they utilize all available longitudinal data (see Table 1). When comparing Pearson correlations and polychoric correlations, we find attenuation of correlations if Pearson correlations were opted for analyses due to the fact that measurements are non-normal (as in Hamagami, 1998). Table 4a is a list of the correlations of GPA over grade levels, and these are strong and positive (~r=+0.5 to +0.6). However, the use of ordinal scoring in GPA* yields a slightly higher correlation in every case. Table 4b is a list of the correlations of the WCESD over grade levels, and these are almost as strong and positive (~r=+0.4 to +0.5). Similar to GPA, however, the use of ordinal scores in WCESD* yields a slightly higher correlation in every case, suggesting that using the WCESD* is more accurate. The critical cross-correlations over time among these measures is listed in Table 4c for selected pairs of variables: (1) GPA[t] and WCESD[t] and (2) GPA[t]* and WCESD[t]*. The GPA[t] and WCESD[t] correlations are largely low and negative (~r=−0.06 to −0.15), and the use of the ordinal scaling does not seem to change the simple relationships very much (~r=−.04 to −.22). These differences in the patterns of correlations between Pearson and polychoric approaches indicate that dynamic characteristics derived from two different approaches may not be exactly the same.

Results from Univariate Dynamic Models of Grade Point Averages Over Four Grade Levels

The first set of longitudinal results of Table 5 is based on alternative change models for the GPA trajectories (in Figure 1a). The first three models (5a, 5b, 5c) assume interval scaled data and models are fit in increasing order of complexity. First, a baseline model with intercepts only is fitted (not shown) and this yields χ²=398 on df=11. The first model listed in Table 5a is the linear change model with one slope (labeled Model 5a) and fits much better with χ²=48 on df=8 (so ε=0.027), so the change in fit is large as well (Δχ²=350 on Δdf=3). This is remarkably small misfit for such a large sample size (N>7,000). The mean intercept for the 9^th grade is reasonable (µ₀=2.65) and the mean slope is positive but small (µ₁=0.09) indicating only small average changes over grade levels. The variability in these components shows somewhat large initial differences (σ₀²=0.42) with small systematic changes (σ₁²=0.02) and larger random changes (ψ²=0.22). The second model (5b) forces the systematic slope components to be zero, but allows an autoregressive component (β=0.037) to allow changes which accumulate. This auto-regression AR(1) model does not seem to fit the GPA data so well (χ²=114 on df=8 so ε=0.044). The third model (5c), termed a Dual change, allows both linear and autoregressive changes to occur, and this leads to the best fit (χ²=24 on df=7, so ε=0.019). This model suggests more complex changes due to the negative mean slope (µ₁=−1.79) combined with positive autoregressive changes (β=0.69), implying that the GPA would go down over grade levels except for the impact of the prior grades GPA.

Table 5.

Alternative Latent Curve Results from Fitting Univariate Dual Change Score Model to Different Scalings of Grade Point Averages (GPAs) (Ordinal GPA^*)

Parameters & Fit	(a) Interval GPA Linear Change	(b) Interval GPA AR(1) Change	(c) Interval GPA Dual Change	(d) Ordinal GPA* Linear Change	(e) Ordinal GPA* AR(1) Change	(f) Ordinal GPA* Dual Change
Fixed Effects
Mean intercept, µ0	2.65 (211)	2.69 (201)	2.68 (210)	=0	=0	=0
Mean slope, µ1	0.09 (17.)	=0	−1.79 (3.3)	0.14 (14)	=0	0.07 (4.6)
Constant change, α	=1	=0	=1	=1	=0	=1
Proportion change, β	=0	0.037 (15)	0.69 (3.4)	=0	=0.69 (3.2)	0.84 (3.3)
Scaling coefficients, T	=1	=1	=1	−1.8, −;1.3 −.70, −.30 .06, .66 1.2, 1.8	−2.0, −;1.5 −.77, −.31 .07, .75 1.3, 2.0	−1.9, −;1.4 −.80, −.30 .03, .67 1.2, 1.9
Variable Intercepts, µ	=0	−0.07 (3.6)	=0	=0	0.16 (15)	=0
Random Effects
Intercept Variance, σ02	0.42 (25)	0.42 (25)	0.40 (25)	=1	= 1	=1
Slope variance, σ12	0.02 (5.1)	=0	1.22 (2.1)	0.04 (6.3)	=0	0.78 (1.81)
Common slope-level, σ01	−0.05 (7)	=0	−0.29 (4.1)	−0.11 (8.7)	=0	−.88 (−3.6)
Unique variance, ψ2	.22 (35)	.027 (38)	.22 (35)	0.48 (18)	0.70 (27)	0.53 (18)
Residual Variance, σe2	=0	−0.03 (5.7)	=0	=0	−0.05 (2.9)	=0
Goodness of Fit
Misfit index χ2 / df	48./8	114./8	24./7	174./26	246./26	94./25
Change in fit Δχ2 / Δdf	350./3	284./3	24./1; 90./1	985./3	913./3	80/1; 152./1
WLSM scaling factor κ	1	1	1	0.723	0.739	0.651
RMSEA ε	.027	.044	.019	.029	.034	.020

Note: Weighted least squares mean (WLSM) estimator based on weighted least squares plus mean adjusted variances. Sample size N=6,896, 15 patterns of incomplete data; Level Only Baseline for the two scalings are GPA=398/11 with ε=0.071, and GPA

^*=1159/29, κ=0.871, ε=0.075. Obtain Technical Appendix (from authors) for Mplus input and output. AR = autoregression. Root Mean Square Error of Approximation = RMSEA.

The second set of three models (Table 5d, 5e, 5f) assume some ordinal thresholds are needed and then re-examines the same change models. Here we need to place several additional constraints on the latent variables to assure identification (i.e., µ₀=0, σ₀²=1) and estimate the 8 thresholds (τ₁−τ₈). While we could allow the thresholds to change over grade levels, we do not consider this possibility here, and this assumption of scale invariance over grade levels leads to additional misfit (but see McArdle, 2007). The scaling coefficients (described earlier) range about −2 to +2 but suggest an unequal distance between GPA points. The baseline model with intercepts only is fitted (not shown) and this yields χ²=1159 on df=29, so the ordinal linear model fitted to these is a great improvement in fit (i.e., χ²=174 on df=26, so Δχ²=985 on Δdf=3), with parameters representing some positive changes (µ₁=0.14, σ₁²=0.04) and larger random changes (ψ²=0.48). (We note that the kurtosis scaling coefficient for the WLSM estimator is reported (ω4=0.723, but, since our overall results will remain the same with or without this correction, this was not applied to adjust the chi-square tests.)

The next model (5e) is the same, but allows proportional auto-regressive changes without slopes, and it does not fit as well. The final model (5f) allows both types of changes to the ordinal scales, and it fits much better (i.e., χ²=94 on df=25, so Δχ²=80 on Δdf=1). Assuming this is our final GPA model, we have: (1) unequal distances in GPA scaling, (2) small positive changes in slopes over grade levels with large variations (µ₁=0.07, σ₁²=0.78), (3) large positive proportional changes from one GPA level to another (β=0.84), and (4) even larger random changes (ψ²=0.70). In this comparison, the first three models for GPA suggest the dual change is needed – all models for ordinal GPA* suggest unequal but ordered intervals, and the dual change model fits best. A plot of the expected values from this GPA* model is drawn in Figure 6a and this shows a small but significantly positive shift in the mean over grade levels, with increasing individual differences in trajectories.

Figure 6.

Expected longitudinal trajectories on the two key indicators variable for a random subset of n=30 persons. Figure 6a: Expected longitudinal trajectories for GPA* (from Table 5, Model 5d); Figure 6b: Expected longitudinal trajectories for WCESD* (from Table 6, Model 6d).

Results for Univariate Dynamic Models of Depressive Symptoms Over Four Grade Levels

The second set of longitudinal results of Table 6 is based on alternative change models for the WCESD trajectories (in Figure 1b). The first three models (6a, 6b, 6c) assume interval scaled data and models are fit in increasing order of complexity. First, a baseline model with intercepts only is fitted (not shown) and this yields χ²=74 on df=11. The first model listed in Table 6a is the linear change model with one slope (Model 6a) and fits much better with χ²=31 on df=8 (so ε=0.027), so the change in fit is large too (Δχ²=43 on Δdf=3). This is also a remarkably small misfit for such a large sample size (N>7,000). The mean intercept for the 9^th grade is reasonable (µ₀=1.48 days) and the mean slope is negative but small (µ₁=−0.03) indicating only small average changes over grade levels. The variability in these components shows somewhat large initial differences (σ₀²=0.57) with small systematic changes (σ₁²=0.01) and larger random changes (ψ²=0.49). The second model (6b) forces the systematic slope components to be zero, but allows an autoregressive component (β=−0.13) to allow changes to accumulate and level off. This AR(1) model seems to fit the WCESD data very well (χ²=21 on df=8 so ε=0.02). The third model, termed a Dual change, allows both linear and autoregressive changes to occur, and this leads to the best fit (χ²=29 on df=7 so ε=0.02). This model suggests more complex changes due to the negative mean slope (µ₁=−1.48) combined with positive autoregressive changes (β=0.03), implying more complex grade level patterns in the WCESD; however, this model is not an improvement in fit. Indeed, the interval WCESD seems to fluctuate from one time to the next without a systematic linear change.

Table 6.

Alternative Latent Curve Results from Fitting Univariate Dual Change Score Model to Interval and Ordinal Scalings of the Weighted Center for Epidemiologic Studies-Depression (WCESD) Scale (rescaled version of 13 items of Factor 1)

Parameters & Fit	(a) Interval WCESD No AR Change	(b) Interval WCESD AR(1) Change	(c) Interval WCESD Dual Change	(d) Ordinal WCESD* Linear Change	(e) Ordinal WCESD* AR(1) Change	(f) Ordinal WCESD* Dual Change
Fixed Effects
Mean intercept, µ0	1.48 (91)	1.60 (100)	1.47 (103)	=0	=0	=0
Mean slope, µ1	−0.03 (4.3)	=0	−1.48 (−9.1)	−0.46 (2.5)	=0	−0.04 (1.5)
Constant change, α	=1	=0	=1	=1	=0	=1
Proportion change, β	=0	−0.13 (4.0)	0.03 (0.8)	=0	−0.07 (2.0)	0.03 (0.4)
Scaling coefficients, T	=1	=1	=1	0.5, 1.4 2.0, 2.7, 3.6	0.5, 1.4 2.0 2.6, 3.4	0.5, 1.4 2.0 2.7, 3.6
Variable Intercepts, µ	=0	0.18 (3.4)	=0	=0	−0.05 (2.6)	=0
Random Effects
Intercept Variance, σ02	0.57 (20)	0.51 (15)	0.53 (22)	=1	=1	=1
Slope Variance, σ12	0.01 (1.2)	=0	0.56 (17)	0.011 (0.6)	=0	0.10 (0.3)
Common slope-level, σ01	−0.04 (20)	=0	−0.54 (20)	−0.04 (1.1)	=0	−0.30 (0.5)
Unique Variance, ψ2	0.49 (38)	0.44 (19)	0.50 (37)	0.78 (8.8)	0.67 (7.0)	0.77 (9.7)
Residual Variance, σe2	=0	0.06 (2.0)	=0	=0	0.11 (1.7)	=0
Goodness of Fit
Misfit index χ2 / df	31.3 / 8	21.9 / 8	29.2 / 7	13.7 / 17	10.7 / 17	13.8 / 16
Change in fit Δχ2 / Δdf	42.7 / 3	51.1 / 3	1.9/1; −8.3/1	47.3 / 3	50.3 / 3	−0.1/1;−2.9/1
WLSM scaling factor κ	1	1	1	0.772	0.796	0.734
RMSEA ε	0.02	0.02	0.02	0.00	0.00	0.00

Note: Weighted least squares mean (WLSM) estimator based on weighted least squares plus mean adjusted variances. Sample size N=6,942, 15 patterns of incomplete data; Level Only Baseline for the two scalings are WCESD=74./11 with ε=0.03, and WCESD

^*=61./20, m=0.900, ε=0.02; AR = auto-regression; Root Mean Square Error of Approximation = RMSEA.

The second set of three models (6d, 6e, 6f) assumes some ordinal thresholds are needed and then re-examines the same change models. Here we need to place several additional constraints on the latent variables to assure identification (i.e., µ₀=0, σ₀²=1) and estimate the 5 thresholds (τ₁−τ₅). While we could allow the thresholds to change over grade levels, we do not consider this possibility here, and this assumption of scale invariance over grade levels leads to very little misfit. The estimated scaling coefficients (described earlier) range about 0 to +4 but suggest an unequal distance between WCESD points. The baseline model with intercepts only is fitted (not shown) and this yields χ²=61 on df=29, and therefore, the ordinal linear model fitted to WCESD* is a minor improvement in fit (i.e., χ²=14 on df=17, so Δχ²=47 on Δdf=12), with parameters representing some negative changes (µ₁=−0.46, σ₁²=0.01) and larger random changes (ψ²=0.78). (Again, we note that the kurtosis scaling coefficient for the WLSM estimator is reported [ω4=0.772], because this has an effect on the resulting chi-square tests.)

The next model (6e) is the same, but allows proportional auto-regressive changes without slopes, and it fits only slightly better (i.e., χ²=11 on df=17). The final model (6f) allows both types of changes to the ordinal scales, and it fits about the same (i.e., χ²=14 on df=16). Assuming this is our final WCESD* model, we find: (1) unequal distances in WCESD scaling, (2) small negative changes in slopes over grade levels with large variations (µ₁=−0.04, σ₁²=0.10), (3) small positive proportional changes from one WCESD level to another (β=0.03), and (4) even larger random changes (ψ²=0.77). In this comparison, the first three models for WCESD suggest that only the autoregressive part of the dual change is needed. All models for ordinal WCESD* suggest unequal but ordered intervals, and the dual change model is possible. A plot of the expected values from this WCESD* model is drawn in Figure 6b and this shows a small but significantly negative shift in the mean over grades, with increasing individual differences in trajectories.

Results from Bivariate Dynamic Latent Change Models

The results of Table 7 give the SEM parameter estimates for a dynamic system where GPA and WCESD are allowed to impact the trajectory of each another over 9^th to 12^th grades based on the full bivariate dynamic path diagram of Figure 5. The first model (Table 7a) is based on interval scaling of both variables, GPA and WCESD as observed, and the second model (7b) is based on estimation using the ordinal concepts developed up to this point. (The authors provide an Mplus computer program for these models in a Technical Appendix on their website). Perhaps it is obvious, but the dynamic results differ depending upon how the variables are scaled.

Table 7.

Dynamic Structural Equation Model (SEM) Results from a Bivariate Dual Change Score Model for Interval and Ordinal Scalings of Grade Point Averages (GPAs) and Weighted Center for Epidemiologic Studies-Depression (WCESD) Scale, including Alternative Misfits

	(a) Interval Scaling		(b) Ordinal* Scaling
Parameters	GPA	WCESD	GPA*	WCESD*
Fixed Effects
Mean intercept, µ0	2.68 (202)	1.48 (81)	=0 (=0)	=0 (=0)
Mean slope, µ1	−0.66 (−.58)	0.45 (.35)	0.026 (1.00)	−0.052 (−2.34)
Constant change, α	=1	=1	=1	=1
Proportional change, β	0.607 (2.57)	0.140 (.22)	−0.109 (0.27)	−0.010 (−0.02)
Coupling, γ GPA → WCESD	0.25 (−1.05)		0.074 (−0.37)
Coupling, γ WCESD → GPA	0.63 (−1.19)		2.170 (−2.57)
Scaling coefficients, T			−1.8, −1.4, −0.7, −0.3, 0.01, 0.6, 1.1, 1.7	0.5, 1.4, 2.0, 2.7, 3.6
Random Effects
Intercept variance, σ02	0.40 (24)	0.56 (15)	=1 (=0)	=1 (=0)
Slope variance, σ12	0.44 (1.2)	0.05 (.38)	4.58 (1.3)	0.01 (0.71)
Cova. Slope & Level, σ01	−0.31 (3.7)	−0.12 (.39)	−0.45 (−1.5)	−0.03 (−0.07)
Unique variance, ψ2	0.22 (35)	0.49 (35)	0.43 (14.7)	0.81 (13.1)
Goodness-of-Fit
“Dual Coupling” Misfit	55.9 / 23 / 0.014		82.6 / 50 / 0.009
“No GPA→ WCESD”	56.7 / 24 / 0.014		82.0 / 51 / 0.009
“No WCESD→ GPA”	57.7 / 24 / 0.014		113. / 51 / 0.013
“No Couplings” Misfit	58.0 / 25 / 0.014		111. / 52 / 0.013
“No Cross-Lags” Misfit	83.0 / 27 / 0.017		191. / 54 / 0.019
“No Slopes” Misfit	168. / 32 / 0.024		1172. / 59 / 0.060

Notes: “Dual” model sample size is N=7,258 with 130 patterns of incomplete data; Ordinal ω4= .725; Not all model parameters are listed here; Obtain Technical Appendix (from authors) for Mplus input and output.

In the Interval measurement model (7a), we use the scale of measurement as it is calculated from the scores in the data, and this assumes an equal interval between score points for both GPA and WCESD. Of course, our prior plots and models fitted have suggested this is largely an incorrect assumption for both variables. Nevertheless, since interval scaling is typically assumed, we start from this point. As a result, we observe strong dynamic parameters with GPA, little or no dynamic action of the WCESD, and little or no systematic coupling across variables. The impact of GPA on the changes in WCESD is now negligible (γ=−0.25, t~1), and the impact of WCESD on the changes in GPA, while seeming a bit larger, is also negligible (γ=−0.63, t~1). The overall model fits the data well (χ²=56 on df=23, ε=0.014), but a model with either or both couplings set to zero (χ²=57 on df=24, or χ²=58 on df=25) fit about the same (ε=0.014). In contrast, a model where we assume no cross-lagged impacts at all (i.e., a “parallel process” model) does lead to a substantial loss of fit (χ²=83 on df=27) and a model assuming no slopes at all (i.e., a standard cross-lagged regression) is even worse (χ²=168 on df=32). Therefore, while there are some dynamic influences operating in the interval scaling, the direction of impacts over grade levels in not very clear – GPA and WCESD appear to be correlated by not dependent processes.

In the Ordinal measurement model (Table 7b), we do not assume the scale points have equal distance among them, but, as defined earlier, we estimate the differences using the thresholds (τ). This use of a latent variable measurement model for the GPA* and the WCESD* requires some kinds of identification constraints and we employ the ones used earlier (µ₀=0, σ₀²=1), but now for both variables. When the dynamic model is estimated for these ordinal latent variables, a result emerges: the impact of GPA* on the changes in WCESD* is clearly negligible (γ=−0.07, t<1), but the impact of WCESD* on the changes in GPA* is now significant and large (γ=−2.17, t>2.5). The fits listed show models where: (a) the overall model fits the data well (χ²=83 on df=50, ε=0.009), (b) a GPA*→ WCESD* coupling set to zero fits just as well (χ²=82 on df=51), (c) the WCESD*→ GPA* coupling set to zero does not fit as well (χ²=113 on df=51), and (d) both couplings set to zero does not fit either (χ²=111 on df=52). In addition, a model where we assume no cross-lagged impacts at all (i.e., a “parallel process” model) leads to a substantial loss of fit (χ²=191, on df=54) and a model assuming no slopes at all (i.e., a standard cross-lagged regression) is even worse (χ²=1172 on df=59). Therefore, in this ordinal scaling there seems to be directional dynamic influences operating – the direction of impacts accumulated over all grade levels suggests that WCESD*→ GPA* and not the other way around.

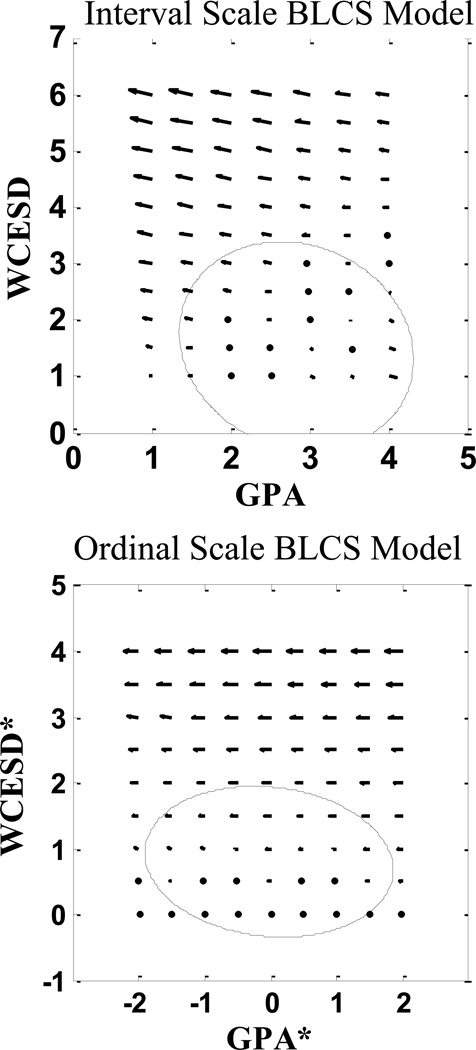
The use of a vector field plot was introduced to assist in the interpretation of the size of the impacts of the dynamic results (see Boker & McArdle, 2005). In Figure 7, these kinds of vector field plots are displayed for both the Interval model (Table 7a, Figure 7a) and for the Ordinal model (Table 7b, Figure 7b). In both plots we derive the expected direction of the trajectory for all points across a reasonable span of scale points. We then display these expectations as small arrows (i.e., directional derivatives) and we interpret the overall picture as in terms of the overall flow of the arrows. We include a 95% confidence ellipsoid around the starting points based on the available data, but we recognize that expectation outside of these boundaries may be among the most interesting flows in the diagram. The first display (Figure 7a) shows the Interval model with very little cross-variable movement, especially inside the 95% bounds of the observed data. The second display (Figure 7b) shows the Ordinal model has a little trace of cross-variable movement, where the GPA* is moving down for increasing levels of WCESD*. In both cases there is exaggerated movement outside the 95% bounds of the observed data, but these arrows reflect expectations for scores that do not appear in the current data. There does not appear to be any dynamic action in the Interval model, but there is some important dynamic action in the Ordinal model where the WCESD* effects changes in the GPA* and not the other way around.

Figure 7.

Vector field plots of expected longitudinal trajectories from the Interval and Ordinal bivariate latent change score (BLCS) models (see Table 7). Figure 7a: Interval Scale. Figure 7b: Ordinal Scale.

Results for Group Differences in Linear Dynamic Models

To add to our understanding of the dynamics, we can compare demographic groups, such as Hawaiians and Non-Hawaiians, and Females versus Males. There are several ways to consider group differences in the bivariate latent difference scores models, and we present a few of these analyses next (for details, see McArdle, 2009; McArdle & Hamagami, 1996). In one form of a multi-level DSEM, we simply use the group information to describe the distribution of the latent level and latent slopes. This is equivalent to suggesting that the dynamic process based on the coupling coefficients is invariant over groups, but that the position of the groups may differ in the vector field (i.e., different 95% confidence ellipsoids). A more flexible way to deal with these dynamic models is to examine the possibility of qualitative differences in dynamic systems among the WCESD* and GPA* longitudinal processes over the groups – that is, we ask, “Do the dynamics operate the same way in each sub-group?” One practical way to examine this form of invariance is to split up the data into groups, allow the dynamics to differ, and see if these relaxed assumptions improve the model fit substantially. This simple strategy requires a multiple group approach and, to retain power within each group, many participants are needed within in each group (McArdle & Hamagami, 1996). By splitting up the data into only four groups based only on Ethnicity and Gender we can meet the sample size requirements in the HHSHS. Results for this multiple group form of group dynamics is presented in Table 8 and Figure 8.

Table 8.

Maximum Likelihood Estimate-Missing at Random (MLE-MAR) Estimates of Dynamical Parameters (and z-values) based on Four Separate Bivariate Latent Change Score Models with Fixed Ordinal Measurement Model (Threshold Parameters based on Table 7)

	(a) Male Hawaiian (n=2,531)	(b) Male Non-Hawaiian (n=1,192)	(c) Female Hawaiian (n=2,286)	(d) Female Non-Hawaiian (n=1,184)
µWCESD	−.16	−.10	−.09	−.11
	(2.37)	(1.20)	(3.32)	(1.07)
µGPA	.04	.08	−.02	.002
	(1.50)	(1.91)	(.40)	(.04)
βWCESD	−.98	−1.02	−.86	−.65
	(11.1)	(9.61)	(3.79)	(3.78)
βGPA	.42	.26	−.07	.25
	(1.09)	(.73)	(.18)	(.67)
γGPA →WCESD	−.45	−.22	−.34	.15
	(1.76)	( .77)	(.69)	(.33)
γWCESD →GPA	−.72	−.92	−.99	−.65
	(2.72)	(6.22)	(7.24)	(2.78)
χ2	81	74	42	63
df	52	51a	52	50b
εa	.015	.014	.000	.015

Notes:

^aindicates that there is no response in one category in WCESD, thus one less df; ε_a = Root Mean Square Error of Approximation

^bindicates that there is no response in the last category in WCESD in Grades 9 and 10, with the highest threshold parameter rendered un-estimable;

Variances of all slope components are fixed at 1.0 for simplicity; εa = Root Mean Square Error of Approximation

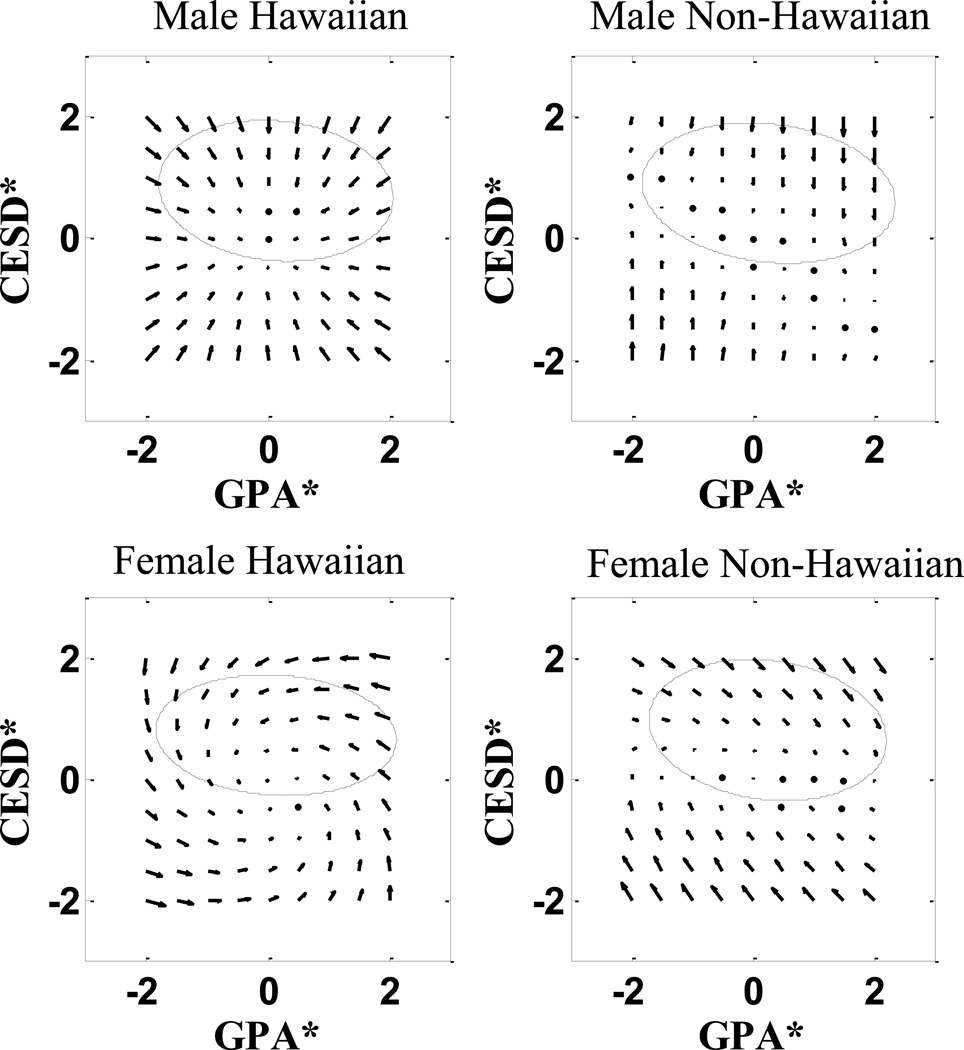
Figure 8.

Vector field plots of expected longitudinal trajectories from the multiple group bivariate latent change score (BLCS) models (see Table 8).

The resultant bivariate dynamics for the four adolescent groups are first listed separately in Table 8 – i.e., results are listed for the Male-Hawaiian adolescent group (Table 8a and Figure 8a), the Male Non-Hawaiian group (Table 8b and Figure 8b), and so on. In all groups, the status of WCESD* dictates how both WCESD* and GPA* change. WCESD* alone seems to decline itself, while GPA* is negatively influenced by the status of depression. The significant negative coupling of WCESD* on a change score of GPA* intimates that a change in GPA* is solely based on the previous state of WCESD*. The higher the depressive state at the current state, the larger the negative change in GPA*. While the plots in Figure 8 are not exactly the same, they are all very similar.

We started with the separate models of Table 8 and added invariance constraints to the four-group model, and we found: (1) A model which is invariant over Ethnicity yields a relatively small loss of fit of Δχ² =50 on Δdf = 13; and (2) A model which is invariant over Gender yields a relatively large loss of fit of Δχ² =321 on Δdf = 13. As a result, the idea that these subgroups should be treated as one large group having equivalent dynamic systems is a reasonable one, except for some notable Gender differences. That is, while there are slightly different parameters for Hawaiian and Non-Hawaiians, there is little evidence for differences in dynamic systems for different Ethnic groups. However, it appears Males and Females are operating on slightly different dynamic systems and should probably not be combined.

Finally, to check our within-time equality constraints (on βs and γs) we examined the equality of dynamic constraints over time. In the previous models listed above we required the same dynamic result to appear over every time interval – from 9^th to 10^th, 10^th to 11^th, and 11^th to 12^th. In these final analyses, we relaxed these dynamic assumptions, looked at the groups as a whole, and within each separate sub-group, and we basically found no evidence for differential dynamics over grade level or time.

Discussion

The primary issue raised in this paper is not a new one – “Does depression lead to poor academic achievement OR does poor academic achievement lead to depression?” Of course, it would not be ethical to deal with this kind of question on a randomized experimental trial design (see McArdle & Prindle, 2008). As a practical alternative, we dealt with this substantive question on a statistical basis by using contemporary models with three features: (1) A large set of relevant data was collected on adolescents using a cohort sequential design with intentionally incomplete pieces. (2) An accounting was made of scale differences between GPA and CESD. (3) A linear dynamic model was fitted, and examined in several ways, including some accounting for group differences. The overall result differs from the previous models in at least three important ways – dealing with incomplete data, scaling issues, and dynamic inferences. First, we used all the data at all occasions of measurement in an attempt to provide the best estimates available for any model fitted.

Second, we demonstrated that that the scaling of the variables can make a difference in the dynamic interpretation between academic achievement (GPA) and depressive symptoms (CESD). From our results, we learned that the scaling of the WCESD is highly skewed (see Figure 3) and we know this limits the inferences that can be made using standard interval score models. In addition, the categories of the GPA scale used here were also not equal, and this led to additional limits. It is not so surprising that when we examined alternative latent change models for either variable, we found that both the form and size of the changes were related to the measurement or scaling of the variables used in the change model. But the biggest differences arose when we tried to link the repeated measures data from one grade level to the next over both variables. Here we first established no dynamic linkage in the interval scaled data. However, when we used an ordinal scaling of both variables, we found out that prior levels of WCESD* lead to subsequent GPA* changes in the next grade level. Any true dynamic expression, no matter how large, could have been masked by impoverished measurement. The typical GPA and/or CESD scaling may be considered in this respect. That is, it may be that the constructs of achievement and depression are clearly linked over time, but the typical measurement with GPA and the CESD may not be the best way to understand these processes. Perhaps the fact that we cannot fit a good dynamic expression of change without good measurement of the construct should not be a great surprise either.

And third, in general, affective states of youth in our sample from Hawai‘i seemed to manifest in how they focused on school performances. This has many implications from clinical and prevention standpoints (see also Hishinuma et al., in press). For example, screening for depressive symptoms, major depression, and dysthymia, in conjunction with appropriate identification and treatment may prevent future poor academic performance and perhaps prevent academic failure and other comorbid delinquency behaviors (e.g., dropping out of school, substance use, suicide). In addition, given that depression is typically internalized and often not identified by schools aside from the outward manifestations of depression (e.g., changes in patterns in eating and sleeping), decreases in academic achievement may be a marker for schools that depressive symptoms may have preceded or are currently occurring and causing the lowered academic performance.

In our final analyses, we learned more about gender differences and ethnicity differences. In these analyses, we found the ethnic differences were not apparent, but the gender differences were large from a number of points of view. That is, the females seemed to be experiencing both more of, and a potentially more virulent form of an impact of increasing depressive symptoms leading to lowering of changes in academic achievement. These finding suggest that screening for prevention and treatment may be particularly important for girls.

There are many limitations of the modeling approach used here, some of these based on the current analyses and some based on the available data. The statistical model used is fairly flexible, but it still presumes invariance at several levels largely because parameter identification becomes much more difficult when more complexity is added. Our initial assumptions about interval scaling were relaxed and made ordinal, but the results presented here did not fully evaluate the assumptions of an invariant over-grade measurement model, and these assumptions are worthwhile examining in more detail. In addition, for example, in all the DSEMs fitted here, we assumed a dynamic process that takes the same amount of time no matter what pair of grade levels we were considering. We recognize that it is possible that more changes occur between some grade levels (i.e., Grades 9 and 10) than between others (i.e., Grades 10 and 11), or that the changes between longer times is not a simple accumulation (i.e., Grades 9 to 11 is a function of the other times).

The data we used were somewhat limited as well. For example, the assumption of invariance over different patterns of incomplete data is likely to be incorrect to some degree and we know that specific forms of self-selection effects can lead to parameter bias (see McArdle & Hamgami, 1992). There were also no other measured variables defined in this system, although surely there are other sources to the changes in both GPA and CESD (Hishinuma, Foster et al., 2001). For example, it is likely that sources of individual differences outside the school setting are responsible for the additional influences, and we have not tried to take into account other sources of family support (but see Andrade et al., 2006). Finally, the group differences models only attempted to account for observed group differences in ethnicity and gender, and it is likely that latent sub-groups or classes of similar groups of adolescents were involved (see Flahrety, 2008; McArdle & Prindle, 2008; Van Horn et al., 2009). It is possible for example, to isolate groups of adolescents for whom GPA → ΔDepression, and to find others for whom Depression→ ΔGPA. For all of these reasons, the substantive results presented may not replicate in further analyses of key sub-groups.

The dynamic analyses presented here clearly pointed out a few problems that can be overcome by using contemporary modeling procedures. This DSEM approach can be used to turn important developmental questions about temporal sequences into statistically powerful hypotheses. The fact that this can be done in the presence of ordinal level measurement and large amounts of incomplete data was also demonstrated, and this is a necessity for most real life-situations. We hope this approach can be useful for many other studies where multivariate longitudinal data have been collected to gain some insight into an ongoing developmental process. Such findings, in turn, should have both scientific and applied value.