Abstract
The performance of computer aided ECG analysis depends on the precise and accurate delineation of QRS-complexes. This paper presents an application of K-Nearest Neighbor (KNN) algorithm as a classifier for detection of QRS-complex in ECG. The proposed algorithm is evaluated on two manually annotated standard databases such as CSE and MIT-BIH Arrhythmia database. In this work, a digital band-pass filter is used to reduce false detection caused by interference present in ECG signal and further gradient of the signal is used as a feature for QRS-detection. In addition the accuracy of KNN based classifier is largely dependent on the value of K and type of distance metric. The value of K = 3 and Euclidean distance metric has been proposed for the KNN classifier, using fivefold cross-validation. The detection rates of 99.89% and 99.81% are achieved for CSE and MIT-BIH databases respectively. The QRS detector obtained a sensitivity Se = 99.86% and specificity Sp = 99.86% for CSE database, and Se = 99.81% and Sp = 99.86% for MIT-BIH Arrhythmia database. A comparison is also made between proposed algorithm and other published work using CSE and MIT-BIH Arrhythmia databases. These results clearly establishes KNN algorithm for reliable and accurate QRS-detection.
Keywords: ECG, QRS detection, KNN, Classifier, Cross-validation, Gradient
Introduction
The function of human body is frequently associated with signals of electrical, chemical, or acoustic origin. These signals convey information which may not be immediately perceived but which is hidden in the signal’s structure and reflect properties of their associated underlying biological systems. Extracting useful information from these biomedical signals has been found very helpful in explaining and identifying various pathological conditions. The most important category of the biomedical signal is the signals which are originated from the heart’s electrical activity. The heart is the one of the most important organs of the human body hence it is termed as a vital organ. It responds to body’s needs by adjusting its rate moment to moment, relative to respiration, physical activity, the sleep cycle and other factors. Thus for determining the heart’s ongoing functional variability there is a need of long-term measurements, computer driven calculations and detection of subtle cyclical patterns. This electrical activity of the human heart, though it is quite low in amplitude (about 1 mV) can be detected on the body surface and recorded as an electrocardiogram (ECG) signal. The ECG, i.e. voltage measured as a function of time, arise because active tissues within the heart generate electrical currents, which flow most intensively within the heart muscle itself, and with lesser intensity throughout the body. The flow of current creates voltages between the sites on the body surface where the electrodes are placed. In this regard the ECG has been established as a fast and reliable tool for deciphering the current status of the heart and has been also widely used in prognosis and diagnosis of various cardiovascular diseases and abnormalities such as myocardial ischemia and infarction, ventricular hypertrophy, and conduction problems. In general the normal ECG signal consists of P, QRS and T waves and in particular the QRS-complex reflects the electrical activity within the heart during the ventricular contraction, the time of its occurrence as well as its shape provide much information about the current state of the heart. The QRS interval is a measure of the total duration of ventricular tissue depolarization. The normal QRS interval is 0.06–0.10 s in the adult. Due to its characteristic shape it serves as the basis for the automated determination of the heart rate, as an entry point for classification schemes of the cardiac disease diagnosis. Thus, QRS detection provides the fundamental reference for almost all automated ECG analysis algorithms. The ECG signal is only of the order of 1 mV in amplitude, thus it is most susceptible to interference from biological and environmental sources such as motion artifacts, skin potentials, muscle noise, power-line interference, and radio frequency interference. These types of interferences are always accompanying the ECG acquisition and recording. That is why removal or suppression of the noise is required to be performed before QRS detection. A wide diversity of algorithms have been reported in the literature, based on mathematical transformation [1–3] and pattern recognition [4], artificial neural networks [5–7], statistical methods [8,9], for QRS detection. The heuristic methods [10–12] were also widely used in classifying the ECG signals. But the performance of these heuristic approaches is based on the ample choice of the bandwidth of the band pass filtering and the duration of the moving window used for integration. However, this choice is not, completely successful since large bandwidth passes large amount of noise whereas narrow bandwidth attenuates the QRS high frequency component. Similarly, large moving window duration increases the false positive QRS-complexes detected while small duration causes missed QRS-complexes. This is mainly due to the time variant characteristic of the QRS-complex. Later on wavelet transform (WT) was proposed to overcome the drawbacks of this fixed filtering bandwidth and moving window duration [13–16]. In order to further improve the detection accuracy, new signal analysis technique based on empirical mode decomposition has been proposed for detection of QRS-complexes [17].
Friesen et al. [18] have presented a comparison of nine QRS detection algorithms based on: (i) amplitude and first derivative, (ii) first derivative only, (iii) first and second derivative and (iv) digital filtering.
Kohler et al. [19] proposed an extensive review of various approaches of QRS detection based on: (i) signal derivatives and digital filters, (ii) wavelet-based QRS detection, (iii) neural network approaches, (iv) additional approaches like adaptive filters, hidden Markov models, mathematical morphology, matched filters, genetic algorithms, Hilbert transform-based QRS detection, etc.
Previously, KNN method has been used in applications such as data mining, statistical pattern recognition, image processing, recognition of handwriting, ECG disease classification. This work is primarily motivated by the desire to design an algorithm for precise and accurate delineation of QRS-complexes which serves as a reference for the performance of automated ECG analysis. Thus, the aim of this work is to explore the merits of KNN algorithm as an ECG delineator and to demonstrate its superior performance over other published works for CSE database and MIT-BIH Arrhythmia database (the golden standard for QRS detection).
The KNN method is an instance based learning method that stores all available data points (examples) and classifies new data points based on similarity measure. The idea underlying the KNN method is to assign new unclassified examples to the class to which the majority of its K nearest neighbors belongs. This algorithm proves to be very effective, in terms of reducing the misclassification error, when the number of samples in training dataset is large. Another advantage of the KNN method over many other supervised learning methods like support vector machine (SVM), decision tree, neural network, etc., is that it can easily deal with problems in which the class size is three and higher [20].
In KNN, the each training data consists of a set of vectors and every vector has its own positive or negative class label, where K represents the number of neighbors. In all the classification techniques based on KNN, the classification accuracy largely depends on the value of K and the type of distance metrics used for computing nearest distance. Thus, in this work, an attempt has also been made to find out the optimal value of K and distance metric using fivefold cross-validation for achieving the highest classification accuracy. After evaluating these best possible values of K and distance metric, a KNN algorithm has been used for QRS detection.
Further, the accuracy of the KNN algorithm can be severely degraded by the presence of (i) noisy data, (ii) irrelevant features, and (iii) non-consistency of feature scales with their importance. Thus, for an efficient KNN based classification, (i) digital filtering has been used to reduce the noise, and (ii) the gradient of the signal has been used as a feature for QRS detection which serves to reduce the computational burden on the KNN classifier.
Overview of K-Nearest Neighbor algorithm
The KNN is one of prospective statistical classification algorithms used for classifying objects based on closest training examples in the feature space. It is a lazy learning algorithm where the KNN function is approximated locally and all computations are deferred until classification. No actual model or learning is performed during the training phase, although a training dataset is required, it is used solely to populate a sample of the search space with instances whose class is known, for this reason, this algorithm is also known as lazy learning algorithm. It means that the training data points are not used to do any generalization and all the training data is needed during the testing phase. When an instance whose class is unknown is presented for evaluation, the algorithm computes its K closest neighbors, and the class is assigned by voting among those neighbors. In KNN algorithm, training phase is very fast but testing phase is costly in terms of both time and memory [21].
The KNN algorithm consists of two phases: Training phase and Classification phase. In training phase, the training examples are vectors (each with a class label) in a multidimensional feature space. In this phase, the feature vectors and class labels of training samples are stored. In the classification phase, K is a user-defined constant, a query or test point (unlabelled vector) is classified by assigning a label, which is the most recurrent among the K training samples nearest to that query point. In other words, the KNN method compares the query point or an input feature vector with a library of reference vectors, and the query point is labeled with the nearest class of library feature vector. This way of categorizing query points based on their distance to points in a training data set is a simple, yet an effective way of classifying new points.
Parameter K and distance metric
One of the advantages of the KNN method in classifying the objects is that it requires only few parameters to tune: K and the distance metric, for achieving sufficiently high classification accuracy. Thus, in KNN based implementations the best choice of K and distance metric for computing the nearest distance is a critical task. Generally, larger values of K reduce the effect of noise on the classification, but make boundaries between classes less distinct. The special case where the class is predicted to be the class of the closest training sample (i.e. when K = 1) is called the nearest neighbor algorithm. In binary classification problems, it is helpful to choose K to be an odd number as it avoids tied votes. Thus, the value of K is defined in such a way that it produces the highest correct classification rate [21]. In this work the different values of K which have been tested are 1, 3, 5, 7 and 9. Further, the different distance metrics which are used in this work are Euclidean distance, City Block and Correlation. The brief explanation of these distance metrics is as follows:
Distance metrics
Given an [mx × n] data matrix X, which is treated as [mx(1 × n)] row vectors x1, x2, … , xmx, and [my × n] data matrix Y, which is treated as [my(1 × n)] row vectors y1, y2, … , ymy, the various distances between the vector xs and yt are defined as follows:
Euclidean distance metric (EU)
This is the most usual way of computing a distance between two objects. It examines the root of square differences between coordinates of a pair of objects and is defined using the following equation [22]:
| (1) |
City Block distance metric (CB)
It is based on Taxicab geometry, first considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates defined using the following equation:
| (2) |
The City Block distance metric is also known as Manhattan distance, boxcar distance, absolute value distance. It represents distance between points in a city road grid. While the Euclidean corresponds to the length of the shortest path between two points (i.e. “as the crow flies”), the City Block distance refers to the sum of distances along each dimension (i.e. “walking round the block”).
Correlation distance metric (CO)
It is one minus the sample correlation between points (treated as sequences of values) and is defined using the following equation:
| (3) |
where
It is important to mention here that the performance of classifiers is usually dependent upon the value of K and distance metric. In this work these values are evolved through cross-validation, which involves the determination of classification accuracy for multiple partitions of the input samples used in training. The cross-validation is mainly used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. In general, one round of cross-validation involves partitioning a sample of data into complementary subsets, performing the analysis on one subset called the training set, and validating the analysis on the other subset called the testing set or validation set. Further, to reduce variability, multiple rounds of cross-validation are performed using different partitions, and the validation results are averaged over the rounds.
In k-fold cross-validation, the original sample is randomly partitioned into k subsamples. Of the k subsamples, a single subsample is retained as the validation data for testing the model, and the remaining (k − 1) subsamples are used as training data. The cross-validation process is then repeated k-times (the folds), with each of the k subsamples used exactly once as the validation data. The k results from the folds then can be averaged to produce a single estimation.
Methodology
In this section, we describe the proposed algorithm for the detection of QRS-complex in CSE and MIT-BIH databases using KNN classifier. The algorithm schematic and the results for 12-lead ECG CSE database are shown in Figs. 1 and 2 respectively. Although the algorithm is designed for use on 12-lead ECG data at a time using CSE database and on 2-lead ECG data using MIT-BIH database, the results for one lead are included here (in this case lead V6 of record no. MO1_036 of CSE database) to demonstrate its effectiveness in identification of QRS-complex in ECG wave.
Fig. 1.

Schematic representation of intermediate steps for KNN algorithm implementation.
Fig. 2.
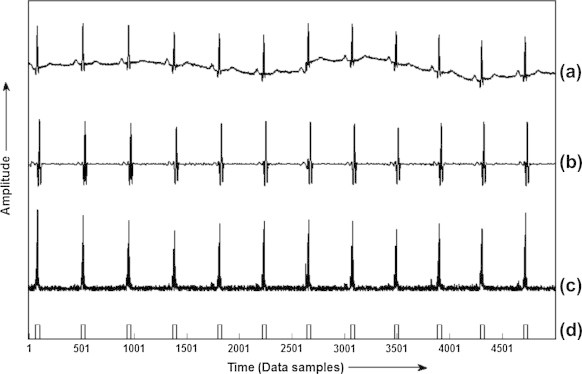
Results obtained at each step of the algorithm for lead V6 of record MO1_036 of CSE database: (a) raw ECG, (b) filtered ECG, (c) gradient curve of the ECG signal and (d) QRS locations.
ECG databases
The databases used for the validation of the algorithm for QRS detection are CSE and MIT-BIH Arrhythmia.
CSE is Common Standards for Quantitative Electrocardiography Database. There are three CSE reference data sets [23]. The first data set (CSE DS-1) consists of 3-lead ECGs, and has been recorded simultaneously in the standard sequence. In the second data set (CSE DS-2), all the leads, i.e. standard 12 leads plus 3 Frank leads are recorded simultaneously. A third CSE database (DS-3) has been developed for the assessment of diagnostic ECG and evaluates the performance of computer measurement programs. This database comprises multi-lead recordings of the standard ECG. All the data have been sampled at 500 Hz. The multi-lead measurement database is composed of original and artificial ECG recordings. This database has been split into two equal sets, i.e. data set three and data set four. Each set consists of ECG recordings of 125 patients. File name starts with the character MA and MO. The record length for these cases is in principle 10 s for each lead. These ECGs have been analyzed by a group of five referee cardiologists and eleven computer programmers. In this paper CSE DS-3 original 125 files has been used for QRS detection.
MIT-BIH Arrhythmia database was also considered for validation of this proposed algorithm. This database consists of 48 half-hour recordings for a total of 24 h of ECG data. Each one has a duration of 30 min and include two leads – the modified limb lead-II and one of the modified leads V1, V2, V4 or V5 [24], sampled at 360 Hz with resolution of 5 μV/bit. Two cardiologists have annotated all beats. This 24 h MIT-BIH database contains more than 109,000 beats.
ECG signal pre-processing
A raw digital ECG signal of a record is acquired as shown in Fig. 2a. This signal is often contaminated by disturbance such as power-line interference; muscle noise and baseline wander. In order to attenuate noise, the signal is bandpass filtered.
Bandpass filter
The bandpass filter reduces the influence of muscle noise, 50 Hz interference, baseline wander, and T-wave interference. The desirable passband to maximize the QRS energy is approximately 5–15 Hz. For the databases used in this work, a bandpass filter is used to achieve 3 dB passband from 5 to 12 Hz, and is composed of cascaded highpass and lowpass filters [11].
Lowpass filter
A lowpass filter is designed with a cut-off frequency of 11 Hz and the gain of 36 with filter processing delay of six samples.
The transfer function of the second order lowpass filter is
| (4) |
The amplitude response is
| (5) |
where T is the sampling period. The difference equation of the filter is
| (6) |
Highpass filter
The design of the highpass filter is based on subtracting the output of a first-order lowpass filter from an allpass filter. The low cut-off frequency of the filter is about 5 Hz, the gain is 32 and the delay is 16 samples.
The transfer function for such a highpass filter is
| (7) |
The amplitude response is
| (8) |
The difference equation is
| (9) |
The filtered ECG signal after removal of power-line interference and baseline wander is shown in Fig. 2b.
QRS-complex detection algorithm using gradient as feature signal
Gradient calculation
The gradient is a vector, has both direction and units, that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change. The gradient of any function f, defined using Eq. (10) is the vector field whose components are the partial derivatives of f.
| (10) |
In mathematics, gradient is widely used in measuring the degree of inclination, steepness or the rate of ascent or descent. A higher gradient value indicates a steeper incline. Thus it is clear that if the gradient of any signal under test is calculated, then any part of the signal which is having a high slope will have a higher value of gradient. The gradient of the curve as shown in Fig. 3, at point A is the same as that of the tangent at point A. Drawing tangents is a rather cumbersome method of obtaining gradients. Hence, the solution is differentiation. Differentiation allows to find the rate of change. Here in case of ECG signal, it allows to find the rate of change of amplitude of QRS-complex with respect to time samples. Thus, the QRS-complex as the most prominent wave component of ECG wave, having high slope and amplitude as compared to the rest of the wave components results in higher value of gradient than non-QRS regions. Further, the gradient also assists in the formation of decision boundaries and this in turn helps in reducing the computational burden of a classifier. Therefore based upon this fact, in this part of the work an attempt has been made to use the gradient as a feature vector for the detection of QRS-complexes [25].
Fig. 3.
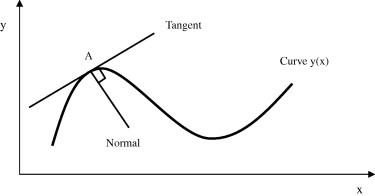
Gradient of a curve.
The gradient at each point in the ECG signal, will show the direction the signal rises most quickly and the magnitude of the gradient will determine how fast the signal rises in that direction. Moreover, the gradient is also being used to measure how a signal changes in other directions, rather than just the direction of greatest change, i.e. in the region of QRS-complex. Thus in order to enhance the signal in the region of QRS-complex, the gradient of an ECG signal at each sampling instant is calculated using Eq. (10). The gradient values so obtained are then normalized as depicted in Fig. 2c [9].
Selection of K and distance metric
It is not known beforehand which value of K and the type of distance metric are the best for this problem of component wave detection. Thus, the objective of this part of the work is to obtain best value of K and optimal distance metric, using cross-validation, so that the classifier can accurately predict the unknown data (testing data). In the present study fivefold cross-validation approach has been used to select the best K value and type of distance metric. In this approach, the original sample/data is randomly partitioned into five subsamples, of the five subsamples, a single subsample is retained as the validation data for testing the classifier, and the remaining subsamples are used as training data. The cross-validation process is then repeated five times (the folds), with each of the five subsamples used exactly once as the validation data. The results from the fivefolds are then averaged to produce a single estimation. Thus, each instance of the whole training set is predicted once so the cross-validation accuracy is the percentage of data which are correctly classified.
Using fivefold cross-validation algorithm the results which are obtained in terms of averaged classification accuracy, for five different values of K, i.e. 1, 3, 5, 7 and 9 using three different methods of computing the nearest distance, i.e. Euclidean (EU), City-Block (CB), and Correlation (CO), are shown in Table 1. After analyzing the results given in Table 1, it is found that the averaged classification accuracy obtained using EU distance metric for K = 3 is highest, i.e. 99.76% in comparison to CB (99.73%) and CO (99.74%) distance metrics for the same value of K. Also the averaged classification rate obtained using EU method is higher than CB and CO methods for all the values of K. Thus it has been established that in terms of classification accuracy obtained using fivefold cross-validation, the optimal value of K is 3 and type of distance metric is Euclidean.
Table 1.
Averaged classification accuracy using fivefold cross-validation for different values of K and distance metrics.
| Distance metrics | K = 1 | K = 3 | K = 5 | K = 7 | K = 9 |
|---|---|---|---|---|---|
| Euclidean (EU) | 99.67 | 99.76 | 99.73 | 99.73 | 99.72 |
| City Block (CB) | 99.55 | 99.73 | 99.71 | 99.71 | 99.71 |
| Correlation (CO) | 99.58 | 99.74 | 99.73 | 99.72 | 99.72 |
Training phase
After obtaining the optimal value of K and type of distance metric, the KNN classifier is now trained. The record no. MA1_001 of CSE database and record no. 100 of MIT-BIH database were used for training the classifier.
The training phase for KNN consists of storing all known instances and their class labels. Here, in this phase, a [m × n] training matrix is formed, consisting of m training instances of n features. The number of training instances (m) is equal to the number of samples of selected portions of ECGs, i.e. for CSE database the value of m = 5000 and for MIT-BIH database m = 650,000. The value of n, which is the normalized gradient value of each lead of the ECG at a training instance, for a CSE 12-lead ECG database is taken as 12, whereas for MIT-BIH Arrhythmia 2-lead database is 2. If the training instance belongs to QRS region, the training label vector is set to 1 and if it belongs to non-QRS region it is set to −1.
Classification phase
A basic rule in classification analysis is that the testing is not made for data samples that are used for training or learning. Instead, testing is made for samples that are kept out of training process. This was due to the reason that if testing is made for samples used in training or learning, the accuracy will be artificially biased upward.
Thus based upon this rule, after training the KNN, each record of the CSE and MIT-BIH databases is tested for the detection of the QRS-complexes. Here, in case of CSE database, 10 s duration data has been used for testing while for MIT-BIH database whole file of 30 min duration is used for testing. After testing, a train of 1’s is obtained at the output of KNN classifier. Then this train of 1’s is picked and by using their duration, average pulse duration of 1’s is evaluated. Those trains of 1’s, whose duration turns out to be more than the average pulse duration are detected as QRS-complex and the other are discarded. The locations of the QRS-complexes, as detected by KNN, are shown by the curve Fig. 2d.
Results and discussion
Although patterns of QRS-complexes hold considerable promise for clarifying issues in clinical applications, the inaccurate detection and quantification of these patterns may obscure critical issues and may impede rather than foster the development of computerized ECG analysis in clinical settings. Thus by keeping this thing in consideration, the evaluation of the performance of the proposed algorithm for QRS-complex detection has been done using 125 original 12-leads ECG recording of dataset-3 of CSE multi-lead measurement library and 48 half-an-hour 2-leads recording of MIT-BIH Arrhythmia database. Here, detection is said to be true positive (TP) if the algorithm correctly detects the QRS-complex, false negative (FN) if algorithm fails to identify QRS-complex, and false positive (FP) if the algorithm detects non-QRS-complex as QRS-complex. Further, the parameters which are used to evaluate the performance of our proposed algorithm are: detection rate, sensitivity (Se) and specificity (Sp). The detection rate, sensitivity and specificity have been calculated using the Eqs. (11)–(13) respectively [10].
| (11) |
| (12) |
| (13) |
The quantitative values of the results of QRS detection using proposed algorithm for all the records of CSE database, i.e. from MO1_001 to MO1_125 are given in Table 2. After analyzing the results given in Table 2 it has been found that this algorithm correctly detects the QRS-complexes in all the records except in record no. MO1_053, MO1_109, MO1_111 and MO1_124. In MO1_053 and MO1_109 it detects 01 FN beat each and in MO1_111 and MO1_124 it detects 01 FP beat each. Further, by using Eqs. (11)–(13), the detection rate of 99.89%, Se of 99.86% and Sp of 99.86% has been achieved. In addition a comparative table showing the results of QRS detection using our proposed algorithm and other published works for CSE data base is also given in Table 3 [9,26,1,27,4,28,29,5]. The results clearly show that the proposed algorithm gives the improved detection rate of 99.89%. In terms of visual representation of the results, the results for record number MO1_008 of all the 12-leads of CSE database is shown in Fig. 4. It has been seen that the proposed classifier detects all the QRS-complexes without any false positive and false negative detection. Further, the results of QRS detection for record number MO1_109 of CSE database is given in Fig. 5, demonstrates that the proposed KNN classifier fails to detect one QRS-complex, due to its very low amplitude in most of the leads, and it is termed as false negative (FN). However, all the QRS-complexes are accurately detected. Similarly the results for the detection of QRS-complexes of record number MO1_124 of CSE database shown in Fig. 6, reveals that the algorithm detects one extra non-QRS-complex, termed as false positive (FP).
Table 2.
Results of evaluating the KNN algorithm using CSE database.
| Record | Actual peak | Detected peak | TP | FP | FN | Detection rate (%) |
|---|---|---|---|---|---|---|
| MO1_001 | 11 | 11 | 11 | – | – | 100 |
| MO1_002 | 19 | 19 | 19 | – | – | 100 |
| MO1_003 | 17 | 17 | 17 | – | – | 100 |
| MO1_004 | 12 | 12 | 12 | – | – | 100 |
| MO1_005 | 17 | 17 | 17 | – | – | 100 |
| MO1_006 | 16 | 16 | 16 | – | – | 100 |
| MO1_007 | 17 | 17 | 17 | – | – | 100 |
| MO1_008 | 10 | 10 | 10 | – | – | 100 |
| MO1_009 | 12 | 12 | 12 | – | – | 100 |
| MO1_010 | 07 | 07 | 07 | – | – | 100 |
| MO1_011 | 15 | 15 | 15 | – | – | 100 |
| MO1_012 | 13 | 13 | 13 | – | – | 100 |
| MO1_013 | 12 | 12 | 12 | – | – | 100 |
| MO1_014 | 08 | 08 | 08 | – | – | 100 |
| MO1_015 | 06 | 06 | 06 | – | – | 100 |
| MO1_016 | 16 | 16 | 16 | – | – | 100 |
| MO1_017 | 10 | 10 | 10 | – | – | 100 |
| MO1_018 | 15 | 15 | 15 | – | – | 100 |
| MO1_019 | 13 | 13 | 13 | – | – | 100 |
| MO1_020 | 22 | 22 | 22 | – | – | 100 |
| MO1_021 | 07 | 07 | 07 | – | – | 100 |
| MO1_022 | 12 | 12 | 12 | – | – | 100 |
| MO1_023 | 08 | 08 | 08 | – | – | 100 |
| MO1_024 | 09 | 09 | 09 | – | – | 100 |
| MO1_025 | 10 | 10 | 10 | – | – | 100 |
| MO1_026 | 13 | 13 | 13 | – | – | 100 |
| MO1_027 | 14 | 14 | 14 | – | – | 100 |
| MO1_028 | 10 | 10 | 10 | – | – | 100 |
| MO1_029 | 10 | 10 | 10 | – | – | 100 |
| MO1_030 | 12 | 12 | 12 | – | – | 100 |
| MO1_031 | 11 | 11 | 11 | – | – | 100 |
| MO1_032 | 14 | 14 | 14 | – | – | 100 |
| MO1_033 | 09 | 09 | 09 | – | – | 100 |
| MO1_034 | 12 | 12 | 12 | – | – | 100 |
| MO1_035 | 11 | 11 | 11 | – | – | 100 |
| MO1_036 | 12 | 12 | 12 | – | – | 100 |
| MO1_037 | 13 | 13 | 13 | – | – | 100 |
| MO1_038 | 11 | 11 | 11 | – | – | 100 |
| MO1_039 | 09 | 09 | 09 | – | – | 100 |
| MO1_040 | 12 | 12 | 12 | – | – | 100 |
| MO1_041 | 11 | 11 | 11 | – | – | 100 |
| MO1_042 | 11 | 11 | 11 | – | – | 100 |
| MO1_043 | 10 | 10 | 10 | – | – | 100 |
| MO1_044 | 08 | 08 | 08 | – | – | 100 |
| MO1_045 | 13 | 13 | 13 | – | – | 100 |
| MO1_046 | 12 | 12 | 12 | – | – | 100 |
| MO1_047 | 16 | 16 | 16 | – | – | 100 |
| MO1_048 | 10 | 10 | 10 | – | – | 100 |
| MO1_049 | 11 | 11 | 11 | – | – | 100 |
| MO1_050 | 08 | 08 | 08 | – | – | 100 |
| MO1_051 | 20 | 20 | 20 | – | – | 100 |
| MO1_052 | 15 | 15 | 15 | – | – | 100 |
| MO1_053 | 17 | 16 | 16 | – | 01 | 94.11 |
| MO1_054 | 07 | 07 | 07 | – | – | 100 |
| MO1_055 | 09 | 09 | 09 | – | – | 100 |
| MO1_056 | 10 | 10 | 10 | – | – | 100 |
| MO1_057 | 10 | 10 | 10 | – | – | 100 |
| MO1_058 | 15 | 15 | 15 | – | – | 100 |
| MO1_059 | 08 | 08 | 08 | – | – | 100 |
| MO1_060 | 12 | 12 | 12 | – | – | 100 |
| MO1_061 | 13 | 13 | 13 | – | – | 100 |
| MO1_062 | 11 | 11 | 11 | – | – | 100 |
| MO1_063 | 09 | 09 | 09 | – | – | 100 |
| MO1_064 | 11 | 11 | 11 | – | – | 100 |
| MO1_065 | 12 | 12 | 12 | – | – | 100 |
| MO1_066 | 10 | 10 | 10 | – | – | 100 |
| MO1_067 | 12 | 12 | 12 | – | – | 100 |
| MO1_068 | 16 | 16 | 16 | – | – | 100 |
| MO1_069 | 13 | 13 | 13 | – | – | 100 |
| MO1_070 | 12 | 12 | 12 | – | – | 100 |
| MO1_071 | 14 | 14 | 14 | – | – | 100 |
| MO1_072 | 11 | 11 | 11 | – | – | 100 |
| MO1_073 | 13 | 13 | 13 | – | – | 100 |
| MO1_074 | 10 | 10 | 10 | – | – | 100 |
| MO1_075 | 13 | 13 | 13 | – | – | 100 |
| MO1_076 | 13 | 13 | 13 | – | – | 100 |
| MO1_077 | 12 | 12 | 12 | – | – | 100 |
| MO1_078 | 07 | 07 | 07 | – | – | 100 |
| MO1_079 | 09 | 09 | 09 | – | – | 100 |
| MO1_080 | 09 | 09 | 09 | – | – | 100 |
| MO1_081 | 12 | 12 | 12 | – | – | 100 |
| MO1_082 | 09 | 09 | 09 | – | – | 100 |
| MO1_083 | 15 | 15 | 15 | – | – | 100 |
| MO1_084 | 10 | 10 | 10 | – | – | 100 |
| MO1_085 | 11 | 11 | 11 | – | – | 100 |
| MO1_086 | 09 | 09 | 09 | – | – | 100 |
| MO1_087 | 09 | 09 | 09 | – | – | 100 |
| MO1_088 | 09 | 09 | 09 | – | – | 100 |
| MO1_089 | 06 | 06 | 06 | – | – | 100 |
| MO1_090 | 08 | 08 | 08 | – | – | 100 |
| MO1_091 | 09 | 09 | 09 | – | – | 100 |
| MO1_092 | 11 | 11 | 11 | – | – | 100 |
| MO1_093 | 09 | 09 | 09 | – | – | 100 |
| MO1_094 | 10 | 10 | 10 | – | – | 100 |
| MO1_095 | 08 | 08 | 08 | – | – | 100 |
| MO1_096 | 08 | 08 | 08 | – | – | 100 |
| MO1_097 | 09 | 09 | 09 | – | – | 100 |
| MO1_098 | 11 | 11 | 11 | – | – | 100 |
| MO1_099 | 10 | 10 | 10 | – | – | 100 |
| MO1_100 | 15 | 15 | 15 | – | – | 100 |
| MO1_101 | 16 | 16 | 16 | – | – | 100 |
| MO1_102 | 16 | 16 | 16 | – | – | 100 |
| MO1_103 | 11 | 11 | 11 | – | – | 100 |
| MO1_104 | 08 | 08 | 08 | – | – | 100 |
| MO1_105 | 14 | 14 | 14 | – | – | 100 |
| MO1_106 | 10 | 10 | 10 | – | – | 100 |
| MO1_107 | 14 | 14 | 14 | – | – | 100 |
| MO1_108 | 16 | 16 | 16 | – | – | 100 |
| MO1_109 | 15 | 14 | 14 | – | 01 | 93.33 |
| MO1_110 | 15 | 15 | 15 | – | – | 100 |
| MO1_111 | 20 | 21 | 20 | 01 | – | 100 |
| MO1_112 | 13 | 13 | 13 | – | – | 100 |
| MO1_113 | 17 | 17 | 17 | – | – | 100 |
| MO1_114 | 11 | 11 | 11 | – | – | 100 |
| MO1_115 | 20 | 20 | 20 | – | – | 100 |
| MO1_116 | 13 | 13 | 13 | – | – | 100 |
| MO1_117 | 12 | 12 | 12 | – | – | 100 |
| MO1_118 | 11 | 11 | 11 | – | – | 100 |
| MO1_119 | 18 | 18 | 18 | – | – | 100 |
| MO1_120 | 09 | 09 | 09 | – | – | 100 |
| MO1_121 | 10 | 10 | 10 | – | – | 100 |
| MO1_122 | 15 | 15 | 15 | – | – | 100 |
| MO1_123 | 13 | 13 | 13 | – | – | 100 |
| MO1_124 | 11 | 12 | 11 | 01 | – | 100 |
| MO1_125 | 12 | 12 | 12 | – | – | 100 |
| Total | 1488 | 1488 | 1486 | 02 | 02 | 99.89% |
Table 3.
Comparison of proposed KNN algorithm with other QRS detection algorithms using CSE database.
| Database | QRS detector | Reference | Detection rate (%) |
|---|---|---|---|
| CSE database | KNN algorithm | Using proposed algorithm | 99.89 |
| SVM algorithm | [9] | 99.75 | |
| Length and energy transformation | [26] | 99.60 | |
| Time recursive prediction technique | [1] | 99.00 | |
| K-means algorithm | [27] | 98.66 | |
| Bottom up approach | [4] | 98.49 | |
| Mathematical morphology | [28] | 99.38 | |
| An integrated pattern recognition method | [29] | 99.83 | |
| Predictive neural network based technique to detect QRS complexes | [5] | 98.96 |
Fig. 4.
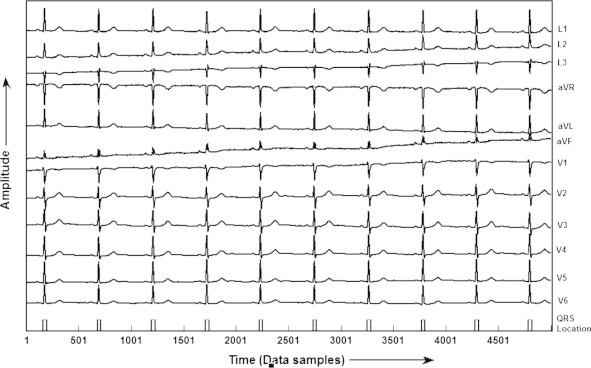
QRS detection in record MO1_008 of CSE database.
Fig. 5.
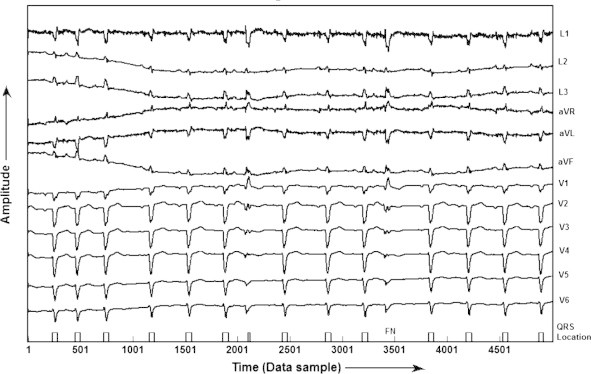
QRS detection in record MO1_109 of CSE database.
Fig. 6.
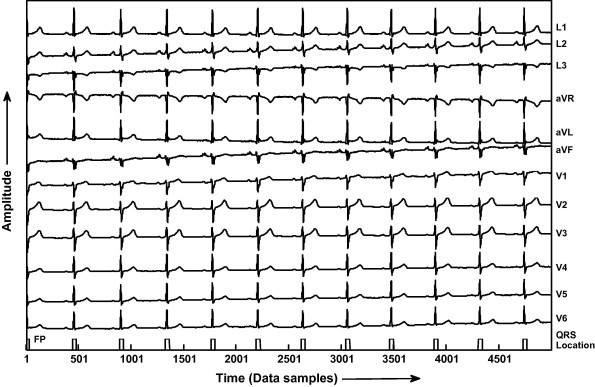
QRS detection in record MO1_124 of CSE database.
Furthermore, in order to validate the results, same algorithm has been applied to MIT-BIH Arrhythmia database for QRS detection. The results given in Table 4, summarizes the performance of our proposed algorithm. It has been shown that the detection rate of 99.81% is achieved with 151 false positive (FP) beats and 207 false negative (FN) beats. In addition, the Se of 99.81% and Sp of 99.86% has been achieved using this algorithm. In addition, the results of QRS detection for record number 201 of MIT-BIH database is given in Fig. 7, which shows that the proposed KNN classifier fails to detect one QRS-complex, due to its very low amplitude, and it is termed as false negative (FN). Fig. 8 shows the detection of QRS-complex of record no. 207 of MIT-BIH database.
Table 4.
Results of evaluating the KNN algorithm using MIT-BIH Arrhythmia database.
| Data no. | Actual peaks | Detected peaks | TP | FP | FN | Det. rate (%) |
|---|---|---|---|---|---|---|
| 100 | 2273 | 2273 | 2273 | 00 | 00 | 100 |
| 101 | 1865 | 1865 | 1865 | 00 | 00 | 100 |
| 102 | 2187 | 2187 | 2187 | 00 | 00 | 100 |
| 103 | 2084 | 2084 | 2084 | 00 | 00 | 100 |
| 104 | 2229 | 2218 | 2214 | 04 | 15 | 99.33 |
| 105 | 2572 | 2557 | 2560 | 01 | 12 | 99.53 |
| 106 | 2027 | 2033 | 2026 | 07 | 01 | 99.95 |
| 107 | 2137 | 2137 | 2137 | 00 | 00 | 100 |
| 108 | 1763 | 1753 | 1751 | 02 | 12 | 99.32 |
| 109 | 2532 | 2532 | 2532 | 00 | 00 | 100 |
| 111 | 2124 | 2124 | 2124 | 00 | 00 | 100 |
| 112 | 2539 | 2539 | 2538 | 01 | 01 | 99.96 |
| 113 | 1795 | 1795 | 1795 | 00 | 00 | 100 |
| 114 | 1879 | 1879 | 1872 | 07 | 07 | 99.63 |
| 115 | 1953 | 1953 | 1953 | 00 | 00 | 100 |
| 116 | 2412 | 2411 | 2411 | 00 | 01 | 99.96 |
| 117 | 1535 | 1537 | 1535 | 02 | 00 | 100 |
| 118 | 2278 | 2280 | 2278 | 02 | 00 | 100 |
| 119 | 1987 | 1997 | 1987 | 10 | 00 | 100 |
| 121 | 1863 | 1863 | 1863 | 00 | 00 | 100 |
| 122 | 2476 | 2476 | 2476 | 00 | 00 | 100 |
| 123 | 1518 | 1518 | 1518 | 00 | 00 | 100 |
| 124 | 1619 | 1619 | 1619 | 00 | 00 | 100 |
| 200 | 2601 | 2598 | 2583 | 15 | 18 | 99.31 |
| 201 | 1963 | 1947 | 1943 | 04 | 20 | 98.98 |
| 202 | 2136 | 2145 | 2135 | 10 | 01 | 99.95 |
| 203 | 2980 | 2975 | 2965 | 10 | 15 | 99.49 |
| 205 | 2656 | 2654 | 2653 | 01 | 03 | 99.88 |
| 207 | 2332 | 2325 | 2312 | 13 | 20 | 99.14 |
| 208 | 2955 | 2955 | 2951 | 04 | 04 | 99.86 |
| 209 | 3005 | 3006 | 3004 | 02 | 01 | 99.96 |
| 210 | 2650 | 2645 | 2643 | 02 | 07 | 99.73 |
| 212 | 2748 | 2749 | 2747 | 02 | 01 | 99.96 |
| 213 | 3251 | 3254 | 3249 | 05 | 02 | 99.94 |
| 214 | 2262 | 2264 | 2262 | 02 | 00 | 100 |
| 215 | 3363 | 3364 | 3361 | 03 | 02 | 99.94 |
| 217 | 2208 | 2202 | 2199 | 03 | 09 | 99.59 |
| 219 | 2154 | 2146 | 2144 | 02 | 10 | 99.53 |
| 220 | 2048 | 2049 | 2045 | 04 | 03 | 99.85 |
| 221 | 2427 | 2427 | 2423 | 04 | 04 | 99.83 |
| 222 | 2483 | 2476 | 2468 | 08 | 15 | 99.39 |
| 223 | 2605 | 2604 | 2598 | 06 | 07 | 99.73 |
| 228 | 2053 | 2052 | 2047 | 05 | 06 | 99.70 |
| 230 | 2256 | 2255 | 2255 | 00 | 01 | 99.95 |
| 231 | 1571 | 1571 | 1571 | 00 | 00 | 100 |
| 232 | 1780 | 1779 | 1776 | 03 | 04 | 99.77 |
| 233 | 3079 | 3079 | 3075 | 04 | 04 | 99.87 |
| 234 | 2753 | 2755 | 2752 | 03 | 01 | 99.96 |
| 48 patients | 109,966 | 109,910 | 109,759 | 151 | 207 | 99.81 |
Fig. 7.
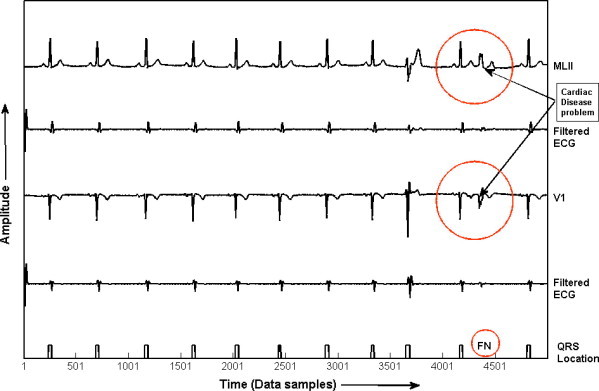
QRS detection in record no. 201 of MIT-BIH Arrhythmia database.
Fig. 8.
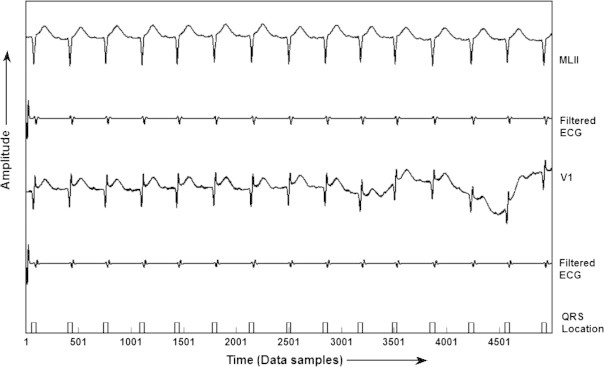
QRS detection in record no. 207 of MIT-BIH Arrhythmia database.
The detection performance of our proposed algorithm in comparison to other published works tested on MIT-BIH Arrhythmia database is also given in Table 5 [11,12,6,13,30,14,16,15,10,17,31,32]. The percentage of sensitivity/rate of accurate QRS detection given in Table 5 is not directly comparable, because, different number of beats has been used by different researchers. In this work an entire available recordings of MIT-BIH Arrhythmia database have been considered in comparison to the first 5 min of records of MIT-BIH database, used as a learning period in some earlier published works, and were not considered in the validation. Further, precautions have also been taken in reporting the accurate number of total beats on the account of false positive and false negative beats.
Table 5.
Comparison of proposed KNN algorithm with other QRS detection algorithms using MIT-BIH Arrhythmia database.
| Database | QRS detector | Reference | Detection rate (%) |
|---|---|---|---|
| MIT-BIH database (109,966 beats) | KNN algorithm | Using proposed algorithm | 99.81 |
| MIT-BIH database (109,809 beats) | A real-time QRS detection based upon digital analysis of slope, amplitude and width | [11] | 99.30 |
| MIT-BIH database (109,267 beats) | QRS detection using optimized decision rule process | [12] | 99.46 |
| MIT-BIH database (Record 105) | NN based adaptive matched filtering for QRS detection | [6] | 99.50 |
| MIT-BIH database (104,181 beats) | Detection of ECG characteristic points using wavelet transform | [13] | 99.83 |
| MIT-BIH database (2572 beats) | QRS detection based on optimized prefiltering in conjunction with matched filter and dual edge threshold | [30] | 97.80 |
| MIT-BIH database (14,481 beats) | Use of wavelet transform for ECG characterization | [14] | 98.78 |
| MIT-BIH database (103,763 beats) | WT based QRS detection | [16] | 99.80 |
| MIT-BIH database (109,428 beats) | WT based QRS detection | [15] | 99.66 |
| MIT-BIH database (110,050 beats) | QRS detection using combined adaptive threshold | [10] | 99.74 |
| MIT-BIH database (110,050) | Empirical mode decomposition | [17] | 99.84 |
| MIT-BIH database (109488) | Multi wavelet packet decomposition | [31] | 99.14 |
| MIT-BIH database (109,481) | Shannon energy envelope (SEE) estimator | [32] | 99.80 |
Thus, as established using all the actual 125 records of CSE database of 10 s duration and all 48 ECG recordings of MIT-BIH Arrhythmia database of 30 min duration, the proposed algorithm accurately detects all the QRS-complexes. Hence, it is capable of detecting all kinds of morphologies of QRS-complexes, which has a direct bearing on the ECG interpretations.
Conclusion
The present paper lays much emphasis on (i) the algorithmic considerations of proposed algorithm, (ii) its methodological aspects related to the classification and (iii) its capabilities of detecting QRS-complexes leading to the ability to precisely discriminate between pathologies. This paper proposes a new method for QRS detection using KNN classifier. The results has been validated on two different standard annotated ECG databases, (i) 125 original 12-leads ECG recording of dataset-3 of CSE multi-lead measurement library and (ii) 48 half-an-hour 2-leads recording of MIT-BIH Arrhythmia database. The purpose of using these databases of different sampling rates is to take into consideration the wide diversity of morphologies of ECG signals. In this work gradient of an ECG signal has been calculated and used for the generation of a feature signal for the KNN classifier. Further, for the accurate detection of QRS-complexes, an optimal value of K, i.e. 3 and type of distance metric for computing the nearest distance, i.e. Euclidean has been proposed using fivefold cross-validation for the KNN classifier. The efficacy of the proposed value of K and type of distance metric has been demonstrated by performing the comparative analysis between five different values of K, i.e. 1, 3, 5, 7 and 9 and three types of distance metrics, i.e. Euclidian, City block and Correlation distance. Looking to the performance of the proposed algorithm, which gives the detection rate of 99.89% on CSE DS-3 and 99.81% on MIT-BIH Arrhythmia databases, prove the efficacy of KNN algorithm for the accurate and reliable detection of QRS-complexes. Further, the training done on a dataset is equally applicable for other datasets having same sample rate.
The results have also been compared with other contemporary published works and authenticated that this algorithm outperforms the other existing algorithms (which includes even the algorithms designed exclusively for real-time applications) for the detection of QRS-complexes. Thus, it is possible that this algorithm of QRS detection is capable of enhancing specific rhythms in ECG signals, which are in turn proves helpful in accurately detecting the QRS-complexes. Hence, this method of detection of QRS-complexes leads to a better visual and automated ECG analysis, which is not only desirable in basic physiology studies, but also a prerequisite for a widespread utilization of QRS detection techniques in clinical studies like heart rate variability, where simplicity and effectiveness of information are of primary importance.
Footnotes
Peer review under responsibility of Cario University.

References
- 1.Kyrkos A., Giakoumakis E.A., Carayannis G. QRS detection through time recursive prediction technique. Signal Process. 1988;15:429–436. [Google Scholar]
- 2.Murthy I.S.N., Prasad G.S.S.D. Analysis ECG from pole zero models. IEEE Trans Biomed Eng. 1992;39:741–751. doi: 10.1109/10.142649. [DOI] [PubMed] [Google Scholar]
- 3.Mehta S.S., Lingayat N.S. Combined entropy based method for detection of QRS complexes in 12-lead electrocardiogram using SVM. Comput Biol Med. 2008;38:138–145. doi: 10.1016/j.compbiomed.2007.08.003. [DOI] [PubMed] [Google Scholar]
- 4.Trahanias P.E., Skordalalkis E. Bottom up approach to the ECG pattern-recognition problem. Med Biol Eng Comput. 1989;27:221–229. doi: 10.1007/BF02441478. [DOI] [PubMed] [Google Scholar]
- 5.Vijaya G., Vinod K., Verma H.K. ANN-based QRS-complex analysis of ECG. J Med Eng Technol. 1998;22:160–167. doi: 10.3109/03091909809032534. [DOI] [PubMed] [Google Scholar]
- 6.Xue Q., Hu Y.M., Tompkins W.J. Neural network based adaptive matched filtering for QRS detection. IEEE Trans Biomed Eng. 1992;39:317–329. doi: 10.1109/10.126604. [DOI] [PubMed] [Google Scholar]
- 7.Mehta SS, Dave V, Vyas SD, Chouhan VS. Detection of QRS-complexes in 12-lead ECG using error back propagation neural network. In: Int cong on bio and med eng, Singapore; 2002.
- 8.Mehta S.S., Lingayat N.S. Development of entropy based algorithm for cardiac beat detection in 12-lead electrocardiogram. Signal Process. 2007;87:3190–3201. [Google Scholar]
- 9.Mehta S.S., Lingayat N.S. Development of SVM based classification techniques for the Delineation of wave components in 12-lead electrocardiogram. Biomed Signal Process Control. 2008;3:341–349. [Google Scholar]
- 10.Christov Ivaylo I. Real time electrocardiogram QRS detection using combine adaptive threshold. Biomed Eng. 2004;3:28. doi: 10.1186/1475-925X-3-28. [Online] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pan J., Tompkins W.J. A real time QRS detection algorithm. IEEE Trans Biomed Eng. 1985;32:230–236. doi: 10.1109/TBME.1985.325532. [DOI] [PubMed] [Google Scholar]
- 12.Hamilton P.S., Tompkin W.J. Quantitative investigation of QRS detection rules using MIT/BIH Arrhythmia database. IEEE Trans BME. 1986;33:1157–1165. doi: 10.1109/tbme.1986.325695. [DOI] [PubMed] [Google Scholar]
- 13.Li C., Zheng C., Tai C. Detection of ECG characteristic points using wavelet transforms. IEEE Trans BME. 1995;42:21–28. doi: 10.1109/10.362922. [DOI] [PubMed] [Google Scholar]
- 14.Sahambi J.S., Tondon S.N., Bhat R.K.P. Using wavelet transforms for ECG characterization – an on-line digital signal processing system. IEEE Eng Med Biol. 1997:77–83. doi: 10.1109/51.566158. [DOI] [PubMed] [Google Scholar]
- 15.Pablo J.M., Almeida R., Olmos S.S., Rocha A.P., Laguna P. A wavelet-based ECG delineator: evaluation on standard database. IEEE Trans BME. 2004;51:570–580. doi: 10.1109/TBME.2003.821031. [DOI] [PubMed] [Google Scholar]
- 16.Saxena S.C., Vinod K., Hamde S.T. QRS detection using new wavelets. J Med Eng Technol. 2002;26:7–15. doi: 10.1080/03091900110096038. [DOI] [PubMed] [Google Scholar]
- 17.Hadj Slimane Z.-E., Amine N.-A. QRS complex detection using empirical mode decomposition. Digital Signal Process. 2010;20:1221–1228. [Google Scholar]
- 18.Friesen G.M., Thomas C.J., Jadallah M.A., Yates S.L., Quint S.R., Nagle H.T. A comparison of the noise sensitivity of nine QRS detection algorithm. IEEE Trans Biomed Eng. 1990;37:85–98. doi: 10.1109/10.43620. [DOI] [PubMed] [Google Scholar]
- 19.Kohler B.-U., Hennig C., Orglmeister R. The principles of software QRS detection. IEEE Eng Med Biol Mag. 2002;21:42–57. doi: 10.1109/51.993193. [DOI] [PubMed] [Google Scholar]
- 20.Yazdani A, Ebrahimi T, Hoffmann U. Classification of EEG signals using Dempster Shafer theory and a K-nearest neighbor classifier. In: Proc of the 4th int IEEE EMBS conf on neural engineering, Antalya, Turkey; April 29–May 2, 2009. p. 327–30.
- 21.Thirumuruganathan S. A detailed introduction to K-nearest neighbor (KNN) algorithm; 2010.
- 22.Karimifard S, Ahmadian A, Khoshnevisan M, Nambakhsh MS. Morphological heart arrhythmia detection using Hermitian basis functions and KNN classifier. In: Proceedings of the 28th IEEE EMBS annual international conference, New York City, USA; August 30–September 3, 2006 p. 1367–70. [DOI] [PubMed]
- 23.Willems J.L., Arnaud P., Van Bemmel J.H., Bourdillon P.J., Degani R., Denis B. A reference database for multilead electrocardiographic computer measurement programs. J Am Coll Cardiol. 1987;10:1313–1321. doi: 10.1016/s0735-1097(87)80136-5. [DOI] [PubMed] [Google Scholar]
- 24.Massachusetts Institute of Technology. MIT-BIH ECG database. <http://www.physionet.org/cgi-bin/atm/ATM>.
- 25.Chouhan V.S., Mehta S.S. Detection of QRS complexes in 12-lead ECG using adaptive quantized threshold. Int J Comput Sci Network Security. 2008;8(1):155–163. [Google Scholar]
- 26.Gritzali F. Towards a generalized scheme for QRS detection in ECG waveforms. Signal Process. 1998;15:183–192. [Google Scholar]
- 27.Mehta S.S., Shete D.A., Lingayat N.S., Chouhan V.S. K-means algorithm for the detection and delineation of QRS-complexes in electrocardiogram. Elsevier IRBM. 2010;31:48–54. [Google Scholar]
- 28.Trahanias P.E. An approach to QRS-complex detection using mathematical morphology. IEEE Trans Biomed Eng. 1993;40:201–205. doi: 10.1109/10.212060. [DOI] [PubMed] [Google Scholar]
- 29.Mehta S.S., Saxena S.C., Verma H.K. Computer-aided interpretation of ECG for diagnostics. Int J Syst Sci. 1996;27:43–58. [Google Scholar]
- 30.Antti Ruha, Sallinen S., Nissila S. A real-time microprocessor QRS detector system with a 1ms timing accuracy for the measurement of ambulatory HRV. IEEE Trans BME. 1997;44:159–167. doi: 10.1109/10.554762. [DOI] [PubMed] [Google Scholar]
- 31.Chouakri S.A., Bereksi-Reguig F., Taleb-Ahmed A. QRS complex detection based on multiwavelet packet decomposition. Appl Math Comput. 2011;217:9508–9525. [Google Scholar]
- 32.Sabarimalai M.M., Soman K.P. A novel method for detecting R-peaks in electrocardiogram (ECG) signal. Biomed. Signal Process. Control. 2012;7(2):112–128. [Google Scholar]


