What do we learn from repeated population analyses?

Abstract

Population analyses are performed on new and existing drugs. They play an important role in quantifying the time course of drug effects and provide a means of understanding the impact of variability between individuals on dosing requirements. For some drugs there have been several population analyses reported in the literature. It is important to understand how repeated population analyses can value add and what authors and readers can consider when reviewing such analyses. The purpose of this review is to explore what is learnt from repeated population analyses and provide an understanding of how the value-added nature of these analyses can be considered.

Introduction

The safe and effective use of medicines requires the right drug for the right individual at the right dose. The choice of drug is driven, largely, by the evidence base supporting its safety and effectiveness. The choice of dosing regimen, on the other hand, requires a quantitative understanding of the expected magnitude of drug effects for a given dose, the time course over which desired and adverse effects are likely to occur and how variability in drug exposure and response between patients impacts on dosing requirements. Understanding and quantifying these factors is therefore critical to determine how best to construct dosing regimens that will meet individual patient's needs. Understanding variability in the time course and magnitude of drug effects relates to the pharmacokinetic (PK) and pharmacodynamic (PD) properties of the drug (readers interested in learning more about PK–PD are referred to a recent viewpoint on PK–PD [1]). Quantifying variability in the time course and magnitude of drug effects requires knowledge of the typical effect size in the population and the variability around this effect size both of which may change over time. Variability in response arises from both predictable sources (covariates), e.g. renal function, and non-predictable sources that appear random.

Population analyses have become an established statistical tool for understanding and quantifying the time course of drug effects, and the impact of variability between individuals on drug response. Population analysis techniques are used to quantify both the mean population effect and also to understand the sources of variability around the mean effect (readers who are interested in learning more about population analysis are referred to a recent viewpoint [2]). Since the early work of Sheiner [3] the application of population analysis techniques has become widespread with a seemingly exponential growth in published reports in the literature (Figure 1). Multiple population analyses have been conducted for some drugs and, in some cases, different models have been developed. It is unclear how repeated population analyses for the same drug compare in terms of predictive performance and whether they can be used to confirm or deny beliefs about the system that transcends a specific drug. Of particular importance in the clinical setting is the question of whether variability between trial populations will influence the utility of any population analysis to predict drug response across different clinical settings.

Figure 1.

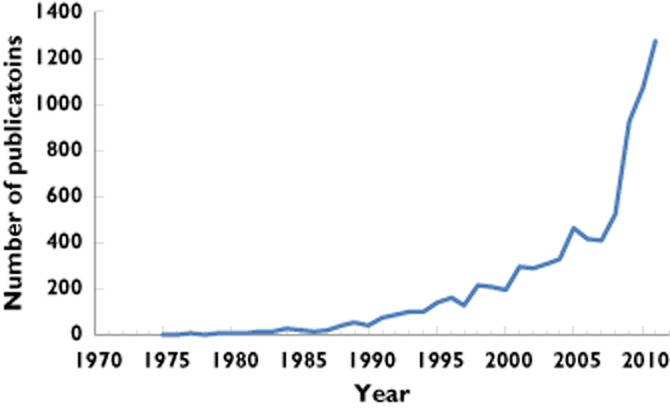
Number of publications per year that relate to population analyses (based on MEDLINE and EMBASE citations)

The primary reasons for conducting a population analysis are to identify and describe sources of variability in drug exposure and response and to provide an accurate description of the mean response across individuals and for each individual. The ability of a population analyses to provide information relevant to the reader will therefore depend on the characteristics of the study population. Rarely are studies designed solely for the purpose of identifying and quantifying the influence of covariates. Generally population analyses are conducted either as an additional analysis on top of a study that was designed for another purpose (e.g. Bruno et al. analyzed the TIMI study [4]) or to quantify a specific source of potential variability, e.g. renal function (e.g. Green et al. assessed the specific influence of renal function [5]). In the former case the covariates that are identified and the sources of variability that are quantified will depend on the study population and may not necessarily reflect all new study populations. It is expected therefore that population analyses may need to be repeated on a specific drug across different settings in order to characterize fully the time course of drug effects. A search using MEDLINE indicates that population analyses have been repeated for many drugs (see Table 1).

Table 1.

Examples of drugs with multiple published population analyses for select therapeutic classes

Drug class	Top drugs	Number of published population analyses
Oncology	Carboplatin	28
	Cyclophosphamide	22
	Etoposide	16
	Docetaxel	30
	Paclitaxel	22
Antiretrovirals	Zidovudine	5
	Didanosine	10
	Efavirenz	19
	Nelfinavir	6
	Nevirapine	11
Anaesthetics	Propofol	44
	Remifentanil	21
	Alfentanil	12
Antibiotics	Gentamicin	26
	Vancomycin	23
	Tobramycin	12
	Amikacin	11
	Meropenem	14
Immunosuppressants	Ciclosporin	48
	Tacrolimus	39
	Mycophenolate	25
	Sirolimus	7
Anticoagulants	Enoxaparin	11
	Warfarin	9
Antidepressants/mood stabilisers	Lithium	5
	Paroxetine	3
Antipsychotics	Clozapine	5
	Respiradone	9

*We have not attempted an exhaustive search of the literature so the numbers of publications are indicative only and the choice of drugs do not necessarily represent all agents in the class. Searches were performed in MEDLINE using MeSH terms: nonmem, Monolix, (non-linear adj2 hierarchical) and model.

In this work we explore how we learn from repeated population analyses. We hope to provide insight into the importance of repeated analyses and also provide a framework for interpreting the results of multiple studies. We have chosen an example drug, enoxaparin, to explore this process, understanding that the results here will not necessarily be representative of all drugs. Enoxparin is a low molecular weight heparin anticoagulant that is used in the initial treatment phase of deep vein thrombosis, pulmonary embolism and acute coronary syndromes. It is also used in the prevention of deep vein thrombosis post-surgery. Like all anticoagulants the choice of dosing regimen is a balance between the risk of bleeding and ongoing thrombotic episodes. Enoxaparin provides a good learning opportunity as the PD biomarker of effect (anti-Xa activity) is also the marker for its PK properties. Hence the PK–PD of enoxaparin can be characterized from a single response model making interpretation of the population analysis simpler.

Methods

A literature review was conducted using MEDLINE (1950–2012) and EMBASE (1947–2012) databases to identify all published population analyses for enoxaparin. MESH terms (enoxaparin, anticoagulants, dose–response relationship, statistical models, biological models, population, algorithms, pharmacokinetics) and keywords (population adj2 pharmacokinetic, nonmem, Monolix or PPharm, non-linear adj2 hierarchical) were used. In addition, key articles were identified and mined for papers.

The analysis of the studies was divided into two parts (i) updating inference from the studies and (ii) comparison of the predictive distributions from the models.

Updating inference from multiple studies

Part 1 provides a setting to compare important inferences that arise from the studies, for instance, identification of new covariates or assessment of the influence of special populations. This part was assessed by summarizing the findings of each study and assessing new and important inferences that occurred chronologically over the period of the publications.

Comparison of the predictive distributions from different population analyses

Part 2 provides a setting to evaluate learning associated with the statistical and structural models that underpin the population analyses. This was assessed by comparing the distribution of model-predicted anti-Xa concentrations (a measure of enoxaparin response) from each published population analysis.

For the purposes of this analysis, it was assumed that published models for enoxaparin were a sufficient summary of their data and hence that a predictive distribution of simulated anti-Xa concentrations under each model would be a sufficient representation of the important features of the model and their original data. An additional assumption of this work was that the published population analyses for enoxaparin were intended by the authors to be (also) used for the prediction of drug response into new clinical settings.

The time course of distributions of predicted anti-Xa concentrations were assessed informally by comparing the 2.5^th, 50^th and 97.5^th percentiles of the predicted data for each model. The resulting plots were termed visual predictive distributions (VPDs). Note that a VPD is methodologically identical to a VPC (visual predictive check) but since there are no actual data presented in this work we have dropped the term check and are considering now the time course of distribution of predictions of enoxaparin anti-Xa concentrations rather than checking the performance of any model against data under which it was built.

All simulations were conducted in MATLAB (2012b). Two plots were generated, (i) VPD plots for individual models and (ii) empirical joint VPD for the disposition model.

VPD plots for individual models

Details of the structural and error models and estimates of all fixed effect and random effect parameters for each population analysis for enoxaparin were reconstructed in MATLAB. The base models, i.e. parameter estimates before accounting for covariates, were not published in all cases so all VPDs were generated using the full covariate model. The demographic details were standardized for each study to represent a typical individual in that study. All predicted anti-Xa concentrations were normalized by dose. All covariate models were normalized to their centred values resulting in their effect being ignored. The covariate models and centred values are summarized in Table 2.

Table 2.

Covariate models for enoxaparin and centred/normalised values for each study

Reference	Covariate models	Centred/ normalized value
Schoemaker & Cohen [6]	Nil	Nil
Bruno et al. [4]	CL = 0.733 + 0.0043*(WT–82)+0.0034*(CLcr–87.9)	WT = 82 kg CLcr = 87.9 ml min−1
Green & Duffull [7]	CL = 1.03*LBW/70 Vc = 3.67*WT/70	LBW = 70 kg WT = 70 kg
Hulot et al. [8]	CL = 0.70*(Scr/97)−0.51 V = 6.65*(WT/72)1.72	Scr = 97 μmol l−1 WT = 72 kg
Green et al. [5]	CL = 0.681*(CLcr/80)+0.229 V = 5.22*WT/80	CLcr = 80 ml min−1 WT = 80 kg
Hulot et al. [9]	CL = 0.74*(WT_Scr ratio/0.79)0.24 V = 5.25*(WT/73)1.49	WT = 73 kg WT_Scr ratio = 0.79
Sanchez-Pena et al. [11]	CL = 1.20*(WT/75)0.9 V = 2.9*(WT/75)0.7	WT = 75 kg
Berges et al. [13]	CL = 0.70*(WT/65)0.78*(CLcr/69)0.25 Vc = 6.43*(WT/65)1.25	WT = 65 kg CLcr = 69 ml min−1
Barras et al. [15]	CL = 0.3*(CLcr/70)+0.42*(LBW/55) Vc = 3.43*LBW/55;	LBW = 55 kg CLcr = 70 ml min−1

CL, clearance; CL_cr, creatinine clearance; LBW, lean body weight; S_cr, serum creatinine concentration; V, volume (1 compartment model); V_c, central volume (2 compartment model); WT, weight.

A VPD plot was generated for each study by simulating anti-Xa concentrations for 1000 individuals. The simulations were conducted under a single fixed dose of 7000 IU and the predicted anti-Xa concentrations were normalized by this dose. The VPD plots included the 2.5^th, 50^th and 97.5^th percentiles of the predicted anti-Xa concentrations at 0, 10 min, 30 min, 1, 2, 3, 4, 6, 8, 12, 18 and 24 h post-dose.

Empirical joint VPD for the disposition model

An empirical joint VPD plot was generated by combining the 2.5^th, 50^th and 97.5^th prediction intervals generated from 1000 predicted anti-Xa concentrations for each study into a single figure. All predicted anti-Xa concentrations were normalized by dose. All covariate models were normalized to their centred values resulting in their effect being ignored (see Table 2).

A summary VPD plot was created by calculating the empirical interquartile range (IQR) for the 2.5^th, 50^th and 97.5^th percentiles over the nine studies at the following times: 0, 1, 6, 30 min, 1, 2, 3, 4, 6, 8, 12, 18 and 24 h post-dose.

In the published studies, enoxaparin was administered by both subcutaneous and intravenous bolus injection. Since the disposition kinetics of enoxaparin are unaffected by the input process then all input processes were converted to an i.v. bolus model, achieved by fixing the duration of an infusion to 1 min or the value of the absorption rate constant to 1000 h⁻¹. This allows all published models to be included in the joint VPDs.

Results

Identification of inference from the studies

Twelve studies [4–15] were identified from the search of MEDLINE and EMBASE databases (Table 3). Three did not provide sufficient model details to enable simulation [10,12,14] and were not included in this analysis.

Table 3.

Characteristic findings of the population analyses for enoxaparin in chronological order of publication

Ref	Year	Design	Model	Covariates identified	Population studied	Purpose of study
Schoemaker & Cohen [6]*	1996	n = 12	2 compartment or 1 compartment + baseline	Nil	HV	Tutorial
Bruno et al. [4]†	2003	n = 448 s.c., 1 mg kg−1 every 12 h,	1 compartment (FO – I/O)	V | WT CL | WT, CLcr‡.	Phase III	Covariate identification and bleeding risk estimation
Green & Duffull [7]	2003	n = 96 s.c., 1 mg kg−1 every 12 h	2 compartment (FO – I/O)	CL | LBW V | WT	DVT, PE, ACS, prophylaxis	Identify dosing regimen for obesity
Hulot et al. [8]	2004	n = 60 s.c., 1 mg kg−1 MD	1 compartment (FO – I/O)	V | WT CL | Scr, SEX	ACS	Covariate identification
Green et al. [5]	2005	n = 38 Dosing based on WT, CLcr	2 compartment (FO – I/O)	CL | CLcr(LBW) V | WT	ACS	Covariate identification
Hulot et al. ¶ [9]	2005	n = 532, s.c.	1 compartment (FO – I/O)	V | WT CL | CLCR	ACS	Identify dosing regimen for renal dysfunction.
Kane-Gill et al. [10]	2005	n = 67, CIVI	1 compartment (ZO/FO – I/O)	Nil	DVT, PE, ACS, AF	Safety and effect of renal dysfunction.
Sanchez-Pena et al. [11]	2005	n = 556, IIVI	1 compartment (ZO/FO – I/O)	CL | WT0.9 V | WT0.7	PCI	Characterize PK after IVI
Feng et al. [12]	2006	n = 83 (35 from Green et al. [5]	2 compartment (FO,ZO/FO – I/O),	CL | CLcr V | WT	GM, ICU	Identify dosing regimen for CIVI.
Berges et al. [13]	2007	n = 189 s.c., 40 mg every 24 h	2 compartment (FO – I/O)	CL | WT,CLcr§ V | WT	VT prophylaxis	Influence of age.
Lebaudy et al. [14]	2008	n = 113 s.c., variety of doses	1 compartment (FO – I/O)	CL | CLcr (PREGNANCY), V | WT(PREG)	Current VT or hyper VT state	Identify influence of pregnancy.
Barras et al. [15]	2009	n = 118	2 compartment (FO – I/O)	CL | LBW, CLcr V | LBW	DVT, PE, ACS, AF	Bleeding risk estimation

All studies except Schoemaker & Cohen [6] and Sanchez-Pena et al. [11] were multiple dose. CL_cr, creatinine clearance; WT, weight. ‘|’ = conditioned on.

^*Data from Stiekema et al. 1993 [18].

^†Originally reported in Retout et al. 2002 [19].

^‡SEX and AGE were also identified but coefficients not reported. CIVI, continuous intravenous infusion; GM, general medical; ICU, intensive care unit; IIVI, intermittent intravenous infusion; s.c., subcutaneous.

^§Using the simplified MDRD equation. ACS, acute coronary syndrome; AF, atrial fibrillation; DVT, deep vein thrombosis; FO–I/O, first order input and output; HV, healthy volunteers; PCI, percutaneous coronary intervention; PE, pulmonary embolism; PREG, pregnancy; VT, venous thromboembolism; ZO, zero order. ¶60 patients were from the study of Hulot et al. [8].

Over the 12 studies two central covariates were identified, an estimate of glomerular filtration rate (eGFR) and two size descriptors total body weight (WT) and lean body weight (LBW). CL_cr was identified from seven studies as a significant covariate [4,5,9,12–15]. In one additional study an inverse relationship with serum creatinine was identified as a covariate for CL [8], in this case this is a simplification of most eGFR formula and hence can be considered as if it were an eGFR. Only the study of Barras et al. [15] found both LBW and eGFR on CL. Volume was best described by either WT or LBW.

No new covariates were identified after 2003 (the third population analysis).

In general the indications were consistent across studies and consisted of pulmonary embolism, acute coronary syndrome, deep vein thrombosis and atrial fibrillation, with one study selecting patients undergoing percutaneous coronary intervention.

In contrast, special populations continued to be studied over the whole publication period. The first special population was studied by Green & Duffull in 2003 [7] who investigated the influence of obesity on the disposition of enoxaparin. Following this, elderly [8,13], renally impaired [5,9] and pregnant [14] populations were also studied. These analyses provided significant insight into the disposition of enoxaparin. It was found that using (the appropriate) eGFR, which accounts for structural and functional changes with these special populations, was sufficient for predicting parameter values without the need for additional covariates.

In other cases the population analyses was conducted as part of a wider aim. In three cases safety and bleeding risks [10,13,15] were identified as the primary aim and the population analysis was conducted in support of these claims.

Comparison of the predictive distributions from the studies

VPD plots for individual models

VPDs over time are shown for the nine models available for consideration (Figure 2). We see that many of the models provide similar dose normalized exposure profiles with exceptions of Green et al. [5] and Berges et al. [13] which appear to have lower exposure and Sanchez-Pena et al. [11] that describes a higher exposure compared with other studies. We note here that the study of Green et al. [5] was small (n = 38) and was designed to assess renal clearance and hence heterogeneity would be expected to be low. The study of Berges et al. [13] differs in that it was based on prophylactic dosing. All profiles were normalized based on the standard patient in each study group.

Figure 2.

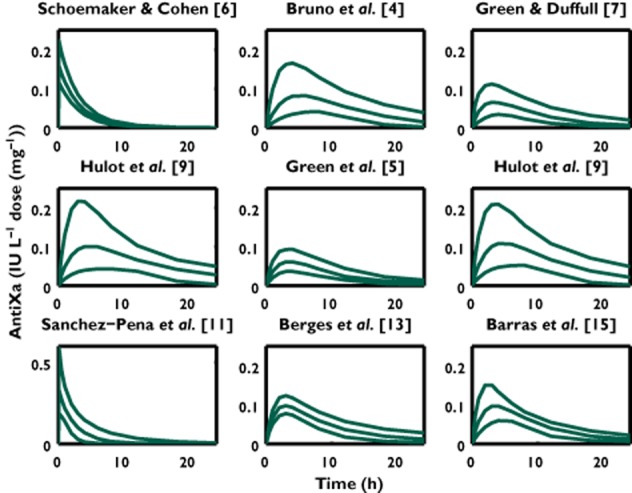
VPDs for each enoxaparin population analysis. Enoxaparin was administered by subcutaneous injection in all studies expect Schoemaker & Cohen [6] and Sanchez-Pena et al. [11]. The lines represent the 2.5^th, 50^th and 97.5^th percentiles of the predicted anti-Xa concentrations

Empirical joint VPD for the disposition model

The disposition profile is presented in Figure 3. We see here that the IQR bands around the upper (97.5^th) middle (50^th) and lower (2.5^th) percentiles are relatively narrow across studies. It is apparent that the time exposure profiles are relatively similar across studies. It is not unreasonable to conclude that the studies are with few exceptions relatively homogenous. A more detailed VPD could be constructed if the data were available for each study and then combined allowing for a study effect. This would provide additional benefits for researchers thinking of conducting further population analyses whereby decisions could be made about the probability that value adding a population analysis would provide significant new inference. In the absence of data sharing then an empirical joint VPD, such as provided here, provides some support for the degree of similarity across studies.

Figure 3.

The interquartile range (IQR) of the 2.5^th, 50^th and 97.5^th percentiles of the predicted anti-Xa concentrations for the joint VPD combining all enoxaparin population analyses. The green lines represent the IQR for the 97.5^th percentile, the blue lines represent the IQR for the 50^th percentile, the orange lines represent the IQR for the 2.5^th percentile. For the purposes of this VPD an intravenous bolus dose was assumed for all studies. , 2.5^th IQR; , 2.5^th percentile; , 2.5^th IQR; , 50^th IQR; , 50^th percentile; , 50^th IQR; , 97.5^th IQR; , 97.5^th percentile; , 97.5^th IQR

Discussion

The goal of population analyses is to make inference about new patient groups who have not (yet) been studied. This inference may be in the form of a dosing recommendation that may appear in the drug label or the probability that a particular dosing regimen may provide a specific effect level. Both of these decisions are based on quantification of the central tendency of the time course of drug effects as well as heterogeneity between patients. Population analyses require PK and PD data which are inherently expensive to collect and complicated to analyze. Hence we see a tendency for researchers to focus on a specific question, such as dosing in renal dysfunction, rather than general questions, such as dosing in a population of adults across all phenotypic groups, concurrent conditions and co-medications. It is therefore expected that each population analysis will provide information about a specific set of study conditions and repeated analyses are therefore both expected and desirable.

In the example reviewed here we see that enoxaparin has 12 population analyses of which nine provide sufficient information in order that the population model can be completely characterized. Enoxaparin was chosen due to its relative simplicity, in that the PK and PD measures are the same. We see that the benefits of repeated population PK studies in terms of covariate identification are realized within the first three to four studies. While further studies did not elicit any new relationships they did provide valuable information about the influence of various special populations (e.g. pregnancy). Importantly researchers continued to review new populations of patients to identify the potential for differences in exposure–response relationships. It appears from this work that special populations tended to be addressed later in the analyses after main covariates have been established.

Similarly we see that the time course of predicted exposure profiles was relatively similar for subcutaneous administration and when shown jointly appeared to provide similar time–exposure profiles. All profiles were dose normalized and based on the standard patient in each study group. It is seen that each study population has a different standard patient which will bias the profiles in this analysis. This highlights the importance of reporting both the best base model (i.e. model without covariates) and the best covariate model. The former provides valuable information on the time–exposure profile that should in theory encompass all new patients whereas the latter provides information about the influence of various covariates on the time–exposure profile, thereby providing the basis for assessing dosing in different settings. Based on the available information with enoxaparin it would be expected that the new information learnt from the different time–exposure profiles would diminish as more population analyses were available and indeed probably may not benefit greatly after the fourth study. We see the importance of considering special populations with the profile of Sanchez-Pena et al. [11] showing a much higher than expected time–exposure profile than would be expected given the administration route. A more formal analysis could be undertaken if the data sets were made available for future researchers or previous work could be incorporated within the framework of a fully Bayesian analysis in the form of an appropriately weighted prior. This would allow combined analyses to be cumulated so that each population studied could contribute to our overall understanding and the influence of a study effect identified. It would also allow for covariate effects to be identified over more diverse populations. In the absence the availability of pooling data the researcher is left with uncertainty about what can be learned from future analyses.

These results are for illustrative purposes and do not necessarily reflect other drugs or other settings. For instance a change in assay procedure (e.g. for ciclosporin) has necessitated new analyses to re-identify exposure–response relationships [16]. In other circumstances drug–drug interactions may occur as a result in a change of practice, for instance a change in the combined use of ciclosporin and mycophenolate will affect conclusions about the exposure relationship with mycophenolate [17], or due to the introduction of new agents.

Conclusion

In this work we consider the potential importance of repeated population analyses. We identify different reasons for the need for such repeated analyses and the importance for authors to identify the value added reasons for their analysis. While it appears that the drug is well characterized within the first few repeated analyses and further work on the base and covariate model is probably unhelpful at this stage it is important to note that learning over special populations continues throughout the time course of published population analyses.

Competing Interests

Both authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare no support from any organization for the submitted work, no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years and no other relationships or activities that could appear to have influenced the submitted work.