Combining the ‘bottom up’ and ‘top down’ approaches in pharmacokinetic modelling: fitting PBPK models to observed clinical data

Abstract

Pharmacokinetic models range from being entirely exploratory and empirical, to semi-mechanistic and ultimately complex physiologically based pharmacokinetic (PBPK) models. This choice is conditional on the modelling purpose as well as the amount and quality of the available data. The main advantage of PBPK models is that they can be used to extrapolate outside the studied population and experimental conditions. The trade-off for this advantage is a complex system of differential equations with a considerable number of model parameters. When these parameters cannot be informed from in vitro or in silico experiments they are usually optimized with respect to observed clinical data. Parameter estimation in complex models is a challenging task associated with many methodological issues which are discussed here with specific recommendations. Concepts such as structural and practical identifiability are described with regards to PBPK modelling and the value of experimental design and sensitivity analyses is sketched out. Parameter estimation approaches are discussed, while we also highlight the importance of not neglecting the covariance structure between model parameters and the uncertainty and population variability that is associated with them. Finally the possibility of using model order reduction techniques and minimal semi-mechanistic models that retain the physiological-mechanistic nature only in the parts of the model which are relevant to the desired modelling purpose is emphasized. Careful attention to all the above issues allows us to integrate successfully information from in vitro or in silico experiments together with information deriving from observed clinical data and develop mechanistically sound models with clinical relevance.

Introduction

Pharmacokinetics is the study of the processes that determine the concentration–time course of an administered drug inside the body. As variation in systemic concentration partly accounts for the variability in therapeutic response, it is reasonable to develop pharmacokinetic models in order to interpret mathematically and predict concentration–time profiles. The complexity of these pharmacokinetic models can range from being entirely ‘exploratory’ and empirical, to semi-mechanistic and ultimately complex physiologically based pharmacokinetic (PBPK) models [1]. This choice is conditional on the goal of the modelling exercise as well as the amount and quality of the available data. In other words, pharmacokinetic models can be built based mainly on the observed clinical data (‘top down’ approach) or based on our broader understanding of the human body and its mechanisms (‘bottom up’ approach) [2]. PBPK models have a physiologically pragmatic compartmental structure based on the actual anatomical characteristics of the body and its organs/tissues [3,4]. The concept of PBPK modelling can be traced back many decades [5] and for many years its applications were mainly related to environmental toxicology research [6,7]. With regards to the pharmaceutical area, until recently PBPK research was mainly carried out in academia. However, this approach has been much more popular and appealing during the last decade, with applications in both drug development and regulatory science [8,9]. This trend can be mainly attributed to three factors. Firstly, advances in computer science and the development of modelling and simulation tools facilitated the PBPK approach in terms of speed, accuracy and accessibility. Secondly, in the past, PBPK models were heavily reliant on animal tissue data in order to extrapolate to humans [10,11]. The development of in silico methods to predict drug–tissue affinity and distribution [12,13] alleviated PBPK from the cost, time and ethical constraints related to the intensive sampling of animal tissues. Finally, the development and refinement of in vitro-in vivo extrapolation (IVIVE) methods allows a more accurate prediction of processes involved in absorption, distribution, metabolism and excretion (ADME) of a compound [14–16].

PBPK models employ a richer information content than empirical models with regards to the anatomy and physiology of the underlying system and consequently they can predict drug exposure in inaccessible tissues where the drug acts or exerts its toxicity [17]. In recent years the latter has motivated the move from traditional perfusion limited PBPK models to transporter-incorporated permeability limited models of certain organs [18]. However, the main advantage of PBPK models over their empirical counterparts is that they provide a rationale to extrapolate not only from animal to human, but also in special populations such as paediatrics [19,20] or the obese [21] and in complex scenarios such as drug–drug interactions [22]. On the contrary, empirical models can be safely used only for interpolation within the studied population and experimental conditions [23]. Nevertheless, these advantages do not come without cost. Physiologically based models are systems of differential equations involving a considerable number of parameters which come from disparate research fields. These parameters can be broadly classified as system-related (e.g. blood flows, organ volumes) and drug-related (e.g. intrinsic metabolic clearance). System-related parameter values for a PBPK model can be extracted from several publications [24–26]. However, it should be noted that these values usually refer to an ‘average individual’ and data for special populations and different disease states are difficult to find. Moreover, as PBPK model complexity is increasing there is a need for more sophisticated system-related parameters (e.g. absolute abundances of hepatic transporters), the determination of which is very challenging. Drug-related parameters have to be extrapolated from in vitro experimental data, which may be limited especially in the first stages of drug development. Moreover, even when the in vitro data are available, the extrapolated model parameters will always carry a certain degree of error due to the uncertainty in the in vitro results or inappropriate system-related scaling factors. In practice, when in vivo data are available, parameters which are either unknown or uncertain are determined through simulation and calibration or more sophisticated parameter estimation techniques [27]. Although such a ‘middle out’ approach is very beneficial, as it permits the application of PBPK models with all the merits described above, it is also prone to limitations which should not be overlooked.

Structural identifiability

The concept of structural identifiability (also referred in the literature as ‘a priori identifiabilty’) [28,29] is important to ensure that the unknown model parameters of interest are uniquely identifiable from a specified experiment, assuming noise-free data. This notion particularly applies in PBPK modelling. In the absence of a unique correspondence between parameter values and the observed output, it is impossible for the researcher to quantify the physiological process that involves the unidentifiable parameter. More importantly, extrapolation to species or populations outside the studied conditions may be unjustified and dangerous. The reader is referred to [30,31] for further information with regards to identifiability analysis techniques in PBPK models. In practice indications for identifiability issues are failure of the optimization procedure to converge, parameter values sensitive to the initial estimates used for optimization and highly correlated parameter estimates [30]. However, it should be noted that structural identifiability analysis is an element of the experimental design and is recommended to be performed at an early stage. One of the possible solutions to resolve identifiability issues is to provide additional information either by perturbing the experimental design [32] (e.g. by sampling in an additional tissue compartment), or by applying a Bayesian framework where prior knowledge about model parameters is utilized [33].

Numerical sensitivity

Even when the model is itself structurally identifiable, it may suffer from practical non-identifiabilities [34]. These difficulties arise mainly from two sources, separately and in combination: (i) due to an insufficient number and quality of observations and (ii) due to lack of sensitivity of the model's output to differences in the values of the parameter. Both of these conditions particularly apply in PBPK modelling. Ethical and experimental considerations may affect the quantity and quality of the data, whilst the physiological-anatomical topology of the estimated parameter is remote from the model's observed output (usually plasma). Practical non-identifiability is usually manifested with increased uncertainty (standard errors) in the parameter estimates and/or problems in the optimization routines to converge to a minimum, as the objective function related to an insensitive model parameter is relatively flat. However, there are measures to avoid these difficulties. Firstly, one of the remedies lies again in the experimental design, as an optimal design approach can be used to optimize sampling collections and thus improve the information content of the data [35]. Secondly, before any attempt to estimate an unknown parameter, it is recommended that a sensitivity analysis is performed in order to investigate if the output is sensitive to the unknown model parameter. Sensitivity analysis is a method that examines how the variation in the output of the model can be attributed, qualitatively or quantitatively, to different sources of variation [36]. The reader is referred to [36] for a comprehensive review of the different methods and technical issues related to sensitivity analysis and to [37,38] for applications in PBPK modelling.

Finally it should be noted here that although a good fit to plasma concentration profiles is a good diagnostic of the PBPK model's performance, it is not necessarily sufficient to regard the model adequate, as particular parameter values might be estimated to be outside their true physiological space in order to provide a good fit. Therefore it is recommended as good practice firstly to assess if the parameter estimates are physiologically plausible and secondly to evaluate the model's predictive performance in situations where some of the pathways of the system are perturbed (e.g. in drug–drug interactions or genetic polymorphisms).

Correlation between parameters upon estimation

An additional issue that should be considered when attempting to estimate parameters in a PBPK model is that some of these parameters are intrinsically correlated, through the underlying physiology [2]. High correlation between model parameters, when neglected, may result in biased, imprecise and sometimes non-physiologically realistic parameter estimates. Therefore, in the case of two highly correlated parameters it is usually recommended either to use a physiologically plausible value extracted from the literature for one of them, or to reparameterize the model in terms of a composite variable. An example of the latter is to parameterize the model in terms of the intrinsic clearance of a compound per pmol of enzyme, instead of separately estimating a different clearance in each eliminating tissue as a separate parameter.

Parameter estimation approaches, uncertainty and variability

As discussed in the previous sections, parameter estimation in PBPK models is challenging because of the large number of involved parameters and the relatively small amount of observed data usually available. Several approaches have been performed in the literature in order to fit PBPK models to observed data. More specifically, one of the proposed methods is to optimize all model parameters together, termed as ‘global optimization’, using Monte Carlo optimization or the simplex method [39]. It should be noted that this approach may provide unrealistic parameters for some of the well defined physiological parameters (e.g. flows and volumes) possibly due to identifiability problems, and therefore it is recommended that these parameters should be constrained (see discussion in [39]). Alternatively, more modern methods such as genetic algorithms, which are based on the concept of natural selection [40], can be applied to optimize simultaneously many parameters in these complex models [41]. However the approach which is more commonly used, is to fix most of the model parameters (to values known from physiology or previous in vitro and in vivo experiments) and optimize only a few unknown model parameters [42]. This is usually done either by a trial and error visual calibration to the observed concentration profiles or by more formal statistical approaches, such as non-linear least squares and maximum likelihood methods. However, this approach is not without limitations and extreme care should be taken when these parameter estimates are used for extrapolation. It should be recognized that with such an approach the parameter estimates are conditional on the values that have been assumed for the fixed parameters [39,43]. Nevertheless, many of these fixed parameters in complex PBPK models involving IVIVE may carry a certain degree of inaccuracy and/or imprecision as with every experimentally obtained result. In addition, as model parameters might be correlated through the underlying system physiology, fixing some of them while optimizing for others distorts the covariance structure of the parameters and may lead to biased estimates [44]. Finally, it should be pointed out that as with any optimized parameter, the fitted estimate itself is always accompanied with a level of uncertainty which derives from imperfect data or any model mis-specifications [45]. It is striking that a large fraction of the recently published PBPK models (in the pharmaceutical arena) that performed parameter optimization estimation do not report any uncertainty on the fitted estimate, while only a few do [46,47]. Reporting a single value for an estimated parameter gives no idea how reliable this estimate is. More importantly, when this parameter is related to a mechanistic hypothesis, which is a subject of extrapolation, any conclusions or predictions cannot be trusted. On such occasions, sensitivity analysis is again a powerful tool to examine different scenarios and support any conclusions.

At this point it should be mentioned that the term uncertainty mentioned above is clearly distinct from the term variability and the reader is referred to [48] for an excellent discussion related to these two terms in PBPK modelling and simulation. Briefly, variability refers to differences attributable to environmental or genetic factors and is a fundamental property of the studied system that cannot be reduced. On the contrary uncertainty is variation that derives from errors in the experimental procedure, measurement, modelling and assumptions of the studied system. It is not itself a system property and it can be reduced through optimization of the experiment. Although difficult, it is desirable to disentangle and separate uncertainty and variability in a parameter estimation process. Ideally, it is desirable to derive parameter estimates not only for the ‘average individual’, but also their distribution in the population. However, a part of the observed variability is a priori related to differences in key system related parameters mechanistically affected by well established covariates (e.g. age, weight) and this information should not be neglected [2,49].

In the majority of published studies using PBPK modelling only a structural model is developed allowing only ‘average individual’ predictions. In practice, clinical data that are used for fitting are extracted from published studies and therefore only average population and no individual concentration profiles are usually available. It should be noted that in this case, not only is inter-individual variability on model parameters unattainable, but also parameter estimates might be biased as averaging of data can produce a distorted picture of the individual model function [50]. In addition, it is commonly observed in the PBPK modelling literature, that even when individual data are available, these are treated as if they arise from the same unique human/animal, an approach usually referred to as ‘naive pooled data’. However the limitations of such an approach have been repeatedly described and the use of hierarchical population modelling is strongly recommended [51,52].

The Bayesian perspective

Many of the shortcomings mentioned in the above section can be avoided when a Bayesian approach is combined with population hierarchical modelling. As explained before, the information contained in the available data is usually insufficient to estimate the numerous parameters in a complex PBPK model. In addition these parameters are mechanistic in nature and thus prior information about their range can be extracted from physiology literature, in vitro experiments and previously published models. Therefore, it makes sense to use the current data in order to update any prior information and beliefs with regards to the model parameters. This Bayesian approach rather than providing single point estimates, outputs statistical distributions of the model parameter values (called ‘posterior distributions’), which are consistent both with the fitted data and prior knowledge. When this approach is combined with a hierarchical population model, it yields posterior distributions not only at the individual but also at the population level [53,54]. In a typical Bayesian analysis these distributions are produced by Markov-chain Monte Carlo (MCMC) methods. The reader is referred to [44] for an introduction on the Bayesian hierarchical approach and to [33,43,55–58] for related applications in physiologically based toxicokinetic and pharmacokinetic modelling.

The advantages of an approach that uses prior information in PBPK modelling can be summarized as follows: it is natural in that it updates prior beliefs in the light of new data, it sets biologically plausible ranges for the well known physiological parameters and it can stabilize the estimation procedure in terms of identifiability with regards to parameters that cannot be informed from the available data. However, the approach does have a number of problems. The first is that sometimes it is difficult to summarize prior knowledge in terms of appropriate statistical prior distributions. This particularly applies to the contemporary IVIVE incorporated PBPK models, where most of the prior information with regards to drug-related parameters comes from in silico methods and in vitro experiments, which either produce point estimates (e.g. mechanistic predictions of partition coefficients) or estimates in which uncertainty and variability cannot be separated (e.g. intrinsic clearance predictions from pooled human liver microsomes). In addition it should be noted that if the analyzed data do not contain enough information with regards to the model parameters upon estimation, these parameter estimates will shrink towards the prior information which could not be updated. Finally, one of the most important shortcomings is that the Bayesian population approach is very computationally intensive and time-consuming, even with present day fast computers [59,60].

In order to overcome this latter obstacle without losing the advantages of using prior information, a maximum a posteriori (MAP) estimation method can be applied, which is commonly referred to in population pharmacokinetics literature with the contradictory phrase ‘use of frequentist priors’. This method was introduced by Gisleskog et al. [61], as a way to stabilize a sparse data population analysis with information from previous studies when the data from the latter are inaccessible or impractical to pool. Briefly, this is achieved by incorporating a penalty term on the objective function upon minimization, which reflects a representation of the available prior knowledge with regards to model parameters. However, this approach should be clearly distinguished from a Bayesian method in that it does not assume a distribution governing randomness on the parameter estimate, but rather outputs point parameter estimates which are considered as unknown constants in the model. Nevertheless, this method has been successfully applied in PBPK modelling [59] providing parameter estimates which were in close agreement with those from a typical Bayesian analysis [56], but with a substantial improvement in computation times.

Overparameterization, lumping and semi-mechanistic approach

In practice, in a typical pharmacokinetic study it is not usually achievable (or statistically significant) to fit more than three exponentials to a plasma concentration profile, even with reasonably noise free data sampled over a long period after the dose [32]. Therefore, complex PBPK models with numerous compartments and parameters can be considered as a priori overparameterized. The increased dimensionality of such models cause computational and numerical problems during estimation and therefore simpler but still physiologically satisfactory models are desired. This can be achieved with model order reduction techniques, which aim to reduce formally the dimensionality of a system of differential equations without losing the key dynamic information [62]. One of these methods, that is proper lumping of tissue compartments, has been applied in PBPK to derive simpler models with kinetic behaviour similar to that of the original complex model and a formal methodology for this procedure has been proposed [63]. Other lumping procedures have been also applied to PBPK models [64,65], with the latter being appealing in that it imposes fewer restrictions on lumping conditions and allows concentration predictions in the tissues of the original non-lumped model. However, it should be stated that lumping procedures are valid only locally in the parameter space for a particular set of parameter values [66]. This is of high importance in the context of PBPK models where most of the model parameters are not precisely known and carry a certain degree of uncertainty and variability. In order to address this issue to some extent, a Bayesian automated lumping method has been proposed [67] that is optimal on average as it makes compromises between the different parameter values.

Finally, an appealing approach that avoids some of the parameter estimation difficulties in complex PBPK models is the use of minimal or semi-mechanistic models. These models offer great flexibility as they retain their physiological mechanistic nature only in the parts of the model that are relevant to the desired modelling purpose (see [68] as an example). In the same vein a generalized minimal PBPK model was recently published [69] that allows the estimation of physiologically relevant pharmacokinetic parameters and offers a reasonable alternative to full PBPK modelling when only plasma concentration data are available.

Conclusions and recommendations

Until recently PBPK models were mainly used to simulate concentration profiles using parameter values informed from in vitro or in silico experiments. Parameter estimation in these complex models from observed clinical data was rarely carried out and simpler empirical compartmental models were mainly utilized for this purpose. However, depending on the modelling purpose there are situations where mechanistic modelling offers advantages and a trend towards it has been recently observed. Therefore the combination of physiologically based modelling with parameter estimation techniques seems to be the way forward and already its impact on the PBPK literature progressively increases. An overview of this ‘middle out’ approach together with some of the key concepts described in this manuscript is schematically presented in Figure 1. Although such an approach is not without limitations, some of which were raised here, further methodology research in this field and the rapid advances in computer science can address many of them. The main advantage of this approach is that it allows us to integrate information from in vitro or in silico experiments together with information deriving from observed clinical data and therefore develop mechanistically sound models with clinical relevance. Subsequently, it is apparent that ‘bottom up’ and ‘top down’ modelling strategies, which were traditionally separated, need to approach and borrow skills from each other.

Figure 1.

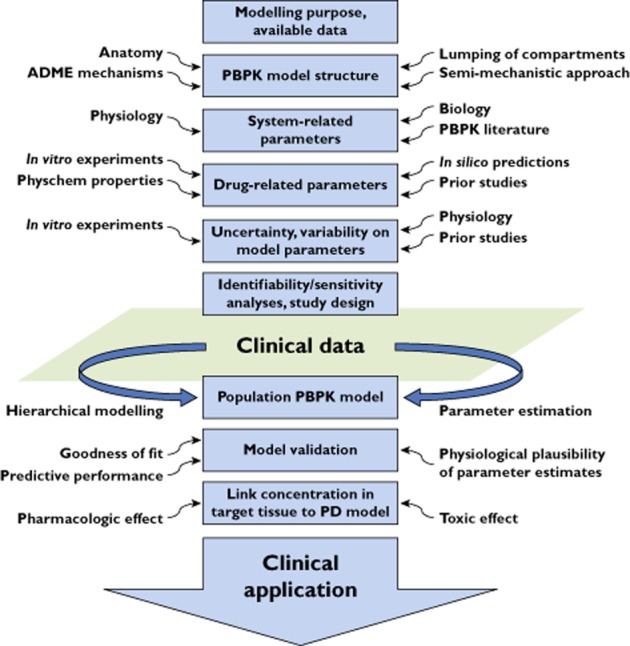
An overview of the ‘middle out’ approach

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare no support from any organization for the submitted work. AR-H is an employee of the University of Manchester and part time secondee to Simcyp Limited (a Certara Company). Simcyp's research is funded by a consortium of pharma companies. NT received support from Eli Lilly and Company. No other relationships or activities that could appear to have influenced the submitted work.