Population pharmacokinetic–pharmacodynamic modelling in oncology: a tool for predicting clinical response

Abstract

In oncology trials, overall survival (OS) is considered the most reliable and preferred endpoint to evaluate the benefit of drug treatment. Other relevant variables are also collected from patients for a given drug and its indication, and it is important to characterize the dynamic effects and links between these variables in order to improve the speed and efficiency of clinical oncology drug development. However, the drug-induced effects and causal relationships are often difficult to interpret because of temporal differences. To address this, population pharmacokinetic–pharmacodynamic (PKPD) modelling and parametric time-to-event (TTE) models are becoming more frequently applied. Population PKPD and TTE models allow for exploration towards describing the data, understanding the disease and drug action over time, investigating relevance of biomarkers, quantifying patient variability and in designing successful trials. In addition, development of models characterizing both desired and adverse effects in a modelling framework support exploration of risk-benefit of different dosing schedules. In this review, we have summarized population PKPD modelling analyses describing tumour, tumour marker and biomarker responses, as well as adverse effects, from anticancer drug treatment data. Various model-based metrics used to drive PD response and predict OS for oncology drugs and their indications are also discussed.

Introduction

Cancer remains an unmet medical need [1]. Not only is there a need to develop new drugs in oncology, but also to improve the speed and efficiency of clinical oncology drug development [2]. In the current paradigm, overall survival (OS), i.e. the time from randomization until death from any cause, is considered the most reliable and preferred endpoint to evaluate treatment benefit in oncology [3]. However, it may take years for OS data to become mature such that statistical conclusions can be drawn. Drug approval (pending) may therefore be granted based on an improvement in progression-free survival (PFS, time from randomization until objective tumour progression or death [3]). Support of PFS as a surrogate for OS, however, has been shown only with advanced colorectal and advanced ovarian cancers [4].

There are practical challenges for oncologic drug development – it may be difficult to characterize the dose–response relationship as often only one or two doses are studied in the target patient population, and placebo data are rarely available. There is also typically a narrow therapeutic index in that drug concentrations that cause tumour shrinkage may also cause adverse effects. In recent years, population pharmacokinetic–pharmacodynamic (PKPD) modelling has become a key tool towards streamlining oncologic drug development through early understanding, identification and quantification of various dose–response relationships. Population PKPD modelling provides a systematic way to develop and assess model-based metrics as ‘drivers’ for various responses to treatment which can then be evaluated as predictors for survival in parametric time-to-event (TTE) models.

In this review, we present clinical oncology analyses that incorporate population PKPD modelling approaches to describe tumour, tumour marker and biomarker responses, as well as adverse effects, and highlight analyses that assess model-based metrics and baseline patient factors as predictors of OS. We also discuss three population PKPD models that are frequently applied in clinical oncology drug development: (1) the tumour growth inhibition (TGI) model for tumour response, (2) the indirect response (IDR) model for biomarker response and (3) the myelosuppression model for leukocyte, neutrophil and platelet responses.

Shown in Figure 1 is a proposed modelling framework, expanded from Bruno & Claret [5], which encapsulates this review and illustrates a methodology towards establishing quantitative relationships between model-based metrics and treatment outcome. We refer the reader to reviews on population PK [6,7], PKPD [8–11] and model-based drug development [12–15] which have nicely presented these concepts. The similarity among measurements and endpoints for oncology, regardless of cancer type, makes this an applicable framework for clinical drug development programmes. For example, 1) for solid tumours, tumour sum of longest diameter (SLD) measurements are used as an indication of treatment effect, 2) circulating biomarkers, predictive of drug mechanism of action, are assessed as early indicators of treatment effect, 3) adverse effects, such as chemotherapy-induced myelosuppression, are noted across many cancer treatments and 4) PFS and OS are primary clinical endpoints for evaluating treatment success.

Figure 1.

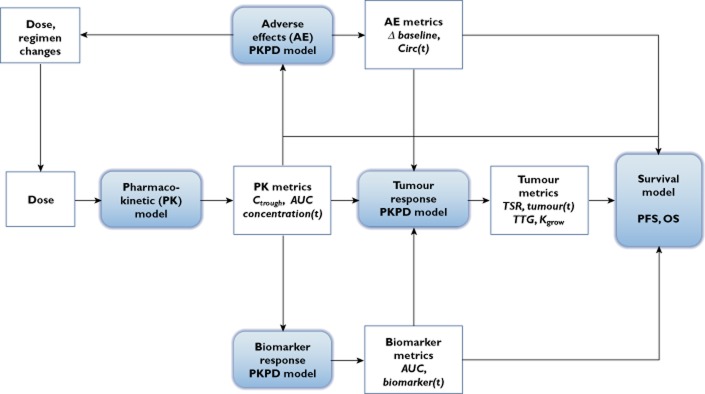
Model-based framework for clinical oncology drug development. From development of a population PK model, PK metrics can be implemented into PKPD models for various responses, i.e. adverse effects, tumour and biomarker responses, and also assessed as predictors for survival. PKPD models can support dose and regimen changes, as well as provide model-based metrics that can be assessed as drivers for other PD responses and as predictors for survival. Δ baseline: change from baseline; AUC: area under the curve; biomarker(t): biomarker time course; Circ(t): circulating blood cell (e.g. platelets, neutrophils) time course; Concentration(t): Drug concentration–time course; C_trough: drug trough concentrations; K_grow: tumour growth rate constant parameter; OS: overall survival; PFS: progression-free survival; PKPD: pharmacokinetic-pharmacodynamic; Tumour(t): tumour time course; TSR: tumour size ratio; TTG: time to tumour growth

Population PKPD modelling

As shown in Figure 1, a population PK model, typically described using compartments, is developed from drug concentration–time data. PK parameters (e.g. clearance (CL) and volume of distribution (V)) and their variability are estimated and individual patient PK parameters can be obtained. Individual patient characteristics (i.e. covariates), such as weight, creatinine clearance, etc., can be tested and implemented into the model to explain the between patient variability [7]. The development of a population PK model that well describes the drug concentration–time data implies an understanding of how the body is processing the drug.

Following this analysis, pharmacometricians may attempt to incorporate PK model-based metrics to describe the drug concentration–effect (i.e. PKPD) relationship(s). ‘PD’ refers to pharmacodynamic variable, and herein we have reviewed PD measurements associated with tumour burden, biomarker and adverse effects. During PKPD model building, PK metrics can be tested as ‘drivers’ of the specific PD response. These include fixed time point descriptors (e.g. C_max, C_trough), summary measurements of overall exposure (e.g. AUC, C_ss) and the model-predicted drug concentration–time (t) curve. Factors such as the drug mechanism of action and the time frame of PD response, as it relates to the driver and dosing scheme, should be considered when assessing drivers of PD response. As shown in Figure 1, metrics derived from the adverse effect and biomarker PKPD models can also be assessed as drivers for tumour responses, similar to PK metrics. These analyses can confirm or drive new hypotheses as to how the drug is reducing tumour burden and may provide an early indication of anti-tumour efficacy. The development of clinical oncology PKPD models may help to design subsequent trials towards minimizing toxicity and optimizing efficacy through establishment of an optimal dose, optimal regimen, for the optimal patient.

Population modelling of tumour size

In oncology, the Response Evaluation Criteria in Solid Tumours (RECIST; currently version 1.1) is used to describe tumour response to treatment [16]. Tumour progression is defined as a > 20% increase in tumour SLD over baseline (or from best response), with a minimum 5 mm absolute increase, or appearance of any new lesions. However, RECIST 1.1 is not an optimal assessment of drug efficacy: 1) information is lost when the continuous tumour SLD data are categorized, including information on the initial tumour burden, 2) the number of metastases, or metastatic location, is not considered and 3) with regard to anti-angiogenic therapies, where drug effect is cytostatic rather than cytotoxic, a change in tumour size may not adequately assess treatment efficacy [17]. PKPD modelling of longitudinal tumour SLD data on a continuous scale preserves relevant information, and the outcome of other doses and schedules than those investigated can be more accurately explored.

Table 1 shows representative analyses, for a diversity of solid tumour types and treatment drugs, in which the time course of longitudinal tumour SLD was described by population PKPD models. In 2008, Tham et al. [18] proposed a model describing gemcitabine effect on tumour size in patients with non-small cell lung cancer (NSCLC). Tumour response was characterized by a Gompertz-like model (equation 1) in which the drug effect (Effect), described by an E_max model, inhibited tumour growth

Table 1.

Population analyses of clinical tumour SLD response

Tumour type	Treatment	PD measurement (s)	Driver of PD response	Model type	Predictors for survival
					Model-based	Other	Reference
NSCLC	Gemcitabine + carboplatin	Tumour SLD	Dose, AUC	Gompertz-like	–	–	Tham et al., 2008 [18]
NSCLC	Various chemotherapies	Tumour SLD	None; dose-independent	Linear growth; exp shrinkage	TSR (week 8)	ECOG, tumour SLD0	Wang et al., 2009 [19]
NSCLC	C/P or C/P + bevacizumab or C/P + motesanib	Tumour SLD	None; dose-independent	Linear growth; exp shrinkage	TSR (week 8)	ECOG, tumour SLD0	Claret et al., 2012 [20]
RCC	Sorafenib	Tumour SLD	None; dose-independent	Linear growth; exp shrinkage	–	–	Maitland et al., 2013 [21]
Metastatic RCC	Everolimus	Tumour SLD	Dose history	Linear growth; exp shrinkage	–	–	Stein et al., 2012 [22]
CRC	Capecitabine; Fluorouracil	Tumour SLD	Daily dose	TGI	TSR (week 7)	Tumour SLD0	Claret et al., 2009 [23]
Thyroid cancer	Motesanib	Tumour SLD	AUCss	TGI	TSR (week 8)	ECOG, tumour SLD0	Lu et al., 2010 [26] Claret et al., 2010 [65]
GIST	Sunitinib	Tumour SLD	Daily AUC, sVEGFR-3(t), sKIT(t)	TGI	–	Tumour SLD0	Hansson et al., 2011 [24], Hansson 2012 [29]
GIST, metastatic RCC	Sunitinib	Tumour SLD	Concentration(t)	TGI	–	AUCss	Houk et al., 2010 [25]
mCRC	Bevacizumab + chemotherapy	Tumour SLD	Constant exposure	TGI with constant exposure	TTG, TSR (week 6)(*), log(G)(*),	ECOG, tumour SLD0(*), treatment arm(*), number of organs	Claret et al., 2013 [28]
Metastatic breast cancer	Capecitabine or docetaxel or capecitabine + docetaxel	Tumour SLD	Dose history	TGI with Gompertz growth	–	–	Frances et al., 2011 [30]
Low-grade glioma	Procarbazine, nitrosourea, vincristine	Tumour MTD	Dose	TGI with quiescent compartment	–	–	Ribba et al., 2012 [31]
Metastatic breast cancer	Capecitabine + docetaxel	Tumour SLD	Dose	TGI	TSR (week 6)	Tumour SLD0, ECOG, number of metastasis, study effect	Bruno et al., 2012 [32]
Ovarian	C/P; carboplatin/pegylated liposomal doxorubicin	Tumour SLD	Dose history	IDR I	–	–	Wilbaux et al., 2011 [39]

AUC, area under the drug concentration curve; C/P, carboplatin/paclitaxel; CRC, colorectal cancer; ECOG, Eastern Cooperative Oncology Group performance status; exp, exponential; GIST, gastro-intestinal stromal tumour; IDR, indirect response model; log(G), log of the tumour growth rate; MTD, mean tumour diameter; NSCLC, non-small cell lung carcinoma; PD, pharmacodynamic; RCC, renal cell carcinoma; sKIT, soluble stem cell factor receptor; SLD, sum of longest diameters; SLD₀, baseline sum of longest diameters; sVEGFR-3, soluble vascular endothelial growth factor receptor 3; TGI, tumour growth inhibition model; TSR, tumour size ratio; TTG, time to tumour growth.

^(*)Survival analysis was performed using non-parametric methods.

(1)

SLD(t) is the tumour size at time t, the inverse of turnover is a second order rate constant, and SLD₀ is the tumour size at baseline. Drug exposure in an effect compartment accounted for the slow onset of tumour response and the delay in tumour regrowth after washout. A Gompertz model has the characteristic of approaching an asymptote, i.e. a maximal tumour size. However, due to the lack of repeated pretreatment measurements and data from placebo treatment in the study, the rate of tumour growth at baseline could not be estimated and a zero net growth at baseline was assumed. The model parameterization could therefore not explain tumour growth above baseline, as when drug effect wears off, tumour size would eventually approach an asymptote equal to SLD₀. The data the model was developed from showed, however, no clear evidence of tumour regrowth and the model successfully described the tumour SLD time course. The analysis also demonstrated that gemcitabine dose and gemcitabine AUC were equally good predictors of changes in tumour SLD and better than AUC of gemcitabine metabolites.

Wang et al. [19] suggested a model with exponential drug-dependent shrinkage and linear growth with time (equation 2) to describe tumour SLD data from four clinical trials of patients with NSCLC treated with various chemotherapies or placebo.

(2)

SR was a drug-dependent, but dose-independent, tumour shrinkage rate constant. PR, the tumour progression rate constant, described tumour growth as independent of size. This model structure also described data from NSCLC patients treated with carboplatin/paclitaxel alone or in combination with bevacizumab or motesanib [20], as well as data from renal cell carcinoma (RCC) patients treated with sorafenib [21], where the tumour natural growth was first characterized using data from placebo-treated patients. Of note, this initial version of the model did not include dose or drug exposure as predictors and therefore could not be used to simulate tumour response under other dosing regimens. However, a dose–effect or drug exposure–effect could replace the shrinkage parameter (SR), and Stein et al. [22] have applied a model with dose-dependent exponential tumour shrinkage and linear tumour growth to tumour SLD data from metastatic RCC patients treated with everolimus.

In 2009, the tumour growth inhibition (TGI) model was developed by Claret et al. [23] on data from colorectal cancer patients receiving capecitabine on a schedule of 2 weeks on, 1 week off, or 5-fluorouracil (5-FU) on days 1 to 5 every 4 weeks. This model has been subsequently applied by several investigators to several cancer types and drugs. The TGI model is described by equation 3 and the model structure is presented in Figure 2A.

Figure 2.

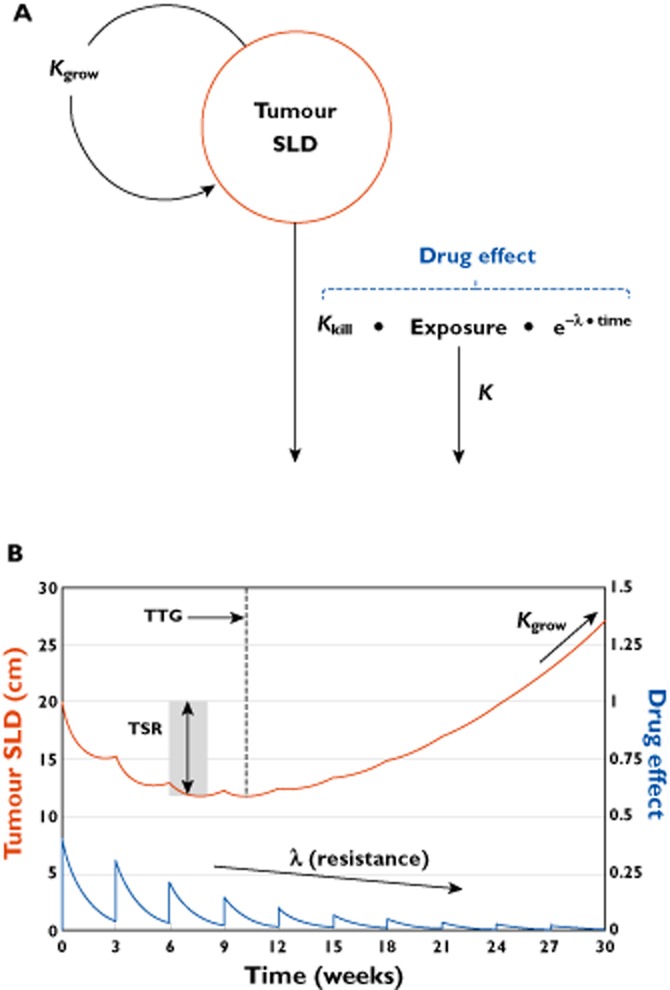
TGI model structure and representative plot. (A) Compartmental representation of the TGI model. K_grow: tumour growth rate constant; Exposure: drug exposure metric; K: drug exposure elimination rate constant; K_kill: tumour kill rate constant; λ: drug resistance parameter. K_grow, K_kill, and λ are model parameters to be estimated. K describes drug elimination in cases where the PKPD driver is dynamic and may be estimated or fixed based on the drug elimination half-life; the K parameter was not in the original publication [23] (i.e. K = 0), but can be applied to characterize reduction in exposure. (B) TGI model-predicted tumour SLD (red curve) and drug effect (blue curve) time courses for a once every 3 week (q3w) drug treatment. TSR: tumour size ratio from baseline, typically assessed after 1 or 2 treatment cycles (6–8 weeks); TTG: time to tumour growth. TSR, TTG, K_grow, and tumour SLD time course are metrics that can be assessed as predictors for survival

(3)

From equation 3, the TGI model assumes that, in the absence of treatment, tumour SLD increases exponentially according to a disease-specific first order growth rate constant K_grow. The tumour SLD doubling rate can readily be derived as ln(2)/K_grow. Drug-related tumour shrinkage is accounted for by a metric for drug exposure (e.g. dose [23], daily AUC accounting for off-treatment periods [24], model-predicted drug concentration [25], AUC at steady-state [26]) and a drug-specific cell kill rate constant (K_kill). Diminishing of drug effect is described by a time-dependent mono-exponential function defined by the parameter λ, which is assumed to start acting at the start of treatment and to be independent of dosing schedule and drug exposure during the trial. The λ parameter may also reflect tumour heterogeneity in drug sensitivity within the tumour at start of treatment, i.e. the most sensitive tumour cells are killed off during the initial treatment, while the cells remaining are less affected by drug and thereby the tumour appears to become resistance to the treatment.

Figure 2B shows a representative plot of drug effect and tumour SLD time course simulated using the TGI model. In this version of the model, the drug exposure is assumed to decrease mono-exponentially via the K parameter, allowing for treatment washout. Several tumour metrics have been derived from the TGI model for assessment as predictors for OS (discussed later in ‘Modelling of overall survival’ section). These metrics, illustrated in Figure 2B, include the tumour time course, the tumour size ratio (TSR), the time to tumour growth (TTG) and K_grow [27,28]. TSR is the change in tumour SLD from baseline at a certain time point, e.g. after one or two treatment cycles (i.e. 6–8 weeks). TTG corresponds to the time of a patient's tumour SLD nadir, at which there is no net tumour growth (i.e. dSLD/dt = 0). If constant exposure is assumed in equation 3, TTG can be directly derived from the individual patient parameter estimates: TTG = [log(K_kill•Exposure) − log(K_grow)]/λ [27].

Using the TGI model approach, Hansson et al. [24,29] showed that model-predicted changes in soluble biomarkers from baseline over time can be better predictors of tumour SLD time-courses than measures of drug exposure. Their study was based on data from gastro-intestinal stromal tumour (GIST) patients treated with sunitinib under different treatment schedules. In the final model for tumour SLD, variable-specific K_kill parameters described the relationship between drivers of tumour response (i.e. relative change in stem cell factor receptor (sKIT), daily AUC, and the relative change in the soluble vascular endothelial growth factor (VEGF) receptor 3 (sVEGFR-3), and tumour SLD. The use of model-predicted exposure-driven time courses for the predictors allows for simulations of tumour SLD under new dosing schedules.

Frances et al. [30] developed a variant of the TGI model (equation 4) for metastatic breast cancer patients treated with capecitabine (C) and/or docetaxel (D).

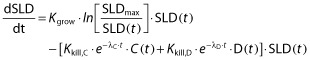(4)

K_kill,C and K_kill,D are efficacy rate constants of the two drugs and λ_C and λ_D are drug-specific resistance parameters. This model included a Gompertz growth, where the proliferation was dependent on the rate constant K_grow and an estimated maximum tumour burden SLD_max, resulting in that tumour growth rate slowed down as the tumour size increased. When administered in combination, the analysis identified a synergistic anti-tumour effect of the two drugs but no diminished effect of capecitabine was supported by the data (λ_C was 0).

Ribba et al. [31] proposed a model for low grade glioma treated with chemotherapy or radiotherapy to provide a biological interpretation for the prolonged response following cessation of treatment. In this model, proliferative cells grow according to a logistic function but can transition to quiescence. By damaging DNA, the treatment affects both proliferative and quiescent/non-proliferative tissue. While damaged proliferative tissue is directly eliminated, damaged quiescent cells are either eliminated or can repair their DNA damages and re-enter the cell cycle and return to the proliferative state. Bruno et al. [32] described SLD data from metastatic breast cancer patients treated with a combination of docetaxel and capecitabine using the TGI model assuming an additive effect of both drugs and resistance development for both drugs.

In oncology, patients who progress on placebo are generally switched to treatment and patients on treatment showing disease progression (i.e. tumour growth or regrowth, new lesions) usually drop out from the study; the natural tumour size growth is often difficult to assess. This explains the variety of models that have been applied to characterize tumour growth on data from clinical trials (linear, exponential, logistic, Gompertz, etc.). It also has the consequence that growth-related parameters can be difficult to estimate precisely and thereby the possibilities to describe accurately changes related to the drug effect may be limited. Noteworthy, neglecting informative dropout due to disease progression can potentially bias tumour growth and/or tumour shrinkage parameter estimates [33]. To be accurate, simulation-based tumour model evaluation or simulation of tumour SLD for new trials should take into account the frequency and time course of dropout, which is dependent on tumour SLD, and can be described, e.g. by a TTE or logistic regression model [34].

Population modelling of tumour markers

Currently, a number of circulating tumour markers are used in clinical practice for some cancer types to diagnose cancer, monitor treatment response, plan treatment and detect disease progression or relapses. These tumour markers are produced in high amount by cancer cells or by other cells of the body in response to cancer. Examples include prostate specific antigen (PSA) in prostate cancer, M-protein in myeloma, cancer antigen 125 (CA-125) in ovarian cancer and carcinoembryonic antigen (CEA) in colorectal cancer. These tumour markers are readily measured in blood, and may be more indicative of the overall cancer burden in the body compared with tumour SLD. Tumour SLD measurements, according to RECIST 1.1, only assess a maximum of five target lesions [16], and traditional two dimensional scans do not reveal changes in tumour density or metabolic activity [35]. Tumour SLD measurements are also subjective, costly and evaluations are limited to every 6 to 8 weeks. Shown in Table 2 are clinical analyses in which the time-course of a tumour marker was described by a population modelling approach.

Table 2.

Population analyses of clinical tumour marker response

Tumour type	Treatment	PD measurement (s)	Driver of PD response	Model type	Predictors for survival		Reference
					Model-based	Other
Prostate	Prostatectomy	PSA	None	Two compartment	CLPSA (*)	–	You et al., 2009 [36]
NSGCT	Bleomycin, etoposide, cisplatin	AFP	None	One compartment	AUCAFG-hCG (*)	–	You et al., 2010 [37]
		hCG	None	One compartment
Multiple myeloma	Dexamethasone	M-protein	Dose	TGI	–	–	Jonsson et al., 2010 [38]
Ovarian	C/P; carboplatin/pegylated liposomal doxorubicin	CA-125	Tumour(t)	IDR III	–	–	Wilbaux et al., 2011 [39]

AFP, alpha fetoprotein; AUC, area under the concentration curve; C/P, carboplatin/paclitaxel; CA125, cancer antigen 125; CL, clearance; hCG, human chorionic gonadotropin; IDR, indirect response model; NSGCT, non-seminomatous germ cell tumour; PD, pharmacodynamics; PSA, prostate-specific antigen; TGI, tumour growth inhibition model.

^(*)Survival analysis was performed using non-parametric methods.

PSA is often elevated in men with prostate cancer or other prostate disorders. You et al. [36] utilized population models to describe PSA levels after prostatectomy in prostate cancer patients. The decline in PSA levels over time was modelled using a two compartment (bi-exponential) model. Similarly, You et al. [37] modelled alpha-fetoprotein (AFP) and human chorionic gonadotropin (hCG) levels in non-seminomatous germ cell tumour patients treated with conventional chemotherapy using mono-exponential models.

In multiple myeloma, excessive amounts of monoclonal immunoglobulin proteins (M-protein) are produced by malignant plasma cells. The M-protein concentration–time curves are similar in shape to tumour SLD–time curves, with some patients appearing to progress with increasing M-protein concentrations after developing resistance, some patients responding to treatment with decreasing M-protein and some patients progressing directly from the start of the study. A drug exposure-driven model, with the same parameterization as the TGI model (equation 3), was applied by Jonsson et al. [38] to describe the time course of M-protein levels in multiple myeloma patients treated with dexamethasone.

CA-125 is a protein that has been shown to play a role in advancing tumour genesis and tumour proliferation which may be elevated in blood serum in some cancers such as ovarian cancer. Wilbaux et al. [39] developed a joint model for drug exposure, tumour SLD and CA-125 concentration following chemotherapy in relapsed ovarian cancer. Tumour SLD was described by an indirect response (IDR) model (see next section and Table 1) where the drug inhibits the production of tumour growth (K_in). Model-predicted tumour SLD stimulated the production of CA-125, which turnover was quantitatively characterized by another IDR model.

Population modelling of biomarkers

From the National Cancer Institute, a biomarker is defined as ‘a biological molecule found in blood, other body fluids or tissues that is a sign of a normal or abnormal process, or of a condition or disease. A biomarker may be used to see how well the body responds to a treatment for a disease or condition’ (http://www.cancer.gov/dictionary). Biomarkers may be assessed early in drug development to indicate that drug has reached its target and elicited some response. Table 3 shows representative analyses in which the time course of a biomarker was described by population PKPD models. The majority of these studies involved VEGF-related biomarkers and utilized the family of indirect response (IDR) models outlined by Sharma & Jusko [40].

Table 3.

Population analyses of clinical biomarker response

Tumour type	Treatment	PD measurement (s)	Driver of PD response	Model type	Predictors for survival		Reference
					Model-based	Other
Healthy volunteers	Sunitinib	VEGF-A	Concentration(t)	transduction function	–	–	Lindauer et al., 2010 [42]
		sVEGFR-2	Concentration(t)	IDR I
mCRC	Sunitinib	sVEGFR-2	Concentration(t)	IDR I	Concentration(t), AUC (*)	Age	Kanefendt et al., 2012 [44]
		sVEGFR-3	Concentration(t)	IDR I
GIST	Sunitinib	VEGF	Daily AUC	IDR II	sVEGFR-3(t)	tumour SLD0	Hansson et al., 2011 [24], Hansson 2012 [29]
		sVEGFR-2	Daily AUC	IDR I
		sVEGFR-3	Daily AUC	IDR I
		sKIT	Daily AUC	IDR I
Solid tumours; lymphomas	E7820	α2-integrin	Concentration(t)	IDR I	–	–	Keizer et al., 2011 [47]

AUC, area under the curve; GIST, gastro-intestinal stromal tumour; IDR, indirect response; mCRC, metastatic colorectal cancer; sKIT, soluble stem cell factor receptor; SLD, sum of longest tumour diameters; SLD₀, baseline sum of longest diameters; sVEGFR-2,3, soluble vascular endothelial growth factor receptor 2, 3; VEGF, vascular endothelial growth factor.

^(*)Survival analysis was performed using non-parametric methods.

The IDR models and equations are presented in Figure 3. Briefly, in the absence of drug, the rate of biomarker change is described by a zero order rate constant for production of the response, K_in, and a first order rate constant for loss of the response, K_out. The biomarker baseline is typically assumed to be constant over time and can be derived as the ratio K_in : K_out, although disease progression or circadian rhythm in production or elimination can be accounted for [41]. The drug effect is commonly defined as a function of drug exposure (e.g. model-predicted drug concentration or daily AUC) and modelled to inhibit (models I and II) or stimulate (models III and IV) the production or loss of biomarker response (Figure 3A). In Figure 3A, the drug effect is parameterized as an E_max model where I_max and S_max are the maximal fractional ability of drug to inhibit and stimulate, respectively; IC₅₀ and SC₅₀ are exposures that produce 50% of maximum inhibition and stimulation, respectively. If the mechanism of action of a drug is known a priori, the appropriate IDR model (I-IV) can be implemented. Otherwise, the model that best fits the data is typically selected. Representative IDR model-predicted time courses of biomarkers and drug effect are shown in Figure 3B for an inhibitory effect on K_in (IDR I) and K_out (IDR II).

Figure 3.

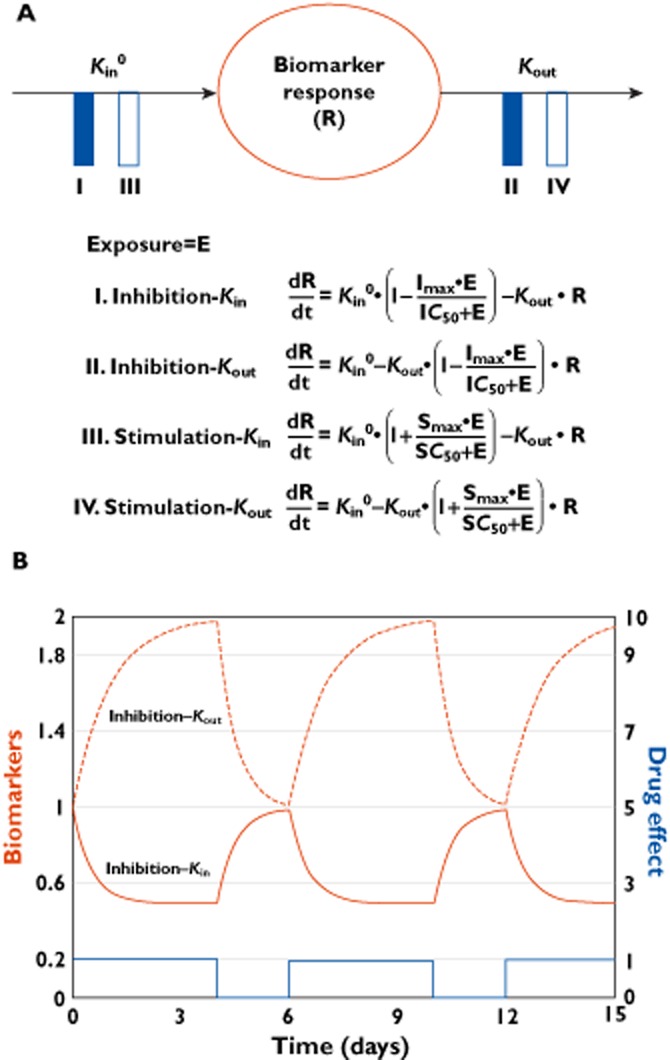
IDR model structure and representative plot. (A) Compartmental representation of the IDR models and associated equations. E: drug exposure; R: biomarker response; K_in: zero order rate constant for production of response; K_out: first order rate constant for loss of the response. The drug effect is exemplified by an E_max model where I_max or S_max are maximal fractional ability of drug to inhibit or stimulate, respectively and IC₅₀ or SC₅₀, are exposures that produces 50% of maximum inhibition or stimulation, respectively. K_in, K_out, IC₅₀ (or SC₅₀), and I_max (or S_max) are model parameters to be estimated. (B) IDR model-predicted biomarker time courses for inhibition of K_in (IDR I, solid red curve) and inhibition of K_out (IDR II, dashed red curve) and drug effect time course (blue curve) for a 4 day constant rate drug input with 2 day washout interval

Population PKPD models have been developed to identify biomarker relationships during treatment with sunitinib, a multi-targeted tyrosine kinase inhibitor, in different populations. In a small cohort of healthy volunteers, model-predicted concentrations of sunitinib and its active metabolite were used as drivers for modelling the time course of two candidate biomarkers, VEGF-A and its soluble receptor sVEGFR-2, after sunitinib administration over 3–5 days [42]. The sVEGFR-2 time course was described by an IDR model with inhibition of its production while the VEGF-A time course was described by a sunitinib-induced transduction function driving the delayed increase in the biomarker [43]. Kanefendt et al. [44] used the same sVEGFR-2 IDR model structure to describe sVEGFR-2 and sVEGFR-3 data in patients with metastatic colorectal cancer treated with sunitinib.

Hansson et al. [24,29] fitted IDR models to the time courses of VEGF, sVEGFR-2, sVEGFR-3 and sKIT in GIST patients treated with sunitinib. A linear disease progression model described the increase in VEGF and sKIT levels over the study period in placebo patients. The biomarkers were estimated to have varying turnover times (3.8 to 101 days for VEGF and sKIT, respectively) and this was also reflected in the degree of fluctuation in the concentration during off treatment periods. Based on the biomarker analysis and the correlations between the biomarker responses, Hansson et al. proposed a unique analytical framework in which the relationships between model-predicted time courses of drug exposure, four biomarkers, tumour SLD, four adverse effects and survival were investigated. Model-predicted changes in sKIT and sVEGFR-3 from baseline over time, in addition to daily AUC, were included as predictors of tumour response in a TGI model. The relative change in sVEGFR-3 was also a better predictor than daily AUC for several common adverse effects of sunitinib (myelosuppression, fatigue and hand-foot syndrome) [29,45].

For GIST patients treated with sunitinib, a PKPD model has also been developed to characterize tumour glucose metabolism as determined by the maximum standardized uptake value (SUV) assessed by fluorodeoxyglucose positron emission tomography (FDG-PET), which has been proposed as a potential biomarker to assess early response to targeted therapies [46]. Daily AUC was found to be more predictive of SUV changes than model-predicted time courses of anti-angiogenic biomarkers or sKIT.

These sunitinib analyses support the use of population PKPD modelling for biomarkers to 1) investigate which biomarkers are of value to be collected, 2) better understand the mechanism of action of the drug in vivo, 3) early assess treatment efficacy and 4) predict long term clinical outcome. Population PKPD models of biomarkers have also been used to integrate preclinical and early clinical phase data and serve as a proof of mechanism. This was illustrated in a study on an investigational anti-angiogenic drug E7820 [47]. An IDR model described the drug effect on platelet α₂-integrin expression inhibition in mice, which was subsequently used to drive tumour growth inhibition. The developed model successfully fitted data from phase I cancer patients and simulations from the biomarker–tumour size relationships determined in mice allowed for identification of doses at which tumour stasis could be met in man.

Population modelling of adverse effects

Shown in Table 4 are clinical analyses in which the time course of an adverse effect was described by a population modelling approach. For chemotherapy, myelosuppression is a common adverse effect. Myelosuppression is a condition in which the proliferation of blood cells in the bone marrow is reduced, resulting in fewer circulating red blood cells, leukocytes (60–70% neutrophils) and/or platelets. Given that chemotherapy typically affects rapidly proliferating cells and the importance for neutrophils and platelets in fighting infections and in blood clotting, respectively, myelosuppression is dose limiting for many anticancer agents.

Table 4.

Population analyses of clinical adverse effects

Tumour type	Treatment	PD measurement (s)	Driver of PD response	Model type	Predictors for survival		Reference
					Model-based	Other
Not reported	Docetaxel, paclitaxel, etoposide, DMDC, irinotecan vinflunine	Leukocytes	Concentration(t)	MS	–	–	Friberg et al., 2002 [48]
		Neutrophils	Concentration(t)	MS
Breast cancer	FEC, docetaxel	Neutrophils	Concentration(t)	MS (modified)	–	–	Quartino et al., 2011 [56]
MBC	T-DM1	Platelets	Concentration(t)	MS (modified)	–	–	Bender et al.,2012 [55]
Non-myeloid malignancies	Darbepoetin alfa	Hemoglobin	Concentration(t)	IDR III (modified)	–	–	Agoram et al.,2006 [57]
Solid tumours	Trabectedin	ALT	Concentration(t)	IDR III (modified)	–	–	Fetterly et al., 2008 [58]
GIST, mRCC	Sunitinib	Δ dBP	Concentrationtrough	Direct Emax	–	–	Houk et al., 2010 [25]
GIST	Sunitinib	Neutrophils	sVEGFR-3(t)	MS	Neutrophil(t), dBP(t)	tumour SLD0	Hansson et al., 2012 [45]
		dBP	Concentration(t)	IDR III
		Fatigue, HFS	sVEGFR-3(t)	Prop odds with Markov
CRC	Capecitabine	HFS	Cumulative dose	Prop odds with Markov	–	–	Henin et al., 2009 [61]
Solid tumours	Irinotecan	Diarrhoea score	AUC	Prop odds	–	–	Xie et al., 2002 [60]

Δ dBP, change in diastolic blood pressure from baseline; ALT, alanine aminotransferase; AUC, area under curve; CRC, colorectal cancer; dBP, diastolic blood pressure; FEC, Fluorouracil (5FU), epirubicin and cyclophosphamide; GIST, gastro-intestinal stromal tumour; HFS, hand-and-foot syndrome, IDR, indirect response model; MBC, metastatic breast cancer; MS, myelosuppression model; mRCC, metastatic renal cell carcinoma; Markov, modification of Prop odds modelling where scores are not independent from one time to the other; Prop odds, proportional odds ratio model for categorical scores; SLD₀, baseline sum of longest diameters; sVEGFR-3, soluble vascular endothelial growth factor receptor 3.

A myelosuppression model was developed by Friberg et al. [48] in 2002 based on leukocyte and neutrophil data from six chemotherapeutic agents. This model has been widely used to characterize neutrophil [49–53], leukocyte [54] and platelet [50,53,55] responses. As shown in Figure 4A, the myelosuppression model is a physiologically based based model, with components of blood cell precursor proliferation, maturation, blood cell circulation and a feedback mechanism, that aim to separate system-related parameters from drug-related parameters. From a population PK model, central compartment concentrations (C_drug) are derived and induce cell kill by a linear (Slope • C_drug (t)), or by a (sigmoid) E_max drug effect. The model consists of a proliferation cell pool (Prol) compartment, three transit compartments (T₁, T₂, and T₃) mimicking the maturation of the non-proliferative cells and a blood circulation compartment (Circ) where the measurements (e.g. neutrophil counts) have been observed over time. Prior to drug treatment, the system is assumed to be at steady-state and intercompartmental transfer rate constants (K_tr) are set to be equal. The feedback process is governed by the parameter (γ), which stimulates the proliferation rate as circulating cell levels are depleted and slows down proliferation when the circulating neutrophil counts are above the baseline value.

Figure 4.

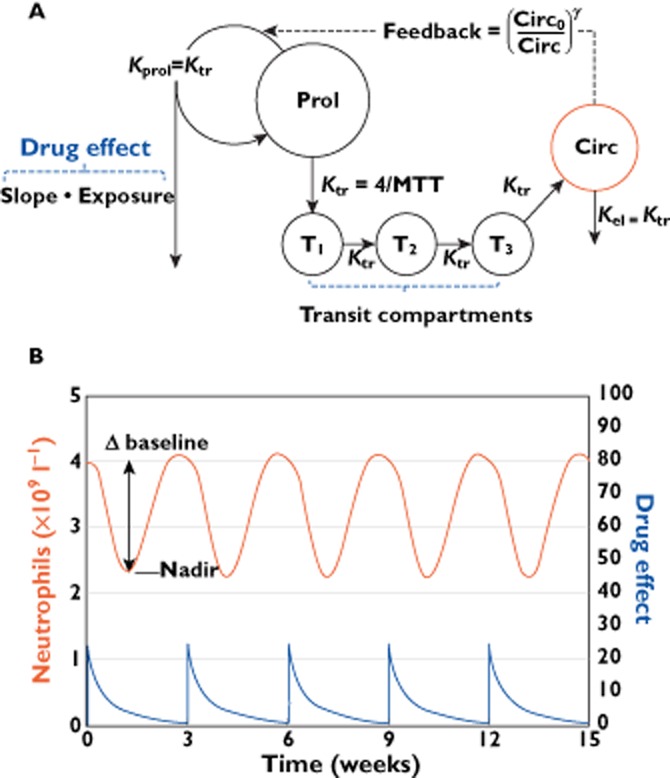
Myelosuppression model structure and representative plot. (A) Compartmental representation of the of the myelosuppression model. Prol: proliferation cell pool compartment; T₁, T₂ and T₃: transit compartments; Circ: blood circulation compartment; Drug effect: slope•exposure; Exposure:, e.g. the drug–concentration time course; Slope: drug inhibition constant; Circ₀: baseline neutrophil count; γ: feedback term; MTT: mean transit time, derived as K_tr/(n + 1), where n is the number of transit compartments. Slope, MTT, Circ₀ and γ are model parameters to be estimated. (B) Myelosuppression model-predicted neutrophil (red curve) and drug effect (blue curve) time courses for a once every 3 weeks drug treatment. Δ baseline may be calculated from the model-predicted (baseline-nadir)/baseline

Shown in Figure 4B is a representative model-predicted neutrophil and drug effect–time course, for a once every 3 weeks intravenous drug treatment. Model-based metrics that may be assessed as indirect measures of drug exposure to predict response in models of other variables include the neutrophil–time course (red line) and the percent change from baseline at nadir (Δ baseline).

The model described by Friberg et al. [48] aimed to be relatively simple with few estimated parameters thereby being applicable in a range of different situations, including model fitting to sparse data. The mechanism-based nature allows however for addition to the structure based on other types of data. One example of an addition to the myelosuppression model is the work by Quartino et al. [56] which incorporated granulocyte stimulating colony factor (G-CSF) measurements. A turnover model of G-CSF, where G-CSF elimination was dependent on the circulating neutrophil counts, replaced the feedback function and provided a more mechanistic interpretation which may allow for improved predictive capacity of chemotherapy-induced myelosuppression. To describe the effect of TDM-1 on platelets, Bender et al. [55] modelled the proliferation compartment as composed of one drug sensitive and one drug non-sensitive lineage, in order to capture the downward drift in platelet nadir, seen in some patients.

Similar to leukocytes, platelets and neutrophils, other drug concentration-driven responses associated with adverse effects from anticancer drugs include haemoglobin reduction (anaemia), elevated liver enzymes (alanine aminotransferase; ALT) and elevated diastolic blood pressure (dBP). These variables have been described by the IDR (or modified IDR) model approach. In patients with chemotherapy-induced anaemia, Agoram et al. [57] used IDR III to describe the haemoglobin time course upon stimulation of its production by darbopoeitin alfa. In patients with trabectedin-induced liver toxicity, Fetterly et al. [58] modelled the time course of ALT using IDR III. Keizer et al. [59], and subsequently Hansson et al. [45], used IDR III to describe the dBP time course after E7080 and sunitinib administration, respectively. Houk et al. [25] also modelled dBP after sunitinib treatment, using a direct E_max model to describe the relationship between trough concentrations and the change in dBP from baseline. These continuous type adverse effects are often categorized into the degree of severity, but by retaining them on a continuous scale, the information is preserved and thereby more useful for predictions of different scenarios.

Some toxicities do not have underlying continuous measurements (e.g. fatigue, hand-and-foot syndrome (HFS), diarrhoea), and are instead only graded using ordered categorical scoring systems; grade 0 refers to no toxicity, and then grades increase in order of toxicity severity. To model ordered categorical scores with a population approach, investigators have used a proportional odds model to predict the probability of having a certain toxicity score. Xie et al. [60] applied such a model to predict diarrhoea after receiving irinotecan using AUC as a driver of response. If subsequent toxicity scores are not independent, i.e. the probability of a certain score is related to a previous score, a Markov model extension may be used. Henin et al. [61] developed a proportional odds ratio model with a Markov process to predict HFS in patients receiving capecitabine using cumulative dose as a driver of response. Hansson et al. [45] applied the same type of model on fatigue and HFS data in patients receiving sunitinib, where sVEGFR-3 was driving the drug effect.

Modelling of overall survival (OS)

In previous sections we have discussed the development of population PKPD models of tumour SLD, tumour markers, biomarkers and adverse effects, and the model-based metrics that can be derived. As illustrated in Figure 1 and listed in Tables 4, these metrics can subsequently be evaluated and implemented into parametric TTE models as predictors for OS, thus providing a model-based prediction for survival benefit. We introduce the basic concepts regarding modelling of survival below, and refer the reader to a recent tutorial on TTE analysis for pharmacometricians [62] and a textbook on modelling survival data [63] for further background.

Shown in equation 5 is the hazard function, h(t), describing the instantaneous rate at which an event (in our case, death) occurs.

(5)

The baseline hazard h₀(t) is defined by one or more estimated parameters, and x₁, x₂, … x_n represent a set of predictors (e.g. one of the metrics in Tables 4 that were related to OS). These predictors may be a derived constant value for each patient (e.g. TSR, Δ baseline), an individual parameter estimate (e.g. K_grow, slope), or a time varying metric (e.g. tumour(t), biomarker(t)) from the population PKPD models. Additionally, patient baseline characteristics (e.g. ECOG status, observed tumour size at baseline, number of lesions, etc.) are frequently assessed as predictors. Incorporation of relevant predictors in the final survival model can be decided according to the log-likelihood ratio test and goodness-of-fit plots, e.g. in a visual predictive check comparing simulated Kaplan–Meier curves with the observed survival data [64]. The impact of the predictors is determined by the size of the respective coefficients β₁, β₂, …, β_n, which are estimated from the data [62].

Shown in Table 1 are examples of tumour SLD-related predictors for survival, both model-based metrics and patient baseline characteristics. Relative or absolute changes from baseline in a variable over time (e.g. tumour SLD) may reflect the drug-induced effect better than the absolute values and thereby be better predictors of outcome. This is often the case when baseline measurements are highly variable, as is for tumour SLD. Indeed, TSR (e.g. at week 6–8) was identified as a predictor for OS in NSCLC [19,20], colorectal cancer [23,28] and metastatic breast cancer [32].

In the analysis by Claret et al. [23], SLD₀ and the model-predicted TSR at week 7 were identified as predictors of OS in the 5-FU arm using a parametric drug-independent survival model. The modelling framework for analysis was used to predict survival in a phase III trial of capecitabine vs. 5-FU. The same approach has been applied to thyroid cancer patients treated with motasenib [26,65] where the probability and duration of dose reduction and interruption were also modelled. Application of this modelling framework has therefore been demonstrated to leverage information from phase II trials to predict phase III outcomes and thereby support end-of-phase II decisions and guide clinical trial design (e.g. dose selection for phase III studies). Further, Bruno et al. [32] found the TSR at week 6 to be predictive of OS and PFS. Using simulations, the authors determined the capecitabine dose that would show non-inferiority to the dose currently registered, when used in combination with docetaxel.

There are drawbacks with TSR in that it is determined at a fixed time point, and thereby can be the same value for a drug with slow drug effect rate and low resistance development as for another drug with a fast drug effect rate and high rate of resistance development. It is not possible to ascertain whether tumour SLD is in a declining or increasing phase at week 6–8. In addition, TSR is typically also applied to predict survival at time points preceding week 6–8, i.e. before the predictor can be determined, and thereby limit its use for simulation. Lastly, changes in treatment after the evaluation time point are not considered, which could be of importance when predicting survival in cancers with longer survival times.

In addition to TSR, the model-based metrics of tumour growth rate and TTG were shown as predictors for survival in a parametric TTE analysis of colorectal cancer data [28]. Tumour growth rate was also shown to be predictive in a correlation analysis of prostate cancer data [66]. TTG is derived using the TGI modelling approach, and this metric summarizes a patient's tumour growth rate, tumour growth inhibition rate and drug efficacy decay [28]. TTG is a measurement in time units, as survival, and may therefore provide the TTE model of OS with more information on when an event will happen compared with TSR. The TTG metric does have similar limitations as TSR, i.e. it is a constant value metric that is used to predict survival also at time points before the metric has occurred, and TTG may be the same value even for patients with vastly different tumour responses (i.e. the extent of tumour shrinkage is not considered). Ultimately, using the full model-based time course (i.e. tumour(t)) as a continuous predictor of survival in parametric TTE models is most useful for simulations of different scenarios since all information contained in the tumour profiles is retained.

Tumour markers have also been related to OS in TTE models (Table 2). These markers (e.g. M-protein, PSA, AFP, hCG) may be more reflective of overall tumour body burden than tumour SLD measurements, and thus survival, providing a convenient and cost-effective alternative to assess therapeutic efficacy. In You et al. [36], several metrics (e.g. PSA clearance (CL_PSA), half-life, AUC) were derived and investigated as prognostic factors for clinical outcome using non-parametric analyses. CL_PSA was found to be a predictor for survival in which patients with lower CL_PSA had a reduced chance for biochemical relapse-free survival. In You et al. [37], the combined model-predicted AUC of AFP and hCG was found to be a predictor for PFS using non-parametric analyses. In Bruno et al. [67], the week 8 change in M-protein from baseline, along with other baseline patient factors, predicted survival in phase III patients with multiple myeloma treated with dexamethasone alone or in combination with lenalidomide. OS and PFS were subsequently simulated for patients in phase I and II studies of another drug, pomalidomide, using interim M-protein data. Simulation results were shown to be similar to actual OS and PFS, supporting the use of M-protein as a biomarker of response in multiple myeloma. The modelling approach may be used to guide end-of-phase II decisions for candidate drugs in multiple myeloma.

Regarding biomarker response, sunitinib AUC [44] and sVEGFR-3(t) [29] have been identified as predictors for OS in mCRC and GIST, respectively (Table 3). Using a parametric TTE model, the model-predicted change in sVEGFR-3 from baseline was found to be a better predictor of OS as compared with change in tumour SLD or sKIT. This finding differed from the results of a traditional statistical analysis where sKIT was reported to be a better predictor of OS than sVEGFR-3 [68]. This may be explained by the fact that only discrete (trough) time points were used in the traditional analysis, and the difference in turnover times between the biomarkers was not considered. A biomarker with a long turnover time like sKIT (101 days) is less sensitive to sampling in off treatment periods as compared with a biomarker with shorter turnover time, like sVEGFR-3 (17 days). Integration of the whole biomarker response by a model-based approach allows for biomarkers with shorter turnover time to be appropriately evaluated, regardless of the time of measurement. Population PKPD modelling of biomarkers in oncology is relatively new, and further work is needed to identify readily measurable, circulating biomarkers that can be used as predictors for treatment responses and as early indicators for survival benefit.

Overall, parametric TTE models offer an evaluation and understanding of survival in a population through testing the predictive ability of patient baseline or time-varying covariates, as well as model-based metrics. TTE models can be used to conduct simulations to predict survival in a new setting, explore different dosing schedules, predict long term clinical outcome in phase III studies based on short term phase II data [23,28], or in the development of guidelines to be applied in clinical practice. It should be noted that we have documented only those predictors which were determined using population PKPD and parametric TTE analysis. Other investigators have identified prognostic indicators (e.g. albumin [69], α₁-acid glycoprotein (AAG) [70]), and predictive indicators (e.g. neutropenia [71], drug trough concentrations [72]) for survival from non-parametric, retrospective analyses of clinical trial data. These indicators should be considered when designing and analyzing new trials.

Discussion

In clinical oncology drug development, a wide range of variables are being collected for a given drug and indication. It is necessary to characterize these factors, and the links between them, to improve understanding and guide future interventions. In this review, we have listed the currently identified PD drivers of response and predictors of OS for oncology drugs and their cancer indication (Tables 4).

The three highlighted PKPD models (TGI, IDR and myelosuppression) have parameters with some mechanistic interpretation and are relatively simple with few parameters and one to five differential equations. These models are readily modifiable if given additional data [56] and/or the need for additional mechanistic detail [55,57]. Application of structural PKPD models should streamline data analysis and allow comparison of results across drugs and indications. For example, the first order tumour growth rate (K_grow) from the TGI model provides tumour doubling times for various cancer types. Comparison of the slope parameter, from the myelosuppression model, may give an indication on the relative toxicity between different anticancer drugs. The magnitude of the estimated variability in these parameters, from the population modelling approach, provides information on the range of patient responses to expect.

We note that the drivers of PD response range from model-predicted time courses, to exposure (e.g. AUC, dose), to none, i.e. ‘dose independent’ (Tables 4). The possibility to apply different drivers is, of course, dependent on what type of data are available and the sampling frequency. For tumour SLD measurements, which are typically made once every 6 or 8 weeks, daily drug AUC may suffice as the PD driver. However, to characterize schedule dependence, there is a need to use the drug–concentration time profile to drive the response. For myelosuppression, in which blood cell counts are readily available and the effect delay is in the order of days, a drug concentration–time course driven response is often applied. Thus, simulation of response and outcomes under other dose and regimens have been used to minimize side effects [73] and optimize drug treatment for individual patients.

The population PKPD and TTE modelling examples presented herein support linking drug exposure with PD response, and linking PD response with survival. This is in order to explain and forecast patient response to drug treatment in oncology, with the ultimate goal of predicting and improving survival by bringing the ‘right drug to the right patient at the right dose’. We propose that investigators consider this framework (Figure 1) for model-based clinical oncology drug development for application in clinical protocol design and analyses. These framework and modelling approaches can readily be extended to combination drug treatment to account for drug–drug interaction in PK and/or PD. Further, we support the use of time courses of time-varying predictors to improve the predictive and simulation value of the models. With a fully integrated modelling framework, both the benefits and risks of a different dosing strategy can be explored, which is of special importance in oncology where a range of outcome measures are being applied and different types of adverse effects are limiting.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare no support from any organization for the submitted work, no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years and no other relationships or activities that could appear to have influenced the submitted work.