The role of concentration−effect relationships in the assessment of QT_c interval prolongation

Abstract

Population pharmacokinetic and pharmacokinetic−pharmacodynamic (PKPD) modelling has been widely used in clinical research. Yet, its application in the evaluation of cardiovascular safety remains limited, particularly in the evaluation of pro-arrhythmic effects. Here we discuss the advantages of disadvantages of population PKPD modelling and simulation, a paradigm built around the knowledge of the concentration−effect relationship as the basis for decision making in drug development and its utility as a guide to drug safety. A wide-ranging review of the literature was performed on the experimental protocols currently used to characterize the potential for QT interval prolongation, both pre-clinically and clinically. Focus was given to the role of modelling and simulation for design optimization and subsequent analysis and interpretation of the data, discriminating drug from system specific properties. Cardiovascular safety remains one of the major sources of attrition in drug development with stringent regulatory requirements. However, despite the myriad of tests, data are not integrated systematically to ensure accurate translation of the observed drug effects in clinically relevant conditions. The thorough QT study addresses a critical regulatory question but does not necessarily reflect knowledge of the underlying pharmacology and has limitations in its ability to address fundamental clinical questions. It is also prone to issues of multiplicity. Population approaches offer a paradigm for the evaluation of drug safety built around the knowledge of the concentration−effect relationship. It enables quantitative assessment of the probability of QT_c interval prolongation in patients, providing better guidance to regulatory labelling and understanding of benefit/risk in specific populations.

Introduction

Predicting the cardiac safety risk of drugs in the general population in a strictly quantitative manner is technically challenging. Drug trials conducted in the pre-marketing period are often designed sub-optimally to detect adverse drug reactions (ADRs) such as cardiac arrhythmias [1], which may show low incidence or display a signal which may go undetected during treatment. Two key regulatory guidelines exist which delineate the strategy by which cardiac safety is assessed during drug development. The first focuses on the preclinical evaluation of cardiac pro-arrhythmic risk [2], whereas the second on the requirements for the evaluation of pro-arrhythmic risk in humans [3]. Despite the concern about the pro-arrhythmic properties of drugs and its impact on cardiovascular safety, little has been done to promote the assessment of causality, i.e. drug-relatedness during the evaluation of QT_c interval prolongation. According to the ICH-E14, drug-induced effects are defined statistically rather than pharmacologically in that the effect size is determined relative to placebo after correction for differences in baseline. The approach assesses drug effects as a discrete variable, preventing direct inferences from underlying pharmacokinetic−pharmacodynamic (PKPD) relationships [4].

Improved decision-making during drug development relies on the availability of appropriate evidence of efficacy and safety prior to the approval process. Here we do not delve into further discussions about whether QT_c prolongation or baseline QT values are the best predictors of arrhythmic events and cardiovascular risk [5,6]. It has been demonstrated that not all drugs that prolong the QT interval to the same amount carry the same risk of inducing torsade de pointes (TdP) and TdP itself does not occur in all subjects with the same prolongation of the QT interval [7,8]. Nevertheless, it should be clear to readers that the current practice is based on the assumption that increase ≥10 ms relative to baseline QT interval is potentially predictive of specific ADRs, such as TdP and has labelling implications for drugs. Irrespective of the prognostic value of the aforementioned measures, achieving a better understanding of the concentration−effect relationship on specific safety parameters, including the QT interval, is particularly beneficial since this can support further evaluation of causality. In this context, it has been shown that PKPD relationships can provide clinically valuable information for drug developers, regulators and clinicians [9,10]. In this review, we explore the advantages and disadvantages of population approaches to determining the QT_c prolongation potential of novel compounds in clinical development and provide an overview of the requirements for systematic use of clinical trial simulations for the evaluation of drug effects on QT_c interval. For the sake of clarity, methodological, pharmacological and clinical aspects are discussed separately.

The physiological and pharmacological basis of pro-arrhythmic effects

The QT interval represents the duration of the ventricular action potential in normal sinus rhythm and normal values are dependent on the resting heart rate (described by the RR interval). Higher heart rates are associated with a shorter QT interval and as such a correction factor has to be applied to numerically describe the QT interval accurately, referred to as the corrected QT interval (QT_c) [11,12]. The evaluation of a drug's potential to prolong the QT_c is relevant because TdP requires prolongation of the QT interval as an antecedent event (Figure 1). QT_c therefore remains the only clinical surrogate for torsadogenicity, even though QT interval prolongation itself is not necessarily harmful [13]. In addition, TdP undergoes morphological evolution, degrading into ventricular fibrillation in about 20% of cases. As a result cardiac arrest or sudden death become potential outcomes with mortality estimates in the region of 10% [14]. The potential clinical problem is not just related to cardiovascular drugs. A review of the FDA safety database over 30 years revealed 2194 cases of which the most common agents were cardiac drugs (26.2%), CNS drugs (21.9%) and anti-infective agents (19.0%). Moreover, 11.7% were determined to be associated with drug interactions [14].

Figure 1.

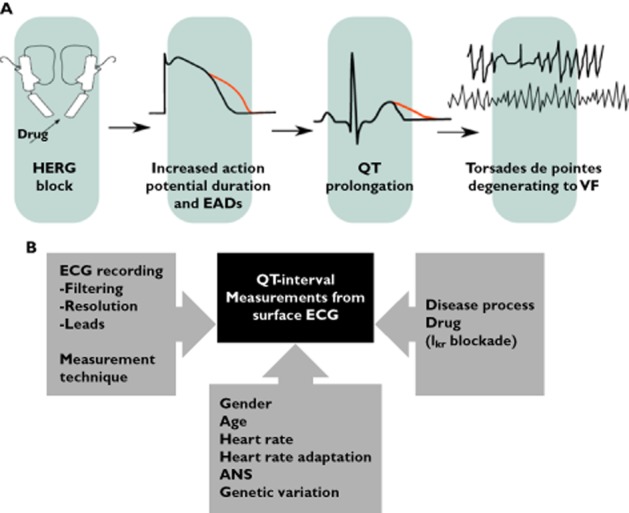
A) The cardiac sequelae of blockade of the HERG channel. Blockade of the HERG channel results in prolongation (in red) of the cardiac action potential leading to early after depolarizations (not shown). QT interval prolongation occurs secondary to these changes and ultimately leads to torsade de pointes (TdP). In the example above the TdP degenerates to ventricular fibrillation (VF). B) Summary of the potential areas of concern where significant impact can be made to the observed QT interval data, including the algorithm used for ECG recordings, the technique selected to correct measurement bias, the nature of the disease that influence ECG values, and various other covariates that can impact the recordings (modified from Totterman [68])

Current approaches to cardiac safety evaluation

Historically, the identification of a compound's propensity to induce TdP has been elucidated through experimentation using empirical protocols or by inference from knowledge about class effects. More recently guidance has been provided from regulatory agencies which outlines the strategy for the evaluation of QT_c prolongation, arguably the most significant of which is the ICH E14. Since then the evaluation of the potential for torsadogenicity during clinical development has been centred on the thorough QT (TQT) study. The TQT study is designed to detect (and ideally rule out) small changes in the QT_c interval. It is usually a double-blind, double-dummy design consisting of three arms, the investigational product, placebo and an active control (e.g. moxifloxacin), which is included in order to demonstrate assay sensitivity. An active comparator is sometimes employed if a drug exists in the same class that has a known QT prolongation effect. The study drug is investigated at therapeutic (usually highest therapeutic dose) and supra-therapeutic doses. In addition, heart rate effects on QT_c interval are characterized using Bazett's and Fridericia's correction factors under the assumption that these are sufficiently robust to account for interindividual differences. From a clinical and pharmacological perspective, the crux of the problem is that the primary analysis of a TQT study is based on the ‘double-delta’ method [15]. The approach relies on the assessment of the upper bound of the 95% one-sided confidence interval for the largest time-matched mean treatment effect on the QT_c interval. The results must exclude a 10 ms increase in QT_c interval if the drug is to be deemed safe, i.e. a negative study. In fact, the one-sided 95% confidence interval should exclude an effect of >10 ms for every single measurement. Whereas this is thought to be the most suitable approach, it can lead to multiplicity issues and positive bias [16,17]. Clearly, an important limitation of the proposed double-delta method is the absence of concentration−QT relationships. Indeed, the role of exposure−response analysis as a tool to interpret QT data from TQT studies has been recently highlighted by academic and regulatory experts [18]. From a scientific perspective, it means that any regulatory review of QT study based on the evidence gathered in such a trial does not fully address the issue of causality, providing a clear, quantifiable measure of risk. This issue is very well illustrated by the clinical data collected during the TQT study for sitagliptin (Figure 2).

Figure 2.

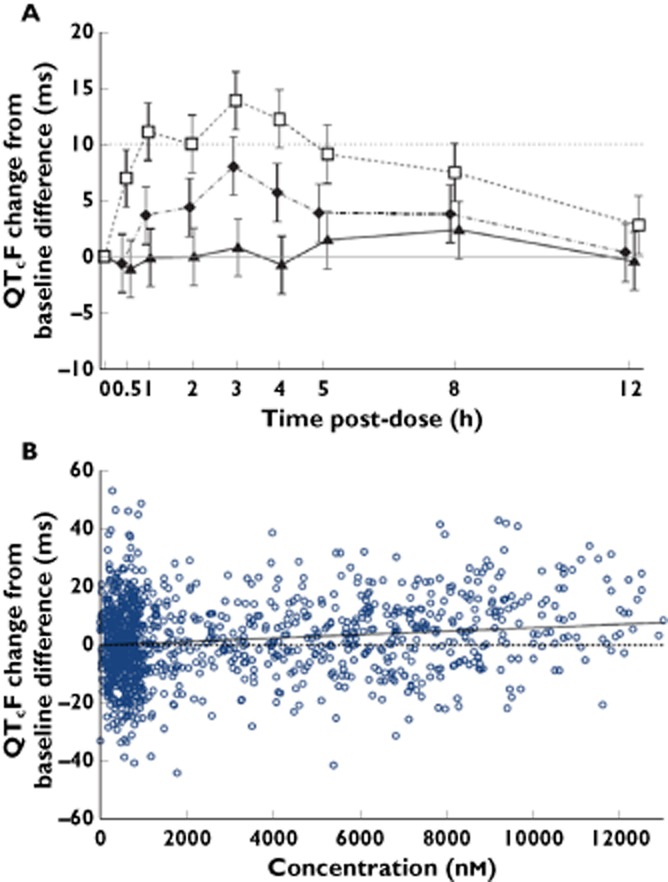
An example of the utility of understanding concentration−effect relationships during the evaluation of QT_c prolongation. In the upper panel (A), the supratherapeutic dose of 800 mg of MK-0431 (sitagliptin) crosses the 10 ms boundary at the fourth time point resulting in a positive TQT study, at exposure levels equivalent to an 11-fold higher dose than predicted clinically. A PK/QT_c model was used to describe the relationship between sitagliptin plasma concentrations and placebo-subtracted QT_cF change from baseline following single oral doses of 100 mg and 800 mg. The lower panel (B) illustrates that subsequent analysis of the concentration−effect relationship utilizing a linear PKPD model does not result in prolongation of the QT_c for therapeutic concentrations of sitagliptin (Reprinted with permission from Bloomfield et al. [69]). , 100 mg MK-0431; , 800 mg MK-0431; , moxifloxacin; , observed; , predicted mean; , slope = 0

Advantages and limitations of PKPD relationships when assessing QT interval prolongation

Since drugs that prolong the QT_c interval have been shown to do so in a concentration-dependent manner [19,20], understanding of the underlying concentration−effect relationship for QT_c prolongation opens up the potential to explore causality and to discriminate drug effects from other sources of variability, something that standard methods and experimental protocols are unable to do adequately [21]. Moreover it is possible to establish correlations between the PKPD relationships across species (Figure 3). By contrast, the TQT study addresses a critical regulatory question and advantageously relies on very few assumptions. However, it does not reflect knowledge of the underlying pharmacology and has limitations in its ability to address some fundamental clinical questions. The E14 guidance itself identifies the potential advantages of establishing the relationships between plasma drug concentrations and QT_c changes, but the proposed methodology is rather rudimentary. Given that drug concentration data are routinely collected during the TQT study, there has been, however, increasing acceptance by regulatory agencies of the value of additional analysis based on the concentration−QT effect relationship [18]. One example of this is the case of the muscarinic receptor antagonist imidafenacin for overactive bladder. It was approved in Japan at doses of 0.1 mg twice daily in 2007, i.e. prior to implementation of ICH E14 guidance. In order to update the labelling to include doses of 0.2 mg a long term dose escalation study using the same population as the pivotal phase 3 trial was conducted. A population pharmacokinetic model was updated using data from 90 healthy volunteers and 852 patients across nine clinical studies including the new dosing data. QT_c data before treatment and at relevant time points post-dose generated 1103 measurements which were used for a concentration−QT analysis. No concentration dependent QT_c prolongation relationship was observed and the data were used to form part of the labelling update package [22].

Figure 3.

A) Goodness-of-fit plots show the model-predicted vs. observed QT_c interval and B) the corresponding probability curves for QT_c interval prolongation ≥10 ms vs. the predicted plasma concentrations of cisapride, d,l-sotalol and moxifloxacin respectively. Black dots and dotted lines represent values for conscious dogs, grey dots and solid lines depict data in healthy subjects. (Reprinted with permission from Chain and Dubois et al. [40])

From a clinical perspective, assessing the risk of drug induced TdP, a relatively rare event, by delineating the frequency and duration of QT interval prolongation at supratherapeutic doses in a very small number of relatively healthy subjects is limiting and not as useful as characterizing how changes in the drug exposure alter the QT interval. Patients with co-morbidities, particularly cardiac ones, are often excluded from these studies, as are females and the elderly. Such populations are known to have different QT dynamic properties and clinical risk levels [23]. These studies also exclude subjects with pharmacological or physiological predisposing factors to adverse events such as patients receiving drugs with a propensity for drug−drug interactions or patients with electrolyte imbalances. As such, clinically relevant extrinsic determinants of variability are not accounted for, limiting therefore the ability to generalize the findings in a TQT study to real-life conditions. Furthermore, the TQT study relies on demonstrating a change in the QT_c interval of less than 10 ms across all sampling times during the course of the intervention, despite lack of evidence for a strict correlation between a 10 ms prolongation and fatal arrhythmia [24].

In relation to general issues of study design and analysis, it should be noted that the TQT study depends on the detection of small changes in the QT_c interval using supratherapeutic drug doses. Such an approach may be prone to high false positive rates and biased estimates [25]. The extent to which bias occurs is variable and can be affected by the study design (particularly in parallel trial designs which have inherent large variability), sample size and patient characteristics [4,26]. Consequently, adequate powering for some TQT study designs often results in very large and expensive trials.

A regulatory dilemma therefore exists since a false positive could result in cessation of development or inappropriately restrictive labelling of a drug. Alternatively, the change may be drug-induced but inappropriately ascribed to a spontaneous variation when in fact a serious hazard may exist [27]. Issues of multiplicity also exist by virtue of the analysis requiring an exclusion of a >10 ms time difference at multiple time points. In fact, it is known that increasing the number of time points, increases the false positive rate when the recommended intersection union test (IUT) is used [25]. In addition, one needs to assume comparable drug effects in healthy subjects and in the target patient population, which may not be necessarily appropriate.

Despite the advantages of the PKPD modelling, the approach can have some important limitations. The major constraints are often related to experimental design. Typical TQT protocols are not optimized to enable the assessment of exposure−response relationships and therefore, to allow one to establish correlations between drug concentrations and QT_c interval prolongation. One of the main implications of such a shortcoming is the biased estimation of the pro-arrhythmic effect [25]. This is particularly important if the causal agent(s) are the metabolites, rather than the parent drug. Similarly, time-dependent changes in ion channel expression on cardiac tissue may lead to altered response over time, which may not correlate directly with drug exposure. Such limitations can be overcome by careful consideration of the modelling requirements and assumptions. Population PKPD modelling can be performed using data from multiple studies, yielding more relevant information than traditional random effects meta-analyses.

Another limitation is the variability in QT_c measurement and the potential role of covariates, such as demographic characteristics (e.g. gender, ethnicity) [26,28] and disease conditions [29], which can become important confounders when looking for drug-induced changes of around 10 ms. Whereas the efficiency of PKPD-guided designs can been demonstrated theoretically, these issues still represent an obstacle for the implementation of clinical protocols. These points are briefly discussed in the next paragraphs.

Methodological considerations on the use of PKPD modelling

Defining exposure-response relationships in a quantitative manner is central to utilizing experimental data in a way that informs or enhances decision making in drug development and clinical practice [30]. Population PKPD modelling approaches have evolved as a tool to support evidence generation and facilitate the interpretation of experimental data as well as explore hypothetical or extreme conditions, which would not be desirable, necessary or ethical in humans. However, in contrast to the wide range of applications in which efficacy has been evaluated [31–33], the use of population approaches for the systematic characterization of QT interval prolongation remains limited. This is partly explained by the focus of the TQT study on hypothesis testing using a frequentist statistical approach. More than ever, there is clear need for methodological approaches that provide mechanistic insight, rather than simply support statistical inference [10].

From a scientific perspective, one of the major shortcomings in the TQT study is the assessment of drug effects as a discrete, rather than a continuous measure. Nominal doses are used instead of exposure, making the clinical interpretation of pro-arrhythmic risk difficult. On the contrary, population models allow for the integration of data from measurements of all time points and across treatment groups. It also enables one to predict drug effects for clinical scenarios in which the exposure may be different from those observed in a controlled trial, e.g. drug−drug interactions and certain co-morbid conditions, i.e. in situations where metabolic clearance is altered [34]. For drugs with highly variable pharmacokinetics, such a method has enormous clinical value [25].

There are a few published studies exploring the use of PKPD models on QT_c interval prolongation [26,35–37]. Yet, despite their findings, such knowledge has not been systematically used to translate drug effects into labelling recommendations with regard to dose selection and benefit−risk for specific subgroups or populations. One example is that of ranolazine, a drug used for chronic angina. A population modelling approach utilized data pooled from 18 clinical studies. A linear model was used to characterize the concentration–effect relationship and it was found that the QT_c interval increased by 2.6 ms per mg ml⁻¹ of drug. A sub-analysis of patients with mild to moderate hepatic impairment revealed an increase of 7.1 ms per mg ml⁻¹ of drug. The labelling of ranolazine utilized these data as the basis for contraindicating its use in patients with clinically significant hepatic failure [18]. More so, the knowledge of the PKPD relationship allows the risk to be communicated in a way that is relevant to clinicians. Since ranolazine has large between-subject variability in drug concentrations, the population distribution of pharmacokinetic data enabled the concentration−QT relationship to be expressed as a probability of prolonging the QT_c interval in the general population as well as special groups. This has a different clinical utility than merely characterizing the maximum mean change in QT_c interval at clinical and/or supratherapeutic doses.

Special cases also exist whereby a more detailed understanding of the PKPD relationship can help with understanding the implications for drug development and subsequent planning. An example of this is when a drug shows intrinsic chronotropic effect. It is essential to be able disentangle the effects on the heart rate from the heart rate correction applied (using the various formulae) for calculation of the QT_c interval if the effect on cardiac conduction is to be characterized accurately.

It should be noted, however, that from a conceptual point of view, the risk associated with a novel therapeutic agent cannot be delineated unless the drug-specific and system-specific parameters are distinguished. As such, the quantitative assessment of PKPD relationships using model-based techniques is central to discriminating drug effects from other sources of variability. In fact, this concept has been recently illustrated by the use of an integrated Bayesian approach in which drug-specific parameters were describe separately from other system variables such as heart rate and circadian rhythm [15]. An important feature of the aforementioned approach is the possibility to incorporate prior knowledge regarding system-specific parameters and thereby optimize experimental protocol design. This approach also enables the prediction of the required exposure to induce a clinically relevant increase in the QT_c interval.

Statistical concepts in modelling and simulation

Whereas a detailed technical discussion of the methodologies currently available for the assessment of PKPD relationships is beyond the scope of this review, a few important concepts underpinning model identification and parameter estimation are summarized below. They are meant to provide the reader with further understanding of the opportunities and limitations associated with the use of hierachical (population) models.

Non-linear hierarchical modelling

In recent years, the use of hierarchical models has increased considerably as a tool for the characterization of exposure−response relationships and other medical applications [38]. The key difference between classical statistical testing and model-based approaches is the possibility to explore and explain variability in a physiologically and clinically plausible manner. Moreover, when applied in conjunction with Bayesian methodologies, estimates can be obtained which allow direct interpretation of probability. The statistical reasoning behind this is that traditional statistics relies on the likelihood, i.e. the probability of observing the data given a range of parameter values. Bayesian statistics, however, rely on the posterior distribution, which is the distribution of the parameters (i.e. parameter space) given the observed data [31]. Another important aspect of the application of hierarchical (population) models is the focus on the population rather than the individual as the object of the investigation. The approach is particularly suitable when information on individual subjects is limited. Regardless of the density of the data, population models describing concentration−effect relationships should be considered an ideal tool to translate between species (i.e. non-clinical to clinical data) and between clinical trials and the real life population. Lastly, it should be noted that the availability of hierarchical models offers an important opportunity as a study optimization tool (e.g. dose selection, sampling times, treatment duration and population size). These models can also be used to support prediction and extrapolation of data across different age groups, dosing regimens and formulations or delivery forms. Moreover, population models may enable extrapolation of long term efficacy and safety based on short term pharmacokinetic and treatment response data.

Clinical trial simulations

In contrast to meta-analysis, clinical trial simulation (CTS) allows for the investigation of the impact of a range of design characteristics on the power to detect a treatment effect prior to exposing patients to an experimental drug. In a field where most clinical trials have a conservative design, this methodology offers a unique opportunity to evaluate innovative designs. Rather than performing power calculations which only take sample size and endpoint variability into account, CTS allows calculation of power taking into account a multitude of other factors [39]. In general, CTS utilizes two types of model. First, a drug−action (PKPD) model is considered, which comprises pharmacokinetic and pharmacodynamic factors. In chronic diseases the model also accounts for disease progression (Figure 4). Unfortunately, the lack of knowledge about the mechanisms underlying treatment response in many therapeutic indications has prevented the development of mechanistic models. Hence, examples often refer to standard statistical models, such as, for example, the mixed model for repeated measures (MMRM). Such statistical models have, however, a downside in that they often do not incorporate concentration−effect relationships. Secondly, CTS requires a trial execution model. These models simulate other important aspects of the trial, such as dropout, compliance and protocol deviations. Thereby, one can determine all possible outcomes under candidate trial designs, allowing different trial designs to be compared in a strictly quantitative manner. Thus far, very few examples exist in which relevant design factors have been evaluated prospectively as part of the planning of a cardiovascular safety trial.

Figure 4.

The diagram depicts the major components of a clinical trial simulation (CTS). In model-based drug development, CTS can be used to characterize the interactions between drug and disease, enabling among other things the assessment of disease-modifying effects, dose selection and covariate effects (e.g. age, body weight). In conjunction with a trial model, CTS allows the evaluation of such interactions, taking into account uncertainty and trial design factors, including the implications of different statistical methods for the analysis of the data (Reprinted with permission from Gobburu et al. [39])

It is also important to stress that CTS allows investigation of factors that cannot be scrutinized by meta-analysis or empirical design. First, designs which have not been implemented cannot be included in a meta-analysis. Second, it is difficult to separate the influence of multiple design factors, whereas CTS allows evaluation of a single factor at a time. Although meta-analyses may provide valuable information about differences in patient populations and treatment response, it is unfortunate that many investigators consider overall publication review sufficient to gather evidence on the role of design factors, as often suggested in the discussion of meta-analysis results.

If simulated data is to be exchangeable with actual patient data, it is imperative that not only model parameters are unbiased, but that estimates of variability are also accurate. Often interpretation of statistical model results focuses on the predicted values of the treatment effect. This does not necessarily mean that response distributions reflect what occurs in the true patient population. In fact, it is not infrequent to see model misspecifications being corrected by inflated estimates of variability. It is therefore critical for clinicians to understand that standard goodness-of-fit criteria do not take simulation characteristics into account and may therefore not be indicative of the best model. A comparison between simulated and original data can be performed using graphical and statistical tools.

CTS relies on the availability of accurate model parameter and corresponding distributions to investigate ‘what if’ scenarios across a different range of conditions or design features, such as population size, stratification levels, dose range, sampling scheme, and even different endpoints. One of the main advantages of such a virtual or statistical experiment is the possibility to predict ‘trial performance’ and so to identify potential limitations in study and protocol design prior to its implementation and decide if the trial should be performed. In fact, some clinical trial simulations have been evaluated against outcomes from real trials.

Population PKPD modelling and simulation as a tool for integration of safety data during drug development

A major limitation with most models is that they only provide a description of the PKPD relationship. They do not indicate whether development of the drug should be stopped or continued, or what the associated risks are. In fact, most of the proposed models in the published literature have been used as data analysis methodology. By contrast, we envisage the application of population modelling and simulation as a tool for data integration and decision making (Figure 5). PKPD models can provide the basis for a more comprehensive safety pharmacology evaluation which includes assessment of the drug properties in vivo in non-clinical species as well as in humans, supporting the translation of drug effects across species [40]. Utilizing such approaches may ultimately lead to better decision making in the drug development process [41]. Moreover, population PKPD models can be parameterized in such a way that data can be effectively integrated across different phases of drug development, enabling the assessment of cardiac risk in relevant groups in the target population [42].

Figure 5.

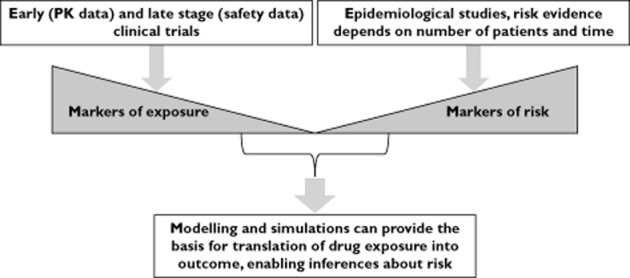
Inferential methods are essential to establish causality during signal detection. The use of markers of exposure in conjunction with population PKPD modelling provides the basis for the characterization of concentration−effect relationships. On the other hand, epidemiological data can be used to establish the correlation between markers of risk and drug-induced treatment effects in subjects and experimental conditions which may not have been tested initially during drug development. In addition, evaluating risk by modelling and simulation also offers the possibility to discriminate between drug and systems or patient specific properties

PKPD modelling has already proven to add considerable value for informed decision making regarding the safety profile of drug candidates [43,44]. In their recent paper, Parkinson and colleagues investigated and quantified the translational relationship for concentration−QT_c response between dogs and humans for different compounds with differing ion channel pharmacology, including one drug that shortens the QT_c interval. The study has not only highlighted the role of the dog as a predictive model for humans, but also showed whether the observed responses were independent of the underlying pharmacology [45]. The study demonstrated a similar relationship between dog and human independent of the underlying pharmacology at low free drug concentrations and for changes in the QT_c interval up to 10 ms but slight differences at higher exposures. The authors recommended a more detailed mechanism-based model using a wider range of drug classes to confirm the predictive value of the model. In addition to characterizing between species differences, population PKPD modelling can also be used to assess in vitro−in vivo correlations. In a recent publication, clinical QT prolongation has been predicted from hERG data [46], but this might be limited to selective hERG blockers.

Another example is the recent evaluation of cardiovascular safety of losmapimod, in which a population PKPD modelling approach utilizing data from six phase 1 studies was used to gain an early insight into the potential effect of the agent on QT_c interval and to explore relevant covariates. The availability of a concentration−effect relationship for QT_c interval prolongation enabled the assessment of the probability of observing a QT effect in a TQT study in doses up to 60 mg (i.e. supratherapeutic doses), thereby providing confidence in dose selection for the progression of the development programme [[47] ].

Unfortunately, despite the added value PKPD modelling for the evaluation of concentration−effect relationships, no final consensus has been reached within the regulatory agencies in support of the generation of safety data in an integrated way [20,48]. Guidelines still focus on the availability of a series of discreet, independent studies [2,3]. In contrast to quantitative estimates of the pro-arrhythmic effects at therapeutically relevant levels, the various in vitro and in vivo studies simply provide qualitative data for the progression of the compound into the clinical phase, during which the TQT study is often required as a confirmatory step.

From a translational pharmacology perspective, it should also be mentioned that population models enable the identification of covariate effects and therefore provide quantitative estimates of the contribution of patient-specific characteristics, discriminating them from drug-specific effects [49]. Consequently, it is possible to establish correlations between concentration−response relationships across species.

Yet, publications on interspecies correlations for cardiovascular effects are limited and the relationship of exposure−response across species is not entirely understood [44]. Nevertheless, cross-species scaling of pharmacology in recent examples suggests that allometric scaling of data obtained in pre-clinical models may be suitable to predict not only pharmacokinetics but also drug effects in humans [10,50].

Clearly, the use of modelling and simulation to elucidate differences between species imposes fundamental changes to the way experimental safety data are generated. Current toxicological based approaches using extremely high dose levels do not allow for the evaluation of drug effects at exposure levels that are relevant to the clinical setting. Moreover, pharmacokinetic information is often missing or insufficient to ensure accurate prediction of drug concentrations throughout the course of treatment.

In contrast to the limitations in translating preclinical drug effects to humans, the use of PKPD modelling in early clinical development may allow a reduction in the costs associated with progressing compounds unnecessarily. In fact, early clinical development is often the only stage in drug development in which supra-therapeutic doses are explored, therefore providing a valuable opportunity for quantifying QT_c effect at relevant exposure levels. One example of the utility of this approach is the evaluation of simulation scenarios in which individual QT and RR interval profiles are generated for a virtual population of healthy subjects and patients, including profiles of patients who would not typically be included in a TQT study. Such scenarios allow one to assess virtually the liability to QT_c interval prolongation across a range of conditions that may not be easily controlled or stratified for in a clinical trial (Figure 6). In this case a dedicated TQT study could be implemented only as a confirmatory step.

Figure 6.

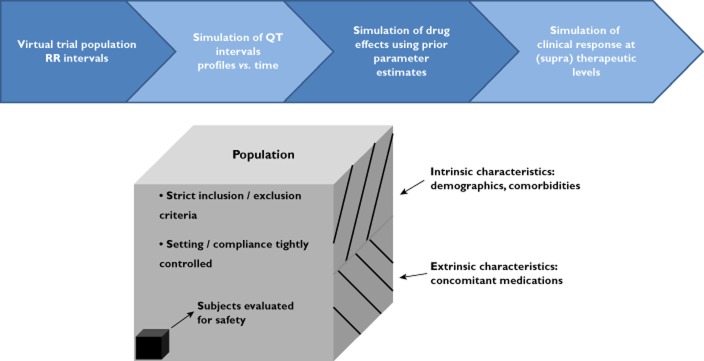
A schematic flow chart demonstrating the steps required for integration of multiple sources of data in a Bayesian PKPD model to build a clinical trial simulation (CTS) for QT_c prolongation in a representative population. The diagram highlights the fact that clinical trials and in particular the TQT trial design yields estimates of drug effects on a restricted subset of the population. Simulation scenarios allow for inferences to be made about the true safety profile of a new chemical entity in the overall population (with different demographic characteristics, comorbidities and concomitant medication usage), i.e. discriminating drug-specific properties from other sources of variability in QT_c interval

From a methodological perspective, models can take into consideration hysteresis and other time-dependent factors affecting the concentration−effect curve, which need to be accounted for to assess accurately the magnitude of drug-induced ECG changes [[51] ]. PKPD modelling can also overcome issues of multiplicity testing. In conjunction with Bayesian statistics, other experimental issues, such as statistical power and sensitivity, can be addressed in a more robust manner [52,53]. Another important aspect of Bayesian statistics in the implementation of population PKPD models is the possibility to use prior information to support parameter estimation. This is a particularly powerful resource when considering so-called system-specific properties and other trial design aspects, e.g. effect size and variability of the positive control. Using MCMC simulations, one can evaluate not only the experimental conditions, but also consider additional scenarios to quantify the contribution and consequences of other factors such as the distribution of baseline values and known covariate effects (e.g. age, gender). An elegant application of these concepts has been illustrated by Friberg et al. who evaluated the implications for QT_c interval across a wide range of doses of citalopram [54] (Figure 7).

Figure 7.

A) Simulated plasma concentrations (········) and QT intervals (------) vs. time for a patient with typical PK and PD parameters after an overdose of citalopram (1200 mg). The RR interval was fixed at 760 ms for the purposes of this simulation exercise. B) Simulated probability over time for having a QT≥ 447 ms for a predefined RR interval of 760 ms. Ten different dose levels are shown, ranging from 100 mg to 1800 mg. In the simulations all patients were assumed to be 30-year-old women who were also taking citalopram therapeutically. (Slightly modified with permission from Friberg et al. [54])

Lastly, it should be noted that PKPD relationships offer an alternative to some important practical and ethical limitations imposed by rigid study designs. Model-based meta-analysis using individual level patient data can provide evidence on the clinical relevance of drug effects taking into account the underlying differences in protocol and study design. One of the best examples on the use of modelling and simulation to investigate pooled data is the work by Florian et al., who have characterized the pro-arrhythmic effects of methadone in methadone maintenance treatment patients [55]. Their analysis was prompted by the ongoing discussion about the reassessment of the risk of cardiac arrhythmias in methadone users. The authors acknowledge that a thorough QT study with single dose or steady-state dosing of methadone in healthy volunteers is not feasible and that previous attempts to correlate the QT-prolonging effects of methadone with dosage and plasma methadone concentrations were of limited value due to the lack of replicate QT measurements at baseline and at multiple time points after dosing for the same individual (Figure 8). This type of analysis yields important new information and guides health care providers in the safe use of drugs, in particular by highlighting the links between dose, exposure and the risk of QT prolongation.

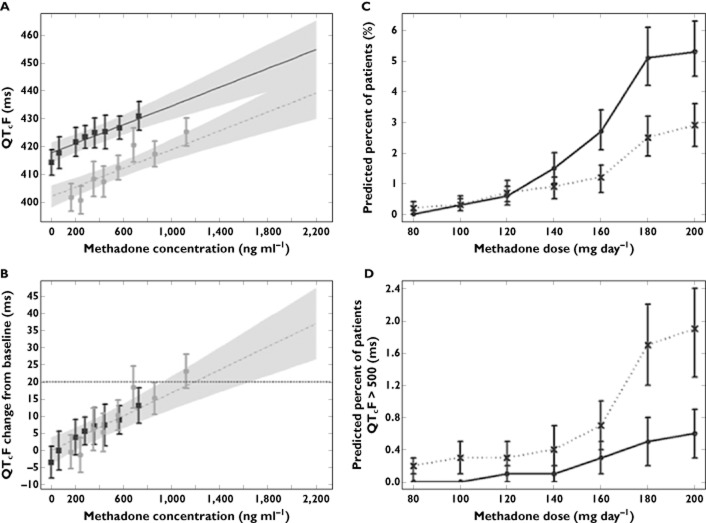
Figure 8.

Concentration-related effects of methadone on the QT interval (left panels). (A) Quantile plot showing the median and 90% CI for the linear concentration–QT_cF relationship with study-specific intercepts. (B) Quantile plot showing the median and 90% CIs for the linear concentration–ΔQT_cF relationship. Observed data from the Martell and DDI trials (squares) and Eap trial (circles) were grouped into eight quantiles and plotted as mean values± 90% CI. The shaded area encompasses the methadone concentration range observed from the pooled clinical trials. In addition, results of outlier analysis are shown as the percentages of simulated patients exceeding different QT-related risk thresholds for each methadone dose (right panels). (C) ΔQT_cF > 60 ms (dotted line) and QT_cF >480 (solid line). (D) QT_cF >500 ms for mean population baseline values of 407 ms (dotted line) and 421 ms (solid line). QT_cF, Fridericia rate-corrected QT. CI, confidence interval; DDI, drug–drug interaction; QT_cF, Fridericia rate corrected QT. (Slightly modified with permission from Florian et al. [55])

Opportunities for the characterization of drug-induced effects in clinical practice

Whilst the sensitivity of the proposed data analysis methods has been the subject of debate in numerous publications [56–58], less attention has been paid to the implications of overlooking the underlying concentration−QT_c effect relationship and consequently to the availability of supporting evidence for extrapolation of the findings to real life conditions, i.e. post-approval in clinical practice [15,18]. In fact, from a clinical standpoint one should raise questions about the reliability of the inferences made from pre-approval clinical trials. Given the patient population enrolled, the background noise and the relatively low frequency of clinically relevant arrhythmogenic effects, clinical trials may or may not accurately detect the frequency and intensity of QT_c interval prolongation in the target population.

Although it may be understandable and desirable to characterize a drug's safety profile by using healthy subjects, inclusion/exclusion criteria can undoubtedly lead to a somewhat biased estimation of the drug effects in the patient population who will receive the treatment after approval. In particular, the exclusion of severely ill subgroups or those with higher risk factors for TdP is usually not factored in a quantitative manner when evaluating clinical trial results. These subgroups include females, elderly subjects, those with predisposed cardiac or non-cardiac diseases associated with diminished repolarization reserve, those with pharmacogenetic defects of drug metabolizing enzymes or pharmacological targets, such as the potassium channels, those susceptible to bradycardia or electrolyte imbalance or those receiving drugs with a potential for pharmacokinetic or pharmacodynamic interactions [59,60]. In addition, little importance has been given to the role of other factors contributing to QT_c interval prolongation in the patient population, as compared with the observed drug effect in healthy subjects [30]. Consequently, no formal procedures exist to mitigate the impact of such differences or support the management of cardiovascular risk in the target population.

To address these concerns, Chain et al. [[42] ] have recently proposed the use of imputation procedures together with the predicted concentration−effect relationship to identify the effect of other influential covariates contributing to QT_c interval prolongation in patients. In contrast to previous applications of modelling and simulation [61–64], simulations are used to explore the role of design factors that have been omitted or excluded from randomized trials. Using d,l-sotalol as a paradigm compound, the authors introduced the concept of not-in-trial simulations as a tool for the evaluation of QT_c interval prolongation in real life conditions (Figure 9). Their findings show that co-morbidities and co-medications can have a significant contribution to the observed QT prolongation in the overall population. The impact of such factors cannot be derived empirically from TQT trials in healthy subjects. From a drug development and risk management perspective, the approach represents a natural extension of ongoing efforts within the pharmaceutical industry to improve safety signal detection [65–67] and can be applied to evaluate special cases even before drug approval.

Figure 9.

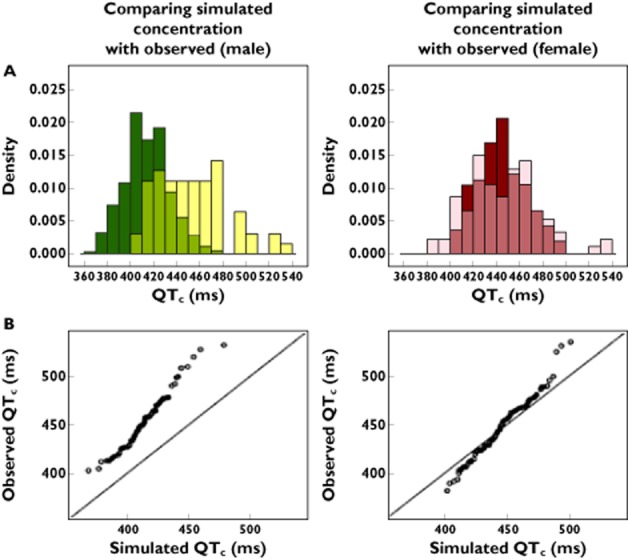
(A) Not-in-trial simulation results show overlapping distributions and discrepancies between observed and predicted QT_c interval in the male population (left panel) and female population (right panel). The darker colours represent the predicted drug-induced QT_c values and the light colours represent the observed overall QT_c intervals. The medium shades denote the overlapping areas. (B) QQ-plots comparing the distributions of the QT_c values for male population (left) and female population (right). The deviation from the identity line reflects the residual difference between the observed QT_c intervals and model-predicted sotalol effects under the assumption of comparable pharmacokinetic−pharmacodynamic relationship, as determined in phase I clinical trials (with permission from Chain et al. [42])

Conclusions

Clear shortcomings from various aspects of the ICH E14 guideline have been identified that limit its clinical value. The use of population PKPD modelling offers an alternative approach to the evaluation of pro-arrhythmic effects. It is evident that the use of concentration−effect relationships underpins the concept of causality, enabling informed decisions and recommendations to be made to drug developers, regulators, patients and prescribers about safe use of a medicinal product. Similar recommendations cannot be achieved by the currently accepted double-delta method. Moreover, the use of a Bayesian approach shows superior accuracy and precision in predicting actual QT_c interval prolongation over the entire time course of observations, not just at discrete time points. Another advantage to using a model-based approach is its ability to integrate information across phases of development, across compounds as well as between different species before embarking on any confirmatory study.

The examples used to illustrate modelling and simulation concepts highlight the need for a new paradigm for the assessment of cardiovascular safety, in which evidence generation does not prevail over the role of evidence synthesis, which is by far more encompassing and informative. Clinical researchers, health care providers, regulatory authorities and policy makers have to realise the implications of experimental design to the generation of evidence under controlled conditions, as in the case of randomised clinical trials. Differences in the patient population during drug evaluation (pre-launch) and clinical use (post-launch) cannot be overlooked. Intrinsic and extrinsic factors or covariates contribute to treatment outcome, which in turn alter, counteract or mitigate drug related effects. Hence, as suggested, there is a gap in the translation of safety findings from non-clinical species to clinical trials to real-life conditions, which must be accounted for in risk management. During clinical development one needs to learn before embarking into confirmatory trials. Therefore, focus should be given to data integration (evidence synthesis) and accurate assessment of the underlying PKPD relationships. In any case, the ability to discriminate between drug- and system-specific parameters will remain critical for the success of a model-based approach.

Competing Interests

Both authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare no conflict of interest. There are no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years and no other relationships or activities that could appear to have influenced the submitted work.