Model-based evaluation of drug-induced QTc prolongation for compounds in early development

Abstract

AIMS

Significant differences between dogs and humans have been observed in the concentration–QTc effect relationship of compounds with known pro-arrhythmic properties. These findings suggest that interspecies differences must be considered when evaluating drug effects. The aim of this study was to evaluate the performance of a model-based approach to assess the risk of QTc prolongation for three investigational compounds (NCE01, NCE02 and NCE03).

METHODS

Pharmacokinetic and pharmacodynamic data from experiments in conscious dogs and healthy subjects were included in this analysis. Pharmacokinetic modelling and deconvolution methods were applied to derive drug concentrations at the time of each QT measurement. An integrated pharmacokinetic–pharmacodynamic (PKPD) model was then used to describe QT prolongation. A threshold of ≥10 ms was used to characterize the probability of QTc prolongation.

RESULTS

The PKPD relationships of all three compounds were successfully described in both species. A strong effect was observed after administration of NCE01 to dogs and humans, with a slope of 0.0061 and 0.0662 ms nm⁻¹, respectively, and maximal probability of QTc prolongation ≥10 ms at peak concentration. For NCE02 and NCE03, QTc-shortening and borderline QT effects were observed both in dogs and humans, as described by negative or very shallow slopes (NCE02, −0.00098 and −0.01 ms nm⁻¹; NCE03, 0.00064 and −0.0002 ms nm⁻¹).

CONCLUSIONS

Whilst NEC01 shows clear pro-arrhythmic effects, the liability for QT/QTc prolongation for NCE02 and NCE03 can be deemed low at the expected therapeutic exposure. Moreover, our results show the advantages of an integrated PKPD approach as the basis for translating pro-arrhythmic effects from dogs to humans.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• The use of model-based approaches for the screening of molecules in safety pharmacology is rather limited.

• A previous investigation has shown the feasibility of characterizing pharmacokinetic–pharmacodynamic relationships as the basis for evaluation of the pro-arrhythmic risk in dogs and humans.

• The magnitude of the drug effects on QT/QTc interval varies across species as a result of the underlying differences in pharmacokinetics, pharmacodynamics and homeostasis.

WHAT THIS STUDY ADDS

• Our study confirms the feasibility of applying pharmacokinetic–pharmacodynamic modelling to assess the liability for QT/QTc interval prolongation during the early stages of development of novel candidate molecules.

• The proposed approach appears to be sensitive to drug effects of varying magnitude. Moreover, it disentangles system-specific from drug-specific properties, enabling comparison of the pro-arrhythmic activity across species.

• Accurate assessment of pharmacokinetics and understanding of the therapeutic exposure are critical for the interpretation of preclinical findings and decision-making regarding the progression of novel molecules into clinical development.

Introduction

Assessment of the propensity for QT/QTc interval prolongation is a mandatory step in drug development owing to its supposed prognostic value for the risk of fatal supraventricular arrhythmia [1]. Often, the pharmacological mechanism underlying drug-induced QT prolongation is a disturbance in the complex cardiac ion current and, more specifically, inhibition of the Human-Ether-a-Go-Go related Gene (hERG)-mediated K⁺ current [2,3]. Given the potential safety implications of QT/QTc prolongation, an increase ≥10 ms has been defined as the acceptable threshold for safety [4,5]. However, little effort has been made to establish how such a threshold relates to the real risk of pro-arrhythmic events in patients or whether similar levels ought to be considered for the evaluation of drug-induced effects in preclinical species.

Undoubtedly, prediction of the propensity for QT/QTc prolongation remains a major milestone in preclinical drug development, because it would be desirable to discard compounds that are likely to show clinically relevant QTc interval prolongation in humans. In fact, during the screening of candidate molecules, the beagle dog is the most common species used for the in vivo evaluation of safety pharmacology. This choice is based on the supposed similarity in the electrophysiology of the heart in dogs and humans [6]. However, little is known in quantitative terms about the sensitivity and specificity of these labour-intensive experiments [7]. In a recent investigation, we have shown significant differences in the concentration–effect relationships of moxifloxacin, d,l-sotalol and cisapride between dogs and humans [8]. Multiple factors can be considered that explain the translational gap between preclinical species and humans, including differences in heart rate, circadian variation and tissue receptor density [9,10]. Despite such differences, we have proposed the use of a model-based approach for the evaluation of concentration–effect relationships as the basis for the extrapolation between preclinical species and humans [11,12]. Pharmacokinetic–pharmacodynamic (PKPD) modelling offers the following possibilities: (i) to correlate drug exposure with QT effect; (ii) to quantify interspecies differences in pro-arrhythmic activity; and (iii) most importantly, to assess the liability for QT prolongation (i.e. the probability of ≥10 ms increase of QT/QTc interval).

In fact, the use of modelling as an alternative approach to the intersection union test, currently recommended by the ICH E14 guideline, has been gaining wide scientific recognition. One of the first examples of the approach is illustrated by Friberg et al., who described the delayed effects of citalopram on QTc interval following overdoses [13,14]. Ollerstam et al. also derived a model to describe the effect of dofetilide and placebo on the QTc interval in conscious telemetered dogs [15]. More recently, Tsong et al. applied a linear concentration–response model to moxifloxacin and eight test drugs [16]. The investigation revealed some weaknesses in the prediction of the maximal QTc interval change but suggested the possibility for improved estimates if more robust models are considered. In this context, we would like to emphasize the potential advantages of Bayesian hierarchical models for the characterization of concentration–effect relationships in early drug development. In conjunction with suitable parameterization, Bayesian methods allow formal incorporation of prior knowledge during parameter estimation procedures. The model proposed previously for the assessment of the liability for QT/QTc interval prolongation was based on a clear distinction between drug- and system-specific parameters [11]. Such a distinction ensures that drug-specific properties are disentangled from experimental and species-related variability [8,11]. Moreover, any knowledge about system-specific parameters (e.g. from past experiments) can be introduced as prior distributions to inform parameter estimation, increasing the precision of estimates, especially when small sample sizes are used.

A natural question that arises from the findings described so far is: are the differences in the PKPD relationships observed between dogs and humans systematic or not? Evidence of systematic differences would enable one to consider the use of an allometric or correlation factor to predict drug effects in humans based on experimental data in dogs. Although differences may exist in baseline function, and receptor densities may vary, it can be anticipated that such a correlation might be used to reflect the underlying mechanisms associated with QTc interval prolongation in vivo [17]. This point is particularly relevant for compounds with known activity on different ion channels, for which in vitro experiments cannot provide an accurate estimate of the drug effects in vivo [18–20].

The objective of the present investigation was therefore to assess the value of in vivo safety pharmacology protocols in dogs to predict the liability for QTc interval prolongation of new compounds in humans. A selection of three compounds with different safety pharmacology profiles was included in the analysis to assess the sensitivity of the approach to detect drug effects for compounds that show a low or borderline QTc interval-prolonging effect. Ultimately, we aim to explore the feasibility of a wider use of this Bayesian PKPD modelling approach to support decision-making during the screening of candidate molecules in early drug development.

Methods

Experimental data

Data from three compounds in development were provided by the participating partners in the TIPharma consortium (http://www.tipharma.com). They are coded as NCE01, NCE02 and NCE03 and have been selected based on the primary objective of this investigation, i.e. to explore the sensitivity of the approach for compounds that show no effect, low or borderline QTc interval-prolonging effect.

Preclinical protocols

A four-way crossover design was used for the evaluation of QTc interval in conscious, freely moving beagle dogs. All dogs were chronically instrumented with radio telemetry probes measuring blood pressure (BP), electrocardiogram (ECG) and body temperature (T). The ECG electrodes were placed in a lead II position. Animals were administered vehicle, a subtherapeutic, a therapeutic and a supratherapeutic oral dose of each compound. All experiments were approved by the ethical committees and performed under Good Laboratory Practice (GLP) regulations. Further details on the experimental design and data acquisition are summarized in Table 1A.

Table 1.

Treatment, experimental variables and sampling scheme details for preclinical experiments in conscious dogs (A) and clinical studies in healthy subjects (B)

A. Dogs	NCE01	NCE02	NCE03
Number of animals	4	6	4
Dose (mg kg−1)	Vehicle, 2.15, 4.3	Vehicle, 4, 20, 100	vehicle, 10, 30, 100, 1000
PK sampling times (h)	Predose, 0.5, 1.0, 1.5, 2, 6, 24	0, 1, 3, 6, 17, 24	0, 0.5, 1, 2, 4, 8, 24, 36, 48
PD sampling times	−1, −0.75, −0.5, −0.25, 0, 0.5, 1.0, 1.5, 2.0, 2.5, 3, 4, 5, 6, 10, 12, 16, 20	0.5, 1, 2, 3, 4, 6, 8, 12, 16, 20, 24	Every 30 min, for 20 h
PK data, vital signs, demographic covariates, ECG parameters	Plasma drug concentration, clock time, heart rate, blood pressure, body weight, QT, RR

B. Healthy subjects	NCE01	NCE02	NCE03
Number of subjects	29	64	16
Gender	Male	Male	Male: 16
Age (years)	Mean = 25 (range: 20–37)	Mean = 27 (range: 20–45)	Mean = 33 (range: 22–54)
Dose (mg)	Placebo, 10, 30, 70, 90, 180, 360, 430, 500	Placebo, 3, 6, 12, 24, 48, 95, 190	Placebo, 100, 200, 400, 800, 1600, 2800, 4000, 5000
PK sampling times (h)	0, 0.33, 0.67, 1.00, 1.33, 1.67, 2.0, 2.5, 3, 4, 5, 6, 8, 12, 24, 36, 48	0, 0.33, 0.67, 1.00, 1.33, 1.67, 2.0, 2.5, 3, 4, 5, 6, 8, 12, 24, 36, 48	0, 0.5, 1.0, 1.5, 2, 3, 4, 6, 8, 10, 12, 24, 30, 48
PD sampling times (h)	−1, 0.17, 0.33, 0.50, 0.67, 0.83, 1.00, 1.25, 1.50, 1.75, 2.0, 2.5, 3.0, 3.5, 4, 6, 8, 10, 12, 24, 36	0–1 (42 samples), 1.02, 1.03, 1.05, 1.07, 1.08, 1.10, 1.12, 1.13, 1.15, 1.17, 1.18, 1.20, 1.22, 1.23, 1.25, 1.50, 1.52, 1.53, 1.55, 1.57, 1.58, 1.60, 1.62, 1.63, 1.65, 1.67, 1.68, 1.70, 1.72, 1.73, 1.75, 1.77, 1.78, 1.80, 1.82, 1.83, 1.85, 1.87, 1.88, 1.90, 1.92, 1.93, 1.95, 1.97, 1.98, 2.00, 2.02, 2.03, 2.05, 2.07, 2.08, 2.10, 2.12, 2.13, 2.15, 2.17, 2.18, 2.20, 2.22, 2.23, 2.25, 2.27, 2.28, 2.30, 2.32, 2.33, 2.35, 2.37, 2.38, 2.40, 2.42, 3.0, 3.5, 4, 6, 8, 12, 24	0, 0.5, 1.0, 1.5, 2, 3, 4, 5, 6, 8, 10, 12, 24
PK data, vital signs, demographic covariates, ECG parameters	Plasma drug concentration, heart rate, body weight, QT, QTc[B], QTc[F], RR

PD, pharmacodynamic; PK, pharmacokinetic; QTc_[B], Bazett-corrected QTc interval; QTc_[F], Fredericia-corrected QT interval.

Clinical protocols

All three of the clinical protocols were phase I studies in healthy volunteers. The NCE02 and NCE03 data were extracted from randomized, double-blind, placebo-controlled study designs. For NCE02, subjects received either one placebo dose or one active oral treatment. For NCE03, each subject received one placebo dose and one to four oral doses of the active treatment. All studies were performed in accordance with the Declaration of Helsinki and its subsequent revisions. Further details about the experimental design and data acquisition are summarized in Table 1B.

Pharmacokinetic sampling procedures and bioanalysis

In vivo preclinical protocols in dogs

The analyses of plasma samples for NCE01 and NCE02 were performed at Drug Metabolism and Pharmacokinetics (DMPK), AstraZeneca R&D Södertälje, Sweden, whereas NCE03 was analysed at Drug Metabolism and Pharmacokinetics (DMPK), GlaxoSmithKline R&D, Ware, UK. The bioanalysis was performed in accordance with GLP using a method based on protein precipitation and liquid chromatography–tandem mass spectrometry (LC-MS/MS). Sampling times are listed for each study in Table 1.

Clinical studies in healthy subjects

Drugs were administered in ascending doses as usually performed in phase I studies. Blood samples for pharmacokinetics were drawn from a forearm directly into Vacutainer tubes with K₂-EDTA and centrifuged within 30 min from collection for 10 min at 4°C at 1500g. The plasma was then frozen at −20°C. For NCE01 and NCE02, blood samples were left to clot at room temperature. After clot retraction occurred, samples were centrifuged at 4°C at 1500g for 10 min with the minimum of delay. Serum (∼1 ml) was carefully pipetted into prelabelled Nunc 1.8 ml polypropylene tubes and then frozen in an upright position at −20°C until assay. All samples were kept frozen in Cardice pellets during transit and transport to various analysis facilities. Compounds were analysed using liquid chromatography tandem mass spectrometry (LC-MS/MS).

Electrocardiographic monitoring and sampling

In vivo preclinical protocols in dogs

Telemetric recordings of the ECG were performed in conscious dogs [15,21]. In brief, dogs were implanted with a telemetric transmitter under general anaesthesia. The transmitter was placed in the peritoneal cavity, and electrodes were placed in lead II configuration. The sensor catheter was implanted into the femoral artery. Telemetric transmitters were implanted at least 10 days before start of recording and, during this time, all dogs were trained for the experimental conditions.

A Latin-square crossover design was used for the experiments, where each animal received each dose of the active compound and placebo at least 3 days apart. ECG (lead II) was recorded in a continuous fashion from 1 h pre-dose to 24 h post-dose. The data were recorded and analysed using the Notocord data acquisition system (HEM software, Notocord Inc., Croissy-sur-Seine, France). The Dataquest Open ART™ software (St. Paul, MN, USA) was then used to set up and calibrate the telemetry systems. The QT interval duration was measured for every wave complex. An average of five consecutive wave complexes were used in the final analysis. The placement of the ECG calipers was checked and manually corrected if deemed necessary. Individual correction methods for the QTc interval were applied in the final dataset for NCE01 [22], whereas Van de Water correction factor was used for NCE02. In spite of the different methods used to correct for heart rate, the RR intervals were within the 400–1300 ms range where both methods show acceptable performance according to Ollerstam et al. [22]. Yet, for the current PKPD analysis the corrected QT values were used only for visual checking purposes.

Clinical studies in healthy subjects

The clinical protocols were based on a randomized, double-blind, placebo-controlled study design. All studies were performed in accordance with the ethical principles that have their origin in the Declaration of Helsinki and that are consistent with International Conference on Harmonisation (ICH)/GCP. Alcohol and nicotine use were not allowed during the trial, whereas strenuous physical activity was prohibited within 7 days before dosing until completion of the trial. All meals were nutritionally standardized and served at the time of dosing, 4, 6, 9 and 12h after drug administration. ECG was collected during resting conditions with the subjects in a supine position for several minutes prior to the measurements. Triplicate 12-lead ECGs were recorded over 10 s for QT, QTc_[B] (Bazett corrected), QTc_[F] (Fredericia corrected) and RR interval. For the PKPD analysis, the mean of the triplicate measurements from lead II was used.

Pharmacokinetic modelling

Time-matched concentration and QT interval values were required for the characterization of the pharmacokinetic–pharmacodynamic relationships; therefore, pharmacokinetic models were used to impute and simulate drug concentrations at each ECG recording time. Pharmacokinetic data analysis was performed using nonlinear mixed-effects techniques in NONMEM VII (ICON, Hanover, MD, USA) and deconvolution methodology in WinNONLIN 4.2. Model validation was based on goodness-of-fit diagnostics and normalized prediction distribution errors. Where applicable, an overview of the models is shown with the corresponding pharmacokinetic parameters for each compound (Table 2A,B).

Table 2.

Pharmacokinetic models and parameters describing the time course of drug concentrations in plasma after administration of oral doses of NCE01, NCE02 and NCE03 in conscious dogs (A) and healthy subjects (B)

A. Dogs	NCE01	NCE02	NCE03
Model structure	–	One-compartment model	–
Graphical representation	–		–
Parameterization	–	CL*, Vc*, KA	–
Interindividual variability	–	CL, Vc, KA	–
Covariates	–	Body weight	–

B. Healthy subjects	NCE01	NCE02	NCE03
Model structure	–	Dual absorption, two-compartment model	One-compartment model
Graphical representation	–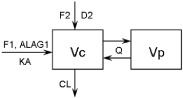
Parameterization	–	CL, Vc, Vp, Q, KA, F1, F2, D2, ALAG1	CL, Vc, KA, F1
Interindividual variability	–	CL, Vc, Vp, F1, F2	CL, Vc, KA
Covariates	–	Body weight	–

ALAG, lag time; CL, clearance; D2, duration of zero-order input into compartment 2; F1, bioavailability relative to compartment 1; F2, bioavailability relative to compartment 2; KA, absorption rate constant; Q, intercompartmental clearance; Vc, volume of distribution for the central compartment; Vp, volume of distribution for the peripheral compartment. *CL and V parameters were obtained using individual data fitting in WINNONLIN 4.2.

Pharmacokinetic–pharmacodynamic modelling

Although the same PKPD model was used to describe the effect of the drug on QT/QTc interval, each drug was analysed separately. A Bayesian adaptation of a hierarchical model previously described by Chain et al. [8] was used. The model is comprised of three components, including an individual correction factor for RR interval (heart rate), an oscillatory component describing the circadian variation and a truncated E_max model, as shown by Equation 1:

(1)

where QT_c0 (in milliseconds) is the intercept of the QT–RR relationship [23] (sex was included as a covariate for this parameter), RR (in seconds) is the interval between successive R waves, α is the individual heart rate correction factor, A (in milliseconds) is the amplitude of circadian rhythm, t is the clock time, ϕ is the phase, slope (in milliseconds per nanomolar) is the linear pharmacodynamic relationship, and C is the predicted drug concentration (nanomolar) at the time of QT measurements. Further details about the model-building and validation can be found elsewhere [8,11].

Probability of ≥5 and ≥10 ms QT/QTc interval prolongation

One of the advantages of the present approach is the possibility of characterizing drug effect in a quantitative manner and expressing it in terms of the probability relative to a clinically relevant threshold. In our analysis, the liability for QT/QTc interval prolongation was based on the assessment of the probability associated with an increase ≥10 ms in QT interval, irrespective of the baseline QTc values (Equation 2A). Given that drugs which show borderline or small pro-arrhythmic effects will not reach such a threshold, we have also considered a lower boundary to evaluate the liability for an increase in QT ≥5 ms when the probability of ≥10 ms is lower than 0.5 (Equation 2B). The analysis was performed with a step function in WinBUGS 1.4.2 (The WinBUGS Project, MRC Biostatistics Unit, Cambridge, UK) using the slope and an interindividual correction factor for gender differences at the following concentrations: 50, 200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000, 2500, 3000, 3500, 4000, 6000, 7000, 9000, 10 000, 15 000, 30 000, 60 000, 100 000, 120 000, 130 000, 140 000, 150 000 and 160 000 nm. The concentration values were chosen in such a way that data points spread across the sigmoid curve.

(2A)

(2B)

where 0.00001 is set as an arbitrary small number to avoid computational errors associated with numerical difficulties (i.e. division by zero), F(gender) is the gender specific population estimate for the baseline QTc interval (QT_c0), 5 and 10 ms refers to the QTc interval prolongation threshold of interest, C is the drug concentration, and slope is the QT increase per unit drug concentration.

Results

Pharmacokinetic modelling

The time course of drug concentrations in plasma was characterized for each compound separately, using nonlinear mixed-effects modelling where possible or deconvolution techniques. A summary of the pharmacokinetic models and final parameter estimates is shown in Tables 2A,B and 3A,B, respectively. Model performance and diagnostics are presented together with the predicted profiles in Figure 1A–C. Given that most of the pharmacokinetic samples were taken at different time points relative to the ECG recordings, individual predicted concentrations were required to generate time-matched data for subsequent evaluation of drug effects by PKPD modelling.

Table 3.

Summary of PK parameter estimates for NCE01, NCE02 and NCE03 in dogs (A) and healthy subjects (B)

A	Dogs
Parameters	NCE01	NCE02	NCE03
	Mean	Mean	Mean
CL (l h−1)	1.596	–	–
Vc (l)	5.575	–	–
AUC (nm h)	–	7506 (2.15 mg kg−1) 15 982 (4.3 mg kg−1)	29 631 (10 mg kg−1) 66 264 (30 mg kg−1) 91 407 (100 mg kg−1) 88 058 (1000 mg kg−1)
t1/2 (h)	–	4.4 (2.15 mg kg−1) 4.7 (4.3 mg kg−1)	4.6 (10 mg kg−1) 7.7 (30 mg kg−1) 9.3 (100 mg kg−1) 17.0 (1000 mg kg−1)
KA (h−1)	0.57	–	–
F	–	–	–

B	Healthy subjects
Parameters	NCE01	NCE02		NCE03
	Mean	Mean	IIV%	Mean	IIV%
CL (l h−1)	45–57	16.45	43.6	0.0232	27.7
Vc (l)	–	12.91	98.5	0.957	60.5
Intercept BW on Vc	–	2.60	–	–	–
Vp (l)	–	105.72	33.2	–	–
Intercept BW on Vp	–	0.86	–	–	–
Vss (l)	260–344	–	–	–	–
Q (l h−1)	–	19.99	–	–	–
KA (h−1)	0.57	0.40	–	0.96	77.5
F	F1 (360 mg) 0.38	F1 (<48 mg) 0.29	366.5	F1 (≤400 mg) 1	–
	F2 (450 mg) 0.54	F2 (<48 mg) 0.71	335.3	F1 (400–2800 mg) 0.39	–
	–	F1 (≥48 mg) 0.75	73.5	F1 (>2800 mg) 0.18	–
	–	F2 (≥48 mg) 0.06	80.0	–	–
D2 (h)	–	D2 (<48 mg) 0.83	–	–	–
	–	D2 (≥48 mg) 0.55	–	–	–
ALAG1 (h)	–	(≥48 mg) 0.55	–	–	–

ALAG, lag time; AUC, area under the concentration curve; BW, bodyweight; CL, clearance; D2, duration of zero-order input into compartment 2; F1, bioavailability relative to compartment 1; F2, bioavailability relative to compartment 2; IIV%, interindividual variability for parameter estimate; KA, absorption rate constant; Q, intercompartmental clearance; t_1/2, elimination half-life; Vc, volume of distribution for the central compartment; Vp, volume of distribution for the peripheral compartment.

Figure 1.

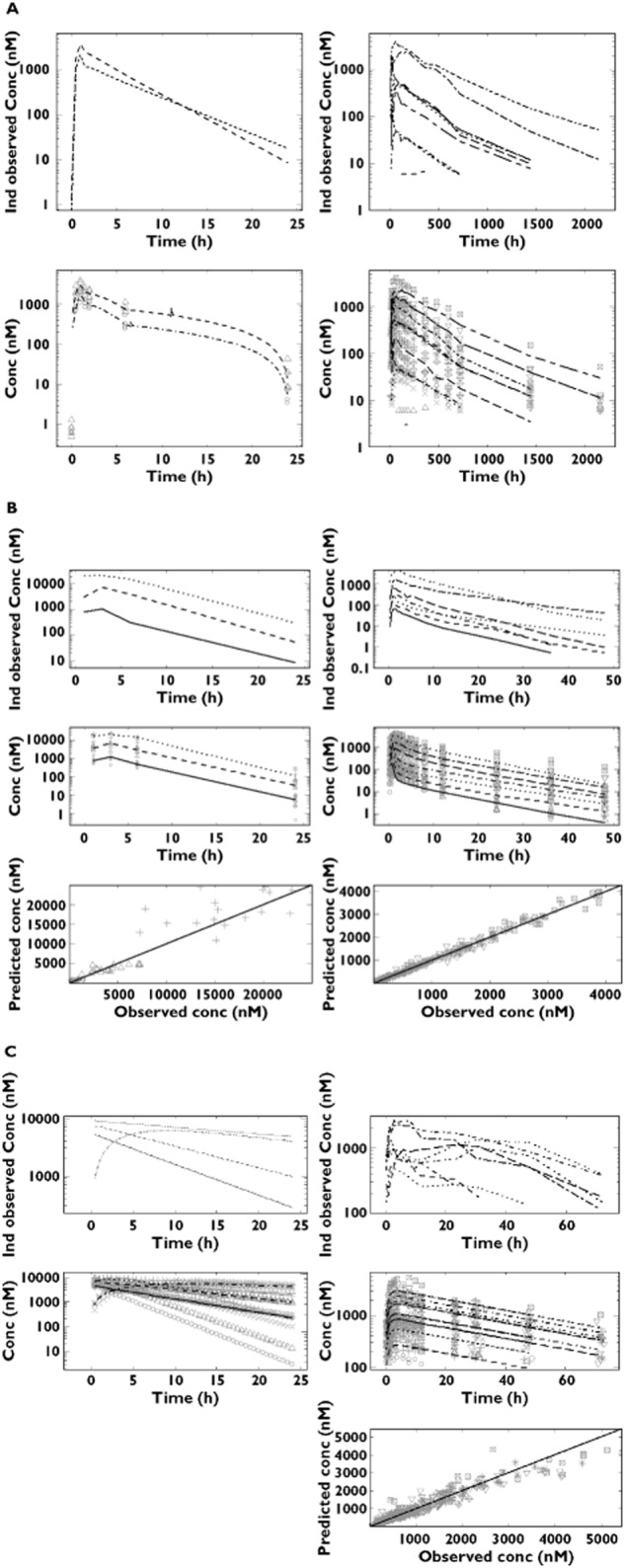
Pharmacokinetic analysis for conscious dogs (left) and healthy subjects (right). The lines represent the regression for the population prediction using the model parameters. Dots show the observed concentration data on the corresponding time intervals. (A) NCE01: individual observed concentrations vs. time for a typical subject (upper panels) and observed population median concentrations vs. time (lower panels). Symbols depict different dose levels, as follows: ○ and for 2.15 mg kg⁻¹, △ and for 4.3 mg kg⁻¹ in conscious dogs, and △ and for 10 mg, + and for 30 mg, x and for 70 mg, ◇ and for 90 mg, ▽ and for 180 mg, and for 360 mg, * and for 430 mg, and ⊕ and for 500 mg in healthy subjects. (B) NCE02: individual predicted concentration vs. time (upper panels), population predicted concentration vs. time (middle panels) and individual predicted vs. observed concentrations (lower panels). Symbols depict different dose levels, as follows: ○ and for 11 μm kg⁻¹, △ and for 54 μm kg⁻¹, + and for 270 μm kg⁻¹ in conscious dogs, and ○ and for 3 mg, △ and for 6 mg, + and for 12 mg, x and for 24 mg, ◇ and for 48 mg, ▽ and for 95 mg, and for 190 mg in healthy subjects. (C) NCE03: individual predicted concentration vs. time (upper panels), population predicted concentration vs. time (middle panels) and individual predicted vs. observed concentrations (lower panels). Symbols depict different dose levels, as follows: ○ and for 10 mg kg⁻¹, △ and for 30 mg kg⁻¹, + and for 100 mg kg⁻¹, x and for 1000 mg kg⁻¹ in conscious dogs, and ○ and for 100 mg, △ and for 200 mg, + and for 400 mg, x and for 800 mg, ◇ and for 1600 mg, ▽ and for 2800 mg, and for 4000 mg, * and for 5000 mg in healthy subjects

Pharmacokinetic and pharmacodynamic modelling

The analysis was performed using the recorded ECG measurements and predicted drug concentrations at the corresponding time of sampling. If model parameters could not be estimated accurately, concentrations were imputed by deconvolution techniques, as indicated above. In most cases, system-specific parameters, i.e. baseline QT (QT_c0), the QT–RR correction factor (α), the amplitude (A) and phase (ϕ), showed values within the same range within each species. Small differences were found in QT_c0 in dogs due to a possible age difference between the studies. In addition, the observed variation in A and ϕ could be explained by different sampling schemes used in each experimental protocol. As shown in Table 4, however, the main difference was found in the drug-specific parameter (slope), which varied significantly both across compounds and between dogs and humans.

Table 4.

Mean parameter estimates and 95% credible intervals of the PKPD model after oral administration of NCE01, NCE02 and NCE03 to dogs (A) and healthy subjects (B)

A	Dogs
Parameters	NCE01 (n = 4, occ = 3)	NCE02 (n = 6, occ = 4)	NCE03 (n = 4, occ = 5)
QTc0 (ms)	243.5 (238.5–248.5)	261 (252–270)	250 (248–252)
α	0.234 (0.142–0.385)	0.20 (0.31–0.48)	0.26 (0.17–0.42)
A (ms)	9.16 (4.26–18.09)	4.3 (1.8–8.6)	4.2 (2.5–7.1)
ϕ (h)	16.40 (10.16–26.08)	4.42 (0.59–9.09)	9 (5–16)
Slope (ms nm−1)	0.0061 (0.0022–0.016)	−0.00098 (−0.00206 to 0.00064)	0.00064 (−0.0009 to 0.0043)
BSV (QTc0; %)	6.4 (6.3–6.5)	6.19 (6.08–6.30)	6.32 (6.29–6.35)
BSV (α; %)	110 (43−181)	82 (35–219)	99 (40–270)
BSV (A; %)	9.29 (7.08−16.11)	7.2 (5.3–11.6)	6.2 (4.6–10.1)
BSV (ϕ; %)	8.86 (4.9–19.44)	24.23 (9.19–156.7)	13.4 (6.8–33.2)
BSV (slope; %)	37.14 (21.0–102.3)	33 (21–60)	42.5 (26.7–79.5)
Residual error (ms)	9 (8–10)	7.3 (6.7–8.0)	4.5 (4.3–4.7)
Prob effect ≥10 ms at Cmax	1	0.03	0.3
Prob effect ≥5 ms at Cmax	1	0.05	0.54
Cmax (nm)	3877	25 030	9123

B	Healthy subjects
Parameters	NCE01 (n = 43*)	NCE02 (n = 56)	NCE03 (n = 35)
QTc0 (ms)	379 (371–386)	380 (378–382)	385 (379–392)
α	0.30 (0.27–0.33)	0.22 (0.20–0.24)	0.24 (0.22–0.26)
A (ms)	5.75 (2.60–10.55)	7.9 (6.8–9.3)	4.9 (3.8–6.3)
ϕ (h)	28.2 (22.2–39.3)	4.4 (3.3–5.7)	9.7 (8.1–10.9)
Slope (ms nm−1)	0.0662 (0.0496–0.0809)	−0.010 (−0.013 to −0.007)	−0.0002 (−0.0010 to 0.0007)
BSV (QTc0; %)	5.19 (5.08–5.13)	5.13 (5.11–5.15)	5.09 (5.05–5.14)
BSV (α; %)	59 (40–92)	140 (110–190)	80 (50–120)
BSV (A; %)	11.8 (8.6−17.0)	12.6 (10.8–15.2)	8.7 (5.4–12.0)
BSV (ϕ; %)	7.4 (4.6–13.6)	62.6 (42.7–97.0)	10.2 (7.2–15.1)
BSV (slope; %)	389 (227–708)	286.4 (223.5–378.7)	32.3 (22.0–46.6)
Residual error (ms)	8.9 (8.4–9.4)	4.3 (4.2–4.5)	63.3 (57.4–69.9)
Probability of effect ≥10 ms at Cmax	1.0	0	0
Cmax (nm)	3981	3970	4308

α, individual heart rate correction factor; ϕ, phase of the circadian rhythm; A, amplitude; BSV, between-subject variability; C_max, peak concentration; OCC, occasions. *29 healthy subjects received multiple dose levels, but dosing events were treated as different individuals for the purposes of the analysis.

In addition to the typical Bayesian criteria for parameter convergence and model acceptance 24–27, goodness-of-fit plots were generated for each compound and summarized in Figure 2. In principle, the larger the positive value of the slope, the stronger the effect of the drug on the QTc interval. Drugs showing slope value around zero will produce no effect or borderline effect on QTc interval. Eventually, estimation of negative values for the slope indicates a possible shortening effect on the QT/QTc interval. Hence, our findings corroborate the sensitivity of the method to assess the pro-arrhythmic properties of molecules with minor or no QT-prolonging effects. NCE01 can be considered a QTc-prolonging compound, whereas NCE02 appeared to have QT-shortening properties. No clear effects on QTc interval were observed after administration of NCE03, because the maximal probability reached only 0.3. Such an estimate suggests that some pro-arrhythmic activity may be present, but it is not pronounced enough to result in QTc prolongation ≥10 ms. In fact, this borderline effect is demonstrated by the higher probability values obtained when a threshold of ≥5 ms was used. The estimated probability at peak concentrations of QT interval prolongation and the corresponding PKPD parameters are summarized in Table 4.

Figure 2.

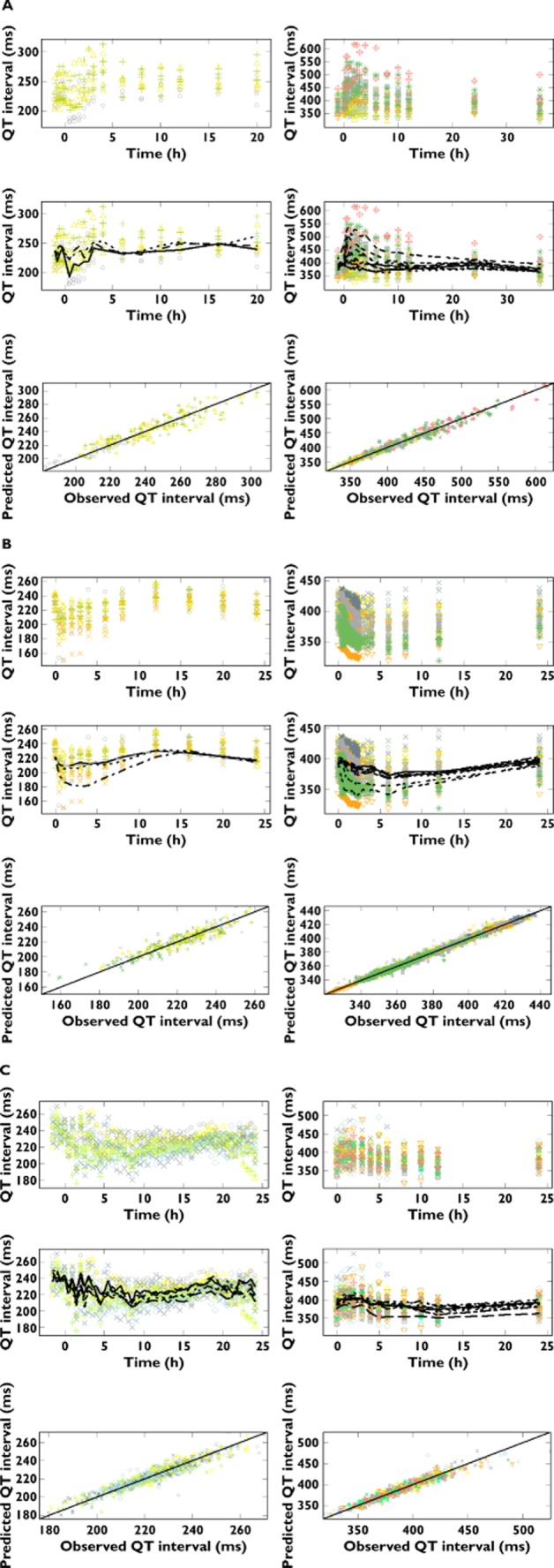
Pharmacokinetic–pharmacodynamic relationship between QTc interval and plasma concentrations for conscious dogs (left) and healthy subjects (right). The top panels depict the observed QT intervals vs. time stratified by dose, whilst the middle and lower panels show the observed QT intervals vs. population prediction stratified by dose and the observed vs. the predicted individual QT intervals, respectively. (A) NCE01; symbols depict different dose levels, as follows: ○ and for placebo, △ and for 2.15 mg kg⁻¹, + and for 4.3 mg kg⁻¹ in conscious dogs, and ○ and for placebo, △ and for 10 mg, + and for 30 mg, x and for 70 mg, ◇ and for 90 mg, ▽ and for 180 mg, and for 360 mg, * and for 430 mg, ⊕ and for 500 mg in healthy subjects. (B) NCE02; symbols depict different dose levels, as follows: ○ and for placebo, △ and for 11 μm kg⁻¹, + and for 54 μm kg⁻¹, x and for 270 μm kg⁻¹ in conscious dogs, and ○ and for placebo, △ and for 3 mg, + and for 6 mg, x and for 12 mg, ◇ and for 24 mg, ▿ and for 48 mg, and for 95 mg, * and for 190 mg in healthy subjects. (C) NCE03; symbols depict different dose levels, as follows: ○ and for placebo, △ and for 10 mg kg⁻¹, + and for 30 mg kg⁻¹, x and for 100 mg kg⁻¹, ◇ and for 1000 mg kg⁻¹ in conscious dogs, and ○ and for placebo, △ and for 100 mg, + and for 200 mg, x and for 400 mg, ◇ and for 800 mg, ▿ and for 1600 mg, and for 2800 mg, * and for 4000 mg, ⊕ and for 5000 mg in healthy subjects. The lines represent the regression for the population prediction using the model parameters. Dots show the observed QT interval and the corresponding (predicted) individual concentration data

Discussion

Pharmacokinetic–pharmacodynamic modelling

In this study, we have shown the application of a Bayesian hierarchical model to describe the relationship between drug concentration and QTc interval prolongation for three new compounds in conscious dogs and their correlation with the pharmacological effects in humans at comparable exposure ranges. As indicated in our initial publication [8], the availability of a common model to assess drug effects in dogs and humans and the explicit distinction between drug- and system-specific parameters allow direct inferences to be made about the probability of drug-induced QTc interval prolongation in humans. Moreover, these results appear to confirm our earlier findings with d,l-sotalol, cisapride and moxifloxacin, in that dogs are apparently less sensitive to QT/QTc prolongation than humans [8]. These differences are evident when comparing the estimated slope values and the corresponding liability for QT/QTc interval prolongation, expressed as probability of increase ≥10 ms. In addition, our findings suggest that the model parameterization is robust enough not only to demonstrate significant and no drug effects (i.e. true-positive and true-negative results), it also detects adverse changes such as QT shortening.

It was also evident from the analysis that accurate interpretation of the preclinical findings requires some knowledge about the expected therapeutic range, which was expected to be known given the range of doses selected for the phase I studies. Currently, based on preclinical results it is not possible to quantify fully the liability for QT/QTc interval prolongation in humans without some certainty about the clinically relevant levels. Inferences from extremely high dose levels, often used in toxicology experiments, may lead to biased conclusions about the magnitude of the effect on QTc interval and its clinical implication. In addition, we recommend that a lower threshold is evaluated when probability values between 0.1 and <0.5 are observed for exceeding ≥10 ms. In this way, it is possible to assess the magnitude of potential pro-arrhythmic effects for compounds with borderline activity, as shown for NCE03.

We acknowledge that the evidence from three compounds with unknown mechanisms of action is not sufficient to establish the sensitivity and specificity of the method. These results provide, however, further motivation to explore the feasibility of using a conceptual framework for future evaluation of the pro-arrhythmic potential of candidate molecules, in which drug-specific parameters are used to scale up or translate the effects observed in dogs [17]. The approach consists in the use of simulation scenarios in which pharmacokinetic profiles in humans are simulated, taking into account the putative drug effects, as defined by the drug-specific parameter in our model (i.e. slope). In addition, it should be noted that based on the present parameterization, it is possible to evaluate the pro-arrhythmic effects of a drug also from a medical perspective; for instance, to assess correlations between drug exposure and abnormal or extreme QT values. In this context, one could generate, for example, probability curves for observing QT intervals >500 ms.

From a drug development perspective, our approach appears to overcome one of the main limitations of earlier PKPD models in preclinical research, i.e. their use as a screening tool in early drug development. Usually, different PKPD models are required to describe preclinical and clinical data. In other cases, additional in vitro data have been used to correlate findings across species [9,15,28]. Furthermore, the choice of parameterization in these analyses does not allow for the reuse of the model for a different compound or compound class, defeating the main purpose of such an analysis.

The proposed approach also prevents some of the pitfalls from inaccuracies in current experimental protocols [29]. Although some criticism may be made regarding the lack of a more mechanistic parameterization of the effects on repolarization, the use of a slope provides a strong basis for the generalizability of the approach, irrespective of the underlying receptor–ligand interaction [30,31]. In terms of sensitivity and specificity, we anticipate another important advantage over current drug-screening strategies, which rely on the identification of molecules with low-potency hERG-blocking activity whilst retaining desirable therapeutic properties. In fact, our results raise questions about the predictive value hERG safety margins, which are currently used in conjunction with in vivo nonclinical data to establish the liability for QT/QTc interval prolongation in humans [2].

Experimental design requirements

The pharmacokinetic data used as input for the assessment of the PKPD relationships were derived taking into account between-subject variability in drug exposure and assuming that any effects were associated with the parent drug, rather than with potential metabolites. It should be highlighted that despite the possibility of mean or typical population data when describing pharmacokinetics, overlooking variability in drug disposition may lead to biased conclusions about a compound's liability for QT/QTc interval prolongation. It is therefore essential that individual predicted concentrations are used. This imposes a slightly different experimental protocol than what is typically done in safety pharmacology, i.e. drug exposure is imputed from satellite animals in other toxicology protocols, where pharmacokinetic sampling is required. It should be recognized that individual pharmacokinetic profiles may be effective in disentangling spurious noise from the large inter- and intra-individual variability in ECG recording [32]. In addition, the availability of individual concentration vs. time profiles provides further insight into the role of other moieties, such as metabolites, in the onset and maintenance of effects.

With regard to the use of empirical sampling schemes, we have highlighted in a previous publication that the choice for limited or sparse sampling (usually three to eight samples) without clear understanding of the pharmacokinetic properties in the species of interest renders the assessment of PKPD relationships rather difficult and imprecise. Optimal design concepts should be used to prevent or overcome these issues [8,33,34]. Sampling matrices can also be considered, in which some blood samples are collected during ECG monitoring and additional samples are taken on a separate occasion after or before the safety experiment.

Prediction of QT/QTc interval in humans

The ultimate goal of this research project is to evaluate the feasibility of translating drug effects in conscious dogs to humans in terms of a decision algorithm. Such an algorithm should allow one to establish the liability for QT/QTc interval prolongation and, consequently, determine whether or not a compound should progress in development or be terminated. Currently, neither the use of a thorough QT study in late clinical development nor the exclusion of molecules with hERG channel affinity during drug screening are appropriate filters for decision-making purposes. Thorough QT studies have been shown to be highly cost ineffective, whereas relying on hERG-binding findings at experimental exposure levels that may not be clinically relevant creates unnecessarily high attrition rates.

Undoubtedly, there are many complexities in trying to establish interspecies correlations, particularly when compounds show multiple binding sites and/or metabolites are shown to have ion channel inhibitory properties [35,36]. In these cases, the solution is possibly to investigate further the underlying causes of torsades de pointes, with the aim of being able to predict torsades de pointes, rather than using an imperfect surrogate marker, i.e. QTc interval prolongation [29]. As long as such a marker is not available, it seems obvious that fit-for-purpose protocols are needed that enable the characterization of the underlying PKPD relationships.

In summary, NEC01, NCE02 and NCE03 have shown distinctive pro-arrhythmic activity, with QTc prolongation, no and borderline QT-prolonging effects, respectively. The PKPD relationships were successfully described by a single structural model with acceptable precision in prediction. The probability of an increase in QT/QTc interval ≥10 ms was evident for NCE01, whilst this threshold was not achieved for NCE02 and NCE03 in either species. Together with the evidence of model performance for compounds with known pro-arrhythmic effects, our approach seems to offer the basis for accurate safety screening of novel molecules. Most importantly, the method can be implemented easily within pharmaceutical research and development.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare: VFSD had support from Top Institute Pharma, The Netherlands for the submitted work; no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years; no other relationships or activities that could appear to have influenced the submitted work.