ON CLASSES OF EQUIVALENCE AND IDENTIFIABILITY OF AGE-DEPENDENT BRANCHING PROCESSES

Abstract

Age-dependent branching processes are increasingly used in analyses of biological data. Despite being central to most statistical procedures, the identifiability of these models has not been studied. In this paper, we partition a family of age-dependent branching processes into equivalence classes over which the distribution of the population size remains identical. This result is applicable to study identifiability of the offspring and lifespan distributions for parametric families of branching processes. For example, we identify classes of Markov processes that are not identifiable. We show that age-dependent processes with (non-exponential) gamma distributed lifespan are identifiable and that Smith-Martin processes are not always identifiable.

1. Introduction

Let Z(t) denote the size of a population governed by an age-dependent branching process started at t = 0 with a single particle or cell of age 0. Upon completion of its lifespan, every cell produces a random number of offspring ξ ∈ = {0, 1, 2, …, J}, where J is a given positive integer. Let p := (p₀, …, p_J), where p_j := 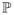(ξ = j), j ∈ , denote the offspring distribution. Put h(u; p) := p_ju^j, u ∈ [−1, 1], and μ := (ξ) = jp_j for its probability generating function (p.g.f.) and expectation. A cell that produces a single offspring (ξ = 1) is said to be quiescent. This feature is relevant when modeling tumor growth ([1]; see also [5]). Throughout, we shall implicitly assume that p₁ ∈ [0, 1). Put (p) := {j ∈ : p_j > 0}. For every j ∈ (p), let G_j(t) := 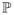(τ ≤ t|ξ = j), t ≥ 0, denote the conditional cumulative distribution function (c.d.f.) of the lifespan τ, given ξ = j. Write for the class all absolutely continuous (a.c.) c.d.f. F that are proper and satisfy F(0+) = 0 (the assumption of a.c. is not needed but simplifies the presentation). Assume that G_j ∈ , j ∈ (p). As usual, every cell evolves independently of all other cells. Put G = {G_j, j ∈ (p)}. We shall refer to C = (p, G) as the characteristics of the process. The process is of Bellman-Harris type if the c.d.f. G_j are identical for all j ∈ (p). Otherwise it allows the lifespan and offspring to be dependent, and belongs to the class of Sevastyanov processes [7, 4, 3].

In this paper, we study the following question: are there distinct characteristics (p, G) under which the distribution of the process Z(t) is identical? This question is relevant to the problem of model identifiability, which is a central prerequisite to most statistical procedures. Although age-dependent branching processes are widely used in biology, this question does not appear to have been studied for this class of models [2, 5, 9]. Answering this question will inform us about what can or cannot be estimated by only observing Z(t), a situation that arises frequently in cell biology.

Let denote the class of all processes that satisfy the above assumptions. It will be useful to define a subclass of processes included in , say , with characteristics (p, G) satisfying p₁ = 0. We shall say that two processes with characteristics (p, G) and (p̂, Ĝ) are equivalent if, for all t ≥ 0, the distribution of Z(t) is the same under either characteristics. Let denote the collection of processes included in that are equivalent to the process with characteristics (p, G). It forms an equivalence class, and our objective is to identify all the processes included in this class for any admissible set of characteristics (p, G). If the class includes processes other than the process with characteristics (p, G), then p and G cannot be unequivocally identified by the marginal distribution of Z(t) for all t ≥ 0.

We construct the class in the next section. We proceed in three steps. Firstly, we identify a collection of equivalent processes (Section 2.1). Next, by inverting the transformation that defines this collection about a properly chosen process, we find a larger collection of equivalent processes (Section 2.2). Finally, we prove, when J = 2, which is typical of most biological applications, and J = 3, that the larger collection is identical to (Section 2.3). Each equivalence class contains a single process such that p₁ = 0. When J = 2, the equivalence classes are fully characterized by the expectation and the variance of Z(t) (Section 2.4). Our results are applicable to study identifiability of families of parametric models. For example, we find that the Markov version of the process is not always identifiable (Section 3.1). The age-dependent process with (non-exponential) gamma distributed lifespan is identifiable (Section 3.2). We also find that the Smith-Martin process is not always identifiable (Section 3.3).

2. Main results

2.1. A collection of equivalent processes

For every p₁ ∈ [0, 1) and a ∈ [0, p₁], define $p^{(a)}=(p_0^{(a)},\dots ,p_J^{(a)})$, where

$$p_j^{(a)}:=\{\begin{array}{ll}\frac{p_j}{1-a}\hfill & j\in \mathcal{J}\backslash \{1\}\hfill \\ \frac{p_1-a}{1-a}\hfill & j=1.\hfill \end{array}$$ (1)

Notice that (p)\{1} = (p^(a))\{1}. By convention, when p₁ = 0, G₁ will denote any c.d.f. in . For every t ≥ 0, j ∈ (p), a ∈ [0, p₁], put

$$G_j^{(a)}(t):=(1-a)G_j\ast \sum _{k=0}^{\infty }{a}^k{G}_1^{\ast k}(t),$$ (2)

where $G_j\ast G_1(t):={\int }_0^t{G}_j(t-x){dG}_1(x)$ denotes the convolution of G_j and F₁, and where $G_1^{\ast k}(t):={\int }_0^t{G}_1^{\ast (k-1)}(t-x){dG}_1(x)$ is the k-fold convolution of G₁ with itself. For every p₁ ∈ [0, 1) and a ∈ [0, p₁], it can be verified that $G_j^{(a)}$ is the c.d.f. of a proper distribution; it can be interpreted as the c.d.f. of a (non-Markov) phase-type distribution, and the Laplace transform of $g_j^{(a)}(t):=d{G}_j^{(a)}(t)/dt$ is:

$${\mathcal{L}}_{g_j^{(a)}}(s)=\frac{(1-a){\mathcal{L}}_{g_j}(s)}{1-a{\mathcal{L}}_{g_1}(s)},$$ (3)

where is the Laplace transforms of g_j(t) := dG_j(t)/dt. Write $G^{(a)}=\{G_j^{(a)},j\in {\mathcal{J}}^{\ast }(p^{(a)})\}$ and C^(a) = (p^(a), G^(a)).

Let denote the collection of processes with characteristics (p^(a), G^(a)), a ∈ [0, p₁]. Since (p⁽⁰⁾, G⁽⁰⁾) = (p, G), includes the process with characteristics (p, G). Thus it is never empty. Moreover, since $p_1^{(p_1)}=0$, always includes at least one process from . This process will play a central role in constructing .

Theorem 1

For all t ≥ 0, the distribution of the population size process Z(t) is identical under all processes included in ; that is, ⊆ .

Proof

Let Φ_C(u, t) := {u^Z(t)|Z(0) = 1}, u ∈ [−1, 1] and t ≥ 0, denote the p.g.f. of Z(t) under the process with characteristics C. Conditioning on the lifespan of the cell initiating the population yields

$${\mathrm{\Phi }}_C(u,t)=u\left\{1-\sum _{j\in {\mathcal{J}}^{\ast }(p)}{p}_j{G}_j(t)\right\}+\sum _{j\in {\mathcal{J}}^{\ast }(p)}{p}_j{\int }_0^t{\mathrm{\Phi }}_C{(u,t-x)}^j{dG}_j(x).$$ (4)

For every j ∈ and u ∈ [−1, 1], let ${\mathcal{L}}_{{\mathrm{\Phi }}_C^j}(u,s):={\int }_0^{\infty }{e}^{-st}{\mathrm{\Phi }}_C{(u,t)}^{j}dt$ denote the Laplace transform of Φ_C(u, t)^j. Put ${\mathcal{L}}_{{\mathrm{\Phi }}_C}(u,t)={\mathcal{L}}_{{\mathrm{\Phi }}_C^1}(u,t)$. Since |Φ_C(u, t)| ≤ 1 for every u ∈ [−1, 1], and t ≥ 0, we have that ${\mathcal{L}}_{{\mathrm{\Phi }}_C^j}(u,s)<\infty$ for every s > 0. Also, it follows from eqn. (4) that (u, s), s > 0, satisfies:

$${\mathcal{L}}_{{\mathrm{\Phi }}_C}(u,s)=\frac{u}{s}\left\{1-\sum _{j\in {\mathcal{J}}^{\ast }(p)}{p}_j{\mathcal{L}}_{g_j}(s)\right\}+\sum _{j\in {\mathcal{J}}^{\ast }(p)}{p}_j{\mathcal{L}}_{{\mathrm{\Phi }}_C^j}(u,s){\mathcal{L}}_{g_j}(s).$$ (5)

For every a ∈ [0, p₁], eqn. (5) can be rearranged into

$$\begin{array}{l}\{1-a{\mathcal{L}}_{g_1}(s)\}{\mathcal{L}}_{{\mathrm{\Phi }}_C}(u,s)=\frac{u}{s}\left\{1-\sum _{j\in {\mathcal{J}}^{\ast }(p)\backslash \{1\}}{p}_j{\mathcal{L}}_{g_j}(s)-p_1{\mathcal{L}}_{g_1}(s)\right\}\\ +\sum _{j\in {\mathcal{J}}^{\ast }(p)\backslash \{1\}}{p}_j{\mathcal{L}}_{{\mathrm{\Phi }}_C^j}(u,s){\mathcal{L}}_{g_j}(s)+(p_1-a){\mathcal{L}}_{{\mathrm{\Phi }}_C}(u,s){\mathcal{L}}_{g_1}(s).\end{array}$$

Dividing both sides of the equation by 1 − a (s) yields

$$\begin{array}{l}{\mathcal{L}}_{{\mathrm{\Phi }}_C}(u,s)=\frac{u}{s}\{\frac{1}{1-a{\mathcal{L}}_{g_1}(s)}-\sum _{j\in {\mathcal{J}}^{\ast }(p^{(a)})\backslash \{1\}}\frac{p_j}{1-a}\frac{(1-a){\mathcal{L}}_{g_j}(s)}{1-a{\mathcal{L}}_{g_1}(s)}\\ -\frac{p_1-a}{1-a}\frac{(1-a){\mathcal{L}}_{g_1}(s)}{1-a{\mathcal{L}}_{g_1}(s)}-\frac{a{\mathcal{L}}_{g_1}(s)}{1-a{\mathcal{L}}_{g_1}(s)}\}\\ +\sum _{j\in {\mathcal{J}}^{\ast }(p^{(a)})\backslash \{1\}}\frac{p_j}{1-a}\frac{(1-a){\mathcal{L}}_{g_j}(s)}{1-a{\mathcal{L}}_{g_1}(s)}{\mathcal{L}}_{{\mathrm{\Phi }}_C^j}(u,s)+\frac{p_1-a}{1-a}\frac{(1-a){\mathcal{L}}_{f_1}(s)}{1-a{\mathcal{L}}_{g_1}(s)}{\mathcal{L}}_{{\mathrm{\Phi }}_C}(u,s)\\ =\frac{u}{s}\left\{1-\sum _{j\in {\mathcal{J}}^{\ast }(p^{(a)})}{p}_j^{(a)}(\theta ){\mathcal{L}}_{g_j^{(a)}}(s)\right\}+\sum _{j\in {\mathcal{J}}^{\ast }(p^{(a)})}{p}_j^{(a)}{\mathcal{L}}_{{\mathrm{\Phi }}_C^j}(u,s){\mathcal{L}}_{g_j^{(a)}}(s).\end{array}$$ (6)

By comparing eqns. (5) and (6), we deduce that (u, s) = (u, s), hence the processes with characteristics (p, G) and (p^(a), G^(a)), a ∈ [0, p₁], are equivalent.

2.2. A larger collection of equivalent processes

By inverting the transformation (p, G) → (p^(a), G^(a)), a ∈ [0, p₁], about a properly chosen process in , we will construct a collection of equivalent processes that is larger than . Setting a = p₁ in eqns. (1) and (3) yields

$$\begin{array}{l}{p}_j^{(p_1)}=\{\begin{array}{ll}\frac{p_j}{1-p_1}\hfill & j\in \mathcal{J}\backslash \{1\}\hfill \\ 0\hfill & j=1,\hfill \end{array}\\ {\mathcal{L}}_{g_j^{(p_1)}}(s)=\frac{(1-p_1){\mathcal{L}}_{g_j}(s)}{1-p_1{\mathcal{L}}_{g_1}(s)},j\in {\mathcal{J}}^{\ast }(p)\backslash \{1\},\end{array}$$

which identifies a process in . We remark that Φ_C^(p1)(u, t) does not depend on $G_1^{(p_1)}$. Also, any process with characteristics (p̂, Ĝ) that satisfy

$$\{\begin{array}{ll}{\widehat{p}}_j^{({\widehat{p}}_1)}=p_j^{(p_1)}\hfill & j\in \mathcal{J}\backslash \{1\}\hfill \\ {\mathcal{L}}_{{\widehat{g}}_j^{({\widehat{p}}_1)}}(s)={\mathcal{L}}_{g_j^{(p_1)}}(s)\hfill & j\in {\mathcal{J}}^{\ast }(p)\backslash \{1\}\hfill \end{array}$$ (7)

belongs to because Φ_Ĉ(u, t) = Φ_Ĉ^(p̂1)(u, t) = Φ_C^(p1)(u, t) = Φ_C(u, t). By solving eqns. (7) we find that (p̂, Ĝ) satisfies

$$\{\begin{array}{ll}{\widehat{p}}_j=p_j^{(p_1)}(1-{\widehat{p}}_1)\hfill & j\in \mathcal{J}\backslash \{1\}\hfill \\ {\mathcal{L}}_{{\widehat{g}}_j}(s)={\mathcal{L}}_{g_j}^{(p_1)}(s)\{1-{\widehat{p}}_1{\mathcal{L}}_{{\widehat{g}}_1}(s)\}/(1-{\widehat{p}}_1)\hfill & j\in {\mathcal{J}}^{\ast }(p)\backslash \{1\},\hfill \end{array}$$ (8)

where p̂₁ ∈ [0, 1) and Ĝ₁ ∈ , and where ⊆ is a set of distributions such that (s), j ∈ (p̂)\{1}, are the Laplace transforms of distributions in . Write (p_{p̂1, Ĝ1}, G_{p̂1, Ĝ1}) for any characteristics that satisfy eqns. (8). Then, the collection of processes

$${\overline{\mathcal{S}}}_{p,G}:=\underset{{\widehat{p}}_1\in [0,1)}{\cup }\underset{{\widehat{G}}_1\in {\mathcal{D}}_{p,G}}{\cup }\left\{\text{process}\text{with}\text{characteristics}(p_{{\widehat{p}}_1,{\widehat{G}}_1},G_{{\widehat{p}}_1,{\widehat{G}}_1})\right\}$$

is included in . It is also clear that ⊂ .

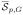2.3. Exhaustivity of 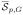when J = 2 and J = 3

Our final step toward identifying is to prove that it coincides with 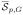. Let ${\mathrm{\Phi }}_C^{(k)}(u,t):={\partial }^k{\mathrm{\Phi }}_C(u,t)/\partial u^k$ denote the k-th order partial derivative of Φ_C(u, t), k = 1, 2 ···. Let $m_k(t):=\mathbb{E}[{\prod }_{l=0}^{k-1}\{Z(t)-l\}\mid Z(0)=1]$, t ≥ 0, k = 1, 2 ···, denote the k-th order factorial moment of Z(t) under the process with characteristics C, and write m(t) = m₁(t). We have that m_k(t) = Φ^(k)(1, t). Differentiating both sides of eqn. (4) with respect to u at u = 1 yields the following integral equation for the expectation of the process:

$$m(t)=1-\sum _{j\in {\mathcal{J}}^{\ast }(p)}{p}_j{G}_j(t)+\sum _{j\in {\mathcal{J}}^{\ast }(p)}{jp}_j{\int }_0^{t}m(t-x){dG}_j(x).$$ (9)

The second and third order factorial moments satisfy

$$m_2(t)=\sum _{j\in {\mathcal{J}}^{\ast }(p)}{jp}_j{\int }_0^t{m}_2(t-x){dG}_j(x)+\sum _{j\in {\mathcal{J}}^{\ast }(p)}j(j-1)p_j{\int }_0^t{m}^2(t-x){dG}_j(x),$$ (10)

and

$$\begin{array}{l}{m}_3(t)=\sum _{j\in {\mathcal{J}}^{\ast }(p)}{jp}_j{\int }_0^t{m}_3(t-x){dG}_j(x)\\ +\sum _{j\in {\mathcal{J}}^{\ast }(p)}3j(j-1)p_j{\int }_0^{t}m(t-x)m_2(t-x){dG}_j(x)\\ +\sum _{j\in {\mathcal{J}}^{\ast }(p)}j(j-1)(j-2)p_j{\int }_0^{t}m{(t-x)}^3{dG}_j(x).\end{array}$$ (11)

Let (s) denote the Laplace transform of m^k(t), k = 1, 2, 3. Taking the Laplace transform of both sides of eqns. (9–11) and rearranging the terms yields

$${\mathcal{L}}_m(s)=\frac{1-{\sum }_{j\in {\mathcal{J}}^{\ast }(p)}{p}_j{\mathcal{L}}_{g_j}(s)}{s\{1-{\sum }_{j\in {\mathcal{J}}^{\ast }(p)}{jp}_j{\mathcal{L}}_{g_j}(s)\}},$$ (12)

$${\mathcal{L}}_{m_2}(s)=\frac{{\mathcal{L}}_{m^2}(s){\sum }_{j\in {\mathcal{J}}^{\ast }(p)}j(j-1)p_j{\mathcal{L}}_{g_j}(s)}{1-{\sum }_{j\in {\mathcal{J}}^{\ast }(p)}{jp}_j{\mathcal{L}}_{g_j}(s)},$$ (13)

and

$${\mathcal{L}}_{m_3}(s)=\frac{{\mathcal{L}}_{m^3}(s){\sum }_{j\in {\mathcal{J}}^{\ast }(p)}j(j-1)(j-2)p_j{\mathcal{L}}_{g_j}(s)}{1-{\sum }_{j\in {\mathcal{J}}^{\ast }(p)}{jp}_j{\mathcal{L}}_{g_j}(s)}+\frac{3{\mathcal{L}}_{m{m}_2}(s){\mathcal{L}}_{m_2}(s)}{{\mathcal{L}}_{m^2}(s)},$$ (14)

where (s) denotes the Laplace transform of m(t)m₂(t).

Lemma 1

Suppose that J = 2 or J = 3. For every admissible (p, G), the equivalence class includes a single process in .

Proof

Assume first that J = 3. Consider two processes in with characteristics C = (p, G) and Ĉ = (p̂, Ĝ). Thus, p₁ = 0 and p̂₁ = 0. Suppose that these processes are equivalent; that is, they both belong to . Then Φ_C(u, t) = Φ_Ĉ(u, t) and ${\mathrm{\Phi }}_C^{(k)}(1,t)={\mathrm{\Phi }}_{\widehat{C}}^{(k)}(1,t)$, u ∈ [−1, 1], t ≥ 0, and k = 1, 2, 3. Write m̂_k(t) for the k-th order factorial moment of the process with characteristics Ĉ. Hence, ${\mathcal{L}}_{{\mathrm{\Phi }}_C^{(k)}}(s)={\mathcal{L}}_{{\mathrm{\Phi }}_{\widehat{C}}^{(k)}}(s)$, which, using Identities (12–14), yields

$$\{\begin{array}{ccc}\frac{1-p_0{\mathcal{L}}_{g_0}(s)-p_2{\mathcal{L}}_{g_2}(s)-p_3{\mathcal{L}}_{g_3}(s)}{d(s)}& =& \frac{1-{\widehat{p}}_0{\mathcal{L}}_{{\widehat{g}}_0}(s)-{\widehat{p}}_2{\mathcal{L}}_{{\widehat{g}}_2}(s)-{\widehat{p}}_3{\mathcal{L}}_{{\widehat{g}}_3}(s)}{\widehat{d}(s)}\\ \frac{{\mathcal{L}}_{m^2}(s)\{2p_2{\mathcal{L}}_{g_2}(s)+6p_3{\mathcal{L}}_{g_3}(s)\}}{d(s)}& =& \frac{{\mathcal{L}}_{m^2}(s;\widehat{C})\{2{\widehat{p}}_2{\mathcal{L}}_{{\widehat{g}}_2}(s)+6{\widehat{p}}_3{\mathcal{L}}_{{\widehat{g}}_3}(s)\}}{\widehat{d}(s)}\\ \frac{6{\mathcal{L}}_{m^3}(s)p_3{\mathcal{L}}_{g_3}(s)}{d(s)}+\frac{3{\mathcal{L}}_{m{m}_2}(s){\mathcal{L}}_{m_2}(s)}{{\mathcal{L}}_{m^2}(s)}& =& \frac{6{\mathcal{L}}_{{\widehat{m}}^3}(s){\widehat{p}}_3{\mathcal{L}}_{{\widehat{g}}_3}(s)}{\widehat{d}(s)}+\frac{3{\mathcal{L}}_{\widehat{m}{\widehat{m}}_2}(s;){\mathcal{L}}_{{\widehat{m}}_2}(s)}{{\mathcal{L}}_{{\widehat{m}}^2}(s)},\end{array}$$

where d(s) = 1 − 2p₂ (s) − 3p₃ (s) and d̂(s) = 1 − 2p̂₂ (s) − 3p̂₃ (s). Since (s) = (s), k = 1, 2, 3, and (s) = (s), the above system reduces to

$$p_j{\mathcal{L}}_{g_j}(s)/d(s)={\widehat{p}}_j{\mathcal{L}}_{{\widehat{g}}_j}(s)/\widehat{d}(s)j=0,2,3.$$ (15)

The above equations obtained when j = 2, 3 yield

$$\{\begin{array}{ccc}{p}_2{\mathcal{L}}_{g_2}(s)-3p_2{\mathcal{L}}_{g_2}(s){\widehat{p}}_3{\mathcal{L}}_{{\widehat{g}}_3}(s)& =& {\widehat{p}}_2{\mathcal{L}}_{{\widehat{g}}_2}(s)-3{\widehat{p}}_2{\mathcal{L}}_{{\widehat{g}}_2}(s)p_3{\mathcal{L}}_{g_3}(s)\\ p_3{\mathcal{L}}_{g_3}(s)-2p_3{\mathcal{L}}_{g_3}(s){\widehat{p}}_2{\mathcal{L}}_{{\widehat{g}}_2}(s)& =& {\widehat{p}}_3{\mathcal{L}}_{{\widehat{g}}_3}(s)-2{\widehat{p}}_3{\mathcal{L}}_{{\widehat{g}}_3}(s)p_2{\mathcal{L}}_{g_2}(s),\end{array}$$

which implies that 2p₂ (s) + 3p₃ (s) = 2p̂₂ (s) + 3p̂₃ (s), hence d(s) = d̂(s), and the system of equations (15) reduces to p_j (s) = p̂_j (s), j = 0, 2, 3. Hence (p̂, Ĝ) = (p, G) since the distributions G_j and Ĝ_j, j ∈ (p), are all proper. This completes the proof when J = 3. The case J = 2 is treated similarly except that we only use the first and second equations of the system (15), and we set p₃ = p̂₃ = 0.

Theorem 2

We have 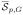= for every admissible (p, G) when J = 2 and J = 3.

Proof

We already know that 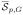⊆ . To prove that the converse holds true, let (p̂, Ĝ) denote the characteristics of any process included in . Then, by construction, the process with characteristics (p̂^(p̂₁), Ĝ^(p̂₁)) belongs to . We also know from Lemma 1 that (p̂^(p̂₁), Ĝ^(p̂₁)) = (p^(p₁), G^(p₁)). Hence the process with characteristics (p̂, Ĝ) belongs to 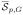, which implies that ⊆ 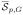. This completes the proof.

2.4. Characterization of using moments when J = 2

In data analyses, model parameters are sometimes estimated using moments of the process rather than its distribution. Then, a relevant question is which moments are sufficient to fully characterize the equivalence class ? We show below that the answer is simply the expectation and variance when J = 2. This property does not appear to generalize when J > 2, however.

Theorem 3

Assume that J = 2 and that the marginal distribution of {Z(t), t ≥ 0}, is determined by its moments. Then, = {processes with characteristics (p̂, Ĝ) : m̂(t) = m(t), m̂₂(t) = m₂(t), t ≥ 0}.

Proof

To simplify the presentation, we assume, when p_j = 0, that G_j is any arbitrary c.d.f in . For k = 2, 3 ···, it can be shown by induction and using the identity $m_k(t)={\mathrm{\Phi }}_C^{(k)}(1,t)$ that

$$m_k(t)=p_2{\int }_0^t\sum _{r=1}^{\lfloor k/2\rfloor }{c}_{kr}{m}_r(t-x)m_{k-r}(t-x){dG}_2(x)+\sum _{j=1}^2{jp}_j{\int }_0^t{m}_k(t-x){dG}_j(x),$$

where ⌊k/2⌋ denotes the largest integer less than or equal to k/2, and c_kr are some positive integers. Then,

$${\mathcal{L}}_{m_k}(s)=p_2{l}_k(s){\mathcal{L}}_{g_2}(s)+{\mathcal{L}}_{m_k}(s)\sum _{j=1}^2{jp}_j{\mathcal{L}}_{g_j}(s),$$ (16)

where l_k(s) is the Laplace transform of ${\sum }_{r=1}^{\lfloor k/2\rfloor }{c}_{kr}{m}_r(t)m_{k-r}(t)$. Hence,

$${\mathcal{L}}_{m_k}(s)=\frac{l_k(s)p_2{\mathcal{L}}_{g_2}(s)}{1-{\sum }_{j=1}^2{jp}_j{\stackrel{\sim }{\mathcal{L}}}_{g_j}(s)}.$$

Let Ĉ = (p̂, Ĝ) denote the characteristics of any process in . Then Φ_Ĉ(u, t) = Φ_C(u, t), t ≥ 0, u ∈ [−1, 1]. By assumption, Φ_c(u, t) is determined by its moments. Hence, = {processes with characteristics (p̂, Ĝ) : m̂_k(t) = m_k(t), t ≥ 0, k ∈ }, where = {1, 2 ···}. We notice that m̂_k(t) = m_k(t) implies that (s) = (s) and l̂_k(s) = l_k(s), k ∈ , from which we deduce, when k = 2, that

$$\frac{p_2{\mathcal{L}}_{g_2}(s)}{1-{\sum }_{j=1}^2{jp}_j{\mathcal{L}}_{g_j}(s)}=\frac{{\widehat{p}}_2{\mathcal{L}}_{{\widehat{g}}_2}(s)}{1-{\sum }_{j=1}^{2}j{\widehat{p}}_j{\mathcal{L}}_{{\widehat{g}}_j}(s)},$$ (17)

and, when k = 3, 4 ···, that

$$\frac{l_k(s)p_2{\mathcal{L}}_{g_2}(s)}{1-{\sum }_{j=1}^2{jp}_j{\mathcal{L}}_{g_j}(s)}=\frac{l_k(s){\widehat{p}}_2{\mathcal{L}}_{{\widehat{g}}_2}(s)}{1-{\sum }_{j=1}^{2}j{\widehat{p}}_j{\mathcal{L}}_{{\widehat{g}}_j}(s)}.$$ (18)

Eqns. (17) and (18) are clearly equivalent when l_k(s) ≠ 0. When l_k(s) = 0, we deduce from eqn. (16) that (s) = 0 and m_k(t) = 0, k = 3, 4 ···. Thus, in either case, we conclude that = {processes with characteristics (p̂, Ĝ) : m̂_k(t) = m_k(t), t ≥ 0, k =1, 2}, which completes the proof.

3. Application to model identifiability

Results obtained in Section 2 are applicable to study identifiability of branching processes when specific parametric assumptions are made about the lifespan distributions. To shorten the discussion, we only consider the case where J = 2.

3.1. Exponentially distributed lifespan

We assume here that τ is conditionally exponentially distributed, given {ξ = j}: G_j(t) = 1 − e^−ψ_jt, t ≥ 0, for some ${\psi }_j\in {ℝ}_{+}^{\ast }$, j ∈ (p). The resulting class of processes is denoted by . We remark that (s) = ψ_j/(ψ_j + s), j ∈ (p). It is defined for s ∈ (−ψ_j, ∞), and extendable to s ∈ (−∞, −ψ_j) ∪ (−ψ_j, ∞) by analytic continuation.

For every admissible (p, G), let ${\mathcal{C}}_{p,G}^{\mathcal{M}}={\mathcal{C}}_{p,G}\cap \mathcal{M}$ denote the class of all processes included in that are equivalent to the process with characteristics (p, G). We say that the characteristics (p, G) are identified by {Z(t), t ≥ 0} if and only if ${\mathcal{C}}_{p,G}^{\mathcal{M}}$ includes only the process with characteristics (p, G). To establish identifiability of (p, G), or lack thereof, it suffices to construct the class ${\mathcal{C}}_{p,G}^{\mathcal{M}}$. Let (p̂ Ĝ) denote the characteristics of any process in ${\mathcal{C}}_{p,G}^{\mathcal{M}}$. Then Ĝ_j, j ∈ (p̂), is exponential.

Assume first that p₁ = 0. If p̂₁ = 0, Lemma 1 implies that (p̂, Ĝ) = (p, G). If p̂₁ ∈ (0, 1), we know from Theorem 2 and eqn. (8) that for every j ∈ (p)\{1},

$$\frac{(1-{\widehat{p}}_1){\widehat{\psi }}_j}{{\widehat{\psi }}_j+s}=\frac{{\psi }_j}{{\psi }_j+s}\left(1-\frac{{\widehat{p}}_1{\widehat{\psi }}_1}{{\widehat{\psi }}_1+s}\right).$$

Rearranging the terms in the above identity leads to the polynomial equation

$$(1-{\widehat{p}}_1){\widehat{\psi }}_j({\psi }_j+s)({\widehat{\psi }}_1+s)={\psi }_j\{(1-{\widehat{p}}_1){\widehat{\psi }}_1+s\}({\widehat{\psi }}_j+s).$$ (19)

This identity holds if and only if ψ̂_j = ψ̂₁ = ψ_j/(1 − p̂₁). Hence, for any j₁, j₂ ∈ (p), ψ_j1 = ψ_j2, and the process with the characteristics (p, G) must be Bellman-Harris. Write ψ := ψ_j, j ∈ (p), and we have ψ̂_j = ψ/(1 − p̂₁). Using the first equation in (8), we deduce that p̂_j = p_j(1 − p̂₁), p̂₁ ∈ (0, 1).

Assume next that p₁ ∈ (0, 1). If p̂₁ = 0, a similar line of arguments shows that the process with characteristics (p̂, Ĝ) satisfying ψ̂_j = ψ(1 − p₁), p̂_j = p_j/(1 − p₁), j ∈ (p){1}, belongs to ${\mathcal{C}}_{p,G}^{\mathcal{M}}$ if ψ_j = ψ, j ∈ (p)

Now assume that p₁ ∈ (0, 1) and p̂₁ ∈ (0, 1). Then, for every j ∈ (p), we have

$$\frac{(1-{\widehat{p}}_1){\widehat{\psi }}_j}{{\widehat{\psi }}_j+s}=\frac{(1-p_1){\psi }_j}{{\psi }_j+s}\left(1-\frac{{\widehat{p}}_1{\widehat{\psi }}_1}{{\widehat{\psi }}_1+s}\right)/\left(1-\frac{p_1{\psi }_1}{{\psi }_1+s}\right).$$

Rearranging the terms in the above identity leads to the polynomial equation

$$(1-{\widehat{p}}_1){\widehat{\psi }}_j\{(1-p_1){\psi }_1+s\}({\psi }_j+s)({\widehat{\psi }}_1+s)=(1-p_1){\psi }_j\{(1-{\widehat{p}}_1){\widehat{\psi }}_1+s\}({\widehat{\psi }}_j+s)({\psi }_1+s).$$ (20)

Solving this equation together with the first equation in (8) for each j ∈ (p)\{1} separately leads to three admissible sets of equations, denoted by A_j, B_j and C_j (indexed by j):

$$(A_j)\{\begin{array}{l}(1-{\widehat{p}}_1){\widehat{\psi }}_j=(1-p_1){\psi }_j\hfill \\ {\widehat{\psi }}_1={\psi }_1\hfill \\ {\widehat{\psi }}_j={\psi }_j\hfill \\ (1-{\widehat{p}}_1){\widehat{\psi }}_1=(1-p_1){\psi }_1\hfill \\ {\widehat{p}}_j/(1-{\widehat{p}}_1)=p_j/(1-p_1),\hfill \end{array}(B_j)\{\begin{array}{l}(1-{\widehat{p}}_1){\widehat{\psi }}_j=(1-p_1){\psi }_j\hfill \\ {\psi }_1={\psi }_j\hfill \\ {\widehat{\psi }}_1={\widehat{\psi }}_2\hfill \\ (1-p_1){\psi }_j=(1-{\widehat{p}}_1){\widehat{\psi }}_j\hfill \\ {\widehat{p}}_j/(1-{\widehat{p}}_1)=p_j/(1-p_1),\hfill \end{array}$$ (21)

and

$$(C_j)\{\begin{array}{l}(1-{\widehat{p}}_1){\widehat{\psi }}_2=(1-p_1){\psi }_2\hfill \\ {\widehat{\psi }}_1={\psi }_1\hfill \\ {\psi }_2=(1-{\widehat{p}}_1){\widehat{\psi }}_1\hfill \\ {\widehat{\psi }}_2=(1-p_1){\psi }_1\hfill \\ {\widehat{p}}_j/(1-{\widehat{p}}_1)=p_j/(1-p_1).\hfill \end{array}$$ (22)

Assume first that p₀p₂ > 0. Then the collection of Markov processes that are equivalent to the process with characteristics (p, G) is determined by simultaneously solving the equations X₀ and Y₂, where X and Y stand symbolically for either A, B, or C. There are 9 such combinations:

• For equations A₀ and A₂, it is easy to show that the only solution is (p̂, Ĝ) = (p, G). Thus, here, (p̂, Ĝ) identifies the process with characteristics (p, G).

• Equations B₀ and B₂ admit solutions if and only if ψ_j = ψ, j ∈ (p); that is, the process with characteristics (p, G) must be Bellman-Harris. When this condition is met, the solutions to the two equations satisfy ψ̂_j = ψ̂, j ∈ (p), where ψ̂ = ψ(1 − p₁)/(1 − p̂₁), p̂_j = p_j(1 − p̂₁)/(1 − p₁), and p̂₁ ∈ (0, 1). Thus, any Markov Bellman-Harris process admits infinitely many equivalent processes in , which are also (Markov) Bellman-Harris.

• Equations C₀ and C₂ admit solutions if and only if ψ₀ = ψ₂ and ψ₀ ≤ ψ₁. Under these constraints, the unique solution to the two sets of equations is: ψ̂₁ = ψ₁, ψ̂₀ = ψ̂₂ = (1 − p₁)ψ₁, p̂₁ = 1 − ψ₀/ψ₁, and p̂_j = p_jψ₀/{(1 − p₁)ψ₁}, j = 0, 2. This solution always differs from (p, G), except when p₁ = 1 − ψ₀/ψ₁. Thus, processes that satisfy the conditions ψ₀ = ψ₂ and ψ₀ ≤ ψ₁ are identifiable only if p₁ = 1 − ψ₀/ψ₁. Otherwise, there exists a unique (p̂, Ĝ) that differs from (p, G) under which the distribution of the process Z(t) does not change.

• Any other pair of equations admits solutions only under specific restrictions on (p, G). For example, equations A₀ and B₂ will have a solution provided that ψ₁ = ψ₂. When the conditions are met, the only solution to the equations is (p̂, Ĝ) = (p, G), and, therefore, identifies the initial process.

When either p₀ = 0 or p₂ = 0, we obtain the same set of solutions as above (details are omitted). We summarize the above findings in the following Corollary:

Corollary 1

Suppose that J = 2 and, for every j ∈ (p), that G_j(t) = 1 − e^−ψ_jt, t ≥ 0, for some ${\psi }_j\in {ℝ}_{+}^{\ast }$. Then, (p, G) is uniquely identified by the process {Z(t), t ≥ 0}, except in the following cases:

• Case 1: If ψ_j = ψ, j ∈ (p) (Bellman-Harris case), then ${\mathcal{C}}_{p,G}^{\mathcal{M}}$ includes the Markov processes with characteristics (p̂, Ĝ) ∈ {p̂₁ ∈ [0, 1), p̂_j = p_j(1 − p̂₁)/(1 − p₁), j ∈ (p)\{1}, ψ̂_j = ψ(1 − p₁)/(1 − p̂₁), j ∈ (p̂)}.

• Case 2: If ψ_j = ψ, j ∈ (p)\{1}, p₁ ∈ (0, 1), ψ < ψ₁, and p₁ ≠ 1 − ψ/ψ₁ (“extended” Bellman-Harris case), then ${\mathcal{C}}_{p,G}^{\mathcal{M}}$ consists of the processes in with characteristics (p, G) and (p̂, Ĝ) where p̂₁ = 1 − ψ/ψ₁, p̂_j = p_jψ/{(1 − p₁)ψ₁}, ψ̂₁ = ψ₁, ψ̂₀ = ψ̂₂ = (1 − p₁)ψ₁, j ∈ (p)\{1}.

Remark 1

Corollary 1 identifies two classes of processes in that are not identifiable. The characteristics of the equivalent processes differ widely over when (p, G) identifies a Bellman-Harris process. As an illustration, consider the Markov process with offspring distribution $p=(\frac{1}{5},\frac{1}{2},\frac{3}{10})$ and exponentially distributed lifespan with parameters ψ₀ = ψ₁ = ψ₂ = 1. This process is of Bellman-Harris type. The class of processes in equivalent to this process is determined by Case 1 of Corollary 1, and it includes the processes with offspring distributions $\widehat{p}=[\frac{2}{5}(1-{\widehat{p}}_1),{\widehat{p}}_1,\frac{3}{5}(1-{\widehat{p}}_1)]$ and exponentially distributed lifespan with parameters ${\widehat{\psi }}_0={\widehat{\psi }}_1={\widehat{\psi }}_2=\frac{1}{2(1-{\widehat{p}}_1)}$, where p̂₁ ∈ [0, 1). In particular, if p̂₁ = 0, we obtain the process parameterized by $\widehat{p}=(\frac{2}{5},0,\frac{3}{5})$ and ψ̂₀ = ψ̂₂ = 0.5, which belongs to . Figure 1.A displays examples of probability density functions ĝ₂ for a sample of processes that belong to the equivalence class. Figures 1.B–C show the set of probability density functions ĝ₂ when the Bellman-Harris structure of the process is relaxed. For example, in Figure 1.B, we set ψ₁ = 1.5 (all other parameter values are identical to those used in Figure 1.A), and find using Case 2 of Corollary 1 that the class of equivalent Markov processes includes a second process with offspring distribution $\widehat{p}=(\frac{4}{15},\frac{1}{3},\frac{2}{5})$ and exponentially distributed lifespan with parameters ψ̂₁ = 1.5, and ψ̂₀ = ψ̂₂ = 0.75. In Figure 1.C, we set ψ₁ = 0.5, while in Figure 1.D, we set ψ₁ = 1 and ψ₀ = 2. In these two cases, the class of equivalent processes includes only the original process, which is therefore identifiable.

Figure 1.

Representation of the set of probability density functions ĝ₂ over the class of equivalent processes for four Markov processes: (A) ψ₀ = ψ₁ = ψ₂ = 1 (Bellman-Harris process); (B) ψ₀ = ψ₂ = 1 and ψ₁ = 1.5 (> ψ₀ and > ψ₂) (“extended” Bellman-Harris process); (C) ψ₀ = ψ₂ = 1 and ψ₁ < 1 (“extended” Bellman-Harris process); (D) ψ₀ ≠ ψ₂, ψ₁ > 0, ψ₂ = 1. We set $p_1=\frac{1}{2}$ in all cases. Each plot shows g₂ and ĝ₂ (whenever ∃ĝ₂ ≠ g₂) for: the process with characteristics (p, G) (solid line); representative processes of the equivalence class (dashed grey lines); equivalent Markov process in (dashed black lines). The model is non-identifiable in cases (A) and (B), and identifiable in cases (C) and (D).

Remark 2

From a statistical standpoint, when Z(t) is observed at discrete time points, the likelihood function can be solely expressed using the marginal distribution of {Z(t), t ≥ 0}, and the model parameters are therefore not always identifiable. The maximum likelihood estimator is not consistent, at least in the traditional sense [6]. If modeling quiescence is not of primary interest this non-identifiability issue may be avoided by imposing p̂₁ = p₁ = 0. Under such a restriction, the interpretation of G_j, j ∈ (p), may change because the time to producing j offspring could now include a resting phase latently embedded in the lifespan.

3.2. Gamma distributed lifespan

We now extend the Markov process by assuming that the lifespan is gamma distributed: $G_j(t):={\int }_0^t\frac{{\kappa }_j^{{\omega }_j}}{\mathrm{\Gamma }({\omega }_j)}{x}^{{\omega }_j-1}{e}^{-{\kappa }_{j}x}dx$ for some ${\psi }_j:=({\omega }_j,{\kappa }_j)\in {ℝ}_{+}^{\ast }\times {ℝ}_{+}^{\ast }$, j ∈ (p). We have ${\mathcal{L}}_{g_j}(s)={\kappa }_j^{{\omega }_j}/{({\kappa }_j+s)}^{{\omega }_j}$, defined for s ∈ (−κ_j, ∞), but also extendable to s ∈ (−∞, −κ_j) ∪ (−κ_j, ∞) by analytic continuation. The assumption of gamma distributed lifespan is frequently made in practice [3, 9]. We obtain the Markov process of the previous section if ω_j = 1, j ∈ (p). We show, when ω_j ≠ 1, that it is identifiable:

Corollary 2

Suppose that J = 2 and, for every j ∈ (p), that G_j is a gamma distribution with parameters κ_j > 0, ω_j > 0 and ω_j ≠ 1. Then, (p, G) is uniquely identified by the process {Z(t), t ≥ 0}.

Proof

Let (p̂, Ĝ) denote the characteristics of any process included in . Assume first that p₁ = 0. If p̂₁ = 0, Lemma 1 implies that (p̂, Ĝ) = (p, G). If p̂₁ ∈ (0, 1), eqn. (7) gives

$$(1-{\widehat{p}}_1){\left(\frac{{\widehat{\kappa }}_j}{{\widehat{\kappa }}_j+s}\right)}^{{\widehat{\omega }}_j}={\left(\frac{{\kappa }_j}{{\kappa }_j+s}\right)}^{{\omega }_j}\left\{1-{\widehat{p}}_1{\left(\frac{{\widehat{\kappa }}_1}{{\widehat{\kappa }}_1+s}\right)}^{{\omega }_1}\right\}.$$

Rearranging the terms in the above identity leads to the equation

$$(1-{\widehat{p}}_1){\widehat{\kappa }}_j^{{\widehat{\omega }}_j}{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}{({\kappa }_j+s)}^{{\omega }_j}={\kappa }_j^{{\omega }_j}{({\widehat{\kappa }}_j+s)}^{{\widehat{\omega }}_j}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}\}.$$ (23)

Dividing both sides of eqn. (23) by (κ̂₁ + s)^ω̂₁ (κ_j + s)^ω_j and letting s → ∞ yields

$$(1-{\widehat{p}}_1){\widehat{\kappa }}_j^{{\widehat{\omega }}_j}={\kappa }_j^{{\omega }_j}\underset{s\to \infty }{lim}\left\{\frac{{({\widehat{\kappa }}_j+s)}^{{\widehat{\omega }}_j}}{{({\kappa }_j+s)}^{{\omega }_j}}-\frac{{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}{({\widehat{\kappa }}_j+s)}^{{\widehat{\omega }}_j}}{{({\kappa }_j+s)}^{{\omega }_j}{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}}\right\}.$$

In order for the R.H.S. to converge to a constant, we must have ω̂_j = ω_j, which implies that $(1-{\widehat{p}}_1){\widehat{\kappa }}_j^{{\widehat{\omega }}_j}={\kappa }_j^{{\omega }_j}$. Then, eqn. (23) reduces to ${({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}{({\kappa }_j+s)}^{{\omega }_j}={({\widehat{\kappa }}_j+s)}^{{\omega }_j}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}\}$. Setting s = −κ̂₁ gives ${\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}{({\widehat{\kappa }}_j-{\widehat{\kappa }}_1)}^{{\omega }_j}=0$, from which we deduce that κ̂_j = κ̂₁, and eqn. (23) reduces further to ${({\kappa }_j+s)}^{{\omega }_j}={({\widehat{\kappa }}_1+s)}^{{\omega }_j}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}{({\widehat{\kappa }}_1+s)}^{-{\widehat{\omega }}_1}$. Letting s → −κ̂₁, the L.H.S. converges to (κ_j − κ̂₁)^ω_j whereas the R.H.S. diverges to −∞. Hence, eqn. (23) has no admissible solutions.

Assume next that p₁ ∈ (0, 1). If p̂₁ = 0, a similar line of arguments shows that there are no admissible solutions. If p̂₁ ∈ (0, 1), eqn. (7) gives

$$\frac{(1-{\widehat{p}}_1){\left(\frac{{\widehat{\kappa }}_j}{{\widehat{\kappa }}_j+s}\right)}^{{\widehat{\omega }}_j}}{1-{\widehat{p}}_1{\left(\frac{{\widehat{\kappa }}_1}{{\widehat{\kappa }}_1+s}\right)}^{{\widehat{\omega }}_1}}=\frac{(1-p_1){\left(\frac{{\kappa }_j}{{\kappa }_j+s}\right)}^{{\omega }_j}}{1-p_1{\left(\frac{{\kappa }_1}{{\kappa }_1+s}\right)}^{{\omega }_1}}.$$

Rearranging the terms in the above identity leads to the equation

$$(1-p_1){\kappa }_j^{{\omega }_j}{({\kappa }_1+s)}^{{\omega }_1}{({\widehat{\kappa }}_j+s)}^{{\widehat{\omega }}_j}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}\}=(1-{\widehat{p}}_1){\widehat{\kappa }}_j^{{\omega }_j}{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}{({\kappa }_j+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}.$$ (24)

Divide both sides of eqn. (24) by (κ₁ +s)^ω₁ (κ̂₁ +s)^ω̂₁ (κ̂_j +s)^ω̂_j and let s → ∞. Then

$$(1-p_1){\kappa }_j^{{\omega }_j}=(1-{\widehat{p}}_1){\widehat{\kappa }}_j^{{\widehat{\omega }}_j}\underset{s\to \infty }{lim}\left\{\frac{{({\kappa }_j+s)}^{{\omega }_j}}{{({\widehat{\kappa }}_j+s)}^{{\widehat{\omega }}_j}}-\frac{p_1{\kappa }_1^{{\omega }_1}{({\kappa }_j+s)}^{{\omega }_j}}{{({\widehat{\kappa }}_j+s)}^{{\widehat{\omega }}_j}{({\kappa }_1+s)}^{{\omega }_1}}\right\}.$$ (25)

In order for the R.H.S. to converge to a constant, we must have ω_j = ω̂_j, which implies that $(1-p_1){\kappa }_j^{{\omega }_j}=(1-{\widehat{p}}_1){\widehat{\kappa }}_j^{{\widehat{\omega }}_j}$. Then, eqn. (24) reduces to

$${({\kappa }_1+s)}^{{\omega }_1}{({\widehat{\kappa }}_j+s)}^{{\omega }_j}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}\}={({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}{({\kappa }_j+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}.$$ (26)

Setting s = −κ₁ gives $-p_1{\kappa }_1^{{\omega }_1}{({\widehat{\kappa }}_1-{\kappa }_1)}^{{\widehat{\omega }}_1}{({\kappa }_j-{\kappa }_1)}^{{\omega }_j}=0$, from which we deduce that either κ̂₁ = κ₁ or κ_j = κ₁. We study these two cases separately.

• Case 1: κ̂₁ = κ₁. Assume first that ω₁ > ω̂₁. Eqn. (26) becomes

  $${({\kappa }_1+s)}^{{\omega }_1-{\widehat{\omega }}_1}{({\widehat{\kappa }}_j+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\kappa }_1^{{\widehat{\omega }}_1}\}={({\kappa }_j+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}.$$ (27)
  Setting s = −κ₁ gives $p_1{\kappa }_1^{{\omega }_1}({\kappa }_j-{\kappa }_1)=0$. Hence, we must have κ₁ = κ_j, and eqn. (27) becomes

  $${({\kappa }_1+s)}^{{\omega }_1-{\widehat{\omega }}_1}{({\widehat{\kappa }}_j+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\kappa }_1^{{\widehat{\omega }}_1}\}={({\kappa }_1+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}.$$ (28)

  We distinguish two sets of solutions:

  1. If κ̂_j = κ₁, eqn. (28) reduces to ${({\kappa }_1+s)}^{{\omega }_1-{\widehat{\omega }}_1}\{{({\kappa }_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\kappa }_1^{{\widehat{\omega }}_1}\}=\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}$. Setting s = −κ₁ yields $p_1{\kappa }_1^{{\omega }_1}=0$, which is not admissible here because p₁κ₁ > 0.

  2. If κ̂_j ≠ κ₁, dividing both sides of eqn. (28) by (κ₁ + s)^ω_j and letting s → −κ₁ entails that ω_j = ω₁ − ω̂₁ > 0, and eqn. (28) reduces to ${({\widehat{\kappa }}_j+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\kappa }_1^{{\widehat{\omega }}_1}\}={({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}$. Differentiating both sides of the equation with respect to s gives

     $${\omega }_j{({\widehat{\kappa }}_j+s)}^{{\omega }_j-1}\{{({\kappa }_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\kappa }_1^{{\widehat{\omega }}_1}\}+{\widehat{\omega }}_1{({\widehat{\kappa }}_j+s)}^{{\omega }_j}{({\kappa }_1+s)}^{{\widehat{\omega }}_1-1}={\omega }_1{({\kappa }_1+s)}^{{\omega }_1-1}.$$

     Letting s → −κ̂_j, the L.H.S. of the equation converges to 0 if ω_j > 1 and diverges to −∞ if 0 < ω_j < 1, whereas the R.H.S. converges to ω₁(κ₁ − κ̂_j)^ω₁−1 ∈ (0, ∞). Hence, eqn. (26) has no admissible solutions in this case either. By using a similar line of arguments, one can show that eqn. (26) has no admissible solutions either when ω₁ < ω̂₁.

     When ω̂₁ = ω₁, eqn. (26) reduces to

     $${({\widehat{\kappa }}_j+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\omega }_1}-{\widehat{p}}_1{\kappa }_1^{{\omega }_1}\}={({\kappa }_j+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}.$$ (29)
     If κ̂_j ≠ κ_j, setting s = −κ̂_j gives ${({\kappa }_1-{\widehat{\kappa }}_j)}^{{\omega }_1}=p_1{\kappa }_1^{{\omega }_1}$ and setting s = −κ_j gives ${({\kappa }_1-{\kappa }_j)}^{{\omega }_1}={\widehat{p}}_1{\kappa }_1^{{\omega }_1}$. This implies that κ₁ ≠ κ̂_j and κ₁ ≠ κ_j. Taking the derivative with respect to s on both sides of eqn. (29) yields

     $$\begin{array}{l}{\omega }_j{({\widehat{\kappa }}_j+s)}^{{\omega }_j-1}\{{({\kappa }_1+s)}^{{\omega }_1}-{({\kappa }_1-{\kappa }_j)}^{{\omega }_1}\}+{\omega }_1{({\widehat{\kappa }}_j+s)}^{{\omega }_j}{({\kappa }_1+s)}^{{\omega }_1-1}\\ ={\omega }_j{({\kappa }_j+s)}^{{\omega }_j-1}\{{({\kappa }_1+s)}^{{\omega }_1}-{({\kappa }_1-{\widehat{\kappa }}_j)}^{{\omega }_1}\}+{\omega }_1{({\kappa }_j+s)}^{{\omega }_j}{({\kappa }_1+s)}^{{\omega }_1-1}.\end{array}$$ (30)

     As s → −κ̂_j, the L.H.S. of eqn. (30) converges to 0 if ω_j > 1 and diverges to −∞ if 0 < ω_j < 1, whereas the R.H.S. converges to ω₁(κ_j − κ̂_j)^ω_j (κ₁ − κ̂_j)^ω₁−1 ∈ (0, ∞). Hence, eqn. (29) has no admissible solutions.

     If κ̂_j = κ_j, then (κ̂_i, ω̂_i) = (κ_i, ω_i), i = 1, j. We also deduce from eqn. (29) that p̂₁ = p₁. Hence p̂_j = p_j using eqn. (19).

• Case 2: κ̂₁ ≠ κ₁ and κ_j = κ₁. Eqn. (26) reduces to

  $${({\kappa }_1+s)}^{{\omega }_1}{({\widehat{\kappa }}_j+s)}^{{\omega }_j}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}\}={({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}{({\kappa }_1+s)}^{{\omega }_j}\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}.$$ (31)
  Setting s = −κ̂₁ gives ${\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}{({\kappa }_1-{\widehat{\kappa }}_1)}^{{\omega }_1}{({\widehat{\kappa }}_j-{\widehat{\kappa }}_1)}^{{\omega }_j}=0$. Because κ̂₁ ≠ κ₁, we must have κ̂₁ = κ̂_j, and eqn. (31) reduces to

  $${({\kappa }_1+s)}^{{\omega }_1-{\omega }_j}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\omega }_1}\}={({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1-{\omega }_j}\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}.$$ (32)

  We consider the following cases separately:

  1. If ω₁ > ω_j, setting s = −κ₁ yields $p_1{\kappa }_1^{{\omega }_1}{({\widehat{\kappa }}_1-{\kappa }_1)}^{{\widehat{\omega }}_1-{\omega }_j}=0$, which has no admissible solutions.

  2. If ω̂₁ > ω_j, setting s = −κ̂₁ yields ${\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}{({\kappa }_1-{\widehat{\kappa }}_1)}^{{\omega }_1-{\omega }_j}=0$, which has no admissible solutions.

  3. If ω_j > ω₁ and ω_j > ω̂₁, eqn. (32) can be rewritten as

     $${({\widehat{\kappa }}_1+s)}^{{\omega }_j-{\widehat{\omega }}_1}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}\}={({\kappa }_1+s)}^{{\omega }_j-{\omega }_1}\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}.$$ (33)
     Setting s = −κ̂₁ yields ${({\kappa }_1-{\widehat{\kappa }}_1)}^{{\omega }_1}=p_1{\kappa }_1^{{\omega }_1}$, and setting s = −κ₁ yields ${({\widehat{\kappa }}_1-{\kappa }_1)}^{{\widehat{\omega }}_1}={\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}$. Differentiating eqn. (33) w.r.t. s gives

     $$\begin{array}{l}({\omega }_j-{\widehat{\omega }}_1){({\widehat{\kappa }}_1+s)}^{{\omega }_j-{\widehat{\omega }}_1-1}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{({\widehat{\kappa }}_1-{\widehat{\kappa }}_1)}^{{\widehat{\omega }}_1}\}+{\widehat{\omega }}_1{({\widehat{\kappa }}_1+s)}^{{\omega }_j-1}\\ =({\omega }_j-{\omega }_1){({\kappa }_1+s)}^{{\omega }_j-{\omega }_1-1}\{{({\kappa }_1+s)}^{{\omega }_1}-{({\kappa }_1-{\widehat{\kappa }}_1)}^{{\omega }_1}\}+{\omega }_1{({\kappa }_1+s)}^{{\omega }_j-1}.\end{array}$$

     Letting s → −κ̂₁, the L.H.S. of the equation either converges to 0 (if ω_j − ω̂₁ > 1) or diverges to −∞ (if ω_j − ω̂₁ < 1), whereas the R.H.S. converges to ω₁(κ₁ − κ̂₁)^ω_j−1 ∈ (0, ∞). Hence, eqn. (33) has no admissible solutions.

  4. If ω_j = ω₁ and ω_j > ω̂₁, eqn. (32) can be rewritten as

     $${({\widehat{\kappa }}_1+s)}^{{\omega }_j-{\widehat{\omega }}_1}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}\}=\{{({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}\}.$$ (34)
     Taking the derivative with respect to s on both sides of eqn. (34) gives

     $$({\omega }_j-{\widehat{\omega }}_1){({\widehat{\kappa }}_1+s)}^{{\omega }_j-{\widehat{\omega }}_1-1}\{{({\widehat{\kappa }}_1+s)}^{{\widehat{\omega }}_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\widehat{\omega }}_1}\}+{\widehat{\omega }}_1{({\widehat{\kappa }}_1+s)}^{{\omega }_j-1}={\omega }_1{({\kappa }_1+s)}^{{\omega }_1-1}.$$

     Letting s → −κ̂₁, the L.H.S. of the equation either converges to 0 (if ω_j − ω̂₁ > 1) or diverges to −∞ (if ω_j − ω̂₁ < 1), whereas the R.H.S. converges to ω₁(κ₁ − κ̂₁)^ω_j−1 ∈ (0, ∞). Hence, eqn. (34) has no admissible solutions. The case ω_j > ω₁ and ω_j = ω̂₁ is handled similarly, and has no solutions either.

  5. If ω_j = ω₁ and ω_j = ω̂₁, eqn. (32) reduces to ${({\widehat{\kappa }}_1+s)}^{{\omega }_1}-{\widehat{p}}_1{\widehat{\kappa }}_1^{{\omega }_1}={({\kappa }_1+s)}^{{\omega }_1}-p_1{\kappa }_1^{{\omega }_1}$, which has no admissible solutions because κ̂₁ ≠ κ₁.

3.3. A Smith-Martin process

We consider a generalization of the Smith-Martin (S.M.) model originally proposed in [8]. The process assumes that, conditional on ξ = j, j ∈ (p), the lifespan takes the form τ = τ_Aj + δ_j, where τ_Aj follows an exponential distribution with parameter ψ_j, and where δ_j is a non-negative constant. In the original formulation of the model, τ_A2 represents essentially the duration spent by the cell in the G₀/G₁ phases, and δ₂ is the time spent by the cell in the S, G₂, M (and part of G₁) phases. Here, (s) = e^−δ_jsψ_j/(ψ_j + s), where it can be extended to s ∈ ℝ\{−ψ_j} by analytic continuation. This process is identical to the process of Section 3.1 if δ_j = 0, j ∈ (p). Let denote the family of S.M. processes. Write ${\mathcal{C}}_{p,G}^{\mathcal{S}\mathcal{M}}={\mathcal{C}}_{p,G}\cap {\mathcal{M}}^{\mathcal{S}\mathcal{M}}$ for the class of S.M. processes equivalent to the process with characteristics (p, G). This process is not always identifiable:

Corollary 3

Suppose that J = 2 and, for every j ∈ (p), that G_j(t) = 1−e^{−ψ_j(t−δ_j)} (t ≥ δ_j). Then, (p, G) is uniquely identified by {Z(t), t ≥ 0} except:

• Case 1: If ψ_j = ψ, j ∈ (p), and δ₁ = 0 when p₁ = 0 (Bellman-Harris case), ${\mathcal{C}}_{p,G}^{\mathcal{S}\mathcal{M}}$ includes the S.M. processes with characteristics (p̂, Ĝ) ∈ {p̂₁ ∈ (0, 1), p̂_j = p_j(1−p̂₁)/(1−p₁), δ̂₁ = 0, δ̂_j = δ_j, ψ̂₁ = ψ̂_j = ψ(1−p₁)/(1−p̂₁), j ∈ (p)\{1}} ∪ {p̂₁ = 0, p̂_j = p_j/(1 − p₁), δ̂_j = δ_j, ψ̂_j = ψ(1 − p₁), j ∈ (p)\{1}}.

• Case 2. If p₁ ∈ (0, 1), p₁ ≠ 1 − ψ/ψ₁, δ₁ = 0, ψ_j = ψ, j ∈ (p)\{1}, and ψ < ψ₁ (“extended” Bellman-Harris case), ${\mathcal{C}}_{p,G}^{\mathcal{S}\mathcal{M}}$ consists of the S.M. processes with characteristics (p, G) and (p̂, Ĝ) where p̂₁ = 1−ψ/ψ₁, p̂_j = p_jψ/{(1−p₁)ψ₁}, δ̂₁ = 0, δ̂_j = δ_j, ψ̂₁ = ψ₁, ψ̂_j = (1 − p₁)ψ₁, j ∈ {0, 2}.

Proof

Let (p̂, Ĝ) denote the characteristics of any process in . Assume first that p₁ = 0. If p̂₁ = 0, Lemma 1 yields (p̂, Ĝ) = (p, G). If p̂₁ ∈ (0, 1), eqn. (8) gives

$$(1-{\widehat{p}}_1)\frac{e^{-{\widehat{\delta }}_{j}s}{\widehat{\psi }}_j}{{\widehat{\psi }}_j+s}=\frac{e^{-{\delta }_{j}s}{\psi }_j}{{\psi }_j+s}\left\{1-{\widehat{p}}_1\frac{e^{-{\widehat{\delta }}_{1}s}{\widehat{\psi }}_1}{{\widehat{\psi }}_1+s}\right\}.$$ (35)

Taking the logarithm of both sides of the equation, we obtain

$$-{\widehat{\delta }}_{j}s+log{\widehat{\psi }}_j(1-{\widehat{p}}_1)-log({\widehat{\psi }}_j+s)=-{\delta }_{j}s-log({\psi }_j+s)+log{\psi }_j\left(1-{\widehat{p}}_1\frac{e^{-{\widehat{\delta }}_{1}s}{\widehat{\psi }}_1}{{\widehat{\psi }}_1+s}\right).$$

Dividing both sides of the equation by s and letting s → ∞ entails that δ̂_j = δ_j, and eqn. (35) reduces to (1−p̂₁)ψ̂_j(ψ_j+s)(ψ̂₁+s)−ψ_j(ψ̂_j+s)(ψ̂₁+s) = ψ_j(ψ̂_j+s)p̂₁ψ̂₁e^−δ̂₁s. Taking again the logarithm of both sides of the equation, dividing by s, and letting s → ∞ yields δ̂₁ = 0. Hence, eqn. (35) leads to eqn. (19), from which we deduce that ψ̂₁ = ψ̂_j = ψ/(1 − p̂₁), where ψ: = ψ_j, j ∈ (p), and p̂_j = p_j(1 − p̂₁), p̂₁ ∈ (0, 1). This proves part of Case 1 of Corollary 3.

Assume next that p₁ ∈ (0, 1). If p̂₁ = 0, the same line of arguments applies, and, by symmetry, we find that the process with characteristics (p̂, Ĝ) satisfying δ̂_j = δ_j, ψ̂_j = ψ(1 − p₁), and p̂_j = p_j/(1 − p₁), j ∈ (p)\{1}, belongs to ${\mathcal{C}}_{p,G}^{\mathcal{S}\mathcal{M}}$ if ψ_j = ψ, j ∈ (p), and δ₁ = 0. This proves also part of Case 1.

Assume now that p₁ ∈ (0, 1) and p̂₁ ∈ (0, 1). Then, for every j ∈ (p)\{1}, eqn. (7) gives

$$(1-{\widehat{p}}_1)\frac{e^{-{\widehat{\delta }}_{j}s}{\widehat{\psi }}_j}{{\widehat{\psi }}_j+s}\left\{1-p_1\frac{e^{-{\delta }_{1}s}{\psi }_1}{{\psi }_1+s}\right\}=(1-p_1)\frac{e^{-{\delta }_{j}s}{\psi }_j}{{\psi }_j+s}\left\{1-{\widehat{p}}_1\frac{e^{-{\widehat{\delta }}_{1}s}{\widehat{\psi }}_1}{{\widehat{\psi }}_1+s}\right\}.$$ (36)

Taking the logarithm, dividing both sides of eqn. (36) by s, and letting s → ∞ implies that δ̂_j = δ_j, and eqn. (36) reduces to

$$(1-{\widehat{p}}_1)\frac{{\widehat{\psi }}_j}{{\widehat{\psi }}_j+s}\left\{1-p_1\frac{e^{-{\delta }_{1}s}{\psi }_1}{{\psi }_1+s}\right\}=(1-p_1)\frac{{\psi }_j}{{\psi }_j+s}\left\{1-{\widehat{p}}_1\frac{e^{-{\widehat{\delta }}_{1}s}{\widehat{\psi }}_1}{{\widehat{\psi }}_1+s}\right\}.$$

Multiplying both sides by s and letting s → ∞, we obtain that (1 − p̂₁)ψ̂_j = (1 − p₁)ψ_j. Then eqn. (36) becomes

$$({\psi }_j-{\widehat{\psi }}_j)({\psi }_1+s)({\widehat{\psi }}_1+s)=p_1{\psi }_1{e}^{-{\delta }_{1}s}({\psi }_j+s)({\widehat{\psi }}_1+s)-{\widehat{p}}_1{\widehat{\psi }}_1{e}^{-{\widehat{\delta }}_{1}s}({\widehat{\psi }}_j+s)({\psi }_1+s).$$ (37)

We distinguish four sets of solutions:

1. If δ₁ > 0 and δ̂₁ > 0, dividing both sides of eqn. (37) by s² and letting s → ∞ yields ψ̂_j = ψ_j. Then, eqn. (37) reduces to p₁ψ₁e^−δ₁s (ψ̂₁+s) = p̂₁ψ̂₁e^−δ̂₁s (ψ₁+s), from which we deduce that δ̂₁ = δ₁, p̂₁ = p₁, and ψ̂₁ = ψ₁. Hence, (p̂, Ĝ) = (p, G).

2. If δ₁ > 0 and δ̂₁ = 0, rearranging the terms of eqn. (37) leads to (ψ₁ + s){(ψ_j − ψ̂_j)(ψ̂₁ + s) + p̂₁ψ̂₁(ψ̂_j + s)} = p₁ψ₁e^−δ₁s(ψ_j + s)(ψ̂₁ + s). Letting s → ∞, the L.H.S of the equation diverges to infinity, whereas the R.H.S. converges to zero. Hence, eqn. (37) has no admissible solutions.

3. If δ₁ = 0 and δ̂₁ > 0, a similar line of arguments shows that eqn. (37) has no admissible solutions.

4. If δ₁ = 0 and δ̂₁ = 0, eqn. (37) is equivalent to eqn. (20). The values of p̂ and ψ̂_j, j ∈ (p̂) that solves the equation are given in Corollary 1, and leads to part of Case 1 and to Case 2.