Skip to main content
PMC home page
Journal of Cerebral Blood Flow & Metabolism logoLink to Journal of Cerebral Blood Flow & Metabolism
. 2014 Nov 5;35(1):148–156. doi: 10.1038/jcbfm.2014.191

Noninvasive blood-free full quantification of positron emission tomography radioligand binding

Francesca Zanderigo 1,*, R Todd Ogden 2,3,4, Ramin V Parsey 5
PMCID: PMC4294408  PMID: 25370860

Abstract

Full quantification of a positron emission tomography (PET) radioligand binding to its target is preferred because it requires the fewest assumptions, but generally involves measuring the concentration of free radioligand in the arterial plasma by collecting blood samples from the subject's radial artery during the scan, and performing metabolite analysis. This invasive, costly procedure deters subjects' participation, and requires specialized staff and equipment. Simultaneous estimation (SIME) can fully quantify binding using only PET data from multiple brain regions and one individual anchor value, which is based on a single arterial blood sample. Drawing this sample can still be challenging in clinical settings, particularly when using simultaneous PET/magnetic resonance scanners. Here we propose a methodology for full quantification of binding that does not require any blood samples. The methodology substitutes the SIME blood-based anchor with a value predicted using multiple linear regression of noninvasive, easy-to-collect variables related to the radioligand blood concentration, and individual metabolism, such as injected dose, body mass index, or body surface area. As a study case, we show here the methodology in comparison to analysis with full arterial-line blood sampling in a cohort of 23 available scans with [11C]CUMI-101, a partial agonist of the serotonin 5-HT1A receptors.

Keywords: binding, blood free, brain, full quantification, PET, serotonin

Introduction

Positron emission tomography (PET) is a nuclear imaging technology that uses radioactively labeled molecules (radioligands), that are injected into the body and bind, although not exclusively, to a specific target, to quantify in vivo biologic processes, such as blood flow, metabolism, and the distribution of proteins in the brain. Positron emission tomography is an invaluable tool to establish the genetic and cellular basis of brain diseases.1, 2, 3

Fully quantitative PET measures a series of binding potentials between radioligand and target to indirectly determine the available amount of the target.1 These potentials are in various ways related to the density of available target (Bmax) through the affinity of the radioligand for the available binding sites1 (1/KD). The binding potential called BPf (BPf = Bmax/KD) is the outcome measure most directly related to the density of available target.1 Other binding potentials called BPp and nondisplaceable binding potential BPND (BPp=fP × Bmax/KD; BPND=fND × Bmax/KD) each include an additional term unrelated to the target density: the radioligand plasma free fraction fP, and the radioligand intracerebral free fraction fND, respectively.

Estimating BPf and BPp generally requires measuring the concentration of free (unbound to plasma proteins) radioligand in the arterial plasma (metabolite-corrected input function, cIF) by collecting blood samples from the subject's radial artery at several times during the scan, measuring the radioligand concentration in these samples, and performing a separate metabolite analysis to determine the fraction of unmetabolized parent compound. This invasive and costly procedure deters subjects' participation, and requires highly specialized medical staff and equipment. Nondisplaceable binding potential can be measured without taking blood samples during scanning using reference region approaches4, 5, 6, 7, 8, 9, 10, 11 (RRAs). However, to be valid, RRAs require the existence of a measurable, valid, and reliable reference region in the brain that is devoid of the target, and for comparisons to be valid, its properties must be independent of treatment effects and groups.1, 12 A region meeting these criteria has not yet been identified, or might not exist, for many radioligands,13, 14, 15, 16, 17, 18 including [11C]CUMI-101 (CUMI), a partial agonist of the serotonin 5-HT1A receptor, which is implicated in the pathophysiology of numerous neuropsychiatric disorders.3 Even if such a region exists, identification and validation can be difficult. Erroneously designating a region as a reference results in biased estimates of the PET outcomes,19, 20, 21, 22 and the validity of resulting conclusions may be called into question.

As an alternative, simultaneous estimation (SIME) can fully quantify the radioligand total volume of distribution (VT), which will subsequently allow estimation of any of the three binding potentials.2 Simultaneous estimation only requires time-activity curves from multiple brain regions along with one individual ‘anchor' value to ensure model identifiability. This anchor value may be based on a single arterial blood sample taken at some time after the injection.2 Simultaneous estimation is based on a certain parametric model for the cIF, and incorporates the parameters describing this model together with the parameters related to VT and the binding potentials into an overall cost function involving multiple regions, which is then optimized during the model fitting process. Because it still requires at least one anchor point, SIME does not obviate the need to draw any blood during the scanning. Although it is an improvement to draw only one arterial sample, this procedure is still challenging in clinical settings, particularly when using simultaneous PET/magnetic resonance scanners.

Here we propose a new methodology for full quantification of VT (and therefore binding potentials, specifically the BPf) that obviates the need for any blood sampling. The methodology uses multiple linear regression of noninvasive and easy-to-collect variables, such as injected dose (ID), body mass index (BMI), and body surface area (BSA), and can be trained with a limited number of scans that have full blood sampling data available. We show here the methodology in the study case of CUMI.

Materials and Methods

Subjects

Data for this methodological paper were previously collected for other independent studies. Twenty-three available scans with CUMI were examined, including 18 acquired in a test–retest study3 (9 healthy controls, 2 scans each) and 5 other independently acquired patients with major depressive disorder. The studies were performed in accordance with the Declaration of Helsinki and The Institutional Review Boards of Columbia University Medical Center and New York State Psychiatric Institute approved the protocol. Subjects gave written informed consent after receiving an explanation of the study.

Positron Emission Tomography Protocol

Radioligand preparation, emission data acquisition and reconstruction, and determination and fit of the cIF were obtained as previously described for CUMI.3, 23 Briefly, a venous catheter was used to inject the radioligand, and an arterial catheter to obtain arterial samples for measuring the input function. Positron emission tomography was performed with the ECAT HR+ (Siemens/CTI, Knoxville, TN, USA). A 10-minute transmission scan was obtained before radioligand injection. At the end of the transmission scan, CUMI was administered intravenously as a bolus over 30 seconds. Emission data were collected in three-dimensional mode for 120 minutes, with 21 frames of increasing duration: 3 at 20 seconds, 3 at 1 minute, 3 at 2 minutes, 2 at 5 minutes, and 10 at 10 minutes. Images were reconstructed to a 128 × 128 matrix (pixel size of 2.5 × 2.5 mm2). Reconstruction was performed with attenuation correction using the transmission data, and scatter correction was performed using model-based scatter correction.24 The reconstruction filter and estimated image filter were Shepp 0.5 (2.5 full width at half maximum), Z filter was all pass 0.4 (2.0 full width at half maximum), and zoom factor was 4.0, leading to a final image resolution of 5.1 mm full width at half maximum at the center of the field of view.

Input Function Measurement and Metabolite Correction

Arterial samples were collected with an automated sampling system every 5 seconds for the first 2 minutes, and manually thereafter for a total of 31 samples. Centrifuged plasma samples were collected in 200 mL aliquots, and the radioactivity was measured in a well counter. After initial extraction, the percentage of CUMI radioactivity in plasma was determined by high-performance liquid chromatography.25 Six of these samples were used to measure the unmetabolized parent compound fractions. These fractions were then fitted with a Hill function.3, 26 The final product of the fitted unmetabolized fraction and the total plasma counts was fit with a straight line from time zero to the plasma peak and the sum of three exponentials from the peak to the end (see below for details on the model). The fitted values were used as input to the analyses that are here referred to as analyses with full blood sampling.

Image Analysis

Images were analyzed using Matlab Release 2013b (The MathWorks, MA, USA) with extensions to FMRIB's linear image registration tool version 5.2 (ref. 27), brain extraction tool version 1.2 (ref. 28). Motion correction was applied. Thirteen anatomic target regions were identified21, 29 and selected for their known high concentration of 5-HT1A receptors as assessed with [11C]WAY-100635 (ref. 22) and CUMI:3 hippocampus, entorhinal cortex, insula, posterior parahippocampal gyrus, temporal, amygdala, medial prefrontal cortex, cingulate, orbital, dorsolateral prefrontal cortex, parietal, raphe nucleus, and occipital. In addition, the gray matter of the cerebellum (GCER) was selected as the reference region.3

Simultaneous Estimation

Simultaneous estimation assumes a certain parametric model, common to all the brain regions, for cIF, and incorporates the free parameters of the model together with the parameters related to the binding into a single cost function, which is optimized during the model fitting process.2 Here the model is the same assumed to fit the cIF when full blood sampling data are available: 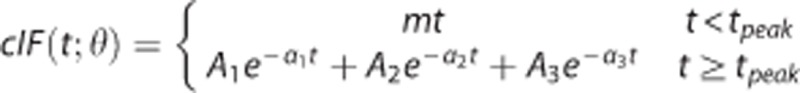Inline graphic, with tpeak the time of the cIF peak, and θ=(m;tpeak;A1;A2;A3;α1;α2;α3) the vector of free parameters of the cIF model, which include the slope m of the prepeak phase, and the scale (A1;A2;A3) and rate constants (α1;α2;α3) of the three-exponential function after the peak. This model has been used extensively in full arterial-line blood sampling PET studies. The cost function that is optimized is then:

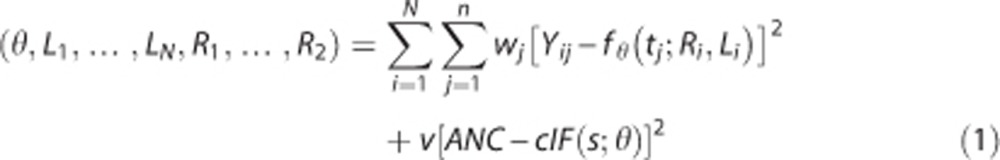graphic file with name jcbfm2014191e2.jpg

where 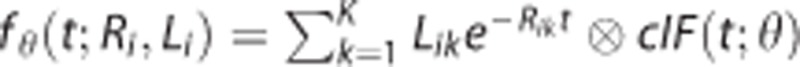Inline graphic is the compartment model describing the radioligand kinetics1, 12 in region i: K is the number of tissue compartments (two-tissue compartment, K=2, for CUMI3), and the macroparameters Li=(Li1,…,Lik) and Ri=(Ri1,…,Rik) depend on the rate constants (K1 through k4) of the particular compartmental structure12 (for CUMI, 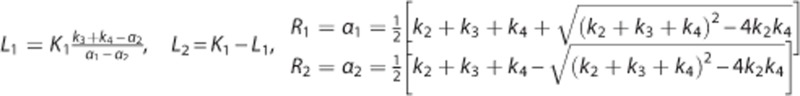Inline graphic). Yij is the measured PET signal in region i at time tj; and (w1,…,wn) are a set of known weights, which we take to be equal to the square root of the corresponding scanning time frame durations.3 ANC represents the available (blood-based or predicted) anchor at time s after injection, and the weight v, that we set to be relatively large (i.e., 100 and 1,000; see details in the Results section), ensures that the estimated cIF passes very close to the anchor point.2 In the case of CUMI, we take s to be 60 minutes after injection.30

As compared with the analysis with full blood sampling data, SIME increases the number of unknown parameters that needs to be estimated and, accordingly, the computational complexity required for optimization. Therefore, SIME is here implemented with a robust optimization algorithm known as simulated annealing,31 which is more suitable for complex optimizations than standard nonlinear regression techniques, such as those based on the Newton–Raphson algorithm. The name simulated annealing comes from the analogy of annealing two materials by heating at a high temperature and then slowly cooling them down. Following this analogy, in the simulated annealing algorithm, the set of parameters is treated as a state and the objective function Φ as the energy of the state. The algorithm travels iteratively through the parameter space by randomly choosing a new ‘candidate state' (determined by a new set of parameters) at each step. The new state is accepted with probability given by the Metropolis criterion: 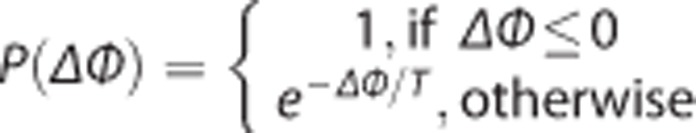Inline graphic, where ΔΦ is the decrease in the value of Φ that would result from moving to the new state and T, the temperature of the system, which is gradually decreased at each step. At high temperature (corresponding to early steps in the algorithm), the Metropolis criterion allows the algorithm to escape local minima by sometimes accepting ‘uphill' movements. As the temperature decreases, the algorithm becomes gradually more selective for ‘downhill' movements.

For this study, the simulated annealing algorithm was implemented similar to that described by Wong et al,32 with initial temperature set to T=100. Starting values for the parameters are chosen randomly, constrained according to limits derived from results of modeling data with full blood sampling. In particular, each parameter is constrained to be positive, and its upper limit is set considerably higher than any of the corresponding parameters estimated with full blood sampling data. The choice of limits does not appreciably affect the results, because as part of the simulated annealing algorithm these limits are iteratively reduced until convergence. For each of the iterations, the candidate state is calculated by perturbing one current parameter value based on a uniform distribution with a range that is specific to each parameter. This range is set to the limits described above for the first set of iterations and is gradually tightened as the algorithm progresses. The candidate parameter vector is ‘accepted' (and thus replaces the previous parameter values) with probability P(ΔΦ). This perturbation and acceptance/rejection step is repeated 20 times for each parameter, and the algorithm works through each parameter in turn. After one round of searches through all the parameters, the algorithm adjusts the vector of ranges so that the acceptance rate of new candidates is ~50%. After 10 rounds of adjusting the range vector, the current value of the parameters is stored as an intermediate solution and the temperature is decreased by a factor of 0.8. The algorithm continues until the objective function evaluated at the last four intermediate solutions differs by <10−5. The maximum number of iterations is set at 5 × 106, which is high enough to ensure that the algorithm does not prematurely terminate.

Simulated annealing performance in terms of convergence can be affected by factors such as initial temperature T, rate of cooling, and the number of steps between cooling, but most importantly the kinetic diversity of the brain regions that are simultaneously estimated.2, 30 Here, we automatically select the regions for SIME using a data-driven voxel-based algorithm30 that determines five subject-specific regions via k-means clustering of gray and white matter voxels. Computational time for one study is on average ~15 minutes when five regions are used for optimization.

Blood-Based Anchor

One arterial blood sample, taken after injection of the radioligand at a time that is optimized according to the radioligand in hand,2 is used to determine the total radioactivity of the radioligand in the plasma, and the corresponding unmetabolized fraction, following the same methodology described above for the analysis with multiple blood samples. The product of the total radioactivity of the radioligand in the plasma and the corresponding unmetabolized fraction represents the cIF at that time.2 In the case of CUMI, one sample is taken 60 minutes after injection.30 The sample may also be used to measure the radioligand free fraction in the plasma (fP), necessary to calculate BPf.1

Predicted Anchor

Simultaneous estimation can be performed completely blood free by substituting the required anchor, heretofore based on a single arterial blood sample, with its predicted value. The prediction is performed using multiple linear regression, using as predictors noninvasive and easily collectable variables and biometrics that are related to the radioligand injection and the individual metabolism of each subject. We explored here three simple variables: radioligand ID, and two aggregate measures indicative of individual metabolism, BMI (BMI=weight[lbs]·703/(height[in]),2 ref. 33), and BSA (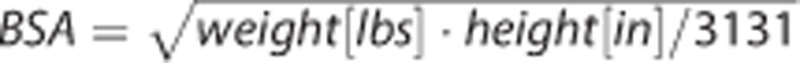Inline graphic, ref. 34). An initial dataset of scans with full arterial blood sampling data available is randomly divided into selection and validation subsets. Different multiple linear models of the noninvasive variables and biometrics are trained using the selection subset, and their performance are compared with that of analysis with full blood sampling data, to select the best predicting model.

Free Fraction Considerations

If the model is trained to predict anchor values that do not contain any information relative to fP, the proposed methodology allows calculating only VT and BPp. BPp is calculated as BPp=VT−VTref, with VTref the VT in the reference region, assumed to represent the nonspecific binding of the radioligand common across all regions.1, 3 However, calculating BPf also requires the determination of fP, as BPf=BPp/fP=(VT−VTref)/fP (ref. 1). Alternatively, the model can be trained to predict an anchor equal to the cIF at the time of sampling after injection multiplied by fP. It can be easily proved mathematically that this alternative anchor allows estimating BPf.

Application to CUMI

We collected ID, and calculated BMI and BSA, for all the available scans. First, we randomly divided the scans into model-selection (18 scans) and model-validation (5 scans) groups, to have enough scans available to train the predicting models, while excluding a few subjects from the training process to realistically measure out-of-sample prediction errors. Then, we randomly further divided the model-selection group into model-selection training (12 scans) and model-selection testing (6 scans) subgroups, repeating the subgrouping for a sufficiently high number of distinct instances (50). In each of these 50 distinct instances, we trained three linear models of ID, BMI, and/or BSA using the model-selection training group:

graphic file with name jcbfm2014191e7.jpg
graphic file with name jcbfm2014191e8.jpg
graphic file with name jcbfm2014191e9.jpg

where y is the vector of blood-based anchors (including or not fP), and ID, BMI, and BSA are vectors containing the corresponding ID, BMI, and BSA values, respectively. Each model contains a variable that is related to the CUMI injection (ID), and at least one variable related to the metabolism of each subject (BMI and or BSA). In each of the 50 runs, we compared the performance of the models using the model-selection testing group using correlation (r) between predicted and blood-based anchors, slope and intercept of the regression analysis (blood-based anchors are designated the independent variable), mean and standard deviation (s.d.) of the difference between predicted and blood-based anchors, and Akaike information criterion.35 The selected model in each case was finally trained using the whole model–selection group, and applied to the model-validation group initially set aside.

Comparison with Full Blood Sampling Analysis

For all scans, we ran SIME using blood-based and both versions of predicted anchors, here called cIF60 and cIF60·fP, respectively, since for CUMI the sample is taken 60 minutes after injection.30 To isolate the effect of the predicted anchor values, the clusters extracted via k-means to run SIME were kept the same for each subject across different SIME runs. The predicted cIF was then used to determine the input function for the likelihood estimation in graphical analysis36 (LEGA) to calculate VT for cIF60, and BPf for cIF60·fP, in the 13 target regions. Quantification of outcomes was repeated using LEGA and the cIF obtained from full blood sampling, after correction for metabolites and fitting as described above. Outcome estimates obtained by SIME with blood-based or predicted anchors were compared with the corresponding ones obtained by analysis with full blood sampling data, based on correlation coefficient (r), slope and intercept of the regression line (outcomes obtained with full arterial-line data are designated the independent variable), and mean and s.d. of the difference between outcomes estimated by SIME with blood-based or predicted anchors and outcomes estimated with full arterial-line data.

Results

Prediction of the Anchor

Injected dose, BMI, and BSA values and their statistics for the subjects in the considered dataset are reported in Table 1. The five scans used as model-validation group are highlighted. The two models that include ID and either BMI or BSA (equations 2 and 3) provide predicted anchor values very close to each other and also close to the blood-derived ones. Increasing the number of predictors from 2 (ID and either BMI or BSA) to 3 (model in equation 4) increases the complexity of the prediction model and its parameters identification, without providing further improvements in the description of the data. Only the results relative to the two simpler models (ID and either BMI or BSA) are therefore presented here, while the results of the model that includes both BMI and BSA are not shown.

Table 1. ID, BMI, and BSA values and their statistics for the subjects in the considered dataset.

Scan # ID BMI BSA
1 12.49 30.04 1.89
2 15.69 30.04 1.89
3 3.53 26.31 1.85
4 7.75 26.31 1.85
5 6.31 23.29 1.70
6 10.65 23.29 1.70
7 6.76 25.10 2.02
8 7.58 25.10 2.02
9 3.29 25.09 1.89
10 15.38 23.63 1.88
11 10.81 23.63 1.88
12 11.4 28.89 2.03
13 12.27 28.89 2.03
14 9.5 24.21 1.78
15 4.15 24.21 1.78
16 6.05 23.99 1.97
17 7.05 23.99 1.97
18 12.49 28.71 1.76
19 13.75 28.71 1.76
20 3.48 23.03 1.62
21 7.20 21.41 1.79
22 4.32 30.18 1.81
23 14.48 26.70 2.22
Min 3.29 21.41 1.62
Max 15.69 30.18 2.22
Mean 8.97 25.86 1.87
Median 7.75 25.10 1.88
s.d. 4.02 2.65 0.14
Open in a new tab

BMI, body mass index; BSA, body surface area; ID, injected dose. ID is measured in μCi, BMI in lb/in2, and BSA in (lb·in)0.5. The five scans used as model-validation group are highlighted.

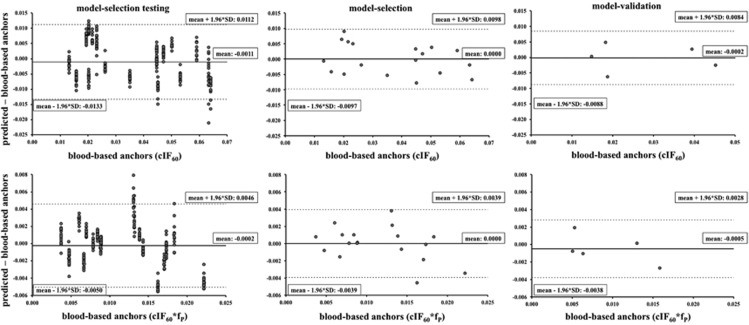
According to the 50-model–selection testing instances, the most accurate, precise, and parsimonious model to predict the anchor cIF60 uses ID and BMI. For this model, Figure 1 (top) shows the Bland–Altman plots37 of predicted minus blood-based cIF60 values versus blood-based cIF60 values in the 50-model–selection testing instances within the model-selection group (vertical clusters of points correspond to the 50 distinct instances of six testing scans), the model-selection group, and the model-validation group. Results in the middle column refer to the predictive model (as selected using the 50 distinct subgrouping instances shown on the left column) trained using the whole model–selection group (18 scans). Results in the right column refer to the trained predictive model as applied to the model-validation group (5 scans), that is initially set aside and never used in the selection or training of the predictive model. No trends in the prediction errors with the amplitude of the anchor to be predicted can be noticed in the model-selection and model-validation groups, although there is an underestimation of the highest anchors in some of the 50-model-selection testing instances. Corresponding mean and intervals of confidence of the vertical axis of the Bland–Altman plots are reported in Table 2 (top), together with the numerical results (r, slope and intercept) of the regression analysis between predicted and blood-based anchors. The results for the other models (ID and BSA) are also reported in Table 2. Correlation is high (>0.95) and slope is close to unity (>0.91) for both the ID and BMI, and the ID and BSA models in the model-selection and model-validation group.

Figure 1.

Figure 1

Open in a new tab

Top panel: Bland–Altman plots of predicted minus blood-based cIF60 values versus blood-based cIF60 values in the 50-model–selection testing instances (cluster of points correspond to the 50 different instances of 6 testing scans) within the model-selection group (left), the model-selection group (middle), and the model-validation group (right); mean and intervals of confidence of the vertical axis are reported in each plot. Bottom panel: corresponding results for cIF60·fP. cIF, metabolite-corrected input function; fp, plasma free fraction.

Table 2. Numerical comparison between blood-based and predicted anchors with the models ID–BSA and ID–BMI for the anchors cIF60 (top) and cIF60·fP (bottom).

  Model-selection testing Model selection Model validation
cIF60
 ID–BMI
  Slope 0.887 0.917 0.990
  Intercept 0.003 0.003 0.000
  r 0.930 0.958 0.953
  Mean −0.0011 0.0000 −0.0002
  s.d. 0.0062 0.0050 0.0044
  Mean + 1.96*s.d. 0.0112 0.0098 0.0084
  Mean − 1.96*s.d. −0.0133 −0.0097 −0.0088
 ID–BSA
  Slope 0.875 0.918 0.984
  Intercept 0.004 0.003 0.000
  r 0.928 0.959 0.954
  Mean −0.0010 0.0000 −0.0001
  s.d. 0.0063 0.0049 0.0043
  Mean + 1.96*s.d. 0.0114 0.0097 0.0084
  Mean − 1.96*s.d. −0.0133 −0.0097 −0.0085
       
cIF60*fP
 ID–BMI
  Slope 0.816 0.875 1.006
  Intercept 0.002 0.001 −0.001
  r 0.880 0.936 0.909
  Mean −0.0005 0.0000 −0.0007
  s.d. 0.0025 0.0019 0.0023
  Mean + 1.96*s.d. 0.0044 0.0037 0.0038
  Mean − 1.96*s.d. −0.0054 −0.0037 −0.0052
 ID–BSA
  Slope 0.832 0.858 0.811
  Intercept 0.002 0.002 0.001
  r 0.884 0.926 0.944
  Mean −0.0002 0.0000 −0.0005
  s.d. 0.0025 0.0020 0.0017
  Mean + 1.96*s.d. 0.0046 0.0039 0.0028
  Mean − 1.96*s.d. −0.0050 −0.0039 −0.0038
Open in a new tab

BMI, body mass index; BSA, body surface area; cIF, metabolite-corrected input function; fP, radioligand-free fraction in the plasma; ID, injected dose; r, correlation coefficient.

According to the 50-model–selection testing instances, the best model to predict the anchor cIF60·fP uses ID and BSA instead (Figure 1, bottom; Table 2, bottom). Also in this case, no trends in the prediction errors with the amplitude of the anchor to be predicted can be noticed in the model-selection and model-validation groups. For both models, the prediction performance only slightly worsens in terms of bias with respect to, and correlation with, the blood-based anchors in all the groups.

Outcomes Quantification: Comparison with Full Blood Sampling

Simultaneous estimation with blood-based anchor

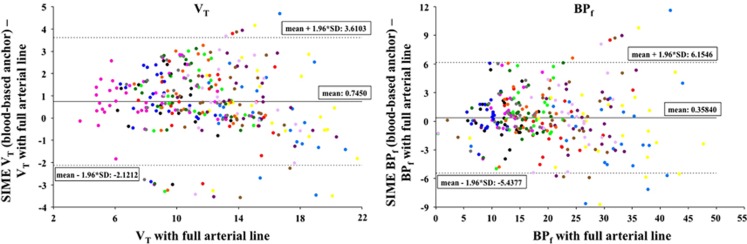
For all scans, cIF was calculated using SIME and the blood-based anchor; the regions used to estimate cIF were three out of five clusters extracted, automatically selected based on the area under the curve of the average (over all voxels in the cluster) time-activity curve.30 The weight v was 100, as previously suggested for SIME.2 This cIF was then used as input function for LEGA. Figure 2 displays the Bland–Altman plots37 of outcome measures estimated with the cIF calculated using SIME minus the same outcome measures estimated with cIF from full blood sampling (y-axis) versus the outcome measures estimated with cIF from full blood sampling (x-axis) in all the 13 target regions and the GCER (only for VT; BPf is zero by definition in the reference region). Points corresponding to different regions are shown in different colors. No trends in the estimation errors with the amplitude of the outcome measure to be estimated can be noticed. Numerical results (r, slope and intercept) of the regression analysis between outcome measures estimated with SIME (in this case with blood-based anchors) and outcome measures estimated with full blood sampling are reported in Table 3. Correlation with estimates from full blood sampling is high (>0.91) for all outcomes, and the bias found for the VT values decreases for BPf (slope is 0.929 and 0.986 for VT and BPf, respectively).

Figure 2.

Figure 2

Open in a new tab

Bland–Altman plots of outcome measures (VT, left; BPf, right) estimated for all scans using LEGA with the cIF calculated using SIME (with blood-based anchors) minus the same outcome measures estimated with cIF from full blood sampling (y-axis), versus the outcome measures estimated with cIF from full blood sampling (x-axis) in all the 13 target regions and the GCER (only for VT; BPf is zero by definition in the reference region). Mean and intervals of confidence of the vertical axis are reported in each plot. Points corresponding to different regions are shown in different colors. BPf, binding potential; cIF, metabolite-corrected input function; GCER, gray matter of the cerebellum; LEGA, likelihood estimation in graphical analysis; SIME, simultaneous estimation; VT, volume of distribution.

Table 3. Numerical results (r, slope and intercept) of the regression analysis between outcome measures estimated with SIME (with blood-based or predicted anchors) and outcome measures estimated with full blood sampling.
  VT BPf
Blood-based anchor
 Slope 0.929 0.986
 Intercept 1.582 0.637
 r 0.916 0.949
     
Predicted anchor
 Model-selection group
  Slope 0.772 0.842
  Intercept 2.838 0.762
  r 0.764 0.937
 Model-validation group
  Slope 0.722 0.836
  Intercept 4.073 1.597
  r 0.828 0.883
Open in a new tab

BPf, binding potential; r, correlation coefficient; SIME, simultaneous estimation; VT, volume of distribution.

Simultaneous estimation with predicted anchor cIF60

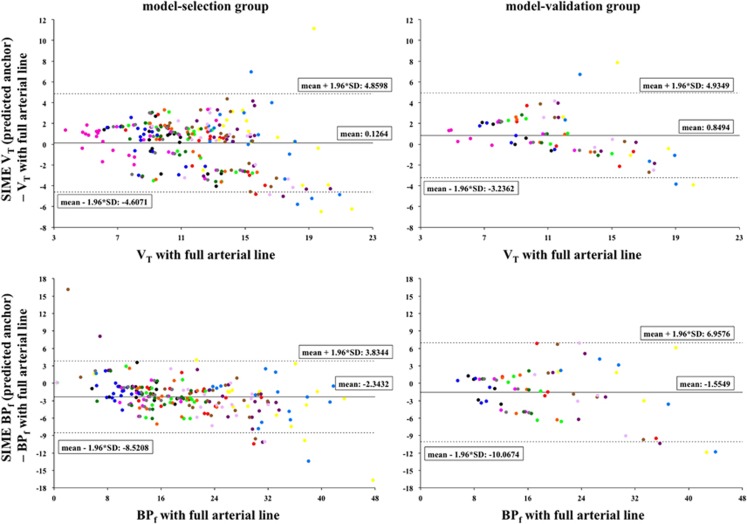
For all scans, cIF was calculated using SIME and the predicted anchor cIF60, the same three regions and weight v used with the blood-based anchors. This cIF was then used as input for LEGA. Figure 3 (top) shows the Bland–Altman plots37 of VT values estimated with the cIF calculated using SIME (with predicted anchors cIF60) minus the same outcome measures estimated with cIF from full blood sampling (y-axis) versus the VT values estimated with cIF from full blood sampling (x-axis) in all the 13 target regions and the GCER. Points corresponding to different regions are shown in different colors. Results are reported separately for the model-selection (left) and the model-validation (right) groups. A tendency to underestimate the highest values of VT is visible in both groups, which is confirmed by the slope values of the regression analysis between outcome measures estimated with SIME (in this case with predicted anchors cIF60) and outcome measures estimated with full blood sampling reported in Table 3. Although the bias increases and the correlation decreases as compared with SIME with blood-based anchors, the blood-free estimation of the outcomes is still close to the one obtained with full blood sampling for both groups.

Figure 3.

Figure 3

Open in a new tab

Top panel: Bland–Altman plots of VT values estimated using LEGA with the cIF calculated using SIME (with predicted anchors cIF60) minus the same outcome measures estimated using LEGA with cIF from full blood sampling (y-axis), versus the VT values estimated with cIF from full blood sampling (x-axis) for the model-selection group (18 scans, left) and model-validation group 5 scans, right) in all the 13 target regions and the GCER. Bottom panel: Bland–Altman plots of BPf values estimated using LEGA with the cIF calculated using SIME (with predicted anchors cIF60·fP) minus the same outcome measures estimated using LEGA with cIF from full blood sampling (y-axis), versus the BPf values estimated with cIF from full blood sampling (x-axis) in all the 13 target regions (BPf is zero by definition in the reference region, GCER) for the model-selection group (left) and model-validation group (right). Mean and intervals of confidence of the vertical axis are reported in each plot. Points corresponding to different regions are shown in different colors. BPf, binding potential; cIF, metabolite-corrected input function; GCER, gray matter of the cerebellum; LEGA, likelihood estimation in graphical analysis; SIME, simultaneous estimation; VT, volume of distribution.

Simultaneous estimation with predicted anchor cIF60·fP

For all scans, cIF was calculated using SIME and the predicted anchor cIF60·fP; the regions were all of the five clusters extracted via k-means, to ensure stability in the solutions with this alternative anchor; a weight v of 1,000 was determined to be optimal for this anchor. Figure 3 (bottom) displays the Bland–Altman plots37 of BPf values estimated with the cIF calculated using SIME (in this case with predicted anchors cIF60·fP) minus the same outcome measures estimated with cIF from full blood sampling (y-axis) versus the BPf values estimated with cIF from full blood sampling (x-axis) in all the 13 target regions (BPf is zero by definition in the reference region, GCER). Points corresponding to different regions are shown in different colors. Results are reported separately for the model-selection (left) and the model-validation (right) groups. The bias decreases and correlation improves with respect to the VT case, although performance is still inferior to the one of SIME with blood-based anchors (Table 3). The blood-free estimation of the outcomes is, however, still close to that obtained using full blood sampling for both groups.

We note no particular convergence issues in the simulated annealing for the dataset here presented.

Discussion

We present a methodology to fully quantify both VT and BPf with sufficient accuracy without the need for any blood samples, and showed its application to the radioligand CUMI. The methodology combines SIME with multiple linear regression of noninvasive and easy-to-collect measurements, such as ID, BMI, and BSA, to predict the individual SIME anchor value, which otherwise must be based on blood samples.

BMI and BSA are simple nonlinear models of weight (W) and height (H). We investigated (results not shown) potential benefits of using W and H (rather than BMI or BSA) as separate predictors, and considered 10 different linear models of ID, W, and/or H along with some basic nonlinear transformations of W and H, with increasing number of free parameters. Results suggest that indeed it is possible to predict the anchors needed by SIME by training directly with transformed values of H and W rather than using BMI and BSA. This could potentially give better performance for certain radioligands and/or populations of subjects. However, the advantage of BMI and BSA is that they already aggregate both H and W in a single predictor, and therefore allow the use of more parsimonious (i.e., fewer free parameters) models for the prediction of the anchors than when H and W are treated as separate predictors. Furthermore, BMI and BSA have a physiologic meaning, as they are proxies for the volume into which the dose of radioligand is distributed across when injected; therefore, they can reasonably be expected to be linearly related to the anchor point, as opposed to various arbitrary nonlinear transformations of H and W.

In our proposed methodology, each predictive model is trained using a limited number of scans with arterial blood samples available (here 12), and then applied to all remaining scans. An intrinsic limitation is the unpredictable behavior in a new set of data if the range of values of the independent variables of the model are significantly different from the range of values the model was trained with. In the specific study case, if the values of ID, BMI, and BSA in the new dataset are significantly different from those used to train the model, which can be easily assessed for each new subject before the beginning of the scan, it would be advisable to draw one blood sample at 60 minutes after injection, to ensure higher accuracy in the quantification of the binding potentials. This sample could also be used to help train the model to predict future observations (anchors for future subjects) with higher accuracy. Higher accuracy could also be obtained by considering measures as predictors that are even more specific than BMI and BSA to metabolism and body shape, such as the waist-to-hip ratio.

Higher accuracy (as compared with full blood sampling) could also be achieved by considering more predicted anchors. The emphasis on using only one anchor point for SIME was originally supported by the fact that, mathematically, only one anchor per subject is necessary, and that, in terms of subjects' comfort, there is a significant difference between drawing only one arterial blood sample and drawing multiple samples, to the point that, if multiple samples would be needed, the advantages of using SIME (as compared with complete sampling of the input function) would almost disappear. However, in the new prediction-based approach proposed here, several anchors per subject, at different times of sampling, could potentially be predicted as long as blood data to train the predictive models are available. Each anchor point would be predicted from the noninvasive variables with some error, and therefore adding one or more predicted anchors could help in improving the accuracy of SIME. Predicting multiple anchors from noninvasive variables could also be useful, for example, for methodologies other than SIME, such as some of the image-derived input function approaches, which still need more than one blood sample to scale/correct the recovered input function.38 To put this into practice, however, careful investigation of the relative weights associated (in estimating the final input function) with each of the predicted anchors per subject would be needed.

Another limitation of the proposed study is that 18 of our available CUMI scans correspond to 9 subjects, each recorded twice in a test–retest setup. Nonindependence of the measurements would need to be taken into account in the correlation analyses, if we were making inference (e.g., computing a P-value) on the correlation coefficients. Despite it being computed on nonindependent data, we regard the correlation coefficient (r) as a reasonable measure, especially because we are only comparing it with other correlation coefficients computed under identical circumstances. The reason we did not consider, for example, only the baseline scan for each of the subjects in the test–retest in our dataset is to maintain a sample size large enough to allow for the proposed two-level cross-validation. Furthermore, we note that, although BMI and BSA values are the same for the test and retest scan of each subject, the value of ID, one of the predictors of the anchor for SIME, will generally be different for each scan. Also, the five scans (see Table 1) that constitute the model-validation group (that realistically measure out-of-sample prediction errors, as they are never used in the training of the predictive models) involved five independent subjects.

A further limitation of this study is that, in the absence of a specific model that relates biometrics and metabolite-corrected concentration of radioligand in the plasma, it is not possible to test the methodology on simulated data.

Even with these limitations, and although using SIME with anchor based on only one arterial blood sample already provides a minimally invasive accurate quantification of the binding potentials (Figure 2), there are several experimental settings that would make drawing even that one sample particularly challenging (e.g., novel PET/magnetic resonance imaging scanners). In such a situation, substituting the blood-based anchor with a prediction based on noninvasive variables, while maintaining accuracy in the estimation of outcomes of interest, allows fully quantifying the binding absolutely blood free. This quantification is sufficiently close to the quantification with full arterial-line sampling analysis, especially when the binding potential BPf (Figure 3) is considered.

In the case of CUMI, BPf, which most researchers regard as most closely reflecting in vivo measurements of Bmax and KD and results obtained in vitro,1 represents the ideal outcome.3 In the case of CUMI, RRAs may be also accurately applied11 because of the relatively low percentage of specific binding and high nonspecific binding in the cerebellum, estimated to be 0.09 mL/cm3 based on our in vitro and in vivo studies using [11C]WAY-100635 (ref. 3). However, this still remains to be validated experimentally. Furthermore, although RRAs work satisfactorily for CUMI,11 they only allow estimation of the BPND1, 12. Nondisplaceable binding potential is only linearly related to Bmax and KD through fND, typically assumed to be equal in receptor-rich and receptor-free regions. Furthermore, effective use of BPND as an outcome measure depends most heavily on the assumption that the nondisplaceable uptake is independent of subject groups or treatment effects.1 Therefore for CUMI,11 the blood-free methodology here proposed should be preferred over RRAs.

It could be argued that, even the calculation of BPf as BPf=(VT−VTref)/fP could be biased if the reference region selected to estimate VTref is not an actual reference region. We are currently investigating the extension of SIME to estimate the VTref without need for specifying a reference region.

The methodology proposed here maintains high levels of accuracy in the quantification of the binding to the target receptors, while performing a PET scan more cost-effective and less challenging logistically, at the same time diminishing the burden on the subjects. The methodology can pave the way to a broader use of PET in the investigation of brain diseases, and potentially as a screening tool for clinical diagnosis and personalized treatment.

The results presented here are the first step of an incremental development of the methodology, whose several aspects would benefit from further investigation. The current implementation of SIME considers very relaxed boundaries for the values that the parameters describing cIF can assume. If this allows for more flexibility in describing any possible cIF curve on the one hand, it also increases the likelihood of obtaining locally instead of globally optimal solutions for the estimated cIF on the other. The accuracy of the estimates could be therefore improved by adding more stringent, subject-specific, and data-driven boundaries for the cIF parameters. Also, the model here adopted to describe the cIF contains a discontinuity at the time of the curve peak, and although it has been used extensively in full arterial-line blood sampling situations, within SIME it can generate solutions that do not seem reasonable physiologically. This can lead to increased inaccuracy in the quantification of the binding potentials. It would be valuable to consider alternative models for the cIF, including those commonly adopted for pharmacokinetic analysis,39 and assessing advantages and disadvantages of increasing/decreasing the number of free parameters in the cIF model.

Given that each of the available blood data point that we use for training the predictive model is also measured with some noise, it would also be valuable to determine in each subject an ‘optimal' anchor, independent of the available blood data, and that is defined as the anchor value that would provide nearly the same estimation of a certain outcome measure (e.g., the radioligand VT) as the traditional analysis with full arterial blood sampling data. This can help achieve higher accuracy with SIME, and is part of our planned future investigation.

Future directions of investigation also include the assessment of the precision of the outcome estimates obtained by SIME, which involves bootstrapping of the single blood-based or predicted anchor.40 This could be accomplished for each bootstrap sample in a ‘parametric' bootstrap manner by simulating a single random variable representing the error in predicting the anchor point based on the fitted model. An estimate for the variance of this random variable can be taken from the mean squared error of the regression using the training data.

Future investigations will also involve the validation of the proposed approach on independent sets of data, and the validation and extension of the proposed methodology to other PET radioligands.

Conclusions

It is possible to fully quantify PET outcome measures such as VT and binding potentials without drawing any blood samples from the subject. The proposed methodology, here applied to CUMI as a test case, can be extended to other radioligands, after assessment of its performance in terms of precision and generalization flexibility.

The authors declare no conflict of interest.

References

  1. Innis RB, Cunningham VJ, Delforge J, Fujita M, Gjedde A, Gunn RN, et al. Consensus nomenclature for in vivo imaging of reversibly binding radioligands. J Cereb Blood Flow Metab. 2007;27:1533–1539. doi: 10.1038/sj.jcbfm.9600493. [DOI] [PubMed] [Google Scholar]
  2. Ogden RT, Zanderigo F, Choy S, Mann JJ, Parsey RV. Simultaneous estimation of input functions: an empirical study. J Cereb Blood Flow Metab. 2010;30:816–826. doi: 10.1038/jcbfm.2009.245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Milak MS, DeLorenzo C, Zanderigo F, Prabhakaran J, Kumar JS, Majo VJ, et al. In vivo quantification of human serotonin 1A receptor using 11C-CUMI-101, an agonist PET radiotracer. J Nucl Med. 2010;51:1892–1900. doi: 10.2967/jnumed.110.076257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cunningham VJ, Hume SP, Price GR, Ahier RG, Cremer JE, Jones AK. Compartmental analysis of diprenorphine binding to opiate receptors in the rat in vivo and its comparison with equilibrium data in vitro. J Cereb Blood Flow Metab. 1991;11:1–9. doi: 10.1038/jcbfm.1991.1. [DOI] [PubMed] [Google Scholar]
  5. Hume SP, Myers R, Bloomfield PM, Opacka-Juffry J, Cremer JE, Ahier RG, et al. Quantitation of carbon-11-labeled raclopride in rat striatum using positron emission tomography. Synapse. 1992;12:47–54. doi: 10.1002/syn.890120106. [DOI] [PubMed] [Google Scholar]
  6. Lammertsma AA, Hume SP. Simplified reference tissue model for PET receptor studies. Neuroimage. 1996;4:153–158. doi: 10.1006/nimg.1996.0066. [DOI] [PubMed] [Google Scholar]
  7. Lammertsma AA, Bench CJ, Hume SP, Osman S, Gunn K, Brooks DJ, et al. Comparison of methods for analysis of clinical [11C]raclopride studies. J Cereb Blood Flow Metab. 1996;16:42–52. doi: 10.1097/00004647-199601000-00005. [DOI] [PubMed] [Google Scholar]
  8. Logan J, Fowler JS, Volkow ND, Wang GJ, Ding YS, Alexoff DL. Distribution volume ratios without blood sampling from graphical analysis of PET data. J Cereb Blood Flow Metab. 1996;16:834–840. doi: 10.1097/00004647-199609000-00008. [DOI] [PubMed] [Google Scholar]
  9. Ichise M, Ballinger JR, Golan H, Vines D, Luong A, Tsai S, et al. Noninvasive quantification of dopamine D2 receptors with Iodine-123-IBF SPECT. J Nucl Med. 1996;37:513–520. [PubMed] [Google Scholar]
  10. Ichise M, Liow JS, Lu JQ, Takano A, Model K, Toyama H, et al. Linearized reference tissue parametric imaging methods: application to [11C]DASB positron emission tomography studies of the serotonin transporter in human brain. J Cereb Blood Flow Metab. 2003;23:1096–1112. doi: 10.1097/01.WCB.0000085441.37552.CA. [DOI] [PubMed] [Google Scholar]
  11. Zanderigo F, Ogden RT, Parsey RV. Reference region approaches in PET: a comparative study on multiple radioligands. J Cereb Blood Flow Metab. 2013;33:888–897. doi: 10.1038/jcbfm.2013.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Slifstein M, Laruelle M. Models and methods for derivation of in vivo neuroreceptor parameters with PET and SPECT reversible radiotracers. Nucl Med Biol. 2001;28:595–608. doi: 10.1016/s0969-8051(01)00214-1. [DOI] [PubMed] [Google Scholar]
  13. DeLorenzo C, Kumar JSD, Zanderigo F, Mann JJ, Parsey RV. Modeling considerations for in vivo quantification of the dopamine transporter using [(11)C]PE2I and positron emission tomography. J Cereb Blood Flow Metab. 2009;29:1332–1345. doi: 10.1038/jcbfm.2009.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ametamey SM, Treyer V, Streffer J, Wyss MT, Schmidt M, Blagoev M, et al. Human PET studies of metabotropic glutamate receptor subtype 5 with 11C-ABP688. J Nucl Med. 2007;48:247–252. [PubMed] [Google Scholar]
  15. Parsey RV, Kent JM, Oquendo MA, Richards MC, Pratap M, Cooper TB, et al. Acute occupancy of brain serotonin transporter by sertraline as measured by [11C]DASB and positron emission tomography. Biol Psychiatry. 2006;59:821–828. doi: 10.1016/j.biopsych.2005.08.010. [DOI] [PubMed] [Google Scholar]
  16. Ginovart N, Meyer JH, Boovariwala A, Hussey D, Rabiner EA, Houle S, et al. Positron emission tomography quantification of [11C]-harmine binding to monoamine oxidase-A in the human brain. J Cereb Blood Flow Metab. 2006;26:330–344. doi: 10.1038/sj.jcbfm.9600197. [DOI] [PubMed] [Google Scholar]
  17. Yaqub M, van Berckel BN, Schuitemaker A, Hinz R, Turkheimer FE, Tomasi G, et al. Optimization of supervised cluster analysis for extracting reference tissue input curves in (R)-[(11)C]PK11195 brain PET studies. J Cereb Blood Flow Metab. 2012;32:1600–1608. doi: 10.1038/jcbfm.2012.59. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Henriksen G, Willoch F. Imaging of opioid receptors in the central nervous system. Brain. 2008;131:1171–1196. doi: 10.1093/brain/awm255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Oquendo MA, Hastings RS, Huang YY, Simpson N, Ogden RT, Hu XZ, et al. Brain serotonin transporter binding in depressed patients with bipolar disorder using positron emission tomography. Arch Gen Psychiatry. 2007;64:201–208. doi: 10.1001/archpsyc.64.2.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Parsey RV, Arango V, Olvet DM, Oquendo MA, Van Heertum RL, Mann JJ. Regional heterogeneity of 5-HT1A receptors in human cerebellum as assessed by positron emission tomography. J Cereb Blood Flow Metab. 2005;25:785–793. doi: 10.1038/sj.jcbfm.9600072. [DOI] [PubMed] [Google Scholar]
  21. Parsey RV, Ojha A, Ogden RT, Erlandsson K, Kumar D, Landgrebe M, et al. Metabolite considerations in the in vivo quantification of serotonin transporters using 11C-DASB and PET in humans. J Nucl Med. 2006;47:1796–1802. [PubMed] [Google Scholar]
  22. Parsey RV, Ogden RT, Miller JM, Tin A, Hesselgrave N, Goldstein E, et al. Higher serotonin 1A binding in a second major depression cohort: modeling and reference region considerations. Biol Psychiatry. 2010;68:170–178. doi: 10.1016/j.biopsych.2010.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Milak MS, Severance AJ, Ogden RT, Prabhakaran J, Kumar JS, Majo VJ, et al. Modeling considerations for 11C-CUMI-101, an agonist radiotracer for imaging serotonin 1A receptor in vivo with PET. J Nucl Med. 2008;49:587–596. doi: 10.2967/jnumed.107.046540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Watson CC, Newport D, Casey ME. Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine. Aix-les-bains: France; 1995. A single scatter simulation technique for scatter correction in 3D PET; pp. 215–219. [Google Scholar]
  25. Kumar JS, Prabhakaran J, Majo VJ, Milak MS, Hsiung SC, Tamir H, et al. Synthesis and in vivo evaluation of a novel 5-HT1A receptor agonist radioligand [O-methyl-11C]2-(4-(4-(2-methoxy- phenyl)piperazin-1-yl)butyl)-4-methyl-1,2,4-triazi ne-3,5(2H,4H)dione in non- human primates. Eur J Nucl Med Mol Imaging. 2007;34:1050–1060. doi: 10.1007/s00259-006-0324-y. [DOI] [PubMed] [Google Scholar]
  26. Gunn RN, Sargent PA, Bench CJ, Rabiner EA, Osman S, Pike VW, et al. Tracer kinetic modeling of the 5-HT1A receptor ligand [carbonyl-11C]WAY- 100635 for PET. Neuroimage. 1998;8:426–440. doi: 10.1006/nimg.1998.0379. [DOI] [PubMed] [Google Scholar]
  27. Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
  28. Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Parsey RV, Ogden RT, Mann JJ. Determination of volume of distribution using likelihood estimation in graphical analysis: elimination of estimation bias. J Cereb Blood Flow Metab. 2003;23:1471–1478. doi: 10.1097/01.WCB.0000099460.85708.E1. [DOI] [PubMed] [Google Scholar]
  30. Zanderigo F, Ogden RT, Mann JJ, Parsey RV. A voxel-based clustering approach for the automatic selection of testing regions in the simultaneous estimation of input functions in PET. Neuroimage. 2010;52:S176. [Google Scholar]
  31. Kirkpatrick S, Gelatt CD, Jr., Vecchi MP. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
  32. Wong KP, Meikle SR, Dagan F, Fulham MJ. Estimation of input function and kinetic parameters using simulated annealing: application in a flow model. IEEE Trans Nucl Sci. 2002;49:707–713. [Google Scholar]
  33. Eknoyan G. Adolphe Quetelet (1796–1874)—the average man and indices of obesity. Nephrol Dial Transplant. 2007;23:47–51. doi: 10.1093/ndt/gfm517. [DOI] [PubMed] [Google Scholar]
  34. Mosteller RD. Simplified calculation of body-surface area. N Engl J Med. 1987;317:1098. doi: 10.1056/NEJM198710223171717. [DOI] [PubMed] [Google Scholar]
  35. Akaike H. A new look at the statistical model identification. IEEE Trans Automat Control. 1974;19:716–723. [Google Scholar]
  36. Ogden RT. Estimation of kinetic parameters in graphical analysis of PET imaging data. Stat Med. 2003;22:3557–3568. doi: 10.1002/sim.1562. [DOI] [PubMed] [Google Scholar]
  37. Krouwer JS. Why Bland-Altman plots should use X, not (Y+X)/2 when X is a reference method. Stat Med. 2008;27:778–780. doi: 10.1002/sim.3086. [DOI] [PubMed] [Google Scholar]
  38. Zanotti-Fregonara P, Chen K, Liow JS, Fujita M, Innis RB. Image-derived input function for brain PET studies: many challenges and few opportunities. J Cereb Blood Flow Metab. 2011;31:1986–1998. doi: 10.1038/jcbfm.2011.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Hoeben E, Neyens M, Mannaert E, Schmidt M, Vermeulen A. Population pharmacokinetics of JNJ-37822681, a selective fast-dissociating dopamine d2-receptor antagonist, in healthy subjects and subjects with schizophrenia and dose selection based on simulated d2-receptor occupancy. Clin Pharmacokinet. 2013;52:1005–1015. doi: 10.1007/s40262-013-0084-3. [DOI] [PubMed] [Google Scholar]
  40. Ogden RT, Tarpey T. Estimation in regression models with externally estimated parameters. Biostatistics. 2006;7:115–129. doi: 10.1093/biostatistics/kxi044. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Cerebral Blood Flow & Metabolism are provided here courtesy of SAGE Publications

RESOURCES