A New Paradigm of Interactive Artery/Vein Separation in Non-Contrast Pulmonary CT Imaging using Multi-Scale Topo-Morphologic Opening

Abstract

Distinguishing pulmonary arterial and venous (A/V) trees via in vivo imaging is a critical first step in the quantification of vascular geometry for the purpose of diagnosing several pulmonary diseases and to develop new image-based phenotypes. A multi-scale topo-morphologic opening (MSTMO) algorithm has recently been developed in our laboratory for separating A/V trees via non-contrast pulmonary human CT imaging. The method starts with two sets of seeds – one for each of A/V trees and combines fuzzy distance transform and fuzzy connectivity in conjunction with several morphological operations leading to locally-adaptive iterative multi-scale opening of two mutually conjoined structures. In the current paper, we introduce the methods for handling “local update” and “separators” into our previous theoretical formulation and incorporate the algorithm into an effective graphical user interface (GUI). Results of a comprehensive evaluative study assessing both accuracy and reproducibility of the method under the new setup are presented and also, the effectiveness of the GUI-based system towards improving A/V separation results is examined. Accuracy of the method has been evaluated using mathematical phantoms, CT images of contrast-separated pulmonary A/V casting of a pig’s lung and non-contrast pulmonary human CT imaging. The method has achieved 99% true A/V labeling in the cast phantom and, almost, 92% to 94% true labeling in human lung data. Reproducibility of the method has been evaluated using multiuser A/V separation in human CT data along with contrast-enhanced CT images of a pig’s lung at different positive end-expiratory pressures (PEEPs). The method has achieved, almost, 92% to 98% agreements in multi-user A/V labeling with ICC for A/V measures being over 0.96 to 0.99. Effectiveness of the GUI based method has been evaluated on human data in terms of improvements of accuracy of A/V separation results and results have shown 8% to 22% improvements in true A/V labeling. Both qualitative and quantitative results found are very promising.

I. Introduction

Over the last few decades, availability of a wide spectrum of medical imaging techniques [1] including MR, ultrasound, CT, PET, X- and γ-rays, has rapidly grown, enhancing needs for computerized algorithms to extract various types of quantitative measures from acquired images. Segmentation is a critical task in many quantitative medical imaging applications and, often, the segmentation problem of an individual application is unique in nature. Here, we address the problems related to separating pulmonary artery/vein (A/V) trees via in vivo CT imaging with no contrast. Separating pulmonary A/V trees via CT imaging is a critical first step in the quantification of vascular geometry for purposes of determining, for instance, pulmonary hypertension, pulmonary emboli and more. Separation of A/V trees may also be useful to enhance airway tree segmentation based on the relationship of artery and airway, and to provide landmarks for intra- and inter-subject pulmonary data registration. Also, ability of A/V separation opens opportunities of developing new imaging phenotypes relating A/V tree geometry, topology and branching patterns to study their relation with different diseases and genotypes.

Challenges in A/V separation are multi-folded including: (1) A/V are indistinguishable by their intensity values in non-contrast CT images, (2) often, there is no trace of intensity variation at locations of A/V fusion, (3) the coupling or fusion between A/V trees are tight and complex with arbitrary and multi-scale geometry, especially at branching locations, and (4) limited signal to noise ratio (SNR) and relatively low resolution are typical for in vivo CT imaging. Patient-specific structural variations of vascular trees further complicate the task. Several works have been reported in literature addressing A/V separation using improved image acquisition techniques; a thorough discussion on the difficulties of such approaches, especially for smaller vessels, has been presented by Bemmel et al. [2]. To the best of our knowledge, only a few postprocessing methods have been published for separating A/V trees [2]–[8]. Two of the previous methods [2], [3] have only been applied to MR data and did not use morphological scale information. These methods primarily rely on intensity variations or presence of edge information at adhering locations between A/V trees and may not work for non-contrast CT images where no such intensity variations are present at locations of adherence. Two methods for A/V separation from pulmonary CT images have been presented by Büelow et al. [3] and Yonekura et al. [5]. Büelow et al.’s method for A/V separation is based on prior knowledge of airway tree segmentation which may not produce optimal A/V separation at distal branches in a pulmonary vascular tree. The method by Yonekura et al. [5] is based on specific anatomic features of pulmonary A/V trees and prior airway segmentation. The anatomic knowledge of the spatial relationship between arteries and airways asserting that, in general, airways run in parallel to the arterial tree, was used by several researchers for A/V separation [6]–[8]. A major difficulty with these referenced methods is the nonuniformity of different features over the wide range of scales in a pulmonary tree and may not generalize to A/V separation in other body regions. Absence of contrast agents and tight spatial coupling between A/V trees leads to mutual fusion at the limited resolution of CT imaging, significantly increasing the task of A/V separation.

Theory and algorithms of a multi-scale topo-morphologic opening (MSTMO) [9] was developed in our laboratory to separate A/V trees in non-contrast CT imaging. Although, the method has been applied to separate A/V trees via pulmonary CT imaging, it may also be useful in other applications including tracking living cells in optical microscopic video imaging [10] or tracking moving objects/subjects in video imaging where multiple entities get mutually partially occluded from time to time. Recently, the method has been applied to separate transitional bronchi, alveoli, and terminal artery/vein trees in a high-resolution micro-CT imaging of fixated murine lung specimens [11], [12]. The basic theory of our previously published MSTMO based A/V separation was designed on the observation that: (1) often, A/V structures are fused at in vivo CT resolution and the intensity variations at such fusions may not be a reliable feature to separate the two structures, (2) however, the two conjoined structures may frequently be locally separable using a morphological opening operator of suitable scale not known a priori, (3) wherever the assumption of local separation of two structures is violated, user interaction is needed to manually enforce a separation of the two target structures. Therefore, a smart fusion of the theory and algorithms into a graphical user interface (GUI) framework is essential to convert it into an effective tool for basic medical as well as clinical research.

The purpose of the current paper is to translate the original theory and algorithm of our previously published work [9] to an effective tool by developing an efficient GUI-based system that may be useful in clinical research studies. Another purpose of this paper is to perform comprehensive experiments evaluating both accuracy and reproducibility of the new A/V separation system. Towards this goal, we have designed and developed an inter-linked 2- and 3-D graphical user interface and added new theory and methods for handling “local update” and “separator”. Both accuracy and reproducibility of the new GUI-based A/V separation system has been comprehensively examined. Accuracy of the method has been assessed using mathematical phantoms, CT images of a contrast-separated pig pulmonary vessel cast and non-contrast human pulmonary CT imaging. Reproducibility of the method has been examined using results of mutually-blinded multi-user A/V separation in human CT data as well as for contrast-enhanced CT images of a pig’s lung at different positive end-expiratory pressures (PEEPs). Also, the effectiveness of the GUI-based method has been examined in terms of improvements of A/V separation accuracy. Preliminary results of the GUI system and the animal study was reported in a conference paper [13].

II. Methods and Algorithms

In this section, first, we briefly describe the key ideas and steps in the MSTMO A/V separation algorithm originally presented in [9] and introduce the use of “separator”. Subsequently, we present a new GUI design integrating the MSTMO algorithm into an effective A/V separation system and a new local update technique.

A. Artery/Vein Separation Algorithm

Separation of pulmonary A/V trees in non-contrast multi-detector CT (MDCT) imaging is modeled as a task of opening two intensity-similar tubular tree structures with significant overlaps at various locations and scales. It is solved using the MSTMO algorithm that starts with a fuzzy segmentation of the assembly of A/V trees and two sets of seeds, one for each tree and a common set of separators. In this paper both seeds and separators are indicated manually. An object region starts growing from a seed while a separator is used to create a barrier between two objects. Finally, the method outputs spatially separated A/V trees. The premise of the MSTMO algorithm is built on the assumption that fusions between arteries and veins are locally separable using a morphological operation at a suitable scale. The method solves two fundamental challenges: (1) how to find the optimal suitable scale of morphological operation at a specific location and (2) how to trace continuity of locally separated regions. These challenges are met by combining fuzzy distance transform (FDT) [14], [15], a morphologic feature, with topologic fuzzy connectivity [16]–[22] in conjunction with other morphologic operations to iteratively open finer and finer details starting at large scales and progressing towards smaller ones. Essentially, during a specific iteration, the method applies erosion at an optimal scale, separating the two target structures, which is followed by a constrained dilation maintaining separate identity of individual structures.

Let us consider two intensity-similar cylindrical objects with significant mutual overlap as illustrated in Fig. 1(a). Following the common practice in 3D medical imaging, let us assume that the object in the figure, an assembly of two cylinders, is defined in a cubic grid denoted as the set of points in where is the set of integers. The assembly of the two cylindrical structures in the figure is essentially a fuzzy object = {(p, (p))|p ∈ }, where : → [0, 1] is the membership function. Following our problem definition, intensity variation at fusions of the two cylinders is not a reliable feature to separate them, while the two cylinders may be locally separable using morphological operations at a suitable scale. The central questions are how to determine local scales of these operations and how to combine locally separated regions. The separation process is initiated by selecting of two sets of seeds , ⊂ , one for each object and a common set of separators . Although, single seed is used for each object in Fig. 1(b), in real application, each of , and may contain multiple points. First, the algorithm computes local-scale normalized FDT image of the conjoined object reducing the effects of spatial scale variation [9]. Scale normalized FDT map for an individual object, say , denoted by : → [0, 1] is computed from the common fuzzy object except that ∪ is enforced into background. Subsequently, “morpho-connectivity” at a given point p in an object specified by the set of seeds S, is defined as the largest scale of erosion while preserving a path-connectivity [23], [24] between p and at least one seed point in S. It can be shown that, in a binary image, morph-connectivity is equivalent to fuzzy connectivity on distance transform image; we argue to use fuzzy connectivity on the FDT image as morpho-connectivity for a fuzzy image. Let , : × → [0, 1] denote the morpho-connectivity fuzzy relation on the two target objects as computed from the two scale-normalized FDT maps and , respectively. Following that the two sets seeds and represent two different objects, a locally adaptive threshold on the morpho-connectivity image that barely disconnects the two objects indicates local scale of the optimum erosion separating the two cylinders, see Fig. 1(b). Thus, during the optimum erosion, a point p is assigned to object if there exists an erosion such that p is disconnected from while remaining connected to . Thus, the region assigned to after optimum erosion is defined as follows:

$$R_{\mathcal{A}}=\left\{p\mid \underset{a\in S_{\mathcal{A}}}{max}{\gamma }_{\mathcal{A}}(a,p)>\underset{b\in S_{\mathcal{B}}}{max}{\gamma }_{\mathcal{B}}(b,p)\right\}.$$ (1)

Fig. 1.

A schematic description of the artery/vein separation problem and its solution using a multi-scale topo-morphologic opening algorithm. In (a), hollow dots indicate morphological erosion while the green disks represent multi-scale morphological operators.

It may be noted that although, the set of separators does not appear in the above equation, it contributes in determining the region by influencing the FDP maps and which then define the morpho-connectivity maps and . The immediate next question is how to proceed with separation at lower scales. The difficulty here is that the scale of the annular remainder after erosion (Fig. 1(b)) is at least equal to that of the regions not yet separated. This difficulty is overcome using a constrained dilation filling the annular remainder while maintaining separate identities of the two objects (Fig. 1(c)). Constrained dilation is confined to “morphological neighborhood” [9] ( ) of to match local scales during erosion and dilation steps. Finally, (or ) is extended by the set of points p ∈ ( ) (respectively, points p ∈ ( )) which are strictly closer to (respectively, ) than (respectively, ); see Fig. 1(c).

The above two steps of optimal erosion and constrained dilation lead to an “optimal opening” operation preparing the ground for separation at next finer scales and the method progresses iteratively until the results of separation converges. The convergence of the process is assured by the following facts – (1) the two structures and monotonically expand with iterations, and (2) the scope of the combined object , i.e., the set of points in with non-zero membership value, over which the two structures and may expand is bounded. During each iteration, the morpho-connectivity paths for one object, say , is restricted from entering into the region assigned to its rival object in the previous iteration and thus changing the morpho-connectivity and eventually refining the results separation between and . This task is accomplished by a simple operation of setting values to zero at all locations assigned to in the previous iteration; see [9] for detail.

B. Effective User Interface

An integrated 2D and 3D user interface has been developed in our laboratory allowing simultaneous viewing of 2D and 3D vascular geometry along with current results of A/V separation overlaid in different colors (see Fig. 2). The correspondence of vascular geometry in 3D and three planar views is realized by tagging the 3D cursor with 2D planar cursors indicated with color-matched orthogonal lines. Facilities to select and edit different seeds and separators are supported within the graphical interface along with various display and overlay-related options. A major challenge with the development of the graphical user interface is the time required (approximately 2–3 minutes for a 512 × 512 × 600 CT image of a human lung in a 2.33 GHz intel(R) Xeon(R) CPU running a Linux operating system) to update the A/V separation result in the entire image thus prohibiting interactive editing of seeds and separators. Since a user is often interested in the local changes of A/V separation during the selection or deletion of seeds or separators, we developed the theory and algorithm for local updates, thus facilitating user interaction. The basic idea is to confine the A/V separation over a small local window of size, say, 51 × 51 × 51 so that a user may view local changes in A/V separation at a reasonable speed while editing seeds and global separators. After several edits a user may ask for an update of A/V separation before entering for another round of editing, if needed. It is important to make the following two observations to understand the challenges as well as the solution for the local update algorithm.

Fig. 2.

An integrated 2D and 3D graphical user interface system for A/V separation. The left window illustrates the 2D interface for editing seeds/separators with several features including various overlay options. The window on the right presents 3D rendering of vasculature along with color-coded display of current A/V separation with the cursors in 2D and 3D windows being inter-connected.

1. The local window inherits some A/V separation results from prior selected seeds possibly outside the local space (Fig. 3(b)).

2. A/V separation inside the box needs to be partially or fully overruled with selection or deletion of seeds and separators.

Fig. 3.

Illustration of the steps during local update. (a) Vessel structures without A/V separation; one seed is selected for each of the A/V trees. (b) Results of initial A/V separation; the location with a failure in A/V separation is indicated. (c) Results of local update after adding a new seed. Inherited seeds are indicated with black circles. (d) Results of global update.

The first observation suggests that we need to inherit some seeds in the local space based on global results of A/V separation. However, if all voxels marked as arteries (or veins) are considered as seeds, the algorithm fails to overrule faulty segmentations inside the local space. Therefore, the aim is to use minimum sets of seeds to inherit the global A/V separation in the local space. It may be noted that any branch of an artery or vein must cross the outer surface of the local space to enter inside and therefore, regions of intersection between globally-separated arteries (or veins) and the outer surface of the local space may be used to inherit seeds for arteries (or veins, respectively) during local updates; these seeds will be referred to as inherited seeds. User-specified seeds falling inside the local space are also used in conjunction with inherited seeds for local updates. Further, in an attempt to eliminate adverse effects of inherited seeds, an inherited seed is eliminated if it falls inside the morphological neighborhood of a user-specified seed, which is assumed to be a more accurate seed. Let us consider the example of Fig. 3, which is a 2D representation of a 3D vascular tree. Fig. 3(a) shows the original vasculature along with two seeds – one for arterial tree and another for venous tree. Following the central spirit of MSTMO-based A/V separation, let us assume that the algorithm may correctly solve some crossings but not all. The result of global A/V separation using the initial seed is shown in Fig. 3(b). Note that the branch indicated by an arrow is incorrectly identified as venous tree and a user interaction is needed here. As the user places an arterial seed to rectify the error, a local update process is invoked. It starts with defining a local space, enclosed by the rectangle as shown in Fig. 3(c), with the newly-added seed as the center. After the local update process, A/V trees are separated correctly in local space but the connected A/V structure in the whole image is not updated immediately, as shown in Fig. 3(c). In order to get the new separated A/V trees in the full image, the lengthier global update process is needed, the result of which is shown in Fig. 3(d). Here, it is assumed that the crossing just outside the box is correctly solved by the MSTMO algorithm.

Steps of interactive correction of A/V separation results on a human pulmonary CT data are pictorially illustrated in Fig. 4; here images from different windows are shown in blocks instead of showing the snapshots of the composite software system to facilitate the presentation in a paper format which is much smaller in size as compared to a large display screen. Fig. 4(a) shows the location of mistake in separating a fusion between arterial and venous branches as shown in 3D in Fig. 4(b) and more clearly in a zoomed-in representation in Fig. 4(c). Fig. 4(d–f) show the results of corrected A/V separation after adding a new arterial seed shown in blue in Fig. 4(d). In general, arterial and venous trees are uniformly distributed over the lung region. A trained user looks for locations with higher concentration of either of arterial and venous tree-type in the color-coded 3D rendered view. Once such a location is identified, the user trace for the root where the misclassification took place using the mouse-controlled zoom-in, rotation and translation tools embedded in the GUI system. After locating the root of misclassification as indicated with arrows, the interconnected cursors in both 2D and 3D views are used to add new seeds or separators to rectify the misclassification. Using a slice-by-slice interface, it is difficult locate such misclassification. Despite that 3D views are effective in locating misclassifications, such views are often misleading while adding seeds or separators. Therefore, an integrated 2D-3D GUI may be an optimum choice to improve the performance of user-interaction in artery/vein separation where a 3D interface used to locate the root of misclassification while a 2D interface is used to add seeds and separators to rectify the error. Although the new integrated 2D/3D GUI improves the performance of interactive seeds selection, further research may be needed to further enhance the performance of pulmonary artery/vein separation using automatic seeds selection based anatomic information, e.g., the presence of airways.

Fig. 4.

Illustration of user interaction steps within the A/V separation GUI system. (a) An axial slice view with a visually detected mistake in A/V separation as indicated by an arrow. (b–c) Normal and zoomed in 3D rendering of the A/V separation results with arrows indicating to location of the mistake in A/V separation. (d–f) Same as (a–c) after correcting the mistake using an additional user specified seed.

III. Experiments and Results

In this section, we describe our experimental plans, methods and results conducted to examine the accuracy and reproducibility of A/V separation results with user interaction through a new 2D-3D GUI system described in the previous section and the automated the MSTMO algorithm [9]. Accuracy of the system is evaluated using – (1) computer generated mathematical phantoms, (2) CT images of a pig pulmonary vessel cast phantom with contrast separated A/V trees, and (3) non-contrast human pulmonary CT images with expert labeled A/V trees. Reproducibility of the method is evaluated using – (1) contrast-enhanced CT images of a pig lung at different PEEPs and (2) multi-user A/V separation in non-contrast pulmonary human CT images. Also, we present experimental results evaluating accuracy enhancement using the current GUI framework for A/V separation as compared to slice-by-slice editing of seeds described in our previous paper [9]. In following sections, we describe methods and results of each of these experiments.

A. Accuracy

A major challenge with evaluating the accuracy of an A/V separation system is the difficulty of producing ground truths under the complexity present in human vasculature. To overcome this challenge, we have examined the performance of our A/V separation system using mathematical phantoms, a physical phantom of contrast-separated pulmonary pig A/V trees and also, with expert labeled A/V points in non-contrast human pulmonary CT images. In our previous paper [9], we evaluated the accuracy of the A/V separation method using mathematically generated tubular structure phantoms without any bifurcation. In order to assess the performance of the algorithm in the presence of bifurcations, we generated a new set of mathematical phantoms with bifurcations and different fusion patterns. The in vivo results presented in [9] demonstrate the performance of the algorithm only qualitatively that is based on visual judgment. The purpose of the in vivo accuracy experiment presented here is to quantitatively examine the accuracy of the method based on an independent expert tracking of A/V trees.

1) Computer Generated Phantoms

Five phantom images, each being an assembly of a pair of tubular tree objects running quasi-parallel across the slice direction, were computer-generated with different geometry (Fig. 5). From each base phantom, four different phantoms were generated at different overlaps (Fig. 5) by moving two tubular tree structures closer to each other. The overlap ratio was computed as follows. A tubular tree in a phantom image is represented using its centerline along with a radius associated to each location on the centerline. Let us assume that a phantom image contains two tubular objects , defined as follows:

$$X=\{(c_{X,1},r_{X,1}),(c_{X,2},r_{X,2}),\cdots ,(c_{X,L},r_{X,L})\}$$ (2)

where X ∈ { , }.

Fig. 5.

3D rendering of five computer generated phantoms with bifurcation used in our experiments.

The overlap ratio between two structures is the maximum normalized overlap between them that is defined as follows:

$$\text{overlap}(A,B)=\underset{i,j}{max}\frac{r_{\mathcal{A},i}+r_{\mathcal{B},j}-\mid c_{\mathcal{A},i}-c_{\mathcal{B},j}\mid }{r_{\mathcal{A},i}+r_{\mathcal{B},j}},$$ (3)

where | − | denotes the Euclidean distance between , . Four phantom images were created with overlap ratio at 5, 10, 15, and 25%.

Each phantom image was originally generated at high resolution and then down-sampled using 3 × 3 × 3, 4 × 4 × 4 and 5 × 5 × 5 windows simulating partial volume effects. Each down-sampled image was further degraded with additive white Gaussian noise at SNR of 12. Thus, twelve test phantom images (4 overlap ratios times 3 resolutions) were generated from each base phantom image producing a total of sixty test phantom images. Using the graphical user interface, for each tubular object exactly one seed point was placed on the top-slice (at the largest scale) near the center. Fig. 6 illustrates that, even in the presence of bifurcation, significant overlap, down sampling and random noise, the method separates the two conjoined structures except at small scale regions in the phantom with the highest overlap and downsampling. A similar trend was observed for other phantoms as shown in Fig. 7.

Fig. 6.

Results of applying the MSTMO algorithm to computer-generated phantoms. (a–f) Results of phantoms with 5% overlap at 3 × 3 × 3 (a, b), 4 × 4 × 4 (c, d) and 5 × 5 × 5 (e, f) down sampling. (a,b) 3D rendering of the phantom images before (a) and after (b) applying MSTMO algorithm. On each image, several 2D cross sectional images are presented to illustrate relative overlap at various scales. (g–l), (m–r), (s–x) Same as (a–f) but for 10%, 15%, and 25% overlaps. At 25% overlap and 4 × 4 × 4 and 5 × 5 × 5 downsampling rate, the method has failed to sucessfully separate two objects at small scales.

Fig. 7.

Results of applying the MSTMO algorithm to three computer-generated phantom images. (a)–(f) Results of phantoms with increasing overlap and downsampling rates – (a, b) 10% overlap and 3 × 3 × 3 downsampling; (c, d) 15% overlap and 4 × 4 × 4 downsampling; (e, f) 25% overlap and 5 × 5 × 5 down sampling. (g–l) Same as (a–f) but for another base phantom.

For quantitative evaluation of the system, the ground truth of separation was computed using the information saved during their generation at the original resolution prior to down sampling. For each tubular object in a phantom image, its centerline along with local radii was recorded. Let (c_X,j, r_X,j)|X = , ; j = 1, 2, …, L_X be the points and local radii along the centerline of the object X in a phantom image prior to its downsampling. Let p = (x, y, z) be a point with non-zero intensity value in the corresponding phantom image obtained by down sampling at l × l × l where l=3, 4 or 5. Local-radius-normalized distance of p from the centerline of the object X, denoted by

$$D_X(p,l)=\underset{j=1,2,\cdots ,L_X}{min}\frac{\mid (xl,yl,zl)-c_{X,j}\mid }{r_{X,j}}.$$ (4)

Here, local-radius-normalized distance is used to avoid a bias in separation due to local scale difference between two objects. Finally, a point p is assigned to (or, ) if (p, l) > (p, l) (respectively, (p, l) > (p, l)). Note that in a rare situation of (p, l) = (p, l) (since, c_X,j is a point in the Euclidean 3D space), the point p is not assigned to any of the two objects. Let and denote true separation for the two objects in a phantom image computed as above and let and denote corresponding separation using the MSTMO-based system. True Labeling (TL) and false Labeling (FL) of the computerized separation are defined as follows:

$$\text{True}\text{Labeling}(\text{TL})=\frac{(T_{\mathcal{A}}\cap S_{\mathcal{A}})\cup (T_{\mathcal{B}}\cap S_{\mathcal{B}})}{T_{\mathcal{A}}\cup T_{\mathcal{B}}},$$ (5)

$$\text{False}\text{Labeling}(\text{FL})=\frac{(T_{\mathcal{A}}\cap S_{\mathcal{B}})\cup (T_{\mathcal{B}}\cap S_{\mathcal{A}})}{T_{\mathcal{A}}\cup T_{\mathcal{B}}}.$$ (6)

It may worth indicating that the sum of true and false labeling may not necessarily be equal to ‘1’ as some voxels may be missed in the process of separation. Results of quantitative evaluation of the true and false labeling in the separation result of each phantom image at different down sampling rates using our algorithm are summarized in Table I. The lowest value of true labeling observed in this study was 92.0% achieved for the example of Fig. 5(a) at 5 × 5 × 5 downsampling rate while the highest false labeling was 3.2% observed for the example of Fig. 5(e) at the same downsampling rate. The results demonstrate that, even in the presence of bifurcation, the MSTMO algorithm produces high level of accuracy in spatial delineation of two structures at different downsampling rates and overlap ratios. The performance of the MSTMO algorithm deteriorates with increasing overlap ratios of two structures as well as with increasing downsampling rates.

TABLE I.

Results (range and mean±std) of true and false labeling of two-object separation in tubular tree-like phantoms using the MSTMO algorithm at different downsampling rates.

Downsampling rate	True Labeling(%)range; mean±std	False Labeling(%)range; mean±std
3 × 3 × 3	[94.6,99.9]; 98.8±1.2	[0.1,1.3]; 0.6±0.4
4 × 4 × 4	[93.6,99.8]; 98.4±1.4	[0.1,2.1]; 0.8±0.5
4 × 3 × 4	[92.0,99.6]; 97.5±1.7	[0.2,3.2]; 1.2±0.9

2) Pig Lung Phantom

The purpose of this experiment is to evaluate the method’s accuracy of separating A/V trees under the actual complexity present in pulmonary vasculature. Towards this aim, we generated a physical cast phantom from the pulmonary vasculature of a pig, where true A/V trees are separated using different injected contrast materials. To generate the vessel cast phantom, the animal was first exsanguinated. While maintaining ventilation at low PEEP, the pulmonary vasculature was flushed with 1L 2% Dextran solution and pneumonectomy was performed. While keeping the lungs inflated at approximately 22cm H₂O Pawy, a rapid-hardening methyl methacrylate compound (Orthodontic Resin, DENTSPLY International, York, PA) was injected into the vasculature to create a cast of the pulmonary A/V trees. The casting compound was mixed with red oil paint for the venous (oxygenated) side and blue oil paint for the arterial (deoxygenated) side of the vascular beds. The arterial side was also contrast-enhanced by additional 10 cc of Ethiodol (Savage Laboratories, Melville, NY) to the casting compound (Fig. 8(a)). The vessel cast was scanned on a Siemens Somatom Definition Flash 128 scanner using the following protocol – 120kV, 115 effective mAs, 1 sec rotation speed, pitch factor: 1.0, nominal collimation: 16 × 0.3mm, image matrix: 512 × 512 and (0.34mm)² in-plane resolution. Images were reconstructed at four different slice thicknesses of 0.6, 0.75, 1.0 and 1.5mm to evaluate the performance of the method at different resolutions. Using CT contrast separation of arterial and venous injections (Fig. 8 (b)), true A/V separation (Fig. 8(d)) for each image was obtained using a suitable CT intensity threshold. The effect of distinguishing A/V contrast between A/V trees was subsequently eliminated using a post image processing algorithm (Fig. 8(c, e)) and this contrast-eliminated image was used by the A/V separation system. For each of A/V trees, exactly ten seeds/separators were manually selected on the contrast-eliminated image with our GUI, and the A/V separation was computed (Fig. 8(f)). Results of A/V separation in phantom images at two different resolutions (slice thickness of 0.6 and 1.5mm) are illustrated in Fig. 9. A visual comparison between Fig. 9(b) and (e) clearly demonstrates that vascular tree segmentation captures finer branches at higher levels of tree generation in high resolution image (Fig. 9(b)) as compared to the result obtained at lower resolution (Fig. 9(e)). A more interesting point observed here is that despite a difference in the quality of vascular tree segmentation at two different resolutions, the quality of A/V separation at respective vascular tree is visually similar. This observation has been confirmed in the quantitative results presented in Table II.

Fig. 8.

A/V separation results on a pulmonary pig vessel cast phantom. (a) A photograph of the phantom. (b) A coronal slice from the original CT image of the phantom data with different contrast for A/V trees. (c) Same as (b) after contrast elimination. (d) True A/V separation from the original contrast-separated CT data. (e) 3D rendering of the contrast-eliminated vasculature. (f) A/V separation from (e) using the MSTMO algorithm.

Fig. 9.

Results of A/V separation on a pulmonary pig vessel cast phantoms. (a) A coronal image slice from the CT data of pig lung vessel cast phantom at 0.6mm slice thickness. (b) 3D rendering of vasculature after elimination of contrast separation. (c) Results of A/V separation. (d–f) Same as (a–c) but at 1.5mm slice thickness.

TABLE II.

Results of quantitative accuracy analysis of A/V separation of a pig pulmonary vessel cast phantom reconstructed at different slice thickness.

Slice Thickness (mm)	True Labeling	False Labeling
0.6	99.60%	0.40%
0.75	99.33%	0.67%
1.0	99.14%	0.86%
1.5	99.49%	0.50%

True and false labeling measures of A/V separation were computed to quantitatively assess the method’s accuracy at every slice thickness and spacing. Result of quantitative analysis in phantom images at different resolutions are presented in Table II. As observed in Table II, the method has produced high true labeling (>99%) and low false labeling (<1%) at all resolutions. However, as observed in the A/V separation results in Fig. 9 at different slice thicknesses, at a larger slice thickness, finer branches are missed in the process of vascular segmentation. In other words, slice thickness plays an important role in vascular segmentation at the finer scale. However, after segmentation of vasculature, slice thickness plays only a minimal role in the accuracy of A/V separation at respective vascular details.

3) Pulmonary Human CT Imaging

The purpose of this experiment is to evaluate the accuracy of the MSTMO-based A/V separation system under a clinical setup where the ground truth was obtained by manual labeling. Towards this goal, the thoracic region of three human subjects were imaged on a Siemens Sensation 64 multi-detector CT scanner using the following protocol: 120kV, 100 effective mAs, pitch factor: 1.0, nominal collimation: 64 × 0.6mm, image matrix: 512 × 512 and (0.55mm)² in-plane resolution. The pulmonary vascular tree consisting of both of A/V trees was segmented in a CT image using a previously published method by Shikata et al. [25]. The method uses tree-connectivity on CT intensity data after processing with a tubular enhancement filter resulting in a binary vessel mask. A fuzzy vascular tree segmentation was generated from this vessel mask using the following three steps – (1) determine the mean and standard deviation of intensity values over the segmented vessel mask, (2) dilate the binary vessel mask region by one voxel to include partial-volume voxels, and (3) assign fuzzy membership at each voxel over the dilated vessel mask following a step up Gaussian function with mean and standard deviation parameters as computed in step 1. Approximately 25–35 seeds/separators were manually selected on each of A/V trees in each of left and right lungs, which were subsequently used by MSTMO algorithm to separate A/V trees. Approximately 90 minutes were spent for each of the left and right lungs for each data set to add the seeds and separators through the MSTMO algorithm for complete A/V separation. To examine the accuracy of our A/V separation system, approximately 8K–10K voxels were manually labeled by an expert as arteries or veins. Specifically, 2K-2.5K voxels for arteries and another 2K-2.5K voxels for veins in each of the left and right lungs were labeled by selecting a few points on each slice inside the corresponding structure. Finally, quantitative measures of true labeling and false labeling were computed and the results are presented in Table III. As observed in the table, the method has produced acceptable accuracy of 91.5% or higher true labeling and 7.3% or less false labeling.

TABLE III.

Results of quantitative accuracy analysis of artery/vein separation in pulmonary human CT images.

subject	whole lung		left lung		right lung
	TL	FL	TL	FL	TL	FL
1	92.20%	7.02%	92.74%	6.78%	91.72%	7.22%
2	93.81%	4.36%	96.53%	2.55%	91.83%	5.6%
3	91.79%	4.67%	92.03%	1.40%	91.60%	7.28%

B. Reproducibility

To evaluate the reproducibility of the A/V separation system, we have conducted two different experiments – (1) qualitative assessment of the reproducibility of A/V separation visually matching structures in contrast-enhanced in vivo pulmonary pig CT imaging at different respiratory pressures and (2) quantitative multi-user reproducibility of A/V separation system in human pulmonary CT imaging. These experiments and observed results are described in the following.

1) Pulmonary Pig CT Imaging at Different Respiratory Pressures

An anesthetized pig was imaged in prone body posture at three different PEEPs, 7.5, 12 and 18cm H₂O, with the intravenous infusion of 40 cc at 2.5 cc/sec of contrast agent (Omnipaque, GE Healthcare Inc, Princeton, NJ) into the external jugular vein. This specific contrast protocol was selected to match with clinical practice for evaluating the pulmonary arterial bed to diagnose pulmonary emboli. The following CT protocol was used for imaging: 120kV, 200 effective mAs, pitch factor: 1.0, nominal collimation: 64 × 0.6mm, image matrix: 512 × 512 and (0.47mm)² in-plane resolution. It’s worth mentioning that both the contrast-enhanced in vivo CT imaging described here and pulmonary vessel cast data described in the previous section were performed on the same animal and the in vivo imaging experiments were performed prior to cast generation. Ten seeds/separators were used for each of A/V trees for each data set. Results of reproducibility of A/V separation at different PEEPs using contrast-enhanced pulmonary pig CT data, displayed at visually matched views, are illustrated in Fig. 10. Agreements of A/V separations results at three respiratory pressures are visually apparent and the results are promising.

Fig. 10.

Results of A/V separation on contrast-enhanced in vivo CT images of a pig’s lung at three different PEEPs. (a,d,g) Visually matched coronal slices from original pulmonary CT images at 7.5cm (a), 12cm (d) and 18cm (g) H₂O PEEPs. (b,e,h) 3D rendering of the segmented vasculature from two CT data sets of (a,d,g). (c,f,i) 3D rendering of A/V separation results using the MSTMO algorithm.

2) Multi-User reproducibility on Human CT Data

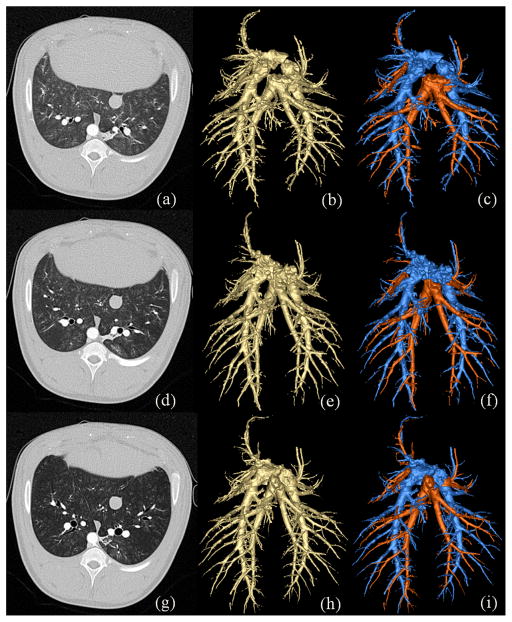
The purpose of this experiment is to quantitatively evaluate multiuser reproducibility of the new pulmonary A/V separation system in human subjects imaged using a clinical CT scan protocol. The reproducibility study was performed on fifteen human pulmonary CT images. Here, all images were acquired using the same CT protocol described in Section III-A3. Also, pulmonary vasculature was segmented in each CT image using the same image processing protocol described in the same section. A coronal image plane of CT data of a human subject is presented in Fig. 11(a) and 3D rendering of segmented vascular trees are presented in Fig. 11(b). Seeds and separators for each of the A/V trees were manually selected by three mutually-blinded experts using the GUI described in Section II-B with built in MSTMO algorithm. A/V separation results from the three mutually blinded experts were used to quantitatively evaluate the reproducibility of the method; colored rendering of A/V separation results by three experts are illustrated in Fig. 11(c–e).

Fig. 11.

Results of A/V separation on pulmonary CT data. (a) A coronal image slice. (b) 3D rendering of the vasculature. (c,d,e) Color-coded rendering of A/V separations using seeds from three independent experts.

Although no true A/V segmentations are available to compare with the results of this experiment, homogeneous distribution of A/V structure complies with biological knowledge of pulmonary A/V distribution. Despite very dense tree structure of pulmonary vasculatures, for most A/V branches, results of separation by three independent experts visually agree. It may be noted that there are a few visible differences in A/V separation results by three experts; however, keeping it in mind that pulmonary vasculature is a complex 3D structure with unknown and multi-scale geometry of coupling between A/V trees, especially, at branching locations, the reproducibility results are visually encouraging. In order to quantitative evaluate the reproducibility of the method, we have defined “agreement” and “disagreement” measurements as follows:

$$\text{Agreement}=\frac{(A_i\cap A_j)\cup (V_i\cup V_j)}{A_i\cup V_i\cup A_j\cup V_j},$$ (7)

$$\text{Disagreement}=\frac{(A_i\cap V_j)\cup (A_j\cup V_i)}{A_i\cup V_i\cup A_j\cup V_j},$$ (8)

where A_x and V_x denote separated A/V using seeds/separators selected by the expert x(x = i or j), i, j ∈ {A, B, C}.

Results of reproducibility analysis of A/V separation for fifteen human CT data in terms of pairwise agreement and disagreement among three experts are summarized in Table IV. The value of agreement was calculated for each pair of experts for each human data and the range as well as mean±std measures were separately computed for left, right and whole lungs. The minimum agreement for the whole lung was 91.6% while the highest agreement value achieved was 98.1% with an average agreement of 95%. The highest disagreement between two experts was 7.5% with an average disagreement of 3.2% for whole lung. Also, we performed an intra-class correlation (ICC) analysis of volume and surface area measurements from A/V separation results by three experts and the results are summarized in Table V. In general, the reproducibility analysis of total volume and surface area measures of A/V trees has resulted high ICC values. Keeping in mind that these results of reproducibility analysis reflect the robustness of the entire process in the presence of human errors as well as effectiveness of the graphical interface, the outcome is very promising.

TABLE IV.

Results of quantitative analysis of agreement and disagreement of A/V separations between each pair of independent mutual blind users among three experts.

lung ⇒	agreement			disagreement
	left	right	whole	left	right	whole
range	[90.2,98.2]	[90.2,98.7]	[91.6,98.1]	[1.2,9.2]	[0.8,8.9]	[1.1,7.5]
mean±std	95.2±1.9	95.4±1.9	95.3±1.6	3.5±1.7	3.0±1.6	3.2±1.5

TABLE V.

Results of intra-class correlation (ICC) analysis of volume and surface area measurements from A/V separation results by three experts.

ICC	left lung		right lung		whole lung
	artery	vein	artery	vein	artery	vein
volume	0.94	0.97	0.98	0.98	0.98	0.97
surface area	0.98	0.96	0.99	0.95	0.99	0.96

C. Effectiveness of the GUI

To evaluate the effectiveness of the proposed GUI, we repeated the same experiment of Section III-A3 except that the ordinary slice by slice interface was used to interactively add seeds and separators. For each dataset, the user was asked to spend approximately 90 minutes to add seeds and separators for each of left and right lungs. Note that a similar amount of time was spent to complete A/V separation using the GUI interface. Results of true labeling and false labeling measures computed using the same ground truth referred to in Section III-A3 are presented in Table VI. A comparison of results presented in Table III and Table VI clearly show enhancement in performance of A/V separation using the integrated 2D–3D GUI. Specifically, over the whole lung, the 2D–3D GUI has resulted 8% to 22% enhancement in the performance of true artery/vein labeling while reducing false labeling by three to five folds.

TABLE VI.

Results of quantitative accuracy analysis of artery/vein separation with user interaction through a slice-by-slice interface without using the presented GUI.

subject	whole lung		left lung		right lung
	TL	FL	TL	FL	TL	FL
1	75.38%	24.14%	83.22%	16.28%	74.26%	25.30%
2	79.01%	20.81%	87.30%	12.31%	77.23%	22.75%
3	84.91%	14.41%	80.38%	18.45%	83.29%	13.23%

IV. Conclusions

In this paper, we have presented a comprehensive system to separate pulmonary arterial and venous trees through non-contrast in vivo CT imaging using the theory of a recently developed multi-scale topo-morphologic opening algorithm [9] embedded into a 2D–3D inter-connected graphical user interface. The steps related to optimal erosion and constrained dilation using morpho-connectivity and fuzzy distance transform within the multi-scale topo-morphologic opening algorithm have been described. Also, we have introduced new theory and methods for handling “local update” and “separators” essential for a practical A/V separation system with an effective user interface. A thorough experimental plan was designed and executed to evaluate both accuracy and reproducibility of the method as well as to examine the effectiveness of the new GUI system. Despite significant overlap, blurring and noise, the method has been found highly accurate (true labeling > 97.5±1.7%) on mathematical phantoms with two intensity-similar objects mutually fused at various scales and locations. Noise and resolution are major issues in CT and the high performance of the current method for degraded phantoms is encouraging and it may be worth investigating the performance of the method in low dose and ultra-low dose CT [26]–[28]. The performance of A/V separation results in such low radiation image may depend on the performance of the first step of segmenting the combined vascular tree. Accuracy of the method was studied on a cast phantom of a pig’s pulmonary vasculature where the truth was obtained from the contrast separation of the arterial and venous trees. The purpose of this experiment was to investigate the method’s performance under the complexity often present in a biological vasculature and the results found (true labeling > 99%) were very promising using only ten seeds for each of A/V trees. Results of accuracy analyses of the method on three human pulmonary non-contrast CT data were satisfactory (true labeling > 91.5%) where the ground truth was generated using seed points selected on each of A/V trees by expert. Results of the reproducibility study of the method on in vivo CT data of a pig’s lung at different positive end-expiratory pressures were visually encouraging. As observed visually, most matching branches were correctly labeled as A/V at all three pressures (7.5, 12 and 18cm H₂O PEEPs). Mutually-blinded multi-user reproducibility of the A/V separation system on human pulmonary data was satisfactory (agreement for the whole lung > 91.6% and ICC of separated A/V volume > 97%). The multi-scale topo-morphologic opening algorithm takes 2–3 minutes to compute for each of left and right lungs in a human pulmonary CT data (size: 512 × 512 × 600). However, it takes approximately 90 minutes for a trained expert to place seeds and separators though the comprehensive A/V separation system with 2D–3D inter-connected graphical user interface. An experiment evaluating the effectiveness of the 2D–3D integrated GUI system has shown that the new interface system may improve 7% to 17% (mean: 12%) improvement in the accuracy (true labeling) of A/V separation results as compared to an ordinary slice by slice user interface system. In order to reduce effects of body motions in A/V separation, it is imperative that the subject remain apneic throughout the scan. This is a requirement for all other image-based pulmonary quantitative measures. With scanning times now on the order of 6 seconds or less on state-of-the-art scanners, this is usually not an issue. There are some issues with cardiogenic motion near the heart, mostly on the left side. Such region specific motion issues will need to be studied more carefully as we begin to utilize this new image analysis methodology. Currently, we are investigating the application of the comprehensive A/V system in a clinical study, and in particular how these volumes related to emphysema origin and progression.