Hierarchical effects of task engagement on amplitude modulation encoding in auditory cortex

Abstract

We recorded from middle lateral belt (ML) and primary (A1) auditory cortical neurons while animals discriminated amplitude-modulated (AM) sounds and also while they sat passively. Engagement in AM discrimination improved ML and A1 neurons' ability to discriminate AM with both firing rate and phase-locking; however, task engagement affected neural AM discrimination differently in the two fields. The results suggest that these two areas utilize different AM coding schemes: a “single mode” in A1 that relies on increased activity for AM relative to unmodulated sounds and a “dual-polar mode” in ML that uses both increases and decreases in neural activity to encode modulation. In the dual-polar ML code, nonsynchronized responses might play a special role. The results are consistent with findings in the primary and secondary somatosensory cortices during discrimination of vibrotactile modulation frequency, implicating a common scheme in the hierarchical processing of temporal information among different modalities. The time course of activity differences between behaving and passive conditions was also distinct in A1 and ML and may have implications for auditory attention. At modulation depths ≥ 16% (approximately behavioral threshold), A1 neurons' improvement in distinguishing AM from unmodulated noise is relatively constant or improves slightly with increasing modulation depth. In ML, improvement during engagement is most pronounced near threshold and disappears at highly suprathreshold depths. This ML effect is evident later in the stimulus, and mainly in nonsynchronized responses. This suggests that attention-related increases in activity are stronger or longer-lasting for more difficult stimuli in ML.

amplitude modulation (AM)—a change in amplitude envelope over time—is an important information-bearing parameter in speech recognition (Rosen 1992; Shannon et al. 1995; Smith et al. 2002; Steinschneider et al. 1999; Van Tasell et al. 1987) and in segregating sound sources in complex listening environments (Bregman et al. 1990; Fishman et al. 2012; Grimault et al. 2002; Micheyl et al. 2013). Accordingly, how auditory cortex (AC) processes AM and other temporal modulations has been studied extensively (Bendor and Wang 2007, 2010; Bieser and Müller-Preuss 1996; Eggermont 1991, 1994; Kajikawa et al. 2008; Liang et al. 2002; Lu et al. 2001; Lu and Wang 2000; Malone et al. 2007; Schreiner and Urbas 1988). Since most AC research was performed in primary auditory cortex (A1), we have yet to form a precise understanding of how temporal sound properties are processed throughout the auditory cortical network.

Macaque AC has been proposed to have three processing stages: 1) a primary stage with three core fields, 2) a secondary stage with seven belt fields, and 3) at least two parabelt fields (Kaas and Hackett 1999, 2000). This classification is based on the anatomical connections between the thalamus, core, belt, and parabelt areas (de la Mothe et al. 2006a, 2006b; Hackett et al. 1998; Morel et al. 1993; Morel and Kaas 1992; Rauschecker et al. 1997; Romanski et al. 1999b) as well as on physiological properties such as first-spike latencies (Lakatos et al. 2005; Recanzone et al. 2000a), the level of spectral integration, and response preference to pure tones and more complex sounds (Imig et al. 1977; Kosaki et al. 1997; Kusmierek and Rauschecker 2009; Lakatos et al. 2005; Petkov et al. 2006; Rauschecker et al. 1995; Rauschecker and Tian 2004; Recanzone et al. 2000a; Wessinger et al. 2001).

In addition to the three-stage hierarchical processing model, AC has been proposed to contain two parallel pathways: anterior AC for sound recognition/categorization, constituting the auditory “what” pathway, and posterior AC for auditory spatial tasks, constituting the auditory “where” pathway (Kaas and Hackett 1999, 2000; Kusmierek et al. 2012; Rauschecker and Tian 2000; Recanzone et al. 2000b; Romanski et al. 1999a, 1999b; Russ et al. 2008; Tian et al. 2001). Tian et al. (2001) have recorded single-unit responses to monkey calls presented at different spatial positions in the anterior-lateral (AL), middle-lateral (ML), and caudal-lateral (CL) belt cortices and shown that AL neurons are more selective for monkey calls than ML or CL, CL neurons have a greater spatial selectivity than AL or ML, and ML neurons show intermediate selectivity to both space and monkey calls. One interpretation of these results is that ML may be the branching point of auditory “what vs. where pathways.” ML is located immediately lateral to A1, and is heavily interconnected with A1 (Morel et al. 1993). Thus sound representations in ML may reflect a transformation one level higher than in A1.

Several studies have demonstrated that neural discrimination ability can improve when animals are actively discriminating sounds versus sitting passively (Fritz et al. 2003; Knudsen and Gentner 2013; Lee and Middlebrooks 2011). Recently, our laboratory has shown that A1 neurons' ability to discriminate AM improves with task engagement compared with a passive listening condition (Niwa et al. 2012a). Here, we examine how this behaviorally modulated improvement in neural AM discriminability evolves at the next processing stage in the auditory cortical hierarchy.

MATERIALS AND METHODS

Subjects

Two female (monkeys W and V) and one male (monkey X) adult rhesus macaque (Macaca mulatta) monkeys were used in this study. ML recording was done in the right hemisphere of monkeys W and X. A1 recording was done in the right hemisphere of all three monkeys. Some analyses from these A1 recordings have been presented previously (Niwa et al. 2012a). We only present new and more detailed analysis of the A1 data (which helps to reveal the differences between A1 and ML) in the present report. All procedures conformed to US Public Health Service (PHS) policy on experimental animal care and were approved by the UC Davis animal care and use committee.

Stimuli

Stimuli were 800-ms sinusoidally amplitude-modulated (AM) broadband noise bursts. Modulation frequencies were 2.5, 5, 10, 15, 20, 30, 60, 120, 250, 500, and 1,000 Hz. Depth sensitivity functions were collected at one fixed modulation frequency with modulation depths of 0% (unmodulated), 6%, 16%, 28%, 40%, 60%, 80%, and 100%. The unmodulated noise served as a comparison to determine how well neurons could determine whether or not a sound was modulated. For all these stimuli the noise carrier was “frozen”; the noise was created using the same random number sequence, producing a stimulus waveform that was identical on all trials, save for the modulation envelope.

Sound generation has been described previously (O'Connor et al. 2010). The sound signals were constructed with MATLAB (MathWorks), digital-to-analog (D/A) converted (Cambridge Electronic Design, model 1401), passed through programmable (TDT Systems PA5) and passive (Leader LAT-45) attenuators, amplified (Radio Shack MPA-200), and delivered to a speaker. We used two different sound booths (IAC: 2.9 × 3.2 × 2.0 m and 1.2 × 0.9 × 2.0 m) equipped with different speakers positioned at ear level. One booth had a Radio Shack PA-110 speaker 1.5 m in front of the subject, while the other had a Radio Shack Optimus Pro-7AV positioned 0.8 m in front of the subject. Sounds were generated at a sampling rate of 100 kHz and had cosine-ramped onsets and offsets with 5.0-ms rise and fall time. Sound intensity was calibrated with a sound-level meter (Bruel & Kjaer model 2231) to 63 dB sound pressure level (SPL) at the approximated midpoint of the animals' two pinnae.

Behavioral Task

The monkeys were trained to discriminate AM noise from unmodulated noise. This also can be regarded as AM detection because subjects detect whether a sound was amplitude modulated. Task specifics were as follows. First, monkeys began a trial by pressing and holding down a lever for at least 500 ms. Then, two 800-ms sounds were presented sequentially with a 400-ms intersound interval (ISI). Within a trial, the first (standard) sound was always unmodulated noise and the second sound (test stimulus) was either another unmodulated noise (nontarget) or an AM noise (target). Note that here we reserve the word “stimulus” for test sound (not the standard). During each recording session, the modulation frequency of target stimuli was set at the best modulation frequency (BMF) of the multiple-unit (MU) response from the same electrode (see Unit Recording). Target modulation depths were 6%, 16%, 28%, 40%, 60%, 80%, and 100%, presented with equal probability. Subjects were trained to release the lever in response to AM targets. They were required to wait for stimulus offset to respond and to respond within an 800-ms response window following the target stimulus offset. When the test stimulus was an unmodulated nontarget (12.5% of the trials), subjects were required to continue depressing the lever for the entire response window. Subjects were given liquid rewards for all correct responses: hits (a lever release for target trials) and correct rejections (withholding lever release for nontarget trials). We notified subjects of incorrect responses—misses (not releasing the lever on target trials) and false alarms (releasing the lever on nontarget trials)—by turning off an incandescent light placed in front of them. Subjects were also given a time-out period of 15–60 s after false alarms. This enabled us to keep the false alarm rates at the relatively low level of ∼10% as reported in Niwa et al. (2012b). Behavioral thresholds were reported in Niwa et al. (2012a).

Unit Recording

The neural recording procedures were described previously (Niwa et al. 2012a, 2012b, 2013), so we will briefly recap them here. To allow AC access, a 2.7-cm-diameter CILUX chamber (Crist Instruments) was implanted over the portion of parietal cortex immediately above AC. The chamber held a plastic grid with 27-gauge holes, covering a 15 × 15-mm area at 1-mm intervals. Each recording day, a stainless steel transdural guide tube was inserted through a grid hole. A tungsten microelectrode (1–4 MΩ, FHC; 0.5–1 MΩ, Alpha-Omega) was put through the guide tube and lowered through parietal cortex into ML or A1 by a hydraulic microdrive (FHC). During this procedure macaques were head-restrained by a titanium post. Electrophysiological signals were amplified (A-M Systems model 1800), filtered (0.3–10 kHz; A-M Systems model 1800 and Krohn-Hite model 3382), and sent to an A/D converter (CED model 1401, 50 kHz sampling rate). Action potentials were assigned to individual neurons on- and off-line with SPIKE2's (CED) waveform-matching algorithm.

At each recording site, we first determined the BMF of MU activity by presenting unmodulated noise and 100% depth, 800-ms AM noise at all modulation frequencies. Receiver operating characteristic (ROC) areas (ROCas), based on both firing rate and vector strength (VS, a measure of phase-locking), were calculated at each modulation frequency (see Neurometric analysis for details). BMF_VS was defined as the modulation frequency with the greatest VS-based ROCa, while BMF_SC was the frequency with the firing-rate-based ROCa most deviant from 0.5. The farther the ROCa from 0.5, the larger the difference between responses to AM and unmodulated noise. This means that the BMF was the modulation frequency at which the unit could best distinguish AM from an unmodulated sound. When BMF_VS and BMF_SC were different, we chose either BMF_VS or BMF_SC as the modulation frequency for the subsequent “AM sensitivity” experiment. This selection was alternated from day to day to avoid a bias toward one of the BMF measures.

After BMF determination, the AM sensitivity of single units (SUs) and MUs was assessed by collecting response vs. modulation depth functions at the BMF during two behavioral conditions: 1) while animals performed the task (behaving condition) and 2) while they were presented with the same stimuli and received randomly timed liquid rewards for sitting quietly (passive condition). The sequence of behaving and passive experiments was alternated daily to eliminate order effects. For recording, the monkeys sat in an acoustically transparent primate chair, with their head restrained to the chair, in a double-walled, sound-attenuated, foam-lined booth.

Data Analysis

Neurometric analysis.

ROC analysis (Green and Swets 1974) was used to quantify how well a neuron distinguishes AM from unmodulated noise. A detailed description of this analysis was presented in Niwa et al. (2012a), so we briefly describe it here. Neural ROCa, in our analysis, represents the neural discriminability of AM noise from unmodulated noise, the probability that an ideal observer can detect a signal (the modulation) based solely on neural responses. An ROCa of 1 (or 0) means the neural response is 100% accurate in predicting whether the sound was modulated; values of 0.5 mean the neural response can only predict at chance level whether the sound was modulated. An ROCa of 1 means the neural response to AM is always greater than the response to unmodulated noise; an ROCa of 0 means the neural response to AM is always less than the unmodulated noise response. To calculate neural ROCa, first we quantify a unit's response to AM (for example, with firing rate) for each trial to create a probability distribution of the neural measure from all repeated trials. In the same way, we also create a probability distribution for the unit's response to unmodulated sound using the same measure. From these two probability distributions, we determine the proportion of trials (P_AM) where the neural response to AM exceeds a criterion level and the proportion of trials (P_unMod) in which neural response to the unmodulated noise carrier exceeds the same criterion value. One hundred pairs of P_AM and P_unMod are determined using 100 criteria values that were selected from the full range of both distributions. P_AM, the proportion of AM trials where the neural response exceeds the criterion, is directly comparable to hit rate for behavior. P_unMod, the proportion of responses to the unmodulated noise carrier that exceed the criterion, is directly comparable to the false alarm rate. The plot of all P_AM and P_unMod pairs forms the neural ROC, and the area under this is called the neural ROCa.

All analyses were also performed with the discriminability index, d′, which also measures how well a neuron discriminates AM from unmodulated noise. d′ is the number of standard deviations separating the means of the AM and unmodulated noise response distributions. An advantage of d′ is that it is unbounded (ROCa is bounded by 0 and 1), so larger differences always result in a larger d′. This allows d′ to distinguish between well-separated distributions for which ROCa has a ceiling (or floor) effect. The disadvantage of d′ is that its relationship to behavioral performance is less straightforward than ROCa. As was seen previously in A1 (Niwa et al. 2012a), differences between behaving and passive conditions were almost always more pronounced with d′, because many neurons show ceiling or floor effects at ROCa of 1 or 0.

Phase-projected vector strength.

Vector strength (VS) measures the degree of a neuron's phase-locking, and is defined as

$$\text{VS}=\frac{\sqrt{{\left({\displaystyle {\sum }_{i=1}^n\text{cos}{\theta }_i}\right)}^2+{\left({\displaystyle {\sum }_{i=1}^n\text{sin}{\theta }_i}\right)}^2}}{n}$$ (1)

where n is the total number of spikes and θ_i is the phase of each spike in radians,

$${\theta }_i=2\pi \frac{\left(t_i\mathit{mod}\mathit{u}\mathit{l}\mathit{o}\hspace{0.17em}p\right)}{p}$$ (2)

where t_i is the time of the spike relative to the stimulus onset and p is the stimulus modulation period (Mardia and Jupp 2000).

VS has problems measuring phase-locking when the number of spikes (n) is small. When spikes are randomly distributed in time VS should be 0, but when working with a small number of spikes VS tends to give values spuriously higher than 0. For example, if a cell fires one spike on a trial, VS would be 1. If a cell fires two spikes randomly, a high VS would also likely result, because the probability that two random spikes fire 180° out of phase with each other (relative to the stimulus modulation period) is low. So for spikes occurring randomly in time, VS will tend toward nonzero values for small numbers of spikes and will get closer to 0 as the number of spikes increases. For determining ROCa, we need to calculate VS on a trial-by-trial basis. Because some SUs fire only a few spikes in a single trial, bias of VS in low-spike-count trials can become a problem.

Phase-projected vector strength (VS_pp; Yin et al. 2011) circumvents this. In determining VS_pp, first VS is calculated for each trial. Then the mean phase angle of each trial is compared with the mean phase angle of all trials (global response), and the standard VS values are penalized if they are not in agreement. VS_pp is calculated on a trial-by-trial basis as follows:

$$\mathrm{V}{\mathrm{S}}_{\mathrm{p}\mathrm{p}}=\mathrm{V}{\mathrm{S}}_{\mathrm{t}}\hspace{0.17em}\cos \left({\phi }_{\mathrm{t}}-{\phi }_{\mathrm{c}}\right)$$ (3)

where VS_t is the standard vector strength per trial, calculated as in Eq. 1, φ_t is the mean phase angle of the trial, and φ_c is the mean phase angle of global response (calculated from the unit's response to 100% AM collapsed across all repeated trials). Whereas VS ranges from 1 to 0, VS_pp may range from 1 (all spikes in phase with the mean phase of the global response) to −1 (all spikes 180° out of phase with the global mean phase), with 0 corresponding to random phase with regard to the global mean phase. Except for the cases of low spike counts, the two VS measures were in good agreement (Yin et al. 2011).

Identification of cortical areas.

ML was identified on the basis of physiological responses to tones and band-pass noise as was done previously (Niwa et al. 2013). First, pure-tone frequency tuning was assessed at (or near) each recording site by varying tone frequency and intensity. An initial estimate of the best frequency (BF) of the site was used to determine the range for the automated procedure where frequencies typically spanned three octaves (usually in 1/5-octave steps) centered on the initial BF estimate, and intensities typically spanned 80 dB with a 10-dB steps between 10 and 90 dB SPL. Tones (100 ms) were presented in a random order and repeated at least twice for each frequency-intensity combination. From a two-dimensional response matrix, the neuron's frequency tuning curve was obtained with the contour line (MATLAB's “contourc” function) at the mean spontaneous rate plus 2 standard deviations. The BF and threshold were determined from this frequency tuning curve. A tonotopic map was created for each animal from the BFs. We determined the location of A1 based on a systematic BF increase from anterior to posterior and approximately constant BF along the medial-lateral axis. The border of A1 and ML was determined based on the lack of response robustness to tones, slower tone response latency, and wider width of frequency tuning for ML locations (Kosaki et al. 1997; Merzenich and Brugge 1973; Morel et al. 1993; Rauschecker et al. 1997; Recanzone et al. 2000a). Putative ML was identified as a narrow strip of 2- to 3-mm width located lateral to the physiologically determined A1/ML border.

When time permitted, we also recorded unit responses to 100-ms band-pass noise (BP noise) having various center frequencies, filter widths (1/3, 1/2, 1, and 2 octaves), and intensities. Intensities typically were the same as for frequency tuning. BP noises were presented in random order and repeated one to three times for each combination of center frequency, filter width, and intensity depending on the available time. Firing rate was calculated with the 0–100 or 0–150 ms window after stimulus onset depending on the response profiles at each recording site. A two-dimensional response matrix (intensity × frequency) was obtained for each filter width size. The frequency tuning curve was estimated in the same way as above for each filter width size, and the BF and the preferred filter width size were determined. The anterior-posterior border of ML (the borders with AL and CL) was estimated with a systematic change in BF using BP noise tuning.

RESULTS

We recorded spiking activity from 57 MUs and 97 SUs in ML of monkeys W and X while they discriminated AM (behaving condition) and while they were passively presented the same AM stimulus set (passive condition). These results were compared to 57 MUs and 142 SUs recorded from A1 of monkeys V, W, and X.

Effect of Engagement on ML Neuron Rate-Based AM Discriminability Depends on Time Period of Stimulus Presentation

Animals' engagement in AM discrimination affects ML neurons' AM discriminability differently during the first (0–400 ms) and second (400–800 ms) halves of the test stimulus. This is exemplified by three ML neurons whose responses are depicted in Figs. 1–3. The neuron in Fig. 1 shows improvement in firing rate-based AM discriminability due to task engagement during the first half of the test stimulus but deterioration during the second half. The neuron in Fig. 2 shows a change in its firing rate response characteristics to modulation depth from monotonically increasing during the first half to nonmonotonic during the second. The neuron in Fig. 3 shows a change in its firing rate response characteristics to modulation depth, from monotonically increasing during the first stimulus half to monotonically decreasing during the second half.

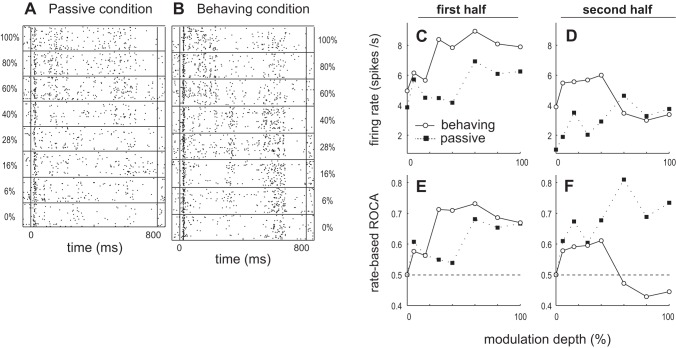
Fig. 1.

Example of the activity of a middle lateral belt (ML) single unit (SU) showing improvement in firing rate-based amplitude modulation (AM) discriminability due to task engagement during the 1st half of the test stimulus but deterioration during the 2nd half. A and B: raster plots of a SU response to 30-Hz AM as modulation depth is varied from 0% (bottom) to 100% (top) in the passive (A) and behaving (B) conditions. C and D: average firing rate during the 1st (C) and 2nd (D) halves of the stimulus plotted as a function of modulation depth for passive and behaving conditions. E and F: receiver operating characteristic (ROC) area (ROCa) based on firing rate during the 1st (E) and 2nd (F) halves of the stimulus plotted as a function of modulation depth for passive and behaving conditions. Neural ROCa yields the probability that an ideal observer would detect modulation based solely on the neural responses. An ROCa of 0.5 corresponds to chance performance. The farther ROCa is from 0.5, the better the neuron is at discriminating AM from an unmodulated sound. An ROCa of 1 or 0 = perfect AM detection, where 1 indicates higher firing rates for modulated sounds than to the unmodulated sound and 0 indicates lower firing rate to modulated sounds.

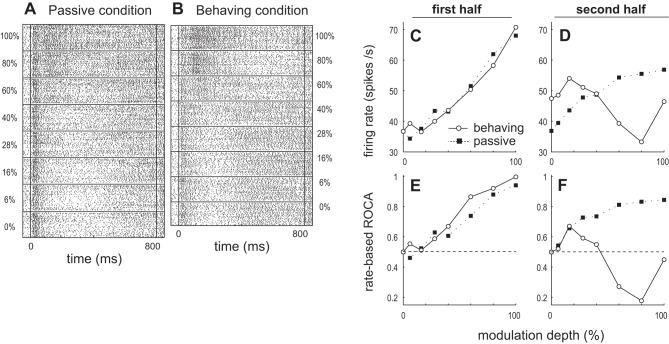
Fig. 3.

Example of an ML SU that shows a change in its firing rate response characteristics to modulation depth from monotonically increasing during the 1st stimulus half to monotonically decreasing during the 2nd half. Data are presented in the same format as Fig. 1.

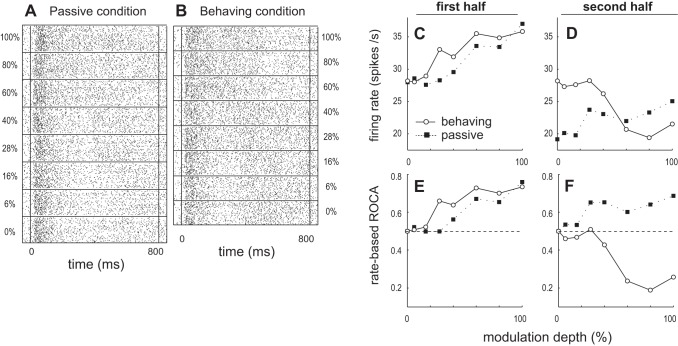
Fig. 2.

Example of an ML SU that shows a change in its firing rate response characteristics to modulation depth from monotonically increasing during the 1st stimulus half to nonmonotonic during the 2nd half. Data are presented in the same format as Fig. 1.

For the ML SU in Fig. 1, in the passive condition the firing rate increases with depth during both first and second halves of the stimuli (Fig. 1, C and D). In the behaving condition the dependence of firing rate on modulation depth appears different than in the passive condition. During the first half, the firing rate roughly increases monotonically with depth (Fig. 1C), as in the passive condition. During the second half, firing rate decreases with increasing depth in the behaving condition (Fig. 1D). The decrease during behavior is largely due to increased activity 500–650 ms after stimulus onset for 0–40% depth in the behaving condition (Fig. 1B), which lessens at higher depths. This pattern of activity between 500 and 650 ms is not seen in the passive condition (Fig. 1A).

During the first half of the stimulus the neuron can better discriminate AM in the behaving than the passive condition. When the SU's firing rates during 0–400 ms in the behaving and passive conditions are compared, the rate response to both unmodulated noise and low-modulation-depth AM (0–16%) is slightly greater in the behaving than passive condition (Fig. 1C). However, at higher modulation depths (particularly at 28–40%) firing rate increases much more in the behaving condition (Fig. 1C). As a result, in this 400-ms window this SU exhibits greater response differences between AM and unmodulated noise in the behaving than the passive condition (Fig. 1C). This suggests that engagement in the AM task improves neural AM discrimination at modulation depths > 16% (which is approximately behavioral threshold) during this portion (the first 400 ms) of the stimulus, which is supported by neurometric analysis (Fig. 1E).

In contrast to the first half of the stimulus, this SU better discriminates AM from unmodulated noise in the passive condition during the second half of the stimulus (Fig. 1F). From 400 to 800 ms after stimulus onset, the response to unmodulated noise was still higher in the behaving than the passive condition, but the response to 60–100% AM was quite similar in both behaving and passive conditions (Fig. 1D). The result is that, during behavior, the firing rate response to 60–100% AM is slightly less than the firing rate response to unmodulated noise during the second half of the stimulus (the last 3 open circles, at 60–100%, are slightly less than first open circle, at 0%, in Fig. 1D). This leads to poorer neural discrimination ability (points closer to ROCa = 0.5) during the second half in the behaving than the passive condition. The neurometric functions appear to show that the neuron weakly discriminates AM with increased firing rate relative to the unmodulated noise response at low depths and with decreased activity relative to the unmodulated noise response at higher depths. This is seen in Fig. 1F as ROCa > 0.5 for 6–40% and < 0.5 for 60–100%. However, these points are all relatively close to ROCa = 0.5.

Figure 2 shows an example neuron that during the 2nd half of the stimulus discriminates AM with increased firing rate relative to the unmodulated noise response at low depths and with decreased activity relative to the unmodulated noise response at higher depths. In this example a permutation test showed that ROCa was significantly above 0.5 in the behaving condition during the second half at 16% depth and significantly below 0.5 at 60 and 80% depths. In the passive condition, this SU and the SU in Fig. 3 monotonically increase firing rate with modulation depth during early and late portions of the stimulus period (Figs. 2 and 3, C and D). Again, in the behaving condition, these SUs monotonically increase firing rate with depth only during the first half of the stimulus (Fig. 2C, Fig. 3C) and not in the second half (Fig. 2D, Fig. 3D). Also during the first 400 ms AM discrimination is better in the behaving condition (Fig. 2E, Fig. 3E), but comparisons of neural discriminability during the 400–800 ms period after stimulus onset are more complicated. The SU in Fig. 3 decreases firing rate relatively monotonically with depth (Fig. 3F). For all three example neurons, firing rate during the 400–800 ms period is greater in the behaving (than passive) condition for 0–40% AM and smaller in the behaving condition for 60–100% AM (Fig. 1D, Fig. 2D, Fig. 3D).

ML Population Summary: Behavioral State Affects Rate-Based AM Discriminability Differently for Neurons with Increasing and Decreasing Rate-Depth Functions

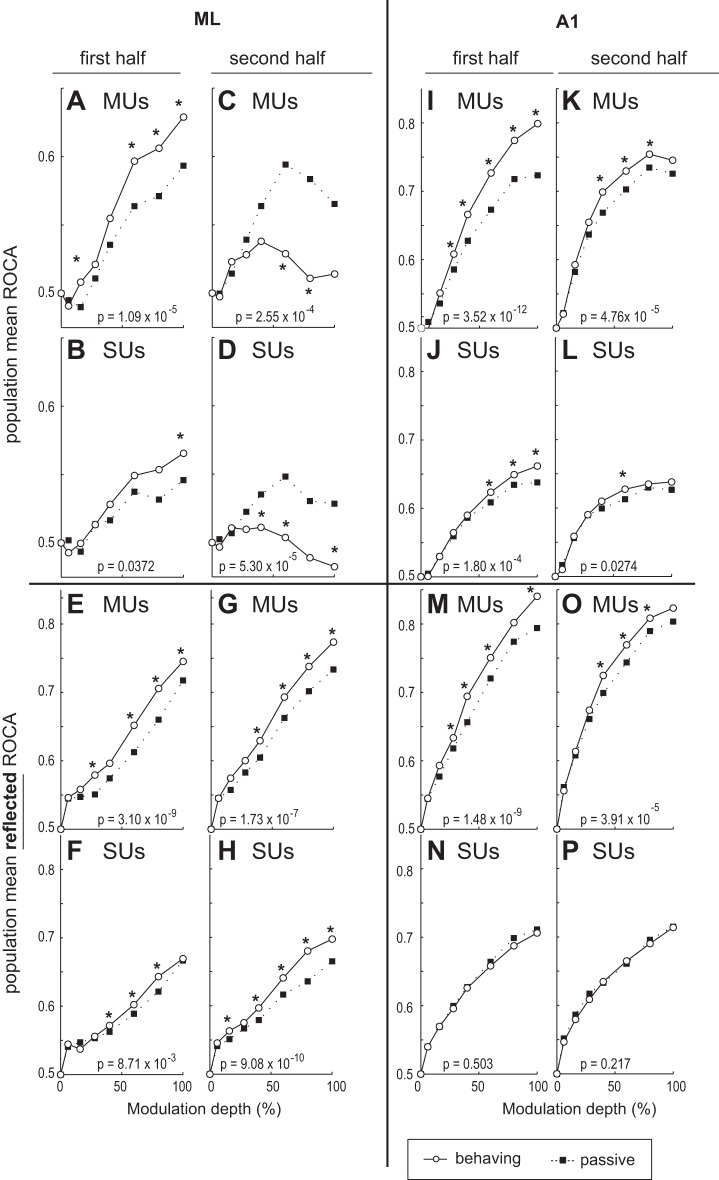
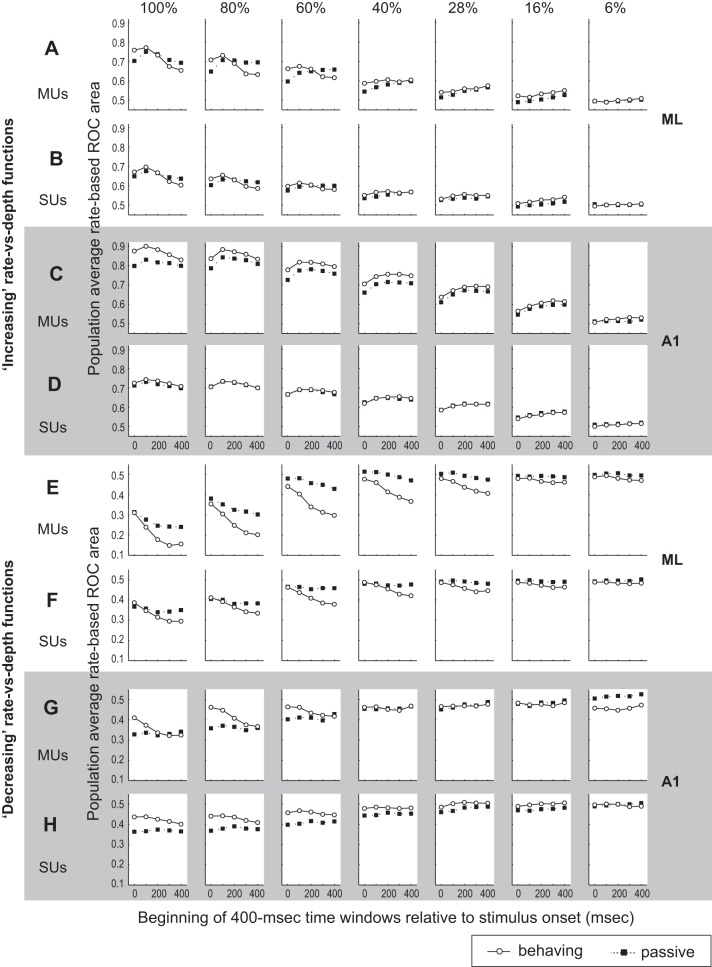
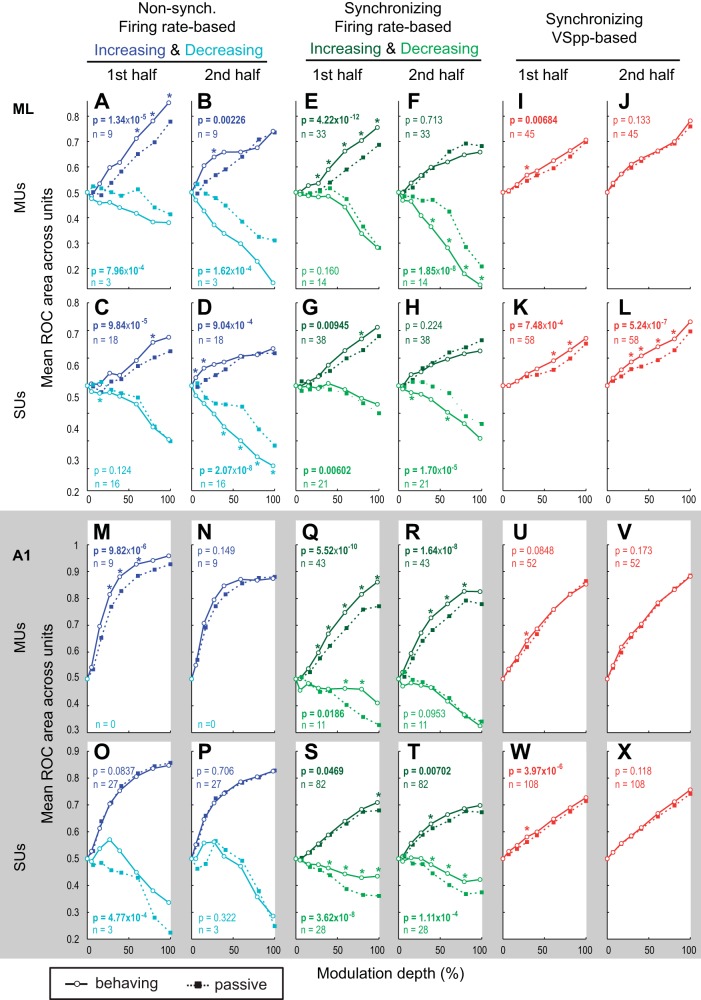
For the entire ML population, the dependence of performance on task engagement is strikingly different during the stimulus's first and second halves. During engagement, neuronal AM sound discrimination improves during the first half and worsens during the second half of the stimulus (Fig. 4, A–D). During the first half, firing rate-based ROCa is significantly greater in the behaving than the passive condition for MUs (Fig. 4A) and SUs (Fig. 4B). On the other hand, during the second half, ML ROCa is significantly worse in the behaving condition (Fig. 4, C and D). Note that Fig. 4, A–D, have a smaller scale than the rest of Fig. 4 to better display ML differences between behaving and passive conditions. Figure 4, A–D, appear to show that task engagement significantly improves rate-based AM discriminability during the first half of the stimulus but significantly impairs it during the second half. This differs from A1, where 1) ROCa monotonically increased with modulation depth for behaving and passive conditions and 2) population ROCa increased for all depths (although not significantly at all depths) in the behaving compared with the passive condition for both halves (albeit smaller improvements were seen for the second half in the behaving compared with the passive condition; Fig. 4, I–L).

Fig. 4.

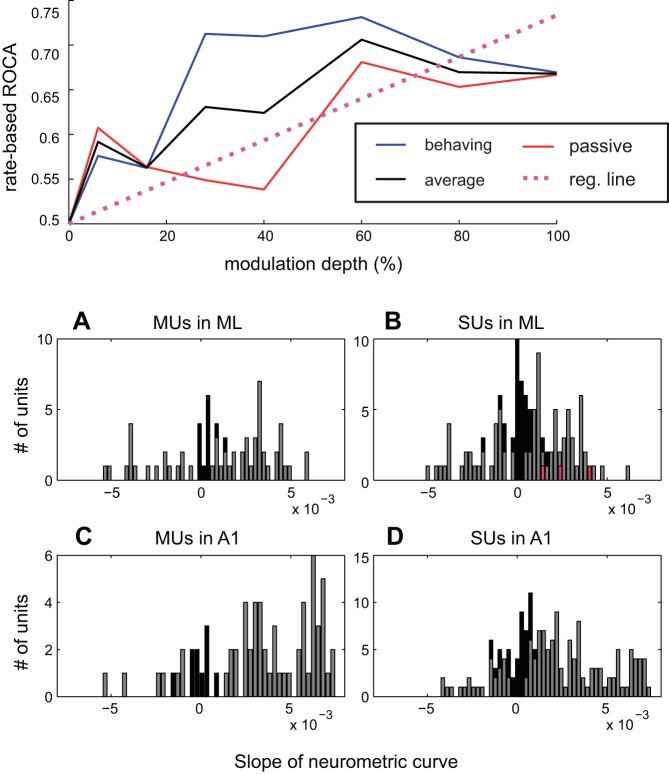
Population ROCa-depth functions for 1st and 2nd halves of the test stimulus in ML and primary auditory cortex (A1) neurons. A and B: ML population mean ROCas based on firing rate during the 1st half of the stimulus plotted as a function of modulation depth for the passive and behaving conditions for all recorded multiunits (MUs; A) and SUs (B) in ML. C and D: population mean, rate-based ROCas for the second 400 ms of the stimulus are shown for MUs (C) and SUs (D). E–H: plots are the same as in A–D except that ROCa is reflected around 0.5. This means the y-axis shows the absolute value of the difference in ROCa from 0.5. So, for example, an ROCa of 0.4 → reflected ROCa of 0.6 and an ROCa of 0.1 → reflected ROCa of 0.9, etc. I–L are the same as A–D except for A1. M–P are the same as E–H except for A1. In all panels, P values denote Wilcoxon signed-rank test comparing collapsed-depth ROC areas between behaving and passive conditions. *Individual modulation depths where a Wilcoxon signed-rank test yielded a value of P < 0.05.

However, when we consider the potential contribution of neurons that encode modulation by decreasing firing for modulated sounds, a different picture emerges. The farther ROCa is from 0.5, the better a unit is at discriminating a modulated from an unmodulated sound. An ROCa of 1 means perfect ability to discriminate AM from an unmodulated sound with increased firing rate for AM; an ROCa of 0 means perfect ability to discriminate AM from an unmodulated sound with decreased firing rate for AM. Therefore reflecting ROCa around 0.5 (Fig. 4, E–H and M–P) for each neuron reveals how well they discriminate AM from an unmodulated noise adjusting for neurons that encode AM with decreased activity. It should be noted that mathematically this is similar to taking the absolute value, so all ROCas will increase, just as the mean of a series of positive and negative numbers will always be smaller than the mean of their absolute values. What is important in Fig. 4, E–H and M–P, is how differences between active and passive change with reflection and how shapes of functions change. When we reflect ROCa in ML, we see significant improvement during the first, and now also during the second, half (Fig. 4, G and H) of the stimulus. Also, the function monotonically increases for reflected ROCa as opposed to the nonmonotonic functions for ROCa (Fig. 4, C and D). For A1, reflecting ROCa (compared to not reflecting) resulted in smaller or no improvements in the passive compared with the behaving condition (Compare Fig. 4, I to M, J to N, K to O, and L to P). We further probe this by analyzing population mean ROCas separately for increasing and decreasing cells, which will allow a clearer picture to emerge.

Separately analyzing cells whose firing rate either increases or decreases as a function of modulation depth is important to understand possible neural codes for AM. In ML some neurons increase firing rate with increasing modulation depth while others decrease firing rate with depth, but most A1 neurons increase firing rate with modulation depth and few decrease (Niwa et al. 2013). The brain could use the ML information for AM discrimination by separately decoding increasing and decreasing functions as two complementary populations of neurons (or subtracting them). Improved AM discriminability for neurons with increasing rate-depth functions would result in increased ROCa (from 0.5), while for neurons with decreasing rate-depth functions improved AM discrimination would yield decreased values below 0.5. If both populations show AM discrimination improvement, the net effect on ROCa of the summed activity across the entire population of neurons would be reduced because the increase in ROCa from cells with increasing functions would cancel the decrease in ROCa by cells with decreasing functions. Therefore, population summaries are presented separately for increasing and decreasing rate functions as well as for the entire ML population, i.e., combining “increasing” and “decreasing” cells (where an increasing cell refers to a neuron with an increasing rate-depth function).

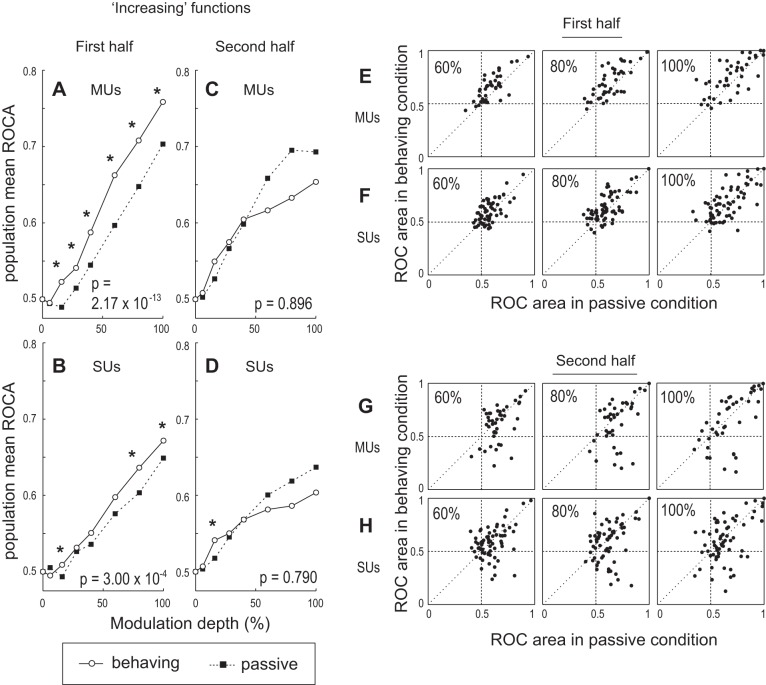
Before showing the population summary for increasing and decreasing functions, we need to discuss how these two groups are defined. As shown by the three SU examples (Figs. 1–3), the slope of neurometric curves for one neuron can change signs between the first and second stimulus halves and between behaving and passive conditions. Since a neuron's response depends on both the time during the stimulus and task conditions, we needed a way to estimate their composite response to modulation depth. To do this, we first created a neurometric firing rate-based ROCa-depth function during the entire stimulus separately for behaving and passive conditions. We then averaged the two functions and calculated the slope with linear regression (Fig. 5, top). We defined a response as “increasing” if it had a positive slope and “decreasing” if it had a negative slope. It is important to note that increases in ROCa from 0.5 correspond to increases in firing rate and decreases in ROCa from 0.5 are decreases in firing rate. All ROCa-depth curves start at 0.5 for 0% depth by definition, so an increasing ROCa-depth curve also would result in an increasing firing rate-depth curve (and vice versa for decreasing). The SU examples from Figs. 1–3 are shown in red in Fig. 5, and all had positive slopes (Fig. 5B; Figs. 1, 2, and 3 neurons' slopes = 0.0023, 0.0041, and 0.0015, respectively). The distribution of the slopes is shown for MUs (Fig. 5A) and for SUs (Fig. 5B) in ML, where 72% of the MU and 63% of the SU recordings had increasing functions. For comparison, the distribution of slopes is also shown for MU (Fig. 5C) and SU (Fig. 5D) recordings in A1, where 81% of MU and 78% of SU recordings had positive slopes. The slope magnitudes in ML were significantly lower than in A1 (P = 0.0013, rank sum test), and the proportion of increasing SU functions in ML was significantly lower than in A1 (P = 0.0067, χ²).

Fig. 5.

Top: demonstration of how the neurometric slope was calculated. A–D: distributions of the slopes of neurometric (ROCa vs. modulation depth) functions by linear regression for MUs in ML (A), SUs in ML (B), MUs in A1 (C), and SUs in A1 (D). The slopes of the 3 examples of Figs. 1–3 are shown in red (Fig. 1 neuron's slope = 0.0023, Fig. 2 neuron's slope = 0.0041, Fig. 3 neuron's slope = 0.0015).

For the population of increasing units in ML, AM discriminability is significantly better in the behaving than the passive condition during the first half (0–400 ms) of the stimulus. During this period, MU firing rate-based ROCa is significantly greater in the behaving than the passive condition for 16–100% AM (Fig. 6A). SUs were also more sensitive in the behaving condition, although fewer depths reached significance (Fig. 6B). To test the overall effect of task engagement, ROCa data were combined across depths in each condition, and a single Wilcoxon signed-rank test was performed. For MUs and SUs, we found a significant increase in across-depth, rate-based ROCa in the behaving compared with the passive condition (Fig. 6, A and B), indicating that task engagement significantly improves neuronal AM discriminability in the first half of the stimulus for increasing cells.

Fig. 6.

Summary of AM discrimination ability for the population of ML cells with increasing rate vs. modulation depth functions. A–D: data are presented in the same format as in Fig. 4, A–D. *Individual modulation depths where a Wilcoxon signed-rank test yielded a value of P < 0.05. P values at bottom right are the P values obtained by collapsing data across all depths. E and F: scatterplots of firing rate-based ROCas during 1st half of the stimulus for 60% (left), 80% (center), and 100% (right) AM for MUs (E) and SUs (F). Each unit's ROCa in the passive condition is plotted on the x-axis and that for the behaving condition on the y-axis. G and H: same as E and F but for ROCa during 2nd half of stimulus. Diagonal line is where ROCa is equal for both conditions, and the quadrants are marked at ROCa = 0.5.

On the other hand, during the second half of the test stimulus there was no significant change in ROCa between the behaving and passive conditions at any individual depth or collapsed over depths for MUs and SUs with increasing rate-depth functions, except for a small difference at 16% (P = 0.0179) for SUs (Fig. 6D). Although no statistically significant difference in ROCa was found between the behaving and passive conditions at high modulation depths (60–100%) during the second half, the population mean ROCa in the behaving condition at these depths appears lower than the ROCa in the passive condition (Fig. 6, C and D). The lack of a significant difference might be due to the large unit-to-unit variability in the change in ROCa between the two conditions. Fig. 6, E and G (MUs) and F and H (SUs), show pairwise comparisons of ROCa between the behaving and passive conditions for all increasing MUs and SUs at 60%, 80%, and 100% depths. Each point on these plots represents a unit, whose ROCa in the behaving condition is given on the y-axis and the passive ROCa on the x-axis. Points falling on the diagonal line indicate no change in ROCa between the two conditions. Points above the diagonal line indicate increased ROCa in the behaving compared with the passive condition, and those below indicate a decrease during behavior. During the second half of the stimulus, points are spread widely across the diagonal line (Fig. 6, G and H), showing unit-to-unit variability in how ROCa changes between the two conditions. However, some neurons' ROCas lie far below the diagonal line, falling into the bottom right quadrant of the plots. These units are largely responsible for pulling down the population mean ROCa for the behaving condition. Units lying in this quadrant fire less to AM than to unmodulated noise in the behaving condition (ROCa < 0.5) but fire more to AM than to noise in the passive condition (ROCa > 0.5); they flip the sign of their response to AM from “positive” (excitatory) in the passive condition to “negative” (suppressive) in the behaving condition during the second half of the stimulus. It is important to remember that classifying a unit's response as increasing or decreasing is based on averaging ROCa for behaving and passive conditions over the entire 800-ms stimulus, which explains why units that decrease during the final 400 ms in the behaving condition can be classified as increasing. The examples shown in Figs. 1–3 are representative of SUs that decrease their activity during the second half of the test stimulus only in the behaving condition (see Figs. 1–3). Interestingly, when the same scatterplots are made for the first half of the stimulus (Fig. 6, E and F), few points fall into the fourth quadrant, suggesting that the reversal of response sign occurs only later during the test stimulus. This effect may occur because AM at the highest modulation depths can be discriminated very easily, and the decision to respond may be made during the stimulus. Also, the fact that the animals are not permitted to respond until after stimulus offset, requiring them to suppress early behavioral responses to AM at higher depths, may cause sustained inhibition of firing to these AM stimuli as the test stimulus continues in time.

For the population of ML units with decreasing rate-depth functions, AM discriminability is significantly better in the behaving than the passive condition during the second half of the stimulus (Fig. 7, C and D); during the first half the effect is weaker for MUs (Fig. 7A) and nonexistent for SUs (Fig. 7B). Remember that for decreasing units lower ROCa (toward 0) means better AM discriminability. During the first half, MU firing rate-based ROCa is significantly lower in the behaving than the passive condition, but the effect is relatively small and limited to near-threshold depths (Fig. 7A). During the second half of the stimulus, MU rate-based ROCa is significantly lower (better) in the behaving than the passive condition at most depths above behavioral threshold (Fig. 7C). For SUs, engagement in the task significantly improves AM discriminability only during the second half of the test stimulus (Fig. 7D).

Fig. 7.

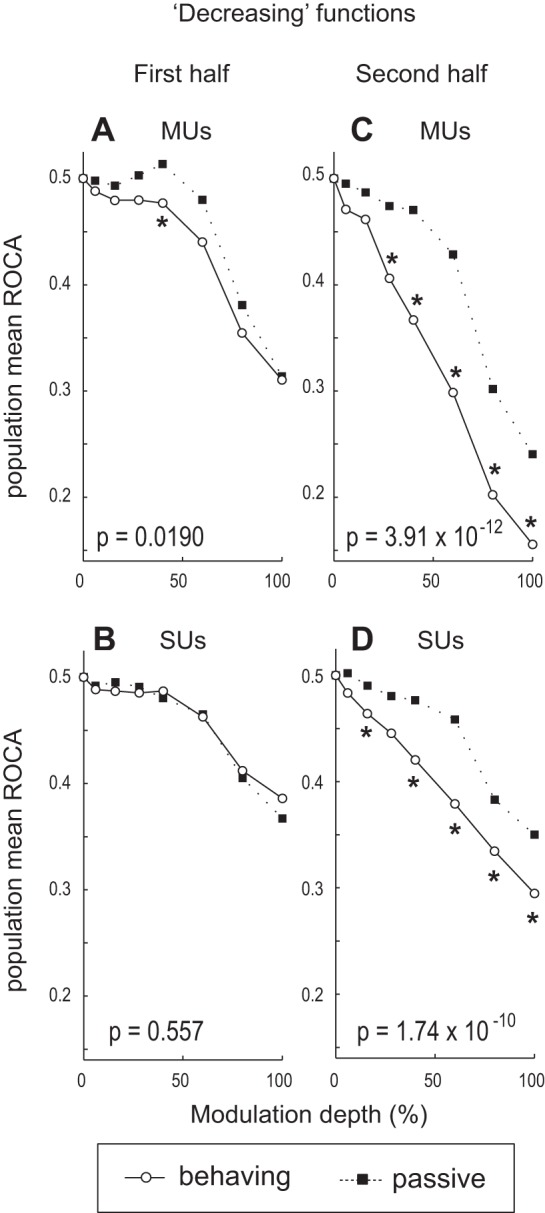
Summary of AM discriminability for the population of ML cells with decreasing rate vs. modulation depth functions. A–D: data are presented in the same format as in Fig. 6, A–D.

Together, these results demonstrate that rate-based AM discriminability for ML cells with increasing rate-depth functions improves under conditions of active engagement early during the stimulus, but the improvement disappears later (Fig. 6). On the other hand, the improvement in rate-based AM discriminability for ML cells with decreasing functions is more pronounced later during the stimulus (Fig. 7).

Comparison of Change in Rate-Based AM Discrimination Over Time Between A1 and ML

We conducted ROC analyses using several time windows for A1 and ML and found that 1) the AM discriminability of cells with increasing rate-depth functions in the behaving condition is more strongly dependent on the time course of stimulus presentation in ML than in A1 and 2) engagement in the AM task affects the AM discriminability of cells with decreasing functions differently in A1 and ML. For this analysis, rate-based ROC areas were calculated with 400-ms time windows beginning at 0, 100, 200, 300, and 400 ms after stimulus onset to determine the change in AM discriminability over time.

For ML increasing units, the discriminability of 100–60% AM stimuli in the behaving condition declines as the time window slides from the start to the end of stimulus presentation for both MUs (Fig. 8A) and SUs (Fig. 8B). Note that the ML population mean AM discriminability in the behaving condition over time actually becomes worse than in the passive, as indicated by the crossing of the two plots (60%-100% depth). In contrast to ML, A1's rate-based AM discriminability at higher depths in the behaving condition always stays at or above the level seen in the passive condition [Fig. 8, C (MUs) and D (SUs)]. The decline in AM discriminability over time in ML in the behaving condition is absent for 6–40% AM stimuli (Fig. 8, A and B). Instead, AM discriminability in the behaving condition appears constant or improves slightly over the time course of stimulus presentation.

Fig. 8.

ROCas (based on firing rate) are calculated in 400-ms time windows starting at various times (0, 100, 200, 300, and 400 ms) after stimulus onset. A–D: population mean rate-based ROC area of “increasing” cells plotted as a function of start time of the windows at each modulation depth (from 100% on left to 6% on right) for the passive and behaving conditions for MUs in ML (A), SUs in ML (B), MUs in A1 (C), and SUs in A1 (D). E–H: population mean rate-based ROCa of “decreasing” cells plotted as a function of start time of the time windows at each modulation depth (from 100% on left to 6% on right) for the passive and behaving conditions for MUs in ML (E), SUs in ML (F), MUs in A1 (G), and SUs in A1 (H).

For ML decreasing units, the population mean ROCa in the behaving condition declines steeply toward 0 as the time window slides from the start to the end of stimulus for both MUs (Fig. 8E) and SUs (Fig. 8F). The decline of ML ROCa in the passive condition is not as steep as in the behaving condition. The result is an increase in the difference in ROCa between these two conditions over time; the improvement in AM discriminability due to engagement in the task is greater later during the stimulus at all depths, for both MUs and SUs (recall that lower ROCa means better discriminability for decreasing units). For A1 decreasing units, the population mean ROCa at 60–100% depth in the behaving condition also declines toward 0 as the time window slides from the start to the end of stimulus (Fig. 8, G and H), while a decline is not clearly seen for the passive condition. The key difference between A1 and ML is that for decreasing functions in A1 ROCa at 60–100% depths in the behaving condition starts much worse (closer to 0.5) than in the passive condition early during the test stimulus and goes toward the passive level over time. Thus in A1 AM discriminability during the early stimulus period is worse in the behaving than the passive condition and improves toward the passive level over time. In ML decreasing functions at higher depths, ROCas for behaving and passive conditions are similar early in the stimulus and over time the behaving condition gains an advantage.

The aggregate results of Fig. 8 suggest that, in ML, decreasing cells improve their AM discriminability throughout the test stimulus, although the improvement is larger later. One interpretation is that in ML both increasing and decreasing cells are suitable and relevant for encoding AM depth.

Rate Response to Unmodulated Noise Increases Later During Stimulus, Causing ROC Areas to Decrease Over Time

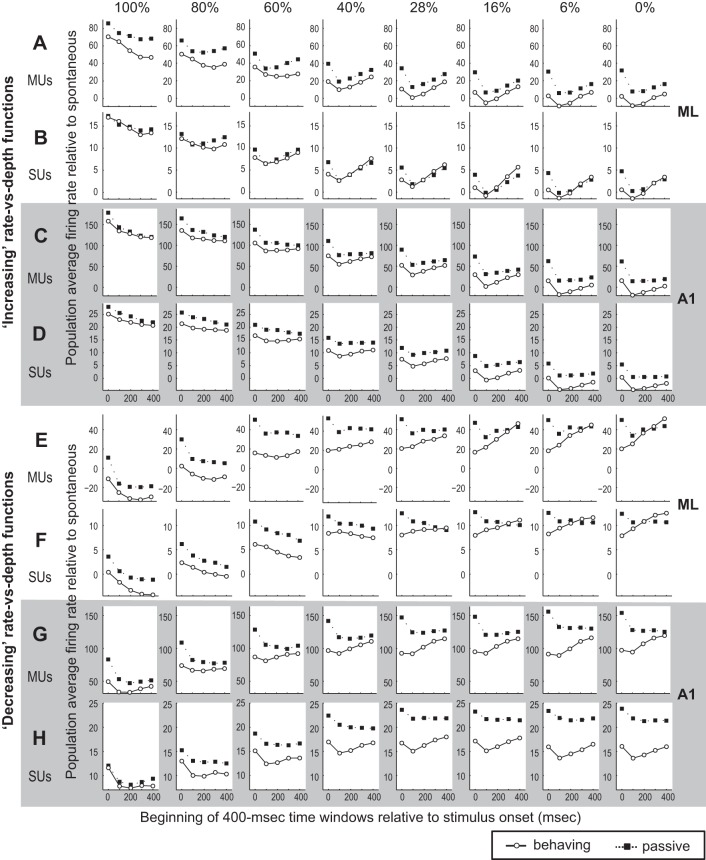
Our analysis revealed that in ML ROCas in the behaving condition appear to decrease over time at a faster pace than in the passive condition. This is true for higher modulation depths and for units with both increasing and decreasing rate-depth functions. The ROCa quantifies the overlap between firing rate distributions in response to AM and unmodulated noise, but it does not explicitly tell us what caused the decline in ROCa. Two possible sources that can cause ROCa to decline are 1) decreased firing rate in response to AM and/or 2) increased firing rate in response to unmodulated noise. The results presented below indicate that the increase in the response to unmodulated noise over time is a major contributor to the decline in ROCa in the behaving condition.

The population average firing rate (relative to spontaneous rate) in the behaving and passive conditions was analyzed with the same time windows as in Fig. 8 and shown separately for cells with increasing (Fig. 9, A–D) and decreasing (Fig. 9, E–H) rate-depth functions. For ML increasing units the population mean firing rate in the behaving condition shows a decrease over time in response to 60–100% AM for MUs (Fig. 9A), while the rate decrease in the passive condition is lesser than in the behaving condition. Thus this difference can contribute to the faster decline in ROCas (steeper slope in curves of Fig. 8) for the behaving condition compared with the passive condition (Fig. 8A). For SUs, the change in population mean firing rate in response to AM at higher modulation depth is similar between behaving and passive conditions (Fig. 9B for SUs), and it seems unlikely that the firing rate change to these AM stimuli is the sole cause of the faster decline (steeper slope) in ROCas in the behaving condition. In response to unmodulated noise (0%), the population average firing rate drops after the 0–400 ms time window, which includes the onset response, then increases over time in both behaving and passive conditions (Fig. 9, A and B). However, the slope of the increase is steeper in the behaving than passive condition for both MUs and SUs. This differential rate of increase for firing rate over time for unmodulated noise in behaving and passive conditions (Fig. 9, A and B, 0%) likely contributes to the steep decline in population average ROCa in the behaving condition for ML cells with increasing functions at higher (60–100%) modulation depths (Fig. 8, A and B).

Fig. 9.

Firing rate relative to spontaneous rate is calculated in 400-ms time windows starting at various times (0, 100, 200, 300, and 400 ms) after stimulus onset. Layout is the same as Fig. 8 except that firing rate rather than ROCa is shown. The firing rate in response to unmodulated noise (0%) is included here, and changes in this contribute to changes in the neuron's ability to detect AM.

For ML cells with decreasing functions, the population average firing rate for unmodulated sound (0%) also increases steeply over time in the behaving condition, while the rate increase is less obvious in the passive condition [Fig. 9, E (MUs) and F (SUs)]. This steep increase in response to unmodulated noise over time (Fig. 9) likely contributes to the steep decline of population average ROCas in the behaving condition for decreasing ML units (Fig. 8, E and F).

In A1, we also observe a similar firing rate increase over time in response to unmodulated noise in the behaving condition for both increasing and decreasing units (Fig. 9, C, D, G, and H). Thus this property—increased responses to unmodulated noise late in the behaving condition—seems general because it is common to both A1 and ML. Note that we also observe a similar increase in firing rate at lower modulation depths (6–28%), suggesting that the increased activity over time may be related to difficulty in detecting AM in these stimuli (also refer to Figs. 1–3).

Which Area Discriminates AM Better Based on Firing Rate: ML or A1?

In addition to the difference in time dependence of AM discriminability, A1 and ML show a significant difference in the overall level of AM discriminability. For increasing units, rate-based ROCa in A1 is significantly greater than that in ML for both MUs and SUs, during both the first and second halves of the test stimulus and in both behaving and passive conditions. In Fig. 10, this can be seen as the increasing functions for all time periods having values significantly greater than 0 at all suprathreshold depths for all four conditions. In contrast, ML only shows an advantage in discrimination for decreasing units during the second half in the behaving condition, while no significant difference between A1 and ML was found for decreasing units during the first half in the behaving condition. In the passive condition, ROCa for 28% AM for decreasing MUs and 60% AM for decreasing SUs was significantly better in A1 than in ML during the first half of the test stimulus, while a significant difference was not found during the second half. Note that in Fig. 10 the scale is twice as large for MUs, reflecting that ROCa differences between A1 and ML were roughly twice as large for MUs as for SUs. The aggregate results show that engagement in the AM task worsens the AM discriminability of decreasing neurons in A1 but improves that of ML decreasing neurons, especially during the later portion of the stimulus, making AM discriminability in ML better than A1 during the later time period. This also implicates the importance of a decreasing rate code in ML but not in A1.

Fig. 10.

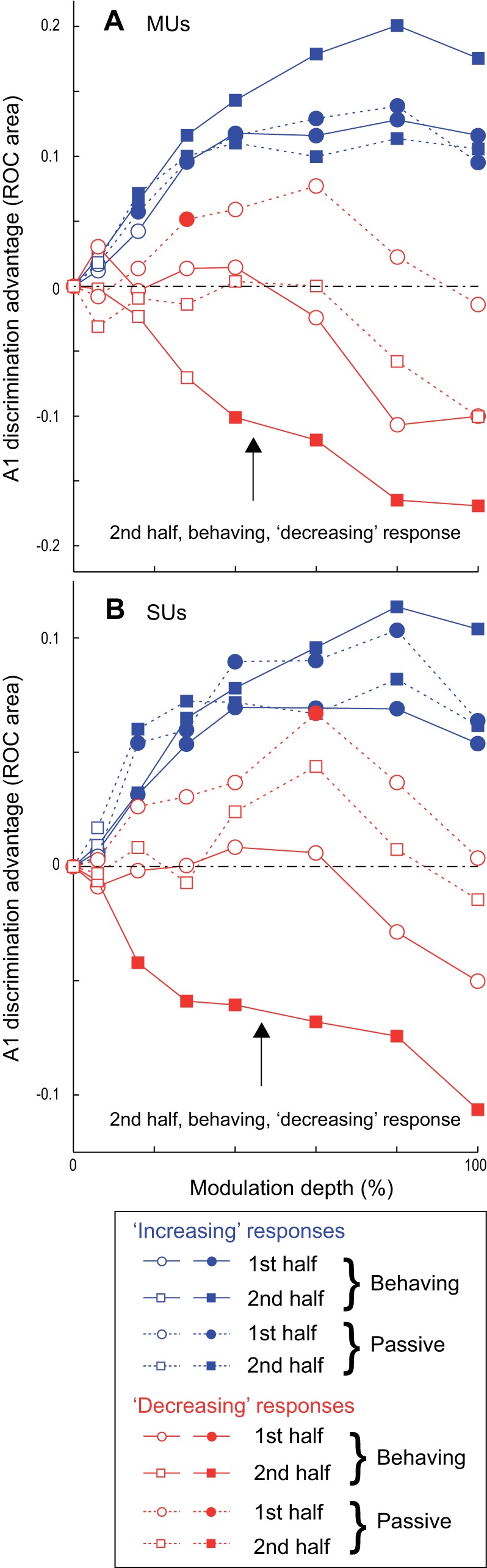
Plot showing the advantage of A1 neurons' ability to discriminate AM compared with ML. For increasing units this is calculated by subtracting ML mean ROCa from A1 ROCa (A1 − ML). Therefore higher values mean that A1 neurons can better discriminate AM than ML neurons. For decreasing units this is calculated by subtracting A1 mean ROCa from ML ROCa (ML − A1). This is required because for decreasing units lower ROCas correspond to better discrimination ability. This was done for both MUs (A) and SUs (B) in the 8 conditions noted in the key. The conditions were created by splitting 3 categories (increasing vs. decreasing, behaving vs. passive, and 1st vs. 2nd half) into the 8 combinations. Filled symbols represent points with significant differences between A1 and ML by a 2-sample t-test (P < 0.05); open symbols represent values not significantly different between A1 and ML.

VS_pp-Based AM Discriminability in ML Improves Because of Animals' Engagement in AM Discrimination Task

We examined whether AM discrimination based on phase-locking improves when animals engage in the AM discrimination task. VS_pp was used as a measure of phase-locking (see materials and methods for details). Figure 11 shows an example SU in ML with improved VS_pp-based AM discrimination due to task engagement. The SU robustly phase-locks to 20-Hz AM at higher modulation depths (Fig. 11, A and B). VS_pp was calculated for each trial in the time window with onset response excluded (time window = 80–800 ms). Trial-averaged VS_pp increased in the behaving condition compared with the passive condition at all depths except 28% and 0% (Fig. 11C). VS_pp-based ROCa increased in the behaving compared with the passive condition at all modulation depths (Fig. 11D), indicating that the AM discrimination based on phase-locking improved for this SU when the animal engaged in the AM task.

Fig. 11.

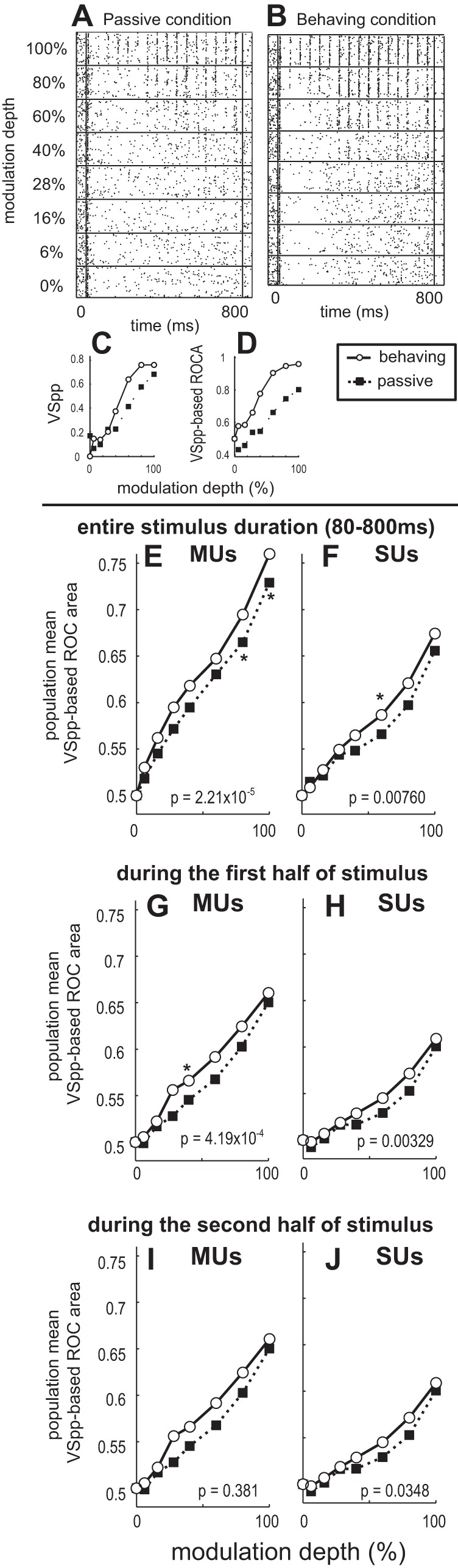
Improved neural discrimination in the behaving compared with the passive condition using vector strength (VS). A–D: example of ML SU that improved phase-locking in the behaving condition. A and B: raster plots of SU response to 15-Hz AM in the passive (A) and behaving (B) conditions. C: phase-projected vector strength (VS_pp) plotted as a function of modulation depth for the passive and behaving conditions. D: ROCa based on VS_pp plotted as a function of modulation depth. Note in D that the behaving point (white circle) is covering the ability to see the passive point (black square) at 0% depth (both behaving and passive are 0.5 for ROCa by definition). E and F: ML population mean ROCas based on VS_pp during the entire stimulus duration (80–800 ms, the onset response is excluded) plotted as a function of modulation depths for the passive and behaving conditions for all recorded MUs (E) and SUs (F). G and H: population mean ROCas based on VS_pp during 1st half of the stimulus (80–400 ms, the onset response is excluded) plotted as a function of modulation depths for the passive and behaving conditions for all recorded MUs (G) and SUs (H). I and J: population mean ROCas based on VS_pp during 2nd half of the stimulus (400–800 ms) plotted as a function of modulation depths for the passive and behaving conditions for all recorded MUs (I) and SUs (J). In all panels, P values are denoted showing Wilcoxon signed-rank test comparing collapsed-depth ROC areas between behaving and passive conditions. *Individual modulation depths where a Wilcoxon signed-rank test yielded a value of P < 0.05.

In ML, the population average VS_pp-based ROCa significantly improves in the behaving condition compared with the passive condition at 100%, 80%, and collapsed depths for MUs (Fig. 11E) and at 60% and collapsed depths for SUs (Fig. 11F). These results indicate that AM discriminability based on phase-locking significantly improves because of engagement in the AM task. Unlike rate-based ROCa, we did not find a decline in VS_pp-based ROCa in the behaving condition during the stimulus (Fig. 11, G–J). However, the improvement in VS_pp-based AM discrimination due to engagement appears to be greater earlier during the stimulus.

Similar to rate-based AM discrimination, A1 and ML show a significant difference in the overall level of AM discrimination based on phase-locking. When VS_pp-based ROCas from the behaving condition are compared, A1 had significantly greater values than ML at 100%, 80%, 60%, 40%, 28%, and 16% for MUs and at 100%, 80%, 60%, and 6% for SUs. These results show that neurons in A1 are significantly better at detecting the presence of AM with phase-locking than those in ML, regardless of the behavioral condition.

Synchronizing vs. Nonsynchronizing Responses

A proposed model of hierarchical processing of temporal modulation involves a transformation from a temporal to a rate code (e.g., from a phase-locking to an average firing rate code). This model is supported by findings that the maximum modulation frequency to which neurons phase-lock decreases and nonsynchronizing responses become more prominent with auditory system ascension. Therefore, neural responses that encode AM exclusively by changing firing rate without synchronizing to the stimulus envelope (nonsynchronized response) are proposed to reflect coding at a more highly processed stage and to have a special role in AM perception (Bartlett and Wang 2007; Bendor and Wang 2007; Liang et al. 2002; Lu et al. 2001). Note that for both synchronized and nonsynchronized responses, some have “increasing” rate-depth functions while others have “decreasing” ones. In the previous sections, we have shown that neural responses with increasing and decreasing rate-depth functions show different task engagement effects. Therefore, we subdivided neural response by type (synchronizing vs. nonsynchronizing) and sign of the rate-depth function slope (increasing vs. decreasing) and examined the effect of task engagement on neuronal AM discrimination (Fig. 12: each row has a ROCa scale for optimum comparison of behaving and passive conditions).

Fig. 12.

Effect of task engagement on AM discriminability shown separately for synchronized/nonsynchronized and increasing/decreasing responses. A and B: ML population mean rate-based ROCas for nonsynchronized responses plotted for increasing (dark blue lines) and decreasing (light blue lines) responses, during 1st half (0–400 ms, A) and 2nd half (400–800 ms, B) for MUs (C and D for SUs). *Depths at which the differences between active and passive were significant (P < 0.05). P values at top of each subplot denote whether differences between active and passive were significant for increasing units collapsed across all depths, and those at bottom of each subplot are for decreasing units collapsed across all depths. E and F: population mean rate-based ROCas for synchronized responses plotted for increasing (dark green lines) and decreasing (light green lines) responses during 1st half (0–400 ms, E) and 2nd half (400–800 ms, F) for MUs in ML (G and H for SUs). Asterisks and P values are formatted as in A–D. I and J: population mean VS_pp-based ROCas for synchronized responses during 1st half (80–400 ms, I) and 2nd half (400–800 ms, J) for MUs in ML (K and L for SUs). M–X: same as A–L, but for A1 units. In all panels, P values are denoted showing Wilcoxon signed-rank test comparing collapsed-depth ROC areas between behaving and passive conditions. *Individual modulation depths where a Wilcoxon signed-rank test yielded a value of P < 0.05.

For increasing ML synchronizing responses, AM discrimination significantly improved with task engagement during the first half of the stimulus, while no significant improvement was found during the second half (Fig. 12, E–H, compare with Fig. 6, A–D, for similarity). In contrast, for ML nonsynchronizing responses with increasing functions, improvements in the rate-based AM discriminability due to task engagement persisted later in the stimulus for AM, but this was true only at near-threshold depths (Fig. 12, A–D). To quantify near-threshold versus suprathreshold effects, we collapsed the three nearest-threshold depths (6%, 16%, and 28%) and the most suprathreshold depths (60%, 80%, and 100%). We then compared active and passive ROCa for ML increasing nonsynchronized units. For both SUs and MUs, there was a significant difference between behaving and passive near threshold (Wilcoxon paired tests, P = 2.8 × 10⁻⁴ SU; P = 3.1 × 10⁻³ MU) but not suprathreshold during the 2nd half of the stimulus (P = 0.16 SU, P = 0.34 MU). A possible interpretation relates to attention. It could be that attention is engaged longer for the more difficult to discriminate, near-threshold, sounds.

For A1 responses with increasing functions, the improvement for nonsynchronizing responses is more pronounced with d′ measures, because their AM discrimination ability is extremely good, and many units encounter a ceiling effect when measured with ROCas (bounded by 1). However, regardless of the measures used, A1 improvement (Fig. 12, M–T) of rate-based AM discrimination does not show as clear or interesting first- and second-half differences as in ML.

For both A1 and ML, nonsynchronizing responses show much better AM sensitivity compared with synchronizing responses regardless of behavioral state.

For responses with decreasing functions, task engagement generally improves rate-based AM discriminability for ML units but degrades it for A1. For ML synchronizing responses with decreasing functions, task engagement significantly improves AM discriminability during the second half of the stimulus but less so during the first (Fig. 12, E–H). For ML nonsynchronizing responses with decreasing functions task engagement significantly improves AM discriminability during the first and second halves of the stimulus, and the improvement is larger during the later period (Fig. 12, A–D). In fact, in the behaving condition during the second half of the stimulus, the mean discrimination ability (distance from ROCa = 0.5) for decreasing ML units is better than that for increasing units. For A1 responses with decreasing functions, regardless of response type (synchronizing or nonsynchronizing), task engagement worsens rate-based AM discrimination, especially during the first half of the stimulus, and the degradation diminishes or disappears in the second half (Fig. 12, M–P and Q–T).

Additionally, we examined whether VS_pp-based AM discriminability improves because of task engagement for synchronizing responses. Note that in the previous section the entire ML population was analyzed (Fig. 11) but here we focus only on units with significant synchronizing responses. We found that VS_pp-based ROCa significantly improved for ML synchronizing responses during the first and the second halves of the stimulus (Fig. 12, I–L). Once again, the effect size and number of significant conditions for VSpp-based ROCa were larger with d′ because many units have an ROCa near 1. For this measure the only condition of the eight conditions shown in Fig. 12, I and J and U and V, not to reach significance was for A1 SUs in the second half of the stimulus; all seven remaining conditions did. Although task engagement has slightly different effects on rate-based and VS_pp-based discrimination, their absolute discriminability levels are roughly comparable, i.e., the population average, rate-based ROCa is comparable to VS_pp-based ones for synchronizing responses (compare Fig. 12, E–H, with Fig. 12, I–L). This suggests that synchronizing responses can encode AM equally well using phase-locking and average firing rate.

DISCUSSION

Differences between A1 and ML were found by investigating how behavioral engagement in AM discrimination affects neurons' ability to discriminate the same sounds. While little is known about attention- and state-related effects in higher auditory areas, these differences appear related to three key issues. First, they may relate to how attention modulates neural responses. The differing response time courses and neural response type differences between ML and A1 may relate to the degree to which this study taps into more selective forms of attention, and possibly the time course of attention including disengagement after a decision is made. Second, the results have implications regarding neural coding. In particular, these results elucidate possible decoding differences, such as simply pooling activity from A1 as opposed to ML, where both increases and decreases in activity must be accounted for by higher areas. Third, the results imply a special role for nonsynchronized responses. Before addressing these issues contrasting A1 and ML, we must relate the results to what is already known in A1, because little is known of attention and engagement effects beyond A1.

Comparing Neural Activity During Passive Listening and Active Behavior in A1

Our results show that engagement in the AM task improves A1 and ML neurons' ability to discriminate AM based on both firing rate and phase-locking. Compared with a passive condition, auditory task engagement can 1) change stimulus-evoked and spontaneous firing rates of AC cells (Benson and Hienz 1978; Hocherman et al. 1976; Miller et al. 1972; Otazu et al. 2009; Pfingst et al. 1977), 2) create facilitative frequency tuning of A1 neurons in tone detection (Fritz et al. 2003; Miller et al. 1972), 3) sharpen spatial tuning of A1 neurons in sound localization (Benson et al. 1981; Lee and Middlebrooks 2011), 4) sharpen frequency tuning (David et al. 2012), and 5) increase neural selectivity for complex sounds (Knudsen and Gentner 2013). Furthermore, Otazu et al. (2009) have shown that the sound-evoked and spontaneous firing rate of A1 neurons is modulated by engagement in either an auditory or an olfactory task, demonstrating that A1 neurons' firing rate can be modulated by attending to nonauditory attributes. It is largely unknown what components in task engagement cause the myriad of observed changes in neural response properties. There are multiple possible contributing sources to the changes observed in our study, including general attention and feature-selective attention.

In A1 attention might activate a multiplicative response increase. Jaramillo and Zador (2011) have shown that temporal expectation improves A1 neurons' frequency discrimination ability by increasing responses at the target frequency and decreasing responses at surrounding frequencies. They conclude that this is consistent with a multiplicative effect. The A1 data we present here and previously (Niwa et al. 2012a) are also consistent with a multiplicative effect, since the engagement effects appear larger for stimuli that evoke higher firing rates. Such multiplicative effects are often thought to be indicative of attention. Our ML data show something different, suggesting feature-selective attention. We believe this because some of the ML effects are most pronounced near threshold and occur for time windows at which stimulus-specific attention is more likely engaged.

Recently, larger neural discrimination improvements have been found for a feature that is selectively attended in contrast to simply attending to sound. Spatial tuning of A1 neurons improved when animals performed a sound periodicity detection task, suggesting a general attention effect rather than a spatial feature-attention effect. However, engagement in a sound localization task improved spatial tuning more than performing the periodicity detection task (Lee and Middlebrooks 2011). This suggests that attention's effects were feature specific.

These results suggest that both general and feature-selective attention influence A1 responses, and are consistent with our A1 results.

Relationship to Plasticity in AC

Our results show rapid changes in neural discrimination when an animal switches between behaving and passive conditions. In addition to immediate attention effects, long-term training could lead to plastic changes that are often highly interrelated with plasticity (Fritz et al. 2007; Polley et al. 2006) that can improve AC neuron discrimination ability (e.g., Jeanne et al. 2011; Thompson et al. 2013). In our animals, plastic changes due to training might be dormant in the passive condition and only activated when the animal engages in the task. This would allow for the cortical circuit in the passive condition to be in a state open to the analysis of many possible signals, but during task performance the circuit is optimized for AM detection.

Comparisons Between A1 and ML

Phase-locking.

An interesting finding in this and an earlier study (Niwa et al. 2012a) is that phase-locking—the precision with which a neuron follows temporal modulation—improves with active engagement. Here we also find that, while in the passive condition ML does not phase-lock as well as A1, ML improves more than A1 with behavioral engagement. This is consistent with A1's ability to improve temporal precision of firing due to training (Fritz et al. 2005; Kilgard et al. 2001; Kilgard and Merzenich 1998; Schnupp et al. 2006). Furthermore, Jakkamsetti et al. (2012) have shown that a higher AC area [rat posterior auditory field (PAF)] normally time-locks worse than A1 but that environmental enrichment improves temporal locking in PAF more than in A1. Finally, in our study phase-locking improves with engagement and becomes as sensitive to AM as firing rate. When combined, all the evidence suggests that learning and attention can improve phase-locking to sound, such improvements are more pronounced in higher cortical areas, and phase-locking could play a meaningful role in sound processing.

Possible implications about attention.

ML increasing cells' AM discriminability during behavior worsens later in the stimulus (Figs. 1–4, Fig. 8), but no such effect was seen in A1. A1 increasing cells' AM discrimination during behavior remains above the passive level throughout the stimulus. The late decline in ML's AM discrimination for increasing units appears greater at higher modulation depths (Fig. 6, C and D, and Fig. 8, A and B). Raw firing rate to AM and unmodulated noise (Fig. 9, A and B) indicates that the late ROCa decline in ML is due to the combination of firing rate decreases to AM and increases to unmodulated noise in the behaving compared with the passive condition. At modulation depths far above the animals' behavioral thresholds, listening to the entire test stimulus is not likely required before making a decision. The observed decrease in AM discriminability may be due to a decrease in attention to high-depth AM later during the stimulus, combined with increased attention to unmodulated noise (particularly later in the stimulus), where animals may be attending more in an attempt to detect AM in the unmodulated stimuli.

Other evidence supporting a different type of attention effect in ML derives from partitioning our analyses by increasing and decreasing units. Nonsynchronized increasing units show the most improvement during behavior later in the stimulus near behavioral threshold (Fig. 12, B and D, and Fig. 6, C and D, show a small effect averaged for all units). This suggests that engagement improves performance in the second half only for the most difficult to discriminate sounds that require the most and longest attention, reflecting its time course. In A1 this effect was not observed.

Overall AM discrimination ability of units.

AM discriminability of units with increasing depth sensitivity functions appears better in A1 than ML. A1 neurons better discriminate AM using phase-locking than ML neurons in both behaving and passive conditions. A1 neurons also better discriminate AM with a rate code with increasing rate-depth functions in both conditions. The exception to A1's better performance is for rate coding using decreasing rate-depth functions. AM discrimination by decreasing cells was significantly better in ML than in A1, although this occurs only during the second half of the test stimulus in the behaving condition. The result suggests that decreasing ML cells may be important for AM detection.

AM coding schemes.

Our results suggest that to decode the population of A1 neurons' activity, aggregate activity increases correspond to more strongly modulated AM. In contrast, in ML the output code is likely the difference in activity between neurons that increase and decrease rate with modulation depth. AM discriminability of decreasing cells in A1 significantly worsens with task engagement (Fig. 8, Fig. 12), while discriminability of ML decreasing cells improves with task engagement (Fig. 7, Fig. 8, Fig. 12). This is another piece of evidence supporting the importance of the rate code carried by decreasing ML cells. It also suggests that, in A1, increases in activity represent modulation, since task engagement actually reduces the performance of decreasing cells in this region by increasing the response to AM during behavior. Therefore, the “reduction” of AM discriminability in A1 decreasing cells is not necessarily bad for AM coding. If one assumes that the brain interprets an increase in A1's aggregate pooled activity (by indiscriminately pooling the activity of all A1 neurons) as evidence of an AM signal, then the reduction of decreasing cells' discriminability can actually render a benefit to the AM discriminability of an A1 population and ultimately to the animal's behavioral performance. The difference in behavioral modulation of decreasing cells' AM discriminability in ML and A1 suggests that different coding schemes are used in these areas; a “single mode” in A1, using only increasing rate, and a “dual-polar mode” in ML, using both increasing and decreasing rate.

The heightened importance of decreasing rate-depth functions in ML is particularly interesting. The emergence of decreasing functions in ML, and the fact that their ability to discriminate AM improves with attention and that they are very sensitive (Fig. 12), may be beneficial for AM coding in ML. While it is well established that positively correlated noise in the activity of similarly tuned neurons limits their coding capacity (Shadlen et al. 1996; Zohary et al. 1994), it has been shown that positively correlated noise among neurons with increasing and decreasing functions can improve their coding efficiency (Romo et al. 2003). Thus the apparent loss of AM discriminability in ML can be at least partially compensated for by the emergence of decreasing functions if the noise in the activity of cells with increasing and decreasing functions is positively correlated.

Comparison to Recent Study Looking at Attention and Nonprimary AC

Recently Dong et al. (2013) compared neural responses in multiple cortical areas while cats discriminated click trains to responses in a passive condition. While some of their results are similar to ours, one apparent discrepancy is that they report increases and decreases in driven responses in lower AC (dorsal tonotopic AC) but only increases in higher ventral nontonotopic AC. Major differences in methods, species, and analysis prevent direct comparison. Their dorsal “lower” cortical area probably includes both A1 and ML in monkeys, and their ventral area is probably much higher than any belt area (perhaps similar to temporal pole or insular cortex in monkeys), so the hierarchical areas between the two studies are not comparable. Their task is relatively easy from a sensory perspective (discriminating 15 Hz from 50 Hz, which is highly suprathreshold) and is unlikely to place high demands on feature-selective attention, whereas our animals are performing around threshold level. For us, particularly in A1, decreases refer to the slope of firing rate vs. modulation depth functions. For them, decreases refer to decreases in activity to both stimuli, not on changes in the neurometric (response vs. frequency) function. Much of the complexity we see occurs between 400 and 800 ms after stimulus onset, while their stimuli are only 320 ms. Finally, comparisons are made difficult by numerous other differences in experimental design: performance level, neuronal inclusion criteria (they only include neurons that fire at least 2 standard deviations above spontaneous level to one of the two stimuli), and species. This highlights that experimental differences can have large impacts on physiological results, particularly attention-related effects that depend critically on the difficulty of discriminating or detecting stimuli.

Is There a Special Role for Nonsynchronized Responses?

AM encoding is hypothesized to transform from temporal to rate-based representations as information is processed from lower to higher auditory areas (Lu and Wang 2004; Nelson and Carney 2004). This is supported by the decrease in the upper limit of modulation frequency to which neurons phase-lock and by the increase in prominence of rate-based AM coding when ascending from lower to higher areas (Blackburn and Sachs 1989; Creutzfeldt et al. 1980; de Ribaupierre et al. 1980; Frisina et al. 1990; Langner and Schreiner 1988; Lu and Wang 2004; Nelson and Carney 2007; Preuss and Muller-Preuss 1990; Rees and Moller 1983; Rouiller et al. 1981) and the emergence of nonsynchronized firing rate encoding of temporal modulation in higher areas (Bendor and Wang 2007; Lu and Wang 2004).

Several lines of evidence support a special contribution for nonsynchronized responses in temporal discrimination. In A1, nonsynchronized (increasing) responses are more sensitive to AM than synchronized responses (Fig. 12) and the nonsynchronized responses increase sensitivity with engagement. Nonsynchronized increasing ML responses, although slightly less sensitive than those in A1, yield similar early-stimulus results. During the second half of the stimulus, ML nonsynchronized increasing responses show depth-dependent improvement in the behaving condition (Fig. 12, B and D), consistent with a more pronounced or longer-lasting attention effect near threshold.

ML nonsynchronized decreasing responses also show large improvements during behavior and are more AM sensitive than synchronizing responses, particularly later in the stimulus (Fig. 12, A–D). Finally, during the entire stimulus, both increasing and decreasing nonsynchronized ML responses improve during behavior (Fig. 12, A–D), whereas for synchronized responses improvements only occur in the first half for increasing and only during the second half for decreasing functions (Fig. 12, E–H). Together these findings suggest that increasing (A1 and ML) and decreasing (ML) nonsynchronized responses have properties that make them particularly well-suited for AM processing. This is further supported by recent studies in behaving cats showing that nonsynchronized responses' discrimination ability more closely match the animal's behavioral performance than synchronized responses (Dong et al. 2011) and nonsynchronized rate responses are modulated by attention but synchronizing ones are not (Dong et al. 2013).

Comparison of ML Activity in Our Task to Somatosensory Cortical Activity During Flutter Frequency Discrimination Tasks

Our study shares similarities with results from the primary and secondary somatosensory cortices (S1 and S2). Romo et al. conducted extensive studies examining the neural codes underlying perception, memory, and decision making during vibrotactile discrimination, where monkeys were trained to report whether the frequency of a first flutter stimulus is greater than the flutter frequency of a second stimulus (Hernandez et al. 2000, 2002, 2010; Luna et al. 2005; Romo et al. 1998, 2002, 2003; Salinas et al. 2000). First, S2 neurons' flutter frequency coding capacity was significantly lower than that of S1 neurons (Salinas et al. 2000); similarly, we find that ML neurons generally have lower AM discriminability than A1 cells. Second, transformation of encoding schemes appears to occur from a single mode of “increasing” rate response in S1 to a dual mode of “increasing” and “decreasing” responses in S2 (Hernandez et al. 2002; Salinas et al. 2000). Salinas et al. (2000) showed that 92% of S1 neurons encoded an increase in flutter frequency with monotonically increasing firing rate and only 8% used decreasing rate. In S2, 58% had increasing rate vs. flutter frequency functions and 42% decreasing. Our results also suggest that the primary sensory area, A1, employs a single-mode encoding with mainly increasing rate-depth functions while the secondary area, ML, employs a dual-polar mode with both increasing and decreasing rate-depth functions. Although our studies and those of the Romo group use different behavioral tasks in different sensory modalities, there is a general principle: a meaningful temporal feature (flutter frequency or modulation depth) in primary sensory cortex is encoded primarily by one type of response—an increase in activity. But in the secondary area two types of responses—activity increases or decreases—encode the feature. The similarities in our results suggest a common scheme in hierarchical processing of temporal information shared in sensory cortices of different modalities.

Hierarchical Processing of Temporal Information in AC

Electrophysiological studies have examined SU responses to AM and other types of temporal modulation across different auditory areas (Bendor and Wang 2007, 2010; Bieser and Müller-Preuss 1996; Eggermont 1991, 1994; Joris et al. 2004; Joris and Yin 1992; Kajikawa et al. 2008; Liang et al. 2002; Lu et al. 2001; Lu and Wang 2000; Malone et al. 2007; Nelson and Carney 2004; Schreiner and Urbas 1988; Scott et al. 2010; Wojtczak et al. 2011). Although we have yet to form a precise understanding of how temporal sound properties are processed in parallel and/or hierarchical AC networks, an interesting trend is evident: a temporal resolution gradient may be present along the posteromedial-to-anterolateral axis on primates' superior temporal gyrus (STG). For example, in awake, nonbehaving squirrel monkey, a gradient of neuron ability to phase-lock to AM was shown across cortical areas, where A1 had the best temporal resolution (Bieser and Müller-Preuss 1996). The areas anterior and lateral to A1 had lower phase-locking-based BMFs, and thus lower temporal resolution. Scott et al. (2010) also showed that in awake, nonbehaving macaques areas anterior and lateral to A1 (areas R and lateral belt cortices) have lower phase-locking BMFs compared with A1 and with an area posteromedial to A1 (CM). This gradient was also shown in human epileptic patients, showing degradation of temporal resolution along the posteromedial to anterolateral direction over the Heschl's gyrus (HG) (Brugge et al. 2009), implicating a flow of temporal processing in the AC hierarchy in the posteromedial-to-anterolateral direction (Gueguin et al. 2007).

Other temporal response properties besides the resolving power for AM frequency exhibit gradients in posterior-to-anterior and/or medial-to-lateral directions over the STG. Neurons' preferred frequency-modulated (FM) frequency decreases in a posterior to anterior direction in the lateral belt (Tian and Rauschecker 2004). In addition, there may be a posterior-to-anterior and/or medial-to-lateral gradient of response latency (Kajikawa et al. 2005, 2008; Kusmierek and Rauschecker 2009; Lakatos et al. 2005; Recanzone et al. 2000a; Scott et al. 2010). Our result showing lower AM discriminability based on phase-locking in ML compared with A1 may be consistent with the idea that temporal response deteriorates in a medial-to-lateral direction.

GRANTS

This work is supported by National Institute on Deafness and Other Communication Disorders Grant DC-02514 (M. L. Sutter) and NRSA F31 DC-008935 (M. Niwa).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: M.N., K.N.O., and M.L.S. conception and design of research; M.N., K.N.O., and E.E. performed experiments; M.N., J.S.J., and M.L.S. analyzed data; M.N. and M.L.S. interpreted results of experiments; M.N. and M.L.S. prepared figures; M.N. and M.L.S. drafted manuscript; M.N., K.N.O., J.S.J., and M.L.S. edited and revised manuscript; M.N., K.N.O., E.E., J.S.J., and M.L.S. approved final version of manuscript.