Abstract
Self-assembly of proteins into amyloid fibrils plays a key role in a multitude of human disorders that range from Alzheimer’s disease to type II diabetes. Compact oligomeric species, observed early during amyloid formation, are reported as the molecular entities responsible for the toxic effects of amyloid self-assembly. However, the relation between early-stage oligomeric aggregates and late-stage rigid fibrils, which are the hallmark structure of amyloid plaques, has remained unclear. We show that these different structures occupy well-defined regions in a peculiar phase diagram. Lysozyme amyloid oligomers and their curvilinear fibrils only form after they cross a salt and protein concentration-dependent threshold. We also determine a boundary for the onset of amyloid oligomer precipitation. The oligomeric aggregates are structurally distinct from rigid fibrils and are metastable against nucleation and growth of rigid fibrils. These experimentally determined boundaries match well with colloidal model predictions that account for salt-modulated charge repulsion. The model also incorporates the metastable and kinetic character of oligomer phases. Similarities and differences of amyloid oligomer assembly to metastable liquid–liquid phase separation of proteins and to surfactant aggregation are discussed.
Introduction
Deposition of plaques composed of protein fibrils is associated with a variety of debilitating human disorders. Examples of these amyloidoses include Alzheimer’s disease, type-II diabetes, cataracts, and senile systemic amyloidosis.1,2 The wide variety of structurally and functionally distinct proteins and peptides capable of forming amyloid fibrils identified by their cross-β sheet architecture implies that polypetides have an intrinsic propensity toward fibril formation.1,3 This intrinsic propensity is exemplified by the increasing number of nondisease associated proteins,4−7 model peptides,8−10 and polyamino acids11 that form amyloid fibrils in vitro. The presence of a nucleation barrier and the highly ordered cross-β sheet structure of amyloid fibrils have led to the further suggestion that amyloid fibril formation represents a generic phase transition similar to bulk crystallization.3,12
Understanding the molecular processes that regulate amyloid formation is complicated by the existence of at least two distinct aggregation pathways. In one pathway, amyloidogenic proteins undergo nucleated polymerization, or variants thereof,12,13 which results in long, rigid fibrils that cause strong thioflavin T (ThT) fluorescence responses. A second oligomeric pathway involves instantaneous growth of small globular intermediates,14,15 which tend to polymerize further into curvilinear fibrils with much weaker ThT responses.16−18 These oligomeric species, in particular, have been implicated as the dominant molecular species responsible for cellular toxicity.19−21 Infrared spectroscopy from Aβ and lysozyme oligomers suggests that these oligomers form antiparallel β-sheets in contrast to the parallel β-sheet structure of their rigid fibril counterparts.17,22,23 This structure is reminiscent of β-barrels and is consistent with high-resolution oligomer structures obtained from amyloidogenic model peptides via X-ray diffraction.24,25
However, a mechanistic understanding of the conditions that promote the formation of oligomers over fibrils, and how these two amyloid structures are related to each other or to their corresponding monomeric species, is lacking. The most comprehensive study to date involves the hemodialysis-related amyloid protein beta-2 microglobulin (B2M). Upon increased acidification, B2M undergoes a transition from soluble monomers (pH > 6) to the formation of amorphous aggregates (pH > 4), then oligomers and short rod-like or longer curvilinear fibrils (pH > 2.5) and, eventually, rigid fibril formation below pH 2.5.18,26 These studies also reported a threshold concentration below which no aggregation occurred. Similar observations of a critical protein or salt concentration below which oligomer formation ceased were reported for amylin27 and lysozyme.28 Precipitation has been independently confirmed for both B2M29 and lysozyme.28 However, the acidification of B2M induces progressive unfolding and alters the monomer net charge. Therefore, the relative contributions of conformational changes versus charge effects on the propensity to form different amyloid structures become difficult to untangle. Formation of distinct amyloid aggregate morphologies and structures upon changes in solution conditions has been reported for multiple proteins. However, these studies did not determine quantitative transition boundaries or did focus on differences in late-stage aggregate phases instead.20,30−32 To address this limitation, we mapped out the critical concentrations for the onset of oligomer formation and for precipitation at fixed pH and temperature, but as a function of protein and salt concentration. We used the readily available amyloid protein hen egg white lysozyme (HEWL) for these material-intensive studies.33−35 These experiments also allowed us to probe the following basic questions: Is the switch from rigid fibril to globular oligomer formation gradual or highly cooperative? Does the transition represent an equilibrium or a kinetic boundary? Do oligomers and their curvilinear fibrils have identical or distinct solubilities? Are they distinct from those for rigid amyloid fibrils? What is the origin of the observed precipitates, and do these precipitates have an internal structure?
We find that the aggregation behavior of HEWL can be described by three phase boundaries that separate the monomer, rigid fibril, oligomer/curvilinear fibrils, and precipitate phases. Of these boundaries, only the monomer-rigid fibril boundary represents a true thermodynamic phase boundary, while the other boundaries are due to kinetically favored metastable states. We present spectroscopic evidence that the precipitates are formed from rapidly assembled oligomers. In addition, we investigated to what extent considerations of colloidal charge interactions replicated the observed transition boundaries. In both cases, the presence of a nucleation barrier retarding one phase allowed us to describe these kinetic boundaries using quasi-equilibrium approximations. Using the Poisson–Boltzmann equation, we considered the effects of colloidal charge repulsion among monomers, when confined in different aggregate morphologies (oligomers or precipitates), as the basis for the observed salt- and protein-concentration dependence of the experimentally determined transitions. The cohesive forces within aggregates, in contrast, were presumed to be independent of solution conditions. The results of these theoretical models are compared with the experimentally determined kinetic phase boundaries for oligomer formation and precipitation.
Experimental Methods
Protein and Chemicals
Two times recrystallized, dialyzed, and lyophilized HEWL was purchased from Worthington Biochemicals (Lakewood, NJ) and used for all experiments. Ultrapure grade ThT was obtained from Anaspec (Freemont, CA). All other chemicals were from Fisher Scientific (Pittsburgh, PA) and were reagent grade or better. All solutions were prepared using 18 MΩ water from a reverse osmosis unit (Barnstead E-pure, Dubuque, IA).
Preparation of HEWL and ThT Solutions
HEWL was dissolved at twice its final concentration in 25 mM KH2PO4 pH 2 buffer and was for a short time placed in a water bath at 42 °C to help dissolve preformed assemblies.36 Samples were successively filtered through 220 nm poly(vinylidene difluoride) (PVDF) (Fisherbrand, Fisher Scientific, Pittsburgh, PA) and 50 nm polyethersulfone (PES) (Tisch Scientific, North Bend, OH) pore size syringe filters. The concentrated HEWL stock was mixed 1:1 with a NaCl/25 mM KH2PO4 pH 2 stock solution, and NaCl concentrations in this salt/buffer stock were at twice the desired final concentration. Actual lysozyme concentrations were determined from UV absorption measurements at 280 nm (a280 = 2.64 mL mg–1 cm–1). ThT stock solutions were prepared by dissolving 1 mM dye in distilled water and passing them through 220 nm syringe filters. Actual ThT concentrations were determined from absorption at λ = 412 nm (ε412 = 32 000 mL mg–1 cm–1). For cross-seeding of fibrils at pH 2, seeds were formed via incubation at 52 °C, pH 2, 1.4 mM lysozyme concentration, 100 mM NaCl for 2.5 days and 300 mM NaCl for 1.5 days.
Curvilinear Fibril Decay Experiments
We generated curvilinear fibril seeds and isolated them from the residual lysozyme monomers via filtration using 100 kDa centrifuge cutoff filters. The thermodynamic stability of these seeds was tested by adding them to a series of solutions at fixed protein concentration (1.4 mM and 0.692 mM). However, a range of salt concentrations (0–300 mM NaCl) was chosen to cross the boundary for rigid filament-to-oligomer formation using 25 mM increments in NaCl concentration. For low protein concentration, NaCl concentration was fixed at 350 mM, and HEWL concentrations varied from 0.5 mM down to 0.035 mM. Total protein concentration was taken as the sum of both monomer and seed concentration. By using this approach, the solution conditions crossed the transition boundary perpendicular to its local slope, and the experimental accuracy improved.
Static and Dynamic Light Scattering
Protein solutions were placed in standard glass cuvettes (Starna Cell, Atascadero, CA) and incubated at 52 °C for 5 days using a dry bath or a thermostatic cuvette holder. Static and dynamic light scattering (SLS and DLS) measurements were carried out using a Zetasizer Nano S (Malvern Instruments, Worchestershire, U.K.) with a temperature-controlled sample compartment. Autocorrelation functions were collected every 5–30 min with acquisition times of 180 s per measurement and were converted into particle-size distributions using the “narrow modes” or “general purpose” algorithms provided with the Zetasizer Nano S. Changes in scattering intensity were monitored simultaneously via the count rates of the avalanche photodiode photon detector. Alternatively, 250 μL of protein solutions was placed in a 96-well glass bottom plate and incubated at 52 °C for 5 days in the thermostated plate holder of a DLS plate reader (DynaPro, Wyatt). Field autocorrelation functions were measured and analyzed identical to single cuvette experiments.
Thioflavin T Fluorescence Spectroscopy
ThT fluorescence measurements were performed using a SpectraMax M5 spectrofluorometer (Molecular Devices). ThT fluorescence was excited at 440 nm, and emission collected at 488 nm. A 250 μL aliquot of the samples was placed in a 96-well glass bottom plate, and ThT stock solution was added, which brought its final concentration to 10 μM. All measurements were done at 52 °C. At elevated protein concentrations (>300 μM) SLS measurements provided a convenient read-out of aggregation behavior, while ThT yielded more reliable signals at low protein concentrations. We previously confirmed that SLS and ThT kinetics generated the same kinetic signature by monitoring both signals under identical solution conditions.17
Fourier-Transform Infrared Spectroscopy (FTIR) of Lysozyme Solutions
Attenuated total reflectance Fourier-transform infrared spectroscopy (ATR-FTIR) was performed on a Bruker Optik Vertex 70 (Ettlingen, Germany) spectrometer with a mid-infrared source and pyroelectric DLATGS (deuterated l-alanine doped triglycene sulfate) detector. Usually, 25–30 μL of protein solution was placed on the thermostated silicon crystal of a BioATRcell II (Harrick Scientific Products, Inc., Pleasantville, NY) accessory. FTIR spectra were acquired between 1,000 cm–1 and 4,000 cm–1 wavenumbers. All spectra were taken at 24 °C with an aperture setting of 8 mm and a scanner velocity of 10 kHz. Typically, 500 scans at 4 cm–1 resolution were recorded, and three such runs were averaged prior to data analysis.
Atomic Force Microscopy
Amyloid fibrils were imaged in air with a MFP-3D atomic-force microscope (Asylum Research, Santa Barbara, CA) using NSC36/NoAl (Mikromasch, San Jose, CA) or PFP-FMR-50 (Nanosensor, Neuchatel, Switzerland) silicon tips with nominal tip radii of 10 and 7 nm, respectively. The cantilever had a typical spring constant and resonance frequency of 2 nN/nm and 70 kHz, respectively. It was driven at 60–70 kHz in alternating current mode and at a scan rate of 0.5 Hz, and images were acquired at 512 × 512 pixel resolution. Raw image data were corrected for image bow and slope. For imaging, 75 μL of sample solutions was diluted 20- to 100-fold into the same salt/buffer combination used during growth, deposited onto freshly cleaved mica for 3–5 min, rinsed with deionized water, and dried with dry nitrogen. Amplitude, phase, and height images were collected for the same sample area. False-color heights were subsequently superimposed over either amplitude or phase images off-line.
Integration of the Poisson–Boltzmann Equation
To compute the electrostatic free energy cost of confining monomers to the volume of an oligomer, we treat the monomers and oligomers as spheres of radius 1.6 nm37 and 3.8 nm,35 with isotropic surface charges of 15e38 and 120e, respectively. We solve for the electrostatic free energy cost within the Poisson–Boltzmann (PB) approximation by numerically integrating the PB equation between two concentric spherical shells. The inner shell is taken to be the radius of the protein or oligomer, while the outer sphere is the effective integration volume. For numerical integration, the outer radius was chosen to exceed the inner radius by 5 λD, where λD is the Debye screening length. This approximation is expected to generate an error on the order of e–5, which is less than 1%. The electrostatic potential determined within this geometry is used as input to calculate the coulomb energy and ion entropy contributions to the electrostatic free energy difference between monomers and oligomers.39 A dielectric constant of 70 was used for water at 50 °C.40 Solution of the nonlinear PB equation and integration of the resulting free energy was performed using the NDSolve and NIntegrate packages in Mathematica.
Results
Morphologies and Kinetics Signatures of Rigid Fibrils, Oligomers and Curvilinear Fibrils, and Precipitates
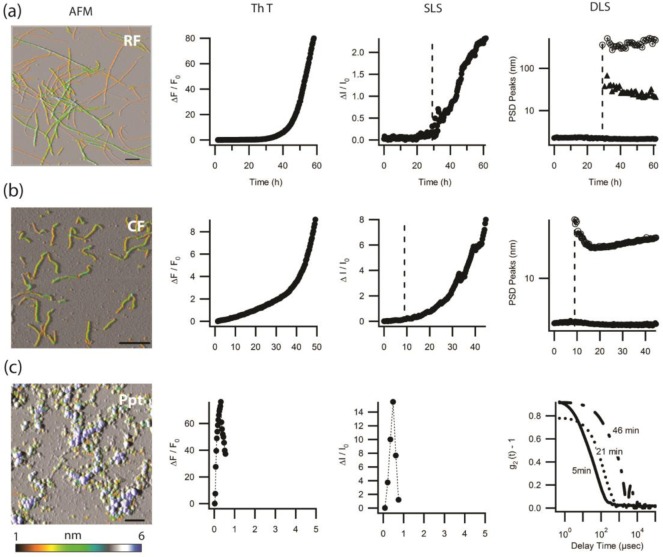
We have previously identified three distinct aggregate morphologies formed by HEWL under the partially denaturing conditions of acidic pH and elevated temperature.28 HEWL will form rigid fibrils (RFs) at low salt, oligomers and curvilinear fibrils (O/CFs) at intermediate salt concentrations, and precipitates (Ppts) at high salt concentrations (Figure 1).17,28 These distinct aggregate morphologies are associated with both unique spectroscopic and kinetics signatures, with details provided in our earlier work.17 Figure 1 summarizes aggregate morphologies associated with each aggregation pathway and their kinetics signatures obtained using SLS and DLS as well as ThT fluorescence. In short, nucleated polymerization of RFs induces a long lag period followed by a sharp upturn in SLS and ThT intensity and the concurrent formation of two new aggregate peaks in DLS (Figure 1a). O/CF assembly, in contrast, induces an instantaneous and gradually accelerating increase in ThT and SLS intensities. Nucleation of CFs, as revealed by DLS, leaves no discernible discontinuity in either the ThT or SLS signals and is therefore commonly missed (Figure 1b). Precipitates, in turn, cause a rapid upturn and subsequent decline in fluorescence and scattering intensities. The corresponding rapid formation of large aggregates causes the DLS field correlation functions to slow down by orders of magnitude (Figure 1c). It is worth noting that we do not observe any mixtures of aggregate states in our experiments, at least not over the time-scales used to determine the initial aggregation pathway.
Figure 1.
Morphology and kinetics of rigid fibrils, oligomers and curvilinear fibrils, and precipitates formed by HEWL. Summary of the distinct morphologies and kinetics signatures associated with growth of (a) RFs, (b) O/CF, and (c) Ppt of HEWL under partially denaturing conditions (pH 2, T = 52 °C). The first column displays atomic force microscopy images of RFs (50 mM NaCl), CFs (200 mM NaCl), and Ppts (400 mM NaCl). The black scale bar in all images represents 300 nm. Aggregate heights in all images are indicated by false-color scale given below images. The subsequent columns show representative ThT responses, SLS intensities, and particle size distribution peaks obtained with DLS. RF growth displays a clear lag period in all three signals. RF nucleation causes the formation of two separate aggregate peaks in DLS, the sizes of which remain essentially stationary. Oligomer formation and subsequent CF nucleation and growth produce continuous increases in ThT and SLS. CF nucleation only generates one aggregate peak and does not yield a discernible discontinuity in ThT or SLS responses. Precipitation, in turn, induces sharp spiking in ThT and SLS signals, with the corresponding DLS autocorrelation functions indicating particle sizes that will settle out of solution, thereby making size determinations unreliable (for further details see refs (17) and (28)).
Kinetic Phase Diagram for HEWL Amyloid Formation: Rigid Fibril-to-Oligomer Transition and Onset of Precipitation
We employed the above multimodal set of assembly-specific kinetic signatures (Figure 1) for high-throughput screening of aggregation pathway for HEWL under partially denaturing conditions (pH 2, T = 52 °C), which were kept fixed unless noted otherwise. A select subset of samples was imaged with atomic force microscopy (AFM) to confirm that aggregate morphologies matched their kinetics signatures. By utilizing the above approach, we mapped out the aggregation behavior of lysozyme covering a range of monomer concentrations that varied from 6 μM to 1.4 mM and NaCl concentrations from 50–800 mM. This encompasses the range of physiological lysozyme and salt concentrations41,42 as well as those used in biophysical studies.34,35,43,44 Figure 2 is a kinetic phase diagram that describes the amyloid aggregates obtained for a given combination of protein and salt concentration. Each dot in Figure 2 typically represents the result of multiple kinetic measurements under these conditions. RFs are the prevailing aggregate phase in the range of low salt or low protein concentrations covered in our experiments. As we will show, RFs also represent the only thermodynamically stable phase. Upon increased salt or protein concentrations, the system sharply and reproducibly switches to amyloid oligomer formation, with subsequent nucleation of curvilinear fibrils (O/CF). We will refer to this boundary as the “critical oligomer concentration” or COC because of its similarities with the critical micelle concentration or CMC in surfactant systems. Further increases in protein or salt concentration induce amorphous Ppt. Precipitation is a fast kinetic transition that occurs at high driving force. Experimentally, it is hard to control because of its sensitivity to subtle variations in quench rates and annealing times. We therefore consider this boundary subject to larger systematic errors than the highly reproducible onset of oligomer formation.
Figure 2.
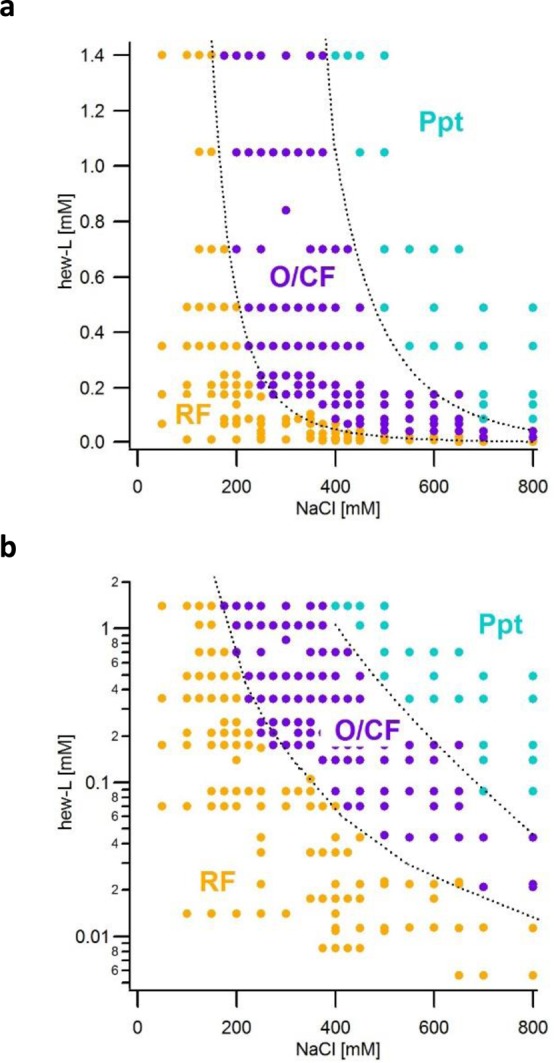
Kinetics phase diagram for RF, oligomer and CF, and precipitate formation of HEWL. (a) Kinetic phase diagram of amyloid aggregate species for HEWL undergoing amyloid growth as a function of protein and NaCl concentrations at pH 2, T = 52 °C. Orange dots represent growth of RFs, purple dots indicate O/CF formation, while blue dots signify Ppt. Aggregate species obtained at a given combination of protein- and salt-concentration were typically determined from multiple kinetics measurements using ThT, SLS, and DLS. Dashed lines are guides to the eye that highlight the well-defined transitions between the three distinct regions in this phase space for each of the three aggregate species. (b) Semilog plot of the same data to highlight data at low protein concentrations.
Amyloid Oligomer and Curvilinear Fibrils Share a Common Transition Boundary
There are three morphologically distinct aggregates that emerge past the COC: amyloid oligomer, CFs, and Ppts. The formation of CFs below the precipitation threshold is separated by a lag period from the onset of oligomer formation.35 This nucleation barrier implies that oligomer concentrations need to exceed an, as yet unknown, solubility limit for CFs. We set out to establish this solubility boundary by seeding solutions with preformed CFs and then delineating their transition from growth to decay. At high protein/low salt concentrations, preformed CFs were diluted into a series of solutions at fixed HEWL concentration but decreasing salt molarity (Figure 3a). Conversely, for low protein/high salt concentrations, CF seeds were diluted with different amounts of buffer solution at fixed salt concentration (data not shown). Using DLS, growth and decay rates of the CF peaks were monitored and extracted from exponential or linear fits to the peak intensities versus time. CF solubility was taken as the extrapolated point where CF growth switched over to decay. Within experimental error, CF solubility matched the COC, and we therefore refer to this region by the single acronym O/CF. This also implies that oligomers under these conditions will always form CFs over time.
Figure 3.
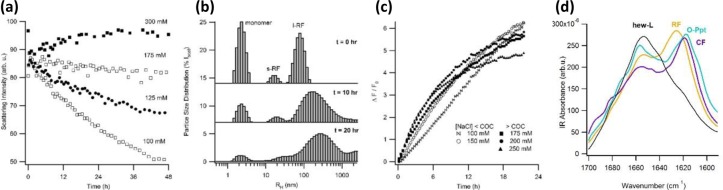
Oligomer versus CF formation, metastability of oligomer phase against RF growth, and amyloid structure of precipitates. (a) CF seeds grown at Clys = 1.4 mM and [NaCl] = 350 mM were subsequently resuspended into solution with [NaCl] that increased from 100–300 mM. The transition from growth to decay of CFs occurred at the same NaCl concentration as delineated by the COC. These data indicate that there is no barrier for oligomer formation and that, within experimental error, the solubility of oligomers is identical to that of CFs. (b,c) RF seeds grown at Clys = 1.4 mM HEWL and [NaCl] = 50 mM were separated from monomers and seeded at 5% into monomer solutions with Clys = 1.4 mM and NaCl between 100 and 250 mM. (b) Changes in the particle size distribution of RFs seeded into 1.4 mM HEWL monomers at [NaCl] = 250 mM s. Both the monomer peak (∼2 nm) and the two aggregate peaks (short and long rigid RFs) are visible right after seeding (0 h). With an increasing incubation period (10 h, 20 h), the area under the RF peak grows at the expense of the monomer peak with very large aggregates that settle out near the end. (c) ThT fluorescence responses for RF seeded into fresh lysozyme (1.1 mM) at NaCl concentrations below (100, 150 mM) and above (175, 200, and 250 mM) the COC. In all cases, RFs continue to grow rapidly. (d) ATR-FTIR spectra within the Amide I band for native HEWL (black), amyloid RFs (orange), CFs (purple), and precipitates (blue) formed under the conditions used to determine the phase diagram in Figure 2. Notice the peaks near 1620 cm–1 in all three aggregate spectra, including that for precipitates, which are considered diagnostic of amyloid beta-sheet structures.
Amyloid Oligomers and Their Curvilinear Fibrils Are Thermodynamically Metastable
The above data indicate that amyloid oligomers and CFs will only form once solution conditions cross the COC. This does not indicate, though, whether the COC is a thermodynamic or kinetic phase boundary. If the COC is a thermodynamic phase boundary, then RFs, which thrive below the COC, should dissolve upon crossing the COC. Alternatively, oligomers and CFs could represent a metastable phase, the formation of which is kinetically favored but thermodynamically unstable against RF growth. To distinguish between these two scenarios, we generated RFs and seeded them into fresh solutions above the COC for oligomer formation. Figure 3, panel b shows the evolution of the particle size distribution of RFs seeded into 1.4 mM monomeric lysozyme at 200 mM NaCl over a time period of 20 h. Clearly, the RF peak continues to grow at the expense of monomeric HEWL. Figure 3, panel c shows corresponding ThT fluorescence data for RFs seeded into HEWL solutions (1.14 mM) at salt concentrations ranging from below (open symbols) to above (filled symbols) the COC located at 175 mM NaCl. In all cases, RFs continued to grow. This implies that the region for RFs/monomer coexistence extends beyond the COC. The formation of RFs well below the COC further indicates that RF solubility is lower than that of O/CFs. Hence, RFs are the thermodynamically stable aggregate phase, and O/CFs represent a kinetically favored, but thermodynamically metastable, aggregate state.
Precipitation Boundary: Structural Analysis via Infrared Spectroscopy
Because of the lack of a Congo-Red response, we had previously presumed that the precipitates were amorphous aggregates formed by denatured monomers.28 The substantial ThT response evoked by precipitates (Figure 1c) raised the question whether the amorphous aggregates, instead, had an underlying amyloid structure. We therefore compared the infrared spectra of amorphous precipitates with those of lysozyme monomers, RFs, and O/CFs using ATR-FTIR. The resulting infrared absorbance within the Amide-I band is shown in Figure 3, panel d. As described previously,17 RFs and O/CFs both developed Amide-I peaks near 1620 cm–1 wavenumber considered diagnostic of intermolecular β-sheet structures of amyloid aggregates.45,46 However, the β-sheet peak for RFs consistently crested about 5 cm–1 to the left from that for O/CFs. Precipitates formed at high salt/protein concentrations developed a similarly pronounced β-sheet peak at the same wavenumber as O/CFs. The weak peak near 1690 cm–1 of O/CFs was less prominent for precipitates, and the peak near 1655 cm–1 suggests that a residual fraction of α-helical structures remains. These differences probably arise from the difficulties of separating precipitates from their monomeric background via cutoff filters, which is less effective than for O/CFs. Nevertheless, the above IR spectra imply that the precipitates share structural characteristics of amyloid aggregates. Their alignment with the O/CF peak in the Amide-I band further implies that the precipitates originated via rapid formation and subsequent precipitation of amyloid oligomers, and we refer to them from here on out as O-Ppts.
Metastable Phase Boundaries for Kinetic Amyloid Oligomer Phases
The above observations suggest that amyloid oligomers form three distinct aggregate structures: individual amyloid oligomers, which under our experimental conditions, further self-assemble into either CFs or O-Ppts. Our data further indicate that individual oligomers and CFs have essentially identical solubilities that result in a single COC boundary. The onset of oligomer precipitation, in turn, is well separated from the COC. In addition, the rapid growth of RFs within the coexistence region for O/CFs implies that RFs represent the thermodynamically stable phase. We therefore assume that RFs form the thermodynamically stable phase throughout the entire phase space, even though the rapid assembly of O-Ppts prevents us from confirming this presumption experimentally. Figure 4 summarizes the corresponding kinetic phase diagram. The thermodynamic stability of RFs through the phase space is suggested by the yellow background shade, which invades the O/CF and O-Ppt regions. The experimentally determined COC and O-Ppt boundary values, as determined from the data in Figure 2, are shown as open purple and blue squares, respectively. The two solid orange squares represent the measured solubilities for CF from the relaxation data in Figure 3, panel a. Figure 4, panel b presents the same data in a semilog plot in order to better resolve the low HEWL concentration range. The solid lines through either data set indicate the theoretical predictions for either transition based on the colloidal-style models of charge repulsion.
Figure 4.
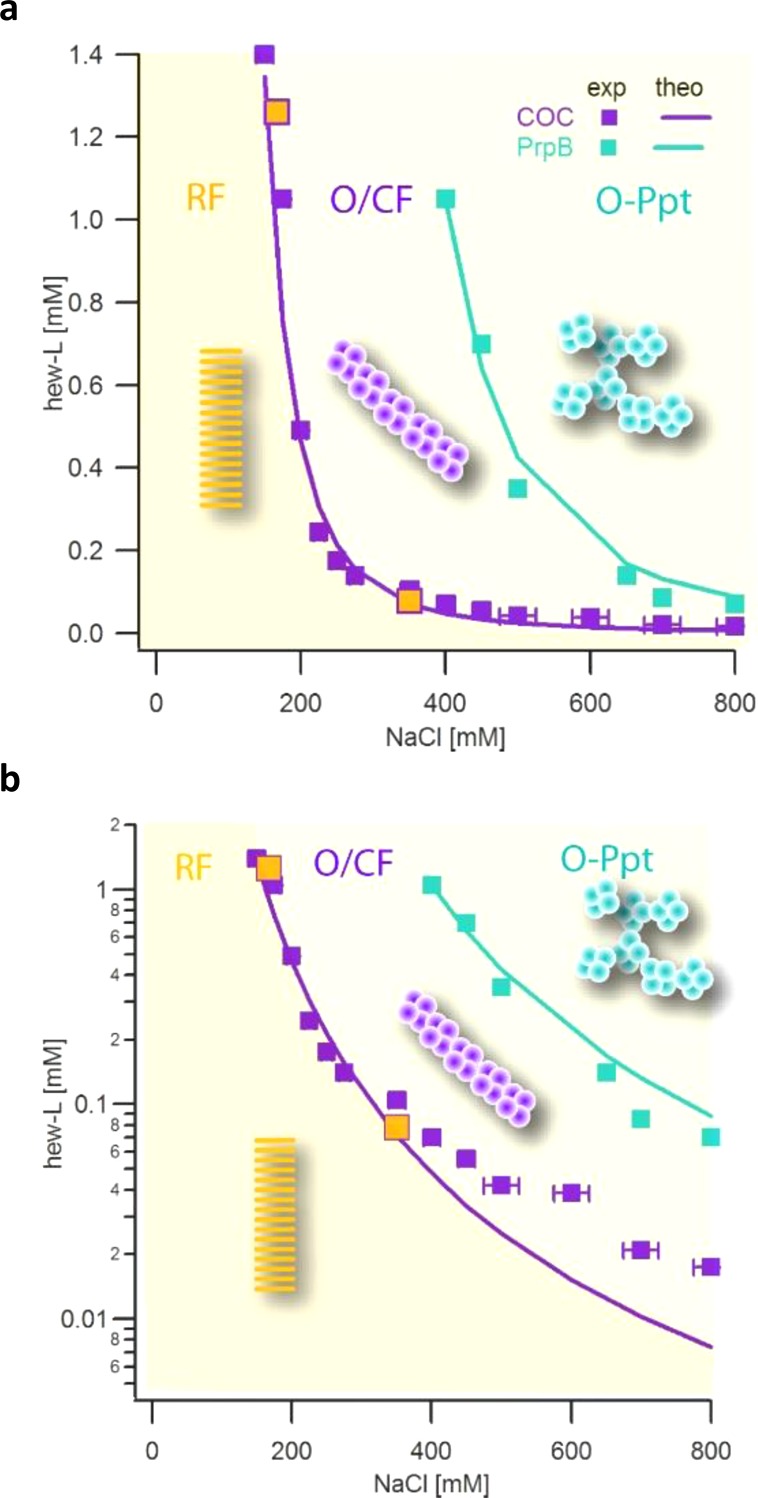
Experimental observations versus theoretical predictions of oligomer phase boundaries. Solid purple squares and their error bars indicate the experimentally determined COC for HEWL amyloid oligomers on a (a) linear and (b) semilogarithmic scale extracted from the data in Figure 2. Filled orange squares display CF solubility determined from relaxation data as those in Figure 3, panel a. Solid blue squares indicate the experimentally determined onset of oligomeric precipitate formation from the data in Figure 2. The yellow background indicates that RFs are the thermodynamic stable phase. The darker yellow shade delineates the region where only RF formation is observed. The lighter shade signifies the region for metastable O/CFs and O-Ppt formation. The solid purple and blue lines through the experimental oligomer phase boundaries are based on theoretical predictions from the colloidal model presented in the text.
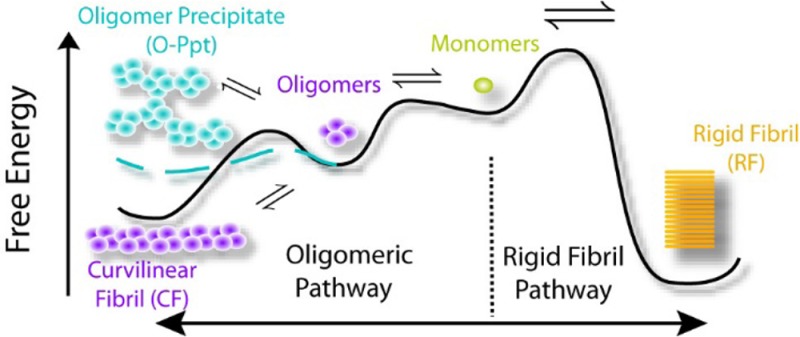
Free Energy Landscape and Colloidal Models of Kinetic Oligomer Phases
Figure 5 shows a schematic of the free energy landscape and the type of amyloid assemblies associated with the minima in this free-energy landscape. Denatured monomers can either assemble into RFs or oligomers and their various assemblies (O, CF, O-Ppt). Our RF seeding experiments (Figure 3b,c) indicate that RFs are the thermodynamic ground state with the lowest free energy. RF formation, however, is kinetically retarded because of a large free energy barrier of nucleation. Amyloid oligomers, in turn, can form nearly instantaneously upon crossing the COC. They can further assemble either into CFs or O-Ppts. The two colloidal models presented below explicitly account for the metastability of the oligomeric phases and their rapid rate of formation. For the COC, we will set up quasi-equilibrium equations for an oligomer–monomer equilibrium. Precipitation of oligomers, in turn, will be modeled as the loss of colloidal stability of the oligomer when compared to the ordered polymerization into CFs.
Figure 5.
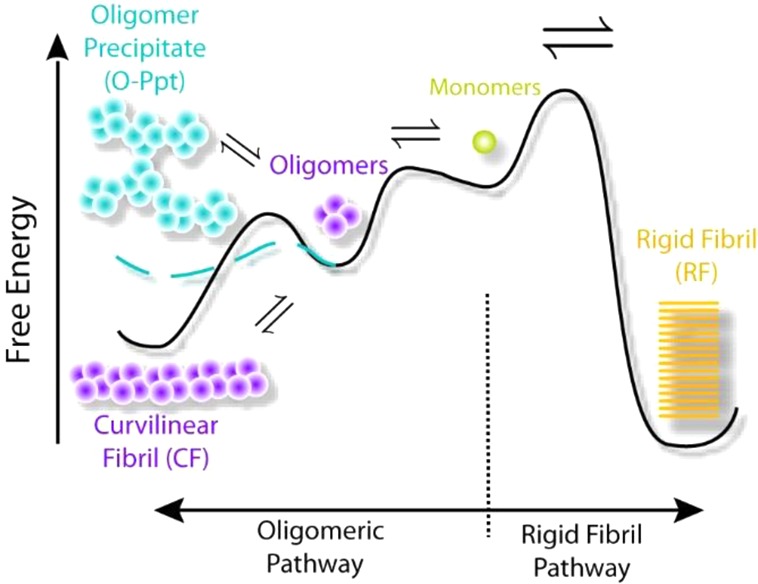
Schematic of the free energy landscape for amyloid aggregate assembly schematic free energy landscape based on the experimental data on HEWL amyloid formation. RFs form the thermodynamic stable state with the lowest free energy minimum. However, they are separated from the (partially denatured) monomers by a high nucleation barrier that retards RF formation compared to the growth kinetics of oligomer phases. Amyloid oligomers, in turn, can form essentially instantaneously upon crossing the COC. They will further self-assemble into CF (lower free energy) separated by only a shallow nucleation barrier. Alternatively, oligomers rapidly coalesce into O-Ppts, as indicated by the blue line. The distinct colors for monomers, RFs, oligomers, and CFs are meant to signify both different aggregate phases and associated changes in monomer structure (see Figure 3d). In contrast, the two colors chosen for CFs and O-Ppts (purple and blue) only highlight different aggregate phases formed by the same amyloid oligomers.
Model of Colloidal Charge Repulsion Reproduces Critical Oligomer Concentration Boundary
To replicate the ionic strength dependence of the COC, we developed a quantitative model of the electrostatic energy cost of confining charged monomers within the volume of an amyloid oligomer. Assuming rapid monomer–oligomer interconversion, the concentration of oligomers is related to the monomer concentration by an equation that takes the form of an nth order reaction equilibrium, that is,
| 1 |
Here, c1 and cn are the monomer and oligomer concentrations in mol/L, respectively, and F(o) is the coalescence free energy of the oligomer discussed below. We chose n = 8 for the number of monomers in an oligomer. This number is based on our previous experimental measurements of the narrow distribution of lysozyme oligomer volumes under these conditions (for details, see ref (35)). This equation predicts a very sharp transition with the oligomer concentration rising as the eighth power of the monomer concentration (Figure 6a). To define a critical oligomer concentration (COC), we use the criterion that equal amounts of protein are in the monomer and oligomer states, c1* = ncn, which yields a critical concentration:
| 2 |
Figure 6.
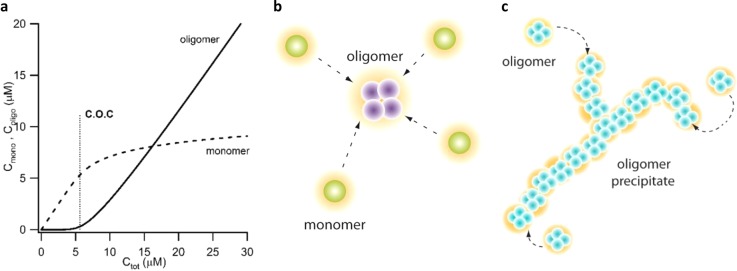
Colloidal model for critical oligomer concentration and onset of oligomer precipitation. (a) Plot of monomer and oligomer concentration versus total protein concentration Ctot for a fixed salt concentration based on eq 1. Notice the highly cooperative transition to oligomer formation with increasing Ctot, which replicates the sharp COC boundary in our experimental data. The COC defined via c1 = ncn is close to the sharp upturn in cn. (b) The colloidal model for amyloid oligomer formation (COC) considers a quasi-equilibrium between charged HEWL monomers and their oligomers (the color change from monomers to oligomers in this schematic does imply an underlying structural change). The model accounts for the salt-dependent cost in free energy of confining n monomers into an n-meric oligomer. Monomers and oligomers are surrounded by an orange cloud that indicates the diffusive screening layer of salt ions. (c) Schematic of the colloidal model used to calculate the contributions of electrostatic repulsion of oligomers condensing into precipitates. The short-range of the Debye layer compared to the size of the precipitates implies that the electrostatic contributions to the free energy are essentially the same for CFs and O-Ppts. This consideration, in turn, leads us to propose an anisotropy in the attractive oligomer interactions as cause for the transition from ordered CF polymerization to precipitation.
Given the steep dependence of cn on c1, the precise choice of definition for the phase boundary is not critical. We are interested in how the COC depends on salt concentration. We split the oligomerization free energy into two parts, Fn(o) = Fnon–ES(o) + FES(o), where Fnon-ES(o) is a nonelectrostatic contribution that is independent of salt concentration. The electrostatic term, FES(o) = Fn – nF1, is the difference in the electrostatic free energy between n like-charged monomers condensed into the volume of one oligomer versus n widely separated monomers (see schematic in Figure 6b). The critical concentration then takes the form
| 3 |
where A is a parameter obtained from fitting the experimentally measured COC value.
Fn and F1 are computed by approximating the protein and oligomer as charged spheres as described in the methods section. We do not expect that the simplifying assumption of a uniformly distributed surface charge significantly affects our results. First, the strong positive charge of lysozyme at pH 2 limits contributions from spatial variations in charge distribution. Second, more than half of the electrostatic contribution to the self-assembly energy comes from the distortion of their Debye screening layers.39 This latter contribution is not sensitive to the precise charge placement on length scales shorter than the Debye length λD. Finally, the product of actual oligomer assembly will have a high (eight-fold) symmetry. The calculated COC values were fit to the experimental data using A = (e(Fnon–ES/kT)/n)1/(n−1) as the only adjustable parameter. The resulting model predictions of the COC are shown in Figure 4 as a solid purple line through the experimental transition values. The model replicates the experimental values remarkably well despite the significant number of simplifying assumptions. Some minor systematic deviations are noticeable in the semilog plot of the phase diagram for high salt and low protein concentrations.
Loss of Colloidal Stability Predicts Onset of Oligomer Precipitation
We attempted to replicate the precipitation boundary using another colloidal model. We observed two distinct modes of supramolecular assembly above the COC: CF polymerization and oligomeric precipitation (OPpt). Given the oligomeric structure of precipitates, this suggests that monomers must first coalesce into oligomers before they assemble into CFs or O-Ppt (Figure 5b). As with RFs versus oligomers, the thermodynamically favorable CFs are kinetically disfavored due to their prolonged lag time, while the O-Ppts appear immediately. The simplest model for the rapid appearance of precipitates would be a diffusion-limited colloidal instability of the oligomers. In diffusion-limited precipitation, the resulting structures have a branched linear morphology with a fractal dimension of 1.8.47 However, the Debye length at the salt concentrations where precipitates are observed is just a few angstroms. As a result, CFs and branched linear precipitates become energetically indistinguishable on the length scale of electrostatic interactions. Hence, the difference between these states must originate, instead, from the nonelectrostatic binding interactions. Assuming anisotropic binding interactions where the oligomers strongly interact in the axial direction and weakly interact along their radial direction could explain the reduced solubility of the CFs relative to the precipitates and their large persistence length relative to the Debye length. We recently postulated similar anisotropy of oligomer interactions in order to explain the prion-like self-replication of lysozyme oligomers under physiological solution conditions.48 Structural support for the polar versus radial anisotropy of amyloid oligomer interactions is provided by the cylindrin structure reported for amyloid oligomers formed by model peptides.25,49
As with the oligomer phase boundary, we model the precipitation boundary as a quasi-equilibrium between two states. The first state is a dilute solution of oligomers. If the concentration of oligomers is cn, then the chemical potential in the solution phase is ln(cn). The second phase is the precipitate. The chemical potential in this state arises primarily from the energetics that form favorable oligomer–oligomer contacts and repulsive electrostatic interactions, that is, μPpt = Frad + FES(Ppt). Here, Frad is the free energy contribution from radial interactions, and FES is that due to electrostatic interactions. Since the time scales for precipitate formation preclude significant annealing, we assume that highly ordered polar contacts will be greatly suppressed compared to the weaker radial contacts. For this reason, we are unable to extract a value for the polar binding energy. The polar binding energy determines the oligomer concentration required for the formation of CFs, which our experiments are unable to resolve from the oligomer formation boundary.
There will also be an entropic contribution to the precipitate chemical potential due to the disordered nature of the precipitate. However, this contribution is a function of the precipitate density that we do not expect to vary over the salt concentrations of interest because of the short screening length. Therefore, the entropic contribution can be absorbed into the unknown parameter Frad. As a crude model, we assume that precipitates will appear when the chemical potential of the solution is greater than that of the precipitate. Therefore, the condition for the onset of precipitation is
| 4 |
Since precipitation occurs when most of the protein is in the oligomer phase, that is, ncn ≈ ctot, we find that precipitation occurs for
| 5 |
where B = neFrad is a parameter that will be obtained by fitting. Since the electrostatic energies of linear assemblies and precipitates are essentially indistinguishable, we used a cylinder geometry to calculate the electrostatic energy contributions to the free energy per molecule.39 The resulting precipitation boundary is superimposed onto the experimental data in Figure 4. Again, the theoretical prediction closely follows the experimental results.
Our expressions for the COC and precipitation boundary contain two free parameters, A and B, which are related to the nonelectrostatic contributions to the oligomerization and precipitation free energies. Since the electrostatic contributions are entirely repulsive, these terms will be dominated by cohesive forces like H-bonds or hydrophobic interactions. Upon fitting eq 3 to the experimentally determined COC, we find that A = 4.3 × 10–8, which corresponds to a nonelectrostatic binding energy of −117 kT. This is partially offset by an electrostatic repulsion that ranges from 84–37 kT as the salt concentration increases from 100–800 mM. Therefore, the net binding energy per protein varies between 4 kT and 10 kT. For the precipitation fitting parameter in eq 5, we find that B = 2.0 × 10–6, which corresponds to Frad = −15.2 kT. With electrostatic repulsion included, the net oligomer–oligomer binding energy varies from 8.9 kT (400 mM salt) to 11.4 kT (800 mM). This is comparable to the binding energy per monomer in the oligomer. Oligomer–oligomer contacts in the precipitate most likely involve multiple monomers that interact by less attractive surfaces.
Discussion
The relationship between rigid amyloid fibrils, which are characteristic of late-stage aggregates, to the toxic, early stage amyloid oligomers, and the conditions that promote the formation of one over the other are critical for our understanding of amyloid self-assembly. By using lysozyme as a model protein, we have mapped out a well-defined transition from rigid fibril to oligomer formation over a wide range of protein and salt concentrations. The data indicate that oligomer formation under denaturing solution conditions is delineated by a well-defined COC. Seeding experiments further established that amyloid oligomers and their curvilinear fibrils represent metastable states, kinetically favored over but located inside the thermodynamic coexistence region of rigid fibrils. Finally, we found that the onset of precipitation was driven by the loss of solubility of rapidly formed oligomeric species. We chose salt and protein concentration as variables and fixed temperature and solution pH, which thereby preserved the (partially denatured) monomer structure and its net charge constant. As a result, we could employ simplified colloidal models of monomer charge interactions to replicate the variation of the COC with protein and salt concentrations. The good agreement with experimental data suggests that charge repulsion plays a critical role in modulating the COC with solution conditions. Models of COCs in relation to the fibril solubility have been studied previously.50,51 However, these earlier works assumed a ternary equilibrium between monomers, oligomers, and fibrils. By considering a quasi-equilibrium between monomer and oligomer states, instead, our analysis directly incorporates the metastability of oligomers with respect to rigid fibril formation. In addition, the anisotropic binding in our model of the oligomers correlates well with the experimentally observed competition between curvilinear fibrils versus precipitate formation.
Conclusions
Our data indicate that amyloid oligomer formation shares intriguing similarities and display important differences with both macroscopic liquid–liquid phase separation in proteins as well as with surfactant self-assembly. First, the formation of metastable oligomers within the coexistence region for mature fibrils resembles the metastable liquid–liquid phases of native proteins located within the crystal–monomer coexistence region.52−54 Such metastable liquid phases have been presumed to be involved in fibril formation as well.55 It is important to remember, though, that the structure of amyloid oligomers confines their spatial extent, and therefore, they cannot coalesce into a uniform extended macroscopic phase. In this regard, the COC of amyloid oligomers more closely resembles the critical micelle concentration of surfactant (or polymeric) systems. Similar to surfactants, amyloid oligomers can also self-assemble into higher-order structures.56 However, micelles are typically the thermodynamic stable aggregate state, while amyloid oligomers are metastable. In addition, the kinetics of amyloid oligomer assembly, when compared to the nearly instantaneous micelle formation in lipids,57 is slow. The relatively slow assembly kinetics for amyloid oligomers likely arise from the significant conformational constraints on their self-assembly due to the complex amphiphilic character of polypetide chains and the steric repulsion among their residues. Despite the complexity of the system, the experimental data and theoretical model suggest that a systematic exploration of the thermodynamics and kinetics of the various aggregate phases of amyloid proteins, and oligomers in particular, can provide important insights into fundamental molecular aspects of amyloid self-assembly and its regulation by the solution environment.
Acknowledgments
We would like to acknowledge the kind access granted to us by Dr. V. Uversky at the USF Health Department of Molecular Medicine to a Wyatt DLS light scattering unit and our colleague Dr. Matthews in the Physics Department at USF for use of the AFM imaging system. This work was supported, in part, by NIH Grant No. R15GM097723 (M.M.) and R01GM107487 (J.D.S.)
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
References
- Kelly J. W. Alternative Conformations of Amyloidogenic Proteins Govern Their Behavior. Curr. Opin. Struct. Biol. 1996, 6, 11–17. [DOI] [PubMed] [Google Scholar]
- Chiti F.; Dobson C. M. Protein Misfolding, Functional Amyloid, and Human Disease. Annu. Rev. Biochem. 2006, 75, 333–366. [DOI] [PubMed] [Google Scholar]
- Dobson C. M. Protein Misfolding, Evolution, and Disease. Trends Biochem. Sci. 1999, 24, 329–332. [DOI] [PubMed] [Google Scholar]
- Jain N.; Bhattacharya M.; Mukhopadhyay S. Chain Collapse of an Amyloidogenic Intrinsically Disordered Protein. Biophys. J. 2011, 101, 1720–1729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gosal W. S.; Clark A. H.; Pudney P. D. A.; Ross-Murphy S. B. Novel Amyloid Fibrillar Networks Derived from a Globular Protein: β-Lactoglobulin. Langmuir 2002, 18, 7174–7181. [Google Scholar]
- Holm N. K.; Jespersen S. K.; Thomassen L. V.; Wolff T. Y.; Sehgal P.; Thomsen L. A.; Christiansen G.; Andersen C. B.; Knudsen A. D.; Otzen D. E. Aggregation and Fibrillation of Bovine Serum Albumin. Biochim. Biophys. Acta, Proteins Proteomics 2007, 1774, 1128–1138. [DOI] [PubMed] [Google Scholar]
- Bromley E. H. C.; Krebs M. R. H.; Donald A. M. Aggregation Across the Length-Scales in β-Lactoglobulin. Faraday Discuss. 2005, 128, 13–27. [DOI] [PubMed] [Google Scholar]
- Lopez de la Paz M.; Goldie K.; Zurdo J.; Lacroix E.; Dobson C. M.; Hoenger A.; Serrano L. De Novo Designed Peptide-Based Amyloid Fibrils. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 16052–16057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lashuel H. A.; LaBrenz S. R.; Woo L.; Serpell L. C.; Kelly J. W. Protofilaments, Filaments, Ribbons, and Fibrils from Peptidomimetic Self-Assembly: Implications for Amyloid Fibril Formation and Materials Science. J. Am. Chem. Soc. 2000, 122, 5262–5277. [DOI] [PubMed] [Google Scholar]
- Makin O. S.; Atkins E.; Sikorski P.; Johansson J.; Serpell L. C. Molecular Basis for Amyloid Fibril Formation and Stability. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 315–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fändrich M.; Dobson C. M. The Behavior of Polyamino Acids Reveals an Inverse Side Chain Effect in Amyloid Structure Formation. EMBO J. 2002, 21, 5682–5690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper J. D.; Lansbury P. T. Models of Amyloid Seeding in Alzheimer’s Disease and Scrapie: Mechanistic Truths and Physiological Consequences of the Time-Dependent Solubility of Amyloid Proteins. Annu. Rev. Biochem. 1997, 66, 385–407. [DOI] [PubMed] [Google Scholar]
- Cohen S. I. A.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. From Macroscopic Measurements to Microscopic Mechanisms of Protein Aggregation. J. Mol. Biol. 2012, 421, 160–171. [DOI] [PubMed] [Google Scholar]
- Dahlgren K. N.; Manelli A. M.; Stine W. B.; Baker J.; Lorinda K.; Krafft G. A.; LaDu M. J. Oligomeric and Fibrillar Species of Amyloid-β Peptides Differentially Affect Neuronal Viability. J. Biol. Chem. 2002, 277, 36046–36053. [DOI] [PubMed] [Google Scholar]
- Walsh D. M.; Klyubin I.; Fadeeva J. V.; Cullen W. K.; Anwyl R.; Wolfe M. S.; Rowan M. J.; Selkoe D. J. Naturally Secreted Oligomers of Amyloid-β Protein Potently Inhibit Hippocampal Long-Term Potentiation in Vivo. Nature 2002, 416, 535–539. [DOI] [PubMed] [Google Scholar]
- Åslund A.; Sigurdson C. J.; Klingstedt T.; Grathwohl S.; Bolmont T.; Dickstein D. L.; Glimsdal E.; Prokop S.; Lindgren M.; Konradsson P.; Holtzman D. M.; Hof P. R.; Heppner F. L.; Gandy S.; Jucker M.; Aguzzi A.; Hammarström P.; Nilsson K. P. R. Novel Pentameric Thiophene Derivatives for in Vitro and in Vivo Optical Imaging of a Plethora of Protein Aggregates in Cerebral Amyloidoses. ACS Chem. Biol. 2009, 4, 673–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foley J.; Hill S. E.; Miti T.; Mulaj M.; Ciesla M.; Robeel R.; Persichilli C.; Raynes R.; Westerheide S.; Muschol M. Structural Fingerprints and their Evolution during Oligomeric versus Oligomer-Free Amyloid Fibril Growth. J. Chem. Phys. 2013, 139, 121901/1–121901/12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gosal W. S.; Morten I. J.; Hewitt E. W.; Smith D. A.; Thompson N. H.; Radford S. E. Competing Pathways Determine Fibril Morphology in the Self-Assembly of β2-Microglobulin into Amyloid. J. Mol. Biol. 2005, 351, 850–864. [DOI] [PubMed] [Google Scholar]
- Klein W. L.; Krafft G. A.; Finch C. E. Targeting Small Aβ Oligomers: The Solution to an Alzheimer’s Disease Conundrum?. Trends Neurosci. 2001, 24, 219–224. [DOI] [PubMed] [Google Scholar]
- Stine W. B. Jr.; Dahlgren K. N.; Krafft G. A.; LaDu M. J. In Vitro Characterization of Conditions for Amyloid-β Peptide Oligomerization and Fibrillogenesis. J. Biol. Chem. 2003, 278, 11612–11622. [DOI] [PubMed] [Google Scholar]
- Uversky V. N. Mysterious Oligomerization of the Amyloidogenic Proteins. FEBS J. 2010, 277, 2940–2953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerf E.; Sarroukh R.; Tamamizu-Kato S.; Breydo L.; Derclaye S.; Dufrêne Y. F.; Narayanaswami V.; Goormaghtigh E.; Ruysschaert J.-M.; Raussens V. Antiparallel β-Sheet: A Signature Structure of the Oligomeric Amyloid β-Peptide. Biochem. J. 2009, 421, 415–423. [DOI] [PubMed] [Google Scholar]
- Zou Y.; Li Y.; Hao W.; Hu X.; Ma G. Parallel β-Sheet Fibril and Antiparallel β-Sheet Oligomer: New Insights into Amyloid Formation of Hen Egg White Lysozyme under Heat and Acidic Condition from FTIR Spectroscopy. J. Phys. Chem. B 2013, 117, 4003–4013. [DOI] [PubMed] [Google Scholar]
- Stroud J. C.; Liu C.; Teng P. K.; Eisenberg D. Toxic Fibrillar Oligomers of Amyloid-β Have Cross-β Structure. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 7717–7722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laganowsky A.; Liu C.; Sawaya M. R.; Whitelegge J. P.; Park J.; Zhao M.; Pensalfini A.; Soriaga A. B.; Landau M.; Teng P. K.; Cascio D.; Glabe C.; Eisenberg D. Atomic View of a Toxic Amyloid Small Oligomer. Science 2012, 335, 1228–1231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahn T. R.; Radford S. E. Folding versus Aggregation: Polypeptide Conformations on Competing Pathways. Arch. Biochem. Biophys. 2008, 469, 100–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhoades E.; Gafni A. Micelle Formation by a Fragment of Human Islet Amyloid Polypeptide. Biophys. J. 2003, 84, 3480–3487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill S. E.; Miti T.; Richmond T.; Muschol M. Spatial Extent of Charge Repulsion Regulates Assembly Pathways for Lysozyme Amyloid Fibrils. PLoS One 2011, 6, e18171.1–e18171.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshimura Y.; Lin Y.; Yagi H.; Lee Y.-H.; Kitayama H.; Sakurai K.; So M.; Ogi H.; Naiki H.; Goto Y. Distinguishing Crystal-Like Amyloid Fibrils and Glass-Like Amorphous Aggregates from Their Kinetics of Formation. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 14446–14451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung J.-M.; Savin G.; Pouzot M.; Schmitt C.; Mezzenga R. Structure of Heat-Induced β-Lactoglobulin Aggregates and Their Complexes with Sodium-Dodecyl Sulfate. Biomacromolecules 2008, 9, 2477–2486. [DOI] [PubMed] [Google Scholar]
- Bolisetty S.; Harnau L.; Jung J.-M.; Mezzenga R. Gelation, Phase Behavior, and Dynamics of β-Lactoglobulin Amyloid Fibrils at Varying Concentrations and Ionic Strengths. Biomacromolecules 2012, 13, 3241–3252. [DOI] [PubMed] [Google Scholar]
- Kodali R.; Wetzel R. Polymorphism in the Intermediates and Products of Amyloid Assembly. Curr. Opin. Struct. Biol. 2007, 17, 48–57. [DOI] [PubMed] [Google Scholar]
- Krebs M. R. H.; Wilkins D. K.; Chung E. W.; Pitkeathly M. C.; Chamberlain A. K.; Zurdo J.; Robinson C. V.; Dobson C. M. Formation and Seeding of Amyloid Fibrils from Wild-Type Hen Lysozyme and a Peptide Fragment from the β-Domain. J. Mol. Biol. 2000, 300, 541–549. [DOI] [PubMed] [Google Scholar]
- Arnaudov L. N.; de Vries R. Thermally Induced Fibrillar Aggregation of Hen Egg White Lysozyme. Biophys. J. 2005, 88, 515–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill S. E.; Robinson J.; Matthews G.; Muschol M. Amyloid Protofibrils of Lysozyme Nucleate and Grow via Oligomer Fusion. Biophys. J. 2009, 96, 3781–3790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parmar A. S.; Gottschall P. E.; Muschol M. Submicron Lysozyme Clusters Distort Kinetics of Crystal Nucleation in Supersaturated Lysozyme Solutions. Biophys. Chem. 2007, 129, 224–234. [DOI] [PubMed] [Google Scholar]
- Schmit J. D.; Dill K. A. The Stabilities of Protein Crystals. J. Phys. Chem. B 2010, 114, 4020–4027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuehner D. E.; Engmann J.; Fergg F.; Wernick M.; Blanch H. W.; Prausnitz J. M. Lysozyme Net Charge and Ion Binding in Concentrated Aqueous Electrolyte Solutions. J. Phys. Chem. B 1999, 103, 1368–1374. [Google Scholar]
- Schmit J. D.; Whitelam S.; Dill K. Electrostatics and Aggregation: How Charge Can Turn a Crystal into a Gel. J. Chem. Phys. 2011, 135, 085103/1–085103/6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malmberg C. G.; Maryott A. A. Dielectric Constant of Water from 0–100 °C. J. Res. Natl. Bur. Stand. 1956, 56, 1–8. [Google Scholar]
- Sasaki S.; Asboe-Hansen G. Serum and Urinary Lysozyme in Patients with Mastocytosis (Urticaria Pigmentosa), Systemic Scleroderma, and Psoriasis1. J. Invest. Dermatol. 1967, 49, 302–305. [Google Scholar]
- Osserman E. F.; Lawlor D. P. Serum and Urinary Lysozyme (Muramidase) in Monocytic and Monomyelocytic Leukemia. J. Exp. Med. 1966, 124, 921–952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frare E.; Polverino de Laureto P.; Zurdo J.; Dobson C. M.; Fontana A. A Highly Amyloidogenic Region of Hen Lysozyme. J. Mol. Biol. 2004, 340, 1153–1165. [DOI] [PubMed] [Google Scholar]
- Chamberlain A. K.; Receveur V.; Spencer A.; Redfield C.; Dobson C. M. Characterization of the Structure and Dynamics of Amyloidogenic Variants of Human Lysozyme by NMR Spectroscopy. Protein Sci. 2001, 10, 2525–2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fändrich M. On the Structural Definition of Amyloid Fibrils and Other Polypeptide Aggregates. Cell. Mol. Life Sci. 2007, 64, 2066–2078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandomeneghi G.; Krebs M. R. H.; McCammon M. G.; Fändrich M. FTIR Reveals Structural Differences between Native β-Sheet Proteins and Amyloid Fibrils. Protein Sci. 2004, 13, 3314–3321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin M. Y.; Lindsay H. M.; Weitz D. A.; Ball R. C.; Klein R.; Meakin P. Universality in Colloid Aggregation. Nature 1989, 339, 360–362. [Google Scholar]
- Mulaj M.; Foley J.; Muschol M. Amyloid Oligomers and Protofibrils, but Not Filaments, Self-Replicate from Native Lysozyme. J. Am. Chem. Soc. 2014, 136, 8947–8956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apostol M. I.; Perry K.; Surewicz W. K. Crystal Structure of a Human Prion Protein Fragment Reveals a Motif for Oligomer Formation. J. Am. Chem. Soc. 2013, 135, 10202–10205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C. F. Isotropic–Nematic Phase Transition in Amyloid Fibrilization. Phys. Rev. E 2009, 80, 031902–031906. [DOI] [PubMed] [Google Scholar]
- Schmit J. D.; Gosh K.; Dill K. Why Do Amyloid Molecules Assemble into Oligomers and Fibrils. Biophys. J. 2011, 100, 450–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muschol M.; Rosenberger F. Liquid–Liquid Phase Separation in Supersaturated Lysozyme Solutions and Associated Precipitate Formation/Crystallization. J. Chem. Phys. 1997, 107, 1953–1962. [Google Scholar]
- Hagen M. H. J.; Frenkel D. Determination of Phase-Diagrams for the Hard-Core Attractive Yukawa System. J. Chem. Phys. 1994, 101, 4093–4097. [Google Scholar]
- Berland C. R.; Thurston G. M.; Kondo M.; Broide M. L.; Pande J.; Ogun O.; Benedek G. B. Solid–Liquid Phase Boundaries of Lens Protein Solutions. Proc. Natl. Acad. Sci. U.S.A. 1992, 89, 1214–1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auer S.; Ricchiuto P.; Kashchiev D. Two-Step Nucleation of Amyloid Fibrils: Omnipresent or Not?. J. Mol. Biol. 2012, 422, 723–730. [DOI] [PubMed] [Google Scholar]
- Jain S.; Bates F. S. On the Origins of Morphological Complexity in Block Copolymer Surfactants. Science 2003, 300, 460–464. [DOI] [PubMed] [Google Scholar]
- Jensen G. V.; Lund R.; Gummel J.; Monkenbusch M.; Narayanan T.; Pedersen J. S. Direct Observation of the Formation of Surfactant Micelles under Nonisothermal Conditions by Synchrotron SAXS. J. Am. Chem. Soc. 2013, 135, 7214–7222. [DOI] [PubMed] [Google Scholar]