Predict Brain MR Image Registration via Sparse Learning of Appearance and Transformation

Abstract

We propose a new approach to register the subject image with the template by leveraging a set of intermediate images that are pre-aligned to the template. We argue that, if points in the subject and the intermediate images share similar local appearances, they may have common correspondence in the template. In this way, we learn the sparse representation of a certain subject point to reveal several similar candidate points in the intermediate images. Each selected intermediate candidate can bridge the correspondence from the subject point to the template space, thus predicting the transformation associated with the subject point at the confidence level that relates to the learned sparse coefficient. Following this strategy, we first predict transformations at selected key points, and retain multiple predictions on each key point, instead of allowing only a single correspondence. Then, by utilizing all key points and their predictions with varying confidences, we adaptively reconstruct the dense transformation field that warps the subject to the template. We further embed the prediction-reconstruction protocol above into a multi-resolution hierarchy. In the final, we refine our estimated transformation field via existing registration method in effective manners. We apply our method to registering brain MR images, and conclude that the proposed framework is competent to improve registration performances substantially.

1. Introduction

Non-rigid pairwise image registration aims to estimate the transformation field following which the moving subject image can deform to the space of the fixed template. The technique of image registration has acted a fundamentally important role in many applications related with medical image analysis during the past decades. After deforming all subject images under consideration to a certain template space, the task to understand the entire image population becomes much easier since the understanding towards a single image can then be propagated to others. Moreover, quantitative evaluations and comparisons upon individual images and image populations can be conducted accurately once all images are carefully registered. In general, the pursuit of accurate registration methods has inspired lots of researches in the area of medical image analysis.

Among existing image registration methods in the literature, most of them regard image registration as a typical optimization problem (Rueckert and Schnabel, 2011; Sotiras et al., 2013), which (1) is favour of higher image similarity between the template and the subject images, (2) imposes certain regularization (i.e., smoothness constraint upon the transformation field usually) in order to suppress unrealistic deformations. The optimization of the transformation field often suffers from the notorious high-dimensional curse, in that (1) the image similarity has to be calculated from the high-dimensional image data and (2) a huge number of parameters need to be optimized for representing the transformation field. The robustness and the accuracy in image registration would especially be challenged, if the variability between the template and the subject is high (e.g., concerning the very complex cortical folding patterns of gyri and sulci in human brain MR images). Then, the determination of the optimal transformation could be easily trapped in local minima/maxima during the optimization.

Recently, several studies show that the challenges in registering a certain subject image to the template can be partially eased by introducing more intermediate images into consideration (Jia et al., 2012b). That is, the intermediate images provide useful guidance at the image scale to the registration of the subject, even though the registration problem is seemingly more complex due to the introduction of the additional intermediate images. The image-scale guidance in general presumes the highly correlated relationship between the entire image appearance and the transformation, as images with similar appearances often have similar transformation fields when registered with an identical template. Therefore, the registration of the subject image can be easily predicted, if there is a certain intermediate image that (1) is similar to the subject and (2) is registered with the template already. In particular, the image-scale guidance can be utilized in two directions as follows.

First, the image guidance to the registration of the specific subject image can be acquired by cherry-picking the intermediate image with the most similar appearances to the subject (Dalal et al., 2010; Hamm et al., 2010; Jia et al., 2011; Munsell et al., 2012; Wolz et al., 2010). The subject can register with the selected intermediate image, and then borrow the pre-existing transformation field that deforms the intermediate image to the template. In this case, the introduction of the intermediate image is able to decompose the registration of the subject into two separate tasks, i.e., to register the subject with the intermediate image and to register the intermediate image with the template. After composing the transformation fields associated with the two tasks, a single transformation then becomes available to initiate the registration of the subject image towards the template. The initial transformation can be further refined via contemporary registration methods in effective manners.

Second, instead of selecting the intermediate image, several models are proposed to generate or simulate the optimal intermediate image, given the subject under consideration (Chou et al., 2013; Kim et al., 2012; Tang et al., 2009). For example, in Kim et al. (2012), support vector regression (SVR) (Drucker et al., 1997) is applied to capture the correlation between features derived from the appearances of a set of training images and the associated transformation fields that register the training images to a certain template. When a new subject image comes, the well-trained regression model can immediately prompt the transformation field according to the appearances of the subject. In the other word, the template can be deformed to derive the simulated intermediate image based on the output of the regression model. The appearances of the simulated intermediate image are usually very similar to the appearances of the subject. Thus, the registration of the subject to the intermediate image is relatively easy, while the transformation field to deform the intermediate image towards the template is already known.

To utilize the intermediate images can effectively improve the performances (i.e., robustness and accuracy) in registering a pair of template and subject images. Obviously, it is critical to acquire the proper intermediate image that optimally approximates the to-be-registered subject image in appearances. Most methods, as described in the above, regard the entire image as a whole. For instance, the intermediate image is selected according to its similarity with respect to the subject that is computed in the image-to-image manner. The evaluation of the image similarity, however, is non-trivial due to the very high dimensionality of the image data. In particular, for brain MR images, high anatomical variations exist within the population. The subject and the intermediate images might share common anatomical structures in certain gyri or sulci, but differ significantly in other areas. As the result, the guidance contributed by specific intermediate images, or the image-scale guidance, might be undermined, since the subject can hardly be approximated by the intermediate images in the entire image space.

Different from the image-scale guidance, we will propose to utilize the patch-scale guidance from the intermediate images for the sake of brain MR image registration in this paper. Note that, in the conventional setting of the image-scale guidance, it is widely accepted that similar images should have similar transformations when registered with an identical template. We further examine this proposition and conclude that, in the patch-scale guidance setting, patches with similar appearances but from different images should also share similar transformation fields when registered to the identical template. Thus, for a certain patch from the to-be-registered subject, its associated transformation can be predicted by identifying patches of similar appearances from the intermediate images. Further, after predicting transformations at an enough number of locations in the to-be-registered subject, the entire transformation field for the subject can be easily reconstructed (i.e., by the means of interpolation).

Our method relies on the point-to-point correspondences that are conveyed by image registration. Specifically, registration estimates the transformation field that deforms each point in the subject to the location of its correspondence in the template. The correspondence is defined such that the two points should be highly alike in terms of their local appearances (i.e., intensities or more sophisticated image context features extracted from the surrounding patches). We presume that all intermediate images are well registered with the template already. Therefore, for points in all intermediate images, their correspondences in the template are apparently available given the existing transformations. Then, for a point in the to-be-registered subject image, we are able to identify the correspondence between the subject point and a certain intermediate point based on the local appearance information of the two points. The correspondence of the intermediate point in the template can also function as the correspondence of the subject point. That is, the subject-template point correspondence is established indirectly and is applicable to the reconstruction of the transformation field for registering the subject. In general, the intermediate images contribute to the registration of the subject with the template by providing the patch-scale guidance, which bridges point-to-point correspondences between the template and the subject.

To effectively utilize the patch-scale guidance from the intermediate images and apply it towards brain MR image registration, we will design a novel prediction-reconstruction strategy, namely the P-R protocol, in this paper. The P-R protocol consists of two coupled steps:

1. Predict the transformations associated with a subset of key points, which are sampled in the image space but cover the entire brain volume;

2. Reconstruct the dense transformation field based on key points and their predicted transformations for registering the subject image with the template.

In the prediction step, it is critical to establish point-to-point correspondences between the subject and the template, by utilizing highly reliable correspondences identified between the subject and the intermediate images. In order to perform correspondence detection rigorously, we have applied the patch-based sparsity learning technique that is widely applied in computer vision (Wright et al., 2010). For a specific subject point, we aim to estimate the linear representation of its surrounding patch given all possible candidate patches from the intermediate images. The optimal linear representation determined by the sparsity learning can locate a sparse set of intermediate patches, the appearances of which are highly similar to the subject patch under consideration. Therefore, all center points of the intermediate patches qualified by the sparse representation can be regarded as the correspondence candidates of the subject point, and then help identify the correspondence of the subject point in the template image. The subject-template point correspondence predicts the transformation, following which the specific subject point is expected to deform.

We apply the prediction procedure upon a subset of selected key points, each of which typically identifies several correspondence candidates in the template space via the sparsity learning technique. In the other word, multiple predictions of the transformation associated with a certain key point can often be collected. Afterwards, we integrate all key points and the multiple predictions of their individual transformations for the reconstruction of the dense transformation field across the entire image space. That is, we compute the varying confidences of individual key points and all of their predicted transformations. Then, we apply an adaptive interpolation approach, which is based on a special family of compact-support radial basis functions (RBFs), to reconstruct the dense transformation field. The reconstruction considers the computed confidences of predictions, as the predicted transformation with a higher confidence plays a more important role. Meanwhile, the reconstructed transformation field is required to be smooth, in order to suppress the unrealistic warping (i.e., folding) of brain tissues.

The P-R protocol is further embedded into a hierarchical framework, namely the P-R hierarchy, which adapts to the typical multi-resolution design in brain MR image registration. Specifically, the P-R protocol first predicts and reconstructs the transformation field at a coarser resolution. Then, the tentatively estimated transformation is further optimized at the finer resolution, where more abundant and detailed image information is taken into consideration. In the other word, the P-R protocol is iterated upon multiple resolutions, i.e., the low, middle, and high resolutions particularly in brain MR image registration. In the final, the reconstructed transformation field can be refined via existing registration methods. The refinement, which aims to boost the quality of the transformation field in registering the subject with the template, can usually be accomplished very effectively.

The manuscript in the next is organized as follows. In Section 2, we will explain the rationale of our method and detail its implementation. Experimental results are reported in Section 3 for the evaluation and the comparison of the performances of the proposed method. Finally, in Section 4, we will conclude this work with extended discussions.

2. Method

We provide an intuitive understanding towards the proposed method and demonstrate its advantages by using a simulated image dataset. As shown in Fig. 1(a), the dataset consists of a root image (highlighted by the red box in the top of the figure) and three branches, each of which consists of 20 images. For convenience, only a limited number of images, including the root and several samples from each branch, are shown in Fig. 1(a). The three branches reflect possible cortical folding patterns in human brains, as more details related with data simulation could be found in Jia et al. (2010).

Figure 1.

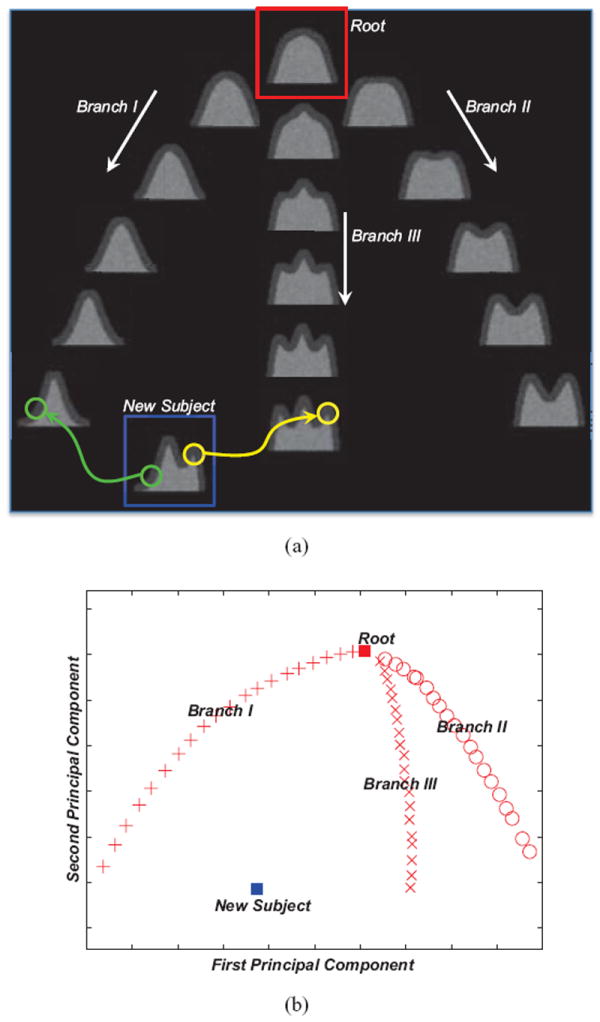
In (a), three branches, as well as the new subject, are simulated by deforming the root. The new subject is able to utilize the patch-scale guidance from individual intermediate images for the registration with the root. The distribution of all images, after being projected to the 2D PCA plane, is shown in (b).

Moreover, we can model the distribution of the entire image dataset in a tree, where all simulated images are expected to register with the root of the tree. The topology of the tree can be easily verified via principal component analysis (PCA). Specifically, by measuring the distance of two images as the sum of squared differences (SSD) of their intensities, we plot the distribution of all simulated images after projecting them onto the 2D plane (c.f., Fig. 1(b)), which is spanned by the first two principal components identified in PCA. The root, as well as three branches of the tree, is clearly visible in the PCA output.

The high inter-image variation could potentially hinder the registration of two images (Jia et al., 2012a; Munsell et al., 2012). For example, in order to register the non-root images with the root directly (i.e., via state-of-the-art methods), we should better utilize the distribution of the dataset (i.e., in the tree structure) and acquire the transformation fields for the non-root images recursively. The reason is that, for each non-root image, from the dataset we are able to identify the intermediate image, which is (1) similar with the non-root image under consideration and (2) more similar with the root than the non-root under consideration. The higher similarity between the intermediate image and the root corresponds to the fact that their registration can usually be done more easily. Bridged by the intermediate image, the registration of the non-root image with the root is thus decomposed into two less challenging subtasks, i.e., to register the non-root subject with the non-root intermediate image and also to register the intermediate image with the root.

Nevertheless, it is non-trivial to identify optimal intermediate images. Given the specific new subject that is highlighted by the blue box in Fig. 1(a), neither already known non-root image is similar enough and thus competent to provide registration guidance at the image scale. On the contrary, the proposed method allows us to utilize the guidance at the patch scale more flexibly. That is, for the green patch in the left part of the new subject, a correspondence patch can be identified from the end image of Branch I to help establish the correspondence between the new subject and the root. Similarly, the yellow patch in the right part can take advantage of the guidance from another intermediate image (i.e., the end image of Branch III). In general, even though we are unable to utilize the image-scale guidance properly, the intermediate images can still contribute at the patch scale to predict the registration of the new subject.

In the next, we will detail the hierarchical predictionreconstruction framework, which is inspired by the above, and apply it to brain MR image registration. For convenience, we will follow the Lagrangian convention to denote the transformation field. In particular, we term the transformation that registers the subject S to the fixed template image T as ϕ(·) : Ω_T → Ω_S, while the point x_T ∈ Ω_T in the template space locates its correspondence at ϕ(x_T) ∈ Ω_S in the subject image space. Reversely, ϕ⁻¹ (·) is capable of deforming the template towards the subject image space. In order to estimate the transformation ϕ(·), we will utilize the patch-scale guidance contributed by the set of intermediate images {M_i∣i = 0, ⋯, M}. For each M_i, the transformation ψ_i (·) that register it with the template is already known. That is, ψ_i(x_T) ∈ Ω_Mi indicates the correspondence of the template point x_T ∈ Ω_T. Note that the template T is also referred as M₀ in this paper, as ψ₀(·) is simply an identity transform that registers the template to itself. In this work, we investigate the prediction of the non-rigid transformation only. Thus all images are necessarily pre-processed, including being aligned to a commons space by affine registration (i.e., FLIRT (Jenkinson and Smith, 2001; Jenkinson et al., 2002)). For easy reference, we also prepare a list of important notations in Table 1.

Table 1.

Summary of important notations in this paper.

Variable	Note	Variable	Note
T	Template image	S	Subject image
Mi	The i-th intermediate image (i is the index)	ΩT, ΩS, ΩMi	Individual image spaces
xT	Template point	xM, x̃M	Points in the intermediate images
xS, x̃S	Points in the subject image	t	Resolution
ϕ(·)	Transformation field to register S with T	ψi(·)	Transformation field to register Mi with T
$\overrightarrow{\varphi }$, ${\overrightarrow{\psi }}_i$	Signature vectors of ϕt(x) and ψi(x)	$\overrightarrow{u}$, ui	Confidence of ψi(x) in prediction
$\overrightarrow{\xi }$, ${\overrightarrow{\theta }}_{\mathit{ij}}$	Signatures of patches at ϕt−1(x) and yij	$\overrightarrow{\nu }$, νij	Confidence of yij in prediction
rc	Maximal radius allowed in correspondence detection	$\overrightarrow{w}$, wij, W	Confidences of combined predictions
K(·), K	RBF kernel function and kernel matrix	σ, c	Control the size of the support of k(·)
${\overrightarrow{\gamma }}_x$, Γ	RBF kernel coefficients	Φ	Predicted transformations

2.1. Prediction Rule and the P-R Protocol

We establish the predictability of the transformation field upon the point correspondences between images, which can be identified from similar patch-scale appearances of corresponding points. Fig. 2 helps illustrate the rationale of our method. In Fig. 2(a) particularly, we enumerate three individual patches (in the top-bottom order) from the template T, a certain intermediate image M_i, and the subject S. All three patches are represented by circles, while their center points are noted by x_T ∈ Ω_T, x̃_Mi ∈ Ω_Mi, x̃_S ∈ Ω_S, respectively. Without losing generality, we define that x_T and x̃_Mi are correspondences to each other such that x̃_Mi = ψ_i(x_T) or $x_T={\psi }_i^{-1}({\stackrel{\sim }{x}}_{M_i})$). Then, assuming that x̃_Mi and x̃_S are also correspondences to each other, we can have ${\varphi }^{-1}({\stackrel{\sim }{x}}_S)={\psi }_i^{-1}({\stackrel{\sim }{x}}_{M_i})$. The reason is straightforward, as x̃_Mi bridges the correspondence between x_T and x̃_S.

Figure 2.

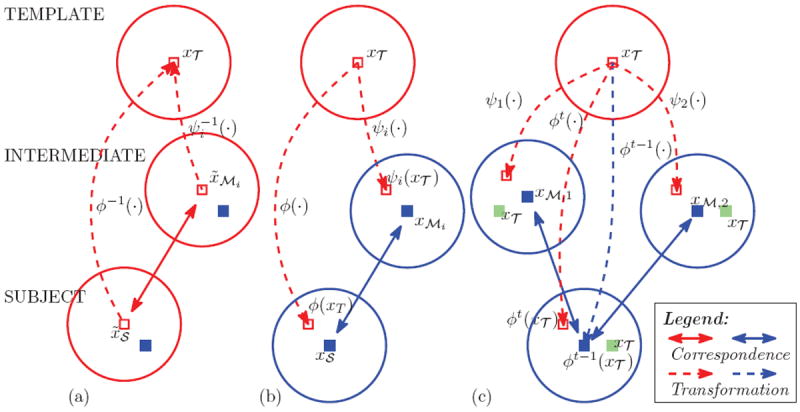
Illustration of the predictability of the transformation: (a) The correspondence between the template point x_T and the subject point x̃_S is established as both points identify x̃_Mi as their correspondence in the intermediate image; (b) The subject transformation ϕ(x_T) is predictable from the intermediate transformation ψ_i(x_T) as in Eq. 1, if x_Mi and x_S are correspondences to each other; (c) Multiple correspondence candidates of x_M might be detected, thus resulting in multiple predictions upon the subject transformation ϕ(x_T).

From the above we are able to predict ϕ⁻¹(·) from the inverted collection $\{{\psi }_i^{-1}(·)\}$. However, it might introduce additional numerical inconsistency to invert the transformation fields. To make our method practically feasible, we can further improve the model to predict ϕ(·) directly from ψ_i(·), instead of its inverse. Specifically, as in Fig. 2(b), we can derive the following proposition.

Proposition 1

If (1) x_Mi ∈ Ω_Mi and x_S ∈ S are correspondences to each other AND (2) x_Mi is spatially close to ψ_i(x_T), then

$$\varphi (x_T)-x_S={\nabla }_{\varphi }(x_T){(\nabla {\psi }_i(x_T))}^{-1}({\psi }_i(x_T)-x_{M_i}),$$ (1)

where ∇ indicates the Jacobian operator.

Proposition 1, the proof of which is shown in Appendix A, allows us to predict and reconstruct ϕ(·) from the collection {ψ_i(·)} of the intermediate images. To handle all variables (i.e., i, x_T, x_Mi, and x_S in Eq. 1) properly, we propose the P-R protocol and apply it to brain MR image registration. The P-R protocol generally consists of two steps, namely the prediction and the reconstruction. In the prediction step, we first select a set of key points from the template image space. More details regarding the selection of key points will be introduced in Section 2.5. Each key point is then fed as an instance of the variable x_T to Eq. 1. We further relate x_S with the tentative estimation of ϕ(x_T) and convert Eq. 1 to the incremental optimization style as

$${\varphi }^t(x_T):={\varphi }^{t-1}(x_T)+\nabla {\varphi }^{t-1}(x_T){(\nabla {\psi }_i(x_T))}^{-1}({\psi }_i(x_T)-x_{M_i}).$$ (2)

Here, t records the timing (or iteration) in optimizing ϕ(·). We also use ∇ϕ^t−1(x_T) to approximate the Jacobian of ϕ^t(x_T) by assuming that ϕ^t(x_T) can only be generated by changing ∇ϕ^t−1 (x_T) mildly. Next, we determine the variables i (as well as ψ_i(x_T)) and x_Mi, such that x_Mi ∈ Ω_Mi is the correspondence to the previously estimated ϕ^t−1(x_T) ∈ Ω_S given the patch-scale appearances of the two center points. In the reconstruction step (Section 2.4), we are able to interpolate the continuous transformation field for the entire image space, based on all key points and their predicted transformations.

Given the key point x_T, several intermediate images with their individual contributions as ψ_i(x_T) might be available. Moreover, multiple instances of x_Mi can potentially be identified as correspondences to ϕ^t−1(x_T) as well. Though the number of correspondences can be arbitrarily reduced to 1 for each instance of x_T, to allow multiple correspondences can greatly improve the robustness and the accuracy for correspondence detection (Chui and Rangarajan, 2003). To this end, we apply the sparsity learning technique (Wright et al., 2010) for the determination of i and x_Mi, while details can be found in Sections 2.2 and 2.3, respectively. In general, the sparsity learning technique allows multiple yet only a limited number of instances of ψ_i(x_T) and x_Mi to contribute to the prediction in Eq. 2. Meanwhile, we are able to attain the confidences to the instances of ψ_i(x_T) and x_Mi that are active in the prediction. The products of the confidences of ψ_i(x_T) and x_Mi are further regarded to measure the confidences of the resulted predictions. All key points and their multiple predicted transformations, along with the varying confidences, are passed to the reconstruction of the dense transformation field.

2.2. Prediction: Determine i and ψ_i(x_T)

The correspondence between ϕ^t−1(x_T) and x_Mi implies that the locations of the two points should be close to each other, especially in brain MR images after affine registration. Therefore, we expect that ψ_i(x_T) can better predict ϕ^t(x_T) if the two transformations are more similar. In Fig. 2(c), for example, we assume that the point ϕ^t−1(x_T) identifies its correspondence x_M,1 from M₁ and another correspondence x_M,2 from M₂. However, the challenges in determining x_M,1 and x_M,2 are different concerning ψ₁(x_T) and ψ₂(x_T). As ψ₂(x_T) is closer to ϕ^t(x_T) than ψ₁(x_T) (in reference to the marked location of x_T), the correspondence detection for x_M,1 thus should be conducted in a much larger area in that ∥x_M,1 − ϕ^t−1(x_T)∥ > ∥x_M,2 − ϕ^t−1(x_T)∥. In this case, ψ₂(x_T) is obviously a better selection for the sake of predicting ϕ(x_T).

In order to determine ψ_i(x_T) that is similar to ϕ^t(x_T) and compute the accompanying confidence, we investigate the sparse representation of ϕ^t(x_T) over the dictionary that is spanned by ψ_i(x_T). Assuming that ϕ^t(x_T) and ψ_i(x_T) are signified by the vectors $\overrightarrow{\varphi }$ and ${\overrightarrow{\psi }}_i$, respectively, we aim to solve

$$\begin{array}{ll}\overrightarrow{u}=& \underset{\overrightarrow{u}}{\mathrm{arg\; min}}{\Vert \overrightarrow{\varphi }-\mathbf{\Psi }\overrightarrow{u}\Vert }^2+\alpha {\Vert \overrightarrow{u}\Vert }_1,\\ \mathrm{s}.\mathrm{t}.& \mathbf{\Psi }=[{\overrightarrow{\psi }}_1,\cdots ,{\overrightarrow{\psi }}_i,\cdots ,{\overrightarrow{\psi }}_M],\\ & \overrightarrow{u}={[u_1,\cdots ,u_i,\cdots ,u_M]}^T,\\ & u_i\ge 0,\forall i.\end{array}$$ (3)

Here, $\overrightarrow{u}$ indicates the vector of the coefficients for the linear representation of $\overrightarrow{\varphi }$ given the dictionary Ψ, which consists of potential contributions from all intermediate images. The l₁ constraint ${\Vert \overrightarrow{u}\Vert }_1$, weighted by the non-negative scalar α, favors a sparse subset of column items from Ψ to represent $\overrightarrow{\varphi }$. The coefficient u_i yielded by the sparsity learning also acts as a similarity indicator between $\overrightarrow{\varphi }$ and ${\overrightarrow{\psi }}_i$ (Wright et al., 2010).

To attribute signatures to both ϕ^t(x_T) and ψ_i(x_T), we vectorize the corresponding transformations into the vectors $\overrightarrow{\varphi }$ and ${\overrightarrow{\psi }}_i$, respectively. On the other hand, $\overrightarrow{\varphi }$ cannot be acquired directly in that ϕ^t(x_T) is still pending for estimation. As an alternative, we generate the signature $\overrightarrow{\varphi }$ from ϕ^t−1(x_T), based on the assumption of the mild changing between ϕ^t−1(x_T) and ϕ^t(x_T). In general, via the optimization in Eq. 3 we are able to identify (or activate) several intermediate images, with their contributions {ψ_i(x_T)} and the non-negative coefficients {u_i}, for the sake of the prediction upon ϕ^t(x_T). We further regard u_i as the measure of the confidence in predicting ϕ^t(x_T) from ψ_i(x_T).

2.3. Prediction: Determine x_Mi

Candidates of x_Mi can be identified via the correspondence detection, centered at the location of ϕ^t−1(x_T), within each active intermediate image after the determination of i (Section 2.2). For convenience, we name all possible candidates of x_Mi as {x_Mij }, as x_Mij indicates the j-th candidate from the i-th intermediate image. The candidate collection {x_Mij } often consists of each grid point x_Mij ∈ Ω_Mi if ∥ϕ^t−1(x_T) − x_Mij∥ ≤ r_c and r_c is the maximally allowed radius for correspondence detection. We define the signatures of the points ϕ^t−1(x_T) and x_Mij as $\overrightarrow{\xi }$ and ${\overrightarrow{\theta }}_{\mathit{ij}}$, respectively, as the similarity between two points can thus be acquired by comparing their signature vectors. In particular, we use the same sparsity learning technique for the purpose

$$\begin{array}{ll}\overrightarrow{\nu }=& \underset{\overrightarrow{\nu }}{\mathrm{arg\; min}}{\Vert \overrightarrow{\xi }-\mathbf{\Theta }\overrightarrow{\nu }\Vert }^2+\beta {\Vert \overrightarrow{\nu }\Vert }_1,\\ \mathrm{s}.\mathrm{t}.& \mathbf{\Theta }=[\cdots ,{\overrightarrow{\theta }}_{1j},\cdots ,{\overrightarrow{\theta }}_{\mathit{ij}},\cdots ,{\overrightarrow{\theta }}_{\mathit{Mj}},\cdots ],\\ & \overrightarrow{\nu }={[\cdots ,{\nu }_{1j},\cdots ,{\nu }_{\mathit{ij}},\cdots ,{\nu }_{\mathit{Mj}},\cdots ]}^T,\\ & {\nu }_{\mathit{ij}}\ge 0,\forall i,j.\end{array}$$ (4)

In Eq. 4, the matrix Θ indicates the dictionary of contributions from the candidate collection {x_Mij}, the vector $\overrightarrow{\nu }$ records the coefficients for the linear sparse representation of $\overrightarrow{\xi }$ given Θ, and the non-negative scalar β controls the sparsity of $\overrightarrow{\nu }$. We define the vectorized patch as the signature (i.e., ${\overrightarrow{\theta }}_{\mathit{ij}}$) for the center point (i.e., x_Mij). Then, ν_ij captures the similarity between the two patches centered at ϕ^t−1(x_T) and x_Mij. Higher ν_ij obviously implies that the correspondence between ϕ^t−1(x_T) and x_Mij is more reliable given their individual patch-scale appearances. As the result, we regard ν_ij as the confidence for predicting ϕ^t(x_T) from x_Mij.

The correspondence detection via Eq. 4 is independent, thus may cause inconsistent outputs for points that are even neighboring to each other. To this end, we enforce the consistency in correspondence detection via the l_2,1-norm constraint (Liu et al., 2009). In particular, we modify the optimization problem in Eq. 4 as

$$\begin{array}{ll}\mathbf{V}=& \underset{\mathbf{v}}{\mathrm{arg\; min}}{\Vert \mathbf{\Xi }-\mathbf{\Theta V}\Vert }^2+\beta {\Vert \mathbf{V}\Vert }_{2,1},\\ \mathrm{s}.\mathrm{t}.& \mathbf{\Xi }=[\cdots ,{\overrightarrow{\xi }}_{x_T+\mathrm{\Delta }},\cdots ],\Vert \mathrm{\Delta }\Vert \le \epsilon ,\\ & \mathbf{\Theta }=[\cdots ,{\overrightarrow{\theta }}_{1j},\cdots ,{\overrightarrow{\theta }}_{\mathit{ij}},\cdots ,{\overrightarrow{\theta }}_{\mathit{Mj}},\cdots ],\\ & \mathbf{V}=[\cdots ,{\overrightarrow{\nu }}_{x_T+\mathrm{\Delta }},\cdots ],\Vert \mathrm{\Delta }\Vert \le \epsilon ,\\ & {\nu }_{x_T+\mathrm{\Delta },\mathit{ij}}\ge 0,\forall \mathrm{\Delta },\forall i,\forall j.\end{array}$$ (5)

Eq. 5 aims to detect correspondence candidates for the centering point x_T, as Δ in the subscript is associated with the point (x_T + Δ) that is neighboring to x_T. Similarly, ${\overrightarrow{\xi }}_{x_T+\mathrm{\Delta }}$ represents the signature vector for (x_T + Δ). The matrix Ξ captures signatures for all points that are located within the radius of ε to the point x_T, while their representation coefficients upon Θ are stored in individual columns of the matrix V. Identical to Eq. 4, the coefficient vector for (x_T + Δ), namely ${\overrightarrow{\nu }}_{x_T+\mathrm{\Delta }}$ is encouraged to be sparse. Meanwhile, we favor that neighboring points should share similar coefficients as their patch-scale appearances could not change drastically. Therefore, besides the l₁ constraint, we enforce the l_2,1 constraint to the matrix V (Liu et al., 2009). That is, each column of V satisfies to the sparsity requirement, while the sparsity patterns of individual columns are expected to be highly similar. In the final, the column for Δ = 0 in V tells all possible correspondence candidates of the point ϕ^t−1(x_T).

Any arbitrary combination of ψ_i(x_T) and x_Mij yields an attempt in predicting ϕ^t(x_T). In particular, we define the confidence w_ij for the attempt as the product of the confidences of ψ_i(x_T) and x_Mij, or w_ij = u_iν_ij. The sparsity enforced in selecting ψ_i(x_T) and x_Mij results in multiple, but a limited number of, predictions with non-zero confidences. In this way, we (1) avoid local minima if only acquiring a single but incorrect prediction for the key point, and (2) suppress a majority of predictions of low reliability. We further normalize the confidence of each key point by w_ij ← w_ij/Σw_ij, to impose equal priors to all key points.

2.4. Reconstruction

We then reconstruct the dense transformation field to fit the multiple predictions of all key points. To this end, we turn to the radial basis function (RBF) for the representation of the transformation field. Suppose that the RBF kernel function is k(·) and ${\overrightarrow{\gamma }}_{x_T}$ is the RBF coefficient vector for the key point x_T, the dense field associated with the arbitrary location $x_T^{\prime }\in {\mathrm{\Omega }}_T$ is then computed by

$$\varphi (x_T^{\prime })=\sum _{x_T}k\left(\Vert x_T^{\prime }-x_T\Vert \right){\overrightarrow{\gamma }}_{x_T}.$$ (6)

We further define the kernel matrix K, in which the entry at the junction of the m-th row and the n-th column is calculated by feeding the Euclidean distance between the m-th and the n-th key points to the kernel function k(·). If only a single prediction was ever attempted for each key point, the residuals for the dense transformation field to fit the predicted transformations of all key points could then be easily computed in the matrix form as ∥Φ − KΓ∥². Here, the predicted transformation (in the transposed row vector form) of the m-th key point is recorded in the m-th row of Φ and its transposed RBF coefficient vector in the m-th row of Γ.

In order to accommodate multiple predictions of each key point, we expand the matrix Φ and further introduce the confidence matrix W for fitting. We enumerate all predictions, as well as the confidences, in Φ and W. Supposing that the p-th row of Φ records a certain prediction for the m-th key point weighted with the confidence w_ij, we set the entry of W at the junction of the p-th row and the m-th column as w_ij and set all other entries in the p-th row as zero. The overall residuals in fitting predictions, weighted by varying confidences, then become ∥Φ − WKΓ∥².

Smoothness regularization is essentially important to the reconstruction of the dense transformation field, in order to suppress any unrealistic warping that might be applied to brain tissues (Rueckert and Schnabel, 2011). To this end, the kernel functions k(·) is usually designed in the style of low-pass filters (Myronenko and Song, 2010). Further, if K is positivedefinite, the regularization can be attained by solving (Girosi et al., 1995)

$$\mathbf{\Gamma }=\underset{\mathbf{\Gamma }}{\mathrm{arg\; min}}{\Vert \mathbf{\Phi }-\mathbf{WK\Gamma }\Vert }^2+\lambda \mathrm{Tr}\left({\mathbf{\Gamma }}^T\mathbf{K\Gamma }\right),$$ (7)

where λ controls the strength of the smoothness constraint. The RBF coefficients Γ, which is needed to generate the dense transformation field according to Eq. 6, are thus solvable in the following

$$\left(\mathbf{K}+\lambda {\left({\mathbf{W}}^T\mathbf{W}\right)}^{-1}\right)\mathbf{\Gamma }={\left({\mathbf{W}}^T\mathbf{W}\right)}^{-1}{\mathbf{W}}^T\mathbf{\Phi }.$$ (8)

In Eq. 8, W^T W is a positive-definite diagonal matrix, where the m-th diagonal entry equals the sum of squares of the confidences for all predictions upon the m-th key point.

The kernel k(·) is designed such that K is positive definite and k(·) has low-pass response. Abundant choices of RBF kernels are available, e.g., the thin plate splines (TPS) with polynomial decay in frequency domain (Bookstein, 1989; Chui and Rangarajan, 2003). Most RBF kernels, however, are globally supported, leading to a very dense matrix K and thus suffering from scalability and numerical instability. As a remedy, we use the compactly supported kernel (Genton et al., 2001) for the reconstruction of the transformation field

$$\begin{array}{l}k(\Vert x_T^{\prime }-x_T\Vert )=\\ \{\begin{array}{ll}\left(1-\frac{{\Vert x_T^{\prime }-x_T\Vert }^2}{c}\right)·\exp \left(-\frac{{\Vert x_T^{\prime }-x_T\Vert }^2}{2{\sigma }^2}\right),& \mathrm{if}\Vert x_T^{\prime }-x_T\Vert \le c;\\ 0,& \mathrm{if}\Vert x_T^{\prime }-x_T\Vert >c.\end{array}\end{array}$$ (9)

The kernel k(·) is obviously a truncated Gaussian, as it cuts to 0 if beyond the compact support $(\Vert x_T^{\prime }-x_T\Vert >c)$. The resulted kernel matrix K is sparse and thus benefits solving Eq. 8.

To alleviate the concern over the optimal parameters of the kernel, we apply the multi-kernel strategy (Floater and Iske, 1996) to recursively reconstruct the transformation field. To derive a set of RBF kernels k_h(·), we fix σ in Eq. 9 and adjust c. The size of the compact support for k_h(·), denoted by c_h, satisfies to c_h = c_h−1/2. For the sake of the reconstruction, we always start with the kernel c₁. Then, the residuals after using the kernel k_h−1(·) are further fitted by the kernel k_h(·), which owns better capability in modeling transformations at higher frequencies. The iterative procedure terminates when the stopping criterion is met, i.e. the residual ∥Φ−WKΓ∥² is tiny enough, or the number of allowed kernels is exhausted. In the final, the dense transformation field is represented by integrating contributions from all kernels involved.

2.5. The P-R Hierarchy

The P-R protocol can be naturally embedded into a hierarchical framework in order to better tackle the high complexity in brain MR image registration. The hierarchy gives a schematic solution that supports multi-resolution optimization upon the transformation field. That is, the transformation field predicted in an early level can initialize the next level of the higher resolution. In particular, by relating the variable t in Eq. 2 to the low-middle-high resolutions, we summarize the P-R hierarchy as follows

1: Load T, S, {M_i}, and {ψ_i(·)};

2: Initialize ϕ(·) to the identity transform;

3: Select a set of template key points X ⊂ Ω_T;

4: for level ∈ {1, 2, 3} do

5:  Select a subset of key points X_level ⊂ X;

6:  for x_T ∈ X_level do

7:   Determine i to activate ψ_i(x_T) (c.f. Eq. 3);

8:   Determine x_Mi as correspondence candidates of ϕ^level−1(x_T) (c.f. Eq. 5);

9:   Acquire multiple predictions of ϕ^level(x_T) (c.f. Eq. 2);

10:  end for

11:  Reconstruct the dense transformation field ϕ^level(·) (c.f. Section 2.4);

12: end for

13: Save ϕ³(·) as the final output of ϕ(·).

The hierarchy above functions in the way similar to state-of-the-art multi-resolution image registration methods, which are needed for registering all intermediate images with the template and for refining the transformation field predicted by our method. In particular, we use HAMMER (Shen and Davatzikos, 2002) to register all intermediate images to the template, and HAMMER explicitly matches correspondence points for estimating the transformation field in registration. The resulted transformation fields of the intermediate images are then used for the prediction of the transformation that registers a new subject with the template.

The key points are abundant in context information and thus crucial to accurate alignment of neuroanatomical structures. Meanwhile, the set of key points X can be pre-computed once the template image is fixed. As in HAMMER, the key points are mostly located from the transitions of individual brain tissues (i.e., white matter, grey matter, and cerebrospinal fluid). Then, we can acquire X_level that corresponds to a certain resolution by sampling X randomly. The subset of key points X_level enlarges its size gradually when the level increases (i.e., 1.0×10⁴ for the size of X₁, 4.0×10⁴ for X₂, and 1.6×10⁵ for X₃ in the end). For other parameters, each key point is signified by its surrounding 5×5×5 patch, while its correspondence candidates are considered within the 9 × 9 × 9 neighborhood only. We set α = 0.35 in Eq. 3 and β = 0.1 in Eq. 5 empirically. The configuration in reconstructing the dense transformation field will be verified in Section 3.1. In the final, after the P-R hierarchy predicts the dense transformation field that registers the subject with the template, we further refine the estimated transformation field, e.g., by feeding the transformation field as the initialization and running diffeomorphic Demons (Vercauteren et al., 2009) and HAMMER (Shen and Davatzikos, 2002) at the high resolution only, respectively.

3. Experimental Results

In this section, we apply the proposed P-R hierarchy to both simulated and real datasets for the evaluation and the comparison of its performances. For the sake of refining the transformation predicted by our method, we use two state-of-the-art registration methods, i.e., diffeomorphic Demons (Vercauteren et al., 2009) and HAMMER (Shen and Davatzikos, 2002). The refinements are conducted within the original image resolution (or the high resolution) only and following the recommended configurations of the two methods. Details related to the experiments on the individual datasets are reported in the following.

3.1. Simulated Data

We independently simulate two sets of transformation fields, as each set consists of 100 fields represented by B-Splines. The two image datasets are then generated by deforming a preselected template in accordance to all simulated transformation fields. The template serving both simulations is arbitrary and the same, which is the fourth image in the LONI LPBA40 dataset (Shattuck et al., 2008). In the pre-processing steps, the template is isotropically resampled to the size of 220×220×184 and the spacing of 1 × 1 × 1mm³. The control points of B-Splines in simulating transformation fields are placed 8mm apart isotropically. In the first simulation set, the B-Spline coefficients for control points along all axes are uniformly sampled from −10mm to +10mm. More drastic deformations are simulated in the second set, as the coefficients are sampled from −20mm to +20mm. Exemplar slices from the template and simulated images are shown in Fig. 3, where the appearance differences between each simulated image and the template is clearly larger in the second simulation set than in the first set.

Figure 3.

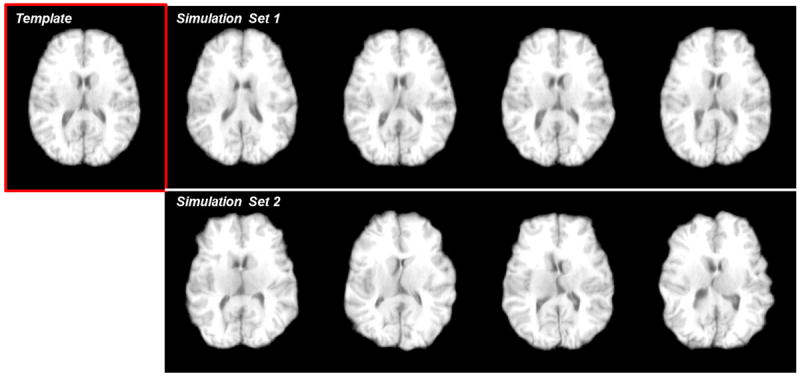
The template (highlighted by the red box) and samples of the simulated images for Section 3.1. In the first set, the B-Spline coefficients of the control points are uniformly sampled from −10mm to +10mm. In the second set, the coefficients are sampled from −20mm to +20mm. All control points are placed 8mm apart isotropically.

From all simulated images, we can designate one as the subject. Other images in the same simulation set are then used as the intermediate. The transformation field that registers each intermediate image to the template is acquired by inverting the transformation field used for simulation directly by ITK (http://www.itk.org). Moreover, we regard the inverse of the simulated field of the subject as the groundtruth, against which the transformation produced in image registration can be quantitatively compared. Registration tasks and subsequent evaluations related to the two sets are conducted independently, though both sets share the same template. In each set, we randomly select 10 different subjects in order to repeat our tests.

There are two specific aims in the quantitative comparisons upon the simulated datasets. First, we break down our method and test the performance gains of its two major components, i.e., transformation prediction of the key points and reconstruction of the dense transformation field. Second, we combine our method with the refinement via state-of-the-art methods, and demonstrate the superiority of applying the patch-scale guidance to image registration over (1) the conventional direct registration and (2) the indirect registration with the image-scale guidance.

3.1.1. Errors of Predicted and Reconstructed Transformations

First, we examine the predicted transformation for each key point (located in the template image space) and compute the error with respect to the groundtruth. For each subject, we calculate the mean error for all key points. The errors are further averaged across all 10 testing subjects in each simulation set. The errors are summarized in Table 2, where we “downgrade” the proposed method for comparison. In particular, we loosen the requirements upon the consistency of correspondence detection for the downgraded method, which thus complies with the model in Eq. 4, instead of Eq. 5 in our full method. From the table, we observe that

1. The proposed full method (Set 1: 1.951mm; Set 2: 2.619mm) results in lower prediction errors than the downgraded method (Set 1: 2.117mm; Set 2: 3.203mm) on both simulation sets, implying the effectiveness of the neighborhood consistency enforced in Eq. 5.

2. Even though the appearance variation of the simulated images could be high especially in the second simulation set, our method is still capable of predicting the transformations of the key points by utilizing the patch-scale guidance from the intermediate images in a robust manner. The predictions are used for the reconstruction of the dense transformation field and subsequent refinement.

Table 2.

Errors (mm) of the predicted transformations of the key points.

Predicted by	Downgraded Method (c.f., Eq. 4)	Our Full Method (c.f., Eq. 5)
Simulatation Set 1	2.117 ± 0.980	1.951 ± 0.963
Simulatation Set 2	3.203 ± 1.715	2.619 ± 1.464

Second, we compute the errors related to the reconstruction of the dense transformation fields, based on the predictions of our full method (c.f., the right column in Table 2). As in Section 2.4, we use a set of compactly supported RBF kernels for the reconstruction of the transformation field, based on the key points and their previously predicted transformations. The error between each reconstructed transformation field and the groundtruth is then computed. The mean errors across all testing subjects, as well as the standard deviation, are provided in Table 3. Comparisons between our method and two alternative reconstruction methods are also conducted in the table.

1. We compare our method with TPS, which is often applied for interpolating the transformation field in the literature (Rohr et al., 2001; Chui and Rangarajan, 2003; Wu et al., 2010; Yap et al., 2010). In our experiment, we adopt the configurations and the parameters that are recommended in Wu et al. (2010).

2. We can also use a single RBF kernel, instead of multiple kernels in our method, to reconstruct the field. The optimal parameters (i.e., c and λ) are determined for each simulation set such that (1) no folding occurs in the predicted transformation field due to λ and (2) the residual error is minimal by manually inspecting outputs of different parameters.

3. For our method, we cascade 3 compactly supported kernels (λ = 0.05) and set c₁ = 10mm for the first kernel. The settings are then adjusted automatically following the strategy in Section 2.4.

Table 3.

Errors (unit: mm) of the reconstructed transformation fields.

Reconstructed by	TPS	Single Kernel	Our Method (Multiple Kernels)
Simulatation Set 1	3.472 ± 1.284	2.934 ± 0.932 (c = 9mm, λ = 0.05)	2.785 ± 0.908
Simulatation Set 2	4.991 ± 1.848	4.732 ± 1.692 (c = 7mm, λ = 0.05)	4.266 ± 1.539

From the results in Table 3, we can observe that

1. Our method (Set 1: 2.785mm; Set 2: 4.266mm) consistently yields lower reconstruction errors on both simulation sets, compared to two alternative reconstruction methods. The results suggest that our method could predict a more accurate transformation field for initializing the subsequent refinement.

2. The optimal parameters of the single-kernel-based reconstruction are different for two sets, implying the necessity to tune parameter per dataset. On the contrary, though we arbitrarily apply the same configuration to two sets in our method, we are still able to acquire lower reconstruction errors. To this end, we argue that our method is less sensitive to parameter tuning, which is practically more feasible.

3. The TPS-based reconstruction yields high errors, which are partly due to its scalability issue. In fact, the dense kernel matrix in the TPS-based reconstruction requires us to partition the image space into several blocks (Wu et al., 2010). The transformation fields in individual blocks are independently interpolated and then integrated. Distortions and errors are thus introduced to the adjacency of neighboring blocks inevitably. However, since the RBF kernel is compactly supported in our method, we can take advantage of the sparse kernel matrix and thus solve the problem much more conveniently.

4. We also note that only non-rigid transformations are simulated and need to be estimated in our experiment. Therefore, the capability of TPS to reconstruct affine and non-rigid transformations simultaneously has become redundant in our study.

3.1.2. Errors of Refined Transformations

Given the transformation field reconstructed by the proposed method (c.f. the right column in Table 3), we continue the refinement through Demons (Vercauteren et al., 2009) and HAMMER (Shen and Davatzikos, 2002), respectively. Each refined transformation field is compared with the groundtruth, as the residual errors between the two fields can be calculated. The errors averaged across all testing subjects are summarized in Table 4, where comparisons to the alternative methods are also conducted.

1. We compare our method (utilizing the patch-scale guidance from the intermediate images) with the conventional registration scheme, where the subject is directly registered with the template without using any guidance.

2. Meanwhile, we compare the proposed method to the case where the image-scale guidance, instead of the patch-scale guidance in our method, is applied. In particular, we use the SSD metric, which is popular in the literature, to measure the distance between images. The optimal intermediate image providing the image-scale guidance to each subject is determined such that the distance between the intermediate image and the subject is minimal. After predicting the transformation field based on the image-scale guidance, the same procedure with our method is used for the refinement of the predicted transformation field.

Table 4.

Errors (unit: mm) of the refined (or directly registered) transformation fields.

Refined by Demons	No Guidance (Direct Registration)	Image-Scale Guidance	Our Method (Patch-Scale Guidance)
Simulatation Set 1	0.742 ± 0.172	0.628 ± 0.149	0.592 ± 0.161
Simulatation Set 2	1.175 ± 0.358	1.104 ± 0.331	0.815 ± 0.260
Refined by HAMMER	No Guidance (Direct Registration)	Image-Scale Guidance	Our Method (Patch-Scale Guidance)
Simulatation Set 1	0.499 ± 0.073	0.427 ± 0.071	0.419 ± 0.063
Simulatation Set 2	1.203 ± 0.393	0.923 ± 0.224	0.803 ± 0.210

Based on the observations to Table 4, we are able to conclude that

1. For the first simulation set, the average errors are 0.592mm (refined by Demons) and 0.419mm (refined by HAMMER) for our method. Both errors are lower than the conventional direct registration (0.742mm for Demons, 0.499mm for HAMMER). Similar results can be found for the second simulation set, where the average errors for our method are 0.815mm (refined by Demons) and 0.803mm (refined by HAMMER). Meanwhile, the errors for direct registration are 0.975mm (Demons) and 1.203mm (HAMMER). The results suggest that, by using the transformation field predicted by our method as the initialization, the overall registration performance after refinement can be better than the direct registration.

2. Our method leads to lower errors upon the refined transformation fields by using the patch-scale guidance than the image-scale guidance. Detailed comparisons of the errors can be found in the right two columns in Table 4.

3. We also note that, as the variation of image appearance increases (e.g. in the second simulation set), the performance margin between our method and the image-scale guidance method becomes much wider. The results imply that our method handles large subject-template appearance difference better. A possible reason is that the guidance from a single intermediate image is not fully competent to guide the registration of the subject given the high appearance variation. Nevertheless, in our method, individual key points could take advantages of various intermediate images, resulting in a more flexible and effective utilization of the patch-scale guidance.

In general, we conclude that our method provides good initializations to image registration, as the initialization-refinement strategy can effectively reduce the errors of the transformation fields compared to using the direct registration or the image-scale guidance.

3.2. NIREP NA0 and LONI LPBA40 Data

Our method predicts and reconstructs the transformation field for the subject, which is refined via state-of-the-art registration methods subsequently. Here, we utilize two public datasets, i.e. NIREP NA0 and LONI LPBA40, to demonstrate that the proposed initialization-refinement framework is capable of better registering real brain MR images, compared to the conventional direct registration. To facilitate our experiments, necessary pre-processing (including bias correction, tissue segmentation, affine registration, etc.) is applied to all images in the two datasets. For each dataset, we can randomly designate a template and a subject. Other images in the dataset are then used as the intermediate. Note that the experiments of the two datasets are independently conducted.

After pre-processing, all intermediate images are segmented and then registered with the template via HAMMER (Shen and Davatzikos, 2002), while the key points in the template image space are determined at the same time. The predicted transformation field for the subject can be further refined via existing registration methods, i.e., Demons (Vercauteren et al., 2009) and HAMMER (Shen and Davatzikos, 2002). Moreover, after registering the subject with the template, we adopt the Dice ratio of anatomical ROIs as the indicator of the accuracy of the registration. The Dice ratio measures the overlap of the corresponding ROIs in the deformed subject and the template, as the higher measure typically implies that the two images are registered more accurately (Klein et al., 2009; Rohlfing, 2012). All images in each dataset are tested as the template and the subject exhaustively, as the detailed performances are reported in the following.

NIREP NA0 Dataset

There are 16 images in the NIREP NA0 dataset, each of which is labeled by 32 ROIs. The ROI indices and names are provided in Table 5. We first refine the predicted transformation fields via Demons (Vercauteren et al., 2009). Compared to the direct Demons registration, the overall Dice ratio after refining our prediction increases by 1.49%. Then, we refine the transformation fields via HAMMER (Shen and Davatzikos, 2002). And the overall Dice ratio after refinement is 2.57% higher than directly registering two images via HAMMER. The box and whisker plots of Dice ratios with respect to individual anatomical ROIs are provided in Figs. 4 and 5. In the figures, the median Dice ratio of each ROI is indicated by the circle, while outliers are marked by crosses. We further examine the statistical significance of the improvement of our method over the direct Demons/HAMMER registration via the paired t-tests. When refined by Demons, our method is significantly better (p < 0.05) than the direct Demons registration on 19/32 ROIs. When refined by HAMMER, our method is significantly better (p < 0.05) than direct HAMMER on 16/32 ROIs. The ROIs where our method achieves significantly higher/lower Dice ratios are highlighted by the +/− signs along the horizontal axes of Figs. 4 and 5. Note that ROIs labelled in the NIREP NA0 dataset mostly covers the cortical areas of human brains, while the observation of the improvement of our method is not restricted to specific cortical areas.

Table 5.

List of ROIs in the NIREP NA0 dataset.

Index	ROI	Index	ROI	Index	ROI
1	L Occipital Lobe	2	R Occipital Lobe	3	L Cingulate Gyrus
4	R Cingulate Gyrus	5	L Insula Gyrus	6	R Insula Gyrus
7	L Temporal Gyrus	8	R Temporal Gyrus	9	L Superior Temporal Gyrus
10	R Superior Temporal Gyrus	11	L Infero Temporal Region	12	R Infero Temporal Region
13	L Parahippocampal Gyrus	14	R Parahippocampal Gyrus	15	L Frontal Lobe
16	R Frontal Lobe	17	L Superior Frontal Gyrus	18	R Superior Frontal Gyrus
19	L Middle Frontal Gyrus	20	R Middle Frontal Gyrus	21	L Inferior Gyrus
22	R Inferior Gyrus	23	L Orbital Frontal Gyrus	24	R Orbital Frontal Gyrus
25	L Precentral Gyrus	26	R Precentral Gyrus	27	L Superior Parietal Lobule
28	R Superior Parietal Lobule	29	L Inferior Parietal Lobule	30	R Inferior Parietal Lobule
31	L Postcentral Gyrus	32	R Postcentral Gyrus

Figure 4.

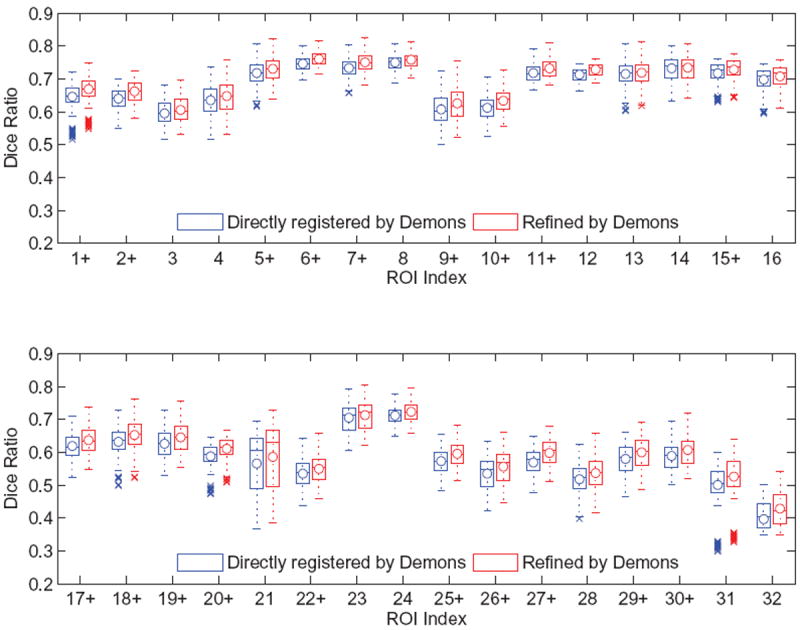
The box and whisker plots of the Dice ratios upon the NIREP NA0 dataset after (1) direct registration by Demons and (2) refining the outputs of our method by Demons. The ROI names corresponding to their indices are listed in Table 5.

Figure 5.

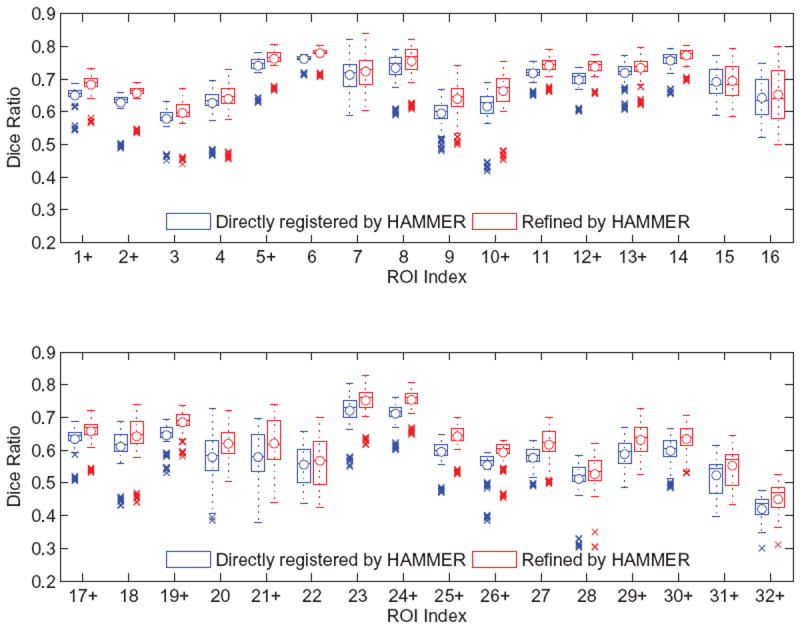
The box and whisker plots of the Dice ratios upon the NIREP NA0 dataset after (1) direct registration by HAMMER and (2) refining the outputs of our method by HAMMER. The ROI names corresponding to their indices are listed in Table 5.

LONI LPBA40 Dataset

The LPBA40 images contains 40 images, each of which is labeled by 54 ROIs. The ROI indices and names are provided in Table 6. Similar to the experiment on the NIREP dataset, we refine the predicted transformation fields via Demons (Vercauteren et al., 2009) and HAMMER (Shen and Davatzikos, 2002), respectively. Compared to the direct registration via Demons, the overall Dice ratio after refining the outputs of our method increases by 1.47%. Compared to the direct registration via HAMMER, the combination of our method and the refinement improves the overall Dice ratio by 1.88%. The box and whisker plots of Dice ratios with respect to individual anatomical ROIs are provided in Figs. 6 and 7. In the figures, the median Dice ratio of each ROI is indicated by the circle, while outliers are marked by crosses. We further examine the statistical significance of the improvement of our method over the direct Demons/HAMMER registration via the paired t-tests. When refined by Demons, our method is significantly better (p < 0.05) than the direct Demons registration on 23/54 ROIs. When refined by HAMMER, our method is significantly better (p < 0.05) than direct HAMMER on 34/54 ROIs, yet worse on 2/54 ROIs. The ROIs where our method achieves significantly higher/lower Dice ratios are highlighted by the +/− signs along the horizontal axes of Figs. 6 and 7. Also, similar with the NIREP NA0 dataset, the improvement of our method can be found across the whole brain, instead of specific anatomical areas.

Table 6.

List of ROIs in the LONI LPBA40 dataset.

Index	ROI	Index	ROI	Index	ROI
1	L Superior Frontal Gyrus	2	R Superior Frontal Gyrus	3	L Middle Frontal Gyrus
4	R Middle Frontal Gyrus	5	L Inferior Frontal Gyrus	6	R Inferior Frontal Gyrus
7	L Precentral Gyrus	8	R Precentral Gyrus	9	L Middle Orbitofrontal Gyrus
10	R Middle Orbitofrontal Gyrus	11	L Lateral Orbitofrontal Gyrus	12	R Lateral Orbitofrontal Gyrus
13	L Gyrus Rectus	14	R Gyrus Rectus	15	L Postcentral Gyrus
16	R Postcentral Gyrus	17	L Superior Parietal Gyrus	18	R Superior Parietal Gyrus
19	L Supramarginal Gyrus	20	R Supramarginal Gyrus	21	L Angular Gyrus
22	R Angular Gyrus	23	L Precuneus	24	R Precuneus
25	L Superior Occipital Gyrus	26	R Superior Occipital Gyrus	27	L Middle Occipital Gyrus
28	R Middle Occipital Gyrus	29	L Inferior Occipital Gyrus	30	R Inferior Occipital Gyrus
31	L Cuneus	32	R Cuneus	33	L Superior Temporal Gyrus
34	R Superior Temporal Gyrus	35	L Middle Temporal Gyrus	36	R Middle Temporal Gyrus
37	L Inferior Temporal Gyrus	38	R Inferior Temporal Gyrus	39	L Parahippocampal Gyrus
40	R Parahippocampal Gyrus	41	L Lingual Gyrus	42	R Lingual Gyrus
43	L Fusiform Gyrus	44	R Fusiform Gyrus	45	L Insular Cortex
46	R Insular Cortex	47	L Cingulate Gyrus	48	R Cindulate Gyrus
49	L Caudate	50	R Caudate	51	L Putamen
52	R Putamen	53	L Hippocampus	54	R Hippocampus

Figure 6.

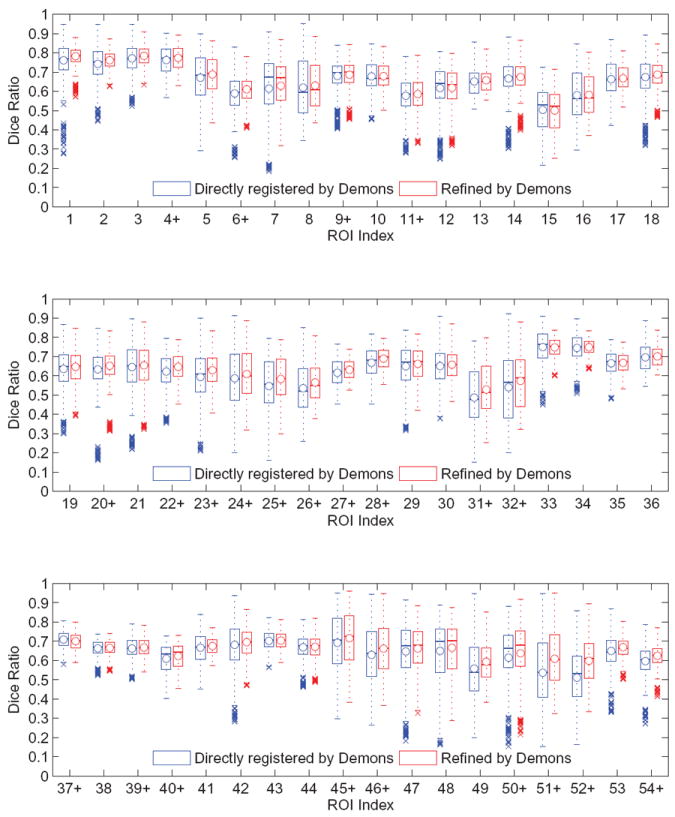
The box and whisker plots of the Dice ratios upon the LONI LPBA40 dataset after (1) direct registration by Demons and (2) refining the outputs of our method by Demons. The ROI names corresponding to their indices are listed in Table 6.

Figure 7.

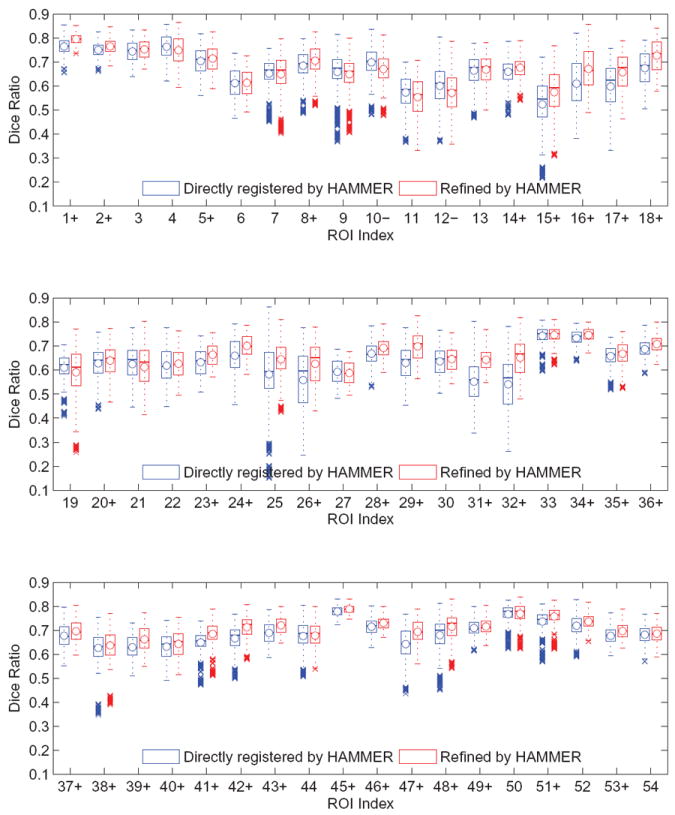
The box and whisker plots of the Dice ratios upon the LONI LPBA40 dataset after (1) direct registration by HAMMER and (2) refining the outputs of our method by HAMMER. The ROI names corresponding to their indices are listed in Table 6.

From the above, we observe that

1. By refining the predicted transformation field, our method yields superior registration accuracy compared to two direct registration methods. The overall Dice ratios after the refinement in our method are significantly higher (p < 0.05) than direct Demons and direct HAMMER, respectively.

2. The numbers of outliers shown are much reduced after the refinement to our method, compared with the direct registration. Meanwhile, the lowest Dice ratio of each ROI in our method is generally higher than the direct registration. The results indicate that our method is effective to handle those difficult registration cases, where extremely low Dice ratios are often produced.

In general, on both two real datasets, the Dice ratios increase by refining the outputs from the proposed method, compared to applying state-of-the-art registration methods directly. Also, our method shows its improved capability of registering “outlier” images. We attribute this improvement to the introduction of the predicted transformation field, which initializes the following refinement.

3.3. ADNI Data

We use the ADNI (Alzheimers Disease Neuroimaging Initiative) data to further demonstrate that our method can effectively utilize the guidance contributed by the intermediate images. From the ADNI cohort, we select 40 images corresponding to normal controls (NC) and 10 images for patients of the Alzheimer’s Disease (AD). All images are properly preprocessed, including bias correction, skull-stripping, tissue segmentation, affine registration, etc. The template is arbitrarily determined to be an NC image, while each time a certain AD image is selected as the subject. All other NC/AD images in the selected dataset serve as the intermediate typically. The test is repeated on all possible subject images.

We compare our method with using the image-scale guidance, where the optimal intermediate image for each subject is determined according to the minimal SSD measure. It is known that the appearances of AD images are often different from those of NC images. For example, as shown by Aljabar et al. (2012), the groups of NC images and AD images are mostly separable on the image manifold which could be learned from simple image distance metric (e.g., SSD). In fact, among all 10 testing cases, 8 subjects identify another AD image as the source of its image-scale guidance, while contributions from the majority of NC images in the dataset are not fully utilized.

We also design a situation where the sources of the patch-scale guidance are limited. That is, since the subject always belong to an AD patient, we arbitrarily remove all NC images from the intermediate image collection. The number of the intermediate images then becomes much smaller, though the appearances of the rest intermediate images are relatively more similar to the subject than the tentatively removed intermediate images. In this way, we can investigate the impacts of different collections of the intermediate images upon the final registration results.

After the subject is aligned with the template in the final, we can compute the Dice overlap ratios of brain tissues (i.e., grey matter and white matter) for quantitative comparison. Note that we carefully check the regularized smoothness of all generated transformation fields. Therefore, the tissue Dice ratio can function as a valid indicator of registration performance in our experiment (Rohlfing, 2012). The results are summarized in Table 7, where we can observe

1. By applying the predicted yet unrefined transformation fields to the subjects, our method achieves the highest tissue Dice ratios compared to using the image-scale guidance and the limited patch-scale guidance. That is, the predictions of our method are the most accurate for registering the subjects with the template.

2. After the refinement via Demons/HAMMER, our method still yields the highest Dice ratios compared to not only using the guidance but also the direct registration. The difference of Dice ratio between our method and each other method is statistically significant (p < 0.05) as revealed by the paired t-test.

3. The results of using the image-scale guidance are generally not satisfactory, as the Dice ratios are lower than other three methods before/after the refinement (or direct registration). A possible reason is that the selected dataset consists of only very few AD images. Since the subjects preferably locate other AD images as the sources of their image-scale guidance, the number of AD images in the dataset might not be enough to provide the guidance properly.

4. By limiting the patch-scale guidance within AD images only, the final registration accuracy is higher than the direct registration and using the image-scale guidance. It is worth noting that, the collection of the intermediate images for the image-scale guidance is much larger than the limited intermediate collection for using the limited patch-scale guidance. However, much better registration quality can still be achieved by a few intermediate images and the mechanism to use the patch-scale guidance.

5. After lifting the limitation upon the intermediate images, our method further improves the registration quality. Although NC images and AD images have different appearances to certain extent, our method allows each AD subject to utilize the guidance from not only other AD images but NC images as well. In this way, our method can utilize more abundant guidance to complete the registration between the subject and the template.

Table 7.

Tissue Dice ratios on the selected ADNI dataset.

Guidance Type	None (Direct Registration)	Image-Scale	Limited Patch-Scale	Our Method (Full Patch-Scale)
	Before Refinement
Grey Matter	–	70.37 ± 5.33	75.03 ± 4.93	77.34 ± 4.20
White Matter	–	71.49 ± 5.29	75.39 ± 4.22	78.18 ± 3.91
	After Refinement/Registration via Demons
Grey Matter	79.35 ± 3.05	78.10 ± 3.29	80.42 ± 2.93	82.83 ± 2.71
White Matter	82.06 ± 1.95	80.72 ± 2.51	82.91 ± 2.62	84.19 ± 2.39
	After Refinement/Registration via HAMMER
Grey Matter	80.77 ± 2.86	77.93 ± 3.20	81.54 ± 2.67	84.10 ± 2.47
White Matter	82.48 ± 1.94	80.31 ± 2.66	83.75 ± 2.19	84.73 ± 2.05

In general, we conclude that our method provides an effective manner to utilize the patch-scale guidance for the sake of registering the subject with the template, even though the two images have large appearance differences. Our results show that the proposed method can achieved higher registration quality compared to (1) the direct registration and (2) using the image-scale guidance.

4. Conclusion and Discussion

We have proposed a novel approach to predict the transformation field for registering a new subject to the template. The prediction utilizes the fact that a point from the subject and another point from the intermediate image should own the same correspondence in the template, if the two points under consideration have similar patch-scale appearances and are correspondences to each other. As the result, by identifying correspondences of subject points in the collection of intermediate images, we are able to predict their associated transformation in registering the subject with the template. The dense transformation field that covers the entire image space can then be reconstructed immediately. We thus propose the P-R protocol and the hierarchical solution for the sake of brain MR image registration. Our method is able to provide satisfactory transformation fields that work as good initializations to the existing registration methods. After refinement, the transformation fields are more accurate in registering the subject, compared to the conventional way in which the subject is registered with the template directly.

Our method owns good scalability in applying the P-R hierarchy to large-scale population of images. As in Sections 2.2 and 2.3, we activate several intermediate images from (ψ_i(x_T)) the pool by determining i (and thus ψ_i(x_T)) first. Then, we identify candidates of x_Mi that are correspondences to ϕ^t−1(x). The order is important. Specifically, the determination of i can be much more efficient than x_Mi, in that the column size of the dictionary Ψ is identical with the number of intermediate images, or O(M). Meanwhile, multiple correspondences may exist in even a single intermediate image. The dictionary Θ has to enumerate all possible instances of y, and thus increases the column size to $O(r_c^{3}M)$ as r_c represents the radius in searching for correspondences. By determining i first, we are able to control the number of activated intermediate images, only from which the contributions to the determination of x_Mi should be counted. Thus, the complexity in determining x_Mi is well scaled regardless of the size of the collection of the intermediate images, as most intermediate images are deactivated already in the determination of x_Mi.

It is worth noting that our method incurs additional computation cost compared to the conventional direct registration, and thus is slower even though we introduce the sequential scheme in determining i and x_Mi. The reason is that we need to identify correspondences between the subject and the intermediate images via sparsity learning in the proposed method; while the conventional registration requires subject-template correspondence information only. However, our method provides a potential solution to tackle the registration task between two images with significantly different appearances, which could be very challenging for direct registration. In our future work, we will apply the proposed method to more applications, including registration of multi-modal images, longitudinal sequences of neonatal data, etc. We will also work on to speed up the proposed method, e.g., by using parallel computation techniques.

Highlights.

1. Initialize brain MR image registration using the transformation field that is predicted by the prediction-reconstruction protocol/hierarchy.

2. Predict point-to-point correspondences between images by using sparsity learning and via bridges of the intermediate images.

3. Reconstruct the transformation field by using compactly supported radial basis kernels.

Appendix A. Proof of Proposition 1

As x_Mi is spatially close to ψ_i(x_T), we can assume that x_Mi = ψ_i(x_T + δx) where δx is a infinitesimal perturbation to x_T. It is implied by ψ_i(·) that the point (x_T + δx) locates its correspondence as x_Mi. Moreover, the points (x_T + δx) and x_S are also correspondences to each other, via the bridge of x_Mi ∈ Ω_Mi. Therefore, we have

$$x_{M_i}={\psi }_i(x_T+\mathit{\delta x})={\psi }_i(x_T)+\nabla {\psi }_i(x_T)\mathit{\delta x}+O(\delta x^T\mathit{\delta x}),$$ (A.1)

$$x_S=\varphi (x_T+\mathit{\delta x})=\varphi (x_T)+\nabla \varphi (x_T)\mathit{\delta x}+O(\delta x^T\mathit{\delta x})$$ (A.2)

We subtract the two equations to eliminate the perturbation variable δx

$${(\nabla {\psi }_i(x_T))}^{-1}(x_{M_i}-{\psi }_i(x_T))={(\nabla \varphi (x_T))}^{-1}(x_S-\varphi (x_T)).$$ (A.3)

Eq. 1 can then be derived after rearranging the above.