Segmentation of Tongue Muscles from Super-Resolution Magnetic Resonance Images

Abstract

Imaging and quantification of tongue anatomy is helpful in surgical planning, post-operative rehabilitation of tongue cancer patients, and studying of how humans adapt and learn new strategies for breathing, swallowing and speaking to compensate for changes in function caused by disease, medical interventions or aging. In vivo acquisition of high-resolution three-dimensional (3D) magnetic resonance (MR) images with clearly visible tongue muscles is currently not feasible because of breathing and involuntary swallowing motions that occur over lengthy imaging times. However, recent advances in image reconstruction now allow the generation of super-resolution 3D MR images from sets of orthogonal images, acquired at a high in-plane resolution and combined using super-resolution techniques. This paper presents, to the best of our knowledge, the first attempt towards automatic tongue muscle segmentation from MR images. We devised a database of ten super-resolution 3D MR images, in which the genioglossus and inferior longitudinalis tongue muscles were manually segmented and annotated with landmarks. We demonstrate the feasibility of segmenting the muscles of interest automatically by applying the landmark-based game-theoretic framework (GTF), where a landmark detector based on Haar-like features and an optimal assignment-based shape representation were integrated. The obtained segmentation results were validated against an independent manual segmentation performed by a second observer, as well as against B-splines and demons atlasing approaches. The segmentation performance resulted in mean Dice coefficients of 85.3%, 81.8%, 78.8% and 75.8% for the second observer, GTF, B-splines atlasing and demons atlasing, respectively. The obtained level of segmentation accuracy indicates that computerized tongue muscle segmentation may be used in surgical planning and treatment outcome analysis of tongue cancer patients, and in studies of normal subjects and subjects with speech and swallowing problems.

1. Introduction

Oral cancer is among the most prevalent cancers in the world, with an estimated 274,000 new cases in 2002 (Parkin et al., 2005) and 264,000 in 2008 (Jemal et al., 2011). Although the mortality rate of oral cancer patients is not considered to be high, the disease and its treatment severely affect their speech, swallowing and mastication, and thus their quality of life. Assessing and understanding the tongue morphology is valuable for proper surgical planning, which may considerably reduce post-operative complications and lead to a faster rehabilitation (Matsui et al., 2007). Besides, quantification of tongue anatomy may help to better understand how humans adapt and learn new strategies for breathing, swallowing and speaking to compensate for changes in function caused by disease, medical interventions or aging. The main imaging modalities that serve these purposes are ultrasound (US) and magnetic resonance (MR) imaging.

During the last couple of decades, real-time US has been the primary imaging modality for providing information on the morphology and motion of the tongue, and thus enabling linguistic and swallowing studies. To perform a computerized analysis of tongue anatomy, Unser and Stone (1992) applied deformable contours, i.e. snakes, to determine tongue boundaries from two-dimensional (2D) US images, which required user interaction to specify the region of interest or correct the snakes if they started to follow wrong boundaries. On the other hand, Akgul et al. (1998) proposed a fully automatic segmentation approach, where snakes were applied to segment US images acquired during speech. The same authors augmented snakes by prior knowledge in the form of predefined speech patterns, which increased the accuracy of tongue boundary detection (Akgul et al., 1998). Li et al. (2005) combined features based on gradients, regions of interest and orientation of boundaries for robust semi-automatic tongue detection. Roussos et al. (2009) proposed to use active appearance models, which allowed tongue segmentation from a limited field of view and extrapolation of tongue boundaries outside the target US image. Fasel and Berry (2010) first filtered US images by applying a type of neural networks called deep belief networks, and then tracked tongue boundaries as paths through the most emphasized image pixels. Tang et al. (2012) modeled 2D tongue movements by Markov random fields and demonstrated the superiority of their segmentation results in comparison to snake-based approaches. Although standard US imaging is inexpensive and noninvasive, the obtained images have a limited field of view and often do not clearly depict important anatomical details, which limit the applicability of US in tongue anatomy studies. By providing better contrast of soft tissues, MR imaging may overcome the drawbacks of US.

Similarly to US images, MR images with short acquisition times facilitate the investigation of tongue motions, including segmentation of the vocal tract (Bresch et al., 2008, Proctor et al., 2010), statistical modeling of speech patterns (Stone et al., 2009), comparison of such patterns between healthy and diseased subjects (Stone et al., 2008), and segmentation of tongue area structures including lips, hard and soft palate, pharyngeal wall, etc. (Bresch and Narayanan, 2009). Chong et al. (2004) applied seeded region growing to semi-automatically segment tongue carcinoma, and validated the obtained results against manual segmentation. Recently, Lee et al. (2013) addressed the problem of tongue segmentation from dynamic three-dimensional (3D) MR images. In this work, a user was required to manually determine the approximate position of the tongue and locate a small number of seed points in the background, which were then propagated to consecutive time frames by non-rigid B-spline registration, and finally used to initialize the random walker segmentation algorithm. In contrast to MR images with low acquisition time, lengthy high-resolution 3D MR imaging preserve a large amount of anatomical detail, which is essential for studying individual tongue muscles. Tongue muscle segmentation obtained from high-resolution 3D MR images with high muscle contrast combined with the whole tongue segmentation and tongue motion estimation, both obtained from dynamic 3D MR images, brings the community closer to automatic computerized analysis of the behavior of individual tongue muscles during speech and mastication. Modern MR protocols allow limited field of view imaging with a resolution of around 1.25 mm³ per voxel, which was demonstrated to be sufficient for in vivo speech studies (Kim et al., 2009). However, the achieved level of contrast and image detail are still not adequate, and make tongue muscle boundaries ambiguously defined and poorly visible for computerized or manual delineation. In vivo acquisition of high-resolution 3D MR images with visible inter-muscle boundaries requires subjects to stay motionless for 4–5 minutes, which is almost impossible due to breathing and involuntary swallowing. Despite the existence of cine and multi-slice MR imaging, up until now this obstacle represented a limitation for visualization and analysis of individual tongue muscles and postoperative monitoring. However, recent achievements in image reconstruction allow the generation of super-resolution 3D MR images of the tongue from sets of orthogonal images, acquired at a lower resolution and combined using super-resolution techniques (Fig. 1) (Woo et al., 2012).

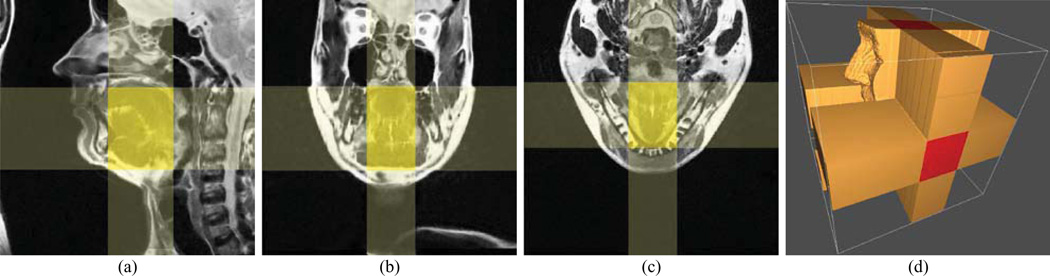
Fig. 1.

An example of a super-resolution 3D MR image of the tongue, reconstructed from sets of orthogonal (a) sagittal, (b) coronal and (c) axial MR images with a limited field of view. The unshaded areas correspond to individual images, the lightly shaded areas to the intersection of two orthogonal images, and the strongly shaded areas to the intersection of three orthogonal images. (d) As a result, only the tongue region is intersected by all orthogonal images, whereas the corners of the volume are not covered by any orthogonal image and therefore represent blank areas.

In this study, we propose, to the best of our knowledge, the first attempt to segment individual tongue muscles from MR images. Tongue muscle segmentation is a challenging task because the tongue is a muscular hydrostat, i.e. a composition of agonist/antagonist muscles without any rigid structures for the muscles to act upon (Levine et al., 2005). Because of this, tongue muscles have a relatively similar physical structure and appearance when observed in MR images, and finding the boundaries of individual muscles in muscular hydrostats is therefore challenging even for an experienced observer. Moreover, non-trivial speech and swallowing motions, and lack of anchor bones are reflected in a complex morphology of tongue muscles. To address these challenges, we propose to apply the game-theoretic framework (GTF) for landmark-based image segmentation, which was already successfully applied to segment lung fields from radiographs, heart ventricles from MR cross-sections, and lumbar vertebrae and femoral heads from computed tomography (CT) images (Ibragimov et al., 2012b, 2014). In the present study, GTF is adapted to segment the genioglossus and inferior longitudinalis tongue muscles from super-resolution 3D MR images. However, poor visibility of tongue muscle boundaries and presence of reconstruction artifacts, such as intensity mismatches, blur, blank image regions, etc., call for improving and extending the original GTF. For this aim, to describe landmarks we first replace individual voxel intensity-based appearance features by more sophisticated Haar-like features, and the consecutive computational costs are reduced by selecting and computing the optimal set of most descriptive Haar-like features for each landmark. Moreover, the landmarks are no longer positioned on the surface of objects of interest, as such surfaces are often poorly visible, but inside and, more importantly, outside of these objects, which makes GTF-based segmentation more universal, accurate and robust. To objectively estimate the performance of GTF, we also apply and evaluate the performance of B-splines and demons atlasing approaches. The obtained results are compared with the inter-observer segmentation variability, which facilitates to understand the complexity of the segmentation problem and its potential for computerized tongue muscle analysis.

The paper is organized as follows. Section II presents the details of GTF, augmented by Haar-like appearance features for landmark detection. Section III focuses on the tongue image database with the corresponding tongue muscle reference segmentation and landmark annotation, and comparison of the obtained results to alternative segmentation approaches. Section IV discusses the obtained results from the perspective of segmentation performance, computation time and applied methodology. We conclude in Section V with directions for future research.

2. Game-Theoretic Segmentation Framework

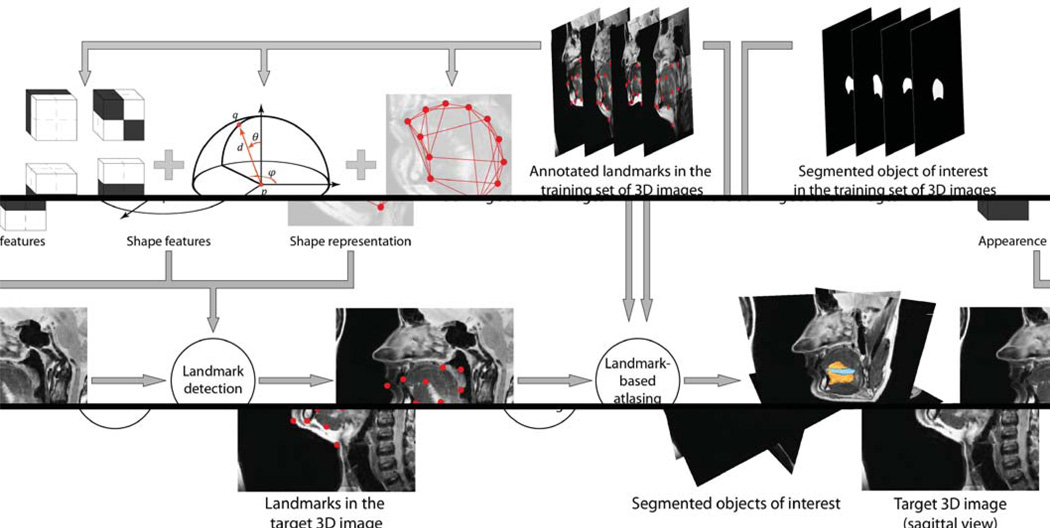
In GTF, segmentation of the object of interest is composed of two steps, namely landmark detection followed by landmark-based atlasing. Each landmark is characterized by its intensity appearance and spatial relationships against other landmarks, both learned from a training set of images, in which the object of interest is already segmented and annotated with corresponding landmarks. For an unknown target image, we first compute the appearance and shape likelihood maps according to the prior knowledge extracted from images in the training set, then apply the appearance likelihood maps to detect landmark candidate points, and finally combine the appearance and shape likelihood maps with a selected graph-based shape representation to obtain the optimal candidate points that represent landmarks. After landmarks are detected, we perform landmark-based atlasing to propagate the segmented object of interest from each image in the training set to the target image. The described framework is schematically shown in Figure 2.

Fig. 2.

A schematic illustration of the game-theoretic framework for landmark-based segmentation of tongue muscles from 3D MR images.

2.1 Appearence Likelihood Maps

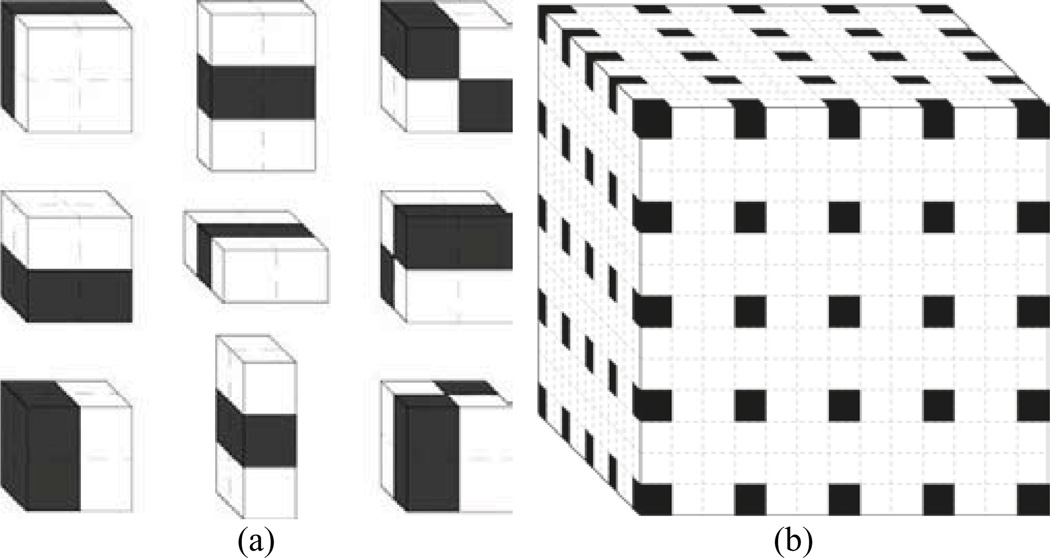
Let the training set of images T consist of super-resolution 3D MR images of the tongue region, and let each image be annotated with a set 𝒫 = {p} of |𝒫| corresponding landmarks that describe the object of interest. Suppose that each landmark p ∈ 𝒫 is associated with some distinctive appearance features, which can be learned from images in the training set and later used to detect the position of the same landmark p in an unknown target image. Local appearance information, such as the intensity of individual voxels, is not descriptive enough, as soft tissues belonging to adjacent anatomical structures often share similar intensities when observed in MR images. Moreover, reconstructed MR images are usually corrupted by intensity artifacts (e.g. intensity inhomogeneity). Therefore, Haar-like features are used instead of individual voxel intensities. Haar-like features are described by linear combinations of the sums of voxel intensities inside adjacent rectangular parallelepipeds (Fig. 3a), with the coefficient of each term of a linear combination being either +1 or −1. As Haar-like features capture larger image regions, they are less sensitive to local intensity variations and therefore provide a more robust description of landmark appearance (Viola and Jones, 2004). Moreover, they can be computed very fast by using an integral representation of the target image (Viola and Jones, 2004). For each landmark p ∈ 𝒫, Haar-like features are extracted at different scales in the neighborhood of the voxel representing landmark p (Fig. 3b). Although such determination is computationally efficient, obtaining all possible features can still be demanding, taking into account the number of landmarks |𝒫| and the size of super-resolution 3D MR images. Among all features, we automatically select |𝒩_p| features with the highest predictive power and use them to define the appearance likelihood map f_p of landmark p by applying Gaussian kernel density estimation:

$$f_p(\nu )=\sum _{k\in {𝒩}_p}\text{exp}(-\frac{{(\mathit{a}(k,\nu )-{\mathit{a}}_p(k))}^2}{2{\mathbf{\sigma }}_p{(k)}^2}),$$ (1)

where a_p(k) is the mean and σ_p(k) is the standard deviation (SD) of the k-th Haar-like feature from set 𝒩_p of features selected for landmark p across all images in the training set, and a(k, ν) is the observed value of the k-th Haar-like feature for an arbitrary point at location ν in the target image. The resulting appearance likelihood map values are normalized against the maximal detected value so that ∀ν: 0 ≤ f_p(ν) ≤ 1.

Fig. 3.

(a) Nine different types of Haar-like features are used to generate appearance likelihood maps. The feature response is the difference between voxel intensities inside shaded and unshaded regions. (b) Haar-like features are computed at 125 voxels (shaded) of the 13³-voxels large landmark neighborhood.

2.2 Shape Likelihood Maps

In general, it cannot be guaranteed that by using only the appearance likelihood map f_p (Eq. 1), the location ν in the target image with f_p(ν) = 1 will best correspond to locations of landmark p in images from the training set. To increase the possibility of finding the best location for landmark p in the target image, spatial relationships against other landmarks are used. We model spatial relationships among landmarks by shape features defined in the polar coordinate system, i.e. we define the distance d, azimuth angle φ and polar angle θ for every pair of landmarks p, q ∈ 𝒫. The probability distribution of a shape feature for a selected pair of landmarks p, q ∈ 𝒫, is estimated by the corresponding histogram H_p,q, generated by Gaussian kernel density estimation:

$$H_{p,q}({\mathit{h}}_{p,q},{\sigma }_H,h)=\sum _{i\in T}\text{exp}(-\frac{{(h-{\mathit{h}}_{p,q}(i))}^2}{2{{\sigma }_H}^2}),$$ (2)

where h_p,q(i) is the feature value for landmarks p,q ∈ 𝒫 in the i-th image from the training set T, h is the observed feature value and σ_H is a predefined SD of the kernel. The histogram is normalized so that Σ H_p,q(h_p,q, σ_H, h) = 1. For every pair of landmarks p and q in images from the training set, and according to Equation 2, we define three histograms: D_p,q(d) = H_p,q(d_p,q, σ_D, d) for the distance d_p,q, Φ_p,q(φ) = H_p,q(φ_p,q, σ_Φ, φ) for the azimuth angle φ_p,q, and θ_p,q(θ) = H_p,q(θ_p,q, σ_θ, θ) for the polar angle θ_p,q. The shape likelihood map g_p,q is obtained as a linear combination of the three shape feature histograms:

$$g_{p,q}(d,\phi ,\theta ,\Delta ,\Upsilon ,\Theta )=[{\lambda }_1{\lambda }_2{\lambda }_3]\left[\begin{array}{c}\hfill D_{p,q}(d·\Delta )\hfill \\ \hfill {\Phi }_{p,q}(\phi +\Upsilon )\hfill \\ \hfill {\theta }_{p,q}(\theta +\Theta )\hfill \end{array}\right],$$ (3)

where parameters λ_i; ${\Sigma }_{i=1}^3{\lambda }_i=1$, ∀ i : λ_i ≥ 0, weight the contribution of each histogram, and Δ, ϒ and Θ scale and/or rotate the system of landmarks p, q ∈ 𝒫 to compensate for the difference in scale and/or rotation between the observed and the average object of interest.

2.3 Shape Representation

The shape of the object of interest described by landmarks can be represented by the complete set of connections among landmarks, i.e. by the complete graph. In such a case, ½|𝒫|(|𝒫| − 1) shape likelihood maps g_p,q (Eq. 3) have to be computed, which is a computationally expensive task. However, by using a shape representation that consists only of the most representative connections among landmarks, not only the computational efficiency can be increased, but also the segmentation accuracy can be improved (Ibragimov et al., 2013, Sawada and Hontani, 2012). Among existing shape representations, the optimal assignment-based graph with landmark clustering (OAG-C) proved highly accurate and computationally efficient (Ibragimov et al., 2014).

In OAG-C, landmarks are first separated into k clusters 𝒞_i; i = 1,2,…k, with each cluster consisting of an equal number k̄ of landmarks (if k̄ · k < |𝒫|, then |𝒫| − k̄ · k dummy landmarks located infinitely far from (or close to) other landmarks are added to 𝒫). To minimize the complexity of OAG-C, the number of clusters is set to $k\approx \sqrt{|𝒫|}$, which implies that the number of landmarks in each cluster is $\mathrm{k̄}\approx \sqrt{|𝒫|}$. For every landmark from each cluster 𝒞_i, intra-cluster connections are established by connecting that landmark with n landmarks from the same cluster 𝒞_i, while inter-cluster connections are established by connecting that landmark with one landmark from every other cluster 𝒞_j. The total number of connections in the resulting shape representation is therefore ½|𝒫|(n +k − 1). For each landmark cluster 𝒞_i, the optimal intra-cluster connections are obtained by:

$$c_i^{*}=\text{arg}\underset{\{c_{p,q}\}}{\text{min}}\sum _{p\in {𝒞}_i}\sum _{q\in {𝒞}_i\backslash \{p\}}{c}_{p,q}·u_{p,q},\forall p\in {𝒞}_i:\sum _{q\in {𝒞}_i\backslash \{p\}}{c}_{p,q}=n,\forall p,q\in {𝒞}_i:0\le c_{p,q}\le 1,c_{p,q}=c_{q,p},$$ (4)

where c_p,q represents the connection between landmarks p and q from cluster 𝒞_i, u_p,q is the distance between the two landmarks that evaluates the connection representativeness, and n is the number of connections per each landmark. The globally optimal solution $c_i^{*}$ is obtained by solving the corresponding transportation problem (Dantzig, 1951), and is represented by a set of functions $\{1_{p,q}^{*}(i)\}$ that indicate whether the connection between landmarks p and q from cluster 𝒞_i is established $(1_{p,q}^{*}(i)=1)$ or not $(1_{p,q}^{*}(i)=0)$. For each pair of landmark clusters 𝒞_i and 𝒞_j, the optimal inter-cluster connections are obtained by:

$$c_{i,j}^{*}=\text{arg}\underset{\{c_{p,q}\}}{\text{min}}\sum _{p\in {𝒞}_i}\sum _{q\in {𝒞}_j}{c}_{p,q}·u_{p,q},\forall p\in {𝒞}_i:{\mathrm{\Sigma }}_{r\in {𝒞}_j}{c}_{p,r}=1,\forall p\in {𝒞}_j:{\mathrm{\Sigma }}_{r\in {𝒞}_i}{c}_{r,q}=1,\forall p\in {𝒞}_i,q\in {𝒞}_j:0\le c_{p,q}\le 1,$$ (5)

where p is a landmark from cluster 𝒞_i and q is a landmark from cluster 𝒞_j. The globally optimal solution $c_{i,j}^{*}$ is found by solving a special case of the corresponding transportation problem called the assignment problem (Kuhn, 2010), and is represented by a set of functions $\{1_{p,q}^{*}(i,j)\}$ that indicate whether the connection between landmark p from cluster 𝒞_i and landmark q from cluster 𝒞_j is established $(1_{p,q}^{*}(i,j)=1)$ or not $(1_{p,q}^{*}(i,j)=0)$. The resulting OAG-C shape representation is obtained by merging the indicator functions of intra-cluster and inter-cluster connections into a single set $\{1_{p,q}^{*}\}$, which contains ½|𝒫|(|𝒫| − 1) elements (i.e. the number of connections in the complete graph) that indicate whether the connection between any chosen pair of landmarks p and q is established or not. Note that the generation of OAG-C does not involve the target image and is therefore performed during the training phase.

2.4 Landmark Detection

To detect landmarks in the target image, appearance likelihood maps f_p (Eq. 1), obtained in the target image for each landmark p ∈ 𝒫, and shape likelihood maps g_p,q (Eqs. 2 and 3), obtained in the target image for each pair of landmarks p,q ∈ 𝒫, are combined with the OAG-C shape representation $\{1_{p,q}^{*}\}$ (Eqs. 4 and 5) (Ibragimov et al., 2014). In GTF (Ibragimov et al., 2012b), landmarks are considered as players, candidate points for landmarks as strategies and likelihoods that candidate points represent landmarks as payoffs. Such reformulations performed for image analysis problems (Bozma and Duncan 1994) allow using concepts from the field of game theory. For each landmark p ∈ 𝒫, the corresponding set of candidate points 𝒮_p = {s_p} is defined at locations of M largest maxima of the corresponding appearance likelihood map f_p (Eq. 1). For each pair of landmarks p, q ∈ 𝒫 with corresponding sets of candidate points 𝒮_p = {s_p} and 𝒮_q = {s_q}, a matrix W_p,q is defined as the partial payoff of landmark p considering appearance likelihood maps of candidate points s_p ∈ 𝒮_p, and shape likelihood maps of candidate points s_p ∈ 𝒮_p and s_q ∈ 𝒮_q:

$$W_{p,q}(s_p,s_q)=(1-\tau )f_p\left({\nu }_{s_p}\right)++\tau g_{p,q}(d_{s_p,s_q},{\phi }_{s_p,s_q},{\theta }_{s_p,s_q},\Delta ,\Upsilon ,\Theta ),$$ (6)

where ν_sp is the location of candidate point s_p for landmark p in the target image, and d_sp,sq, φ_sp,sq and θ_sp,sq are, respectively, the distance, azimuth angle and polar angle between candidate point s_p for landmark p and candidate point s_q for landmark q in the target image. Parameter τ weights the contribution of the appearance and shape likelihood maps; 0 ≤ τ ≤ 1. The set of optimal candidate points ${\sigma }^{*}=\{s_p^{*},s_q^{*},\dots \}$ that represent landmarks in the target image is obtained by maximizing the total payoff of all landmarks:

$${\vartheta }^{*}(𝒫,𝒮,𝒲)=\text{arg}\underset{\omega }{\text{max}}(\sum _{p\in 𝒫}\sum _{q\in 𝒫\backslash \{p\}}{1}_{p,q}^{*}·W_{p,q}(s_p,s_q)),$$ (7)

where ω = {w_p,w_q,…} describes all admissible combinations of payoffs, 𝒮 = 𝒮_p ∪ 𝒮_q ∪ … is the set of candidate points for all landmarks, and 𝒲 = {W_p,q, W_p,r, …, W_q,r, …} is the set of matrices of partial payoff for all pairs of landmarks. The indicator function $1_{p,q}^{*}\in \{1_{p,q}^{*}\}$, obtained from the OAG-C shape representation, determines whether the connection between landmarks p and q in the target image is considered during optimization $(1_{p,q}^{*}=1)$ or not $(1_{p,q}^{*}=0$, and in this case, the corresponding shape likelihood map g_p,q and matrix of partial payoffs W_p,q are not computed).

As Equation 6 represents a non-deterministic polynomial-time hard (NP-hard) problem, only a locally optimal set of candidate points ${\sigma }^{*}=\{s_p^{*},s_q^{*},\dots \}$ can be obtained in polynomial time. The obtained set σ* is further improved by re-evaluating each candidate point $s_p^{*}$ for landmark p within a spatial domain 𝒬_p in the target image that encompasses all candidate points from 𝒮_p. The re-evaluation of optimal candidate points considerably improves the performance of landmark detection (Ibragimov et al., 2012b), while the computational efficiency can be further improved by introducing the game-theoretic concept of strategy dominance (Ibragimov et al., 2014).

2.5 Landmark-Based Atlasing

Segmentation of the object of interest in the target image is obtained by atlasing the segmented objects of interest from images in the training set. For each image in the training set, we first find the B-spline-based non-rigid transformation that aligns landmarks 𝒫 = {p, q, …} in the training image to landmarks ${\sigma }^{*}=\{s_p^{*},s_q^{*},\dots \}$ detected in the target image, and then apply the obtained transformation field to propagate the segmented object of interest in the training image to the target image. By accumulating the propagations of the object of interest over all images in the training set, segmentation of the object of interest in the target image is finally obtained from voxels that correspond to the majority voting of the accumulated propagations.

3. Experiments and Results

3.1 Image Database

A database of 10 super-resolution 3D MR images of the tongue of healthy subjects was used in this study. Each super-resolution 3D MR image was reconstructed from a set of orthogonal sagittal, coronal and axial MR images (Fig. 1), acquired on a Siemens 3 T Tim Trio MR system (Siemens Medical Solutions, Erlangen, Germany) with an 8-channel head and neck coil by applying the T2-weighted turbo spin echo sequence with echo time (TE) of 62 ms, repetition time (TR) of 2500 ms and echo train length (ETL) of 12. The sets of orthogonal images were acquired in a sequence, where the acquisition of each set took on average 100 seconds for 10–24 2D images with a size of 256 × 256 pixels, in-plane pixel size of 0.78 × 0.78 mm and slice thickness of 3 mm, which resulted in reconstructed 3D MR images with a size of 256 × 256 × 256 voxels and isotropic voxel size of 0.78 × 0.78 × 0.78 mm. The tongue is located in the center of the reconstructed image, where all three orthogonal images intersect, meaning that only the tongue region in the 3D image is of super-resolution, whereas the surrounding structures are of lower resolution. The images were acquired from 10 different subjects including five males and five females with the mean (± standard deviation, SD) age of 26.1 ± 3.8 years (range 22–34 years), which were not affected by any tongue, speech or vocal tract disorder, and were not recovering from any tongue related surgery, e.g. glossectomy.

3.2 Reference Segmentation and Landmark Annotation

For each super-resolution 3D MR image in the database, the objects of interest, represented by the genioglossus and inferior longitudinalis tongue muscles, were manually segmented and annotated with corresponding landmarks.¹ Segmentation was performed by an experienced otolaryngologist, who identified the voxels belonging to each muscle without using any image smoothing or volume propagation tools (Table 1). The database represents a relatively heterogeneous subject pool, so that the smallest observed genioglossus and inferior longitudinal muscles were 2- and 3.8-times smaller than, respectively, the largest observed genioglossus and inferior longitudinal muscles. Landmark annotation was performed by placing 46 points on the surface of both muscles, and 319 points on the surface of surrounding structures, such as the mandible, teeth, chin, etc. (Table 2), resulting in 365 landmarks per image. Landmarks were distributed as evenly in space as possible, except in the case of the genioglossus, mandible, teeth and chin. Among the 18 landmarks assigned to the genioglossus, eight were placed along the contour of intersection with its mid-sagittal plane, which can be identified as a visually distinctive region, and 10 on its lateral sides. Among the 47 landmarks assigned to the lower jaw, 33 were placed on the frontal part of the mandible and 14 on the teeth. It has to be noted that landmarks were not placed on wisdom teeth, as they are often removed and therefore may not be present in the target image. The chin was described by 27 landmarks, which were distributed from the lips to the posterior part of the chin. The density of landmark distribution equals to 3.54 mm, meaning that, on average, each voxel from the tongue area has a landmark in its 3.54 mm large neighborhood.

Table 1.

Overview of the reference segmentation of tongue muscles measured in terms of mean (± standard deviation), minimal and maximal muscle volume.

Tongue muscle	Mean volume (mm3)	Min. volume (mm3)	Max. volume (mm3)
Genioglossus	11987 ± 2890	7543	15713
Inferior longitudinalis	2631 ± 1099	1245	4690

Table 2.

Overview of the number of landmarks used to describe the surface of the tongue, individual tongue muscles and surrounding structures.

Location of landmarks	Number of landmarks
Surface of tongue muscles (total)	125
- Genioglossus	18
- Inferior longitudinalis	28
- Digastric	34
- Mylohyoid	16
- Superior longitudinalis	29
Surface of surrounding structures (total)	169
- Mandible (lower jaw)	33
- Teeth (lower jaw)	14
- Chin	27
- Soft palate and mucosa	61
- Submandibular gland	34
Surface of the tongue (total)	71
Total	365

3.3 Experiments

A leave-one-out cross-validation experiment was performed to evaluate the performance of the proposed segmentation framework, which means that GTF was iteratively trained on nine images and used to segment the remaining target image. Each of the |𝒫| = 365 landmarks was searched for within a spatial domain that encompassed that landmark across all images in the training set. For each landmark p ∈ 𝒫, we extracted nine types of Haar-like features (Fig. 3a) at 4-, 8- and 16-voxels large scales, computed at 125 voxels of the 13³-voxels large neighborhood of the voxel representing landmark p (Fig. 3b). Among the resulting 3375 features (9 types × 3 scales × 125 voxels), |𝒩_p| = 200 features with the highest predictive power were automatically selected and used to define the appearance likelihood map f_p of landmark p (Eq. 1), which was further used to select M = 50 candidate points for that landmark in the target image. For each pair of landmarks p, q ∈ 𝒫, a shape likelihood map g_p,q (Eqs. 2 and 3) was defined by using σ_D = 15 mm for the histogram of distances D_p,q, and σ_Φ = σ_θ = 15° for histograms of azimuth angles Φ_p,q and polar angles θ_p,q, and by weighting the contribution of these histograms by λ₁ = 0.7, λ₂ = 0.2 and λ₃ = 0.1 (Ibragimov et al., 2014). The OAG-C shape representation was obtained by applying the k-means algorithm to separate |𝒫|= 365 landmarks into k = 20 clusters, each consisting of k̄ = 19 landmarks (as k̄·k = 380 < |𝒫|, fifteen dummy landmarks were added to corresponding clusters), and then solving the previously described transportation and assignment problems to obtain the set of indicator functions $\{1_{p,q}^{*}\}$ (Eqs. 4 and 5). The generated appearance and shape likelihood maps were incorporated into matrices of partial payoffs W_p,q (Eq. 6) by using τ = 0.8 (Ibragimov et al., 2014), and then combined with the OAG-C shape representation to detect landmarks in the target image (Eq. 7). The segmentation of the object of interest in the target image was finally found by atlasing the segmented objects of interest from images in the training set according to landmarks detected in the target image (Fig. 4a). Note that most of framework parameters, including the number of candidate points M, standard deviations σ_D, σ_Φ and σ_θ for distance and angle likelihood maps, the rule for defining the number of clusters k and number of landmarks per cluster k̄, were adopted from our previous work (Ibragimov et al., 2014).

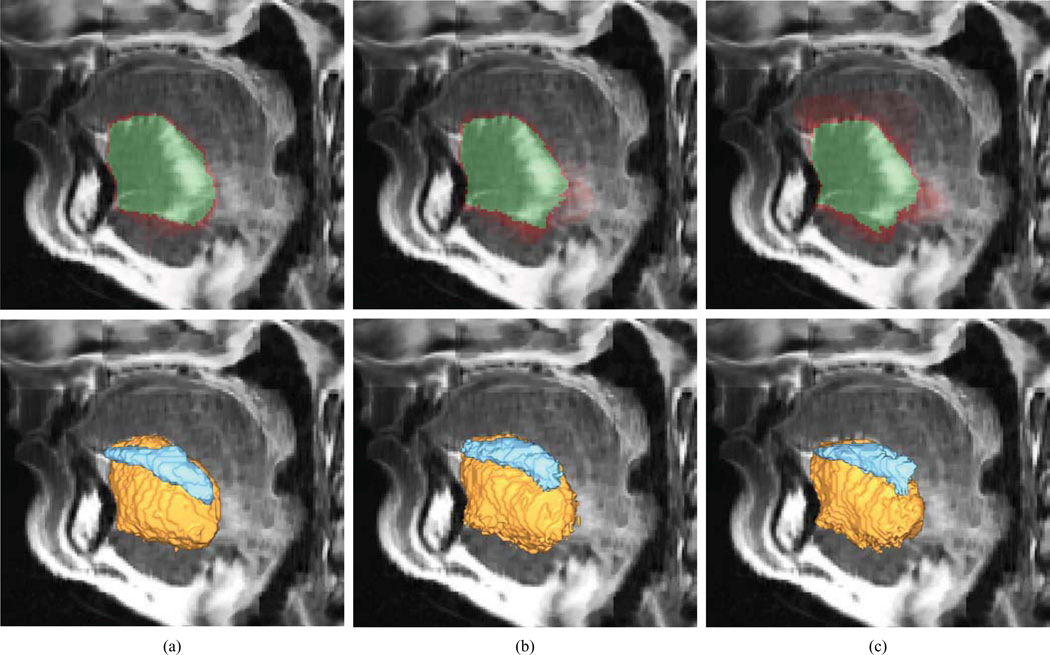
Fig. 4.

Atlasing results for a selected super-resolution 3D MR image of the tongue, shown in a sagittal cross-section and obtained by applying (a) the game-theoretic framework, (b) B-splines atlasing and (c) demons atlasing. In the first row, the results are shown as semi-transparent domains, where the red color indicates the accumulated propagations of reference segmentations from images in the training set, while the green color indicates the majority voting of the accumulated propagations. In the second row, the results are shown as colored volumes, where the yellow color indicates the segmented genioglossus muscle, while the blue color indicates the segmented inferior longitudinalis muscle

To validate the results of GTF segmentation, we compared the obtained results to an independent manual segmentation performed by a second observer, and to the results obtained by two alternative segmentation approaches, namely B-splines and demons atlasing, both of which are registration-based, not landmark-based. For computerized segmentation, images from the database (i.e. the GTF training set) were first registered to the target image using ever B-splines or demons registration and the obtained transformation fields were then used to propagate the segmented objects of interest from images in the database to the target image. Finally, a majority voting of the accumulated propagations was applied to segment the object of interest in the target image (Fig. 4b–c). In the case of B-splines atlasing, a publicly available toolbox (Klein et al., 2010) was used for image registration, which consisted of an initial rigid followed by a B-spline transformation using the advanced mean square and normalized correlation metrics as similarity measures, i.e. as it was recommended for the head and neck segmentation from CT images (Fortunati et al., 2013). In the case of demons atlasing, a publicly available implementation (Kroon) was used for image registration, which consisted of an initial rigid followed by a demons transformation using a voxel velocity field with the Gaussian kernel (SD of 4 voxels) and diffusion regularization (SD of 1 voxel). Moreover, as in the case of GTF each landmark was searched for within a spatial domain that was limited to the region encompassing that landmark across all images in the training set, the images were in the case of B-splines and demons atlasing cropped to a volume of interest containing the tongue in order to ensure a proper comparison of segmentation approaches. Restricting the volume of interest is a valid and safe step for the tongue muscle segmentation problem considering the nature of analyzed images. The original images with high in-plane resolution were acquired in such a way that all of them depict the tongue region. During the reconstruction procedure, the images are combined so that their intersection, i.e. the tongue region, is located in the center of the resulting volume.

3.4 Results

We evaluated the segmentation performance in terms of Dice coefficient κ and symmetric surface distance δ for the genioglossus and inferior longitudinalis muscles (Table 3). For both muscles, the resulting mean (± SD) values were • = 85.3 ± 2.0% and • = 0.79 ± 0.14 mm for the second observer, • = 81.8 ± 3.2% and • = 1.02 ± 0.19 mm for GTF, • = 78.8 ± 5.5% and • = 1.10 ± 0.32 mm for B-splines atlasing, and • = 75.8 ± 6.6% and • = 1.27 ± 0.45 mm for demons atlasing. The results are for a selected image shown in Figure 5.

Table 3.

Segmentation results of the genioglossus and inferior longitudinalis tongue muscles in terms of mean (±standard deviation) Dice coefficient κ and symmetric surface distance δ for the second observer, game-theoretic framework (GTF), B-splines atlasing and demons atlasing.

Method	Genioglossus muscle		Inferior longitudinalis muscle		Both muscles
	κ (%)	δ (mm)	κ (%)	δ (mm)	κ (%)	δ (mm)
Second observer	88.3 ± 1.9	0.71 ± 0.11	69.0 ± 3.7	0.93 ± 0.22	85.3 ± 2.0	0.79 ± 0.14
GTF	84.8 ± 3.7	1.00 ± 0.20	61.4 ± 7.7	1.03 ± 0.18	81.8 ± 3.2	1.02 ± 0.19
B-splines atlasing	81.6 ± 6.1	1.09 ± 0.37	60.5 ± 9.0	1.11 ± 0.31	78.8 ± 5.5	1.10 ± 0.32
Demons atlasing	79.0 ± 6.4	1.26 ± 0.42	53.5 ± 11.9	1.29 ± 0.48	75.8 ± 6.6	1.27 ± 0.45

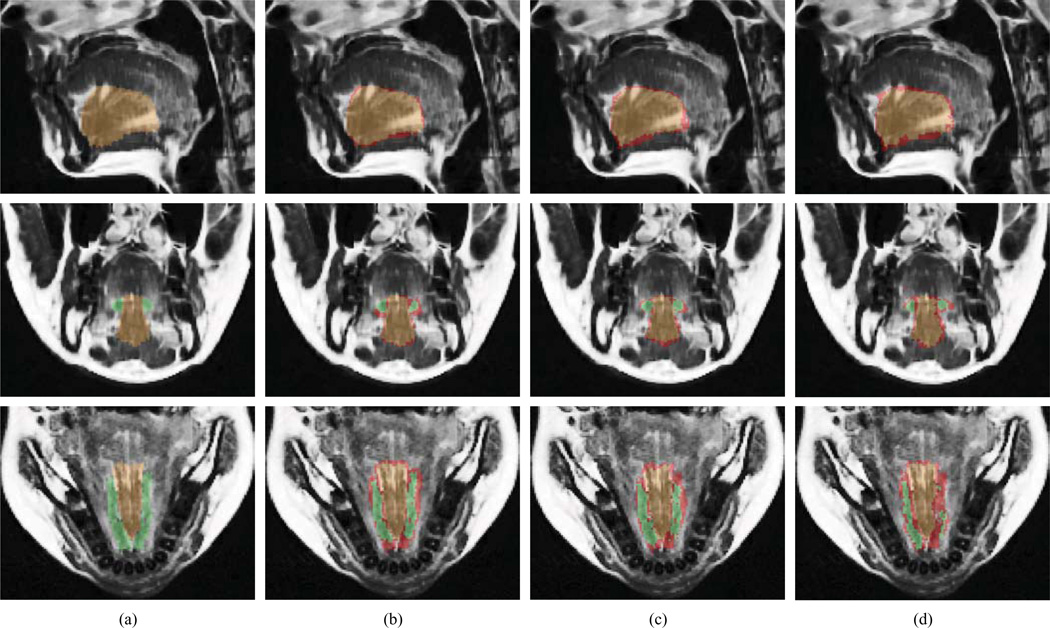
Fig. 5.

Segmentation of genioglossus and inferior longitudinalis tongue muscles for a selected super-resolution 3D MR image, shown in sagittal (top), coronal (middle) and axial (bottom) cross-sections, obtained by (a) manual segmentation, (b) game-theoretic framework, (c) B-splines atlasing and (d) demons atlasing (d). The brown color indicates either the manual segmentation (a) or the overlap between manual and computerized segmentations (b–d) of the genioglossus muscle. The green color indicates either the manual segmentation (a) or the overlap between manual and computerized segmentations (b–d) of the inferior longitudinalis muscle. The red color indicates the disagreement between manual and computerized segmentations.

We additionally evaluated the performance of landmark detection part of GTF. The resulting mean ± SD values of the landmark detection error (i.e. the distance between the detected and reference landmark positions) was 5.63 ± 3.83 mm, while the appearance likelihood value was 0.97 ± 0.04 for the detected landmarks and 0.85 ± 0.11 for the reference landmarks, all computed for the whole set of 365 landmarks. Relatively large values for the landmark detection error do not result in a comparable segmentation error, as landmarks located on object surface are very similar to the neighboring voxels, and can therefore slide along that surface, which increases the landmark detection error but does not considerably affect the segmentation results. The high appearance likelihood value of 0.85 ± 0.11 obtained for the reference landmarks indicates that the selected Haar-like appearance features can correctly model landmarks in the tongue area.

4. Discussion

We presented the first attempt to automatically segment tongue muscles from 3D MR images. Being a muscular hydrostat, the tongue does not contain any bony structures, which are, in general, easier to identify and segment because they have clearly visible boundaries and rigid shape. Moreover, without bony structures to act upon, tongue muscles form a complex system, where each muscle lengthens by acting upon other tongue muscles. Such tongue morphology therefore does not only limit the applicability of computerized segmentation methods based on intensity classification and surface evolution, but makes also manual segmentation challenging. In this study, we addressed this problem by adapting an existing computerized landmark-based segmentation framework to tackle the morphological properties of the tongue and its muscles, and validated the obtained segmentation results against manual and alternative computerized segmentation approaches.

All of the applied segmentation approaches suffer from artifacts in tongue images that are reconstructed from stacks of orthogonal 2D images. As each image has to be acquired in a short time frame, the orthogonal images do not completely cover the imaged 3D volume but overlap only with the tongue region (Fig. 1). This introduces abruptions followed by blank regions, i.e. regions without assigned intensities, in the reconstructed 3D image. These blank regions are located in the eight corners of the 3D image and considerably affect the computation of appearance likelihood maps for voxels close to the tongue surface or on the chin and mandible. Moreover, eventual rotations of the observed anatomy together with the natural variability of the size of the jaw do not allow an observer to estimate the anatomical regions, which will be covered by blank regions. The described limitation is less pronounced in the case of B-splines and demons atlasing, as the 3D images were cropped to the volume of interest containing the tongue. Another disadvantage of reconstructed images is related to intensity mismatches that appear due to slight misalignments of orthogonal images or when intensities of orthogonal images do not perfectly correspond. These mismatches introduce false boundaries and affect the performance of both appearance likelihood maps used in GTF and similarity measures used for registration in B-splines and demons atlasing.

The previously described disadvantages of reconstructed images and poor visibility of inter-muscle boundaries may lead to distorted segmentation results. The number and strength of distortions can be reduced by having a sufficiently large training database. Adding new training images is especially effective for B-splines and demons atlasing approaches, where distorted results for a single registration can be compensated by the remaining correct registrations that form the atlasing procedure. This issue can be additionally addressed by limiting the elasticity of registration transformations, so that the shapes of the depicted objects can be preserved during registration. However, if a false boundary is close to a true one or if the boundary is extremely poorly visible, which often occurs in the case of tongue muscles, distortions may not be avoided. GTF is theoretically more sensitive to distortions, as a single registration is performed after landmarks are detected. If most landmarks located on the periphery of the landmark set are considerably shifted from their actual positions, all training images will be the incorrectly registered to the target image. Similarly to B-splines and demons atlasing, the distortions can be reduced by limiting the elasticity of transformations for landmark-based registration. This implies that the detected landmarks, which are considerably shifted from the landmark set, will not be aligned with corresponding landmarks from the training set if the alignment requires an extremely elastic registration. Although such sensitivity to incorrectly detected landmarks can potentially reduce the segmentation robustness, GTF resulted in a higher mean value and lower SD of the Dice coefficient in comparison to B-splines and demons atlasing. Better results were obtained due to the manual annotation of images in the training set with landmarks that have distinctive appearance and spatial position, which reduces the number of incorrect detections.

Object landmarking has received considerable attention in the literature during the last couple of decades. Landmarks are always defined according to the appearance conditions and/or geometrical conditions, i.e. as points that are clearly visible in the image and/or as points representing curvature extrema, terminal and centerline intersection points (Rohr, 2001). Well-defined landmarks simultaneously satisfy several of the above mentioned conditions and mark anatomically meaningful points (Lu et al., 2009, Proctor et al., 2010, Liu et al., 2010, Donner et al., 2013), object corners and centers (Ibragimov et al., 2012a), and evenly cover object boundaries (Stegmann et al., 2003, van Ginneken et al., 2006). In the present work, all types of landmarks were used, namely anatomically meaningful points (e.g. landmarks marking teeth), object corners and centers (e.g. tongue tip and landmarks on genioglossus mid-sagittal plane), and points evenly distributed on object surfaces (e.g. landmarks on digastric and inferior longitudinalis).

Introducing prior knowledge in the form of landmarks gives a certain advantage to GTF, whereas B-splines and demons atlasing are not supported by any prior knowledge. However, the independence to prior knowledge allows B-splines and demons atlasing approaches to easily incorporate automatically segmented images into the atlas if the obtained segmentation results are of exceptional accuracy. Segmented target images can be also added into GTF to enrich the landmark detection part of the framework, which is however less straightforward. If the results of B-splines or demons atlasing can be quickly visually inspected or automatically validated, it is very time-consuming to ensure the correctness of landmark detection. An automated validation procedure should therefore estimate the detection accuracy relying on partial payoffs for each individual landmark. The optimal candidate points with high payoffs correspond to high appearance and shape likelihood values, and therefore there is a higher probability that they are correctly detected in comparison to the optimal candidate points with low payoffs. This confidence estimation can be transformed into weighting coefficients so that newly detected optimal candidate points can participate in defining the appearance and shape likelihood maps, however, with smaller weighting coefficients than for the manually positioned landmarks.

The segmentation results (Table 3) obtained by all of the applied approaches are promising, with GTF performing better than B-splines or demons atlasing. In terms of the symmetric surface distance, segmentation results were similar for both the genioglossus and inferior longitudinalis muscle. In the case of GTF, the mean values were around δ = 1 mm with a relatively low corresponding SD, which can be considered satisfactory when taking into account image voxel size of 0.78 × 0.78 × 0.78 mm. In terms of the Dice coefficient, segmentation results were, on the other hand, better for the genioglossus than for the inferior longitudinalis muscle. However, the genioglossus is a larger object than the inferior longitudinalis, and larger objects are usually associated with higher Dice coefficients than smaller objects. In fact, the average size of the observed genioglossus muscles was around 11987 mm³, whereas for the observed inferior longitudinalis muscles it was around 2631 mm³. Apart from the difference in size, when observed in MR images the genioglossus has more clearly pronounced lateral boundaries in the region where it is connected with the sublingual gland and inferior longitudinalis. Moreover, there is a visually distinctive area in the mid-superior and mid-posterior part of the muscle (Fig. 5). On the other hand, the inferior longitudinalis can be easily mistaken for the sublingual gland.

All computerized segmentation methods show inferior results in terms of segmentation accuracy and robustness when compared to the performance of the second observer. This fact indicates that there is still room for improvement before computerized tongue muscle segmentation becomes a fully reliable diagnostic tool. On the other hand, the relatively low level of agreement between manual segmentations confirms that the problem is challenging and subject to ambiguities. This observation correlates with the general rule that muscles, lesions, tumors and glands have in MR images relatively blurred boundaries, and therefore cannot be segmented as accurately as bones in CT images. Intensity mismatches, blur and presence of blank regions originating from image reconstruction represent additional obstacles for both manual and computerized segmentation. However, the current results show that computerized tongue muscles segmentation has potential, and that the obtained results can be already used for assisting clinicians in diagnosis and postoperative monitoring.

The applied segmentation approaches are not limited to the genioglossus and inferior longitudinalis muscles. However, to segment a different object of interest, reference segmentations and, in the case of GTF, landmark annotations have to be available. Nevertheless, the inclusion of new objects of interest would not considerably affect the computation time. In the case of GTF, the computation time depends mostly on the number of landmarks, while in the case of B-splines and demons atlasing, it is related to the number of images in the database. According to the applied settings, GTF took on average 6.6 minutes for segmentation (implementation in C++ with code parallelization, execution on a personal computer with Intel Core i7 processor at 2.8 GHz and 8 GB of memory), which proved to be more than 7-times faster in comparison to alternative approaches. However, it must be emphasized that GTF and B-splines atlasing were both implemented in C++ using code parallelization, whereas demons atlasing was implemented in Matlab and without code parallelization. Although direct comparison of computation times is not fully transparent as different programming languages were used, the computational efficiency of GTF is supported by its single registration-based architecture.

5. Conclusion

Computerized segmentation of tongue muscles is valuable not only as a diagnostic tool but also as a support to manual segmentation. This study is the first attempt to automatically segment tongue muscles from 3D MR images. The muscles of interest represented by the genioglossus and inferior longitudinalis were automatically segmented by applying GTF as well as B-splines and demons atlasing. The obtained results were validated against two manual segmentations, one of which was used as a reference standard, whereas the other one served as the inter-observer variability estimation. Although only two tongue muscles were considered as objects of interest, the analyzed segmentation approaches can segment the whole tongue area without computation performance deterioration or training dataset modification. In the case of GTF, this universality is ensured by the fact that landmarks evenly cover not only the muscles of interest, but the whole tongue and some distinguishable anatomical structures around it. In the future, we therefore plan to segment other tongue muscles, such as the superior longitudinalis, hyoglossus, styloglossus, etc., without or with minor training dataset modifications. When a sufficient level of segmentation accuracy is reached, we can focus on analyzing pathological and postoperative cases. Segmentation of tongue muscles from high-resolution MR images combined with whole tongue segmentation from dynamic low-resolution MR images is namely of great importance in oral cancer surgery planning.

Highlights.

• The first attempt to segment tongue muscles from in vivo MR images is presented.

• Haar-like appearance features and optimal assignment-based shape representation are combined with the game-theoretic landmark detection framework.

• The performance of the genioglossus and inferior longitudinalis tongue muscle segmentation is validated by three approaches.

• The images, the corresponding reference segmentations and the manual landmarking data will be publicly released to facilitate the development of new segmentation methods and their objective comparison.