An early prediction of the maximum amplitude of the solar cycle 25

Abstract

A solar activity precursor technique of spotless event has been currently used to predict the strengths and the times of rise of the 11-year coming cycles. This simple statistical method has been previously applied to predict the maximum amplitudes and the times of rises of cycles 22 and 23. The results obtained are successful for both cycles. A developed version of the suggested method was previously used to make an early forecast of the characteristic parameters of the cycle 24. In this work the preliminarily predicted parameters of the cycle 24 are checked using observed values of the spotless events. In addition, the developed method is also applied to forecast the maximum amplitude and time of rise of the 25th solar cycle. The maximum Wolf number and time of rise of the latter cycle are found to be 118.2 and 4.0 years respectively.

Introduction

Solar activity predictions has acquired in recent decades a more prominent status within the scientific community because of its large impact to human technological activity (spacecraft, power grids, human activity in space, etc.) and in certain way living organisms and climate. This interest covers different scales, ranging from predictions of short term space weather events (a few hours or days) to long term forecasts on the amplitude of the following solar cycle several years in advance.

The long term predictions have become relatively popular in the past two decades which usually based on the characteristics of sun spots activity in successive cycles. Many attempts have been devoted to forecast future cycles. For instance, Pesnell [1] recently divided more than 50 predictions for the present solar cycle 24 into different categories:

• 1.Climatology in which the future behavior of the system is a function of average behavior e.g. [2–4].
• 2.Recent climatology: refers to forecast the future behavior is related to that in the recent past e.g. [1].
• 3.Precursor: which look for leading indicator of the solar activity, it has three categories:
• a.Solar magnetic field at minimum ≈ level of the next maximum activity e.g. [5,6].
• b.Geomagnetic activity (aa and Ap indices) near minimum ≈ level of activity near next maximum [7,8].
• c.Spotless event around the preceding minimum [9,10].
• 4.Spectral: it examines a Fourier analysis of sunspot time series for invariant quantities e.g. [11,12].
• 5.Dynamo: It is produced by models capable of integrating conservation equation [13,14].
• 6.Neural Network: It is derived from a set of non-linear data modeling [15].

The present work aims to verify the previous predicted parameter of cycle 24 and predict the timing and strength of the next cycle 25.

Data and method of analysis

The data used in our work are, the monthly mean values of the sunspots numbers, the values of maximum and minimum numbers, the epochs of the minimum and maximum, the times of rise and the dates of the beginning and end of each cycle. The used data are taken from the site of National Geophysical Data Center, USA (ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/SUNSPOT_NUMBER/maxmin.new).

According to Mckonnon [16], the quality of the data is considered as “poor” during 1700–1748, “questionable” during 1749–1817, “good” during 1818–1847 and “reliable” from 1848 onwards.

As we used the count of spotless days around the minimum as a precursor for prediction of the parameters of the new solar cycles, the data covers about 188 years i.e. from cycle 7 up to now.

Preliminary analytical investigations obviously reveled that the shape of the 11-year solar activity cycle is well correlated to the number of spotless events (days) prevailing along the preceding minimum, so our precursor depends on the past behavior of the maximum amplitude of the activity cycles as a function of the number of spotless events along two years intervals around the preceding minimum [9,18,19].

A new approach was also proposed to estimate the spotless events and the maximum amplitude of the next cycle following the current one using the following logarithmic relation

$$\ln ({\text{R}}_{\text{Mn}}/{\text{R}}_{\text{mn}})=a+b({\text{S}}_{\text{omn}}/{\text{S}}_{\text{omn}+1})$$ (1)

where R_Mn and R_mn are the maximum and minimum sunspot numbers of the preceding cycle, S_omn and S_omn+1 are the spotless events at preceding and the following minima of a given cycle.

Results and discussion

Verification of the early predication of cycle 24

Various predictions of the 24th solar activity cycle, using different data sets and methods clearly reveal the contradictory of the results [1,17]. Our preliminary prediction of cycle 24 which was published in 2006 [9] indicates that the maximum amplitude is 90.7 ± 9.2 and the time of rise is 4.6 ± 1.2 years.

As the solar cycle started in 2008, it became possible to use observed values of the spotless events around the minimum to check our previous results through the derived empirical formulae [9] which gives the values:

$${\text{R}}_{\text{M24}}=(183.0482\pm 25.6187)-(0.1733\pm 0.067){\text{S}}_{\text{om}}=91.6\pm 11.3$$ (2)

$${\text{T}}_{\text{r24}}=(2.726\pm 0.4346)+(0.0034\pm 0.0011){\text{S}}_{\text{om}}=4.5\pm 1.2$$ (3)

The results confirm our early prediction and comes into coincidence with the late new prediction of the international panel of experts led by NOAA and sponsored by NASA which gives value of R_M = 90 in May 2013, concluded that this cycle is the lowest of any cycle since 1928.

Our previous predictions of the maximum strengths of solar cycles 22, 23 and 24 in comparison with the international published values are included in Table 1.

Table 1.

Comparison between our predictions and the observed values.

Cycle no.	Observed RM	Predicted RM	Method	Author
22	157.6	153 ± 18	Spotless	Hamid and Galal [18]
23	119.6	134 ± 10.3	Spotless	Hamid [19]
		144.9 ± 22	aamin	Hamid [19]
		132	Neuro–fuzzy model	Attia et al. [20]
24	–	90.7 ± 9.2	Spotless	Hamid and Galal [9]
		90	According to NASA

An early prediction of solar cycle 25

Fig. 1 depicts visually Eq. (1) for solar cycles from 7 to 23. It indicates a best fit as follows:

$$\ln ({\text{R}}_{\text{Mn}}/{\text{R}}_{\text{mn}})=2.1465+0.8856({\text{S}}_{\text{omn}}/{\text{S}}_{\text{omn}+1})$$ (1′)

Fig. 1.

Representation of the logarithmic formula.

Pearson’s correlation coefficient of the above relation c.c. = 1.0.

Fig. 2 shows the variation of the maximum Wolf number (R_M) as a function of spotless events around the preceding minimum. The linear fit can be represented by the following equation:

$${\text{R}}_{\text{M25}}=183.0701-0.1780{\text{S}}_{\text{omn}+1}{\text{R}}_{\text{M25}}=119.2\text{with}\text{c.c.}=-0.68$$ (4)

Fig. 2.

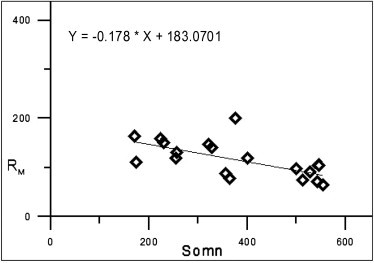
The variation of the maximum Wolf number with the spotless events.

Fig. 3 exhibits the relation between the time of rise and spotless events. It shows a linear fit which can be expressed by the equation:

$${\text{T}}_{\text{r25}}=2.7384+0.0035{\text{S}}_{\text{omn}+1}{\text{T}}_{\text{r25}}=4.0\text{years}\text{with}\text{c.c.}=0.78$$ (5)

Fig. 3.

The variation of time of rise with the spotless events.

It is well known that the modern era of sunspots cycles started from cycle number 10 to present, so we used the data sets for this period to predict the maximum strength and time of rise according to our previous method mentioned before i.e., using Eq. (1) we get,

$$\ln ({\text{R}}_{\text{Mn}}/{\text{R}}_{\text{mn}})=2.1833+0.8814{\text{S}}_{\text{omn}+1}\text{with}\text{c.c.}=0.68$$ (1″)

$${\text{R}}_{\text{M25}}=178.9188-0.1668{\text{S}}_{\text{omn}+1}{\text{R}}_{\text{M25}}=117.2\text{c.c.}=-0.60$$ (6)

$${\text{T}}_{\text{r25}}=2.9316+0.0026{\text{S}}_{\text{omn}+1}{\text{T}}_{\text{r25}}=4.0\text{years}\text{c.c.}=0.61$$ (7)

$${\text{Mean R}}_{\text{M25}}=118.2{\text{Mean T}}_{\text{r25}}=4.0\text{years.}$$

It is noticeable that the results obtained in the latter case are nearly similar to the pervious ones.

Table 2 gives our prediction for cycle 25 in comparison with the published predictions of other authors in chronologic alphabetic order. It is obvious that our results agree with some contributions and disagree with others. In fact the differences of the predicted strengths by different authors may be attributed to the variety of the used techniques and methodology. Although some authors think that cycle 25 could be one of the weakest in centuries [17], in contrast, we think that the next cycle will be relatively stronger than cycle 24 and it will have nearly the same strength of cycle 23, i.e. the sunspot maximum may rebound in the near future.

Table 2.

Predictions of solar cycle 25.

Author	Wolf no. at maximum RM	Duration of rise phase Tr	Year of maximum
Du and Du [4]	111.6 ± 17.4
Quassim [21]	116
Pishkalo [17]	112.3 ± 33.4	4.4 ± 0.7	2023 ± 0.7
Hamid and Galal (2011)	118	4.0	2022–2023

Conclusion

In essence, we may stress the prime importance of further investigation of the spotless sun and its impact to various aspects of our life on the Earth and space environment. It seems that the distribution of spotless events across successive solar cycles are responsible for the variety of their strengths. The more frequently and longer are the spotless events at a given cycle, the smaller the values of the maximum Wolf number reached in it. Prolonged minima of sunspots activity have been observed in the course of history, such as Sporer’s (1430–1510) and Maunder’s (1645–1710) minima, that were accompanied by unstable atmospheric conditions on the Earth.