The long-term variability of cosmic ray protons in the heliosphere: A modeling approach

Abstract

Galactic cosmic rays are charged particles created in our galaxy and beyond. They propagate through interstellar space to eventually reach the heliosphere and Earth. Their transport in the heliosphere is subjected to four modulation processes: diffusion, convection, adiabatic energy changes and particle drifts. Time-dependent changes, caused by solar activity which varies from minimum to maximum every ∼11 years, are reflected in cosmic ray observations at and near Earth and along spacecraft trajectories. Using a time-dependent compound numerical model, the time variation of cosmic ray protons in the heliosphere is studied. It is shown that the modeling approach is successful and can be used to study long-term modulation cycles.

Introduction

The Sun is a rotating magnetic star consisting of a hot plasma entangled with fluctuating magnetic fields. A vast amount of energy is continuously released from the Sun in the form of electromagnetic radiation as well as in the form of charged particles, called the solar wind. The latter is accelerated and ejected omni-directionally into interplanetary space. The region around the Sun filled with the solar wind and its imbedded magnetic field B is known as the heliosphere [1]. This magnetic field, called the heliospheric magnetic field (HMF), remains rooted on the Sun as it rotates, resulting in the formation of an Archimedean spiral, referred to as the ‘Parker spiral’. Turbulent processes that occur on the surface of the Sun cause cyclic variations e.g. in the number of sunspots. Fluctuations in B follow this cycle with an average period of ∼11 years. The direction of B also changes every ∼11 years resulting in polarity cycles of ∼22 years. Positive polarity epochs, indicated by A > 0, are defined as periods when B points outwards in the northern and inwards in the southern heliospheric regions while for A < 0 epochs, the polarity switches; see the top panel in Fig. 1. The thin region where the magnetic polarity abruptly changes creates the heliospheric current sheet (HCS) that becomes increasingly wavy with growing solar activity [1,2]. This waviness is caused by the fact that the magnetic axis of the Sun is tilted with respect to its rotational axis, forming an angle which is equal to the angle α with which the HCS is tilted. This angle is called the HCS tilt angle. Since 1976, values of α have been computed by applying models to solar magnetic field maps as shown in the middle panel of Fig. 1. The time series for α correlate with that for B so α is frequently used in cosmic ray (CR) modulation studies as a proxy for solar activity [1,2]. In terms of α, solar activity is classified as solar minimum when $5°⩽\alpha ⩽30°$, moderate when $30°>\alpha ⩽60°$ and maximum when $60°<\alpha ⩽90°$. Variations in B, observed at Earth as shown in Fig. 1, and changes in α are propagated throughout the heliosphere by the solar wind. For additional background and details, see the reviews by Heber and Potgieter [1,2] and Strauss et al. [3].

Fig. 1.

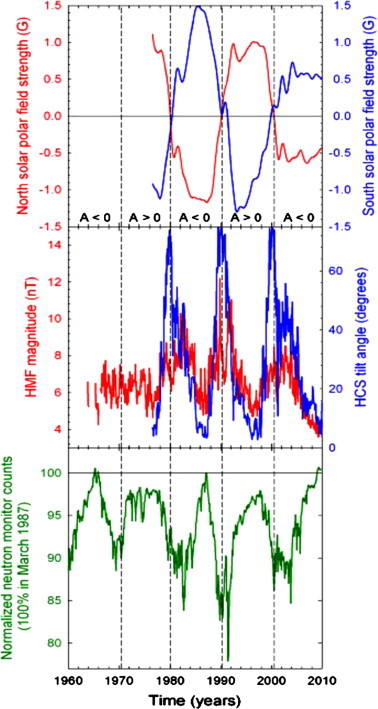
Relation between selected solar activity parameters and CR variations. The top panel shows northern and southern HMF magnitude and polarity; the middle panel the HMF magnitude and the HCS tilt angle at Earth (courtesy of the WSO, http://www.wso.stanford.edu; http://www.cohoweb.gsfc.nasa.gov). The bottom panel shows the normalized Hermanus NM counting rate as a function of time. CR flux observed at the end of 2009 was the highest since the beginning of the space age [3].

Information about the global properties of B, at Earth and in the heliosphere at large, forms important input for various fields of space research including past terrestrial climate effects and very long-term (>100 years) modulation of CRs. Unfortunately records of in situ space measurements of B, and most other indicators of solar activity cover only a few decades so that various models have to be used to reconstruct solar activity parameters via indirect proxies. However, this paper focuses on α and B, as they change with time at Earth, as input for a numerical model describing the global modulation and variability of CRs in the heliosphere. If successful, this approach can be applied for solar activity cycles longer than 22 years.

Modulation of cosmic rays in the heliospheric

Galactic CRs are charged particles that come from outside the heliosphere with energies ranging from ∼10³ eV to as high as 10²⁰ eV [e.g. 4,5]. CRs with kinetic energies E > ∼30 GeV traverse the heliosphere with little effect on their intensity while CRs with lower E are modulated, progressively with decreasing E. The reason is that they get scattered (diffused) by irregularities in B, so that its geometry and magnitude together with the level of variance in B, as a proxy for turbulence, largely determines the passage of CRs inside the heliosphere. This process of changing the intensity with time as a function of energy and position is known as the heliospheric modulation of CRs. Increased solar activity (turbulence) leads to lowering the energy spectrum of CRs, with the largest effects at low energy [see also 1,2].

Ground based observations made since the 1950s when CR detectors, called neutron monitors (NMs) [3], were deployed worldwide, convincingly reflect anti-correlated cycles in the time series of CRs, also in sunspot numbers, in B and in α, as illustrated in Fig. 1. However, there is also a subtle difference in the time histories of CRs and B. The time evolution of CRs at Earth is different in successive activity cycles. In A < 0 epochs, the CR intensity as a function of time is peaked and narrow while in the A > 0 cycles the profiles are much less peaked, as shown in the bottom panel of Fig. 1. This 22-year cycle is caused by reversals in the polarity of B responding to changes in the drift patterns of CRs that reverse every ∼11 years when the polarity of the HMF changes. Galactic CRs thus respond to the curvature and gradients in the HMF and to variations in the HCS. They also diffuse towards the Sun while getting convected back towards the heliospheric boundary by the solar wind, experiencing significant adiabatic energy losses [1,3]. They thus respond to what had happened on the Sun after these solar activity variations reached the Earth. However, the total modulation effect is observed only after these variations have reached the outer heliospheric boundary several months later [6,7].

Modeling transport processes in the heliosphere

The method of describing the transport mechanisms for the modulation of CRs is through a simplified Fokker–Planck type equation, called Parker’s transport equation (TPE) [8]:

$$\frac{\partial f}{\partial t}=\nabla ·({\mathbf{\kappa }}_{\mathbf{s}}·\nabla f)-({\mathbf{V}}_{\mathbf{sw}}+\langle {\mathbf{v}}_d\rangle )·\nabla f+\frac{1}{3}(\nabla ·{\mathbf{V}}_{\mathbf{sw}})\frac{\partial f}{\partial \ln P}$$ (1)

where f(r, P, t) is the cosmic ray distribution function at position r, time t, and rigidity P = pc/Ze of a CR particle with charge Ze, atomic number Z, momentum p, and with c the speed of light. The differential intensity j is commonly used and is given by j = P²f, in units of particles MeV⁻¹ m⁻² s⁻¹ sr⁻¹. The diffusion tensor, in terms of the HMF orientation is given as

$${\mathbf{\kappa }}_{\text{s}}=\left[\begin{array}{ccc}\hfill {\kappa }_{||}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\kappa }_{\perp \theta }\hfill & \hfill {\kappa }_d\hfill \\ \hfill 0\hfill & \hfill -{\kappa }_d\hfill & \hfill {\kappa }_{\perp r}\hfill \end{array}\right]$$ (2)

with κ_|| being the diffusion coefficient parallel to the average background B, with κ_⊥r and κ_⊥θ being the diffusion coefficients perpendicular to B in the radial and polar directions, respectively. The effective diffusion coefficient in the radial direction in a heliocentric, spherical coordinate system is then given by

$${\kappa }_{\mathit{rr}}={\kappa }_{||}{\cos }^2\psi +{\kappa }_{\perp r}{\sin }^2\psi$$ (3)

where ψ is the spiral angle of B, the angle between the radial direction and the averaged direction of B. See also [1,2]. Under the assumption of weak scattering, the drift velocity is given by $\langle {\mathbf{v}}_d\rangle =\nabla \times ({\kappa }_d{\mathbf{e}}_B)$ with the drift coefficient

$${\kappa }_d=\frac{\beta P}{3B}\left[\frac{10{\stackrel{\sim }{P}}^2}{1+10{\stackrel{\sim }{P}}^2}\right]$$ (4)

describing the effects of gradient and curvature drifts. Here, $\stackrel{\sim }{P}=P/P_o$ with P_o = 1.0 GV, β = v/c with v the speed of the CR particle; e_B = B/B is a unit vector in the direction of B. Using α as the only time-dependent parameter, it was shown that time-dependent modulation including gradient, curvature, and HCS drifts could reproduce the basic features of observed CR modulation [9]. However, it was later shown that the model could not reproduce CR variations during a phase of increased solar activity [6,7]. This was especially true when large step decreases in the observed CR intensities occurred prominently during periods of enhanced solar activity. In order to simulate CR intensities during moderate to high solar activity, propagation diffusion barriers (PDBs) had to be introduced [6,9]. These PDBs are in the form of merged interacting regions in the HMF caused by interacting outflows of the solar wind. Regions of fast and slow solar wind speeds are separated by sharp boundaries, resulting in strong longitudinal speed gradients. Fast solar wind speeds are typically ∼800 km s⁻¹, while the slow solar wind speed is ∼400 km s⁻¹. When fast streams of the solar wind run into slower streams ahead of them, interacting regions (IRs) are formed where the magnitude of B and the turbulence are higher. If the structure is stable for several rotations these IRs become corotating interacting regions (CIRs). When two or more CIRs merge, corotating merged interacting regions (CMIRs) form and when they merge, global merged interaction regions (GMIRs) forms which produce very effective CR modulation barriers [10]. Large step decreases of CRs are caused by these PDBs; see the lower panel of Fig. 1. The degree with which GMIRs affect long term modulation depends on the size of the heliosphere (modulation volume), their rate of occurrence, their spatial extent (they may encircle the Sun, stretching up to high heliolatitudes), and how the background B is disturbed consequently. Large GMIRs are not common inside 20 astronomical units (AU), with the Earth at 1 AU. By including a combination of drifts and GMIRs in a comprehensive time-dependent CR model it was shown that it is possible to simulate, to first order, a complete 11 year CR modulation cycle [6,7,9].

Time-dependent modeling of cosmic rays in the heliosphere

The numerical solution of the full TPE (five numerical dimensions) is seldom used because of its complexity so that in order to make progress various approximations have to be introduced. The two-dimensional (2D) compound numerical model used here was developed by Ferreira and Potgieter [6], applied to Ulysses observations by Ndiitwani et al. [7] and recently improved and applied to Voyager 1 and Voyager 2 (V1 and V2) observations by Manuel et al. [11,12]. In this model, azimuthal symmetry is assumed which in turn eliminates cross-terms in the numerical solution of TPE but also reduces its applicability and validity to time scales of one solar rotation or more. The diffusion and drift coefficients used were described in detail by Manuel et al. [11,12] and is not repeated here because of page limitations. It suffices to say that these authors introduced theoretical advances in diffusion and turbulence theory to derive CR transport parameters applicable to the heliosphere in order to establish a time-dependence for the relevant transport parameters used in this compound model. According to this approach, the coefficients in Eq. (2) scale time-dependently as the ratio of the variance in B with respect to the background B.

Results and discussion

The computed proton differential intensities with rigidity 2.5 GV are shown in Fig. 2 as a function of time, compared to 2.5 GV proton observations at Earth (blue line) and along the Ulysses trajectory (red line) [1,13]. Vertical lines indicate the three fast latitude scans (indicated by FLS1,2,3) that Ulysses made in ∼1995, ∼2001 and ∼2007, respectively [1,2]. The HMF switches polarity from A > 0 to A < 0 at the time of year 2000.2 as indicated by the darker vertical line.

Fig. 2.

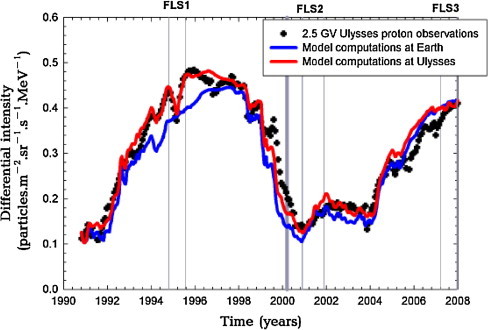
Computations of 2.5 GV proton differential intensities against time compared to proton observations at Earth and along the Ulysses trajectory [13]. Vertical lines indicate the three fast latitude scans that Ulysses made in ∼1995, ∼2001 and ∼2007, respectively. The HMF switches polarity (from A > 0 to A < 0) at 2000.2 as indicated by the darker vertical line.

In Fig. 3 proton observations with E > 70 MeV are shown as a function of time for V1, at Earth by the IMP spacecraft and for 2.5 GV from Ulysses [1,2,13]. These observations are compared with model computations along the V1 trajectory and at Earth. This was done for two approaches in simulating the time dependence of the transport parameters; the previous compound approach [6,7] (solid line) and for the advanced compound approach using improved diffusion theory (dashed line). See Manuel et al. [10,11] for a full discussing of the two approaches. Although the model cannot reproduce variations shorter than one solar rotation, it is quite realistic in producing the 11-year and 22-year cycles, including the two Voyager spacecraft and the latitude dependent modulation observed by Ulysses [1,2,7]. The model is clearly suited to produce CR intensities on a global scale but still needs improvement for increased solar activity conditions when GMIRs seem required to simulate all the larger step decreases.

Fig. 3.

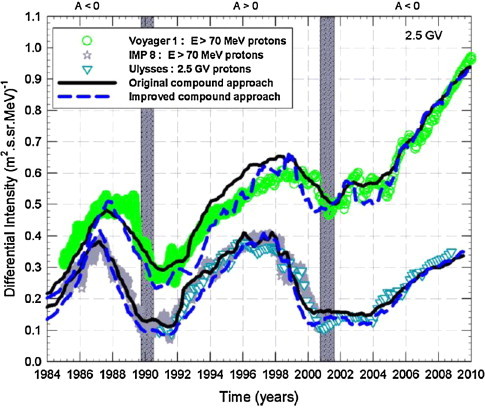
Proton observations with E > 70 MeV from V1 as a function of time (http://www.voyager.gsfc.nasa.gov/heliopause) and at Earth by the IMP satellite [14], as well as at 2.5 GV from Ulysses [1,2,13]. Model computations are shown along the V1 trajectory for the two approaches in simulating the time dependence in the transport parameters, the previous compound approach as the solid line and for the approach incorporating the improved theory as the dashed line.

Conclusions

The modeling approach can successfully reproduce CR intensity variations at Earth, along V1 and V2 trajectories, as well as along the Ulysses trajectory, as shown in comparison with proton observations from IMP, Ulysses, V1 and V2. Input parameters, such as the tilt angle, HMF magnitude and total variance can be extrapolated to predict future CR intensities at Earth and along spacecraft trajectories as well as for past and future solar activity cycles. The model is suitable to study very long-term CR variations, even over centuries, including exceptional periods such as the Maunder Minimum and other grand minima [15].