Broadband optical absorption by tunable Mie resonances in silicon nanocone arrays

Abstract

Nanostructure arrays such as nanowire, nanopillar, and nanocone arrays have been proposed to be promising antireflection structures for photovoltaic applications due to their great light trapping ability. In this paper, the optical properties of Si nanopillar and nanocone arrays in visible and infrared region were studied by both theoretical calculations and experiments. The results show that the Mie resonance can be continuously tuned across a wide range of wavelength by varying the diameter of the nanopillars. However, Si nanopillar array with uniform diameter exhibits only discrete resonance mode, thus can't achieve a high broadband absorption. On the other hand, the Mie resonance wavelength in a Si nanocone array can vary continuously as the diameters of the cross sections increase from the apex to the base. Therefore Si nanocone arrays can strongly interact with the incident light in the broadband spectrum and the absorbance by Si nanocone arrays is higher than 95% over the wavelength from 300 to 2000 nm. In addition to the Mie resonance, the broadband optical absorption of Si nanocone arrays is also affected by Wood-Rayleigh anomaly effect and metal impurities introduced in the fabrication process.

Structures by architectural design at the nanoscale to provide high optical absorbance are important for improving the efficiency of solar cells. In addition to interference-based antireflection coating, silicon-based two-dimensional array of nanostructures, such as nanosphere, nanowire, nanopillar, and especially nanocone, have recently been demonstrated as promising building blocks for high efficiency solar cells due to their broadband low reflectivity for light¹,²,³,⁴,⁵,⁶,⁷,⁸. These nanostructure arrays could be utilized to enhance absorption and to reduce reflectivity in solar cells without introducing extra materials. Since the nanostructure arrays can be added to the outer side of the solar cells, they do not affect the internal morphology of the active-layer. Silicon nanostructures with high absorbance in visible and near infrared region have been reported⁹,¹⁰. Besides applications in solar cells, textured silicon with excellent antireflection ability could also be utilized in hetero-junction photovoltaic cells, photothermal devices and supersensitive photo-detectors. The low reflectivity of Si nanostructure arrays has been attributed to many different factors, including the graded-index coating model²,¹¹,¹² with the mechanism similar to that of the multilayer anti-reflection thin film model, multiple light scattering¹³,¹⁴ where the nanostructure arrays enhanced the scattering (or absorption) path length, and substrate-coupled by Mie resonance⁴,¹⁵ which was usually used to describe small aspect-ratio particles.

Nanostructures can be made in a variety of shapes and sizes which can significantly influence optical properties of the nanostructure arrays¹⁶,¹⁷,¹⁸. The effects of substrate on the optical properties of Si nanoparticles have also been studied in previous works¹⁹,²⁰,²¹. Most theoretical studies so far have focused on nanosphere or nanopillar arrays. However, Si nanocone arrays with high absorbance in a wide wavelength range have recently been reported⁹,¹⁰. Understanding the optical response of nanostructure arrays to solar radiation is still a critical and fundamental step in the design of future generations of high performance solar cells.

In this paper, the optical properties of Si nanopillar and nanocone arrays in visible and infrared region were studied by theoretical calculations and experimental measurements. By simulating the reflectance and absorbance spectra and the electric field distributions of Si nanostructure arrays, we demonstrated that the Mie resonance modes can be tuned by the cross section diameters from the apex to the base in Si nanocone arrays, which resulted in high absorption over a wide range of solar spectrum. It was also shown that the nanocone arrays can act as optical antenna while the incident light is coupled to the Si substrate by the Mie resonance absorption, which increases the efficiency of the solar cells.

Results and Discussion

Fig. 1(a) and (b) illustrate the configuration of nanopillar and nanocone arrays used in the simulations. The array is defined by three parameters: base diameter BD, period P, and height H. For nanocone arrays, the base diameter is always set equal to the period. All arrays were illuminated from the top in air. The incident direction of light is normal to the substrate surface unless otherwise specified.

Figure 1. Schematic of the (a) nanopillar and (b) nanocone arrays.

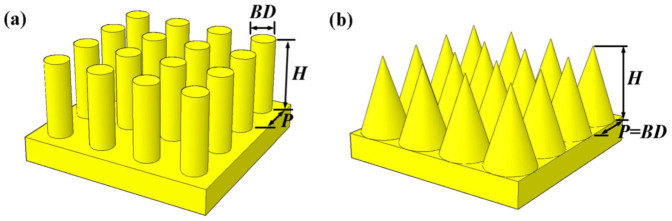
The nanocone is defined by the base diameter BD and the height H.

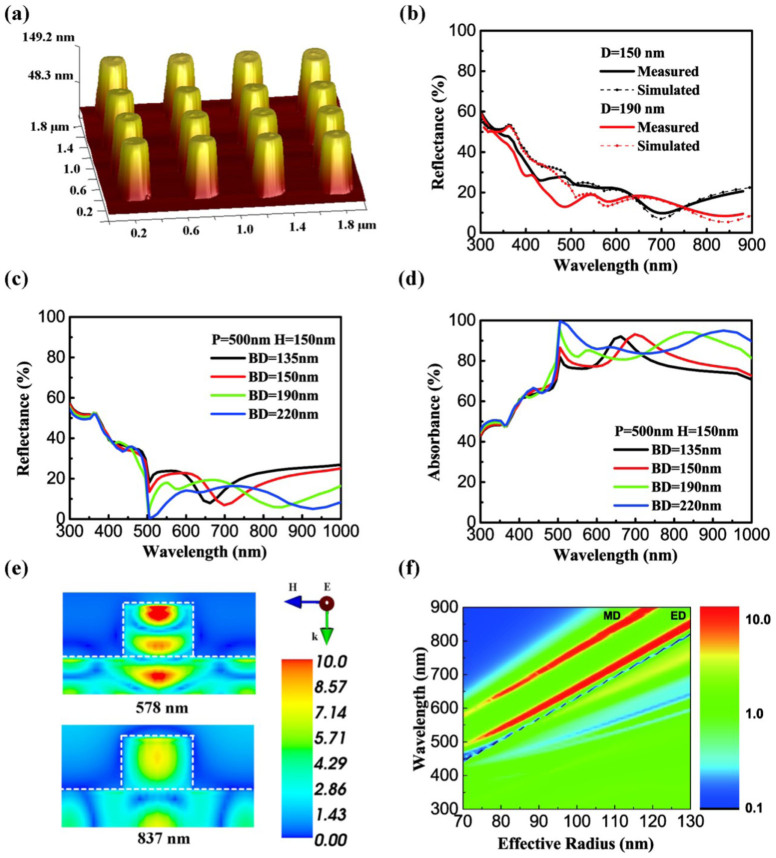
Two different nanopillar array samples were fabricated with H = 150 nm and P = 500 nm, the base diameters are 150 nm and 190 nm, respectively. Fig. 2(a) shows the atomic force microscope (AFM) image of fabricated nanopillar sample with H = 150 nm, P = 500 nm and BD = 190 nm. The measured and simulated reflectance spectra of the nanopillar samples are shown in Fig.2(b), the measured results are in good agreement with the simulations except for the wavelength lower than 500 nm. The discrepancy between experimental and simulated results may be caused by the different dielectric constants between the doped Si (in experiments) and intrinsic Si (in the simulations)²². With increasing diameter, the dip (700 nm for BD = 150 nm sample and 850 nm for BD = 190 nm sample) of reflection resulting from the Mie resonance shows a trend of redshift. Fig. 2(c) and (d) illustrate the simulated reflectance and absorbance spectra of silicon nanopillar arrays with the same period and height but different diameters. The sharp drop in the reflectance around 500 nm is due to Wood-Rayleigh (WR) anomaly effect caused by the periodic structure. WR anomaly occurs when the array period P and wavelength λ satisfy the following equation²³:

where n is the refractive index of the optical medium, k is the order of WR anomaly and θ is the incident angle. For normal incident of light into Si nanopillar arrays, n = 1 and θ = 0, the equation becomes P = kλ. So the dip near 500 nm in Fig. 2(c) is the first order of WR anomaly. In Fig. 2(b) the incident angle is 8 degree so the wavelength of WR is near 570 nm.

Figure 2. Mie resonance and absorbance spectra of the Si nanopillar arrays.

(a) AFM image of the nanopillar sample with BD = 190 nm, H = 150 nm, P = 500 nm. (b) Average value of transverse electric (TE) and transverse magnetic (TM) modes from the simulations is compared with experiment; the incident angle is 8 degree. (c,d) Simulated reflectance and absorbance spectra of silicon nanopillar arrays with different diameters. (e) Electric field distributions (|E|/|E₀|) of Si nanopillar arrays in (b), the diameter is 190 nm. (f) Q_sca of the Si nanopillar with different effective radius. Mie resonance peaks redshift with the effective radius of nanopillar.

Other dips at the wavelengths of 662, 699, 847 and 927 nm in Fig. 2(c) and (d) can be attributed to the Mie resonance effect at base diameter of 135, 150, 190 and 210 nm, respectively²⁴,²⁵. The redshift of Mie resonance modes with increasing particle size is predicted from the simulations. The electric field distributions in Fig. 2(e) provide useful information for understanding the light propagation in the structure. Light at the resonant wavelength is trapped and confined in the pillar and then spreads into the substrate. Fig. 2(f) illustrates the normalized scattering cross section (Q_sca) of the nanopillar arrays with different effective radii. The two red narrow bands represent the first order of the Mie resonance²⁶. The two modes are magnetic dipole (MD) and electric dipole (ED) resonance labeled in the figure. It can be seen that the peaks of Mie resonance could be adjusted by controlling particle parameters. Although Mie resonance effect helps lowering the reflectance of nanopillar arrays, the reflectance is still much higher than that of silicon nanocone structure.

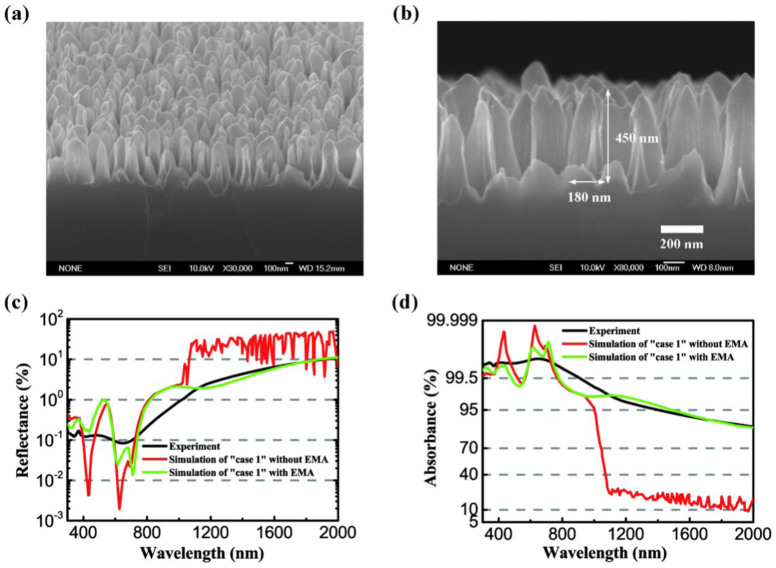
It has been reported that Si nanocone structure can have high absorbance in visible to near infrared wavelength range⁹,¹⁰. This observation is contradictory to the fact that monocrystalline silicon is transparent in the infrared region. To further understand the absorption of nanocone structure in visible and infrared region, the simulations were performed by including the extinction coefficient from the metal silicides through the effective medium approximation (EMA)²⁷ in the infrared region. In this case, the metal silicides are iron and chrome silicides which formed in the surface layer of the nanocone during the samples fabrication. Detailed information for the nanocone sample can be found in recent publication by Qiu et al⁹. The monocrystalline Si nanocone structure was also simulated for comparison. Fig. 3(a) and (b) show a bird's eye view and corresponding cross sectional scanning electron microscope (SEM) image of the prepared silicon nanocone arrays, respectively. The nanocone sample shows certain degree of irregularity. By counting individual particles through SEM image, the nanocone sample is 179.5 ± 18.6 nm in base diameter and 460.4 ± 35.7 nm in height. In order to see the influence of non-uniform nanocone arrays on the optical property, simulations for nanocone arrays with randomness in the heights and base diameters were performed for comparison. The structure (named as “case 1”) is a periodic array consists of 4 nanocones in the unit cell with different heights and diameters (i.e., D₁ = 200 nm, H₁ = 420 nm, D₂ = 160 nm, H₂ = 440 nm, D₃ = 160 nm, H₃ = 460 nm D₄ = 200 nm, H₄ = 480 nm), as illustrated in Supplementary Fig. S3(c). The average base diameter and height of “case 1” are close to those of the experimental sample. As shown in Supplementary Fig. S3(d), the spectrum of “case 1” is smoother and broader than the one from uniform size array. The measured spectrum in the experimental sample is an average over the spectra of various particle sizes and leads to a smooth curve. Fig. 3(c) and (d) give the absorbance and reflectance spectra of “case 1” with and without EMA. The EMA introduced a strong absorbance in infrared region, indicating that the strong absorbance observed by experiment in the infrared region is due to the introduction of impurities during the sample fabrication. For monocrystalline silicon, the light with the wavelengths greater than 1000 nm will penetrate the substrate. Impurities and defects in the sample increased the scattering within the sample and the light was trapped, thus reduced the reflectance and enhanced the absorption in the infrared region. In the visible region, the differences between EMA and monocrystalline silicon are negligible, so EMA will not be taken into account in discussions below.

Figure 3. Silicon nanocone arrays and its reflectance and absorbance spectra in visible and infrared region.

(a,b) SEM image of silicon nanocone array samples. (c,d) Comparisons of reflectance and absorbance spectra between experiment and simulations. The incident angle here is 8 degrees.

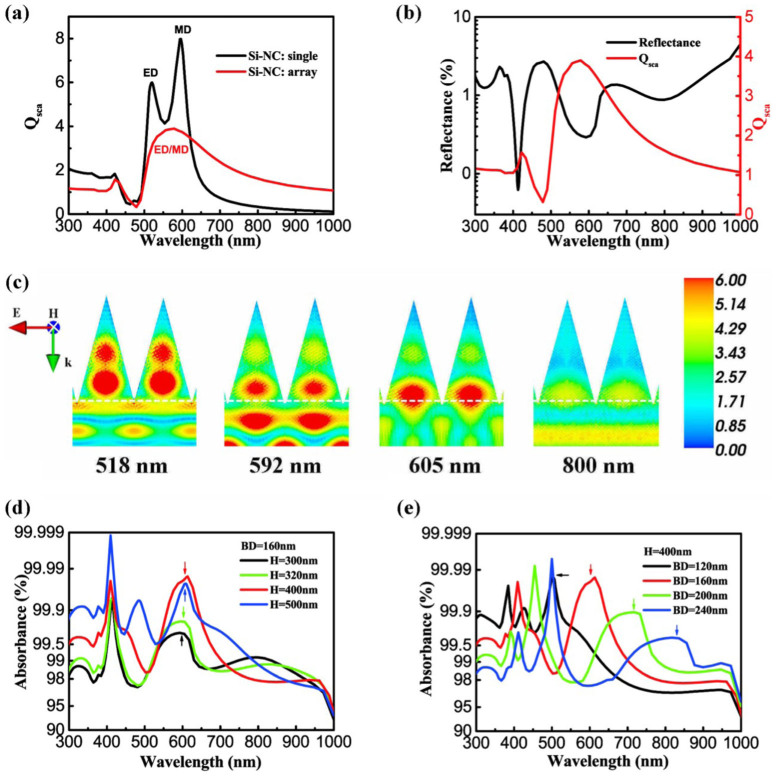
Simulations were also performed to compare the optical response of an isolated nanocone and that of a nanocone array with the same size of 160 nm in base diameter and 300 nm in height. The Q_sca spectra are shown in Fig. 4(a). It is has been shown that conical structures have very similar scattering properties as nanopillars in Fig. 2(f). Furthermore, the compact periodic structure strongly affects the wavelength of Mie resonance. The resonance peaks of nanocone arrays merge into a broader and much stronger feature at 500–1000 nm range, which is in agreement with previous works on nanoparticles¹⁶,¹⁷. The Q_sca and reflectance spectrum (on Si substrate) of nanocone arrays are compared in Fig. 4(b). The reflectance reaches to a minimal value when Q_sca is maximal. The electric field distribution in Fig. 4(c) demonstrates how light was coupled to the substrate by Mie resonances (substrate in this figure is 200 nm thick). With the diameter of the cross section changes continuously from the base to the apex, light with every wavelength could find an optimum resonance condition in nanocone arrays. This leads to the reflectance lower than 2.5% in the whole spectrum and much better performance than nanopillar structures. The resonance mode in the cone overlaps with the substrate and provides a leaky channel for light coupling into the substrate. Because most light will be scattered forward or absorbed, the efficiency of solar cells using the nanocone arrays as the anti-reflection layer will be increased. Besides nanocone structure, other particles with gradual diameter variations could also have the potential to achieve a high broadband absorbance.

Figure 4. Mie resonance and absorbance spectra of the Si nanocone arrays.

(a) Normalized scattering cross section of single Si nanocone (black) and Si nanocone array (red). (b) Relationship between reflectance (black) and normalized scattering cross section (red) of Si nanocone arrays. (c) Electric field distributions (|E|/|E₀|) of Si nanocone arrays at different wavelength, the nanocone is 300 nm in height and 160 nm in base diameter. (d,e) Simulated absorbance spectra of Si nanocone arrays of various heights and base diameters. The arrows indicated the Mie resonance peaks.

The Mie resonances of particle arrays are controlled by particles sizes and the periodicity of the arrays²⁸,²⁹. We have also simulated the dependence of the absorbance on the height and period of nanocone arrays. Fig. 4(e) shows the absorbance of nanocone arrays with different base diameters (or periods); the height is fixed at 400 nm. For periodic nanocone arrays, changing the period does not show significant effects on average absorbance as illustrated in Supplementary Fig. S4(b). But the peaks from Mie resonance (indicated by the arrows) exhibit significant redshift as the base diameter increased. The results of absorbance with the height at the fixed period is shown in Fig. 4(d), the periods of the nanocone arrays are fixed at 160 nm and the height varies from 300 nm to 500 nm. The average absorbance increases with the height, which is enhanced by the larger surface area of the particles³⁰. However, the redshift of Mie resonances (marked with arrows) are hardly observed as the height of the nanocones vary from 300 to 500 nm. The effective radius of nanocone particle with different height is given in Supplementary Table 1. The effective radius is limited by the period, and the Mie resonance peak shows little trends of shifting. In Fig. 4(d) and (e), there are other sharp peaks other than Mie resonance peak. For BD = 160 nm, the peak is at 413 nm, and is shifted as the base diameter (or period) changes. These peaks can be explained by WR anomaly discussed above (see Eq (1)). More details about the origins of all peaks in Fig. 4(e) are given in supplementary Table 2. Absorbance and reflectance (average value of TE and TM modes) spectra simulated for Si nanocone array with P = BD = 160 nm, H = 400 nm at different light incident angles are also shown in Supplementary Fig. S5. The results show that the Si nanocone array exhibits broadband and quasi-omnidirectional (angle of incidence from 0 to 60°) antireflection property.

Conclusions

In summary, Si nanopillar and nanocone arrays with various heights and base diameters were investigated by simulations and experiments. The simulations indicate that the high absorbance of the nanostructure arrays is due to the Mie resonance and WR anomaly effect, which could be tuned by changing the parameters of the nanostructures. The electric field distributions and the large normalized scattering cross section (Q_sca) associated with the Mie resonance modes reveal that coupling of the Mie resonance modes with the Si substrate leads to a strong light trapping effect. The Mie resonant wavelength can be tuned continuously as the diameters of the cross sections in nanocone increase from the apex to the base, resulting in a broadband absorption. The presence of impurities in the nanostructures is beneficial to broaden the absorption to the infrared region. The dependence of these resonances on the geometries of nanostructure arrays provides useful controlling parameters in designing specific wavelength and bandwidth photovoltaic and photothermal devices.

Methods

Fabrication and Measurement

The nanopillar samples were fabricated by reacting ion etching, and the nanocone sample was fabricated using heavy-metal incorporated low-energy Ar+ ion sputtering method¹². The ion beam faced normally to the polished side of the Si sample. The Si sample was fixed by a stainless steel mask consisting of Fe and Cr with a hole of diameter of 1.5 cm in the middle. The reflectance and transmittance spectra of the samples were measured using a UV-vis spectrometer (Perkin Elmer, Lambda 950 with integrating sphere) with non-polarized light source. The surface topography was measured using an Atomic Force Microscope System (Veeco, VT-1000) and Scanning Electron Microscope (Philips, XL30).

Optical Modelling and Simulation

The reflectance and absorbance spectra of the nanostructure arrays are simulated using the transfer matrix method (TMM)³¹,³². The TMM software package was developed by Iowa State University Research Foundation. It can handle the wave scattering by nanostructure arrays, leading to the transmission and reflection spectra. The nanostructure arrays are modeled using the periodic boundary conditions in the in-plane directions. The reflectance and absorbance were calculated with arrays on a 500 μm thick Si substrate. In our simulation, the nanocone structure is approximated by a series of stacking cylinders as shown in Supplementary Fig. S2.

The DDSCAT 7.2 code package was employed to calculate normalized scattering cross section (Q_sca), normalized absorption cross section (Q_abs) and the electric field distributions³³. The DDSCAT package is based on the discrete dipole approximation (DDA); the target is replaced by an array of point dipoles. The electromagnetic scattering problem for an incident wave interacting with this array of point dipoles is then solved. For targets with a substrate, the DDA will consume much longer time because each point of the substrate will be replaced with a dipole. In this case, the thickness of substrate in electric field distribution calculation (Fig. 2(e) and Fig. 4(c)) was set to 200 nm. The quantity being plotted in the electric field distributions is the electric field E normalized to the intensity of incident light E₀ (i.e. |E|/|E₀|).

The dielectric constant of silicon used in the simulations was taken from a book by Palik³⁴.

Author Contributions

Z.Y.W. and S.Y.W. carried out the theoretical analyses; Z.Y.W., R.J.Z. and X.C. performed the optical measurements and surface topography characterization; M.L. synthesized the Si nanocones arrays; Z.Y., K.M.H. and C.Z.W. developed the TMM algorithms and helped theoretical analyses; Y.X.Z. and L.Y.C. discussed and interpreted the results; and Z.Y.W., S.Y.W., C.Z.W., R.J.Z. and Z.Y. co-wrote the paper.

Supplementary Material

Supplementary Information

SUPPLEMENTARY INFO