Abstract
Blind quantum computation (BQC) provides an efficient method for the client who does not have enough sophisticated technology and knowledge to perform universal quantum computation. The single-server BQC protocol requires the client to have some minimum quantum ability, while the double-server BQC protocol makes the client's device completely classical, resorting to the pure and clean Bell state shared by two servers. Here, we provide a deterministic entanglement distillation protocol in a practical noisy environment for the double-server BQC protocol. This protocol can get the pure maximally entangled Bell state. The success probability can reach 100% in principle. The distilled maximally entangled states can be remaind to perform the BQC protocol subsequently. The parties who perform the distillation protocol do not need to exchange the classical information and they learn nothing from the client. It makes this protocol unconditionally secure and suitable for the future BQC protocol.
Blind quantum computation (BQC) is a new type of quantum computation model which can release the client who does not have enough knowledge and sophisticated technology to perform the universal quantum computation1,2,3,4,5,6,7,8,9,10,11,12,13,14,15. A complete BQC comprises two parts. One is the client, say Alice, who has a classical computer and some ability of quantum operation, or she may be completely classical. The other is the fully-fledged quantum computer server owned by Bob. The first BQC protocol was proposed by Childs in 20051. It requires the standard quantum circuit model. In his protocol, Bob needs to perform the quantum gates and Alice requires the quantum memory. In 2006, Arrighi and Salvail proposed another BQC protocol where Alice needs to prepare and measure multiqubit entangled states. It is cheat sensitive for Bob obtaining some information, if he does not mind being caught2. In 2009, Broadbent, Fitzsimons, and Kashefi proposed a different BQC model (BFK protocol)3,16. Their protocol is based on the one-way quantum computation. In their protocol, Alice only requires to generate the single-qubit quantum state and a classical computer. She does not need the quantum memory. Moreover, Bob cannot learn anything from Alice's input, output and her algorithm, which makes it unconditionally secure. Inspired by the BFK protocol, several BQC protocols have been proposed. For instance, Morimae et al. proposed two BQC protocols based on the Affleck-Kennedy-Lieb-Tasaki state4. Fitzsimons and Kashefi constructed a new verifiable BQC protocol based on a new class of resource states6. Morimae and Fujii proposed a BQC protocol in which Alice only makes measurements9. The experimental realization of the BFK protocol based on the optical system was also reported11. Recently, Li et al. proposed the triple-server BQC protocol based on the entanglement swapping15. Actually, the aim of the BQC is to let the client who does not have enough sophisticated quantum technology and knowledge perform the quantum computation. Therefore, the Alice's device and operation is more classical, the protocol is more successful. In BFK protocol, if Bob only has one server, Alice still needs some quantum technology. On the other hand, if two servers are provided which are owned by Bob1 and Bob2, respectively, Alice will not require any quantum technology. She can complete the quantum computation task with a classical computation, resorting to the classical communication. This protocol is called double-server BQC protocol. In double-server BQC protocol, Bob1 and Bob2 should obey a strong assumption that they cannot communicate with each other. If not, they can learn the computation information from Alice and make the computation insecure. Before starting the BQC protocol, they should share the maximally entangled Bell states. Unfortunately, in a realistic environment, the noisy channel will greatly degrade the quality of the entanglement and it will make the whole computation become fail, similar to the non-blind quantum computation. Generally speaking, in double-server BQC protocol, if Bob1 and Bob2 share the mixed entangled states, the Bob2 will obtain the mixed single qubit states, after the Bob1 performing the single qubit measurements. Obviously, these errors always exist in the subsequent single-server BFK protocol, which will ultimately make the whole computation cause error. As pointed out by Refs. 5, 12, it is shown that the double-server BQC protocol is also fault tolerant, but they should require the fidelity of the Bell pairs to be above 99%, even if topological BQC is employed. Therefore, entanglement distillation is required during the noisy double-server BQC protocol.
Entanglement purification is the standard way for distilling the high quality entangled state from a low quality entangled state, which has been widely discussed in current quantum communication17,18,19,20,21,22,23,24,25,26,27,28,29,30. In 1996, Bennett et al. presented the entanglement purification protocol (EPP) with the help of the controlled-not (CNOT) gate17. In 2001, Pan et al. proposed a novel EPP with feasible linear optics20. There are some EPPs based on the nonlinear optics and hyperentanglement22,24,25,26,27. Unfortunately, in a standard EPP, they all need the local operation and classical communication. As pointed out by Morimae and Fujii12, the security of the double-server BQC protocol is not guaranteed in the double-server blind protocol, when the entanglement distillation protocol is required.
Recently, Morimae and Fujii presented a secure entanglement distillation protocol based on the one-way hashing distillation method12. In their protocol, Alice first randomly selects a 2n-bit string s1 and distributes it to two Bobs, respectively. Then each Bob performs certain local unitary operation determined by s1. By measuring a qubit of the single pair, Alice can obtain a bit information from the remained mixed state ensembles. Therefore, by repeating this protocol, they can obtain nS(ρ) bits of information about the mixed states ensembles. At the end of distillation, they can share about n – nS(ρ) pairs.
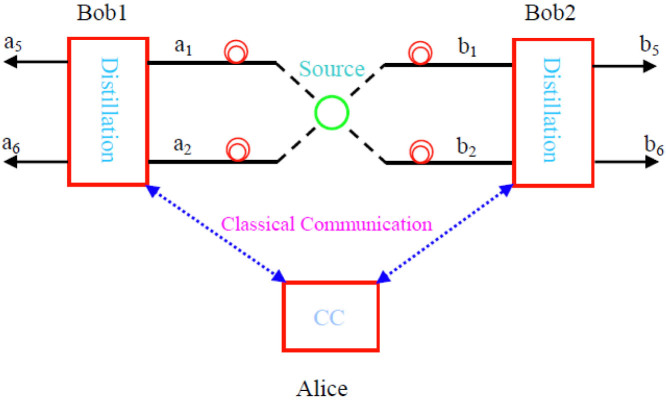
In this paper, we will present another deterministic entanglement distillation protocol for secure double-server BQC protocol. The whole protocol is based on the optical system, because the optical system is suitable for double-server BQC. First, during the standard double-server BQC, two servers say Bob1 and Bob2 should first share the maximally entangled state nonlocally, which is distributed by a trust center12. Photons have natural advantages in carrying and distributing the information for their fast transmission. Second, photons encoded in the polarization degree of freedom are well controlled and manipulated. The first experiment for BQC was also demonstrated in an optical system11. This protocol is quite different from the one-way hashing distillation model and we resort to the hyperentanglement to complete the distillation31,32,33,34. After performing the protocol, Alice can obtain the exact Bell state deterministically. The success probability can reach 100%, in principle, according to the Bobs's measurement results. Moreover, Alice does not feedback any information to Bobs, which makes this distillation secure.
Results
Suppose that both Bobs own the setup of the quantum nondemolition (QND) measurement as shown in Fig. 1. The source (trust center) first generates a pair of hyperentangled state in both polarization and spatial modes, which can be described as
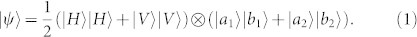 |
Figure 1. Schematic of the principle of the quantum nondemolition (QND) measurement constructed by the cross-Kerr nonlinearity.
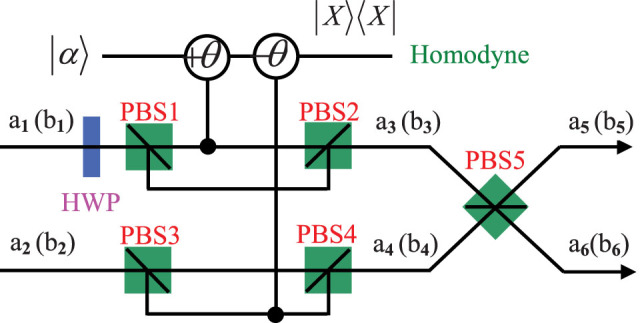
HWP is the half wave plate which can make |H〉 ↔ |V〉. PBS is the polarization beam splitter. It can transmit the |H〉 polarized photon and reflect the |V〉 polarized photon, respectively. |α〉 is the coherent state.
Such state is distributed to Bob1 and Bob2 through the spatial modes a1, a2, b1 and b2, respectively, as shown in Fig. 2. As pointed out in Refs. 22, 25, 27, during the transmission, the spatial entanglement is more robust than polarization entanglement. The noisy channel will lead the polarization part become a mixed state as
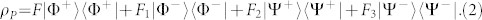 |
Figure 2. Schematic of the principle of the double-server BQC protocol combined with entanglement distillation.
Bob1 and Bob2 can exchange the classical communication with Alice, respectively. But they cannot communicate with each other. CC is a classical computer. Both Bobs own the distillation equipment as shown in Fig. 1.
Here F + F1 + F2 + F3 = 1. |Φ±〉 and |Ψ±〉 are the polarized Bell states with
 |
The whole system ρ = ρP
 ρS can be described as a probabilistic combinations of four pure states17,18,19,20,21,22,23,24,25,26,27,28,29,30. The probability of the state |Φ+〉|Φ+〉s is F. The probability of the state |Φ−〉|Φ+〉s is F1. The probabilities of |Ψ+〉|Φ+〉 s and |Ψ−〉|Φ+〉s are F2 and F3, respectively. Here ρS = |Φ+〉s〈Φ+| with
ρS can be described as a probabilistic combinations of four pure states17,18,19,20,21,22,23,24,25,26,27,28,29,30. The probability of the state |Φ+〉|Φ+〉s is F. The probability of the state |Φ−〉|Φ+〉s is F1. The probabilities of |Ψ+〉|Φ+〉 s and |Ψ−〉|Φ+〉s are F2 and F3, respectively. Here ρS = |Φ+〉s〈Φ+| with 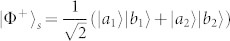 . After passing through the QNDs, the state |Φ+〉|Φ+〉s combined with two coherent states
. After passing through the QNDs, the state |Φ+〉|Φ+〉s combined with two coherent states 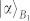 and
and 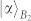 evolves as
evolves as
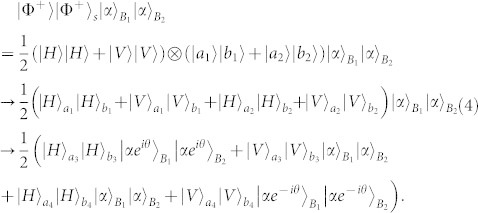 |
The 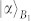 and
and 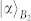 are the coherent states used in the QNDs for Bob1 and Bob2, respectively. On the other hand, the state |Ψ+〉|Φ+〉s combined with two coherent states
are the coherent states used in the QNDs for Bob1 and Bob2, respectively. On the other hand, the state |Ψ+〉|Φ+〉s combined with two coherent states 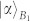 and
and 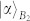 evolves as
evolves as
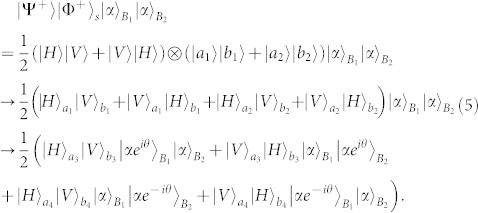 |
If they consider the other items |Φ−〉|Φ+〉s and |Ψ−〉|Φ+〉s, they can obtain the similar results. Then Bob1 and Bob2 both measure the phases of the coherent states with the X quadrature measurement, which makes the |αe±iθ〉 indistinguishable36. Therefore, both Bobs only have two different results, say θ or 0. After the measurement, they both send their measurement results to Alice by classical communication. Finally, Alice can judge the exact Bell state according to the measurement results. In detail, if the measurement results are the same, say both θ or 0, they will obtain |Φ+〉, with the probability of F + F1. Otherwise, if the measurement results are different, say Bob1 is θ and Bob2 is 0, or Bob1 is 0 and Bob2 is θ, they will obtain |Ψ+〉, with the probability of F2 + F3. During the whole protocol, two Bobs do not require to exchange their measurement results and they even do not know the information of the remained Bell state. They can only judge the output modes according to the different phase shift. If the coherent state shows no phase shift, the photon must be in the upper output modes a5(b5). Otherwise, if the coherent state shows θ phase shift, the photon must be in the lower output modes a6(b6). Interestingly, in our protocol, the initial parameters of the mixed state F, F1, F2 and F3 are arbitrary numbers and they only need to satisfy the condition F + F1 + F2 + F3 = 1. Therefore, different from the traditional EPPs17,18,19,20,21, we do not require the polarization part of the mixed state to be entangled.
Combined with the entanglement distillation, the double-server BQC protocol works as follows:
Step 1: As shown in Fig. 2, the entanglement source emits the hyperentangled pairs |ψ〉 to Bob1 and Bob2. They share m pairs of mixed states ρ⊗m, because of the noise.
Step 2: Both Bobs perform the distillation protocol and send the measurement results to Alice. The purified states are 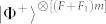 and
and 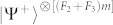 .
.
Step 3: The following steps are the same as the standard BQC protocol1,12. Alice sends Bob1 classical messages 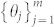 , where θj is randomly chosen by Alice from
, where θj is randomly chosen by Alice from 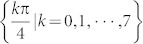 . In detail, if Alice obtains |Φ+〉, she randomly sends Bob1 θj, and if she obtains |Ψ+〉, she randomly sends −θj.
. In detail, if Alice obtains |Φ+〉, she randomly sends Bob1 θj, and if she obtains |Ψ+〉, she randomly sends −θj.
Step 4: Bob measures his qubit in the jth Bell states in the basis 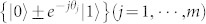 . Here we denote |H〉 ≡ |0〉 and |V〉 ≡ |1〉. After Bob1 performing the measurement, he tells Alice the results
. Here we denote |H〉 ≡ |0〉 and |V〉 ≡ |1〉. After Bob1 performing the measurement, he tells Alice the results 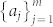 with aj ∈ {0, 1}m.
with aj ∈ {0, 1}m.
Step 5: Alice and Bob2 start to perform the single-server BQC protocol.
In a practical application, the entanglement distillation should be interspersed with the actual computation in order to avoid decoherence. As pointed out by Morimae and Fujii, two Bobs might exchange information about the previous double-server computation during entanglement distillation for the next round of computation, which will make the computation insecure12. This is the reason that the traditional entanglement distillation protocols are unsuitable for double-server BQC protocol, because message exchanges between two Bobs must be done through Alice's mediation17,18,19,20,21,22,23,24,25,26,27,28,29,30. Our double-server BQC combined with entanglement distillation is secure. First, during the distillation, Alice does not feedback any messages to both Bobs. From above description, Once Alice judges the maximally entangled state according to the measurement results coming from two Bobs, the entanglement distillation is finished. In this way, she can start the standard BQC protocol subsequently1,12. Therefore, Bob1 does not have the chance to send any message to Bob2 via Alice. They even do not know the exact information of the purified Bell state. Two Bobs learn nothing from Alice and cannot exchange the message with each other, which essentially means that distillation is secure. Second, once Alice knows the exact information of the distilled maximally entangled states, she can start the standard double-server BQC protocol, whose security is strictly proven and guaranteed in the previous BQC protocols. Third, both Bobs may have the evil intention and send wrong messages to Alice. In this way, Alice will obtain the wrong information about the Bell state, and it will induce the error computation. However, both Bobs still learn nothing from Alice.
Discussion
So far, we have fully described our protocol. It is interesting to compare this protocol with Ref. 12. In Ref. 12 they presented the first secure entanglement distillation protocol based on the one-way hashing distillation method. In their protocol, they require n pairs of degraded mixed states. After repeating their protocol for many rounds, they can finally obtain about n − S(ρ) pairs of maximally entangled states. They also exploit the controlled-not gate to complete the task, which is not experimentally feasible in current technology. Moreover, they require the initial fidelity of the mixed state to be greater than 81%. It will greatly limit the practical application for their protocol in a large noisy quantum channel. Our protocol has several advantages. First, we can obtain the deterministic maximally entangled state with the success probability of 100% in principle. Second, from our description, the initial fidelity F of the mixed state can be arbitrary number, and we even do not require the initial mixed state of the polarization part to be entangled. Third, for each pair of degraded mixed state, the distillation procedure is required to perform for only one step. It greatly reduces the practical operations for each party. Forth, Alice essentially does not need to participate in the distillation, but obtains the results to judge the exact information of the maximally entangled state, while in Ref. 12, Alice should randomly choose a 2n bit string s1 and sends it to two Bobs. Our protocol is simpler than the previous one.
Using spatial entanglement to purify the polarization entanglement has been studied for several groups22,25,26,27. However, their protocols are all unsuitable for BQC protocol. In Ref. 22, the bit-flip error can be well purified by choosing the same output modes. However, they should require the traditional entanglement purification to purify the phase-flip error. The first deterministic and complete entanglement purification using hyperentanglement was first described in Ref. 25. However, they should create the hyperentangled state which is entangled in three degrees of freedom simultaneously. It is still a challenge in current technology. In their protocol, they use the spatial entanglement to purify the bit-flip error, and use the frequency entanglement to purify the phase-flip error. In order to obtain the maximally entangled state, they should exploit the quantum frequency upconversion to erase distinguishability for frequency. It will decrease the fidelity of the entanglement. In Refs. 26, 27, with local operation and classical communication, both bit-flip error and phase-flip error can be corrected in one step. However, the photon pair is destroyed due to the post-selection principle. In the present protocol, the purified photon pair can be remained, resorting to the QND measurement. Moreover, both Bobs do not require to exchange the classical information, which makes it extremely suitable for double-server BQC protocol. In a practical realization, they should generate the hyperentanglement and make the spatial entanglement stable.
The generation of the hyperentanglement with both polarization and spatial degrees of freedom can be well solved with the spontaneous parametric down conversion (SPDC) source20,22. The pump pulse of ultraviolet light goes through a β-barium borate crystal (BBO). It can generate one pair of polarization entangled pairs with probability of p, and is reflected and passes through the crystal a second time and can produce the same photon pairs with the same order of magnitude. This protocol realizes on the hypothesis that the spatial entanglement does not suffer from the noise. Though the spatial entanglement is robust than polarization entanglement, it still will be polluted in noisy channel. Interestingly, it usually suffers from the phase-noise, while the phase-noise can also be well controlled in current technology20,22. Moreover, the experiment for phase-noise measurements showed that the phase in long fibers, such as tens of kilometers, can reach an acceptable stable level on the order of 100 μs35. The other technology challenge may come from the cross-Kerr nonlinearity. Though many quantum information processes with the cross-Kerr nonlinearity were discussed36,37,38,39,40,41, it is still a controversial topic42,44. Shapiro showed that Kerr nonlinearity in a single-photon level cannot contribute the benefit for quantum computation42,43. Gea-Banacloche also argued that it is impossible to obtain a large phase shift via a “giant” Kerr effect in a single wave packets44. As pointed out by Kok et al., in the optical single-photon regime, Kerr phase shift is only about 10−18. On the other hand, in current technology, it is quite a controversial assumption to obtain a clean cross-Kerr nonlinearity45,46. Fortunately, Hofmann showed that with the help of a single two-level atom trapped in a one-side cavity, one can obtain π phase47. Using weak measurement, it is possible to obtain an observable cross-Kerr phase shift with amplification48. As pointed out by Ref. 49, large cross-Kerr nonlinearities were also obtained in a double-quantum-well structure with a four-level, double-type configuration. The “giant” cross-Kerr effect with phase shift of 20 degrees per photon has been observed in current experiment50. Recent work also showed that the Rydberg atom system could generate rather large cross phase between photons51. Therefore, recent theoretical and experimental works based on cross-Kerr nonlinearity may provide its practical application in the future quantum information processing.
In conclusion, we have presented a deterministic entanglement distillation protocol for double-server BQC protocol. After performing the protocol, they can obtain the pure maximally entangled state. The success probability of this protocol can reach 100% in principle. Moreover, Bob1 and Bob2 do not communicate with each other and they also learn nothing from Alice. It makes the protocol unconditionally secure and suitable for future BQC protocol.
Methods
In Fig. 1, it is the QND measurement with the cross-Kerr nonlinearity. As pointed out by Refs. 36, 37, the Hamiltonian of the whole system is 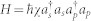 . Here the
. Here the 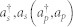 are the creation and destruction operators of the signal (probe) mode. From Fig. 1, if a single photon |V〉 in the spatial mode a1 passes through the equipment, the polarization of the photon will be flipped (|H〉 ↔ |V〉) by half-wave plate (HWP) and transmit through the polarization beam splitter (PBS). The single photon and the coherent state |α〉 will couple with the cross-Kerr nonlinearity and evolve as
are the creation and destruction operators of the signal (probe) mode. From Fig. 1, if a single photon |V〉 in the spatial mode a1 passes through the equipment, the polarization of the photon will be flipped (|H〉 ↔ |V〉) by half-wave plate (HWP) and transmit through the polarization beam splitter (PBS). The single photon and the coherent state |α〉 will couple with the cross-Kerr nonlinearity and evolve as
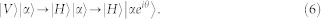 |
It is shown that the single photon state |H〉 is unaffected but the coherent state shows a phase shift directly proportional to the number of the photons. By measuring the phase of the coherent state, one can construct a QND measurement for the single photons.
Author Contributions
Y.B.S. and L.Z. wrote the main manuscript text and prepared figures 1–2. Both authors reviewed the manuscript.
Acknowledgments
This work is supported by the National Natural Science Foundation of China under Grant Nos.11474168 and 61401222, the Qing Lan Project in Jiangsu Province, the 1311 Talent Plan in NJUPT, and a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
References
- Childs A. M. Secure assisted quantum computation. Quantum Info. Comput. 5, 456–466 (2005). [Google Scholar]
- Arrighi P. & Salvail L.. Blind quantum computation. Int. J. Quantum Inform. 4, 883–898 (2006). [Google Scholar]
- Broadbent A., Fitzsimons J. & Kashefi E. Universal blind quantum computation. Proceedings of the 50th Annual IEEE Symposium on Foundations of Computer Science 517–526 (2009). [Google Scholar]
- Morimae T., Dunjko V. & Kashefi E. Ground state blind quantum computation on AKLT state. arXiv: 1009.3486 (2010). [Google Scholar]
- Morimae T. & Fujii K. Blind topological measurement-based quantum computation. Nat. Commun. 3, 1036 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzsimons J. & Kashefi E. Unconditionally verifiable blind computation. arXiv: 1203.5217 (2012). [Google Scholar]
- Morimae T. Continuous-variable blind quantum computation. Phys. Rev. Lett. 109, 230502 (2012). [DOI] [PubMed] [Google Scholar]
- Dunjko V., Kashefi E. & Leverrier A. Blind quantum computing with weak coherent pulses. Phys. Rev. Lett. 108, 200502 (2012). [DOI] [PubMed] [Google Scholar]
- Morimae T. & Fujii K. Blind quantum computation protocol in which Alice only makes measurements. Phys. Rev. A 87, 050301(R) (2013). [Google Scholar]
- Sueki T., Koshiba T. & Morimae T. Ancilla-driven universal blind quantum computation. Phys. Rev. A 87, 060301(R) (2013). [Google Scholar]
- Barz S. et al. Demonstration of Blind Quantum Computing. Science 335, 303–308 (2012). [DOI] [PubMed] [Google Scholar]
- Morimae T. & Fujii K. Secure entanglement distillation for double-server blind quantum computation. Phys. Rev. Lett. 111, 020502 (2013). [DOI] [PubMed] [Google Scholar]
- Giovannetti V., Maccone L., Morimae T. & Rudolph T. G. Efficient universal blind quantum computation. Phys. Rev. Lett. 111, 230501 (2013). [DOI] [PubMed] [Google Scholar]
- Mantri A., Delgado C. A. P. & Fitzsimons J. F. Optimal blind quantum computation. Phys. Rev. Lett. 111, 230502 (2013). [DOI] [PubMed] [Google Scholar]
- Li Q., Chan W. H., Wu C. & Wen Z. Triple-Sever blind quantum computation using entanglement swapping. Phys. Rev. A 89, 040302(R) (2014). [Google Scholar]
- Raussendorf R. & Briegel H. J. A one-way quantum computer. Phys. Rev. Lett. 86, 5188–5191 (2001). [DOI] [PubMed] [Google Scholar]
- Bennett C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76 722–725 (1996). [DOI] [PubMed] [Google Scholar]
- Bennett C. H., DiVincenzo D. P., Smolin J. A. & Wootters W. K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824–3851 (1996). [DOI] [PubMed] [Google Scholar]
- Deutsch D. et al. Quantum privacy amplification and the security of quantum cryptography over noisy channels. Phys. Rev. Lett. 77, 2818–2821 (1996). [DOI] [PubMed] [Google Scholar]
- Pan J. W., Simon C. & Zellinger A. Entanglement purification for quantum communication. Nature 410, 1067–1070 (2001). [DOI] [PubMed] [Google Scholar]
- Pan J. W. et al. Experimental entanglement purification of arbitrary unknown states. Nature 423, 417–422 (2003). [DOI] [PubMed] [Google Scholar]
- Simon C. & Pan J. W. Polarization entanglement purification using spatial entanglement. Phys. Rev. Lett. 89, 257901 (2002). [DOI] [PubMed] [Google Scholar]
- Martín-Delgado M. A. & Navascués M. Entanglement distillation protocols and number theory. Phys. Rev. A 68, 012322 (2003). [Google Scholar]
- Sheng Y. B., Deng F. G. & Zhou H. Y. Efficient polarization-entanglement purification based on parametric down-conversion sources with cross-Kerr nonlinearity. Phys. Rev. A 77, 042308 (2008). [Google Scholar]
- Sheng Y. B. & Deng F. G. Deterministic entanglement purification and complete nonlocal Bell-state analysis with hyperentanglement. Phys. Rev. A 81, 032307 (2010). [Google Scholar]
- Li X. H. Deterministic polarization-entanglement purification using spatial entanglement. Phys. Rev. A 82, 044304 (2010). [Google Scholar]
- Deng F. G. One-step error correction for multipartite polarization entanglement. Phys. Rev. A 83, 062316 (2011). [Google Scholar]
- Wang C., Zhang Y. & Jin G. S. Entanglement purification and concentration of electron-spin entangled states using quantum-dot spins in optical microcavities. Phys. Rev. A 84, 032307 (2011). [Google Scholar]
- Gonta D. & van Loock P. Dynamical entanglement purification using chains of atoms and optical cavities. Phys. Rev. A 84, 042303 (2011). [Google Scholar]
- Gonta D. & van Loock P. High-fidelity entanglement purification using chains of atoms and optical cavities. Phys. Rev. A 86, 052312 (2012). [Google Scholar]
- Barreiro J. T., Langford N. K., Peters N. A. & Kwiat P. G. Generation of hyperentangled photon pairs. Phys. Rev. Lett. 95, 260501 (2005). [DOI] [PubMed] [Google Scholar]
- Schuck C., Huber G., Kurtsiefer C. & Weinfurter H. Complete deterministic linear optics bell state analysis. Phys. Rev. Lett. 96, 190501 (2006). [DOI] [PubMed] [Google Scholar]
- Wei T. C., Barreiro J. T. & Kwiat P. G. Hyperentangled Bell-state analysis. Phys. Rev. A 75, 060305(R) (2007). [Google Scholar]
- Barreiro J. T., Wei T. C. & Kwiat P. G. Beating the channel capacity limit for linear photonic superdense coding. Nat. Phys. 4, 282–286 (2008). [Google Scholar]
- Minář J. et al. Phase-noise measurements in long-fiber interferometers for quantum-repeater applications. Phys. Rev. A 77, 052325 (2008). [Google Scholar]
- Nemoto K. & Munro W. J. Nearly deterministic linear optical controlled-not gate. Phys. Rev. Lett. 93, 250502 (2004). [DOI] [PubMed] [Google Scholar]
- Barrett S. D. et al. Symmetry analyzer for nondestructive Bell-state detection using weak nonlinearities. Phys. Rev. A 71, 060302 (2005). [Google Scholar]
- Lin Q. & He B. Single-photon logic gates using minimal resources. Phys. Rev. A 80, 042310 (2009). [Google Scholar]
- He B., Ren Y. & Bergou J. A. Creation of high-quality long-distance entanglement with flexible resources. Phys. Rev. A 79, 052323 (2009). [Google Scholar]
- He B., Lin Q. & Simon C. Cross-Kerr nonlinearity between continuous-mode coherent states and single photons. Phys. Rev. A 83, 053826 (2011). [Google Scholar]
- He B., Nadeem M. & Bergou J. A. Scheme for generating coherent-state superpositions with realistic cross-Kerr nonlinearity. Phys. Rev. A 79, 035802 (2009). [Google Scholar]
- Shapiro J. H. Single-photon Kerr nonlinearities do not help quantum computation. Phys. Rev. A 73, 062305 (2006). [Google Scholar]
- Shapiro J. H. & Razavi M. Continuous-time cross-phase modulation and quantum computation. New J. Phys. 9, 16 (2007). [Google Scholar]
- Gea-Banacloche J. Impossibility of large phase shifts via the giant Kerr effect with single-photon wave packets. Phys. Rev. A 81, 043823 (2010). [Google Scholar]
- Kok P. et al. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79, 135–174 (2007). [Google Scholar]
- Kok P., Lee H. & Dowling J. P. Single-photon quantum-nondemolition detectors constructed with linear optics and projective measurements. Phys. Rev. A 66, 063814 (2002). [Google Scholar]
- Hofmann H. F., Kojima K., Takeuchi S. & Sasaki K. Optimized phase switching using a single-atom nonlinearity. J. Opt. B 5, 218 (2003). [Google Scholar]
- Feizpour A., Xing X. & Steinberg A. M. Amplifying single-photon nonlinearity using weak measurements. Phys. Rev. Lett. 107, 133603 (2011). [DOI] [PubMed] [Google Scholar]
- Zhu C. & Huang G. Giant kerr nonlinearity, controlled entangled photons and polarization phase gates in coupled quantum-well structures. Opt. Expre. 19, 23364–23376 (2011). [DOI] [PubMed] [Google Scholar]
- Hoi I. C. et al. Giant cross-Kerr effect for propagating microwaves induced by an artificial atom. Phys. Rev. Lett. 111, 053601 (2013). [DOI] [PubMed] [Google Scholar]
- He B. et al. Two-photon dynamics in coherent Rydberg atomic ensemble. Phys. Rev. Lett. 112, 133606 (2014). [DOI] [PubMed] [Google Scholar]