A Risk Model for Lung Cancer Incidence

Abstract

Risk models for lung cancer incidence would be useful for prioritizing individuals for screening and participation in clinical trials of chemoprevention. We present a risk model for lung cancer built using prospective cohort data from a general population which predicts individual incidence in a given time period. We build separate risk models for current and former smokers using 169,035 ever smokers from the multicenter European Prospective Investigation into Cancer and Nutrition (EPIC) and considered a model for never smokers. The data set was split into independent training and test sets. Lung cancer incidence was modeled using survival analysis, stratifying by age started smoking, and for former smokers, also smoking duration. Other risk factors considered were smoking intensity, 10 occupational/environmental exposures previously implicated with lung cancer, and single-nucleotide polymorphisms at two loci identified by genome-wide association studies of lung cancer. Individual risk in the test set was measured by the predicted probability of lung cancer incidence in the year preceding last follow-up time, predictive accuracy was measured by the area under the receiver operator characteristic curve (AUC). Using smoking information alone gave good predictive accuracy: the AUC and 95% confidence interval in ever smokers was 0.843 (0.810–0.875), the Bach model applied to the same data gave an AUC of 0.775 (0.737–0.813). Other risk factors had negligible effect on the AUC, including never smokers for whom prediction was poor. Our model is generalizable and straightforward to implement. Its accuracy can be attributed to its modeling of lifetime exposure to smoking.

Introduction

Lung cancer is the most common cause of cancer mortality in both men and women in the United States, in European men, and the second most lethal cancer in European women (1, 2). The National Lung Screening Trial (3) found that screening using low-dose computed tomography reduces mortality from lung cancer (4). Good prediction models for lung cancer incidence would have an obvious benefit should such screening programs be implemented and could also be used to encourage high-risk individuals to quit smoking, to identify high-risk individuals for increased monitoring by clinicians, to select individuals for participation in clinical trials of chemoprevention and, should such trails prove successful, to select individuals to receive treatment (5–7).

Four previous studies have derived risk models for lung cancer (5–8). The Bach model (5) built their risk models using population-based data on 18,172 subjects enrolled in the Carotene and Retinol Efficacy Trial (CARET)—a randomized trial of lung cancer prevention. The study recruited individuals at high risk of lung cancer: current and former smokers who were either heavy smokers (20+ pack-years) or had been exposed to asbestos; risk was modeled using age, sex, smoking history, and exposure to asbestos. In contrast, the Spitz model (6) used case–control data matched on age (±5 years), sex, ethnicity, and smoking status (never, former, and current). They extended the Bach model by considering other risk factors, identifying emphysema, exposure to dust, exposure to asbestos, and family history of cancer to be predictive risk factors for lung cancer. However, they were unable to estimate the effects of the matching variables in their data, most importantly, the large effects of age and smoking status. Using a subset of the same data, the Spitz model was improved by 2 markers of DNA repair capacity (9). The Liverpool Lung Cancer Project (LLP) model (8) was also constructed using case–control data (matched by year of birth and sex) and considered additional risk factors. The LLP model identified occupational exposure to asbestos, pneumonia, family history of cancer, and prior malignancy to be predictive risk factors for lung cancer. This study was the smallest of the three comprising 579 lung cancer cases. These 3 models were built using data that were not sampled from the general population; therefore, their general applicability is uncertain. Recently, a risk model for lung cancer has been developed using data from the Prostate, Lung, Colorectal, and Ovarian Cancer (PLCO) Screening Trial which uses prospective data from the general population (7). The PLCO model uses logistic regression with spline effects for age, pack-years, smoking duration and smoking quit time, and effects for education, body mass index (BMI), chronic obstructive pulmonary disease (COPD), family history of lung cancer, chest X-ray in the past 3 years, and smoking status. They compared their model with a Cox proportional hazards model.

Here, we build a prediction model for lung cancer incidence using the European Prospective Investigation into Cancer and Nutrition (EPIC) cohort (10). Like the PLCO cohort, EPIC recruited healthy individuals and is prospective, enabling the building of models applicable to the general population. Unlike the PLCO model, we use parametric survival modeling to model the time-dependent nature of the prospective data and capture the risk of age and smoking duration within stratified survival models. Survival models are appropriate for modeling time-to-event data and parametric survival models result in models which are straightforward to apply to external data sets; we provide parameter estimates for our survival models to enable their implementation by other researchers. For each individual in our study, we have detailed information on their smoking history, allowing us to accurately model the effect of smoking on lung cancer risk. In addition, we have information on other exposures previously reported to be associated with lung cancer, including genetic markers (11).

Methods

Study population

EPIC is a multicenter study which recruited healthy participants between 1993 and 1999 across Western Europe, with a limited number of a priori exclusions (prevalent cancers). The majority of participants were aged between 40 and 65 years at recruitment and were recruited predominantly from the general population from a given geographic area (country, region, or city). Our sample population originated from the following recruitment centers: Italy (Florence, Varese, Ragusa, Naples, and Turin), Spain (Asturias, Navarra, Murcia, Granada, and San Sebastian), England (Cambridge, Oxford), the Netherlands (Bilthoven, Utrecht), Greece, Germany (Potsdam, Heidelberg), Denmark (Copenhagen, Aarhus), and Norway (2 recruitment centers covering the north-east and south-west of the country). Detailed individual-level data were collected at recruitment via questionnaire; including, where applicable, the following measures of smoking history: age started smoking, age quit smoking, and smoking intensity in 10 yearly intervals from the age of 20. Anthropometric measurements and blood samples were also taken at recruitment.

Lung cancer cases were identified using population cancer registries (Denmark, Italy, Netherlands, Norway, Spain, and the England), or a combination of health insurance records, cancer and pathology registries and active follow-up of study subjects and their next of kin (Germany and Greece). Follow-up information was updated in 2006. Coding of cases was based on the 2nd revision of the International Classification of Diseases for Oncology (ICD-O-2). Informed consent forms were filled at each local center and the study was approved by the Institutional Review Board at the International Agency for Research on Cancer (IARC; Lyon, France) and local ethical committees.

Exposure to tobacco is measured by cigarette smoke, all smoking variables are defined by cigarette smoking, individuals with missing cigarette smoking information were excluded, this resulted in the exclusion of 27,477 reported current smokers (25% of current smokers) and 35,176 former smokers (29% of reported former smokers). We also excluded individuals who smoked cigars or pipes after quitting cigarette smoking or smoked pipes or cigars before smoking cigarettes, this resulted in the exclusion of a further 1,893 individuals recorded as current smokers (1.7%) and 512 individuals recorded as former smokers (0.42%). We did not exclude individuals who smoked cigars or pipes while also smoking cigarettes, 3,423 current smokers (3.0%), and 44 former smokers (0.003%). After exclusions, our study population consisted of 82,776 current smokers, 86,259 former smokers, and 230,358 never smokers, individuals in all groups were older than 35 years. A description of the study population is shown in Table 1.

Table 1.

Distribution of population variables in the training and test sets by smoking and disease status

	Training set				Test set
	Current smokers		Former smokers		Current smokers		Former smokers
	No lung cancer	Lung cancer	No lung cancer	Lung cancer	No lung cancer	Lung cancer	No lung cancer	Lung cancer	Missing (%)
Total	73,677 (98.9)	820 (1.1)	77,328 (99.61)	304 (0.39)	8,187 (98.89)	92 (1.11)	8,593 (99.61)	34 (0.39)
Number of genotyped individuals, n (%)	508 (44.8)	626 (55.2)	678 (74.34)	234 (25.66)	57 (47.9)	62 (52.1)	72 (72.73)	27 (27.27)	98.83
Sociodemographic
Sex, n (%)
Male	45,647 (99.23)	354 (0.77)	43,178 (99.76)	104 (0.24)	5,073 (99.24)	39 (0.76)	4,870 (99.75)	12 (0.25)	0
Female	70,169 (98.84)	820 (1.16)	74,009 (99.59)	304 (0.41)	7,774 (98.83)	92 (1.17)	8,225 (99.59)	34 (0.41)
Dead at censoring, n (%)a	3,508 (100)	0 (0)	3,319 (100)	0 (0)	413 (100)	0 (0)	368 (100)	0 (0)	0
Age, mean (SD), y	57.5 (8.8)	62 (7.3)	60.5 (9.5)	65.6 (8.8)	57.4 (8.8)	60.6 (8.2)	60.5 (9.6)	65.8 (8.5)	0
Age at recruitment, mean (SD), y	49.5 (8.7)	57.2 (7.2)	52.5 (9.4)	60.8 (8.4)	49.5 (8.8)	56.1 (8.1)	52.5 (9.5)	60.8 (8.3)	0
Follow-up, mean (SD), y	7.9 (2)	4.8 (2.6)	8 (2)	4.8 (2.6)	7.9 (2)	4.5 (2.9)	8 (2)	4.9 (2.3)	0
BMI, mean (SD), kg/m2	25.7 (4.1)	25.7 (4.5)	26.4 (4.1)	26.7 (3.6)	25.7 (4.2)	26 (4.3)	26.3 (4.1)	27 (2.5)	12.56
Education, n (%)
High school and below	60,415 (98.84)	710 (1.16)	56,190 (99.54)	259 (0.46)	6,642 (98.74)	85 (1.26)	6,201 (99.57)	27 (0.43)	4.68
Greater than high school	11,817 (99.32)	81 (0.68)	17,532 (99.89)	20 (0.11)	1,390 (99.57)	6 (0.43)	1,984 (99.7)	6 (0.3)
Medical history
Hay fever, n (%)
No	15,925 (99.1)	145 (0.9)	16,526 (99.73)	45 (0.27)	1,784 (98.84)	21 (1.16)	1,815 (99.78)	4 (0.22)	73.53
Yes	2,664 (99.48)	14 (0.52)	3,963 (99.67)	13 (0.33)	301 (99.34)	2 (0.66)	467 (99.57)	2 (0.43)
Asthma, n (%)
No	30,788 (99.16)	260 (0.84)	27,690 (99.73)	76 (0.27)	3,393 (99.09)	31 (0.91)	3,071 (99.71)	9 (0.29)	61.46
Yes	1,521 (98.51)	23 (1.49)	2,103 (98.92)	23 (1.08)	161 (98.17)	3 (1.83)	269 (99.26)	2 (0.74)
Family history of cancer, n (%)
No	9,730 (98.81)	117 (1.19)	10,880 (99.32)	74 (0.68)	1,098 (99.01)	11 (0.99)	1,235 (99.2)	10 (0.8)	84.02
Yes	1,051 (98.32)	18 (1.68)	1,409 (99.09)	13 (0.91)	121 (99.18)	1 (0.82)	157 (98.74)	2 (1.26)
Smoking exposures
Smoking intensity, mean (SD), cpd	13.5 (7.5)	17.6 (7.4)	13.1 (9.2)	17.8 (10.9)	13.5 (7.4)	17.2 (7.9)	13 (9.2)	17.1 (11.6)	0
Smoking duration, mean (SD), y	30.3 (9.7)	39.5 (8.2)	19 (10.7)	31.4 (12.1)	30.2 (9.8)	38.8 (8.4)	18.9 (10.7)	31.7 (11)	0
Quit time, mean (SD), y	0 (0.1)	0 (0.1)	15 (9.9)	11.9 (9.3)	0 (0.1)	0 (0.1)	15 (9.9)	10.8 (7.4)	0
Age start smoking, mean (SD), y	27.2 (6.1)	22.5 (5.1)	26.5 (4.8)	22.3 (5.2)	27.2 (6.2)	21.8 (4.2)	26.5 (4.9)	23.2 (5.9)	0
Cigarettes per day
≤15	28,222 (98.21)	515 (1.79)	29,174 (99.37)	186 (0.63)	3,203 (98.31)	55 (1.69)	3,242 (99.42)	19 (0.58)	0
>15	45,455 (99.33)	305 (0.67)	48,154 (99.76)	118 (0.24)	4,984 (99.26)	37 (0.74)	5,351 (99.72)	15 (0.28)
Occupational exposures
Silica, n (%)
Not exposed	44,057 (98.64)	609 (1.36)	43,604 (99.51)	216 (0.49)	4,944 (98.58)	71 (1.42)	4,870 (99.47)	26 (0.53)	42.06
Exposed	1,125 (97.74)	26 (2.26)	1,153 (99.31)	8 (0.69)	118 (98.33)	2 (1.67)	104 (99.05)	1 (0.95)
PAH, n (%)
Not exposed	39,750 (98.72)	514 (1.28)	39,620 (99.51)	194 (0.49)	4,419 (98.55)	65 (1.45)	4,412 (99.53)	21 (0.47)	42.06
Exposed	5,432 (97.82)	121 (2.18)	5,137 (99.42)	30 (0.58)	643 (98.77)	8 (1.23)	562 (98.94)	6 (1.06)
Metal, n (%)
Not exposed	32,596 (98.65)	447 (1.35)	34,035 (99.56)	150 (0.44)	3,661 (98.79)	45 (1.21)	3,831 (99.56)	17 (0.44)	46.19
Exposed	6,827 (98)	139 (2)	7,521 (99.31)	52 (0.69)	760 (97.31)	21 (2.69)	806 (99.02)	8 (0.98)
Asbestos, n (%)
Not exposed	39,734 (98.73)	513 (1.27)	38,974 (99.54)	182 (0.46)	4,425 (98.75)	56 (1.25)	4,334 (99.54)	20 (0.46)	42.06
Exposed	5,448 (97.81)	122 (2.19)	5,783 (99.28)	42 (0.72)	637 (97.4)	17 (2.6)	640 (98.92)	7 (1.08)

^aNumbers are taken at time of censoring, cases were censored at diagnosis, before death.

Modeling

Since EPIC is prospective, age of lung cancer incidence was modeled using survival analysis. We split the population into 3 groups: current, former, and never smokers and as in the Spitz model (6), classified former smokers who had quit less than 1 year ago as current smokers. For current and former smokers, we first built models for lung cancer incidence which accounted only for the effect of lifetime exposure to tobacco smoke, we then considered the effects of personal, medical, occupational, environmental, and genetic risk factors. Individuals who were healthy at the last follow-up time or had died or migrated were modeled as censored at the age they left the study, no other outcomes resulted in censoring. The data are left truncated at the age of recruitment; this is accounted for in the model building. We also implement a competing risk model for death before diagnosis of lung cancer.

Exposure to tobacco smoke

The effect of lifetime exposure to cigarette smoke was modeled by considering separately the effects of smoking duration and intensity, measured by the average number of cigarettes smoked per day (cpd). The effects of age start smoking and smoking duration (and functions of these time events) cannot be modeled in a proportional hazards model as they are time-dependent events; therefore, their effects were captured by stratifying. For current smokers, we stratified by age started smoking such that each age of start stratum was assigned its own survival function, thus each current smoker was assigned to the same survival curve throughout their smoking lives. This jointly models the effects of age and smoking duration, accounting for their time-dependent nature.

Similarly, for former smokers, the effects of the time-dependent events, age started smoking and age quit smoking, were captured by stratifying. The relationship between lung cancer risk and duration and age of smoking cessation is uncertain. Some have argued that the risk of lung cancer is a function solely of smoking duration (5, 12), whereas others have argued that the risk of lung cancer continues to reduce the longer the time since cessation (13–15). Others have suggested that age of cessation is an important factor (16) and the Spitz model (6) used age quit as a predictor variable in their risk model for former smokers. We therefore considered models for former smokers that capture these alternative risk models, stratifying only by smoking duration and, in addition, 2 more complete characterization, stratifying by both duration and time since cessation and both duration and age started smoking. The latter 2 models result in many more strata and therefore a degree of data sparsity in some strata which could result in unstable parameter estimates. Therefore, we checked that between strata estimates of risk were biologically plausible, specifically, increased duration results in increased risk. Where biologically unrealistic risks were identified, strata were collapsed to give more robust estimates.

The effect of smoking intensity was modeled as an additive effect on the log hazard. Several studies have indicated that the risk of lung cancer does not increase linearly with smoking intensity (17); we consider 2 approaches to capture this effect (i) by including the square of smoking intensity as an additive effect on the log hazard and (ii) by continuous piecewise linear functions of intensity on the log hazard, defined by knot points between which the relationship is linear. We consider a variety of such functions with 1, 2, and 3 knot points placed in a variety of positions.

In our stratified survival models, an individual’s hazard is given by

$$h(t\mid s,x)=h_j\left(t\right)\exp \left(\beta x\right),$$

where t is the individual’s age, s are the time-related smoking measurements (age start, age quit, etc.) which define the stratum j to which the individual is assigned, h_j is the hazard of stratum j, and x is a matrix of mean centered covariates including smoking intensity, and where applicable other exposures, and β is a vector of covariate effects. Our modeling assumes that covariate effects are identical in all strata and their effect does not vary over time. Throughout, h_j is modeled by the Weibull hazard

$$h_j\left(t\right)=\frac{{\lambda }_j}{{\gamma }_j}{\left(\frac{t}{{\lambda }_j}\right)}^{{\gamma }_j-1},$$

where λ_j and γ_j are the scale and shape parameters of the Weibull hazard for stratum j. We take t to be age in years minus 35 as the fit of the Weibull function is otherwise compromised by the negligible risk of lung cancer at ages less than 35 years old (in our training cohort, the youngest case of lung cancer was 37 years old). The Weibull survival function was chosen as our work is motivated by prediction, and in comparison with the nonparametric Cox survival model, the parametric Weibull survival model gives more robust estimates of the hazard at ages in the extreme of the distribution, where there are typically fewer observations.

Never smokers

The survival model for never smokers did not require stratification and their hazard was modeled by a single Weibull survival function.

Other exposure variables

We explored the effects of personal, medical, occupational, environmental, and genetic exposures in never smokers and whether these exposures improved our models for current and former smokers. We considered exposures for which there exists prior evidence of association with lung cancer, those we had measures of in EPIC were: sex [women at higher risk (refs. 18, 19)], (BMI [high BMI protective (refs. 20, 21)], the following occupational exposures, with individuals recorded as exposed if they had been employed in professions which are known to expose employees to the carcinogens of interest: environmental tobacco smoke (only never smokers), asbestos, silica, metal and polycyclic aromatic hydrocarbons (PAH; ref. 22) and socioeconomic status [SES; high SES protective (ref. 23)]. SES was measured by the level of education attained with levels: completed primary school, technical/professional school, secondary school, and university degree. Preliminary analyses showed that individuals with a university degree were the only SES stratum to show significant associations in the survival models; therefore, to reduce dimensionality, SES was measured as university degree or other. Family history of cancer has also been shown to be associated with risk of lung cancer (6–8); in EPIC, we have records of whether any first-degree relative has had colorectal cancer or breast cancer and we included a binary covariate indicating whether either of these events occurred. We also considered hay fever and asthma (measured as binary yes/no covariates) for which there exists limited evidence of association but were considered by previous risk models (6, 9).

We also investigated the effects of 2 single-nucleotide polymorphisms (SNP) at loci which showed significant association with lung cancer incidence in genome-wide association studies (GWAS); these were rs8034191 on chromosome 15q25 (10, 24, 25) and rs402710 at 5p15 (26, 27). These 2 SNPs were included in 35 SNPs investigated by EPIC in the replication phase of a GWAS in which 2,359 individuals were genotyped; individuals were selected for genotyping by frequency matching cases and controls by sex, age (±3 years), center, referral area (or of residence), and period of recruitment (±6 months; ref. 10). An additive model was fit for both SNPs. The proportional hazards assumption was tested for all covariates (28), for all tests P > 0.05. All models were fit in R (version 2.13.2; ref. 29) using the eha package (version 2.0; ref. 30).

Model choice

A Bayesian perspective was taken to choose between models with different strata characterizing smoking duration. In the Bayesian paradigm, the model with the highest posterior model probability is chosen. Posterior model probabilities of stratified survival models cannot be calculated analytically; however, an approximate Bayesian solution, when one is concerned with future prediction and the range of models considered does not include the true model, can be determined by a cross-validation approach in which the model with the best out-of-sample log likelihood is preferred (31). Specifically, we split the data into 10 equal sized blocks, the model was fit using 9 of the 10 blocks and the log likelihood of the remaining block was calculated from the resultant fit, this was repeated for each block. The models were compared by summing the log likelihood across blocks. Covariate effects for smoking intensity (additive on the log hazard scale), and when significant at P < 0.05, the square of smoking intensity, were included when selecting the best models to characterize the effects of the time-dependent smoking exposures. We next used the same methodology to choose between models for the effect of smoking intensity, comparing the quadratic model and continuous piecewise linear models, using the best fitting models for smoking duration.

Measuring predictive power

To protect against overfitting and best estimate our models’ predictive accuracy in other populations, the EPIC data were split into training and test sets, the training set consisted of a random sample of 90% of each of the cases and controls and the test set, the remaining 10%. The ratio of cases and controls was fixed so as the risk model estimated from the training set reflected the baseline risk observed in our population. Predictive accuracy was measured by comparing predicted and observed 1- and 5-year incidence of lung cancer for all individuals in the test set using the area under the receiver operator characteristic curve (AUC). Specifically, we calculated the probability of lung cancer incidence 1/5 years previous to the last follow-up time, a time at which all individuals are disease-free and are subsequently followed for 1/5 year(s).

To account for individuals who were censored because of death, we treat death as a competing risk. We model age of death using a survival model with the same covariates and stratification as used for the lung cancer incidence model. Probability of yearly incidence of lung cancer is estimated by the product of the probability of lung cancer in the next year and the probability of being alive in 1 year. Applying the Weibull survivor functions for cancer and death, the probability an individual of age = t+35 will be diagnosed in next year is thus given by

$$\begin{array}{cc}\hfill & P\left(\text{diagnosis in}1\text{year from age}t\right)\hfill \\ \hfill & =P\left(\text{cancer in}1\text{year from age}t\right)P\left(\text{alive in}1\text{year from a get}t\right)\hfill \\ \hfill & =p_{\text{cancer}}\left(t\right)(1-p_{\text{death}}(t\left)\right)\hfill \\ \hfill & =\left(1-\frac{S_{\text{cancer}}(t+1)}{S_{\text{cancer}}\left(t\right)}\right)\left(\frac{S_{\text{death}}(t+1)}{S_{\text{death}}\left(t\right)}\right)\hfill \\ \hfill & =\left(1-\exp \left\{\exp ({\beta }_1\times )\left({\left(\frac{t}{{\lambda }_1}\right)}^{{\gamma }_1}-{\left(\frac{t+1}{{\lambda }_1}\right)}^{{\gamma }_1}\right)\right\}\right)\hfill \\ \hfill & \left(\exp \left\{\exp ({\beta }_2\times )\left({\left(\frac{t}{{\lambda }_2}\right)}^{{\gamma }_2}-{\left(\frac{t+1}{{\lambda }_2}\right)}^{{\gamma }_2}\right)\right\}\right)\hfill \end{array}$$ (A)

where S_cancer and S_death are the survivor functions of the cancer and death models, λ and γ are the shape and scale parameters of the Weibull distribution for the lung cancer and death prediction models, indexed by 1 and 2 respectively, x are covariates (including smoking intensity), and β is a vector of covariate effects for the 2 models. To calculate lung cancer incidence for periods of greater than a year, the 1-year cancer and death survival models can be summed over years, for example, 2-year incidence can be calculated as follows:

$$\begin{array}{cc}\hfill & P\left(\text{diagnosis in}2\text{years}\right)\hfill \\ \hfill & =P\left(\text{diagnosis in year}1\right)+P\left(\text{diagnosis in year}2\right)\hfill \\ \hfill & =p_{\text{cancer}}\left(t\right)(1-p_{\text{death}}(t\left)\right)+(1-p_{\text{cancer}}(t\left)\right)\hfill \\ \hfill & (1-p_{\text{death}}(t\left)\right)p_{\text{cancer}}(t+1)(1-p_{\text{death}}(t+1\left)\right)\hfill \end{array}$$ (B)

We compare the accuracy of our model with the Bach model (5) to predict 1- and 5-year incidence of lung cancer. The Bach model similarly calculates 1-year incidence using a competing risk of death within 1 year; therefore, 5-year risk for both models was calculated by extending Equation (B).

To estimate the predictive power of the other exposure variables, we estimated separate models which included each of the covariates, in turn, in the best fitting model which used only smoking information. We applied these models to the test set and compared the resultant AUC with the AUC of the best fitting model which used only smoking information using the deLong method (32) in the R package pROC (version 1.4.4; ref. 33). We also measured the predictive power of covariates using the time-dependent net reclassification index (tdNRI; ref. 34), an extension of the NRI (35) to time-to-event data. The tdNRI is defined at a point in time t (in our application an age) by

$$\begin{array}{cc}\hfill \mathit{tdNRI}\left(t\right)=& P(\text{up}\mid D(t)=1)-P(\text{down}\mid D(t)=1)\hfill \\ \hfill & -P(\text{up}\mid D(t)=0)+p(\text{down}\mid D(t)=0)\hfill \end{array}$$

where up and down refer to those individuals who were reclassified up and down with the introduction of the new covariate into the prediction model, and D (t) is 1 if lung cancer by age t, and 0 otherwise. We calculate tdNRI at 65 years. Because of the small number of observations for some covariates, the significance of the tdNRI was calculated by permutation, reporting P values calculated as the proportion of times the observed tdNRI is greater than the tdNRI from 1,000 permutations of the covariate vector. We also report the P value for association of each exposure variable in the training set. The effect of exposures was assessed using only those individuals for whom measurements of that exposure were available. To maintain the accuracy of the estimated effects of smoking exposures, models including additional covariates were estimated conditional on the effects of smoking exposures estimated using all individuals in the training set.

The risk models presented here are for the models built using the training data, measures of predictive accuracy are from the models’ application to the test set. Preliminary analyses showed that our prediction models of never smokers were poor having AUCs in the region of 0.5, the level expected from a random predictor, therefore results for never smokers are not reported.

Results

Models utilizing only smoking information

Current smokers

A range of strata for age started smoking were considered from less than 16 years old to more than 40 years old in intervals ranging from 1 to 10 years. The strata of the best fitting model are shown in Table 2. Removing the youngest and oldest strata, including additional strata at younger or older ages and including additional strata within the ages spanned by our model decreased the model fit as measured by the out-of-sample log likelihood. These analyses included covariate effects for smoking intensity and square of smoking intensity.

Table 2.

Weibull parameters and HRs of smoking intensity used in Equation (A) for the lung cancer incidence and death models for current and former smokers

	Current smokers
	Lung cancer incidence		Death
	HR (95% CI) β1	P	HR (95% CI) β2	P
Smoking intensity ≤ 15	1.111 (1.084–1.139)	<10−16	1.051 (1.041–1.062)	<10−16
	Weibull hazard parameters		Weibull hazard parameters
Strata	Shape (95% CI) λ1	Scale (95% CI) γ1	Shape (95% CI) λ2	Scale (95% CI) γ2
t ≤ 18	3.819 (3.750–3.869)	0.999 (0.772–1.162)	3.690 (3.659–3.713)	1.220 (1.105–1.302)
18 < t ≤ 20	4.056 (3.966–4.121)	1.071 (0.870–1.215)	3.774 (3.748–3.793)	1.312 (1.210–1.384)
20 < t ≤ 22	4.230 (4.134–4.299)	1.298 (1.144–1.408)	3.859 (3.839–3.873)	1.560 (1.489–1.611)
22 < t ≤ 24	4.339 (4.234–4.414)	1.518 (1.374–1.621)	3.944 (3.924–3.958)	1.775 (1.715–1.818)
24 < t ≤ 26	4.380 (4.258–4.468)	1.679 (1.519–1.794)	3.979 (3.958–3.995)	1.925 (1.865–1.969)
26 < t ≤ 28	4.567 (4.361–4.714)	1.517 (1.294–1.677)	4.049 (4.017–4.071)	1.854 (1.773–1.911)
28 < t ≤ 30	4.506 (4.278–4.670)	1.615 (1.344–1.809)	4.096 (4.049–4.130)	1.838 (1.727–1.917)
30 < t	4.504 (4.317–4.637)	1.684 (1.454–1.848)	4.069 (4.040–4.090)	1.912 (1.835–1.966)
	Former smokers
	Lung cancer incidence		Death
	HR (95% CI) β1	P	HR (95% CI) β2	P
Smoking intensity ≤ 15	1.043 (1.012–1.076)	0.007	1.015 (1.006–1.023)	<10−16
	Weibull hazard parameters		Weibull hazard parameters
Strata	Shape (95% CI) λ1	Scale (95% CI) γ1	Shape (95% CI) λ2	Scale (95% CI) γ2
t ≤ 22; s ≤ 20	4.987 (4.372–5.427)	0.750 (0.359–1.029)	3.754 (3.722–3.776)	1.210 (1.128–1.269)
20 < s ≤ 30	4.723 (4.242–5.066)	0.819 (0.409–1.112)	3.750 (3.726–3.767)	1.511 (1.428–1.570)
30 < s	4.321 (4.140–4.450)	1.032 (0.733–1.246)	3.800 (3.785–3.810)	1.669 (1.603–1.716)
22 < t ≤ 26; s ≤ 20	5.179 (4.537–5.638)	1.165 (0.795–1.430)	4.008 (3.975–4.032)	1.621 (1.555–1.668)
20 < s ≤ 30	4.786 (4.335–5.108)	1.353 (0.989–1.612)	3.975 (3.942–3.998)	1.742 (1.663–1.799)
30 < s ≤ 36	4.651 (4.132–5.022)	1.460 (0.945–1.829)	3.954 (3.921–3.977)	1.835 (1.734–1.907)
36 < s ≤ 42	4.654 (4.034–5.097)	1.318 (0.639–1.804)	3.928 (3.903–3.945)	2.129 (2.018–2.208)
42 < s	4.366 (4.090–4.563)	1.662 (1.136–2.038)	3.982 (3.961–3.998)	2.150 (2.040–2.229)
t > 26; s ≤ 20	5.563 (4.668–6.202)	1.088 (0.640–1.409)	4.123 (4.087–4.148)	1.769 (1.698–1.820)
20 < s ≤ 30	4.680 (4.223–5.007)	1.705 (1.249–2.032)	4.058 (4.026–4.082)	1.865 (1.781–1.926)
30 < s ≤ 36	4.491 (4.062–4.797)	1.879 (1.312–2.283)	4.020 (3.986–4.044)	2.148 (2.027–2.234)
36 < s ≤ 42	4.241 (3.990–4.420)	2.336 (1.754–2.751)	3.999 (3.968–4.021)	2.360 (2.213–2.465)
42 < s	4.177 (4.052–4.266)	2.574 (2.123–2.896)	4.041 (4.007–4.066)	2.490 (2.295–2.629)

NOTE: Parameter estimates are based on maximum likelihood estimates, 95% CIs are in parentheses. Time zero set to 35 years old.

Abbreviations: s, smoking duration; t, age start smoke.

We next compared the quadratic model for the effect of smoking intensity with continuous piecewise linear models using the best fitting stratification for age start described above. Models were compared with single knot points at 5, 10, 15, 20, and 25 cpd; 2 knot points at 5 and 15, 10 and 20, 15 and 25; and 3 knot points at 5, 15, and 25. The best fitting model had a single knot point at 15 cpd. The additional effect of smoking more than 15 cpd was −0.003 (P = 0.9), comparison of this model with one which fixed the effect of more than 15 cpd at 0 (implying no increase in risk beyond 15 cpd) favored the later model, this model was used in further analyses.

Table 2 shows the HRs and 95% confidence intervals (CI) for the effect of smoking intensity and the shape and scale parameters for the Weibull survival functions used in each strata of this model for both the lung cancer incidence model and the death model. There is significant variation in the strata-specific shape and scale parameters, indicating that the model is capturing the effects of age and smoking duration. The effect of smoking intensity is highly significant (P < 10⁻¹⁶).

Former smokers

We compared models which stratified by smoking duration alone (model I), both smoking duration and time since cessation (model II), and one which stratified by both age started smoking and duration (model III). Throughout, 5 strata were used for smoking duration and 3 strata for each of time since cessation and age start smoking. The strata were chosen to balance the number of cases and controls in each. Preliminary analyses revealed that the square of smoking intensity did not have a significant effect in any of the models, therefore, only smoking intensity was used to compare models. Model III gave the best fit to the data. In this model, for individuals who started smoking before 22 years of age, the risk in the upper 2 strata for smoking duration was found to be lower than the risk in the third duration strata, therefore the upper 3 strata were collapsed into one in further analyses. Comparison of the linear model for smoking intensity with continuous piecewise linear models showed that models with a single knot point gave improved fit, however, the difference in model fit between differently positioned knot points was minimal, therefore, for consistency with the model for current smokers, the model with a knot point at 15 cpd and no further increase in effect at higher intensities was chosen. The strata used and their associated shape and scale parameters in the best fitting models for lung cancer incidence and death are shown in Table 2. Also shown in Table 2 is the HR for the effect of smoking intensity, we see that the effects of smoking intensity for both lung cancer incidence and death are less in former smokers than in current smokers.

Effect of additional covariates

Table 3 shows HRs and P values, calculated in the training set, for each covariate when added to the best fitting smoking model and the P value for improvement in AUC and tdNRI, comparing models with and without the additional covariate, calculated in the test set (all model comparisons were for predictions of the same individuals). The effects of sex in current smokers, BMI in both groups, SES in former smokers, and the SNP in 15q25 in current smokers were significant (P < 0.05) when included in the model fit to the training data and were in the direction expected a priori. The effects of hay fever and family history of cancer were also in the direction expected a priori in both current and former smokers but were not significant. However, none of the exposures significantly improved predictions in the test set as measured by the AUC and the improvement in AUC was less than 0.006 for all exposures. The only exposures to significantly improve the tdNRI were education level in current smokers (but not former smokers) and asbestos in former smokers. However, we had minimal power to detect improvement in prediction with the inclusion of exposures due to the limited number of exposed cases.

Table 3.

HRs for effect of exposures in current and former smokers estimated in the training set and their predictive value in the test set

	HR (95% CI)		P		P for improvement in AUC		tdNRI
							Change		P
Covariate	Current	Former	Current	Former	Current	Former	Current	Former	Current	Former
Sex: female 1, male 0.	1.35 (1.16–1.57)	1.2 (0.91–1.59)	0.000126	0.194	−	0.885	−0.346	−0.321	0.99	0.937
BMI	0.963 (0.946–0.98)	0.96 (0.929–0.992)	3.7 × 10−5	0.0148	−	−	−0.0709	−0.206	0.687	0.82
Education level (greater  than high school)	0.944 (0.751–1.19)	0.436 (0.275–0.691)	0.62	0.000418	0.243	−	0.235	−0.0763	0.01	0.637
Hay fever	0.593 (0.335–1.05)	0.901 (0.494–1.64)	0.0728	0.734	+	+	0.233	0.12	0.139	0.366
Asthma	0.85 (0.546–1.32)	1.58 (0.961–2.6)	0.474	0.071	+	+	0.0437	−0.0127	0.346	0.504
Family history of cancer	1.27 (0.758–2.11)	1.23 (0.694–2.16)	0.368	0.484	+	+	−0.217	−0.235	0.9	0.845
Chr15q25	1.13 (1.01–1.27)	1.14 (0.933–1.38)	0.0336	0.202	−	0.726	0.309	0.406	0.381	0.23
Chr5p15	0.954 (0.845–1.08)	1.06 (0.865–1.3)	0.442	0.572	0.765	0.885	1.3	−0.495	0.067	0.808
Occupational exposures
Silica	0.893 (0.602–1.33)	0.851 (0.349–2.07)	0.574	0.722	+	+	−0.0252	−0.0907	0.684	0.945
PAH	0.988 (0.808–1.21)	0.869 (0.586–1.29)	0.906	0.485	0.671	−	0.0177	−0.194	0.428	0.871
Metal	0.961 (0.794–1.16)	1.23 (0.866–1.74)	0.68	0.249	−	0.308	−0.385	0.281	0.996	0.06
Asbestos	0.943 (0.775–1.15)	1.05 (0.738–1.49)	0.558	0.784	−	0.603	−0.24	0.296	0.986	0.029

NOTE: Exposure effects are conditional on lifetime exposure to cigarette smoke. P value for improvement in AUC and tdNRI compares predictive performance of model with and without covariate (tdNRI P values were calculated by permutation). AUC P values are not shown for covariates whose inclusion decreased the AUC (denoted by −) and there were fewer than 5 exposed cases (denoted by +).

Application of model

Because nonsmoking exposures added little predictive power, we report the predictive accuracy using the best fitting models which used only smoking information. These models can be applied to predict the lung cancer risk in a given period of time of any individual for whom their age, average smoking intensity, age started smoking and, for former smokers, duration for which they smoked are known by applying Equations (A) and (B) with shape and scale parameters, given in Table 2, selected according to the smoking profile of the individual; note that effect of smoking intensity is constant above 15 cpd, taking the value attained at 15 cpd.

Characteristics of model

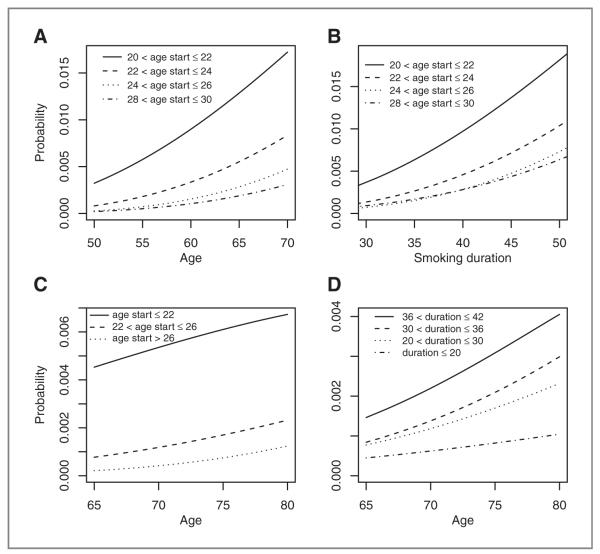
Predicted probabilities of diagnosis of lung cancer in 1 year are shown in Fig. 1 for a variety of smoking profiles. All plots assume an average smoking intensity of 20 cpd. Figure 1A–C highlights an important aspect of our model, the effect of age start smoking, with those starting earlier seemingly at higher risk for both current and former smokers, accounting for the effect of duration. Figure 1A, B and D show the well-known relationship between smoking duration and lung cancer risk.

Figure 1.

Predicted probabilities of 1 year lung cancer incidence, for a variety of smoking profiles, assuming an average smoking intensity of 20 cpd. A, probability of lung cancer in current smokers by age, for different ages of commencement of smoking. B, probability of lung cancer in current smokers by smoking duration, for different ages of commencement of smoking. C, probability of lung cancer in former smokers by age, for different ages of commencement of smoking assuming a smoking duration of 20 to 30 years. D, probability of lung cancer in former smokers by age, for different durations of smoking assuming commencement of smoking between 22 and 26 years old.

Prediction

Table 4 shows the AUC and corresponding 95% CIs of our model and the Bach model (5) applied to the test set for predicting probability of lung cancer in 1 and 5 years; 5-year incidence was calculated for individuals in our test set who were followed for 5 or more years and former smokers who had quit at least 5 years ago, also shown are the numbers of cases and controls in each test set. Results are shown separately for current and former smokers, the combined group of ever smokers and the subset of high-risk ever smokers used in the Bach study: individuals between 50 and 75 years old who have smoked 10 to 60 cpd for 25 to 55 years. Also shown is the P value comparing the AUCs from predictions using the 2 models calculated using the deLong method (32). For all comparisons of 1-year risk, our model gives significantly superior prediction. The predictive accuracy of 5-year incidence is less for both models as would be expected with greater uncertainty over a longer time period. For predicting 5-year risk separately in current and former smokers, the AUCs of the 2 models are not significantly different, however, a more meaningful comparison is within the combined group of ever smokers; in this group, the AUC of our model is significantly superior for both the entire population of ever smokers and the high-risk subgroup. The absolute difference in AUCs of the 2 models for ever smokers and the high-risk subgroup over 1 and 5 years are comparable; however, the significance of the differences is less over 5 years on account of the smaller samples used for these comparisons.

Table 4.

Predictive performance, measured by the AUC, of our model and the Bach model for predicting 1- and 5-year cancer risk in the EPIC test set

	Current smokers	Former smokers	Ever smokers	Bach high-risk group
One year
Controls	8,187	8,593	16,780	4,934
Cases	92	34	126	82
New	0.824 (0.783–0.865)	0.830 (0.762–0.899)	0.843 (0.810–0.875)	0.753 (0.700–0.806)
Bach	0.732 (0.683–0.780)	0.787 (0.710–0.864)	0.775 (0.737–0.813)	0.656 (0.595–0.717)
P	1.25 × 10−5	0.0957	3.91 × 10−6	1.61 × 10−4
Five years
Controls	7,444	6,535	13,979	4,049
Cases	43	10	53	37
New	0.767 (0.701–0.832)	0.715 (0.532–0.898)	0.787 (0.728–0.847)	0.681 (0.597–0.765)
Bach	0.749 (0.686–0.813)	0.753 (0.583–0.922)	0.743 (0.685–0.802)	0.589 (0.510–0.669)
P	0.362	0.118a	0.024	0.0035

NOTE: Bach high-risk group are individuals between 50 and 75 years old who have smoked 10 to 60 cpd for 25 to 55 years. Also shown is the P value for improvement in AUC of our model compared with the Bach model.

^aAUC for 5-year prediction of former smokers is higher using Bach model, therefore P value refers to superiority of Bach model relative to the new model.

Calibration

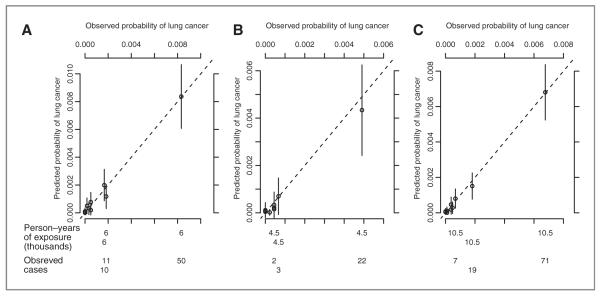
Figure 2 shows a plot of predicted yearly incidence of lung cancer versus observed yearly incidence of lung cancer in current and former smokers and the combined group of ever smokers in the test set. The points, representing deciles of risk, lie around the 45-degree line indicating good calibration of the model.

Figure 2.

Calibration of risk models for (A) current smokers, (B) former smokers, and (C) the combined group of ever smokers. Plots show predicted and observed estimates of 1-year lung cancer incidence in the test set by deciles of predicted risk. Probabilities were calculated for each year each individual was followed. Bars at each decile show the 95% confidence interval for the predicted probability. The observed number of cases and person-years of exposure in the top 3 deciles are shown at the bottom of the figure.

Discussion

Our model is comparable with the Bach model (5) in using prospective cohort data, both can be applied to predict individual risk over any time window and we have shown their accuracy over 1 and 5 years. Both models rely primarily on lifetime exposure to cigarette smoke, however, the Bach model also uses exposure to asbestos. The Bach model was built using individuals between 50 and 75 year old who smoked 10 to 60 cpd for 25 to 55 years, therefore its wider applicability is questionable. In comparison, our model is applicable to all former and current cigarette smokers. We have shown that our model gives significantly superior predictive accuracy, as measured by the AUC, in comparison with the Bach model when applied to the EPIC test set, improving the AUC in the combined group of ever smokers by 0.068 (P = 3.9 × 10⁻⁶) for incidence in 1 year and 0.044 (P = 0.024) for incidence in 5 years. However, it is easier to show good predictive ability in the same population with the same data collection, a fair comparison would require models to be applied to external data.

Other published risk models for lung cancer have used logistic regression modeling to identify risk factors for lung cancer in addition to cigarette smoke, in particular, emphysema (6), COPD (7), pneumonia (8), family history of cancer (6–8), and exposure to asbestos (6) and biomarkers (9) have been found to be good predictors, however, our model which used smoking information alone has comparable predictive accuracy. The Spitz model had an AUC of 0.67 for former smokers (ref. 6) [0.70 using additional biomarkers (ref. 9)] and 0.68 for current smokers (ref. 6) [0.73 using additional biomarkers (ref. 9)]. The LLP model (8) reports an AUC of 0.71 in their combined population of ever and never smokers. The PLCO model (7) reports AUCs of 0.841 in an external replication population which included both ever and never smokers and 0.784, when this population was restricted to ever smokers. The AUC of our model is 0.843 in our test set of ever smokers. The predictive accuracy of our model can be attributed to its modeling of lifetime exposure to cigarette smoke; we jointly model the effects of age, smoking duration, and ages of initiation and cessation of smoking. In comparison, the models built using case–control data (6, 8) have used relatively crude measures of lifetime exposure to cigarette smoke. The PLCO modeling of lifetime exposure to cigarette smoke was more comprehensive, including spline effects for pack-years, smoking duration, and smoking quit time in a logistic regression model; the predictive power of this model is therefore more comparable with ours.

The limited predictive power of nonsmoking exposures in our modeling could be explained by the levels of missing data and the measurement of some exposures in EPIC; our measures of carcinogens, in addition to cigarette smoke, are limited to occupational exposures, therefore, their effects are likely to have been underestimated in our population because of small numbers of individuals employed in high-risk professions, and measurement error in data collection. Our measure of family history of cancer is limited to the number of first-degree relatives who have had either colorectal cancer or breast cancer. Also, because of a lack of follow-up for exposure information, some individuals recorded as current smokers at recruitment will have since ceased smoking. Our model’s generalizability might also be limited as EPIC is not a random sample from the general population. Our model is not applicable to cigar or pipe smokers.

Our modeling found that risk of lung cancer did not increase with a smoking intensity of more than 15 cpd. The dose–response relationship between smoking intensity and lung cancer risk is controversial; others have also observed a leveling-off of risk of lung cancer with increasing intensity, but at 20 cpd (36), however, others have observed an approximately linear relationship (with a slight leveling-off) using serum cotinine as a predictor of lung cancer risk (ref. 37), for a review, see ref. 38).

Our results indicate minimal predictive power of the 2 genetic variants considered in accordance with other studies (39). The SNP rs8034191 at 15q25 is the strongest known genetic risk factor for lung cancer with an estimated OR of 1.29 per allele in Europeans (40). The locus is also known to be associated with smoking status and nicotine dependence (25), recent research has explored whether its association with lung cancer can be explained by its influence on individuals’ smoking behavior alone or whether it also represents an independent risk factor for lung carcinogenesis. Therefore, the limited predictive power of rs8034191 could be explained by our model’s capture of the effect of lifetime smoking exposure. The SNP rs273610 at 5p15 has a relatively small estimated OR of 1.14 per allele in Europeans (40) explaining its more limited predictive power. However, our ability to detect genetic effects was compromised by the small number of genotyped individuals (~3% of the cohort) and the use of a case–control design; possible bias was limited by matching cases and controls by age, sex, recruitment center, and period of recruitment, however, residual bias may remain.

The stratification used in our modeling will result in some loss of information. Strata were chosen to maximize the outof-sample log likelihood and represent a trade-off between closely defined strata with more specific individual estimates and sufficient number of individuals in each strata to give robust parameter estimates. The model could be refined to allow more strata by borrowing information between neighboring strata in a Bayesian framework.

We have shown that the application of standard survival analysis methods, with stratification, provides a framework for accurate and well-calibrated models for lung cancer incidence which are able to include the effects of other exposures. Given the strong predictive power which has been shown for other exposures, we believe that if good measures of these were included in our model, its predictive performance would improve.