BROWNIAN DYNAMICS SIMULATION OF MACROMOLECULE DIFFUSION IN A PROTOCELL

Abstract

The interiors of all living cells are highly crowded with macromolecules, which differs considerably the thermodynamics and kinetics of biological reactions between in vivo and in vitro. For example, the diffusion of green fluorescent protein (GFP) in E. coli is ~10-fold slower than in dilute conditions. In this study, we performed Brownian dynamics (BD) simulations of rigid macromolecules in a crowded environment mimicking the cytosol of E. coli to study the motions of macromolecules. The simulation systems contained 35 70S ribosomes, 750 glycolytic enzymes, 75 GFPs, and 392 tRNAs in a 100 nm × 100 nm × 100 nm simulation box, where the macromolecules were represented by rigid-objects of one bead per amino acid or four beads per nucleotide models. Diffusion tensors of these molecules in dilute solutions were estimated by using a hydrodynamic theory to take into account the diffusion anisotropy of arbitrary shaped objects in the BD simulations. BD simulations of the system where each macromolecule is represented by its Stokes radius were also performed for comparison. Excluded volume effects greatly reduce the mobility of molecules in crowded environments for both molecular-shaped and equivalent sphere systems. Additionally, there were no significant differences in the reduction of diffusivity over the entire range of molecular size between two systems. However, the reduction in diffusion of GFP in these systems was still 4–5 times larger than for the in vivo experiment. We will discuss other plausible factors that might cause the large reduction in diffusion in vivo.

1. Introduction

One of the most characteristic features of the interiors of all living cells is the extremely high total concentration of biological macromolecules. Typically, 20–30% of the total volume of cytoplasm is occupied by a variety of proteins, nucleic acids and other macromolecules. Under these conditions, the distance between neighboring proteins is comparable to the protein size itself, though the molar concentration of each protein ranges from nM to μM. In this crowded, heterogeneous environment, biomolecules work to maintain living systems and they have evolved over several billion years. Therefore, modeling the crowded cellular environment is not only an important first step toward whole cell simulation but also a crucial factor in understanding the nature of living systems.

In this study, we performed Brownian dynamics (BD) simulations of rigid macromolecules in a crowded environment mimicking the cytosol of E. coli to study the motions of macromolecules. BD simulations using an equivalent sphere system, where macromolecules were represented by their Stokes radius were also performed. It has been reported that the diffusion of green fluorescent protein (GFP) in E. coli is ~10-fold slower than in dilute conditions (1, 2). Our aim is to investigate the mechanism(s) that causes this large reduction in diffusion in vivo.

2. Methods

2.1. Estimation of diffusion tensor of a macromolecule from atomic structure

To account for the diffusion anisotropy of macromolecules in our simulation, the diffusion tensors of macromolecules were calculated by using the rigid-particle formalism method (3–5). Here, we will describe this approach briefly. The diffusion of an arbitrarily shaped object undergoing Brownian motion is expressed by a 6 × 6 diffusion tensor, D, which is related to a frictional or resistance tensor, Ξ, through the generalized Einstein relationship, D = k_BT Ξ⁻¹. Both D and Ξ can be partitioned into 3 × 3 sub-matrices, which correspond to translation (tt), rotation (rr), and translation-rotation coupling (tr and rt) tensors:

$$\mathbf{D}=\left(\begin{array}{cc}{\mathbf{D}}_{tt}& {\mathbf{D}}_{rt}\\ {\mathbf{D}}_{tr}& {\mathbf{D}}_{rr}\end{array}\right)=k_{\mathrm{B}}T{\left(\begin{array}{cc}{\mathbf{\Xi }}_{tt}& {\mathbf{\Xi }}_{rt}\\ {\mathbf{\Xi }}_{tr}& {\mathbf{\Xi }}_{rr}\end{array}\right)}^{-1},$$ (1)

where

$${\mathbf{D}}_{rt}={\mathbf{D}}_{tr}^T\text{and}{\mathbf{\Xi }}_{rt}={\mathbf{\Xi }}_{tr}^T.$$ (2)

Here, the superscript T indicates transposition. Translational and rotational diffusion coefficients in a dilute solution are given by

$$D_{0,t}=1/3\text{Tr}\left({\mathbf{D}}_{tt}\right),$$ (3)

$$D_{0,r}=1/3\text{Tr}\left({\mathbf{D}}_{rr}\right),$$ (4)

where Tr is the trace of the tensor.

The components of Ξ can be obtained by the following procedure. From the Cartesian coordinates of the object consisting of N beads with the same radius, a, the 3 × 3 hydrodynamic interaction tensors between beads i and j, T_ij (i, j = 1,…, N) are calculated using the expression formulated by Rotne and Prager (6) and Yamakawa (7), the so-called RPY tensor,

$${\mathbf{T}}_{ij}=\{\begin{array}{ll}\frac{1}{8\pi \eta r_{ij}}\left[\left(\mathbf{I}+\frac{{\mathbf{r}}_{ij}{\mathbf{r}}_{ij}}{{r_{ij}}^2}\right)+\frac{2a^2}{{r_{ij}}^2}\left(\frac{1}{3}\mathbf{I}-\frac{{\mathbf{r}}_{ij}{\mathbf{r}}_{ij}}{{r_{ij}}^2}\right)\right]\hfill & r_{ij}\ge 2a,\hfill \\ \frac{1}{6\pi \eta a}\left[\left(1-\frac{9}{32}\frac{r_{ij}}{a}\right)\mathbf{I}+\frac{3}{32}\frac{{\mathbf{r}}_{ij}{\mathbf{r}}_{ij}}{r_{ij}a}\right]\hfill & r_{ij}<2a.\hfill \end{array}$$ (5)

Here, η is the viscosity of the solvent and r_ij is the distance vector between beads i and j. It is important to note that the radius of bead is the only parameter to be optimized to reproduce hydrodynamic properties in dilute conditions. In what follows, we ignore intermolecular hydrodynamic interactions.

Now, consider a 3N × 3N supermatrix, B, consisting of N × N B_ij blocks at an arbitrary origin O

$$\begin{array}{l}\mathbf{B}=\left(\begin{array}{ccc}{\mathbf{B}}_{11}& \cdots & {\mathbf{B}}_{1N}\\ ⋮& \ddots & ⋮\\ {\mathbf{B}}_{N1}& \cdots & {\mathbf{B}}_{NN}\end{array}\right),\\ {\mathbf{B}}_{ij}={\delta }_{ij}\frac{1}{6\pi \eta a}+\left(1-{\delta }_{ij}\right){\mathbf{T}}_{ij}.\end{array}$$ (6)

Here, δ_ij is the Kronecker delta function. This supermatrix is then inverted to obtain a 3N × 3N supermatrix, C,

$$\mathbf{C}={\mathbf{B}}^{-1}=\left(\begin{array}{ccc}{\mathbf{C}}_{11}& \cdots & {\mathbf{C}}_{1N}\\ ⋮& \ddots & ⋮\\ {\mathbf{C}}_{N1}& \cdots & {\mathbf{C}}_{NN}\end{array}\right),$$ (7)

in which each of the C_ij block is a 3 × 3 matrix. Now, the elements of Ξ can be written as

$$\begin{array}{l}{\mathbf{\Xi }}_{tt}=\sum _i\sum _j{\mathbf{C}}_{ij},\\ {\mathbf{\Xi }}_{tr}=\sum _i\sum _j{\mathbf{U}}_i·{\mathbf{C}}_{ij},\\ {\mathbf{\Xi }}_{rr}=-\sum _i\sum _j{\mathbf{U}}_i·{\mathbf{C}}_{ij}·{\mathbf{U}}_j,\end{array}$$ (8)

where

$${\mathbf{U}}_i=\left(\begin{array}{ccc}0& -z_i& y_i\\ z_i& 0& -x_i\\ -y_i& x_i& 0\end{array}\right).$$ (9)

Here, x_i, y_i, and z_i are the components of the position vector of bead i at origin O.

So far the choice of the origin of the coordinates has been left arbitrary. However, the diffusion tensor, D, especially translational and translation-rotation coupling tensors, depends on the origin. At a certain origin, the so-called center of diffusion Ω, the translational diffusion coefficient reaches a minimum. The position of Ω with respect to the arbitrary origin O, is calculated with the diffusion tensor obtained at O, Do, as

$${\mathbf{R}}_{O\mathit{\Omega }}=\left(\begin{array}{c}{x}_{O\mathit{\Omega }}\\ y_{O\mathit{\Omega }}\\ z_{O\mathit{\Omega }}\end{array}\right)={\left(\begin{array}{ccc}{D}_{rr,O}^{yy}+D_{rr,O}^{zz}& -D_{rr,O}^{xy}& -D_{rr,O}^{xz}\\ -D_{rr,O}^{xy}& D_{rr,O}^{xx}+D_{rr,O}^{zz}& -D_{rr,O}^{yz}\\ -D_{rr,O}^{xz}& -D_{rr,O}^{yz}& D_{rr,O}^{yy}+D_{rr,O}^x\end{array}\right)}^{-1}\left(\begin{array}{c}{D}_{tr,O}^{yz}-D_{tr,O}^{zy}\\ D_{tr,O}^{zx}-D_{tr,O}^{xz}\\ D_{tr,O}^{xy}-D_{tr,O}^{yx}\end{array}\right).$$ (10)

D at the center of diffusion Ω are calculated by

$$\begin{array}{l}{\mathbf{D}}_{tt,\mathit{\Omega }}={\mathbf{D}}_{tt,O}-{\mathbf{U}}_{O\mathit{\Omega }}·{\mathbf{D}}_{rr,O}·{\mathbf{U}}_{O\mathit{\Omega }}+{\mathbf{D}}_{rt,O}·{\mathbf{U}}_{O\mathit{\Omega }}-{\mathbf{U}}_{O\mathit{\Omega }}·{\mathbf{D}}_{tr,O},\\ {\mathbf{D}}_{rt,\mathit{\Omega }}={\mathbf{D}}_{rt,O}-{\mathbf{U}}_{O\mathit{\Omega }}·{\mathbf{D}}_{rr,O},\\ {\mathbf{D}}_{rr,\mathit{\Omega }}={\mathbf{D}}_{rr,O},\end{array}$$ (11)

where

$${\mathbf{U}}_{O\mathit{\Omega }}=\left(\begin{array}{ccc}0& -z_{O\mathit{\Omega }}& y_{O\mathit{\Omega }}\\ z_{O\mathit{\Omega }}& 0& -x_{O\mathit{\Omega }}\\ -y_{O\mathit{\Omega }}& x_{O\mathit{\Omega }}& 0\end{array}\right).$$ (12)

A volume correction term for rotational and intrinsic viscosity estimation is applied in Eq. 8 in some studies (3, 4). However, significant deviations of calculated diffusion properties from experimental values were not observed even without the correction.

2.2. Brownian dynamics for arbitrarily shaped objects

BD is one of the most important simulation approaches to investigate the Brownian motion of arbitrary shaped objects, in which solvent molecules are treated implicitly and the influence of solvent on solute particles is incorporated through frictional and stochastic forces (8). In the high-friction limit, where it is assumed that momentum relaxation is much faster than position relaxation, and when we treat the diffusion tensor as a constant, a BD propagation scheme for an arbitrarily-shaped object can be written as (9)

$${\mathbf{x}}_i={\mathbf{x}}_i^0+\frac{\mathrm{\Delta }t}{k_{\mathrm{B}}T}{\mathbf{D}}_i·{\mathbf{F}}_i^{\mathrm{p}}+{\mathbf{g}}_i(\mathrm{\Delta }t),$$ (13)

where Δt is the time step and x_i is the vector describing the position of the center of diffusion and orientation of the i-th object,

$$\mathbf{x}={(r_1,r_2,r_3,{\varphi }_1,{\varphi }_2,{\varphi }_3)}^T.$$ (14)

Here, r₁, r₂, and r₃ are the position of the center of diffusion, and φ₁, φ₂, φ₃ describe its orientation. F^p is a generalized system force having two components, the force acting on the center of diffusion (f) and the torque (τ):

$${\mathbf{F}}^{\mathrm{p}}={(f_1,f_2,f_3,{\tau }_1,{\tau }_2,{\tau }_3)}^T.$$ (15)

g(Δt) is a 6 × 1 random displacement vector during time step Δt due to the Brownian noise, which satisfies the following relations:

$$\langle {\mathbf{g}}_i(\mathrm{\Delta }t)\rangle =0,\langle {\mathbf{g}}_i(\mathrm{\Delta }t){\mathbf{g}}_j(\mathrm{\Delta }t)\rangle =2{\mathbf{D}}_i\mathrm{\Delta }t{\delta }_{ij}.$$ (16)

Here D_i is the 6 × 6 diffusion tensor of object i at the center of diffusion. Once this diffusion tensor is calculated as described above, we can compute the random displacement vector using a Cholesky decomposition technique (9). The Cholesky decomposition of the diffusion tensor D is determined as

$$\mathbf{D}=\mathbf{S}·{\mathbf{S}}^T,$$ (17)

where S is a lower triangle matrix. The desired vector g(Δt) is then obtained by the following:

$$\mathbf{g}(\mathrm{\Delta }t)=\mathbf{S}·\mathbf{Z},$$ (18)

where Z is a 6 × 1 vector, which has elements chosen from a Gaussian distribution so that

$$\langle {\mathbf{Z}}_i\rangle =0,\langle {\mathbf{Z}}_i{\mathbf{Z}}_j\rangle =2\mathrm{\Delta }t{\delta }_{ij}.i=1,2,\dots ,6.$$ (19)

In BD simulations, quaternions, q = (q₀, q₁, q₂, q₃), were used for handling rotations of rigid objects (8). Diffusion tensors of objects were evaluated in body-fixed frames only once at the start of the simulation. The force and torque on each object calculated in the laboratory or space-fixed frame (f^s or τ^s) were converted to their body-fixed frame (f^b or τ^b) using the rotation matrix Q obtained with quaternions,

$${\mathbf{F}}^{\mathrm{b}}=\left(\begin{array}{c}{\mathbf{f}}^{\mathrm{b}}\\ {\mathbf{\tau }}^{\mathrm{b}}\end{array}\right)=\left(\begin{array}{c}\mathbf{Q}·{\mathbf{f}}^{\mathrm{s}}\\ \mathbf{Q}·{\mathbf{\tau }}^{\mathrm{s}}\end{array}\right).$$ (20)

For each step, quaternions were scaled using Lagrange’s method of undetermined multipliers to satisfy q² = 1 (10).

2.3. Potential function

In this study, we considered only repulsive interactions between intermolecular particles in BD simulations using a soft-sphere potential described by

$$V_{\text{ss}}\left(r_{ij}\right)=\{\begin{array}{ll}{k}_{\text{ss}}{\left(r_{ij}-r_{\mathrm{m}}\right)}^2\hfill & \text{if}{r}_{ij}\le r_{\mathrm{m}}\hfill \\ 0\hfill & \text{if}{r}_{ij}>r_{\mathrm{m}}\hfill \end{array},$$ (21)

where r_ij is the distance between particles i and j, and k_ss is a force constant. r_m is a_i + a_j + Δ, in which a_i and a_j are radii of particles i and j and Δ is an arbitrary parameter representing buffer distance between particles. In this study, Δ of 2 Å and k_ss of 5k_BT/Δ² was used, which means V_ss = 5k_BT at the distance r_ij = a_i + a_j.

2.4. Simulation conditions and analysis

All simulations were performed at 298 K with periodic boundary conditions. For all simulation systems, ten independent simulations were run with different initial configurations. 35 μs simulations were performed with time step of 0.5 ps. Configurations of the systems were sampled every 1 ns. Trajectories for the first 5 μs were discarded for analysis. The translational diffusion coefficient of a particle in three dimensions is estimated by

$$\langle {[\mathbf{r}(t+\tau )-\mathbf{r}(t)]}^2\rangle =6D\tau ,$$ (22)

where r(t) is position of the particle at time t and τ is time interval. 〈 〉 indicates the ensemble average over the same particle type and time t.

3. Results

3.1. Estimation of diffusion tensor of a macromolecule from atomic structure

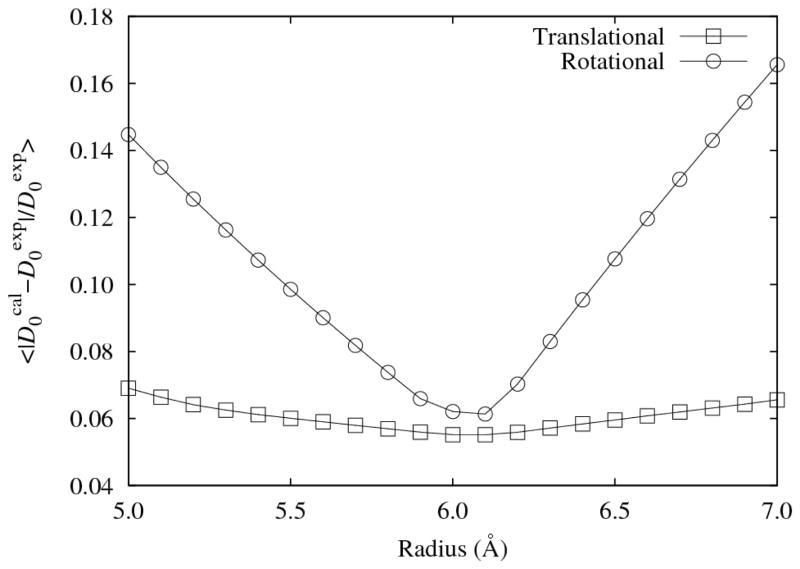
To estimate diffusion tensors of macromolecules from their atomic structures, the rigid-particle formalism was used (3–5). As described in Methods, the particle radius is the only one parameter optimized to reproduce the experimental translational and rotational diffusion coefficients of macromolecules at infinite dilution. The bead radius was optimized using the twelve different proteins whose molecular weight ranges from 6 kDa to 230 kDa, which are the same as those used in Ref. (4) except for lactose dehydrogenase. Proteins were represented by Cα beads. Figure 1 shows that the difference between experimental and calculated diffusion coefficients average over the twelve proteins of Ref. (4) as a function of bead radius. Radius of 6.1 Å gave the minimal error in both translational and rotational diffusion coefficients. For example, the method provided translationla diffusion coefficient for GFP of 8.9 Ų/ns at 293 K, which is excellent agreement with experimental value of 8.7 Ų/ns for this protein in dilute conditions at room temperature (11, 12). In order to simulate the inside of cells, we treat not only proteins but also nucleic acids. Thus, diffusion coefficients of a Phe-tRNA (PDB ID: 1EHZ) were also evaluated using the same method. Nucleic acids were represented by P, C4′, N1, and N9 beads. The bead density of the tRNA was 3.7 beads/nm³, close to the value of proteins averaged over the twelve proteins, 3.5 beads/nm³. Using the same bead radius as proteins, the translational diffusion coefficient of the tRNA is 7.6 Ų/ns at 293 K, which was also in good agreement with experimental value of 7.8 Ų/ns, at the same temperature (13).

Figure 1.

Errors in translational and rotational diffusion coefficients calculated by the rigid-particle formalism as function of bead radius. D₀^cal and D₀^exp represent the translational or rotational diffusion constant in a dilute condition calculated by theory and estimated by experiment, respectively. Values for translational (open squares) and rotational (open circles) diffusion coefficient were averaged over the twelve proteins listed in Table 2 of Ref. (4) except for lactose dehydrogenase. Lines are drawn to guide the eye.

3.2. Construction of the intracellular environment

The size and molecular contents of the E. coli have been estimated by experimentally. To construct a virtual E. coli cytoplasm, we used a statistics data summarized in the CyberCell Database (14). The total cell volume of E. coli is about 1 fL and about 70% of this total volume is cytoplasm, in which the macromolecular concentration reaches 300–400 mg/ml (15). In terms of dry weight, half of that mass is protein and 20% of the protein complement of the cell is ribosomal protein. The number of cytoplasmic proteins excluding ribosomal proteins is roughly 1,000,000. The number of ribosomes consisting 1/3 protein and 2/3 rRNA in mass is about 18,000, which occupies 10% of the total cell volume. tRNAs are also abundant and about 200,000 molecules exist in the cell. Based on these data, a protocell that containing 35 70S ribosomes, 750 enzymes involving in glycolysis which are the most abundant proteins in E. coli cells (16), 75 GFPs for a tracer protein that we can compare to experimental results, and 392 tRNAs in a 100 nm × 100 nm × 100 nm simulation box was constructed (Table 1 and Figure 2 left panel). The total concentration is 271 mg/ml and the volume occupancy reaches at 41% when the radii of all beads were set to 6.1 Å. The simulation box has 1,252 molecules and total 1,279,871 beads. For comparison, simulation systems where each macromolecule was represented by an equivalent sphere with its Stokes radius were also constructed (Figure 2 right panel). Volume occupancy in this system reaches at 45%.

Table 1.

Macromolecules in the simulation system

Name	PDB ID	Molecular weight (Da)	No. of molecules in the system	Stokes radius (Å)†	Translational D0 at 298 K (Å2/ns)
70S ribosome	3I1Q & 3I1R	2,155,152	35	115.2	2.13
Hexokinase	1Q18	72,504	75	34.9	7.02
Glucose-6-phosphate isomerase	1GZV	126,649	75	40.1	6.12
6-phosphofructokinase isozyme 1	1PFK	144,514	75	42.4	5.78
Fructose 1–6 bisphosphate aldolase	1DOS	78,235	75	36.8	6.67
Triosephosphate isomerase	1TRE	54,006	75	31.7	7.73
Glyceraldehyde-3-P dehydrogenase	1S7C	145,013	75	43.1	5.69
Phosphoglycerate kinase	1ZMR	41,287	75	29.2	8.41
Phosphoglycerate mutase	1E58	57,544	75	32.3	7.59
Enolase	1E9I	91,267	75	35.9	6.82
Pyruvate kinase	1PKY	203,184	75	52.9	4.63
GFP	1W7S	26,936	75	24.0	10.2
Phe-tRNA	1EHZ	25,203	196	28.2	8.69
Initial tRNA	3CW5	24,833	196	27.8	8.83

^†Stokes radii were calculated by D₀ = k_BT/6πηa, where a is the Stokes radius.

Figure 2.

Molecular-shaped (left) and equivalent sphere (right) systems. Macromolecules are represented in different colors. These figures were generated by VMD (17).

3.3. Effect of molecular shapes on diffusion

Next, we performed BD simulations using two systems that resemble the E. coli cytoplasm: molecular-shaped and equivalent sphere systems. In order to compare the diffusivity of macromolecules between two systems as well as experiments, we will concentrate on the analysis of the translational diffusion of molecules. Hereafter, diffusion refers to translational diffusion.

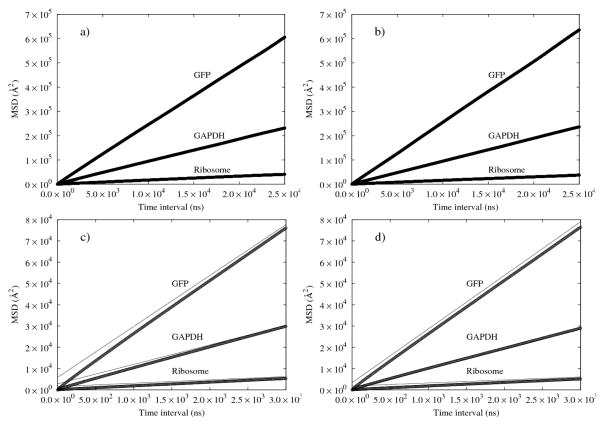
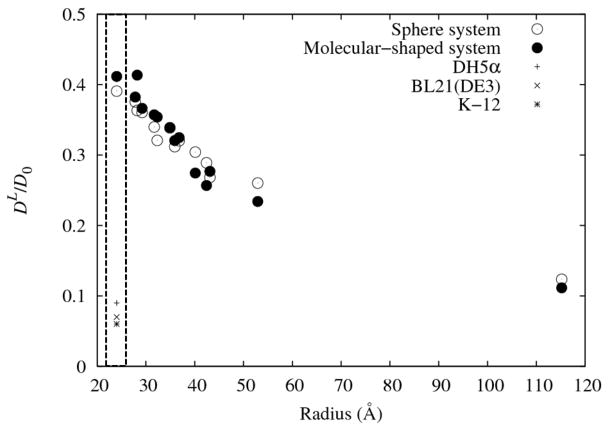
Mean square displacements (MSD) for several macromolecules in the both systems as a function of time are shown in Figure 3. For both systems, as in other simulation studies on diffusion in cytosol-like systems, crossover from anomalous diffusion to normal diffusion were observed for all molecules in short times (18–20). Subsequently, a linear relationship between time and MSD is well observed for long time for all molecules and the diffusion coefficients quickly converged. In Figure 4, the ratio of the long-time translational diffusion coefficients observed in the virtual cytoplasm system to that estimated in dilute solution, D^L/D₀, as a function of Stokes radius is shown. For both systems, the ratio D^L/D₀ decreased with increasing molecular radius, which is qualitatively consistent with other simulation studies (18–20) and experimental results on eukaryotic cells (21). The results of explicit molecular-shaped and the equivalent sphere systems are very close over the entire range of radii. These results suggest that effects of macromolecular shape on molecular diffusion in crowded environments are small and that the single sphere per one molecule model is a reasonable approximation for the analysis of in vivo diffusion.

Figure 3.

MSDs of three macromolecules in sphere system (a, c) and molecular shaped-system (b, d) as a function of time interval, τ. MSDs up to 25 μs are shown in upper graphs (a, b). MSDs over the short-time range are shown in lower graphs (c, d). Solid lines in lower graphs are fitted lines in the time range from 10 to 25 μs. GAPDH represents glyceraldehyde-3-P dehydrogenase.

Figure 4.

The reduction in long-time diffusion coefficient as a function of radius in simulation of sphere and molecular-shaped system with steric repulsion. Open spheres and filled spheres are for the values in sphere system and molecular-shaped systems, respectively. Three values of the reduction in diffusion of GPF measured in vivo of DH5α (1, 2), BL21(DE3) (1, 2s), and K-12 (1, 2) E. coli are also shown for comparison. The values corresponding to GFP diffusivity are surrounded by the dashed line to guide the eye.

In experiments, the reduction in diffusion of GFP is about 0.06–0.09 (11, 12) (see also Figure 4). On the other hand, D^L/D₀ values of GFP obtained in molecular-shaped and sphere systems are 0.4 and 0.42, 5–7 times larger than experiment. This result indicates that (consistent with other studies (18–20)) although excluded volume effects greatly reduce the macromolecules diffusion rate in intracellular environments, they cannot explain the factor of ~10–16 reduction in diffusion constant observed in vivo.

4. Discussion

To investigate a possible cause of the large reduction in diffusion in vivo, we performed BD simulations on two different types of systems: a molecular-shaped system and an equivalent sphere system. Our simulation results provide for two important conclusions: First, excluded volume effects are insufficient to explain the large reduction in diffusion of macromolecules observed in vivo. Second, the one sphere per one molecule model is a good approximation to describe macromolecular diffusion in intracellular environments.

In addition to the excluded volume effects, a number of other factors can affect the nature and magnitude of intracellular diffusion. 1) Hydrodynamic interactions (HI). Effects of HI on dynamics of particles have been well studied in the field of colloidal suspensions. Simulation studies showed that HI greatly reduce the diffusivity of monodisperse colloids especially in dense systems (22, 23). Evaluating HI of an N particle system is computationally expensive scales as O(N³) (22). Therefore, it is very difficult to consider HI in BD of molecular-shaped systems. However, our demonstration of the relatively minor shape effect enables HI to be calculated in a computationally tractable manner for the equivalent sphere system. 2) Non-specific interactions. One fourth of surface residues of proteins are hydrophobic (24); this which could give rise to attractive interactions between molecules. In addition, electrostatic might be important even though they are well screened under physiological conditions (the Debye length is ~8 Å). 3) Viscosity of the cytoplasm. In our simulations, the viscosity of water was used as a parameter in calculating diffusion tensors of molecules and simulations. The in vivo viscosity has been measured by various methods, which indicated that viscosity of the cytoplasm medium is not significantly larger than that of bulk water (21). 4) GFP dimerization. It is well known that GFP tends to dimerize in solutions of low (< 100 mM) ionic strength (25). All of these physical factors will decrease macromolecular diffusivity in vivo. These factors should be examined in further work.

5. Conclusions

Until now, little attention has been paid to the biophysical properties of crowded environments, which have a great impact on biological reactions taking place inside cells. Therefore, modeling these crowding effects is an important first step towards whole cell simulation. In that spirit, by conducting a series of Brownian dynamics simulations, the following conclusions were obtained: First, although excluded volume effects can significantly reduce the diffusivity of macromolecules, this effect is insufficient to explain the large reduction that is observed in vivo. Second, representing a macromolecule by a single equivalent sphere is a reasonable approximation for analyzing diffusion of macromolecules in vivo. Thus, in future work, using our protocell, we shall explore the role of hydrodynamic and electrostatic interactions as in the reduction of in vivo diffusivity.