Biomechanical benefits of the Onion-Skin motor unit control scheme

Abstract

Muscle force is modulated by varying the number of active motor units and their firing rates. For the past five decades, the notion that the magnitude of the firing rates is directly related to motor unit size and recruitment threshold has been widely accepted. This construct, here named the After-hyperpolarization scheme evolved from observations in electrically stimulated cat motoneurons and from reported observations in voluntary contractions in humans. It supports the assumption that the firing rates of motor units match their mechanical properties to “optimize” force production, so that the firing rate range corresponds to that required for force-twitch fusion (tetanization) and effective graduation of muscle force. In contrast, we have shown that, at any time and force during isometric voluntary constant-force contractions in humans, the relationship between firing rate and recruitment threshold is inversely related. We refer to this construct as the Onion-Skin scheme because earlier-recruited motor units always have greater firing rates than latter-recruited ones. By applying a novel mathematical model that calculates the force produced by a muscle for the two schemes we found that the Onion-Skin scheme is more energy efficient, provides smoother muscle force at low to moderate force levels, and appears to be more conducive to evolutionary survival than the After-hyperpolarization scheme.

INTRODUCTION

Muscle force is modulated by varying the number of active motor units and their firing rates. The manner in which motor units are controlled determines the characteristics of the force generated by the muscle that in turn determines the manner in which we interact with our environment and each other.

There is general agreement that, as the excitation to the motoneuron pool increases to produce more force, motor units are recruited in order of increasing size, as described by the “Size Principle” (Henneman, 1957; Hu et al. 2013). As for the firing rate, over the past five decades there has been a common acceptance of the notion promulgated dominantly by Eccles et al. in 1958 that higher-threshold motoneurons have greater firing rates than lower-threshold ones. This notion stems from the observation that, when the nerves of anesthetized cats are electrically stimulated, the larger-diameter (higher-threshold) motoneurons exhibit a shorter after-hyperpolarization (AHP) and greater firing rates than the smaller-diameter (lower-threshold) ones. The lower-threshold motor units have wider and smaller amplitude force twitches than the higher-threshold motor units and require lower firing rates to tetanize (produce twitch fusion). By inference, this arrangement would “optimize” the force generating capacity of the muscle since each motor unit would fire at rates producing twitch fusion and thus contributing its greatest individual force. This hypothesis, which we will refer to as the AHP scheme, was supported by Kernell (1965, 2003) and has been tacitly accepted by many thereafter and adopted in support of their observations in humans (Grimby et al., 1979; Moritz et al., 2005; Oya et al., 2009, among others). However, the empirical studies that reported a linear relation between recruitment threshold and firing rates grouped motor unit data from different subjects and contractions performed on different days or at different force levels (Gydikov and Kosarov, 1974; Grimby et al., 1979; Moritz et al., 2005; Tracy et al. 2005; Barry et al., 2007; Oya et al., 2009; Jesunathadas et al., 2012). But, we make note that this approach is known to introduce inter-subject variability and errors in the analysis (De Luca and Hostage, 2010; De Luca and Contessa, 2012; Hu et al., 2013, 2014b).

We (De Luca et al 1982; De Luca and Hostage, 2010; De Luca and Contessa, 2012) and others (Seyffarth, 1940; Person and Kudina, 1972; Masakado et al., 1995; Stock et al., 2012; Hu et al. 2013, 2014b; De Luca et al. 2014; among others) have shown that, at any time and force during voluntary constant-force contractions in humans, earlier-recruited motor units maintain higher firing rates than later-recruited ones, providing an inverse orderly hierarchy of nested firing rate curves resembling the layers of the skin of an onion. We refer to this construct as the Onion-Skin scheme (De Luca and Erim, 1994).

In this work, we applied a novel model of muscle force generation (Contessa and De Luca, 2013) to compare the force characteristics produced by the two schemes during constant-force contractions. We did so for two muscles: the first dorsal interosseous (FDI) of the hand and the vastus lateralis (VL) of the thigh. These muscles were chosen because they have different properties: the FDI is a smaller muscle commonly involved in precise low-force level activities, and the VL is one of the largest muscles in the body that generates large forces.

METHODS

The model used for the simulation of the firing rate and force behavior of motor units is a modified version of that developed by Contessa and De Luca (2013) for the FDI and VL muscles. The input-output relationship at the motoneuron level, describing the firing behavior of motor units, and the firing rate to force transduction at the muscle fiber level, describing the mechanical properties of motor units, are modeled separately. The model is based on the concept of Common Drive (De Luca et al., 1982b), which describes an excitation, consisting of the sum of all excitatory and inhibitory inputs from the Central and Peripheral Nervous Systems, driving the firing behavior of all motor units in the motoneuron pool of a muscle. The Common Drive will be referred to as the “input excitation”, φ, to the model. It ranges from φ=0, when no motor unit is active and no force is produced, to φ=1, the maximal level of input excitation required to exert maximal force output.

The motoneuron pools of the FDI and VL contain approximately 120 and 600 motor units, respectively (Feinstein et al., 1955; Christensen, 1959). Motor units are activated when the input excitation is greater than or equal to their recruitment threshold value, τ. The range of motor unit recruitment thresholds is between 0-67% maximum voluntary contraction force (MVC) in the FDI and between 0-95% MVC in the VL (De Luca and Hostage, 2010). Smaller motor units are recruited at lower input excitation levels, and as the input excitation increases, higher-threshold motor units are progressively recruited, as described by the following equation derived by De Luca and Kline (2012):

$$\%\text{active MUs}\left(\phi \right)=0.0058s\phi (1-360{\mathrm{e}}^{-5.9\phi })+100(1-{\mathrm{e}}^{-9.8\phi })$$ (1)

where s is the number of spindles in the muscle, with s=34 for the FDI (Smith and Marcarian, 1966) and s=440 for the VL (Voss, 1959).

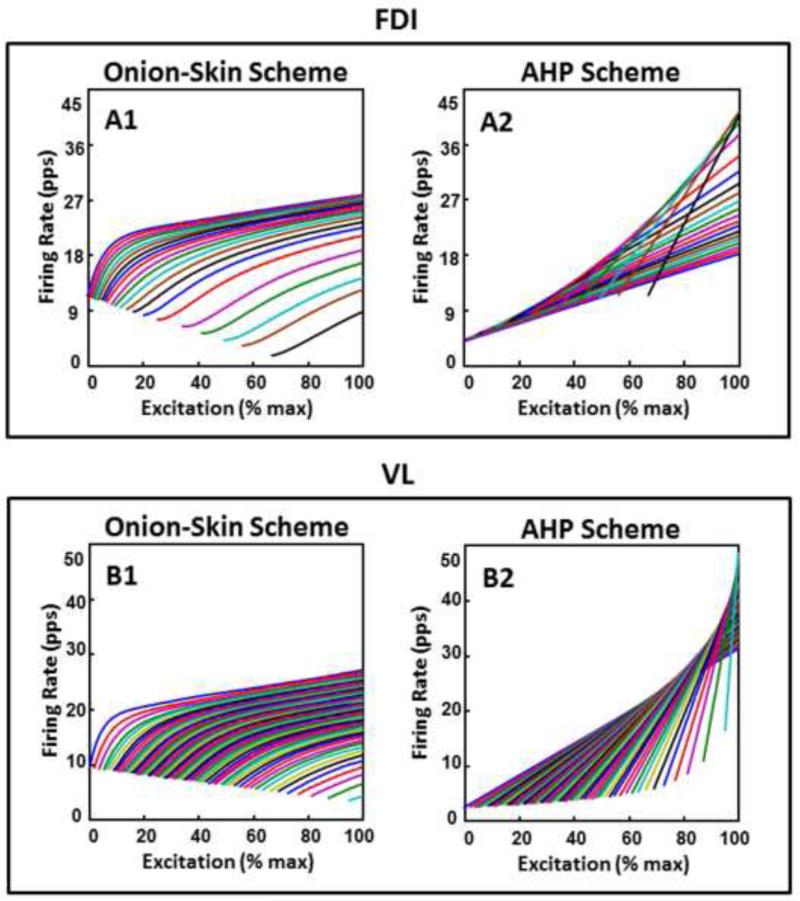
The input excitation also determines the firing rate value λ_i of each active motor unit i. The Onion-Skin scheme describes a hierarchical inverse relationship between the recruitment threshold τ_i and the firing rate λ_i of each motor unit at any input excitation level during a voluntary contraction, thus formulating the “Onion Skin” property (De Luca et al., 1982; De Luca and Erim, 1994). The AHP scheme formulates an opposite arrangement where both the minimal and maximal firing rates of motor units are directly related to recruitment threshold. See the set of trajectories in Figure 1, referred to as the firing rate spectrum, which represents the firing rate pattern of motor units as a function of increasing input excitation in the two schemes and muscles.

Figure 1. Firing rate spectrum for the Onion-Skin scheme and for the After-hyperpolarization (AHP) scheme.

Simulated motor unit firing rate as a function of increasing input excitation to the motoneuron pool of the FDI (top) and VL (bottom) muscles in the Onion-Skin (A1 and B1) and in the AHP (A2 and B2) scheme. This set of trajectories is referred to as the firing rate spectrum. Note that one out of six motor units is shown for clarity.

The equations describing the Onion-Skin scheme were derived by fitting empirical data of motor unit firing rates obtained during voluntary isometric linearly-increasing and constant force contractions in humans with mathematical equations. λ_i is modeled as a function of the input excitation φ and the motor unit recruitment threshold τ_i, as described by the following equations (Contessa and De Luca, 2013) for the FDI:

$${\lambda }_i(\phi ,{\tau }_i)=21+6.9\phi -(23+85{\mathrm{e}}^{-\phi ∕0.3}){\tau }_i-{\mathrm{e}}^{(\tau i-\phi )(0.19\tau i+0.05)}[9.8+6.9\phi +(-8.7-85{\mathrm{e}}^{-\phi ∕0.3}){\tau }_i]$$ (2)

and for the VL:

$${\lambda }_i(\phi ,{\tau }_i)=19+8.0\phi -(21+116{\mathrm{e}}^{-\phi ∕0.2}){\tau }_i-{\mathrm{e}}^{(\tau i-\phi )(0.16\tau i+0.04)}[9.9+8.0\phi +(-14.7-116{\mathrm{e}}^{-\phi ∕0.2}){\tau }_i]$$ (3)

with 0 < τ_i < 1, τ_i+1 < τ_i and 0 ≤ φ ≤ 1.For more details on the numerical values in Equation (2) and (3), refer to Contessa and De Luca (2013).

For the AHP scheme, the relation between the firing rate λ_i of each active motor unit i and the input excitation φ is modeled based on the hypothesis proposed by Eccles et al. (1958) and Kernell (1965, 1979, 2003) that both the minimal and maximal firing rates are greater for later-recruited shorter-duration AHP motor units. Specifically, the minimal firing rate of each motor unit would be close to the frequency at which consecutive force-twitches start to fuse; and the maximal firing rate would be close to the frequency needed for eliciting maximal (fully fused) force (Kernell, 1979, 2003). This construct was hypothesized based on the firing rate behavior of electrically stimulated motoneurons in anaesthetized cats, and it ensures that each motor unit modulates its firing behavior in the steep range of the force-frequency relation (Bawa and Stein, 1976). Based on this hypothesis, the minimal firing rate of each motor unit is calculated by increasing its firing rate until the force twitches start to fuse and the force produced increases in amplitude compared to that of a single twitch. The minimal firing rate, minFR_i, vs. recruitment threshold relation for all motor units could be fitted by a 2^nd order polynomial equation for the FDI:

$$minF{R}_i\left({\tau }_i\right)=-15.81{\tau }_i^2+21.66{\tau }_i+3.02\text{with}{\mathrm{R}}^2=0.99$$ (4)

and by an exponential equation for the VL:

$$minF{R}_i\left({\tau }_i\right)=-2.39{\mathrm{e}}^{\left(1.05\tau i\right)}+0.002{\mathrm{e}}^{\left(9.27\tau i\right)}\text{with}{\mathrm{R}}^2=0.98$$ (5)

The maximal firing rate of each motor unit is calculated by increasing its firing rate to the point where the force produced saturates (fully fused force). The maximal firing rate, maxFR_i, vs. recruitment threshold relation for all motor units was also fitted by a 2^nd order polynomial equation for the FDI:

$$maxF{R}_i\left({\tau }_i\right)=-70.56{\tau }_i^2+81.16{\tau }_i+17.17\text{with}{\mathrm{R}}^2=0.97$$ (6)

and by a linear equation for the VL:

$$maxF{R}_i\left({\tau }_i\right)=18.43{\tau }_i+31.42\text{with}{\mathrm{R}}^2=0.90$$ (7)

A linear firing rate vs. input excitation relation was modeled for all motor units between the minimal firing rate at recruitment and the maximal firing rate at maximal input excitation for both muscles (Kernell, 1979, 2003):

$${\lambda }_i(\phi ,{\tau }_i)={\mathrm{minFR}}_i+[({\mathrm{maxFR}}_i-{\mathrm{minFR}}_i)∕(1-{\tau }_i)](\phi -{\tau }_i)$$ (8)

The above equations for the Onion-Skin and for the AHP schemes provide the average firing rate value of the active motor units at any input excitation level during a contraction. For each active motor unit, a train of firings is then generated with an inter-pulse interval (IPI) that is the inverse of the motor unit average firing rate value. Variability in the firings is introduced by modeling the IPIs between two adjacent firings as a random variable with a Gaussian distribution, as commonly approximated in the past (Dideriksen et al., 2010; Hu et al., 2014a, among others) and a coefficient of variation of 20%.

The motor unit force twitch is modeled based on the equations developed by Raikova and Aladjov (2002):

$$\mathrm{f}\left(\mathrm{t}\right)={\mathrm{pt}}^{\mathrm{m}}{\mathrm{e}}^{-\mathrm{kt}}$$ (9)

with p = Pe^{−kTr(logTr-1)}, m = kTr, k = log2/[Thr – Tr log(Tr + Thr/Tr)]. The three parameters P, Tr and Thr represent the force-twitch amplitude, rise time and half-relaxation time, respectively. Their numerical values were derived from empirical data for the FDI and from simulated data for the VL, as described in Contessa and De Luca (2013). These equations produce progressively higher-amplitude and shorter-duration force-twitches for higher-threshold motor units (Milner-Brown et al., 1973).

The force twitches are then scaled to account for the non-linear summation of force with increasing firing rate (Bawa and Stein, 1976) through multiplication with a force-stimulus rate gain function g. For the FDI, we use the gain function derived by Fuglevand et al. (1993):

$${\mathrm{g}}_{i,j}=[1-{\mathrm{e}}^{-2{(\mathrm{Tri}∕{\mathrm{IPI}}_j)}^3}]∕({\mathrm{Tr}}_i∕{\mathrm{IPI}}_j)\text{when}{\mathrm{Tr}}_i∕{\mathrm{IPI}}_j>0.4\text{and}{\mathrm{g}}_{i,j}=1\text{when}{\mathrm{Tr}}_i∕{\mathrm{IPI}}_j\le 0.4$$ (10)

where g_ij is the gain assigned to the jth firing of motor unit i, Tr_i is the rise time of motor unit i, and IPI_j is the jth interpulse interval.

For the VL muscle, the gain function is based on empirical data from human subjects as derived in Contessa and De Luca (2013):

$${\mathrm{g}}_{i,j}=[1-\mathrm{r}{\mathrm{e}}^{(0.4-\mathrm{Tri}∕{\mathrm{IPI}}_{\mathrm{j}})∕\mathrm{c}}]∕\left[({\mathrm{Tr}}_i∕{\mathrm{IPI}}_j)(1-\mathrm{r})\right]\text{when}{\mathrm{Tr}}_i∕{\mathrm{IPI}}_j>0.4\text{and}{\mathrm{g}}_{i,j}=1\text{when}{\mathrm{Tr}}_i∕{\mathrm{IPI}}_j\le 0.4,\text{with}\mathrm{r}=0.85\text{and}\mathrm{c}=2.13$$ (11)

Finally, the force generated by each motor unit is computed by convolving the noisy impulse train with the scaled motor unit force twitches. Muscle force is obtained by summation of the force contributions of all active motor units; and it is low-pass filtered at 5 Hz to account for the filtering effect of other tissues. The simulated muscle force is normalized in % MVC by dividing it by the value obtained at maximal input excitation (φ=1).

A force feedback loop is implemented to simulate muscle force sustained at given target force levels (in % MVC). At intervals of 0.5 s, the force feedback adjusts the input excitation proportionally to the difference between the average force output and the average target force. At each interval, the simulation is repeated until the error is within a 5% tolerance limit.

For a complete description of the model, refer to Contessa and De Luca (2013).

RESULTS

We mathematically modeled the firing rate characteristics of motor units as a function of increasing input excitation to the motoneuron pool of the FDI and VL muscles for the Onion-Skin (Figure 1, A1 and B1) and for the AHP schemes (Figure 1, A2 and B2), as described by Equations (2), (3), and (8) in the Methods section. The Onion-Skin scheme describes an inverse hierarchical relationship between the recruitment threshold and the firing rate of motoneurons at any time and input excitation value. The AHP-scheme describes an opposite arrangement, where both the minimal and maximal firing rates are greater for later-recruited, shorter-duration AHP motoneurons.

We incorporated these firing rate spectra in our recently developed force model (Contessa and De Luca, 2013), and we simulated the motor unit firing rate and force output at constant levels of input excitation ranging from 5% to 10% and increasing to 100% maximal input excitation in steps of 10% for both schemes. At each input excitation level we calculated: a) the number of active motor units; b) their firing rate; c) their force output; and d) the force output of the whole muscle.

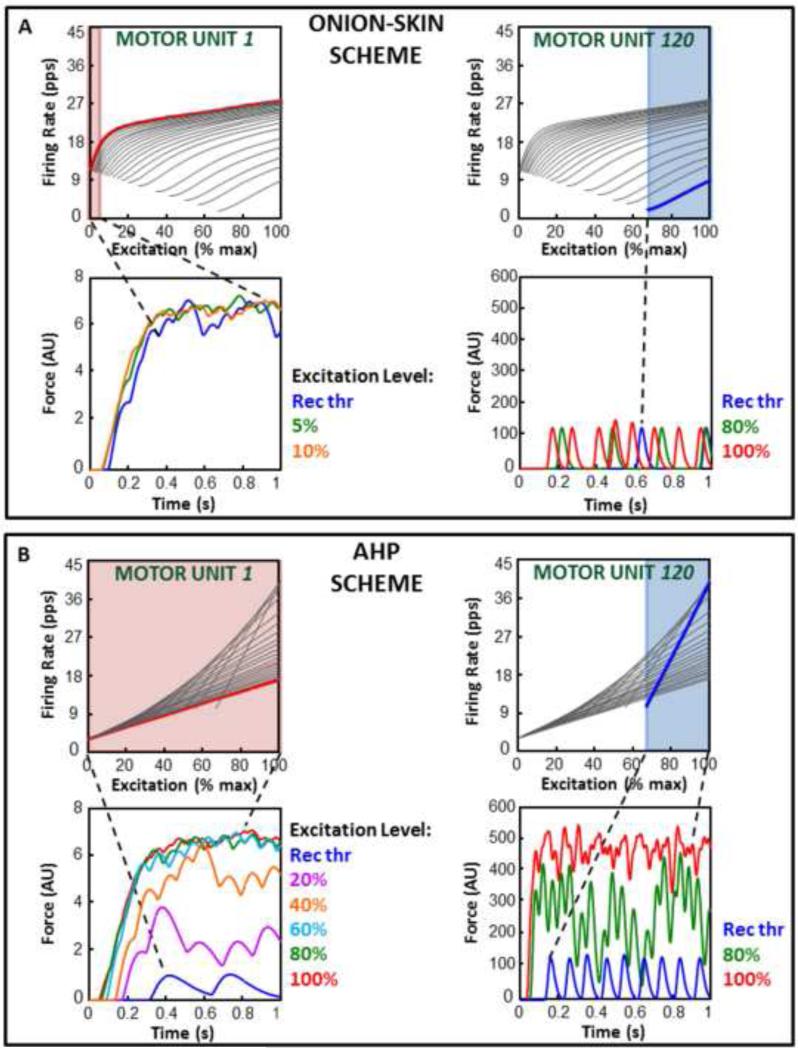
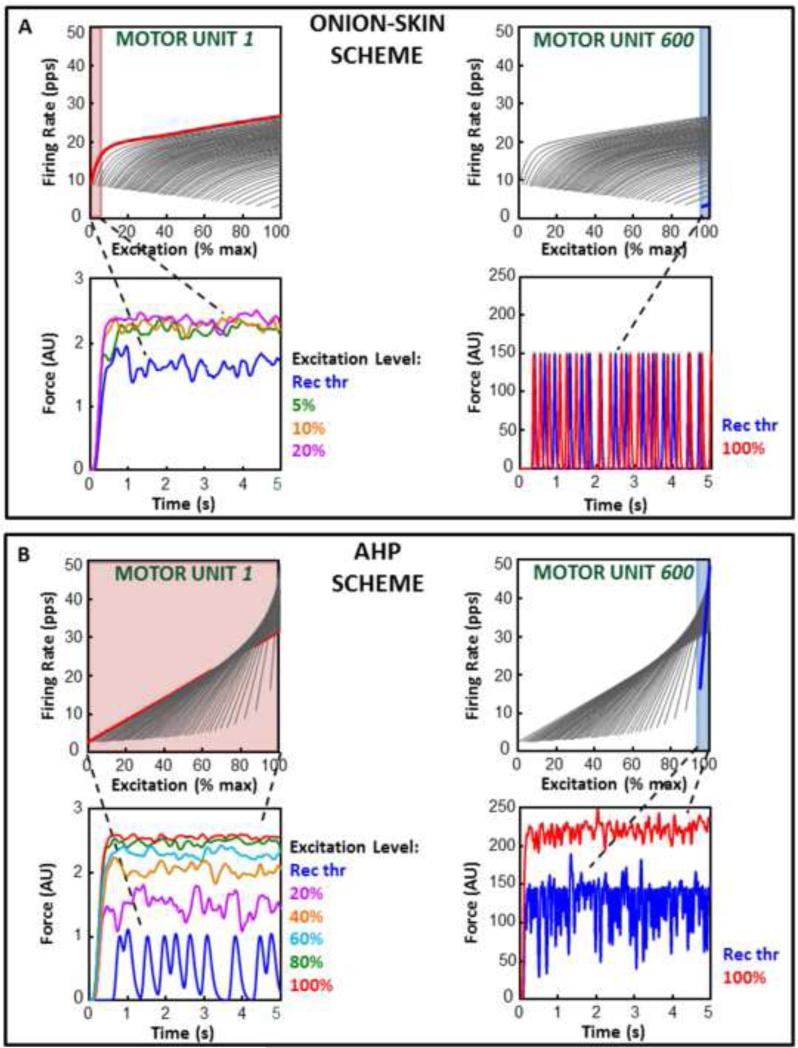
If we focus on the forces produced by the low and high-threshold motor units (Figure 2 for the FDI and Figure 3 for the VL), it can be seen that in the Onion-Skin scheme the force generated by the earliest-recruited motor unit (motor unit #1) is fully fused within 5 to 10% input excitation from its recruitment (red region in Figure 2A and 3A) since a further increase in firing rate does not lead to any changes in the amount of force produced. The force generated by the last-recruited motor unit (motor unit #120 in the FDI and #600 in the VL) does not fully fuse even at maximal input excitation. In contrast, in the AHP scheme, all motor units, including the earliest and latest-recruited ones, fuse around maximal input excitation.

Figure 2. Low and high-threshold motor unit forces for the Onion-Skin and AHP schemes in the FDI.

A and B, bottom panels) Force produced by the first (#1 on the left) and the last (#120 on the right) recruited motor units at increasing input excitation values starting from that at recruitment (Rec Thr). Fully fused force is achieved at maximal input excitation in the AHP scheme (B) for both motor units. It is achieved at low input excitation for motor unit #1, but not for motor unit #120, in the Onion-Skin scheme (A). A and B. top panels) The firing rate trajectories of motor units #1 and #120 are highlighted in the firing rate spectra of the Onion-Skin (A) and AHP (B) schemes. The input excitation range from recruitment to full force fusion, if achieved, is highlighted.

Figure 3. Low and high-threshold motor unit forces for the Onion-Skin and AHP schemes in the VL.

A and B, bottom panels) Force produced by the first (#1 on the left) and the last (#600 on the right) recruited motor unit at increasing input excitation values starting from that at recruitment (Rec Thr). Fully fused force is achieved at maximal input excitation in the AHP scheme (B) for both motor units. It is achieved at low input excitation for motor unit #1, but not for motor unit #600, in the Onion-Skin scheme (A). A and B, top panels) The firing rate trajectories of motor units #1 and #600 are highlighted in the firing rate spectra of the Onion-Skin (A) and AHP (B) schemes. The input excitation range from recruitment to full force fusion, if achieved, is highlighted.

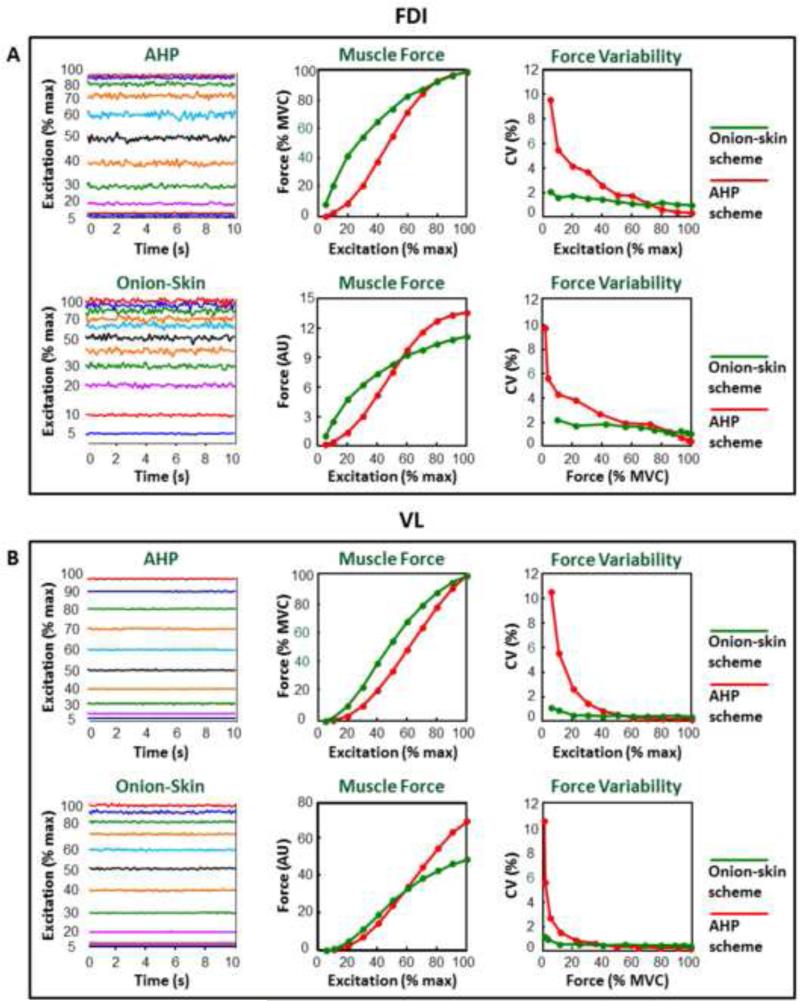
The force generating capacity of the two schemes is compared in Table I and in Figures 4A and 4B for the FDI and VL, respectively. Figure 4 shows: a 10-s interval of muscle force generated at increasing input excitation levels (left panels); the average value of the simulated force as a function of input excitation (middle panels); the coefficient of variation (CV) of the force as a function of increasing input excitation (top) and force (bottom) (right panels).

Table I. Muscle force for the Onion-Skin and AHP schemes at increasing input excitation.

Number of active motor units, average muscle force and CV of the muscle force generated with the AHP (left) and with the Onion-Skin (right) schemes for increasing levels of input excitation to the motoneuron pools of the FDI (top) and VL (bottom) muscles.

			AHP		Onion-Skin
Muscle	Input Excitation Level (%)	# Active Motor Units	Muscle Force (% MVC)	Muscle Force CV (%)	Muscle Force (% MVC)	Muscle Force CV (%)
FDI	5	43	0.92	9.62	8.99	2.11
	10	70	2.88	5.56	21.8	1.61
	20	98	9.68	4.2	41.88	1.78
	30	110	21.53	3.71	55.01	1.54
	40	115	37.67	2.63	65.37	1.52
	50	118	55.17	1.83	74.25	1.31
	60	119	71.44	1.78	82.4	1.14
	70	120	84.67	1.14	87.08	0.98
	80	120	92.96	0.63	92.58	1.2
	90	120	97.35	0.45	96.5	1.06
	100	120	99.12	0.39	99.33	1.01
VL	5	28	0.11	10.6	0.46	1.2
	10	71	0.62	5.61	2.18	0.96
	20	181	3.77	2.72	10.31	0.6
	30	293	10.6	1.54	23.53	0.58
	40	389	21.06	0.92	39.28	0.48
	50	462	34.17	0.63	54.65	0.56
	60	515	48.78	0.39	67.93	0.48
	70	552	63.66	0.33	78.79	0.5
	80	577	77.72	0.29	87.5	0.51
	90	594	90.13	0.28	94.3	0.54
	100	600	98.76	0.26	98.9	0.44

Figure 4. Properties of the muscle force for the Onion-Skin and AHP schemes.

Left panels) A 10-s interval of the muscle force produced by the AHP (top) and Onion-Skin (bottom) schemes at increasing levels of input excitation (5, 10 to 100% in steps of 10% input excitation). Middle panels) Average normalized muscle force (in % MVC, top) and absolute muscle force (in arbitrary unit (AU), bottom) generated by the Onion-Skin (green) and AHP (red) schemes at increasing levels of input excitation. Right panels) Coefficient of variation (CV) of the muscle force produced by the Onion-Skin (green) and AHP (red) schemes at increasing levels of input excitation (top) and muscle force (bottom).

Results from the FDI and VL muscles are presented in panels A and B, respectively.

Note that the Onion-Skin scheme produces more absolute force than the AHP scheme in the range of 0-60% MVC. When approaching maximal input excitation, the AHP scheme is capable of producing greater absolute forces (~20% more in the FDI and ~30% more in the VL) than the Onion-Skin scheme since the forces of all active motor units are fully fused. In contrast, in the Onion-Skin scheme, the later-recruited motor units always maintain a relatively low firing rate that does not provide twitch fusion (see motor unit #120 in Figure 2A for the FDI and motor unit #600 in Figure 2B for the VL).

The Onion-Skin scheme also produces a smoother force throughout most of the force and input excitation range (see Table I). The AHP scheme produces force with greater variability at low force levels approaching the values obtained with the Onion-Skin scheme at about 70% and 50% input excitation in the FDI and VL, respectively (see Table I and Figure 4).

These observations are consistent with previous results of simulation studies (see for instance Hu et al. 2014a).

Another aspect of the two schemes relates to maximal force capacity (Figure 5A, left panels for the FDI and right panels for the VL). In the AHP scheme, motor unit forces are fully fused at 100% input excitation. Hence, muscle force output cannot increase, even if motor unit firing rates are artificially doubled from their value at maximal input excitation. In a similar condition, in the Onion-Skin scheme the whole muscle force output increases from the value at MVC by approximately 20% for the FDI and 30% for the VL.

Figure 5. Maximal force generation capacity and endurance time for the Onion-Skin and AHP schemes.

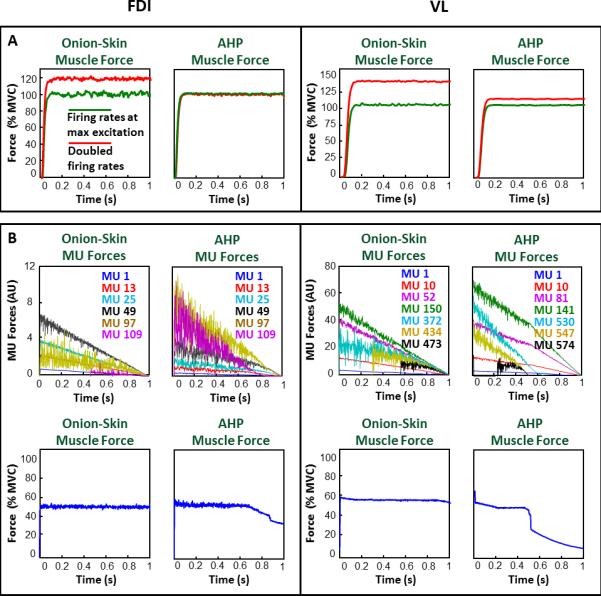
A) Output muscle force for the Onion-Skin and AHP schemes when motor unit firing rates are doubled (red) from their value at maximal input excitation (green) in the FDI (left) and VL (right) muscles. B) Time-dependent motor unit (MU) force (top) and muscle force (bottom) force for the Onion-Skin and AHP schemes in the FDI (left) and VL (right) muscles. Six and seven motor units are shown for clarity in the FDI and VL, respectively. The amplitude of the motor unit force twitches decrease as a function of time, firing rate and recruitment threshold determining different time-varying patterns in the individual MU forces.

We also compared the endurance time provided by the two firing rate schemes during a contraction sustained at 50% MVC. During sustained contractions, the force twitches of the active motor units decrease over time as the muscle fibers fatigue. For similar activation patterns, force generally declines faster for the faster-fatiguing higher-threshold motor units, which are glycolytic in nature, than for the fatigue-resistant lower-threshold ones (Burke, 1981). In our simulation, this characteristic was replicated by modeling the time-dependent decrease in the amplitude of the motor unit force twitches as a function of the motor unit firing rate and recruitment threshold (Small and Stokes, 1992). Note that the same decrease is modeled for both firing rate schemes. The resultant time-varying force output of the individual motor units (Figure 5B, top panels) and of the whole muscle (Figure 5B, bottom panels) during the sustained contraction show the expected force decline. During the sustained contraction, the force feedback of the model maintained the output force at the desired 50% MVC target level. This was achieved by progressively increasing the input excitation to the motoneuron pool, thus recruiting additional motor units and increasing their firing rates, to counterbalance the fatigue-dependent decrease in the amplitude of the motor unit force twitches (Contessa and De Luca, 2013). The muscle endurance limit was reached when the input excitation reached maximal level and the force could no longer be maintained at the desired target. At this point, the feedback allowed a progressively greater mismatch between the target and the muscle force, as evident in Figure 5B for both muscles for the AHP scheme, where the endurance limit is reached earlier than for the Onion-Skin scheme. The forces of the individual motor units, and consequently the force of the whole muscle, decline faster for the higher-threshold faster-firing motor units in the AHP scheme than in the Onion-Skin scheme (see Figure 5B) due to their faster firing rate, and thus faster rate of fatigue. In contrast, in the Onion-Skin scheme, the higher-threshold faster-fatiguing motor units fire slower and fatigue at a slower rate than in the AHP scheme. This arrangement reduces the fatigability of the individual motor units and consequently of the whole muscle.

DISCUSSION

Our analysis revealed a clear distinction between the force generating capacities of the two schemes. The Onion-Skin scheme presented clear evolutionary benefits.

The low-threshold motor units produce more force at lower input excitation levels in the Onion-Skin scheme than in the AHP scheme. Consequently, a fewer number of motor units, with lower recruitment threshold and fatigue-resistant characteristics, are needed in the Onion-Skin scheme to produce a given force at low levels. For example, to produce a 10% MVC force in the FDI muscle, 46 motor units are needed in the Onion-Skin scheme compared to 99 motor units needed in the AHP scheme. Even though motor units fire faster in the Onion-Skin scheme, the fibers comprising these lower-threshold motor units are, in most part, oxidative and can be fueled relatively easily by their abundant blood supply (Burke, 1981). Thus, a fewer number of lower-threshold motor units is able to sustain force production for relatively longer periods of time. Also, the majority of the higher-threshold higher-force producing motor units is not yet active at this low force level and remains available to contribute to higher-force levels. In contrast, in the AHP scheme, a greater number of progressively higher-threshold and more fatigable motor units are already active to sustain even low forces. Thus, the Onion-Skin arrangement provides an economy of force generation at low force levels that is beneficial in activities of daily living. The higher firing rates of the lower-threshold motor units in the Onion-Skin scheme also produce a smoother tetanized force at low to average force levels, the kind used for normal daily activities for precise maneuvering of articulation and for expressive movements.

Additionally, our results show that under voluntary control the Onion-Skin scheme maintains the potential for a “reserve capacity” of force that is not normally accessible, but might be available in extraordinary circumstances (De Luca and Erim, 1994; Contessa and De Luca, 2013). The forces produced by later-recruited motor units never fully fuse, not even at maximal input excitation. These later-recruited not fused motor units are characterized by high amplitude force twitches, and would be capable of providing additional force output if their firing rates were increased. In contrast, in the AHP scheme, the forces produced by all motor units are fully fused at maximal input excitation and no further force increase is possible. The AHP scheme does not allow any muscle reserve capacity, unless it is hypothesized that there exist a “reserved” group of motor units that would remain inactive waiting for the rare circumstance when they might be needed during supra-maximal levels of force production. However, the existence of such mechanism is unlikely, as these normally inactive fibers would atrophy from lack of use, as all muscle fibers do when not activated for prolonged periods of time.

In addition, we have shown that the Onion-Skin scheme produces more force than the AHP scheme in the range of 0-60% MVC, which is the region where the great majority of our functional and expressive tasks are performed. In contrast, the AHP scheme produces more force than the Onion-Skin scheme when approaching maximal force levels, which are rarely used for any functional tasks.

Finally, even if the AHP scheme has the capacity of producing a greater amount of force at high input excitation levels, this force would not be sustainable for a long period of time. The additional force provided by the AHP scheme derives from the faster-firing higher-threshold motor units, which are glycolytic in nature and would quickly exhaust the fuel contained in the muscle cells (Burke, 1981). They would begin to fatigue, decrease the amplitude of their force twitches, and consequently reduce force production (De Luca and Contessa, 2012). This fatiguing effect is less impactful for the slower-firing higher-threshold motor units in the Onion-Skin scheme.

CONCLUSION

In summary, the Onion-Skin scheme is not designed to maximize muscle force, as the AHP scheme has been inferred to do by Kernell (2003). Instead the Onion-Skin scheme provides means to generate force more quickly and more smoothly when force is initiated, and it provides a lower maximal force with the capacity to sustain it over longer time. Also, the higher-threshold motor units maintain a reserve capacity that could be accessible in extreme situations by increasing their firing rates. These features support the flight-or-fight reflexive response in the presence of danger. By balancing a combination of force and duration, the Onion-Skin scheme is mechanically more advantageous and more conducive to evolutionary survival.