Biomechanical Interpretation of a Free-Breathing Lung Motion Model

Abstract

Purpose

To develop a biomechanical model for free-breathing motion and compare it to a published heuristic 5-dimensional free-breathing lung motion model

Method and Material

An ab-initio biomechanical model was developed to describe the motion of lung tissue during free breathing by analyzing the stress-strain relationship inside lung tissue. The first order approximation of the biomechanical model was equivalent to a heuristic 5-dimensional free-breathing lung motion model proposed by Low, et al. in 2005, in which the motion was broken down to a linear expansion component and a hysteresis component. To test the biomechanical model, parameters that characterize expansion, hysteresis and angles between the two motion components were reported independently from and compared between two models.

Results

The biomechanical model agreed well with the heuristic model within 5.5% in the left lungs and 1.5% in the right lungs for patients without lung cancer. The biomechanical model predicted that a histogram of angles between the two motion components should have two peaks at 39.8° and 140.2° in the left lungs and 37.1° and 142.9° in the right lungs. The data from the 5D model verified the existence of those peaks at 41.2° and 148.2° in the left lungs and 40.1° and 140° in the right lungs for patients without lung cancer. Similar results were also observed for the patients with lung cancer, but with greater discrepancies. The maximum likelihood estimation of hysteresis magnitude was reported to be 2.6mm for the lung cancer patients.

Conclusion

The first order approximation of the biomechanical model fit the heuristic 5D model very well. The biomechanical model provided new insights into breathing motion with specific focus on motion trajectory hysteresis.

1. Introduction

Breathing motion affects radiation treatment of lung tumors by averaging and shifting dose distribution over the path of the motion. To compensate for these effects, extra margins are added at the cost of increase lung complications and limiting maximum tumor dose. One possible means of accommodating breathing motion is to reposition the radiation beam following tumor position predicted by a breathing model based on surrogate breathing signals. Currently, breathing motion is mostly modeled as a function of breathing phases on the assumption of regular breathing. This model breaks down for patients, especially those with lung diseases, who breathe irregularly both in magnitude and frequency. A model that accommodates the nonstationary correlation among breathing motion, breathing volume and frequency would be more robust and accurate. A heuristic 5-dimentional free-breathing (respiratory volume, airflow rate and the three coordinates of tissue position at zero respiratory volume and zero airflow rate) lung motion model was previously proposed by Low, et al (Low et al., 2005). The 5D model predicted lung tissue trajectories as functions of respiratory volume and airflow rate,

$$\overrightarrow{X}={\overrightarrow{X}}_0+\overrightarrow{\alpha }V+\overrightarrow{\beta }f$$ (1)

where X⃗ was the tissue trajectory that varied with respiratory volume V and airflow rate f, and X⃗₀ was the tissue reference position defined at zero respiratory volume and zero airflow rate. Respiratory volume in this study was defined as the normal volume of air displaced between respiration at any breathing phase and end of expiration when no extra breathing effort was applied. α⃗ characterized a linear motion due to air filling (motion as a function of respiratory volume) and β⃗ characterized motion hysteresis. Although the accuracy and application of the 5D lung motion model were discussed by Low et al (Low et al., 2010), the physical meaning behind the 5D lung motion model parameters was not described. The goal of this manuscript is to derive the free breathing lung motion model by examining biomechanical lung tissue properties and determine if the biomechanical properties could predict aspects of the motion parameters in the 5D free-breathing model. The stresses on the lung tissue were analyzed to establish the relationship between the driving forces and the resulting deformation. The biomechanical model was compared against the published 5D free-breathing model (Low et al., 2005, Zhao et al., 2009). To distinguish the model developed in this study from the original 5D free-breathing model, the current model was termed the biomechanical model and the original termed the 5D model.

2. Methods

2.1 Theory

2.1.1 Stress Distribution in the Lung

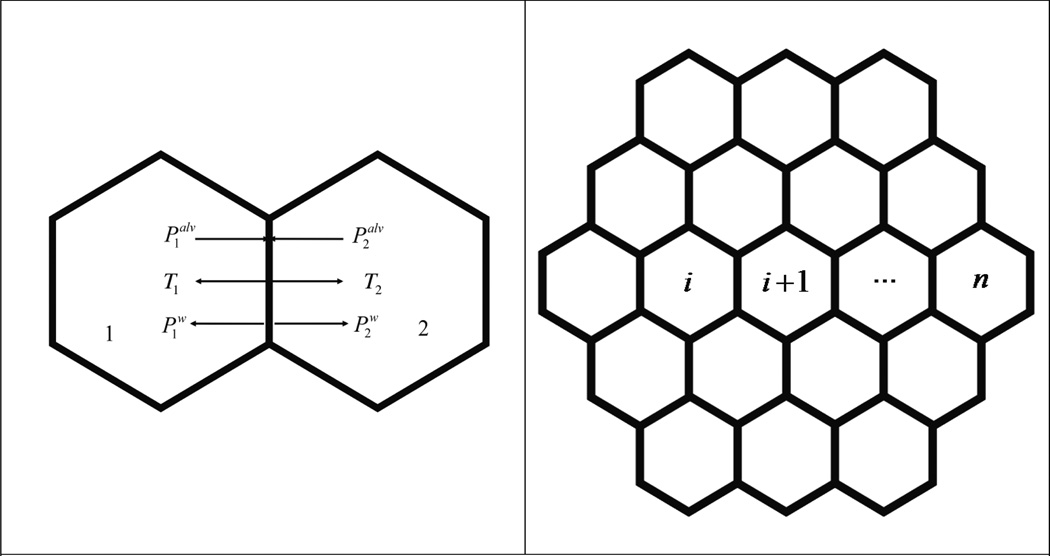
Alveoli have an irregular polyhedral configuration. A close observation of fluorescently labeled lung parenchyma showed a roughly hexagonal arrangement of alveoli (Brewer et al., 2003). In this study, we approximated this structure by employing a simple hexagonal network to model the alveoli arrangement. The projection of this arrangement is illustrated in Fig. 1 (a); the hexagonal-shaped alveolus was subjected to distending stresses that inflate the alveolus on the surfaces, each operating at an angle of 90° with respect to the shared alveolar wall. The distending stresses came from the pressure drop whose direction was determined by the gradient of the pressure across the alveolar cell, which ultimately arose from the pressure drop between the alveolar cell and the pleural wall as will be demonstrated below. The direction of distending stress was normal to the surface upon which it acted.

Fig. 1.

(a) Stresses normal to the wall shared by two adjacent alveoli. P^alv is the alveolar pressure and P^w comes from the surface tension of the liquid membrane that defines the boundary of alveolus. T is the recoil stress from the resistance of the alveolar wall against the deflation or inflation of the alveolus inside.

(b): Arrangement of alveoli on a 2D plane.

A slow breath was broken down into a series of stages where stresses on any alveolar wall were infinitely close to equilibrium,

$$P_1^{\mathit{\text{alv}}}+P_2^w+T_2=P_2^{\mathit{\text{alv}}}+P_1^w+T_1$$ (2)

where $P_1^{\mathit{\text{alv}}}$ and $P_2^{\mathit{\text{alv}}}$ were the alveolar pressures in alveoli 1 and 2 respectively. $P_1^w$ and $P_2^w$ were the radial stresses arising from the surface tension on the alveolar membrane, with subscripts 1 and 2 indicating the source of the surface tension. T₁ and T₂ were resistance from the alveolar wall against inflation and deflation. The source of the recoil stresses was indicated by the subscript. The pressure balance described in equation 2 was achieved only when the airflow rate was infinitesimally slow. As the airflow rate changed during respiration, the pressure drop between the atmosphere and inside of alveoli changed non-uniformly. This slight fluctuation in the alveolar pressure distribution was non-trivial, especially when considering hysteresis, which was hypothesized to be caused by the imbalance of pressure along the moving path.

One question addressed in this study was how the stress that distends the alveolus was related to the pleural pressure. Applying Eq. (2) to a sac of alveoli i as illustrated in Fig. (1b), a series of equations

$$P_i^{\mathit{\text{alv}}}+P_{i+1}^w+T_{i+1}=P_{i+1}^{\mathit{\text{alv}}}+P_i^w+T_i$$

were defined for a chain of alveoli indexed from i to n toward pleural interface on which stresses were specifically given by

$$P_n^{\mathit{\text{alv}}}=P_{pl}+P_n^w+T_n$$

P_pl was the intrapleural pressure.

Fig. 3.

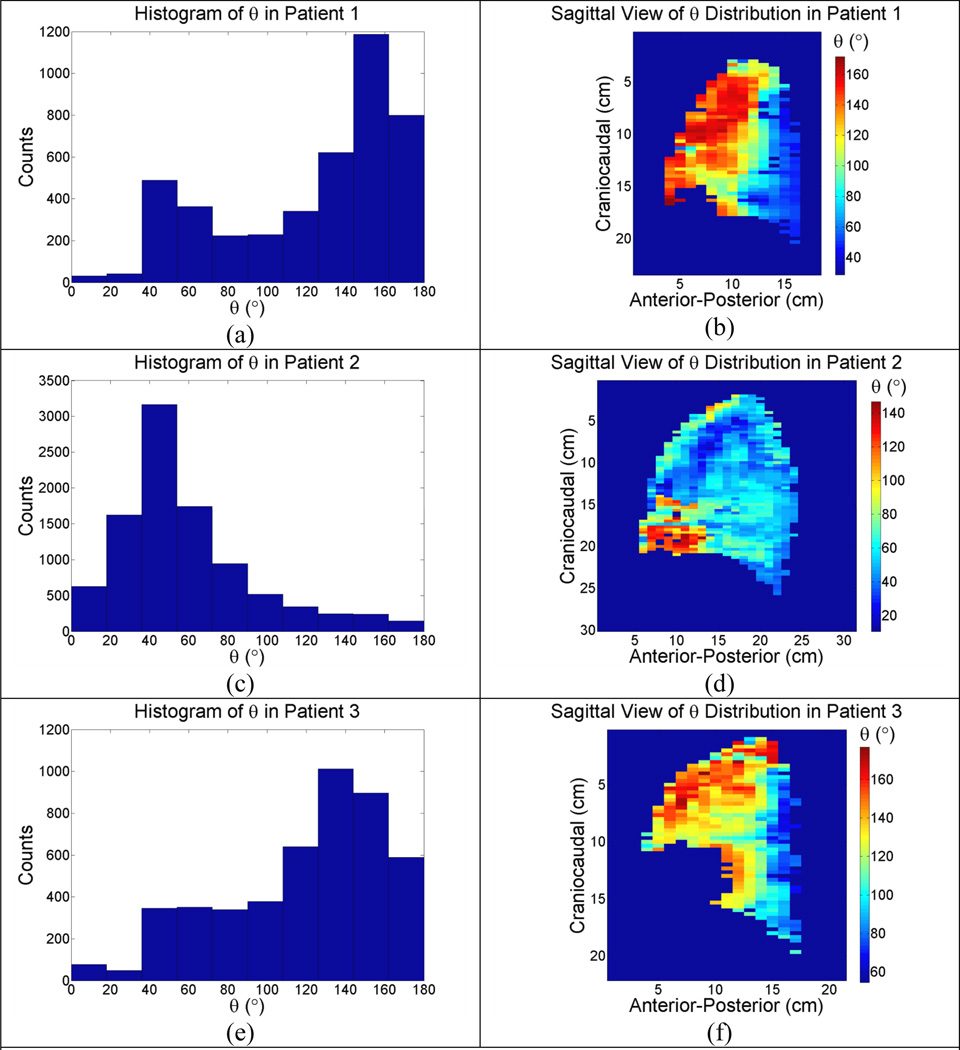
(a)–(f): Sagittal view of unbiased θ distribution in the left lungs of 3 patients.

Summing the equations above resulted in

$$P_i^{\mathit{\text{alv}}}-P_{pl}=P_i^w+T_i$$ (3)

Eq. (3) stated that if a transient balance of stresses was achieved, any alveolus, wherever it was, was exposed to the pleural pressure. The transpulmonary pressure $P_i^{\mathit{\text{alv}}}-P_{pl}$ provided the stress that expanded the alveolar cell. $P_i^w$ and T_i together provided the recoil stress from the i^th alveolar unit. Many publications have described the measurement of recoil stress (Rodarte et al., 1999). The recoil stress was passive and served as the response of lung structure to the transpulmonary pressure that inflated the lung. We hypothesized that under the condition of quiet respiration, the alveolar wall responded fast enough to balance the change of alveolar pressure. The recoil stress was virtually equivalent to the transpulmonary pressure in magnitude under the condition of quiet respiration.

2.1.2 Strain

In this study, we defined a unit tissue as a piece of lung tissue with unit dimensions. The concept of unit tissue was introduced more qualitatively than quantitatively. The unit tissue was small enough to be virtually homogeneous inside, while still containing enough alveoli that its response to stimuli from respiratory muscles was statistically stable. The volume presented by one image voxel acquired from a contemporary CT scanner ranged typically from 1mm³ to 3mm³, and the number of alveoli inside was estimated to be between 125 and 375. Therefore, one voxel in a CT image was regarded statistically as a unit tissue with stable response to stimulus.

A stress vector on any face of the unit tissue could be resolved into two components, a normal stress that followed the expansion of the unit tissue during inspiration and a shear stress that was perpendicular to the normal stress. The latter was a function of air flow since it did not contribute to the change of volume. The stress vector was written

$${\overrightarrow{S}}_n={\overrightarrow{\sigma }}_n(V,f)+\overrightarrow{\tau }(f)$$ (4)

where σ⃗_n(V, f) denoted the normal stress whose magnitude equaled the transpulmonary pressure and τ⃗(f) denoted the shear stress (see appendix for more details).

We hypothesized that breathing motion explicitly depended on the respiratory volume V and airflow rate f. Suppose the strain of the unit tissue was x in the n⃗ direction. As the respiratory volume changed from V to V + δV and the airflow rate changed from f to f + δf, the strain followed from x to x + δx by

$$\delta {\overrightarrow{x}}_n=\frac{{\overrightarrow{\sigma }}_n(V+\delta V,f+\delta f,{\overrightarrow{x}}_0)-{\overrightarrow{\sigma }}_n(V,f,{\overrightarrow{x}}_0)}{E({\overrightarrow{x}}_0)}+\frac{{\overrightarrow{\tau }}_n(f+\delta f,{\overrightarrow{x}}_0)-{\overrightarrow{\tau }}_n(f,{\overrightarrow{x}}_0)}{G({\overrightarrow{x}}_0)}$$ (5)

where x⃗₀ was the location of the tissue at zero respiratory volume and airflow rate. E(x⃗₀) was tissue Young’s modulus and G(x⃗₀) was the shear modulus. δ indicated an infinitesimal variation from the original value. Time was implicit and the change of the strain didn’t necessarily follow the time.

Since it was reasonable to assume that σ⃗_n(V, f, x⃗₀) was differentiable with respect to V and f, the Taylor expansion of σ⃗_n (V + δV, f + δf, x⃗₀) at V = V₀ and f = f₀ was

$${\overrightarrow{\sigma }}_n(V+\delta V,f+\delta f,{\overrightarrow{x}}_0)=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }\frac{{(V+\delta V-V_0)}^i{(f+\delta f-f_0)}^j}{i!j!}\left(\frac{{\partial }^{i+j}{\overrightarrow{\sigma }}_n(V,f,{\overrightarrow{x}}_0)}{\partial V^i\partial f^j}{|}_{\begin{array}{c}V=V_0\hfill \\ f=f_0\hfill \end{array}}\right)$$ (6)

Similarly, the Taylor expansion of τ⃗_n (f + δf, x⃗₀) at f = f₀ was

$${\overrightarrow{\tau }}_n(f+\delta f,{\overrightarrow{x}}_0)=\sum _{j=0}^{\infty }\frac{{(f+\delta f-f_0)}^j}{j!}\left(\frac{{\partial }^j{\overrightarrow{\tau }}_n(f,{\overrightarrow{x}}_0)}{\partial f^j}{|}_{f=f_0}\right)$$ (7)

V₀ and f₀ were selected to minimize the approximation error. The correlation between recoil pressure, lung volume and air flow rate had been previously studied by Stubbs and Hyatt. (Stubbs and Hyatt, 1972). Their results suggested that a linear relationship existed between recoil pressure, lung volume and airflow rate, especially during quiet respiration. Strictly speaking, the response of lung tissue to the respiratory stimulus was nonlinear. However, nonlinear functions like σ⃗_n (V, f, x⃗₀) and τ⃗_n (f, x⃗₀) could be always divided into linear and nonlinear components. We hypothesized that the linear component dominated the breathing motion. Therefore, the first order approximation was applied in Eq. (6) and Eq. (7). Then Eq. (5) was reduced to

$$\delta {\overrightarrow{x}}_n=\frac{1}{E({\overrightarrow{x}}_0)}(\delta V{\frac{\partial {\overrightarrow{\sigma }}_n(V,f_0,{\overrightarrow{x}}_0)}{\partial V}|}_{V=V_0}+\delta f{\frac{\partial {\overrightarrow{\sigma }}_n(V_0,f,{\overrightarrow{x}}_0)}{\partial f}|}_{f=f_0})+\frac{1}{G({\overrightarrow{x}}_0)}\left(\delta f{\frac{\partial {\overrightarrow{\tau }}_n(f,{\overrightarrow{x}}_0)}{\partial f}|}_{f=f_0}\right)$$ (8)

When respiratory volume changes from zero to V and air flow from zero to f, the strain was accumulated to

$$\mathrm{\Delta }{\overrightarrow{x}}_n=\int \delta {\overrightarrow{x}}_n={\int }_0^V\frac{1}{E({\overrightarrow{x}}_0)}\frac{\partial {\overrightarrow{\sigma }}_n(V,f_0,{\overrightarrow{x}}_0)}{\partial V}{|}_{V=V_0}dV+{\int }_0^f\frac{1}{E({\overrightarrow{x}}_0)}\frac{\partial {\overrightarrow{\sigma }}_n(V_0,f,{\overrightarrow{x}}_0)}{\partial f}{|}_{f=f_0}df+{\int }_0^f\frac{1}{G({\overrightarrow{x}}_0)}\frac{\partial {\overrightarrow{\tau }}_n(f,{\overrightarrow{x}}_0)}{\partial f}{|}_{f=f_0}df$$ (9)

where Δx⃗_n was the strain vector of the unit tissue. The total displacement ΔX⃗_n of the unit tissue was accumulated by all pieces of tissue moving behind it,

$$\mathrm{\Delta }{\overrightarrow{X}}_n={\int }_0^{{\overrightarrow{x}}_0}{\int }_0^V\frac{1}{E(\overrightarrow{x})}\frac{\partial {\overrightarrow{\sigma }}_n(V,f_0,\overrightarrow{x})}{\partial V}{|}_{V=V_0}dVd\overrightarrow{x}+{\int }_0^{{\overrightarrow{x}}_0}{\int }_0^f\frac{1}{E(\overrightarrow{x})}\frac{\partial {\overrightarrow{\sigma }}_n(V_0,f,\overrightarrow{x})}{\partial f}{|}_{f=f_0}dfd\overrightarrow{x}+{\int }_0^{{\overrightarrow{x}}_0}{\int }_0^f\frac{1}{G(\overrightarrow{x})}\frac{\partial {\overrightarrow{\tau }}_n(f,\overrightarrow{x})}{\partial f}{|}_{f=f_0}dfd\overrightarrow{x}$$ (10)

where 0 denoted the lung apex which remained stationary during respiration. x⃗ marked the tissues involved in the integrals by specifying their positions at reference respiratory volume and airflow rate.

To further simplify Eq. (10), three variables were introduced

$$\overrightarrow{\alpha }{({\overrightarrow{x}}_0)\equiv {\int }_0^{{\overrightarrow{x}}_0}\frac{1}{E(\overrightarrow{x})}\frac{\partial {\overrightarrow{\sigma }}_n(V,f_0,{\overrightarrow{x}}_0)}{\partial V}|}_{V=V_0}d\overrightarrow{x}$$ (11)

$${\overrightarrow{\beta }}_1{({\overrightarrow{x}}_0)\equiv {\int }_0^{{\overrightarrow{x}}_0}\frac{1}{E(\overrightarrow{x})}\frac{\partial {\overrightarrow{\sigma }}_n(V_0,f,\overrightarrow{x})}{\partial f}|}_{f=f_0}d\overrightarrow{x}$$ (12)

$${\overrightarrow{\beta }}_2{({\overrightarrow{x}}_0)\equiv {\int }_0^{{\overrightarrow{x}}_0}\frac{1}{G(\overrightarrow{x})}\frac{\partial {\overrightarrow{\tau }}_n(f,\overrightarrow{x})}{\partial f}|}_{f=f_0}d\overrightarrow{x}$$ (13)

Since α⃗, β⃗₁ and β⃗₂ were inherent properties of the concerned tissue, which was labelled according to its position x⃗₀ at zero respiratory volume and zero airflow rate, the total displacement vector ΔX⃗_n was reduced to

$$\mathrm{\Delta }{\overrightarrow{X}}_n=\underset{0}{\overset{V}{\int }}\overrightarrow{\alpha }({\overrightarrow{x}}_0)dV+{\int }_0^f{\overrightarrow{\beta }}_1({\overrightarrow{x}}_0)df+{\int }_0^f{\overrightarrow{\beta }}_2({\overrightarrow{x}}_0)df=\overrightarrow{\alpha }({\overrightarrow{x}}_0)V+\overrightarrow{\beta }({\overrightarrow{x}}_0)f$$ (14)

where x⃗₀ was the position of the tissue at zero respiratory volume and zero airflow rate, and β⃗ = β⃗₁ + β⃗₂. This terminology was consistent with the original 5D breathing motion model (Low et al., 2005)

Physiologically, α⃗(x⃗₀) characterized the displacement of lung tissues due to air filling, and β⃗(x⃑₀) characterized the hysteresis motion that was described by Seppenwolde et al. (Seppenwoolde et al., 2002). While α⃗ was determined by the overall integral of the respiratory volume derivative of the normal stress, β⃗ was composed of two independent components, β⃗₁ and β⃗₂. The former was parallel or anti-parallel with α⃗ and the latter was perpendicular to α⃗.

2.1.3 Angle Between α⃗ and β⃗

An evaluation of the terms α⃗ and β⃗ from Eq. (11), Eq. (12), and Eq. (13) was illustrated in Fig.(2). α⃗ was the integral of the respiratory volume derivative of normal stress over the lung space at constant airflow rate, and similarly, β⃗, the combination of β⃗₁ and β⃗₂, was the integral of the airflow rate derivative of stress over the lung space at constant respiratory volume. The α⃗ motion component was contributed to entirely by the change of respiratory volume, or equivalently, the change of lung volume. The β⃗ component, which came from changes of airflow rate during breathing, characterized the hysteresis component of the motion and contributed nothing to the volume change. The β⃗₁ component, which was parallel to α⃗, aligned with the displacement vector that was driven by the normal pressure gradient purely from volume change. Therefore it contributed to a displacement that further inflated or deflated the lung and subsequently changed the volume of any individual piece of tissue on which it worked. However, the changes of volume added up to zero over the whole lung space because, according to the definition, β⃗₁ was the airflow rate derivative of normal stress at a fixed respiratory volume. The β⃗₂ component, which was perpendicular to α⃗, served as a rigid-body rotation of the α⃗ component and did not change the volume of the tissue it worked on. A clinical verification that the summation of β⃗ over the lung space equaled zero was published by Low et al (Low et al., 2010).

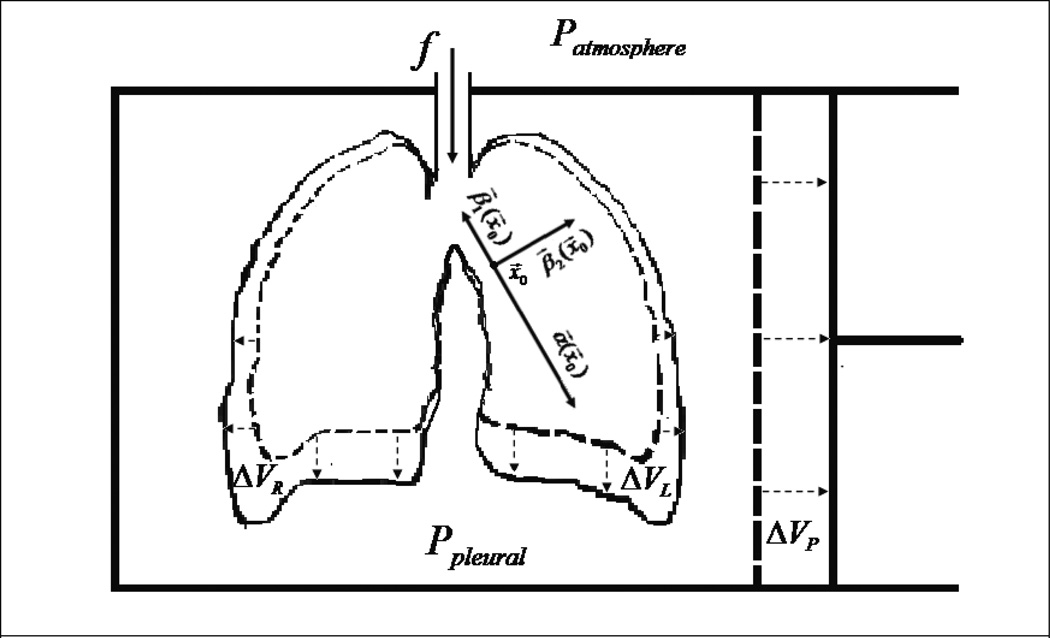
Fig. 2.

Chest wall and respiration muscles are simulated with an airtight container and a piston. V_P is the volume change in thoracic cavity. ΔV_R and ΔV_L are the volume changes in the right lung and the left lung respectively. The displacement of tissue at x⃗₀ is α⃗(x⃗₀)V + β⃗₁(x⃗₀)f + β⃗₂(x⃑₀)f, as described in Eq (14).

In the region where the normal stress decreased as airflow rate increases, the direction of β⃗₁ was anti-parallel to α⃗. In the region where normal stress increased as airflow rate increased, the direction of β⃗₁ was parallel to α⃗. β⃗ lay at a specific angle θ with respect to α⃗ and this angle was predicted and measured as described in section 2.3.

2.2. Model Validation

48 patients were enrolled in an IRB-approved protocol. 28 were lung cancer patients and 20 were non-lung cancer patients. Patients were scanned using a 16-slice CT scanner operating in ciné mode and acquiring scans with a spatial resolution of 0.98 × 0.98 × 1.5 mm³. 25 scans were acquired contiguously at each 24 mm wide couch position. One dataset usually required 8 or 9 couch positions to cover the whole lung. Two external respiratory measurements were simultaneously acquired; the respiratory volume measured using a spirometer (VMM-400, Interface Associates), and a bellows pressure signal measured using a pneumatic belt system that was wrapped around the abdomen. The bellows pressure measurement was correlated with the spirometry measurement to provide the respiratory volume and airflow rate at each scan. (Lu et al., 2005a, Lu et al., 2005b)

2.2.1 Calculations from the heuristic 5D Lung Motion Model

The tissue positions were mapped for each scan using a normalized cross-correlation method (Lewis, 1995). The scan with respiratory volume closest to zero was employed as the reference scan. The remaining scans were sorted according to respiratory volume and categorized into inhalation and exhalation. The position matching was performed in the inhalation and exhalation categories respectively in order of respiratory volume, with zero motion as the initial estimate for the first registration in one category and the result from previous matching as the initial estimate for the remaining registrations in that category.

The registration results, together with the corresponding respiratory volumes and airflow rates were fit to Eq. (1) employing the Nelder-Mead Optimization Algorithm by minimizing the root-mean least-squares average distance between the fitting and measurements for each voxel,

$$\underset{{\overrightarrow{X}}_0,\overrightarrow{\alpha },\overrightarrow{\beta }\in {\Re }^3}{\text{min}}\sum _i\Vert {\overrightarrow{X}}_i-{\overrightarrow{X}}_0-\overrightarrow{\alpha }{\nu }_i-\overrightarrow{\beta }{f}_i\Vert$$ (15)

where X⃗_i was the i^th location of the measurements, and v_i and f_i were the respiratory volume and airflow rate, respectively, for scan i. In this study, 25 scans were obtained for each couch position, so X⃗₀, α⃗ and β⃗ in Eq. (15) were overdetermined to suppress the impact of image motion artifacts and registration errors.

For each dataset, we defined |α⃗|₉₀ and |β⃗|₉₀ as the 90^th percentile of the α⃗ and β⃗ magnitudes, respectively. We selected the 90^th percentile as the indicator to represent the maximum α⃗ and β⃗ magnitudes because it was stable against registration and fitting errors.

2.2.2 Calculations from the biomechanical model

α⃗ and β⃗ characterized the lung tissue response to the change of stresses in the lung parenchyma. Theoretically, they could be predicted through Eq. (11), Eq. (12) and Eq. (13) if the Young’s modulus, shear modulus, respiratory volume, airflow rate derivative of stress, and the distance from the investigated tissue to a fixed reference point were known. Although in-vivo acquisition of patient-specific parameters required in Eq. (11), Eq. (12), and Eq. (13) were infeasible, values in the literature were used here for estimations. The Young’s modulus E was estimated to be 27.65±0.67 cm H₂O for patients with average age of 75 and undergoing quiet breathing (Lai-Fook and Hyatt, 2000). The average respiratory volume derivative of normal stress $\frac{\partial {\sigma }_n}{\partial V}$ was determined to be 3.80 cm H₂O/L by Rodarte et al. (Rodarte et al., 1999). The typical airflow rate derivative of normal stress $\frac{\partial {\sigma }_n}{\partial f}$ was derived to be 0.40 cm H₂O s/L by Stubbs and Hyatt (Stubbs and Hyatt, 1972). Since no published literature data on the shear stress inside of the lung were available, only β⃗₁ could be estimated from published data. The reference point was set at the apex of the lung, which typically exhibited minimal breathing motion. The lung height L₉₀ was defined as the 90^th percentile of distances of all points inside the lung to the reference point. Using these values, |α⃗|₉₀ was predicted using Eq. (11),

$${|\overrightarrow{\alpha }|}_{90}=\frac{L_{90}}{E}\frac{\partial {\sigma }_n}{\partial V}=\frac{3.80}{27.65}{L}_{90}$$ (16)

|β⃗₁|₉₀ was predicted using Eq. (12),

$${\left|{\overrightarrow{\beta }}_1\right|}_{90}=\frac{L_{90}}{E}\frac{\partial {\sigma }_n}{\partial f}=\frac{0.40}{27.65}{L}_{90}$$ (17)

Uncertainties of the model parameters were propagated as

$$\%{|\overrightarrow{\alpha }|}_{90}=\sqrt{{\left(\%\frac{\partial {\sigma }_n}{\partial V}\right)}^2+{(\%E)}^2+{(\%L_{90})}^2}$$ (18)

and

$$\%{\left|{\overrightarrow{\beta }}_1\right|}_{90}=\sqrt{{\left(\%\frac{\partial {\sigma }_n}{\partial f}\right)}^2+{(\%E)}^2+{(\%L_{90})}^2}$$ (19)

where % indicated the percentage uncertainty of the parameter that followed.

2.3 Comparison of α⃗ and β⃗ from 5D model and the biomechanical model

A comparison of the 90^th percentile of |α⃗| from both the 5D model and the biomechanical model was conducted to evaluate how well both models agreed with each other. β⃗ was a vector composed of two orthogonal vectors, β⃗₁ and β⃗₂, and the angle between |β⃗₁| and |β⃗| was given by

$$\text{cos}({\vartheta }_{BM})=\frac{\left|{\overrightarrow{\beta }}_1\right|}{\left|\overrightarrow{\beta }\right|}$$ (20)

The subscript BM indicated the angle was calculated from the biomechanical model. Although β⃗ could be determined by fitting the patient data to the 5D model, it could not be fully determined from the biomechanical model because of the lack of data on shear stress that was necessary to evaluate β⃗₂. Therefore, the angle ϑ_BM was calculated by taking |β⃗₁|₉₀ from the biomechanical model and |β⃗|₉₀ from the 5D model. Assuming that the parameters taken from the literature were averaged over measurements exhibiting a Gaussian distribution, Eq. (12) gave the estimation of |β⃗₁|₉₀ with the maximum likelihood. ϑ_BM from Eq. (20) was consequently the maximum-likelihood angle between α⃗ and β⃗.

An alternative way to calculate the angle between α⃗ and β⃗ was to use only the results from the 5D model. While ϑ_BM indicated the angle between α⃗ and β⃗ that were calculated from the biomechanical model, a new variable ϑ was introduced to indicate the angle between α⃗ and β⃗ that were obtained from the 5D model through

$$\text{cos}(\vartheta )=\frac{\overrightarrow{\alpha }·\overrightarrow{\beta }}{|\overrightarrow{\alpha }|\left|\overrightarrow{\beta }\right|}$$ (21)

Unlike ϑ_BM calculated from published literature data on bulk biomechanical and physiological properties through the biomechanical model, ϑ was obtained from α⃗ and β⃗ throughout the lungs by fitting acquired patient data to the 5D model. Due to the variation of lung properties, ϑ was a distribution instead of a single value. A new parameter ϑ_5D was introduced to indicate the peaks of the ϑ spectrum. ϑ_5D referred to the angle with the maximum likelihood over the spectrum obtained from the 5D model. As demonstrated by the biomechanical model conducted above, β⃗₁ is parallel to α⃗. ϑ_BM, the angle between β⃗ and β⃗₁, is expected to be equal to ϑ_5D that is the angle between α⃗ and β⃗. The comparison of ϑ_BM and ϑ_5D provided another indicator of how well the biomechanical model agreed with the 5D model.

2.4. Zenith angle distribution

Angles between two vectors with randomly assigned components were strongly biased towards 90°. To obtain a meaningful statistic for angles between vectors that reflected the interplay of various biomechanical properties, the angle bias was eliminated by a factor of the sine of the angle.

3. Results

L₉₀ were measured using the CT images. The average value of L₉₀ was 192.3 mm (190.0 mm for lung cancer patients and 195.5 mm for non-lung cancer patients) in the left lung and 191.3 mm (188.3 mm for lung cancer patients and 195.5 for non-lung cancer patients) in the right lung (Table 1).

Table 1.

90th percentile of |α⃗| and |β⃗| in both left and right lungs.

Patient #	Left Lung			Right Lung
	L90(mm)	|α⃗|90 (mm/L)	|β⃗|90 (mm·s/L)	L90(mm)	|α⃗|90 (mm/L)	|β⃗|90 (mm·s/L)
*1	165.2	7.1	2.2	208.0	26.1	3.8
*2	175.0	23.8	2.8	176.2	24.7	2.7
*3	176.3	25.7	2.9	178.2	24.1	2.5
*4	202.8	30.9	2.9	212.6	30.7	3.8
*5	195.5	38.7	5.8	186.1	44.5	5.7
*6	201.1	20.1	3.8	197.3	18.4	5.0
7	183.6	33.1	5.1	172.7	37.3	5.1
*8	185.4	23.2	3.2	178.3	29.5	3.2
9	155.1	19.4	2.5	163.1	18.9	2.0
10	160.6	32.3	6.8	160.7	28.1	7.5
11	174.2	22.1	2.6	162.4	35.8	2.8
*12	214.1	22.5	2.7	216.9	26.8	3.3
13	192.4	34.2	3.6	163.1	31.7	2.8
*14	203.1	21.0	2.2	195.3	29.9	2.4
*15	206.1	26.1	5.5	200.8	34.1	2.6
16	207.5	26.4	3.4	197.5	21.8	2.8
17	207.0	20.5	3.1	203.9	26.2	2.6
18	198.5	17.5	3.2	209.9	26.9	3.2
19	208.7	24.3	4.9	201.3	21.6	4.2
*20	190.4	41.6	5.3	178.6	29.6	5.3
*21	159.0	16.9	5.4	171.8	36.6	5.0
22	253.2	31.6	4.8	265.9	35.2	4.6
*23	179.1	23.0	4.4	180.7	36.6	9.1
*24	177.2	26.0	5.1	170.7	40.9	5.8
25	183.1	25.6	3.9	196.6	30.0	4.3
*26	166.3	39.3	6.1	174.7	55.0	8.4
27	218.8	25.1	2.7	228.6	17.0	1.9
*28	230.9	40.5	3.2	212.7	12.5	1.8
*29	171.3	32.4	3.6	166.0	43.9	3.5
*30	204.0	29.3	4.9	183.9	43.0	6.0
31	173.5	34.3	3.7	161.6	36.0	5.0
32	197.5	17.3	3.6	175.0	17.9	2.8
*33	179.5	45.6	13.4	182.6	39.5	5.9
*34	206.7	14.9	2.7	174.1	14.9	3.7
*35	199.5	16.7	1.6	191.9	30.9	3.9
36	180.5	25.5	3.8	185.1	36.6	3.7
*37	222.3	23.7	2.3	209.8	28.3	2.8
*38	150.1	12.8	3.7	189.7	43.1	4.6
39	242.7	12.6	2.8	245.1	20.6	3.0
*40	209.7	27.0	7.8	200.6	26.5	5.1
*41	192.2	17.3	4.4	193.1	22.2	4.4
*42	183.0	21.8	3.0	161.2	30.5	3.5
*43	172.1	9.1	6.3	171.0	11.0	6.7
44	218.6	21.2	2.6	220.2	29.0	2.5
45	156.4	43.4	5.6	189.7	44.3	5.1
46	166.8	28.1	2.3	170.1	19.6	1.6
47	231.6	15.8	2.6	237.8	11.8	2.7
*48	202.9	38.1	4.9	208.3	19.7	3.8
Mean	192.3	25.5	4.1	191.3	29.2	4.1

Lung cancer patients are indicated with *

Table 2 provided details on model parameters in two subject groups. The average |α⃗|₉₀ in the left lungs as estimated from the biomechanical model was 26.3 mm/L (26.1 mm/L for lung cancer patients and 26.9 mm/L for non-lung cancer patients). The average |α⃗|₉₀ calculated from the 5D model was 25.5 mm/L in the left lungs, with little difference observed between lung cancer patients and non-lung cancer patients. The average discrepancy of |α⃗|₉₀ between the two models was 0.8 mm/L or 3.0% (0.6 mm/L or 2.3% in lung cancer patients and 1.4mm/L or 5.5% in non-lung cancer patients).

Table 2.

	Lung Patients		Non-Lung Patients
	Left	Right	Left	Right
L90 (mm)	190.0±19.7	188.3±15.9	195.5±28.2	195.5±31.2
|α⃗|90 (mm/L)	25.5±10.0*	30.5±10.5*	25.5±7.6*	27.3±8.5*
	26.1+	25.9+	26.9+	26.9+
|β⃗|90 (mm·s/L)	4.4±2.3*	4.4±1.8*	3.7±1.2*	3.5±1.4*
|β⃗1|90 (mm·s/L)	2.7+	2.7+	2.8+	2.8+
θ5D(°)	43.0/150.1*	35.3/129.3*	41.2/148.2*	40.1/140.0*
θBM(°)	51.1/128.9+	52.1/128.9+	39.8/140.2+	37.1/142.9+

Parameters obtained from 5D model (*) and the biomechanical model (⁺) in lung cancer group and non-lung cancer group.

The average |α⃗|₉₀ in the right lungs was 26.2 mm/L from the biomechanical model (25.9 mm/L in lung cancer patients and 26.9 mm/L in non-lung cancer patients). The average |α⃗|₉₀ from the 5D model was 29.2 mm/L (30.5 mm/L in lung cancer patients and 27.3 mm/L in non-lung cancer patients). The average discrepancy of |α⃗|₉₀ between the two models was 3.0 mm/L (4.6 mm/L in lung cancer patients and 0.4 mm/L in non-lung cancer patients), or 11.5% (15% in lung cancer patients and 1.5% in non-lung cancer patients).

The average |β⃗₁|₉₀ from the biomechanical model was 2.8 mm·s/L in the left lungs (2.7 mm·s/L in lung cancer patients and 2.8 mm·s/L in non-lung cancer patients). The average |β⃗|₉₀ from the 5D model was 4.1 mm·s/L (4.4 mm·s/L in lung cancer patients and 3.7 mm·s/L in non-lung cancer patients).

The average |β⃗₁|₉₀ from the biomechanical model was 2.8 mm·s/L in the right lungs (2.7 mm·s/L in the lung cancer patients and 2.8 mm·s/L for in non-lung cancer patients). The average |β⃗|₉₀ measured from the 5D model was 4.1 mm·s/L (4.4 mm·s/L in the lung cancer patients and 3.5 mm·s/L in the non-lung cancer patients) in the left lungs.

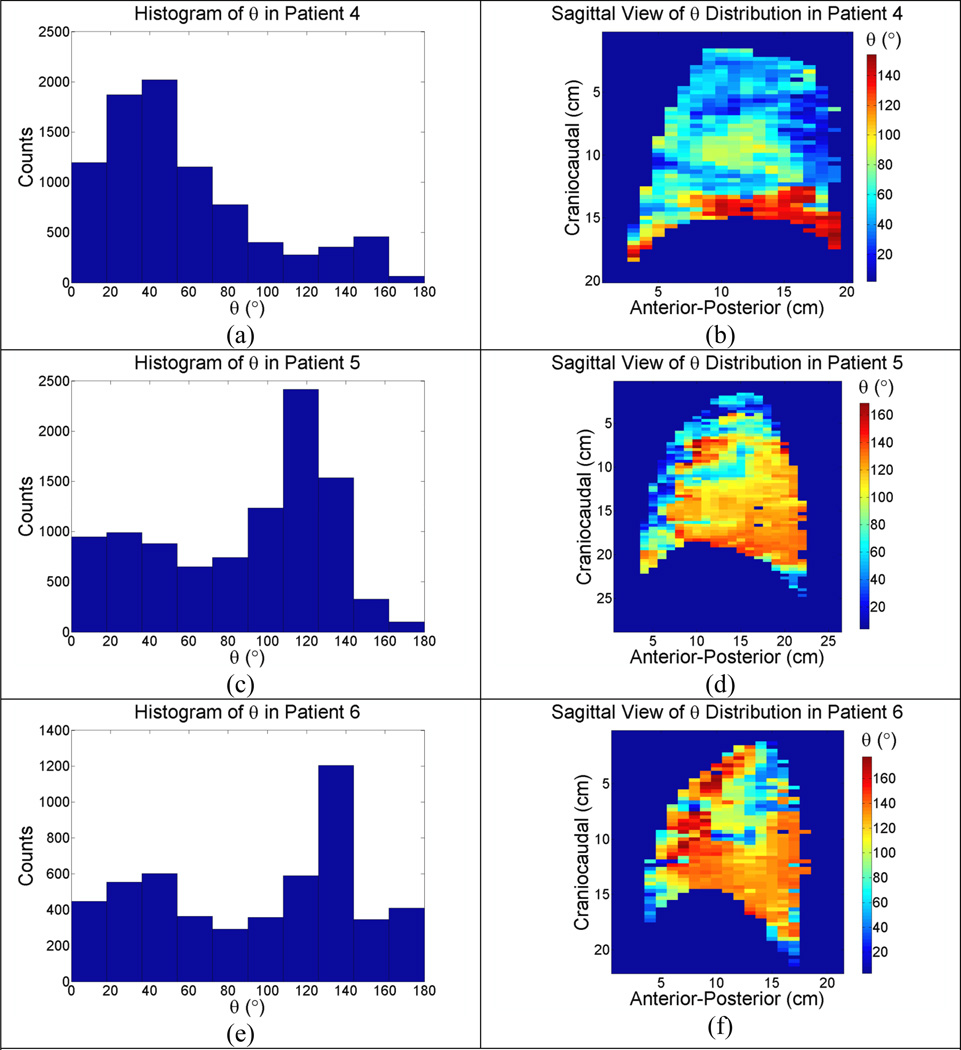
Three typical patterns of the angles between α⃗ and β⃗ for patients, together with the histograms of the angles, were illustrated in Fig. (3) and Fig. (4) for the left and right lungs respectively. Peaks in the histograms were very close to the predictions from the biomechanical model.

Fig. 4.

(a)–(f): Sagittal view of unbiased θ distribution in the right lungs of 3 patients.

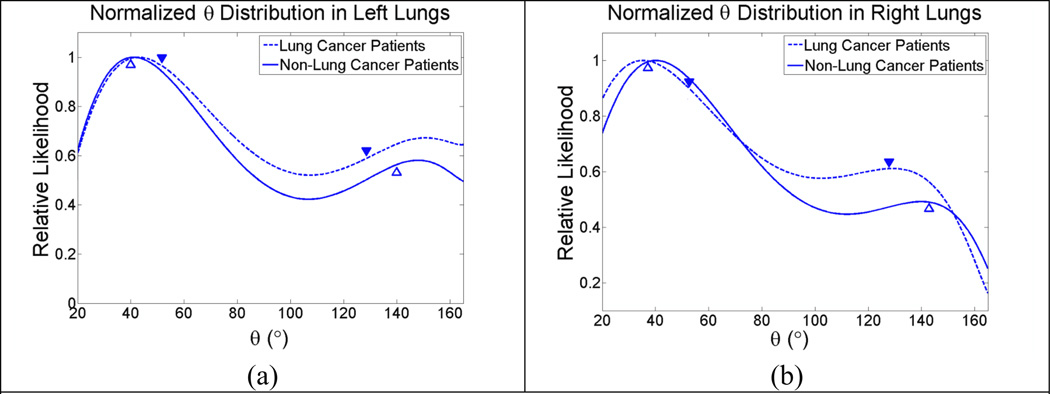
The histograms of ϑ in the left lungs of all patients were illustrated in Fig. (5a) which showed ϑ_5D at 43.0° and 150.1° in the lung cancer patients, and 41.2° and 148.2° in the non-lung cancer patients; the predicted angles ϑ_BM from the biomechanical model were 51.1° and 128.9° in the lung caner patients, and 39.8° 140.2° in the non-lung cancer patients. Fig. (5b) showed similar results in the right lungs, with ϑ_5D at 35.3° and 129.3° in the lung cancer patients, and 40.1° and 140.0° in the non-lung cancer patients; the predicted angles ϑ_BM from the biomechanical model were 52.1° and 128.9° in the lung cancer patients, 37.1° and 142.9° in the non-lung cancer patients.

Fig. 5.

θ from the 5D model in all patients. Predictions from out biomechanical model are indicated with ▼ for lung cancer patients and △ for non-lung cancer patients.(a): Left lungs; (b) Right lungs.

The average maximum respiration volume was 477mL and maximum airflow rate was 468mL/s in the lung cancer group. The maximum likelihood estimation of the distance between trajectories during inhalation and exhalation was 19.4% of the motion magnitude or 2.6mm as determined using average values of |α⃗|₉₀, |β⃗|₉₀ and ϑ_5D Similar results with smaller magnitudes (15.8% and 2.3mm) were measured for the non-lung cancer patients. Because no confidence intervals were available for the published quantities of $\frac{\partial {\sigma }_n}{\partial V}$ and $\frac{\partial {\sigma }_n}{\partial f}$, the minimal percentage uncertainties of |α⃗|₉₀ and |β⃗₁|₉₀ were estimated to be 12.5%, using average %E = 2.4% and %L₉₀ = 12.2% from all patients.

4. Conclusions and Discussion

This study established a link between the heuristic 5D breathing motion model parameters published by Low and lung tissue biomechanical properties such as stress and Young’s modules. Analysis of the published biomechanical properties of lung tissues provided predictions of the 5D model parameters. They were found to be in good agreement with the directly measured parameters, especially for subjects without lung cancer since the parameters that were fed into the biomechanical model are from healthy subjects.

The angle ϑ between α⃗ and β⃗ was an interplay of stress, Young’s modulus and shear modulus. It was a parameter that characterized breathing trajectory elongation. The distance between trajectories during inhalation and exhalation was maximal for tissue with ϑ =90° and minimal with ϑ =0° or 180°. A large portion of the lung exhibited some hysteresis. The estimated hysteresis in the lung cancer group fell within the observed range (Seppenwoolde et al., 2002).

The spectrum of ϑ also provided insight into the stress distribution inside the lung parenchyma. The hysteresis lag in the anterior left lung might be explained by the presence of heart as a geometrical constrain to tissue motion. As the anterior portion of the left lung moved towards the heart, the resistance from the hearts was enhanced by squeezing the lung tissue against the heart. The increased resistance in the anterior portion of the left lung caused the transpulmonary pressure to drop locally, reducing the amount of air moving into the affected region to a level less than without heart as a geometrical constrain. Physiologically, the extra air that would have moved into the squeezed region was now redistributed to regions with less resistance and greater transpulmonary pressure, such as the posterior region. Therefore, in the anterior portion of the left lung, β⃗₁ was most likely to be anti-parallel to the motion of the lung tissue and ϑ_BM was indeed observed to be greater than 90°. As indicated in Fig. (3), the motion of the anterior portion of the left lung was most likely to lag due to the hysteresis component.

Similar phenomena were observed in the inferior and posterior portion of the right lung, but for a different reason. Since the heart impacted breathing motion primarily in the inferior portion of the left lung, the right lung had less geometrical confinement than the left lung does. Instead, gravity played a relatively important role in distributing the air in the right lung. Since the inferior posterior region of the right lung bore more stress from gravity, it had a smaller resting volume at the beginning of inhalation compared to that of the anterior region of the right lung. The elasticity of the lung, which was a monotonically decreasing function of lung volume (Zapletal et al., 1976), had greater elasticity in smaller alveoli than in larger ones. Therefore, the inferior posterior region of the right lung was easier to inflate than the superior and anterior region and consequently received more ventilation. However, the relatively smaller air space and greater ventilation in the inferior posterior region would have escalated the pressure inside of alveolus more than in the superior anterior region as airflow rate increases. The transient greater alveolar pressure would have redistributed the air from region with greater alveolar pressure to region with lower alveolar pressure, and macroscopically from the inferior posterior region to the superior anterior region, to balance the alveolar pressure inside lung parenchyma. Therefore, the motion of the region with better ventilation was subject to a hysteresis lag and ϑ₁ was observed to be greater than 90°, as illustrated in Fig. (4) where a hysteresis lag was present in the inferior posterior region of the right lung. On the other hand, the region with less ventilation would have been boosted by the extra air flow and moved further along the direction than it would have moved at a constant airflow rate.

This study established that the 5D model is the first order approximation of the biomechanical model, which provided not only a physical interpretation of the parameters in the 5D model, but more insights into the breathing motion. One of the applications of the biomechanical model is in vivo measurement of Young’s modulus that characterizes the resistivity of lung parenchyma. Pathological tissues are usually stiffer than normal tissues and the stiffness were observed in patients with lung fibrosis (Levental et al., 2007) and cancer (Paszek et al., 2005, Butcher et al., 2009). According to the biomechanical model, Young’s modulus was linked to the transpulmonary pressure and the divergence of α⃗. By inserting an esophageal balloon to measure transpulmonary pressure while scanning a patient, the patient-specific map of Young’s modulus can be calculated in vivo. If a standard map of Young’s modulus for healthy lungs is established, a patient-specific map of Young’s modulus may aid in the diagnosis of pulmonary diseases. In radiation therapy, specifically, the in vivo acquisition of Young’s modulus will help to monitor radiation-induced damages such as fibrosis, as well as the tumor progression during and after the treatment.

In summary, the hysteresis lag was present in the left lung because the air was redistributed from regions with a greater resistance to regions with lesser resistance. In the right lung, the hysteresis lag was present because the alveolar pressure decreased during airflow rate increase due to the relatively easy and rapid redistribution of air through airways. Both the increase in resistance and the decrease of alveolar pressure lead to a decline in the stress that drove the lung to inflate and deflate.

In this study, a biomechanical model was developed by modeling the lung as an elastic material subjected to driven forces from diaphragm and other breathing muscles. The first order approximation of this biomechanical model led to a lung motion model originally proposed by Low (Low et al., 2005). Two parameters in the biomechanical model, α⃗ and β⃗, were calculated using published literature data on the biomechanical and physiological properties of lung, while the same parameters in the 5D lung motion model were fit using clinical datasets. The two models reached close agreement both on the magnitude of the parameters and on the angle of hysteresis with respect to lung tissue motion.

Appendix

In general, stress is presented by a second-order Cartesian tensor at a point x⃑₀,

$$\overleftrightarrow{S}=\left[\begin{array}{ccc}\hfill s_{11}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill s_{12}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill s_{13}(V,f,{\overrightarrow{x}}_0)\hfill \\ \hfill s_{21}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill s_{22}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill s_{23}(V,f,{\overrightarrow{x}}_0)\hfill \\ \hfill s_{31}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill s_{32}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill s_{33}(V,f,{\overrightarrow{x}}_0)\hfill \end{array}\right],$$ (22)

where s₁₁, s₂₂ and s₃₃ are the stresses normal to the three orthogonal planes. s₁₂ and s₁₃, s₂₁ and s₂₃, s₃₁ and s₃₂ are 3 pairs of shear stresses parallel to the orthogonal planes. We hypothesized that all nine elements in the stress tensor are functions of respiratory volume and air flow.

Introducing

$${\pi }_{ij}=\frac{s_{ij}+s_{ji}}{2}$$ (23)

and

$${\tau }_{ij}=\frac{s_{ij}-s_{ji}}{2}$$ (24)

the stress tensor can be decomposed into a symmetric and anti-symmetric components,

$$\overleftrightarrow{S}={\overleftrightarrow{S}}_{\mathit{\text{symm}}}+{\overleftrightarrow{S}}_{\mathit{\text{anti}}-\mathit{\text{symm}}}=\left[\begin{array}{ccc}\hfill {\pi }_{11}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill {\pi }_{12}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill {\pi }_{13}(V,f,{\overrightarrow{x}}_0)\hfill \\ \hfill {\pi }_{21}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill {\pi }_{22}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill {\pi }_{23}(V,f,{\overrightarrow{x}}_0)\hfill \\ \hfill {\pi }_{31}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill {\pi }_{32}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill {\pi }_{33}(V,f,{\overrightarrow{x}}_0)\hfill \end{array}\right]+\left[\begin{array}{ccc}\hfill 0\hfill & \hfill {\tau }_{12}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill {\tau }_{13}(V,f,{\overrightarrow{x}}_0)\hfill \\ \hfill {\tau }_{21}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill 0\hfill & \hfill {\tau }_{23}(V,f,{\overrightarrow{x}}_0)\hfill \\ \hfill {\tau }_{31}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill {\tau }_{32}(V,f,{\overrightarrow{x}}_0)\hfill & \hfill 0\hfill \end{array}\right]$$ (25)

where S⃡_symm is a symmetric Cauchy stress tensor working on a body that is in equilibrium and satisfies conservation of angular momentum; S⃡_anti-symm is an anti-symmetric Cauchy stress tensor that gives net moments to the body, causing rigid rotation.

A symmetric Cauchy stress tensor can be transformed to a tensor with three orthogonal planes, termed principal planes, on which normal stresses are maintained and shear stresses vanish.

$${\overleftrightarrow{S}}_{\mathit{\text{symm}}}=\left[\begin{array}{ccc}\hfill {\sigma }_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\sigma }_3\hfill \end{array}\right]$$ (26)

where σ₁ ≥ σ₂ ≥ σ₃. Under transient equilibrium of stresses, the magnitude of principal stress is a combination of the pressure across the alveolar wall and the stress from gravity,

$${\sigma }_i=p(V,f)+g_i$$ (27)

where g_i is the pressure component caused by gravity along the principal direction i.

On any plane that passes through a point on which the symmetric Cauchy stress tensor S⃡_symm works, the maximum shear stress τ_max is given by (Chatterjee, 1999)

$${\tau }_{\text{max}}=\frac{1}{2}({\sigma }_1-{\sigma }_3)=\frac{1}{2}(g_1-g_3)$$ (28)

The maximum difference between pressures caused by gravity is given by the stress from the weight of the alveolus on the cross section area. Comparing to the isotropic pressure drop across the alveolar wall caused by the breathing muscles, the anisotropic pressures from gravity is negligible. Ignoring the impact of gravity, the maximum shear stress τ_max goes to zero. Therefore, the principal stress can be simply written as the transpulmonary pressure. The symmetric Cauchy stress tensor S⃡_symm is reduced into

$${\overleftrightarrow{S}}_{\mathit{\text{symm}}}=\left[\begin{array}{ccc}\hfill p(V,f)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill p(V,f)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill p(V,f)\hfill \end{array}\right]$$ (29)

On the other hand, the rigid-rotation tensor S⃡_anti-symm, part of the shear stress in S⃡, comes from the relative motion between adjacent tissues. It is reasonable to assume the correlation between the elements in S⃡_anti-symm and respiratory volume V is negligible based on the observation that the relative motion reaches its minimum at beginning of inhalation and end of exhalation when airflow rate is minimal, and maximum at the middle of inhalation and exhalation when airflow rate is maximal. Therefore S⃡_anti-symm can be parameterized as functions of airflow rate only and reduced to

$${\overleftrightarrow{S}}_{\mathit{\text{anti}}-\mathit{\text{symm}}}=\left[\begin{array}{ccc}\hfill 0\hfill & \hfill {\tau }_{12}(f,{\overrightarrow{x}}_0)\hfill & \hfill {\tau }_{13}(f,{\overrightarrow{x}}_0)\hfill \\ \hfill {\tau }_{21}(f,{\overrightarrow{x}}_0)\hfill & \hfill 0\hfill & \hfill {\tau }_{23}(f,{\overrightarrow{x}}_0)\hfill \\ \hfill {\tau }_{31}(f,{\overrightarrow{x}}_0)\hfill & \hfill {\tau }_{32}(f,{\overrightarrow{x}}_0)\hfill & \hfill 0\hfill \end{array}\right]$$ (30)

The stress tensor S⃡ is a simple combination of Eq. (29) and Eq. (30),

$$\overleftrightarrow{S}=\left[\begin{array}{ccc}\hfill p(V,f)\hfill & \hfill {\tau }_{12}(f,{\overrightarrow{x}}_0)\hfill & \hfill {\tau }_{13}(f,\overrightarrow{x_0})\hfill \\ \hfill {\tau }_{21}(f,\overrightarrow{x_0})\hfill & \hfill p(V,f)\hfill & \hfill {\tau }_{23}(f,\overrightarrow{x_0})\hfill \\ \hfill {\tau }_{31}(f,\overrightarrow{x_0})\hfill & \hfill {\tau }_{32}(f,{\overrightarrow{x}}_0)\hfill & \hfill p(V,f)\hfill \end{array}\right]$$ (31)

The stress vector S⃗_n that works on a plane normal to unit vector n⃗ = (n₁, n₂, n₃) is given by

$${\overrightarrow{S}}_n=\overrightarrow{n}·\overleftrightarrow{S}={\overrightarrow{\sigma }}_n+\overrightarrow{{\tau }_n}$$ (32)

where σ⃗_n is the normal stress that works on the plane, whose magnitude is given by

$$|{\overrightarrow{\sigma }}_n|=\overrightarrow{n}·\overleftrightarrow{S}·\overrightarrow{n}=n_1^{2}p+n_2^{2}p+n_3^{2}p+n_1{n}_2{\tau }_{12}+n_1{n}_2{\tau }_{21}+n_1{n}_3{\tau }_{13}+n_1{n}_3{\tau }_{31}+n_2{n}_3{\tau }_{23}+n_2{n}_3{\tau }_{32}=p(V,f)$$ (33)

τ⃗_n is the shear stress that works on the plane. It is perpendicular to the normal stress σ⃗_n working on the same plane, and its magnitude is given by

$$|{\overrightarrow{\tau }}_n|=\sqrt{|S_n{|}^2-|{\sigma }_n{|}^2}=\sqrt{{\tau }_{12}^2+{\tau }_{13}^2+{\tau }_{23}^2-{(n_3{\tau }_{12}-n_2{\tau }_{13}-n_1{\tau }_{23})}^2}\equiv \tau (f)$$ (34)