Corticokinematic coherence mainly reflects movement-induced proprioceptive feedback

Abstract

Corticokinematic coherence (CKC) reflects coupling between magnetoencephalographic (MEG) signals and hand kinematics, mainly occurring at hand movement frequency (F0) and its first harmonic (F1). Since CKC can be obtained for both active and passive movements, it has been suggested to mainly reflect proprioceptive feedback to the primary sensorimotor (SM1) cortex. However, the directionality of the brain–kinematics coupling has not been previously assessed and was thus quantified in the present study by means of renormalized partial directed coherence (rPDC).

MEG data were obtained from 15 subjects who performed right index-finger movements and whose finger was, in another session, passively moved, with or without tactile input. Four additional subjects underwent the same task with slowly varying movement pace, spanning the 1–5 Hz frequency range. The coupling between SM1 activity recorded with MEG and finger kinematics was assessed with coherence and rPDC.

In all conditions, the afferent rPDC spectrum, which resembled the coherence spectrum, displayed higher values than the efferent rPDC spectrum. The afferent rPDC was 37% higher when tactile input was present, and it was at highest at F1 of the passive conditions; the efferent rPDC level did not differ between conditions. The apparent latency for the afferent input, estimated within the framework of the rPDC analysis, was 50–100 ms.

The higher directional coupling between hand kinematics and SM1 activity in afferent than efferent direction strongly supports the view that CKC mainly reflects movement-related somatosensory proprioceptive afferent input to the contralateral SM1 cortex.

Highlights

• •Neural activity in primary sensorimotor cortex is coupled with hand kinematics.
• •The coupling is stronger in the afferent than in the efferent direction.
• •The afferent delay estimated with phase–frequency plots is 50–100 ms.
• •During movements, <5-Hz sensorimotor activity mainly reflects proprioceptive feedback.

Introduction

During fast repetitive hand movements, neuronal activity from the contralateral primary sensorimotor (SM1) cortex, as measured with magnetoencephalography (MEG), is coherent with hand kinematics at movement frequency (F0) and its first harmonic (F1), a phenomenon referred to as corticokinematic coherence (CKC) (Bourguignon et al., 2011, 2012b; Jerbi et al., 2007). During such repetitive movements, the SM1 cortex phasically produces motor output and integrates somatosensory input in overlapping time windows. Until recently, the brain oscillations emerging from the SM1 cortex at frequencies matching the frequencies of hand kinematics have been thought to be related to encoding of hand kinematics (Bourguignon et al., 2012a, 2012b; Jerbi et al., 2007; Kelso et al., 1998; Waldert et al., 2008), or to be a superposition of motor and somatosensory signals (Muller et al., 2000; Pollok et al., 2003, 2004). The hypothesis of motor encoding would imply descending motor commands that were backed up by monkey recordings showing that the firing rate of some motor-cortex neurons correlates with several kinematics parameters, such as direction (Georgopoulos et al., 1982), speed (Moran and Schwartz, 1999), and acceleration (Ashe and Georgopoulos, 1994; Reina et al., 2001). To which extent CKC reflects motor efferent vs. somatosensory afferent activity had, however, not been quantified.

We recently found evidence for strong involvement of afferent input in the generation of the CKC as both active and passive finger movements lead to similar CKC levels and neuronal generators at the hand area of the contralateral SM1 cortex (Piitulainen et al., 2013). We thus argued that CKC mainly reflects proprioceptive feedback to the SM1 cortex. However, this physiologically well-based interpretation was not backed up by any quantitative analysis of the relative afferent vs. efferent contributions to the CKC, nor was any directionality analysis carried out.

Here, we disentangled the relative contributions of motor output and somatosensory input to CKC by computing the directionality of coupling between MEG signals and finger kinematics. Such quantification can be performed with non-symmetric indices, such as partial directed coherence (PDC), which relies on the concept of Granger-causality to reveal information directionality between processes in a frequency-specific way (Baccala et al., 1998; Sameshima and Baccala, 1999). However, comparison of PDC values is fraught with caveats since a higher PDC value does not necessarily indicate a stronger coupling between the signals (Schelter et al., 2009). Renormalized PDC (rPDC), wherein PDC is normalized so that its null distribution follows a χ² distribution, has been designed to correct this shortcoming, allowing the inference of statistical significance and the comparison of two PDC values reflecting the direction of the information flow (Schelter et al., 2009).

Methods based on the concept of Granger causality were previously used to assess the directionality of the cortex–muscle coherence (Lim et al., 2014; Tsujimoto et al., 2009; Witham et al., 2010, 2011), which reflects coupling between activity of the primary motor cortex and surface electromyogram. During low-force isometric contraction the coherence peaks at ~20 Hz (Conway et al., 1995) and the cortex leads the muscle by about 20 ms to upper limbs and by about 40 ms to lower limbs (Salenius et al., 1997), in agreement with corticomuscular conduction times evident also from other types of measurements (Gross et al., 2000). Proprioceptive feedback does not appear essential for the generation of cortex–muscle coherence since the strength of the coupling assessed with methods based on Granger causality is considerably higher in the efferent direction than in the afferent direction (Lim et al., 2014; Tsujimoto et al., 2009; Witham et al., 2010), and because ischemic sensory deafferentation in the upper limb diminishes but does not abolish cortex–muscle coherence nor alter the frequency of its dominant component (Pohja and Salenius, 2003). Nevertheless, directionality analyses imply that significant coupling to upper-limb muscles exists in both afferent and efferent directions with a similar delay of on average 24 ms for both (Witham et al., 2011). This result argues for the ability of directionality analysis methods to separate the afferent and efferent contributions and to estimate the associated delays, whereas inferences obtained from the phase of the cross-spectrum may fail due to a non-trivial mixing of the afferent and efferent signals (Baker, 2007). Still, methods based on the Granger causality or other measures have not been used to assess the directionality of CKC.

In the present study, we applied rPDC to the previously reported CKC data where subjects performed ~4-Hz right forefinger movements (active) or where their finger was passively moved by an experimenter (passive), with or without tactile input (touch/no-touch) (Piitulainen et al., 2013). Here, rPDC measured the strength of the directional coupling between MEG signals picked up above the SM1 cortex and finger kinematics. To evaluate the relative contributions of motor output and somatosensory feedback, we compared rPDC values in the efferent and afferent directions. In addition, to determine the afferent and efferent delays between finger kinematics and brain signals, and to better link the CKC to movement evoked fields (MEFs) associated with discrete movements (Neshige et al., 1988), we carried out recordings on a new set of subjects who moved at varying rate within the same recording session.

Experimental procedures

Subjects

The dataset related to the first (fixed-pace) experiment is derived from Piitulainen et al. (2013) who studied 15 healthy adults (mean age 29.4 yrs, range 21–38; 8 males, 7 females). According to the Edinburgh handedness scale (Oldfield, 1971), 14 subjects were right-handed and one was ambidextrous.

Four additional healthy right-handed subjects (mean age 30 yrs, range 26–35; 3 males, 1 female) participated in the second (variable-pace) experiment.

The study had a prior approval by the ethics committee of the Helsinki and Uusimaa district, and the subjects gave written informed consent before participation. Subjects were compensated monetarily for the lost working hours and travel expenses.

Experimental protocol

In the fixed-pace experiment described in Piitulainen et al. (2013), subjects performed four randomized movement conditions (active–touch, active–no-touch, passive–touch, and passive–no-touch) involving fast repetitive flexion–extension movements of the metacarpophalangeal joint of the right forefinger for 3.5 min. In touch conditions, the tip of the index finger touched the table on which hand was resting, whereas in no-touch conditions, it did not. In active conditions, the subjects performed self-paced movements, whereas in passive conditions, an investigator moved the subjects' forefinger with a light aluminum stick. Before the recordings, we ensured that the subjects mastered the task. During the recordings, no cues were delivered about the movements. The movement pace was analyzed only afterward, and it ranged from 3 to 5 Hz in all conditions and subjects.

The variable-pace experiment was designed to assess the delay between finger kinematics and MEG signals. Both active–touch and passive–touch movements were performed with smoothly varying rate, spanning frequencies from 1 to 5 Hz in ~20-s-long cycles for 10 min. Subjects were instructed to start with tapping at ~1 Hz and then smoothly increase the pace up to their limit, then slowly decrease the pace back to ~1 Hz, and thereafter again starting the next cycle. The task performance was evaluated similarly as in the fixed-pace experiment. In a few cases, the experimenter asked the subject to start again because online monitoring of the acceleration signals and the video image of the subject indicated deviation from the requested task.

Measurements

The measurements were carried out at the MEG Core of the Brain Research Unit, Aalto University. Cortical activity was recorded with a 306-channel whole-scalp neuromagnetometer (Elekta Neuromag™, Elekta Oy, Helsinki, Finland) and the kinematics of the right forefinger was monitored with a 3-axis accelerometer (ADXL335 iMEMS Accelerometer, Analog Devices, Inc., Norwood, MA, USA) attached to the nail of the forefinger. The recording passband was 0.1–330 Hz for MEG signals and DC–330 Hz for accelerometer signals, and the signals were sampled at 1 kHz.

Data processing

Continuous MEG data were pre-processed off-line using the signal-space-separation method (SSS) to suppress external interferences and to correct for head movements (Taulu et al., 2005). Acceleration (Acc) was computed at every time bin as the Euclidian norm of the three band-passed (1–195 Hz) Acc signals (Bourguignon et al., 2011). Signals from gradiometer pairs indexed by r ∈ {1 : 102} (g_r,1 and g_r,2) were used to estimate the signal of virtual gradiometers in the orientation θ ∈ [0; π]:

$$g_{r,\theta }\left(t\right)=g_{r,1}\left(t\right)cos\theta +g_{r,2}\left(t\right)sin\theta \text{.}$$

Following Halliday et al. (1995), coherence based on the Fourier transform of artifact-free 2-s epochs was then computed between Acc and g_θ:

$$Coh\left(r,f,\theta \right)=\frac{\mathrm{A}\mathrm{c}\mathrm{c}\left(f\right)g_{r,\theta }^{*}{\left(f\right)}^2}{{\left|\mathrm{A}\mathrm{c}\mathrm{c}\left(f\right)\right|}^2{\left|g_{r,\theta }\left(f\right)\right|}^2}\text{,}$$

where * is the Hermitian conjugate and 〈 ⋅ 〉 the mean across epochs. Practically, Coh(r, f, θ) was estimated from the cross-spectral density matrix formed with Acc, g_r,1 and g_r,2, and for θ spanning [0; π] by steps of π/100. The optimum θ and the corresponding coherence value were obtained as follows:

$${\theta }_{\mathrm{opt}}\left(r\right)=\underset{\theta \in \left[0;\pi \right]}{\mathrm{argmax}}Coh{\left(r,f,\theta \right)}_{f\in F}\text{,}$$

$${Coh}_{\mathrm{opt}}\left(r\right)=\underset{\theta \in \left[0;\pi \right]}{max}Coh{\left(r,f,\theta \right)}_{f\in F}\text{,}$$

F = {F0, F1} and 〈 ⋅ 〉 the geometric mean in fixed-pace, and F the frequency range of significant CKC (see Statistical analyses) and 〈 ⋅ 〉 the arithmetic mean in variable-pace. Finally, the optimal gradiometer pair chosen among a pre-selection of 9 gradiometer pairs located above the left rolandic area (R_{left SM1}) was selected as follows:

$$r_{\mathrm{opt}}=\underset{r\in R_{\mathrm{left}\mathrm{S}\mathrm{M}1}}{\mathrm{argmax}}{Coh}_{\mathrm{opt}}\left(r\right)\text{.}$$

Given that CKC mainly arises from the SM1 cortex, the virtual gradiometer $g_{r_{\mathrm{opt}},{\theta }_{\mathit{opt}}\left(r_{\mathrm{opt}}\right)}$ will be referred to as MEG_SM1 signal.

We further set out to estimate the causal influence of Acc and MEG_SM1 signals on one another (in the efferent direction: MEG_SM1 → Acc, and afferent direction: Acc → MEG_SM1). rPDC was chosen as the index of directional influence since it provides good properties, such as inference of statistical significance and comparison of values between conditions (Schelter et al., 2009). The computation of rPDC requires fitting a multivariate autoregressive model to the data, and the order of this model should be high enough to avoid detecting spurious interactions and low enough for true interactions to survive the significance assessment (Schelter et al., 2009; Schneider and Neumaier, 2001; Sommerlade et al., 2009). In addition, the down-sampling applied to the data should afford a temporal resolution better than the expected time-shift between the signals (Florin et al., 2010).

The model order was set to 100 and the model parameters were estimated from Acc and MEG_SM1 signals low-pass filtered at 25 Hz and resampled at 50 Hz with the ARfit package (Schneider and Neumaier, 2001). Across subjects and conditions, the optimal model order range was 41–61 (mean ± SD 50 ± 4) according to Schwarz's Bayesian criterion and 118–195 (149 ± 17) according to Akaike's final prediction error, both implemented in the ARfit package (Schneider and Neumaier, 2001). Adopting model order of 100 therefore represents a good compromise between the two criteria. Furthermore, the chosen parameters (resampling and model order) enable exploring frequencies up to 25 Hz with a 0.5 Hz resolution. Hence, the frequency resolution is the same as used in previous CKC studies (Bourguignon et al., 2011, 2012b; Jerbi et al., 2007), and the down-sampling limits the range of investigated frequencies to 0–25 Hz, range in which the main coherence peaks fall.

As mentioned above, a sensitive issue in Granger-causality-based methods pertains to filtering of the data (Florin et al., 2010). To ensure that our results are not contaminated by filtering or even reflecting some filtering artifacts, we also analyzed the data by increasing the cut-off frequency of our low-pass filter (applied to our data prior to rPDC analysis) from the previous 25 Hz to 50 Hz (with down-sampling at 100 Hz, model order at 200); the proportional increase in all these parameters allowed keeping the 0.5-Hz frequency resolution. The similarity between the rPDC estimated with both sets of parameters was assessed by the correlation coefficient between the corresponding rPDC values pooled across subjects, conditions, and F0/F1.

Finally, the delay between Acc and MEG_SM1 signals in the variable-pace experiment was estimated as described by Campfens et al. (2014). Briefly, the phase of the Fourier-transformed coefficients of the multivariate autoregressive model was plotted as a function of the frequency, and the delay was obtained from the slope (divided by 2π) in the range of 0–10 Hz, using only connected frequency bins of significant coherence. This delay estimation procedure has been shown to perform well under different efferent/afferent coupling strengths (Campfens et al., 2014). Delays estimated in such a way are however “apparent” rather than real latencies, since the estimation is affected by response shape (Hari et al., 1989), and it informs about the timing of the strongest response.

Statistical analyses

The statistical significance of the coherence was assessed under the hypothesis of linear independence (Halliday et al., 1995). To correct for multiple comparisons, the alpha level was set to 0.05 / (N_f × N_s), N_f being the number of frequency bins falling between 0 and 4 × F0 (fixed-pace) or between 0 and 10 Hz (variable-pace), and N_s = 9, the number of sensor pairs included in the analysis.

The statistical significance of rPDC was assessed analytically using the procedure described in Schelter et al. (2006, 2009). Briefly, under the null hypothesis of no directional coupling, rPDC values multiplied by the number of time bins used to fit the autoregressive model have a chi-square distribution with 2 degrees of freedom. To correct for multiple comparisons, the alpha level was set to 0.05 / N_f. Furthermore, the significance of the rPDC was assessed with statistics based on Fourier-transform surrogate data (Faes et al., 2004). Fourier-transform surrogate of a signal is obtained by computing its Fourier-transform, replacing the phase of the Fourier coefficients by random numbers in the range [−π; π], and then computing the inverse Fourier-transform (Faes et al., 2004; Theiler et al., 1992). The procedure of computing the rPDC between Fourier transform surrogate MEG and Acc signals was repeated 1000 times, and the maximum rPDC value across the N_f frequency bins was extracted for each repetition in the afferent and in the efferent directions separately. Significance thresholds at p < 0.05 for the rPDC in the afferent and in the efferent directions were then computed as the 95-percentiles of the corresponding cumulative density functions.

The significance thresholds obtained with the two independent methods (analytical and surrogate-data-based) were very close to each other (ratio between surrogate and analytical threshold 1.09 ± 0.07 in the afferent direction and 1.08 ± 0.08 in the efferent direction; mean ± SD estimated from pooled values across subjects, conditions, and F0/F1). The significance of individual rPDC values was identical with both statistical methods, and thus no further reference will be made to the use of different methods.

Possible differences in the strength of the directional coupling between fixed-pace movement conditions were compared separately using a three-way 2 (active/passive) × 2 (touch/no-touch) × 2 (frequencies, F0 and F1) repeated-measures analysis of variance (ANOVA). The dependent variable was the subjects' individual rPDC. Afferent and efferent connections were tested separately.

We finally compared rPDC in the afferent and efferent directions using paired t-tests. This comparison requires some precautions since the between-signals difference in signal-to-noise ratio (SNR) affects the rPDC differently in the two directions (Schelter et al., 2009). To get around this shortcoming, the comparison between high-SNR Acc and the limited-SNR MEG signals was done with rPDC computed (1) directly (SNR_MEG < SNR_Acc) and (2) after adding noise to Acc signals (SNR_MEG > SNR_Acc). We reasoned that if the same conclusion can be drawn in these two configurations, the effect of SNR will be ruled out. To reach configuration (2), the maximum CKC level across F0 and F1 (Coh) was used to estimate SNR_MEG, and noise was added accordingly to Acc signals. Under the assumptions that (i) Acc signals have infinite SNR, (ii) MEG_SM1 signals are the sum of SM1 activity and of uncorrelated noise, and (iii) coherence between Acc and noiseless-SM1 activity equals one, SNR_MEG = Coh/(1 − Coh). Assumptions (i) and (iii) form the worst-case scenario, leading to a pessimistic SNR estimate. We therefore added noise to Acc signals so that its SNR equaled this pessimistic SNR_MEG in all frequencies; the added noise was computed as the Fourier-transform surrogate Acc signal multiplied by SNR_MEG^−1/2. The simulation was repeated 21 times, and we report the median values to smooth out estimation inaccuracies pertaining to the random character of the added noise. The similarity between the rPDC estimated with noisy and noiseless Acc was assessed by the correlation coefficient between the corresponding rPDC values pooled across subjects, conditions and F0/F1.

Results

Fixed-pace CKC results

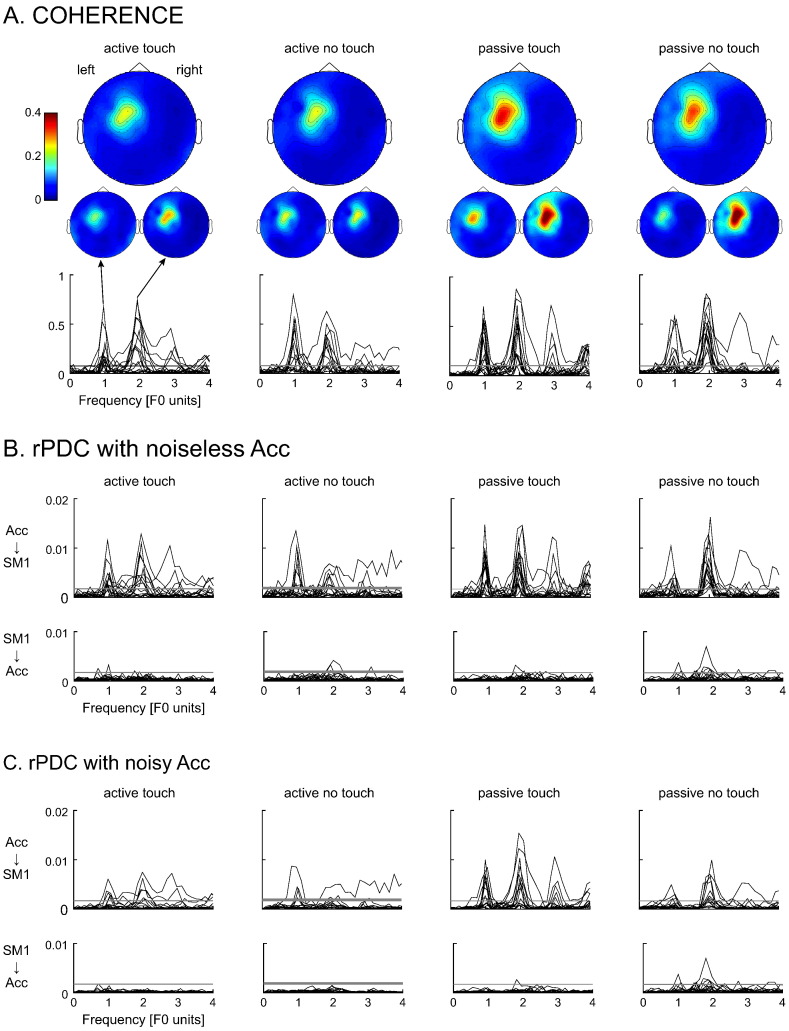
We here first sum up the fixed-pace CKC (coherence between finger kinematics and MEG) results reported by Piitulainen et al. (2013). Fig. 1A illustrates the spatial pattern of CKC at the sensor level. Statistically significant (p < 0.05) CKC peaked at F0 and F1 in all conditions, except in two subjects in active-touch at F0. CKC sources—as reconstructed with dynamic imaging of coherent sources (Gross et al., 2001)—were located in the hand area of the contralateral SM1 cortex, with no spatial differences between the four movement conditions (active/passive with touch/no-touch) at F0 and F1. As reported by Piitulainen et al. (2013), CKC level was statistically significantly affected by the task (active vs. passive) and frequency (F0 vs. F1), with an interaction between them, whereas tactile input (touch vs. no-touch) had no effect.

Fig. 1.

Fixed-pace experiment: coherence spectra and directionality results. A. Coherence spectra (one trace per subject) and associated group-level topographic distribution at F0, F1, and averaged across F0 and F1. B. Renormalized partial directed coherence (rPDC) in the afferent and efferent directions (one trace per subject). C. Same as B with added noise to the accelerometer (Acc) signal. The gray horizontal lines indicate the threshold of statistical significance. SM1: primary sensorimotor.

Afferent and efferent coupling

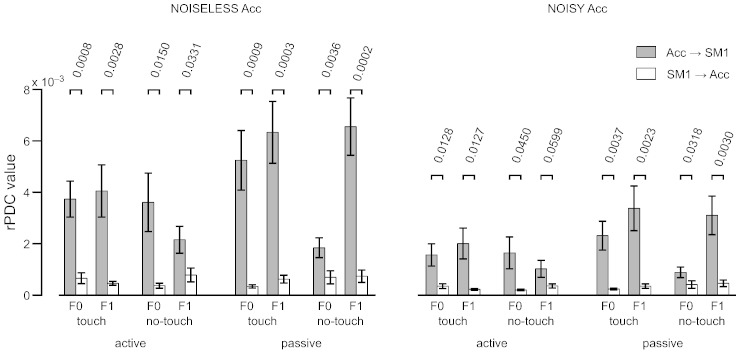
Fig. 1B illustrates the rPDC results and Fig. 2 (left panel) gives the rPDC values for all conditions. Similarly to CKC spectra, the afferent rPDC spectra displayed clear peaks at F0 and F1 in most subjects. The afferent coupling was statistically significant either at F0 or F1 in 13–15 subjects (14 active–touch, 13 active–no-touch, 14 passive–touch, 15 passive–no-touch). The strength of the afferent coupling was affected by the tactile input (touch vs. no-touch, F_1,14 = 7.17, p = 0.018), task (active vs. passive, F_1,14 = 7.12 p = 0.018) and frequency (F0 vs. F1, F_1,14 = 5.62, p = 0.033), with an interaction between task and frequency (F_1,14 = 10.22, p < 0.01). In the rPDC averaged across subjects and conditions, the value was 37% higher in touch (4.8 × 10⁻³) than in no-touch (3.5 × 10⁻³), and the interaction between task and frequency was due to higher rPDC in passive at F1 (6.4 × 10⁻³) than in the other conditions (active at F0: 3.7 × 10⁻³; active at F1: 3.5 × 10⁻³; passive at F0: 3.1 × 10⁻³; p(s) < 0.01); these other conditions showing a similar level of rPDC (p(s) > 0.3). The efferent rPDC was clearly weaker, being statistically significant only in 2–4 subjects (2 active–touch, 3 active–no-touch, 3 passive–touch, 4 passive–no-touch), with no differences between conditions. Paired t-tests demonstrated that the rPDC was 2.7–15.5 times stronger in the afferent direction than in the efferent direction for all conditions, at F0 and F1 (p < 0.05 for all 8 comparisons, see Fig. 2 for exact p-values).

Fig. 2.

Fixed-pace experiment: rPDC values (mean and SEM) between primary sensorimotor (SM1) and acceleration (Acc) signals, for all conditions, and in both noise configurations (noiseless and noisy Acc) 9 p-values of paired t-tests comparing the afferent and efferent rPDC are shown on top of the rPDC values.

Effect of acceleration signal's SNR

Fig. 1C presents the rPDC spectra obtained with noisy Acc signals in all conditions and Fig. 2 (right panel) gives the corresponding rPDC values at F0 and F1. Overall, the results were quite similar, with a correlation between the rPDC values obtained with the two sets of parameters of 0.95 in the afferent direction and 0.89 in the efferent direction. The afferent coupling was statistically significant either at F0 or F1 in 7–12 subjects (7 active–touch, 7 active–no-touch, 12 passive–touch, 10 passive–no-touch). The same effects were identified with the ANOVA analysis of the afferent coupling (tactile input, F_1,14 = 4.86, p = 0.045; task, F_1,14 = 5.10, p = 0.040; frequency, F_1,14 = 6.51, p = 0.023; task and frequency interaction, F_1,14 = 10.04, p < 0.01). The rPDC averaged across subjects and conditions was 39% higher in touch (2.3 × 10⁻³) than in no-touch (1.7 × 10⁻³), and higher in passive at F1 (3.2 × 10⁻³) than in the other conditions (active at F0: 1.6 × 10⁻³; active at F1: 1.6 × 10⁻³; passive at F0: 1.5 × 10⁻³; p(s) < 0.02); these other conditions showing a similar level of rPDC (p(s) > 0.7). The efferent rPDC was significant in 0–2 subjects (1 active–touch, 0 active–no-touch, 1 passive–touch, 2 passive–no-touch), with no differences between conditions. Paired t-tests demonstrated that the rPDC was in all conditions 2.2–9.8 times stronger in afferent than efferent direction. This difference was significant for all conditions but for active-no-touch at F1 (p < 0.05 for all 7 comparisons, p = 0.06 in active–no-touch at F1, see Fig. 2 for exact p-values). The decrease of statistical significance obtained in the noisy configuration is likely due to the high level of noise introduced in the data of subjects displaying relatively weak coherence. Indeed, in all 4 conditions, the maximum coherence was below 0.25 in 4–7 subjects. After adding noise, the coherence decreased below 0.06 and hence, the rPDC analysis was considerably hindered in these subjects.

Effect of low-pass filter

The results obtained with the cut-off of the low pass filter set to 50 Hz were very similar to the ones obtained with the 25-Hz cut-off: the correlation coefficient between the corresponding pooled rPDC values was 0.999 in the afferent direction and 0.996 in the efferent direction. The statistical assessment of individual rPDC values lead to the same results as reported in the Afferent and efferent coupling section. This analysis demonstrates the robustness of our results with respect to the cut-off frequency of the low-pass filter.

Apparent latency

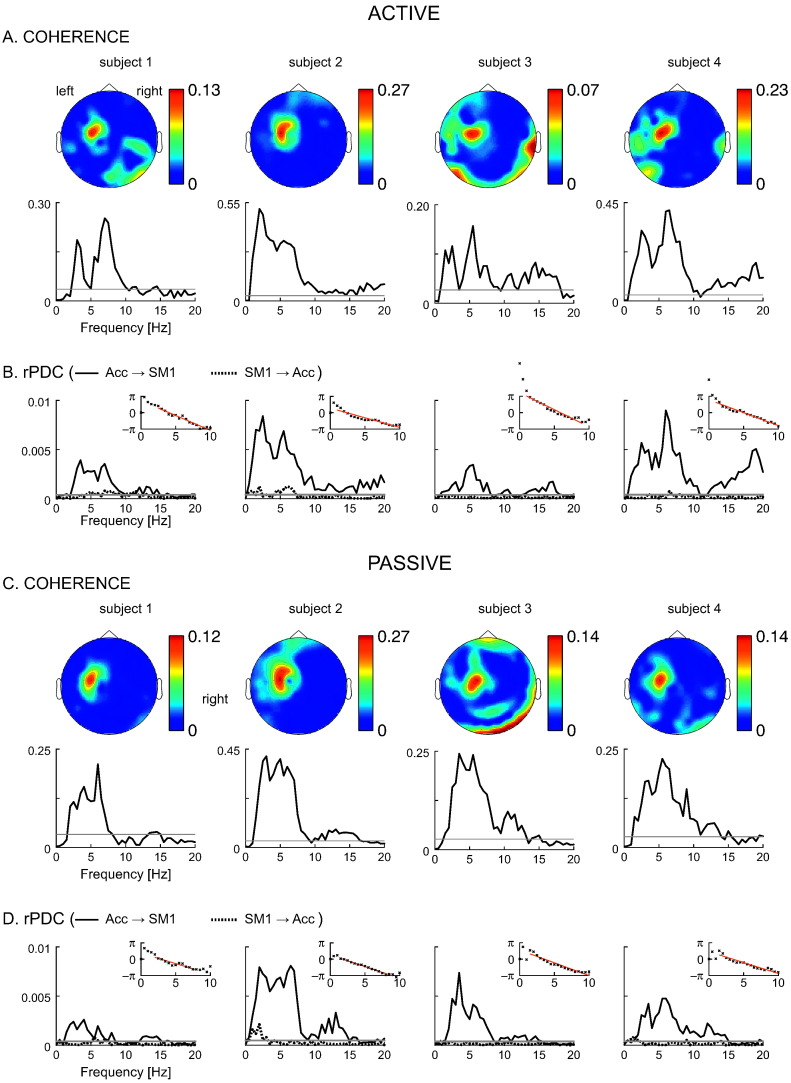
Fig. 3 illustrates the variable-pace results. In this experiment, subjects moved their finger (active) or their finger was moved by an investigator (passive) at slowly varying pace, from ~1 to ~5 Hz and back to ~1 Hz resulting in 9–21 cycles during 10 min (the instructed rate change would have resulted in ~30 cycles). In other words, F0 varied from 1 to 5 Hz. All 4 subjects managed to perform the task and CKC was significant in a wide frequency range corresponding to the variable F0 and higher harmonics (see Fig. 3 and Table 1). The apparent latency between Acc and MEG_SM1 signals—estimated only in the afferent direction since no consistent rPDC was identified in the efferent direction—was 59–104 ms in the active condition and 64–78 ms in the passive condition (see Table 1).

Fig. 3.

Variable-pace experiment: coherence spectra and directionality results. A (active) and C (passive): Coherence spectra and associated topographic distribution in the frequency range of significant coherence. B (active) and D (passive): Renormalized partial directed coherence (rPDC). The smaller insets display the phase–frequency plots of the Fourier coefficients of the multivariate autoregressive model, which were used to estimate the delay through linear regression (red line). The gray horizontal lines indicate the threshold of statistical significance. Acc: accelerometer. SM1: primary sensorimotor.

Table 1.

Summary of variable-pace results.

Condition	Subject	Frequencies [Hz]	Mean coherence	Delay [ms]
Active	S1	2.5–10	0.123	90
	S2	1–10	0.267	59
	S3	1–9	0.067	104
	S4	1–10	0.224	79
Passive	S1	2–8	0.111	64
	S2	1.5–9	0.268	71
	S3	1.5–10	0.133	78
	S4	1.5–10	0.134	66

Discussion

During fast repetitive (active and passive) finger movements, the directional coupling (as measured with rPDC) between finger kinematics and SM1 cortex activity is drastically higher in the afferent than in the efferent direction, thereby strongly supporting the view that CKC mainly reflects movement-induced somatosensory proprioceptive feedback to the contralateral SM1 cortex, with an apparent latency of 50–100 ms. Cutaneous tactile input enhanced afferent coupling, even though it did not affect the CKC level (Piitulainen et al., 2013).

Motor versus proprioceptive contribution to CKC

In our previous study, we argued on the basis of similar coherence strengths and source locations during active and passive movements that CKC mainly reflects proprioceptive feedback to the SM1 cortex (Piitulainen et al., 2013). The present study was designed to obtain quantitative support for this physiologically-based argumentation. By using rPDC, we found that the strength of the directional coupling between hand kinematics and SM1 cortex activity is drastically higher in the afferent than efferent direction, both during active and passive movements. The results remained even when the possible effects of SNR differences between Acc and MEG_SM1 signals were ruled out. This analysis thus strongly supports the view that CKC mainly reflects movement-induced proprioceptive feedback to the contralateral SM1 cortex. Still, motor output might contribute to some extent to the CKC, but this contribution is clearly overshadowed by proprioceptive feedback. This finding, together with the estimated afferent delay of 50–100 ms, suggests that the CKC is closely linked to the movement-evoked fields, MEFs, that are robust evoked responses peaking about 100 ms after movement onset (Kristeva et al., 1991; Neshige et al., 1988; Weinberg et al., 1990), related to muscle contraction and other sources of reafferent signals (Cheyne et al., 1997; Hoshiyama et al., 1997; Kristeva-Feige et al., 1996; Onishi et al., 2006, 2013). Further support for this tight link comes from the findings that the time-courses of MEF and movement velocity are correlated (Kelso et al., 1998), as is the case for the brain signals associated with the CKC (Bradberry et al., 2009, 2010; Jerbi et al., 2007).

Still, we cannot say whether the primary motor, primary somatosensory, or both cortices are the main sources of the CKC since both of them receive afferent proprioceptive projections (Jones et al., 1978), and since the MEG_SM1 signal represents a mixture of activity at least from these two brain areas. Our previous source modeling study failed to segregate the CKC sources to either side of the central sulcus (Piitulainen et al., 2013). Most likely, several areas of the cortical sensorimotor network can contribute to the CKC, as previously suggested (Bourguignon et al., 2012b). Such an assumption is indeed supported by electrocorticographic (ECoG) recordings demonstrating that hand-movement-related evoked responses can be recorded from several sensorimotor regions, including the primary motor and somatosensory cortices, and with lower amplitudes in the pre-motor, posterior parietal and pre-frontal cortices (Ball et al., 2009). These data also agree with findings that MEFs may occur in both primary motor and primary somatosensory cortices, as is evident from recordings of monkey local field potentials and multiunit activity (Arezzo et al., 1977), as well as from human ECoG and EEG recordings (Neshige et al., 1988). Furthermore, an event-related beamforming assessment of MEFs recorded with MEG in humans showed that the first component peaks ~40 ms after movement onset in the primary somatosensory cortex, followed by a second component peaking at ~150 ms in the primary motor cortex (Cheyne et al., 2006).

Similar to the previous CKC results (Piitulainen et al., 2013), the afferent coupling was stronger at F1 than F0 during passive movements whereas no statistical difference was observed during active movements. Although the mechanisms involved in the coupling at F1 are still unsettled, this effect could be explained by the higher regularity of the passive movements compared with the active ones (Piitulainen et al., 2013).

Implication for brain–machine interfaces

Several studies have demonstrated that < 5-Hz MEG/EEG activity can be used to decode movement direction (Hammon et al., 2008; Waldert et al., 2008), or to estimate hand kinematics (Bradberry et al., 2009, 2010). The best decoding accuracy is typically reached during the course of the movement and the associated brain signals have therefore been viewed as promising control signals for brain–machine interfaces (Bradberry et al., 2009, 2010; Jerbi et al., 2011). However, our finding that these movement-related low-frequency brain signals mainly pertain to proprioceptive feedback suggests that brain–machine interfaces based upon these motion-related signals might be impractical in the patient population in need, i.e. the patients unable to move, as no proprioceptive feedback will naturally reach the patients' brain in the absence of movement.

Further studies should clarify whether the direction of even imagined movements could be decoded from low-frequency brain signals. This possibility actually seems likely since movement observation has been shown to lead to coherence between MEG signals from the observer's SM1 cortices and the observed hand kinematics, in the absence of movement of the observer (Bourguignon et al., 2012a). In other words, low-frequency brain signals from the SM1 cortex can in some cases be coherent with some kinematics parameters in the absence of proprioceptive feedback, although the coherence is weaker than with executed movements (Bourguignon et al., 2012a). These contemplations, however, remain to be experimentally supported.

Effect of concomitant tactile stimulation

Our rPDC analysis revealed that tactile input strengthened the coupling between finger kinematics and SM1 activity in the afferent direction, even though tactile input had no effect on the coherence level. The enhanced afferent coupling induced by tactile input cannot be accounted for by differences in movement frequency or regularity since these two parameters were very similar in touch and no-touch conditions (Piitulainen et al., 2013). Of notice, a previous CKC study found an increase of CKC level induced by tactile input but the fast repetitive finger movements used differed between the touch and no touch conditions (Bourguignon et al., 2012b).

In the present fast repetitive finger-tapping task, tactile input represents an additional afferent flow of information to the SM1 cortex, phase-locked to finger's kinematics. Consequently, and as suggested by our rPDC results, brain signals from the SM1 cortex might be better predicted by finger kinematics in the presence of tactile input, probably because of contribution by tactile evoked responses. But, the overall coupling between brain signals and finger kinematics—as measured with CKC—was unaffected by the level of cutaneous input (Piitulainen et al., 2013). It is therefore likely that proprioceptive signals give the basis to establish a strong coupling between brain signals and hand kinematics and that tactile information has limited additional contribution to the overall coupling. Still, the increase in rPDC associated to tactile information shows that rPDC is sensitive to subtle changes in the neuronal information flow.

Delay estimation

The “apparent latency” (see Regan, 1972) between Acc and MEG_SM1 signals was 50–100 ms in the four subjects who performed the variable-pace experiment. This latency appears surprisingly long given that the afferent proprioceptive axons (type Ia fibers) are thick (diameters up to 14 μm; McComas, 1977) and thus very fast conducting (mean velocities of about 75 m/s for median-nerve innervated area; Macefield et al., 1989). Thus proprioceptive input from the upper limb should reach the cortex within ~20 ms, which agrees with the peak latencies of cortical responses to median-nerve stimulation at the wrist (Chiappa, 1997) and to rapid extension of the wrist (Abbruzzese et al., 1985), with the cortex–muscle lags after transcranial magnetic stimulation of the hand primary motor cortex (Rothwell et al., 1991), as well as with the cortex–muscle time lag estimated from corticomuscular coherence to distal hand muscles (Gross et al., 2000; Salenius et al., 1997). Hence, it is likely that the 50–100 ms apparent latency mainly reflects the timing of the strongest cortical response, i.e. the MEF peaking at ~100 ms, rather than the shortest neuronal conduction delay from periphery to the cortex.

Limitations of the study

To render the afferent and the efferent rPDC comparable we added noise to the less noisy signal (i.e. the acceleration). Even though this approach appeared satisfactory in the present study, more elegant methods are needed in the future to allow the direct comparison of directionality parameters, e.g. through properly modeling the effect of SNR on the rPDC.

Although we here demonstrate a predominant contribution of the proprioceptive feedback to the CKC, further studies should identify the tinier role of the efferent motor commands. One possibility would be to use tourniquet ischemia to suppress the proprioceptive feedback, and assess the CKC during passive movements (at the stage when active movements are no more possible due to ischemia) and rPDC.

Finally, the apparent latency of 50–100 ms from Acc to MEG_SMI was estimated from a limited sample of 4 subjects. This latency seemed to be fraught with substantial inter-individual variability, especially in the active condition. Further studies should be designed to estimate more precisely the latency in a larger population.

Conclusions

The present study demonstrates that the coupling between SM1 activity and finger kinematics is predominantly driven by proprioceptive feedback during both active and passive movements. CKC therefore seems to provide a reliable tool to monitor proprioceptive input to the cortex. Our rPDC analysis successfully probed the directionality of information flow, but one should be careful in the interpretation since the SNR affects the rPDC values. Finally, the apparent afferent delay estimated from the phase–frequency plots of autoregressive coefficients yielded values reflecting the timing of the strongest cortical response associated with proprioceptive feedback to the SM1 cortex, revealing a tight link between CKC and MEFs occurring 100 ms after isolated movements.