A model for family-based case–control studies of genetic imprinting and epistasis

Abstract

Genetic imprinting, or called the parent-of-origin effect, has been recognized to play an important role in the formation and pathogenesis of human diseases. Although the epigenetic mechanisms that establish genetic imprinting have been a focus of many genetic studies, our knowledge about the number of imprinting genes and their chromosomal locations and interactions with other genes is still scarce, limiting precise inference of the genetic architecture of complex diseases. In this article, we present a statistical model for testing and estimating the effects of genetic imprinting on complex diseases using a commonly used case–control design with family structure. For each subject sampled from a case and control population, we not only genotype its own single nucleotide polymorphisms (SNPs) but also collect its parents’ genotypes. By tracing the transmission pattern of SNP alleles from parental to offspring generation, the model allows the characterization of genetic imprinting effects based on Pearson tests of a 2 × 2 contingency table. The model is expanded to test the interactions between imprinting effects and additive, dominant and epistatic effects in a complex web of genetic interactions. Statistical properties of the model are investigated, and its practical usefulness is validated by a real data analysis. The model will provide a useful tool for genome-wide association studies aimed to elucidate the picture of genetic control over complex human diseases.

INTRODUCTION

Genetic imprinting arises from a gene when either its maternally or paternally derived copy is expressed while the other copy is silenced [1]. As a consequence of epigenetic marks due to differential DNA methylation during gametogenesis, genetic imprinting has been found to play a pivotal role in regulating the formation, development, function and evolution of complex traits and diseases [2–5]. Tremendous efforts have been made to study the epigenetic and molecular mechanisms of this phenomenon [6], but the number and distribution of imprinted genes and their epistatic interactions are poorly understood, thereby limiting our ability to estimate the effects of imprinting genes on complex traits or diseases. Several authors have used linkage analysis to identify the regions of the genome that contain imprinted sequence variants and further understand the epigenetic variation of complex traits extended the transmission disequilibrium test to test imprinting effects [7–12]. Howey and Cordell reviewed two packages of software for estimating maternal and imprinting effects based on child–parent configurations [13].

As one of the simplest and most powerful approaches for genome-wide identification of disease genes, association studies based on a case–control design have been widely used in human genetics [14]. This design allows the inheritance modes of genetic control to be tested and estimated. Statistical analyses based on a contingency table suggest that some genes function additively, whereas the others function in a dominant or overdominant manner [15]. A recent model by Liu et al. [16] integrates traditional quantitative genetic principles into a case–control design, producing a 2 × 2 contingency table, in which epistasis of different kinds and orders can be characterized. More recently, Zhang et al. [17] have embraced haplotype discovery procedures and Liu et al.’s model to identify genetic interactions between haplotypes located at different positions of the genome. Sui et al. [18] have incorporated DNA methylation mechanisms into Liu et al.’s model, allowing the effect of epigenetic marks on complex disease to be tested.

In this article, we describe a statistical model for estimating genetic imprinting based on a commonly used case–control design by implementing family structure. Unlike classical case–control studies in which random samples of cases and controls are drawn, respectively, from a natural population, a family-based case–control design includes genotyping both these random samples and their parents. By classifying cases and controls into different groups of genotypes at individual genes based on their own genotypes and their parents’ genotypes, we can discern the discrepancy of alleles in their origin, which allows imprinting effects to be characterized. We performed simulation studies to test the statistical behavior of the model and validate its utilization. The new model was used to analyze a real data set collected for inflammatory bowel disease (IBD) [10], leading to the detection of significant imprinting effects at several loci.

BASIC MODEL

Population sampling

The study is based on a case–control study, in which a group of patients (cases) are randomly sampled from a natural population, matched with normal subjects (controls) of a similar size in terms of demographical factors. Genome-wide genotyping is conducted for both case and control groups. For each case and control, their maternal and paternal parents are also genotyped, no matter whether these parents have a disease or are normal. Thus, our case–control design is constructed using random samples of families rather than random samples of individuals from a population.

Consider a single nucleotide polymorphism (SNP) with two alleles, A and a, which generate three genotypes AA (coded as 2), Aa (coded as 1) and aa (coded as 0). Owing to sex-linked selection, the genotypes have different segregating proportions in a population of each sex. Let P₂, P₁, P₀ and Q₂, Q₁, Q₀ denote three genotype frequencies in the female and male population, respectively. A mating between the maternal and paternal parents forms nine different genotypic combinations (Table 1). If the population is at Hardy–Weinberg disequilibrium (HWD), in which the mating is not random, then the frequencies of genotypic combinations are expressed as the products of maternal and paternal genotype frequencies plus disequilibria, D₁, D₂, D₃ and D₄. Let n_ij denote the size of the combination between maternal genotype i and paternal genotype j (i, j = 2, 1, 0), from which the genotype frequencies are estimated as

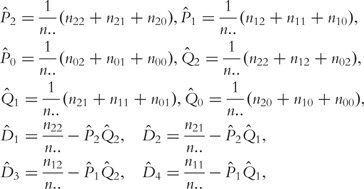(1)

where 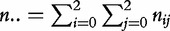is the total number of families sampled for cases or controls.

Table 1:

Mating types of three genotypes, their observations and frequencies under HWD or HWE and no distortion as well as Mendelian ratios of their offspring genotypes

		Frequency		Offspring genotype
Mating type	Observation	HWD	Equilibrium	AA	A|a	a|A	aa
AA × AA	n22	P2Q2 + D1	p2q2	1	0	0	0
AA × Aa	n21	P2Q1 + D2	2p2q(1 – q)			0	0
AA × aa	n20	P2Q0 – D1 – D2	p2(1 – q)2	0	1	0	0
Aa × AA	n12	P1Q2 + D3	2p(1 – p)q2		0		0
Aa × Aa	n11	P1Q1 + D4	4p(1 – p)q(1 – q)
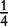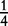Aa × aa	n10	P1Q0 – D3 – D4	2p(1 – p)(1 – q)2	0		0
aa × AA	n02	P0Q2 – D1 – D3	(1 – p)2q2	0	0	1	0
aa × Aa	n01	P0Q1 – D2 – D4	2(1 – p)2q(1 – q)	0	0
aa × aa	n00	P0Q0 + D1 + D2 + D3+D4	(1 – p)2(1 – q)2	0	0	0	1

Note: The parent-of-origin of the alleles for the heterozygous offspring is separated by a vertical line.

If there is a segregation distortion in a unisex population, the genotype frequencies are expressed as P₂ = p² + D_f, P₁ = 2p(1 – p) – 2D_f and P₀ = (1 – p)² + D_f for the female population and Q₂ = q² + D_m, Q₁ = 2q(1 – q) – 2D_m and Q₀ = (1 – q)² + D_m for the male population, respectively, where p and q are the frequency of allele A, and D_f and D_m are the coefficient of distortion in the female and male population, respectively. If the population is at Hardy–Weinberg equilibrium (HWE) and also there is no distortion, we express the genotype frequencies as p² or q² for AA, 2p(1 – p) or 2q(1 – q) for Aa, and (1 – p)² or (1 – q)² for aa (Table 1).

Whether the population is at HWE can be tested by formulating the hypotheses H₀: D₁ = D₂ = D₃ = D₄ = 0 versus H₁: at least one of D’s ≠ 0, from which the log-likelihood ratio test statistic is calculated and compared with a chi-square critical threshold with four degrees of freedom. The HWD test provides basic information about the mating behavior of the original population.

It is also interesting to investigate how the population has diversified between two sexes by testing H₀: p = q and D_f = D_m versus H₁: at least one of equality does not hold. The sex-dependent differences in allele frequency and distortion coefficient can be tested separately. If these tests are significant, this indicates that sex-linked selection has played a pivotal role in affecting the genetic diversity and evolution of populations, which can be thought of an important cause of genetic imprinting.

Offspring genotyping

In Table 1, we also give segregation ratios of offspring genotypes from each mating type under Mendel’s first law. As the genotypes of the parents are known, we can infer the maternal or paternal origin of the alleles in the offspring for all mating types, except for type Aa × Aa in which the parental origin of the alleles for the heterozygous offspring is unknown. For example, type AA (maternal) × Aa (paternal) produces offspring genotype AA and Aa, but it is clear that heterozygote Aa has allele A inherited from the maternal parent and allele a from the paternal parent. We use configuration A|a to separate the parental origin of alleles with one at the left side of the vertical line being from the maternal and the other at the right side from the paternal. Type Aa (maternal) × AA (paternal) produces genotypes AA and Aa, the latter of which should be configuration a|A. For type Aa (maternal) × Aa (paternal), which produces genotypes AA, Aa and aa, we do not know whether a given offspring of Aa is A|a or a|A.

Let n_ijk and m_ijk denote the observations of offspring genotype k (k = 2 for genotype AA, 1 for Aa, 0 for aa) derived from the i × j mating type in the cases and controls, respectively. The total observations for the cases and controls are expressed as 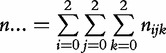and 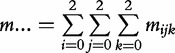. It is not difficult to give the observations of offspring genotypes AA and aa in case and control groups, respectively, by summing the numbers of the corresponding genotypes over all possible mating types. The same thing can be done for two configurations A|a and a|A, but for the offspring heterozygote Aa derived from Aa × Aa, these two configurations, despite mixed, can take a half of n₁₁₁ for each according to Mendel’s segregation ratio. Table 2 presents a 2 × 4 contingency table having four offspring genotypes/configurations in cases and controls, which is generated using observations of offspring genotypes.

Table 2:

Observations for four offspring genotypes/configurations in cases and controls

	AA	A|a	a|A	aa	Total
Case	n2 = n222 + n212 + n122 + n112	n1 = n211 + n201 + n111 + n101	n1′ = n121 + n111 + n021+n011	n0 = n110 + n100 + n010 + n000	R2+
Control	m2 = m222 + m212 + m122 + m112	m1 = m211 + m201 + m111 + m101	m1′ = m121 + m111 + m021 + m011	m0 = m110 + m100+m010 + m000	R1+
	R+2	R+1	R+1′	R+0

Test and estimation

Contingency table for genotypes and configurations

The derivation of our model starts with Table 2. Let R_uv denote the actual frequency of observations in the uth row (u = 1 for cases and 2 for controls) and vth column (v = 2 for AA, 1 for A|a, 1′ for a|A and 0 for aa), let R_u+ and R_+v denote column and row marginals, respectively, and let R₊₊ denote the grand total. If the genotypes/configurations are independent of the disease, then the probability of cell uv is simply the product of the probabilities of marginal categories u and v, expressed as .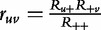

A Pearson statistic for testing the genotype/configuration–disease association can be calculated by

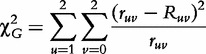(2)

which follows a chi-square distribution with (2 – 1) × (4 – 1) = 3 degrees of freedom. If 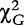>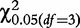, this suggests that the genotypes/configurations are significantly associated with the disease. Otherwise, there is no significant association between the genotypes/configurations and the disease.

Testing imprinting effect

Based on Table 2, we will test various genetic effects, including additive genetic, dominant genetic and imprinting genetic effects. According to Liu et al.’s model, we construct a 2 × 2 contingency table to test the additive effect (a) as

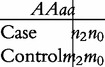(3)

a 2 × 2 contingency table to test the dominant effect (d ) as

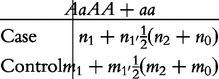(4)

a 2 × 2 contingency table to test the imprinting effect (I ) as

(5)

Chi-square test statistics are calculated for each effect, i.e. 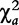, 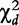and 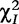, based on the corresponding contingency tables (3)–(5). As cell counts in these tables are formed by a weighted combination of observed cell counts in Table 2, these test statistics may not obey a chi-square distribution with one degree of freedom. Liu et al. [16] have proved that under the null hypothesis, these test statistics are asymptotically smaller than 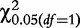. They further derived an approximation approach for determining the critical thresholds.

Estimating imprinting effects

The effect sizes of a, d and I are estimated by odd ratios (OR). A general form of contingency tables (3)–(5) is expressed as the joint distribution of two binary random variables X and Y, i.e.

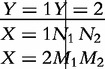from which an OR is calculated as

(6)

describing the extent to which the two variables are related through a particular effect. OR = 1 suggests no relationship. The confidence interval of the OR effect value is calculated as 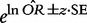, where z is a standard normal deviate corresponding to the level of confidence (z = 1.96, 2.576 for 95% and 99% confidence, respectively), and SE is the standard deviation of OR calculated as .

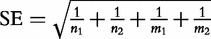Table 3:

Frequencies of different mating types and Mendelian ratios of offspring genotypes when paternal information is missing

Mating			Offspring genotype
Type	Observation	Frequency	AA	A|a	a|A	aa
AA ×–	n2	P2	P2 + P1	P1 + P0	0	0
Aa ×–	n1	P1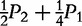
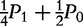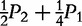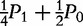aa ×–	n0	P0	0	0	P1 + P2	P0 + P1

Note: n₂., n₁. and n₀. are the cumulative numbers of families with maternal parent AA, Aa and aa, respectively. Genotype frequencies P₂, P₁ and P₀ here are expressed in terms of maternal parents.

Table 4:

Observations for fours offspring genotype/configuration in cases and controls when paternal information is missing

	AA	A|a	a|A	aa	Total
Case	n2 = n2.2 + n1.2	n1 = n2.1 +	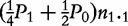n1′ = n0.1 +	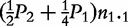n0 = n1.0 + n0.0	R2+
Control	m2 = m2.2 + m1.2	m1= m2.1 +	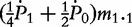m1′ = m0.1 +	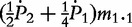m0 = m1.0 + m0.0	R1+
	R+2	R+1	R+1′	R+0

Note: n_i._k and m_i._k are the numbers of offspring genotype k from families with maternal parental genotype i in cases and controls, respectively. 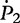, 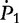and 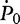are genotype frequencies of AA, Aa and aa in controls.

Table 5:

Population genetic parameters used to simulate family sizes according to Table 1

	Case		Control
Parameter	Female	Male	Female	Male
Mating disequil
D1	0.04		0.05
D2	0.04		0.05
D3	0.04		0.05
D4	0.04		-a
Situation 1
Allele frequency (A)	0.3	0.5	0.5	0.3
Allele frequency (a)	0.7	0.5	0.5	0.7
Distortion Df/Dm	0.05	0.10	0.10	0.05
Situation 2
Allele frequency (A)	0.3	0.3	0.5	0.5
Allele frequency (a)	0.7	0.7	0.5	0.5
Distortion Df/Dm	0.05	0.05	0.10	0.10

^aThis disequilibrium is not fixed, whose value is taken depending on the OR value.

Missing data

In practice, it is possible that some individuals have no information about the genotype of their parents. This missing problem does not affect the grouping of homozygote AA and aa but makes it difficult to distinguish between A|a and a|A. Later in the text, we describe a procedure for constructing a contingency table for four genotypes/configurations when one parent is missing. Consider a family-based control design in which the genotypes of maternal parents are available but those of paternal parents are missing with data structure tabulated in Table 3. In this situation, a 2 × 4 contingency table, as shown in Table 4, can be generated from Table 3.

From Table 4, we can now test and estimate the additive, dominant and imprinting effects at a given SNP using the procedure described earlier in the text. As can be seen, even if the parental information of some families is missing, we can still conduct imprinting test.

Worked example

The model was used to analyze a real data derived from a case–control study with family structure. The study population includes 58 families from the Milton S Hershey Familial Inflammatory Bowel Disease Registry, from which 105 offspring affected with IBD (cases) and 139 matched offspring without IBD (controls) were sampled for SNP genotyping. A total of five SNPs (Arg39Gln, Glu514Gln, Pro979Leu, Gly1066Gly and Pro979Leu) were typed from the candidate gene GLD5 for IBD [19].

None of the five SNPs displays a significant overall genetic effect based on a chi-square test for a 2 × 4 contingency table as shown in Table 2. This table is reorganized to a 2 × 2 contingency table based on additive (3), dominant (4) and imprinting effects (5). It was found that no significant additive and dominant effects exist to affect IBD. But tests for imprinting effects indicate that SNP Arg39Gln triggers a significant imprinting effect on IBD (P = 0.0476), and SNP Gly1066Gly displays a marginally significant imprinting effect (P = 0.0608). The OR values for these SNPs were estimated as 1.5 and 1.7, respectively, suggesting their importance in influencing IBD.

Simulation

We performed simulation studies to investigate the statistical properties of the model. A natural human population was mimicked, from which a panel of unrelated families (each including a male parent, a female parent, and one or more children) is randomly sampled. Given a total of 1000 subjects, the simulation considers two sampling strategies, 1000 × 1 (1000 families with a single child) and 200 × 5 (200 families with five children). For each sampling strategy, we considered two situations in which the same marker is segregating differently in populations of cases and controls but with or without difference between two sexes. The parameters that were used to simulate genotype frequencies of AA, Aa and aa and the size of each mating type for cases and controls are given in Table 5, from which the observations of offspring genotypes/configurations were obtained per Mendel’s segregation ratio.

We will focus on the calculation of the power and false-positive rates of detecting the imprinting effect from the model. The count data in 2 × 2 contingency table (5) were simulated by assuming different ORs. The OR describes and quantifies the extent to which the two variables are related. Values of OR = 1, 1.5, 2.0, 2.5 are regarded as no effect, small effect, moderate effect and large effect, respectively. The count data were simulated under each of these values. To simulate the data under these OR constraints, we relax the disequilibrium D₄ of in the control population. In each situation, simulation was replicated 1000 times to estimate the power of imprinting detection by the new model.

Table 6 gives the results of power calculation from simulated data from 1000 × 1 and 200 × 5 sampling strategies. In general, power is not affected by sex-specific differences in population structure (allele frequencies and distortion degree) because the results are similar in two situations. The strategy of sampling more small families performs better than that of sampling less larger families, especially when the genetic effect is modest. The power to detect the dominance effect is generally larger than that to detect the additive and imprinting effects because more data are used in the former than latter. On the other hand, the model has a small false-positive rate (<0.06 or 0.05) when each of these effects does not exist actually. The main message from the aforementioned simulation is that, for a given sample size, many families each of small size are recommended as a better sampling strategy to detect the additive, dominant and imprinting effects.

Table 6:

Power calculation of imprinting detection under different sampling strategies

Strategy		Situation 1			Situation 2
		a	d	I	a	d	I
200 × 5	OR = 1.0	0.049	0.017	0.045	0.052	0.015	0.052
	OR = 1.5	0.280	0.368	0.279	0.300	0.372	0.290
	OR = 2.0	0.582	0.853	0.569	0.723	0.856	0.557
	OR = 2.5	0.750	0.981	0.749	0.930	0.981	0.687
1000 × 1	OR = 1.0	0.038	0.017	0.043	0.057	0.018	0.041
	OR = 1.5	0.866	0.980	0.872	0.884	0.981	0.885
	OR = 2.0	0.996	1	0.996	1	1	1
	OR = 2.5	1	1	1	1	1	1

INTERACTION MODEL

TWO-LOCUS EFFECTS

The model can be extended to analyze two SNPs simultaneously that may interact with each other to determine the disease. Consider two SNPs, A (with two alleles A, a) and B (with two alleles B, b). At each SNP, genotypes/configurations are denoted as 2 for AA or BB, 1 for A|a or B|b, 1′ for a|A or b|B and 0 for aa or bb. The four haplotypes, AB, Ab, aB and ab, unite to produce 16 diplotypes with genotypic values defined as

where µ is the overall mean; a₁, d₁ and I₁ are the additive, dominant and imprinting effects at SNP A; a₂, d₂ and I₂ are the additive, dominant and imprinting effect at SNP B; i_aa, i_ad, i_aI,i_da, i_dd, i_dI, i_Ia, i_Id and i_II are the additive × additive, additive × dominant, additive × imprinting, dominant × additive, dominant × dominant, dominant × imprinting, imprinting × additive, imprinting × dominant and imprinting × imprinting interaction effects between the two SNPs. These parameters can be solved from the aforemntioned group of equations as

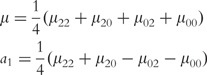(7)

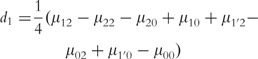(8)

(9)

(10)

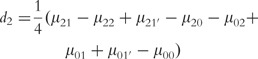(11)

(12)

(13)

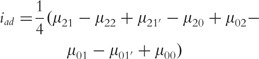(14)

(15)

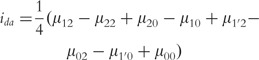(16)

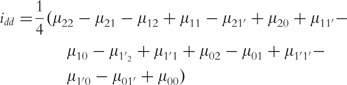(17)

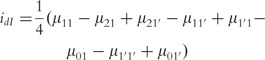(18)

(19)

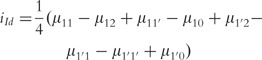(20)

(21)

Later in the text, we describe a procedure for testing each of these effects in a family-based case–control design.

Family structure

We assume that natural selection has driven two sexes to be segregating differently. Let p₁₁ = p₁p₂ + D_F, p₁₀ = p₁(1 − p₂) − D_F, p₀₁ = (1 − p₁)p₂ − D_F and p₀₀ = (1 − p₁)(1 − p₂) + D_F denote the frequencies of four haplotypes AB, Ab, aB and ab at two SNPs, A and B, in the female population, where p₁ and p₂ are the allele frequencies of A and B and D_F is the linkage disequilibrium between the two SNPs [20]. Similarly, we have parameters q₁₁, q₁₀, q₀₁, q₀₀, q₁, q₂ and D_M for the male population.

The two SNPs under consideration produce nine genotypes AABB, AABb, AAaa, AaBB, AaBb, Aabb, aaBB, aaBb and aabb with frequencies denoted as P₂₂, P₂₁, P₂₀, P₁₂, P₁₁, P₁₀, P₀₂, P₀₁ and P₀₀ for the female population and Q₂₂, Q₂₁, Q₂₀, Q₁₂, Q₁₁, Q₁₀, Q₀₂, Q₀₁ and Q₀₀ for the male population. Under non-random mating, these genotypes will form 81 genotype-by-genotype combinations, which frequencies are expressed as the products of maternal genotype frequencies and paternal genotype frequencies plus 64 disequilibria. Using a similar framework in Table 1 and Equation (1), we can estimate sex-dependent genotype frequencies and 64 disequilibria.

If each parent for a mating combination is homozygous for both markers, their offspring will have one genotype. As long as one parent is heterozygous for one marker, the offspring will have two or more genotypes. For one marker, the offspring will have two or more genotypes. However, only when both markers are heterozygous for at least one parent, the genotype frequencies of offspring will be determined by the recombination fraction between the markers (θ). In the Supplementary Material, the structure and frequencies of maternal by paternal genotype combinations under random mating and their offspring genotype frequencies are given. For a double heterozygote AaBb, its observed genotype may be derived from two possible diplotypes, AB|ab or Ab|aB, with different formation frequencies. For the female population, haplotype frequencies produced by each of these two diplotypes are expressed as

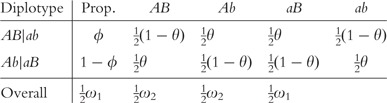with ϕ = p₁₁p₀₀/(p₁₁p₀₀ + p₁₀p₀₁) and ω₁ = (1 − θ)ϕ + θ (1 − ϕ) and ω₂ = θϕ + (1 − θ)(1 − ϕ) that sum to 1. Similarly, for males, we have the recombination fraction ϑ and proportions φ = q₁₁q₀₀/(q₁₁q₀₀ + q₁₀q₀₁), and ϖ₁ = (1 – ϑ)φ + ϑ(1 – φ) and ϖ₂ = ϑφ + (1 – ϑ)(1 – φ).

Let 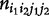denote the size of a particular mating type between maternal genotype i₁i₂ and paternal genotype j₁j₂, with i₁, j₁ = 2 for AA, 1 for Aa and 0 for aa; i₂, j₂ = 2 for BB, 1 for Bb and 0 for bb. Let 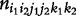denote the number of offspring genotype/configuration k₁k₂ in a family derived from maternal genotype i₁i₂ and paternal genotype j₁j₂, with k₁ = 2 for AA, 1 for A|a, 1′ for a|A and 0 for aa, k₂ = 2 for BB, 1 for B|b, 1′ for b|B and 0 for bb. All possible mating types, their sizes and frequencies, and the frequencies of their offspring genotypes/configurations, can be tabulated as follows:

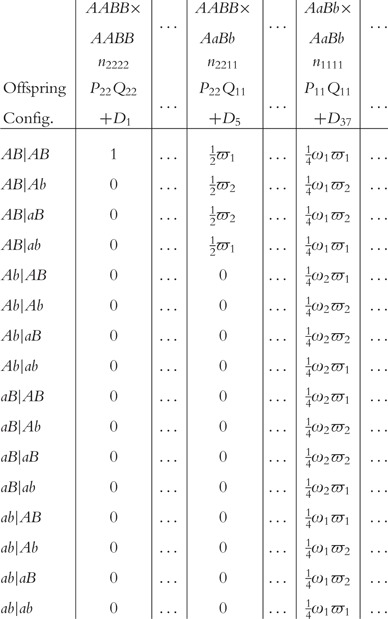where D₁, … , D₅, … , D₃₇, … are the coefficients of disequilibria.

A family design allows the simultaneous estimation of haplotype frequencies and the recombination fraction. By assuming HWD, Li and Wu [20] implemented a two-stage hierarchical EM algorithm to estimate haplotype frequencies (p₁₁, p₁₀, p₀₁, p₀₀) using parental mating type data (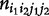) at the upper level, and the recombination fraction (θ) using segregation data of offspring genotypes from each mating type (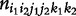). Liu et al. [21] relaxed this assumption to allow the estimation of these parameters. These estimated parameters can be used to construct a contingency table containing 16 diplotypes, with cells for cases expressed as

(22)

Similarly, the observations for controls can also be calculated, expressed as m₂₂, m₂₁, m_21′, m₂₀, m₁₂, m₁₁, m_11′, m₁₀, m_1′2, m_1′1, m_1′1′, m_1′0, m₀₂, m₀₁, m_01′ and m₀₀ for these offspring diplotypes, respectively.

Testing and estimating genetic effects

From contingency table (22), we can formulate a number of tests for the additive, dominant, epistatic and imprinting effects and their mutual interaction effects. This can be done according to the procedure as described in Equations (3)–(5). First, we generate a 2 × 2 contingency table for 15 genetic effects based on the expressions of (7)–(21). Second, the Pearson test statistic is calculated to test the significance of each effect and OR calculated to estimate each effect from these 2 × 2 contingency tables. Testing the additive, dominant and imprinting effects at each SNP and the additive × additive (i_aa), additive × dominant (i_ad), additive × imprinting (i_aI), dominant × additive (i_da), dominant × dominant (i_dd), dominant × imprinting (i_dI), imprinting × additive (i_Ia), imprinting × dominant (i_Id) and imprinting × imprinting interaction effects (i_II) between the two SNPs can be conducted using 2 × 2 contingency tables (23)–(37), respectively, i.e.

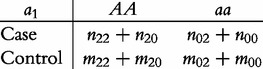(23)

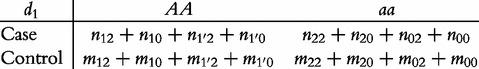(24)

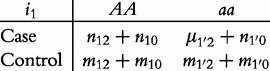(25)

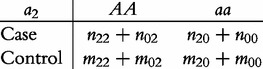(26)

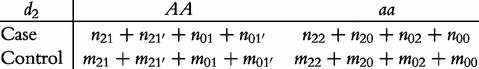(27)

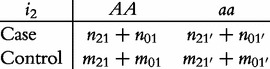(28)

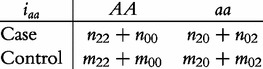(29)

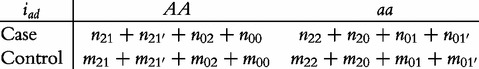(30)

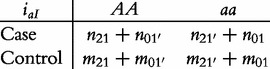(31)

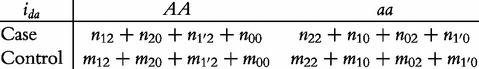(32)

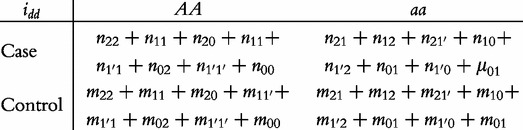(33)

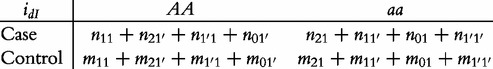(34)

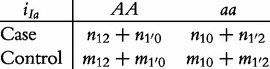(35)

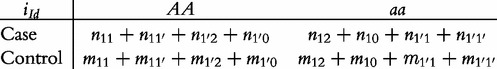(36)

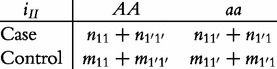(37)

The critical thresholds for the tests of the aforementioned effects can be obtained by an approximation approach derived by Liu et al. [16].

Computer simulation

We further simulated two SNPs to test the epistasis and imprinting effects and their interactions. We assume the two markers, with linkage disequilibrium 0.05 and recombination fraction 0.10, which are segregating with particular allele frequencies in cases and controls. Basic data structure was simulated using the tables given in the Supplementary Material. Here, we focus on the power calculation of additive × dominant (i_ad), imprinting × dominant (i_Id) and imprinting × imprinting effects (i_II). Under OR = 1.0 and 2.0, we simulated a 2 × 2 contingency table based on (33), (36) and (37), respectively. The allele frequencies of SNPs A and B are P = 0.6 (allele A) and q = 0.5 (allele B), respectively, in cases. The allele frequencies in controls were determined by adjusting the OR values. In both cases and controls, no sex-specific differences were assumed.

The model displays low false-positive rates under all sampling strategies. For a given sample size, more families each of small size are recommended because this strategy has better power than fewer large families (Table 7). It seems that imprinting × dominant and imprinting × imprinting effects can be easily detected. To well detect the additive × dominant epistatic effect, more sample size (at least 2000 × 1) is needed. Overall, the model is powerful for detecting epistatic effects and imprinting effects as well as their interaction effects.

Table 7:

Power calculation of epistatic and imprinting effect detection for two associated markers under different sampling strategies

Strategy		iad	iId	iII
200 × 5	OR = 1	0.0016	0.0490	0.0450
	OR = 2	0.0298	0.6796	0.4140
1000 × 1	OR = 1	0.0020	0.0560	0.0380
	OR = 2	0.4340	1	0.9670
2000 × 1	OR = 1	0.0030	0.0470	0.0440
	OR = 2	0.8610	1	1
3000 × 1	OR = 1	0.0040	0.0520	0.0410
	OR = 2	0.984	1	1

DISCUSSION

Given its significance and popularity, genetic imprinting has received tremendous attention in genetic and genomic studies [1,6]. Many studies have focused the molecular mechanisms of this phenomenon and its interplay with epigenetic marks [4]. Its genetic control as a complex trait has also been studied using linkage analysis [7–11,22] and the transmission disequilibrium test [12]. Two packages of software have been written for imprinting estimation [13].

As a powerful genetic tool, genome-wide association studies (GWAS) have been widely used to study the genetic architecture of complex diseases [14]. Thus, the integration of imprinting effect into a GWAS setting should enhance our capacity to study the genetic control of this phenomenon. In this article, we have presented a simple χ² model for testing imprinting effects in a case–control design by incorporating classic quantitative genetic principles into this design. Quantitative genetics and case–control design were regarded as two different areas until several modeling works by Wu and group [15–18]. This study has for the first time integrated imprinting effects into a case–control study by genotyping information for the parents of each case and control. By tracing the parental transmission path of alleles [20], the model is able to separate the effect of the same allele when it comes from different parents.

An important advantage of this model is that it is statistically simple because all tests are reflected in a 2 × 2 contingency table. For this kind of table, we can easily test the association between the two variables, i.e. disease and epigenetic effect in this situation, and estimate the extent of this association using ORs. Conventional log-linear regression models can also be used to test imprinting effects, but it would be time-consuming or even computationally intractable when a number of effects are tested simultaneously [16]. During the model derivation, we assume that the population is at HWE and that sampled families are independent of each other. But in practice, these assumptions may not be true. For a non-equilibrium population, conceptual models have been derived to model allelic and genotype frequencies and zygotic disequilibria [22,23]. When families are related, their structure can be modeled through identical-by-descent alleles [24].

The most meritorious feature of this model lies in its ability to characterize the genetic interactions of imprinting loci distributed throughout the genome. Many imprinted loci have been thought to be highly interacted through the mediation of proteins, RNA and DNA [25–27]. It is possible that these interactions play an important role in the evolution of genetic coadaptation to changing environment [28]. With the availability of whole-genome genotyping and sequencing technologies, it has been possible to comprehend genetic control mechanisms of complex diseases and, ultimately, integrate genetic information into routine clinical therapies for disease treatment and prevention. The model presented here provides a powerful statistical and computational tool for detecting genes that determine complex diseases in an imprinting and interactive way. It will help to elucidate a detailed picture of the genetic architecture for developmental disorders.

SUPPLEMENTARY DATA

Supplementary data are available online at http://bib.oxfordjournals.org/.

Key Points.

• Genetic imprinting is an important phenomenon thought to affect complex diseases in humans.

• Genetic imprinting may operate through interactions with other genetic effects, although this has not been fully explored.

• We describe a statistical model for detecting genetic imprinting and its interactions with additive, dominant and epistatic effects based on a simple 2 × 2 contingency table.

• By incorporating it into GWAS, this model will find its immediate implication for comprehending the genetic architecture of human diseases.

FUNDING

NSF/IOS-0923975 and UL1 TR000127 from the National Center for Advancing Translational Sciences (NCATS). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.

Biographies

Xin Li is a Master’s student in bioinformatics in the Center for Computational Biology at Beijing Forestry University.

Yihan Sui is a fourth-year undergraduate in biological science in the College of Biological Science and Technology at Beijing Forestry University.

Tian Liu is a post-doctoral researcher in statistical genetics in the Center for Lifespan Psychology at Max Planck Institute for Human Development.

Jianxin Wang is a Professor in information science in the College of Information at Beijing Forestry University.

Yongci Li is an Associate Professor in statistics in the College of Science at Beijing Forestry University.

Zhenwu Lin is an Assistant Professor in surgery in the Department of Surgery at Penn State College of Medicine.

John Hegarty is an Assistant Professor in surgery in the Department of Surgery at Penn State College of Medicine.

Walter A. Koltun is a Professor in surgery in the Department of Surgery at Penn State College of Medicine.

Zuoheng Wang is an Assistant Professor in biostatistics in the Department of Biostatistics at Yale University.

Rongling Wu is a Professor in biostatistics and bioinformatics in the Center for Statistical Genetics at Pennsylvania State University.