Abstract
Modern sequencing and genome assembly technologies have provided a wealth of data, which will soon require an analysis by comparison for discovery. Sequence alignment, a fundamental task in bioinformatics research, may be used but with some caveats. Seminal techniques and methods from dynamic programming are proving ineffective for this work owing to their inherent computational expense when processing large amounts of sequence data. These methods are prone to giving misleading information because of genetic recombination, genetic shuffling and other inherent biological events. New approaches from information theory, frequency analysis and data compression are available and provide powerful alternatives to dynamic programming. These new methods are often preferred, as their algorithms are simpler and are not affected by synteny-related problems.
In this review, we provide a detailed discussion of computational tools, which stem from alignment-free methods based on statistical analysis from word frequencies. We provide several clear examples to demonstrate applications and the interpretations over several different areas of alignment-free analysis such as base–base correlations, feature frequency profiles, compositional vectors, an improved string composition and the D2 statistic metric. Additionally, we provide detailed discussion and an example of analysis by Lempel–Ziv techniques from data compression.
Keywords: alignment-free, sequence-alignment, information theory, word-analysis
INTRODUCTION
Gene structure, function and phylogenetic relations are discovered by the basic comparison of known to unknown genetic material across organisms. Sequence comparison is pivotal to the success of basic phylogenetic and metagenomics research. For instance, large portions of common genetic material between organisms provide much evidence to suggest that they are somehow related. Furthermore, similar sequence data fuels conjecture that the associated functions are also similar.
Comparative research came from computer science that provided tools and algorithms to find specific substrings in larger sequences [1] for discovery. For instance, the Knuth–Morris–Pratt algorithm [2] and the Boyer–Moore [3] algorithm were used initially in the 1970’s [4] to locate regions of common DNA by exact matching of larger sequences. Later, a modified version of the Boyer–Moore [5] was applied in the 1980’s. As these algorithms assumed that the input strings contained exact matches, tiny mismatches found in DNA interrupted performance. This led to algorithms for approximate pattern matching [6] and others [7, 8].
Owing to the growth of inexpensive computing and improvements in sequence assembly technologies, there is now more sequence data available to bioinformatics research than ever before. Comparative genomics has been an obstacle to discovery [9, 10] and still manages to be a major factor in more current applications. Some of these applications include sequence assembly [11], evolutionary history comparison involving complications from synteny [12], horizontal gene transfer (HGT) discovery [13, 14], analysis by gene-shuffling [15] and many other applications where proper sequence comparison must be used [16].
Dynamic programming [17] has often been applied to comparing sequences in the aforementioned applications. As global and local alignment algorithms [18, 19] work base-by-base, they stand to be confused by the inherent mismatches, gaps, alternating blocks of sequence material and inversions that are easily found in genetic material. These methods may erroneously conclude that the functionally related sequences are largely unrelated, as they do not demonstrate any statistically significant alignment. Sequence length is also important to address when running an alignment from dynamic programming. For example, local and global, implemented in softwares such as ClustalW [20], have complexities of O(mn), and therefore it is clear that their resource requirements quickly escalate for larger sequences of lengths, m and n. It is often infeasible to perform comparisons of complete genomes by this approach owing to the large amount of time this would involve. For this reason, technologies requiring databases for speed such as BLAST [21], BLASTZ [22] and BLAT [23] have gained popularity. Other methods to help overcome some of the limitations of dynamic programming have come from diverse fields such as cloud computing [24], distributed computing [25] and parallel computing for multiple sequence comparison [26].
Frequency-based algorithms, which are driven by the statistics of word usage or similar, are becoming popular in research for discovery. This is because these approaches are not typically confused by the complexities caused by mismatches, gaps and sequence inversions that are often found between sequences for comparison [27]. For example, these methods function by evaluating the informational content between sequences, and therefore alternating blocks of DNA between two sequences will not be problematic. This form of alignment does not depend on where the features are found in the sequence, only that the sequence contains the features. Methods using frequency analysis also do not suffer from high algorithmic complexities as they are generally linear. They are, therefore, able to process larger sequences with fewer resources than dynamic programming algorithms and do not rely on having database support, as would BLAST, BLASTZ and BLAT. There is clearly a call for an alternative approach for sequence comparison done by methods that are not of dynamic programming, and therefore alignment-free methods are becoming attractive to bioinformatics research where the data are substantial and naturally dynamic.
In this article, we discuss some of the prominent methods stemming from vector or frequency-based analysis such as base–base correlations (BBC), feature frequency profiles (FFPs), compositional vectors (CVs), improved string composition and the D2 statistic metric. These methods have been chosen for discussion because of their simplistic nature and ease of application to research. We provide clear examples for the implementation of these methods and discuss their interpretation. We also provide discussion and an example of a method inspired by the Lempel-Ziv (LZ) compression techniques. This review aims to show how these alignment-free methods are integral to the quantification and discovery of sequence function and structure.
BACKGROUND
Methods for differentiating sequence data by using statistical concepts (factor frequencies and approaches from data compression) have attracted much interest. In their often-cited 2003 publication, Vinga et al. [28] reviewed some related methods, metrics and algorithmic implementations. Mantaci et al. [29] continued by illustrating other methods recently introduced for the alignment-free comparison, which were also based on a statistical approach. The authors organize the comparison algorithms in the following basic groups: (i) count factor frequencies, (ii) data compression and (ii) edit distances or on block edit distance—a special case involving moving entire blocks of a sequence.
Recent developments and the release of new technologies from the scientific community have caused the aforementioned references to become out-dated. Here, we discuss some of the more recent statistical methods, which involve frequency data for comparison. The approaches that we cover were chosen based on their simplicity of application and can be divided into the following categories: factor frequencies [30], composition vectors [31], improved CVs [32], data compression [33–35] and common substrings [6, 36].
FACTOR FREQUENCIES
Producing seminary ideas in 1948, C.E. Shannon’s Information Theory is the branch of mathematics, which is concerned with quantifying information and signal processing [37]. As DNA contains observable structures and patterns [38–40], tools from information theory (e.g. mutual entropy et al.) are appropriate for frequency analysis. Many of these methods break each sequence for comparison into numeric parts such as frequencies from the occurrence of types of words or k-mers (substrings of length k) occurring in the sequences. If two sequences are similar, then the derived k-mer frequencies would have similar distributions to reflect this likeness. If the sequences are different, then so are the frequency distributions.
To perform a k-mer study, the size of the motif is an important factor to consider. When collecting word frequencies from motifs, the size of the motif does make a difference to the results. According to Wu et al. [41], where the length of motif or window size is extensively discussed, there is a general rule of play when collecting word frequencies. When the sequences are obviously different (e.g. they are not related), then size of k-mers or window-size should be short. However, when the sequences are similar (known to be related), then the k-mers or window sizes can be longer. The reader is invited to consult the aforementioned reference for the details behind their general rule.
BBC by analysis of mutual information
Mutual information is a tool from information theory, which measures the amount of common information (or interaction) between two entities. Liu et al. [30] described the development of BBC, an algorithmic approach for determining sequence similarity by mutual information to infer phylogenetic relationships from complete genomes. In their work, an interval is established containing r-bases, making up strings of DNA to be used for multiple sequence comparison. In this interval, a vector is created from all possible joint probabilities of DNA pairs, as the total possible pairs 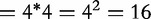 . In their article, they showed that the interval containing these joint probabilities in the sequence can often be expanded to get a better measurement of the difference between sequences.
. In their article, they showed that the interval containing these joint probabilities in the sequence can often be expanded to get a better measurement of the difference between sequences.
For 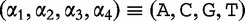 , the probability of finding base
, the probability of finding base 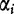 is denoted pi for
is denoted pi for 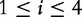 . For
. For 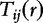 , the average relevance of the two-base combination (the feature) with different gaps from 1 to r (a range of r), the authors define a BBC by the following:
, the average relevance of the two-base combination (the feature) with different gaps from 1 to r (a range of r), the authors define a BBC by the following:
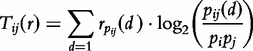 |
(1) |
for 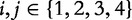 where
where 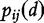 signifies the joint probabilities (e.g. the
signifies the joint probabilities (e.g. the 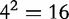 possible length-2 DNA words, which we refer to as features) of bases i and j at a distance of d. A BBC feature constitutes a 16D feature vector,
possible length-2 DNA words, which we refer to as features) of bases i and j at a distance of d. A BBC feature constitutes a 16D feature vector, 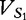 for a sequence S1 having a length of n1.
for a sequence S1 having a length of n1.
The statistical independence of two bases for a sequence of length- l is defined by 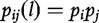 and its deviation is defined,
and its deviation is defined, 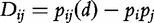 . Let
. Let 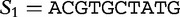 and
and 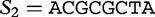 . We find the joint probabilities to populate the vector,
. We find the joint probabilities to populate the vector, 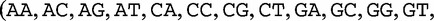
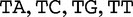 ), with the following equation for frequency,
), with the following equation for frequency, 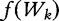 , from [42]:
, from [42]:
| (2) |
where 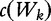 signifies the number of occurrences of a length- k word in a sequence of length- n1. The finalized vectors are the following.
signifies the number of occurrences of a length- k word in a sequence of length- n1. The finalized vectors are the following.
For two sequences S1 and S2 having the same length n1, the authors define the distance 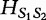 in the following equation.
in the following equation.
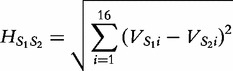 |
(3) |
By this calculation, we find that 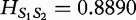 for the example aforementioned. Higher values for this metric indicate a greater spread in the frequency distribution and increasing dissimilarity; however, lower values indicate levels of increasing similarity (e.g. 0 if and only if the distributions being compared are equivalent). The authors note that
for the example aforementioned. Higher values for this metric indicate a greater spread in the frequency distribution and increasing dissimilarity; however, lower values indicate levels of increasing similarity (e.g. 0 if and only if the distributions being compared are equivalent). The authors note that 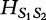 satisfies the definition of a sequence distance because (i)
satisfies the definition of a sequence distance because (i) 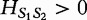 for different sequence lengths;
for different sequence lengths; 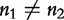 ; (ii)
; (ii) 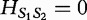 ; (iii)
; (iii) 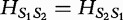 (symmetric); and (iv)
(symmetric); and (iv) 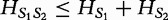 (triangle inequality).
(triangle inequality).
Liu et al. used phylogenetic trees, using branch weights gained from their BBC mutual information calculations. From the sequence data of 48 different Hepatitis E viruses, they constructed a phylogenetic tree, which was consistent with previous studies by diverse approaches [30].
FFPs
In [43], a feature frequency approach (UVWORD) was presented, which compares the DNA words from two sequences. Known as oligonucleotide profiling, the sliding-window method compared the encountered word frequencies of one sequence (the target) with another (the source). The sequence similarity was determined by how many words were common to both sequences. Word-based statistical models were also presented in [42], which investigated the occurrence, type and frequency of overlapping and embedded DNA words for sequence comparison.
Sims et al. [44] were interested in comparing whole genomes, even in situations where there are no common genes with high homology. To do this, they developed a variation of text compression, where the distance between word frequency profiles of two texts would be taken as a measure of dissimilarity. They substituted relative k-mer frequencies (FFP) for word frequencies.
A sliding window of size k is run through the sequence from position 1 to 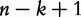 and counts the number of all
and counts the number of all 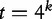 possible k-mers (the total number of features, for example) where four is the number of DNA bases. Although the k-mers extend themselves throughout the entire genome, the window is only allowed to span over the regions, which are completely free of sequencing gaps. The vector
possible k-mers (the total number of features, for example) where four is the number of DNA bases. Although the k-mers extend themselves throughout the entire genome, the window is only allowed to span over the regions, which are completely free of sequencing gaps. The vector 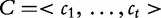 holds the t number of raw frequency counts for all possible words of length- k and is conventionally found by the following equation:
holds the t number of raw frequency counts for all possible words of length- k and is conventionally found by the following equation:
| (4) |
The length of the genome must be considered carefully at this vector-forming stage. If the genomes are of approximately equal length, and a <4-fold difference exists between sequences (four is the number of bases), then the method is conveniently used. However, if the sequences for comparison have extremely different lengths, then it is necessary to implement the block-FFP method, which is similar to the method described by [41]. This pre-processing step works to ensure that diverse genome lengths do not yield misleading results.
This step breaks up each sequence into smaller, manageable fragments of length- n1 (called FFP-blocks). In the case where the length of the shorter sequence is evenly divisible by the length of the longer sequence, the intervals (e.g. blocks) are made so that they have the same length as the shorter sequence. If a sequence (length n2) is not evenly divisible by the shorter sequence (length n1), then the total number of possible blocks for comparative analysis that can be made is n2 modulus n1.
A comparison by frequencies and the Jensen–Shannon Divergence test
Comparing genomes is actually comparing the sets of frequencies, which have been taken over an interval of sequence data. To make this comparison, we will follow Sims et al. [44] approach to use the Jensen–Shannon Divergence (JSD) test. The JSD test is a close relation to the Kullback–Leibler Divergence test, an information theoretic non-symmetric divergence measure of two probability distributions, that is extensively discussed in [45].
Once the vectors have been properly created, we are ready to apply the calculations that determine their distance apart. For two arbitrary vectors, 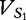 and
and 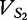 , prepared from sequences S1 and S2 for t, the number of features collected, the JSD is given below:
, prepared from sequences S1 and S2 for t, the number of features collected, the JSD is given below:
| (5) |
where,
| (6) |
for 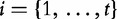 and KL is the Kullback–Leibler Divergence, below.
and KL is the Kullback–Leibler Divergence, below.
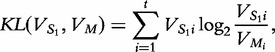 |
(7) |
where t is the number of features.
We now return to our earlier example of the two sequences 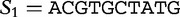 and
and 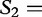
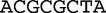 , which we compared by this JSD analysis. In this example, we populate vectors for these sequences using all length-2 words (2mers) in the sequences. The possible 2mers are ordered in the following order:
, which we compared by this JSD analysis. In this example, we populate vectors for these sequences using all length-2 words (2mers) in the sequences. The possible 2mers are ordered in the following order:
The FFP vectors 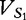 and
and 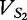 are created and populated by all available 2mers from sequences S1 and S2.
are created and populated by all available 2mers from sequences S1 and S2.
At each position i of both vectors, we apply 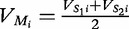 to get an average vector VM. The calculated values for all three vectors are shown in Table 1.
to get an average vector VM. The calculated values for all three vectors are shown in Table 1.
Table 1:
Positions 1 through 16 of the table of vectors for 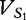 from
from 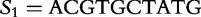 and
and 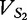 from
from 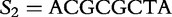 , aligned with position
, aligned with position
| 2mers position i |
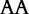 1 1 |
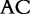 2 2 |
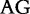 3 3 |
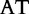 4 4 |
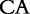 5 5 |
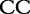 6 6 |
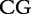 7 7 |
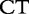 8 8 |
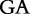 9 9 |
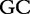 10 10 |
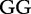 11 11 |
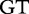 12 12 |
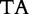 13 13 |
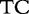 14 14 |
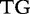 15 15 |
 16 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
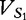 |
0 |  |
0 |  |
0 | 0 |  |
 |
0 |  |
0 |  |
 |
0 |  |
0 |
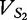 |
0 | 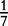 |
0 | 0 | 0 | 0 | 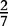 |
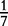 |
0 | 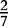 |
0 | 0 | 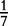 |
0 | 0 | 0 |
| VM | 0 | 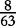 |
0 | 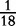 |
0 | 0 | 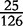 |
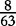 |
0 | 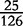 |
0 | 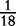 |
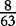 |
0 |  |
0 |
The elements of combined vector M by index are also shown. Frequencies of each 2mer are made by normalizing the occurrences of each 2mer in S1 and S2, respectively, by the total number of 2mer occurrences in each sequence.
To help the reader to keep track of the vectors and their frequencies at each position, we offer Table 1. We apply vectors 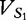 and VM (and then vectors
and VM (and then vectors 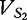 and VM) to Equation (7), which we illustrate below.
and VM) to Equation (7), which we illustrate below.
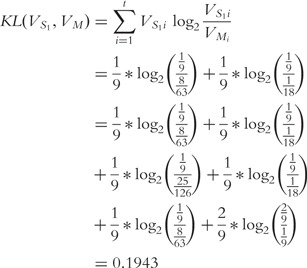 |
Following this theme for sequence S2 (vector 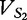 ), we find that
), we find that 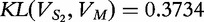 .
.
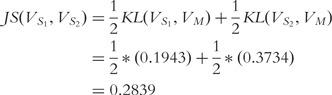 |
Provided the base 2 logarithm is used, the JSD is bounded below by 0 and 1 [45]. Higher values indicate increasing dissimilarity, but lower values indicate increasing similarity (e.g. 0 if and only if the distributions are identical). As 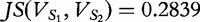 is close to zero, we conclude that the sequences S1 and S2 are similar by this test.
is close to zero, we conclude that the sequences S1 and S2 are similar by this test.
Sims et al. [44] reconstructed phylogenies from concatenated mammalian ‘intronic genomes’ by this method and found that their method closely reflected the accepted evolutionary history and agreed to results from a codon-sequence-based alignment technique [46].
Suffix trees by k-mer frequencies
The abundance of sequence noise (e.g. insertions, mismatches and similar) often necessitates frequency-based analysis. Similar to the work of [44] earlier in the text, another method of applying frequency data have been extensively explored by Soares et al. [47] to measure Euclidean distance between sequence data. When collecting frequency data, typically a window is opened at the beginning of the sequence, and the frequencies are found for all encountered words. The authors depart from this method by presenting a new approach that determines a single optimal word length (k-mers) from which to generate a frequency distribution for application to suffix trees.
To collect these optimal k-mer frequencies, Soares et al. [47] began by determining all words in the DNA alphabet (e.g. {A,C,G,T}) of length- k. An optimal resolution range of k-mers for the given set of genomes was described in [44] and later applied to the work of Soares et al. [47] for instance, 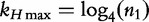 for a sequence of length- n1. To find a value applicable to all sequences under analysis, we choose n1 as the length of the greater sequence and K as the smaller integer greater than
for a sequence of length- n1. To find a value applicable to all sequences under analysis, we choose n1 as the length of the greater sequence and K as the smaller integer greater than 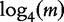 . For m sequences of different lengths, the peak value of word length (K) that is applicable to all sequences of the study is described by the following two equations:
. For m sequences of different lengths, the peak value of word length (K) that is applicable to all sequences of the study is described by the following two equations:
In the logarithmic equation, L is given the smallest integer not less than the calculated value.
The exhaustive lists of DNA L-words for n sequences were created by combinatorial means. For words of length- L, the size of the list can be described mathematically: 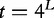 . The frequencies of these words are similarly found as in [44]. Once amassed, they are added to an
. The frequencies of these words are similarly found as in [44]. Once amassed, they are added to an 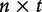 matrix to create a global profile of all L-word frequencies of all input sequences. Next is the development of the genetic distance for the suffix trees. This pairwise standard Euclidean distance between pairs of sequences is calculated by the following:
matrix to create a global profile of all L-word frequencies of all input sequences. Next is the development of the genetic distance for the suffix trees. This pairwise standard Euclidean distance between pairs of sequences is calculated by the following:
| (8) |
for w, representing the k-mer and t representing the exhaustive list of words, respectively, and 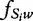 represents the relative frequency of w in the sequence Si. These values may be applied to suffix trees for convenient sequence analysis across large sets of sequences.
represents the relative frequency of w in the sequence Si. These values may be applied to suffix trees for convenient sequence analysis across large sets of sequences.
Composition vectors based on k-mer frequencies
There are two main string composition vectors that we will discuss; the CV and the complete composition vector (CCV). Discussed in [48–50], a k-mer frequency CV for a genomic sequence is a distribution of frequencies of length- k motifs, which are used for comparison across sequences. The CV method contains motif frequencies of the same length, whereas the CCVs contain motif frequencies of unequal length.
The basic steps of creating CVs are the following: (i) find the frequencies of the motifs in a sequence, (ii) create a vector by organizing the frequencies in some order, (iii) compute the distance between every two composition vectors to form a distance matrix, and optionally (iv) construct the phylogenic tree based on the differences. This last step is not essential but may be helpful when evaluating the degree of closeness between a set of sequences.
Creation of Composition Vectors (CVs, CCVs)
The creation of a CCV is similar to that of a CV except that the input frequencies are made from strings of differing lengths. Despite its extra computational expense, the CCV method was found to provide finer evolutionary information than the CV method [32].
Following the discussion from [31, 32], we define S1 to be a sequence consisting of n1 nucleotides and let  to be the observed frequency of the length- k motif in S1. We define
to be the observed frequency of the length- k motif in S1. We define 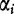 for
for 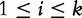 to be a nucleotide such that
to be a nucleotide such that 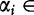 {A, C, G, T} for
{A, C, G, T} for 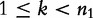 . Next, for some constant K, the largest string length we consider, we define
. Next, for some constant K, the largest string length we consider, we define 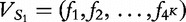 as the combined vector. Finally, we define
as the combined vector. Finally, we define 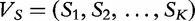 as the combined vector. The vectors,
as the combined vector. The vectors, 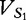 and VS, reflect both random mutation and selection. Lu et al. noted that there is an underestimation of selective evolution for both these vectors when the data are normalized according to Equation (9), which is also discussed in [51] and [52]. For the observed frequency of
and VS, reflect both random mutation and selection. Lu et al. noted that there is an underestimation of selective evolution for both these vectors when the data are normalized according to Equation (9), which is also discussed in [51] and [52]. For the observed frequency of 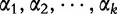 , the normalizing equation is described by the following:
, the normalizing equation is described by the following:
| (9) |
where fe represents the expected frequency and is defined by:
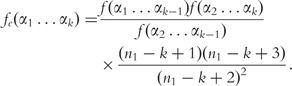 |
for 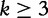 and
and  . Lu et al. [32] note that this normalization method underestimates the actual reality of the data. Next, we describe their modified method, which overcomes this problem.
. Lu et al. [32] note that this normalization method underestimates the actual reality of the data. Next, we describe their modified method, which overcomes this problem.
Creation of improved CCVs
To overcome this setback, Lu et al. [32] propose an improvement to CVs and CCVs. The improved CCV (ICCV) is made assuming that the sequence bases all occur with equal probability, according to the expected frequency of a k-mer string. The variance of frequency of a given sequence S1 of length- n1 is also based on this assumption. We first define the expected motif frequencies and their variance in the vectors. For any given k-mer, a position in the sequence is given as:
for integer i such that 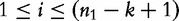 . This upper bound is the maximum observed frequency for a string
. This upper bound is the maximum observed frequency for a string  in S1. Therefore, it can be shown that
in S1. Therefore, it can be shown that
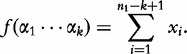 |
(10) |
The expectation and variance of  are described in the following equations.
are described in the following equations.
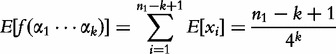 |
(11) |
and the variance;
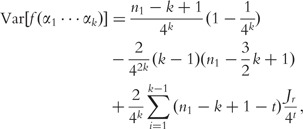 |
where Jr, is defined by the following.
for integer r such that 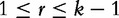 . See [53] for a full derivation. One of the problems with the original CV and CCV concerns the denominator, which requires a square root operation without which Lu et al. warn of a problem of over-estimation. To mitigate the over-estimation problem, the authors apply the data’s expectation and variance to the normalizing equation given later in the text and complete the construction of the ICCV. The normalization of each observed frequency of a k-mer string, knorm is given by the following equation:
. See [53] for a full derivation. One of the problems with the original CV and CCV concerns the denominator, which requires a square root operation without which Lu et al. warn of a problem of over-estimation. To mitigate the over-estimation problem, the authors apply the data’s expectation and variance to the normalizing equation given later in the text and complete the construction of the ICCV. The normalization of each observed frequency of a k-mer string, knorm is given by the following equation:
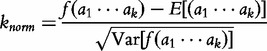 |
(12) |
for 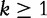 .
.
Distance measurement
We next discuss how the distance between vectors is measured. For two sequences, S1 and S2, let their vectors be defined, 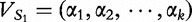 of length- k and
of length- k and 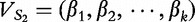 , also of length- k. We define the normalized distance between the vectors by the following:
, also of length- k. We define the normalized distance between the vectors by the following:
| (13) |
where 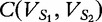 is the cosine distance of the angle between
is the cosine distance of the angle between 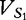 and
and 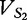 and is described by the following.
and is described by the following.
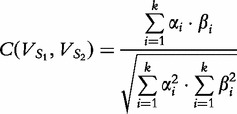 |
(14) |
Lu et al. show that the ICCV method fixes the observed overestimation problems with the previous method and generates more accurate and robust results. They also show that its results are consistent with methods based on alignment by dynamic programming in phylogeny.
A revised string composition method
Chan et al. [31] revisit the composition vector method and apply an analysis of entropy from information theory and operations research. Their method begins by finding the frequencies of each base of a k-string sequence. For example, from  , the base frequencies are the following:
, the base frequencies are the following: 
The second step is to estimate the expected frequency q(u) for each k-string. For this step, the authors suggested determining the relationship between 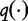 and
and 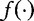 by maximizing the following system of equations from Hua et al. [54]. Here, the entropy in
by maximizing the following system of equations from Hua et al. [54]. Here, the entropy in 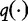 is maximized given the frequency f(v) for all
is maximized given the frequency f(v) for all 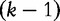 -strings v.
-strings v.
| (15) |
Chan et al. depart from the work of Hua et al. by making no assumptions between 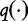 and
and 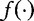 . Instead, they maximized the following equations, which estimate the expected frequencies q(u).
. Instead, they maximized the following equations, which estimate the expected frequencies q(u).
| (16) |
for 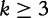 , which was introduced by, Qi et al. [49] and,
, which was introduced by, Qi et al. [49] and,
| (17) |
for 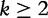 , from Yu et al. [55]. For any k-string u,
, from Yu et al. [55]. For any k-string u,  and
and  represent the left and right nucleotides of the word and
represent the left and right nucleotides of the word and 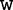 represents the middle
represents the middle 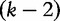 -string located between them. In the second equation, all these elements are assumed to occur independently. From these equations, the authors created a new system of equations (later in the text) to solve where the right-hand side concerns sequence frequencies and the left-hand side concerns the estimations:
-string located between them. In the second equation, all these elements are assumed to occur independently. From these equations, the authors created a new system of equations (later in the text) to solve where the right-hand side concerns sequence frequencies and the left-hand side concerns the estimations:
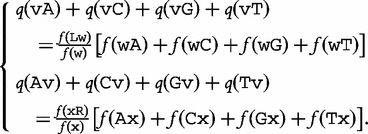 |
(18) |
When this system is maximized, Chan et al. [31] note that the system generates a set of all possible estimation formulas 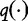 from which one can be selected to maximize the entropy. In general, from any existing estimation formula
from which one can be selected to maximize the entropy. In general, from any existing estimation formula 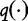 given in terms of
given in terms of 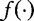 , the authors note that the set of constraints such as the following can be derived:
, the authors note that the set of constraints such as the following can be derived:
| (19) |
where the left- and right-side frequency values, l(v) and r(v) are derived from frequency information (f(v)) for each length-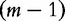 motif v. To obtain the unique q(u) for all u, the following optimization problem is solved:
motif v. To obtain the unique q(u) for all u, the following optimization problem is solved:
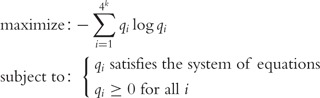 |
where 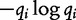 is Shannon’s entropy calculation. The authors apply this information to phylogenetic tree analysis in a similar fashion as we saw in Lu et al. [32].
is Shannon’s entropy calculation. The authors apply this information to phylogenetic tree analysis in a similar fashion as we saw in Lu et al. [32].
Maximum Entropy Principle. After solving the problem aforementioned, a system of noise estimation formulas is provided. Note: a motif appears as the following: 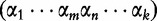 and can be split into to sub words.
and can be split into to sub words.
| (20) |
where, qMEP is the maximized entropy principle score for the sequence data and,
| (21) |
We note that 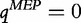 if
if  and that
and that  and
and 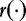 are parametric functions. Different
are parametric functions. Different 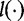 and
and 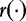 will give different estimation formulas and will have varying levels of success. The authors applied this test to create phylogenetic trees from simulated data sets. Their results showed differentiation of ‘closely related’ sequences.
will give different estimation formulas and will have varying levels of success. The authors applied this test to create phylogenetic trees from simulated data sets. Their results showed differentiation of ‘closely related’ sequences.
D2 statistic
The statistic D2, is the number of approximate word matches of length k between sequences 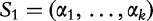 and
and 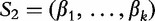 , with
, with 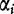 and
and 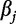 belonging to an alphabet
belonging to an alphabet 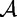 (in this case, the DNA bases), which is distributed according to a letter distribution parameterized by η [56]. This statistic is applied to two populations of differing means, but identical dispersion matrices [57], to determine distance. Recently, the statistic has evolved to provide more exact approximations by asymptotic regimes for uniform and non-uniform distributions [58, 59]. Mathematically, the D2 statistic is defined by the following. From [60], given sequences
(in this case, the DNA bases), which is distributed according to a letter distribution parameterized by η [56]. This statistic is applied to two populations of differing means, but identical dispersion matrices [57], to determine distance. Recently, the statistic has evolved to provide more exact approximations by asymptotic regimes for uniform and non-uniform distributions [58, 59]. Mathematically, the D2 statistic is defined by the following. From [60], given sequences 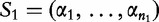 of length- n1 and
of length- n1 and 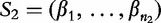 of length- n2 and
of length- n2 and  , then D2 is defined by the following:
, then D2 is defined by the following:
| (22) |
where 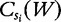 is the number of occurrences of W in sequence Si.
is the number of occurrences of W in sequence Si.
The 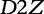 statistic [61] was developed to compare gene regulatory sequences and offered an improvement in performance to D2, but could still fail due to noise complications [62, 60]. To combat this problem of noise, Reinert et al. [60] propose a new statistic
statistic [61] was developed to compare gene regulatory sequences and offered an improvement in performance to D2, but could still fail due to noise complications [62, 60]. To combat this problem of noise, Reinert et al. [60] propose a new statistic 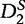 , which is a self-standardized D2.
, which is a self-standardized D2.
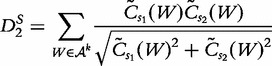 |
(23) |
For 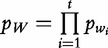 , the probability of occurrence of wi for
, the probability of occurrence of wi for 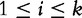 and
and 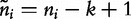 for i sequences, the centralized count variables,
for i sequences, the centralized count variables, 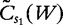 and
and 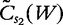 , are therefore denoted by the following.
, are therefore denoted by the following.
Reinert et al. also proposed a second statistic, 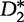 , which we shall presently define. To introduce this statistic, we replace p(a), the unobserved feature probabilities, by
, which we shall presently define. To introduce this statistic, we replace p(a), the unobserved feature probabilities, by 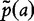 (the observed) for the relative count of letter a in the concatenation of the two sequences that are based on the assumption that the two sequences are independent. We note that these sequences are both independent and contain identically distributed (i.i.d.) bases. The estimated probability of occurrence of
(the observed) for the relative count of letter a in the concatenation of the two sequences that are based on the assumption that the two sequences are independent. We note that these sequences are both independent and contain identically distributed (i.i.d.) bases. The estimated probability of occurrence of 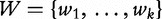 is obtained by
is obtained by 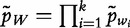 . We now define
. We now define 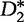 by the following.
by the following.
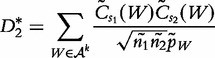 |
(24) |
The authors found that the 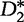 statistic out-performed both the D2 and
statistic out-performed both the D2 and 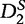 statistics in terms of accurate detection of relatedness between two sequences. The statistical power of both
statistics in terms of accurate detection of relatedness between two sequences. The statistical power of both 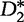 and
and 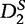 increases with sequence length and tends to 1 as the sequence length tends to infinity under a common motif model. When applied to organizing sequence reads of next-generation sequence assembly tasks, and to phylogeny tasks, the
increases with sequence length and tends to 1 as the sequence length tends to infinity under a common motif model. When applied to organizing sequence reads of next-generation sequence assembly tasks, and to phylogeny tasks, the 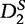 statistic provided a powerful alignment-free comparison tool [63]. However, when studying phenomena in the patten transfer model such as HGT, the power of these statistics declines and converges to a limit that is generally <1 as the sequence length tends to infinity. The primary reason for this limitation is that the means of the word counts in these statistics eventually become increasingly similar to each other. This resemblance works to desensitize the detection of patterns between the sequences.
statistic provided a powerful alignment-free comparison tool [63]. However, when studying phenomena in the patten transfer model such as HGT, the power of these statistics declines and converges to a limit that is generally <1 as the sequence length tends to infinity. The primary reason for this limitation is that the means of the word counts in these statistics eventually become increasingly similar to each other. This resemblance works to desensitize the detection of patterns between the sequences.
To improve the detection of relationships across sequences using alignment-free methods in the pattern transfer model, Liu et al. [64] developed new statistics (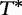 , TS and
, TS and 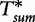 , described later in the text), which they claim have a better statistical power. The authors present them with simulations to demonstrate their power and to show that they are more appropriate for applications where long sequence-lengths are a concern.
, described later in the text), which they claim have a better statistical power. The authors present them with simulations to demonstrate their power and to show that they are more appropriate for applications where long sequence-lengths are a concern.
Based on approximating the mean by a sample mean, the approach of the new statistic is to partition a long sequence of length- n1 into consecutive non-overlapping (discrete) subintervals of length- r, 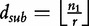 . Then, the
. Then, the 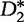 and
and 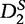 values are calculated over each ith subinterval for word counts w and are denoted
values are calculated over each ith subinterval for word counts w and are denoted 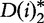 and
and 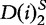 , respectively. For, two sequences of length n1 where,
, respectively. For, two sequences of length n1 where, 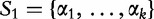 and
and 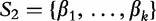 , these statistics are defined by the following equations.
, these statistics are defined by the following equations.
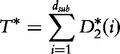 |
(25) |
and
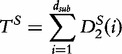 |
(26) |
The final statistic from [64] is drawn over two sequences S1 and S2 of lengths n1 and n2, respectively, to conclude the degree of relatedness.
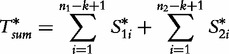 |
(27) |
for,
| (28) |
and
| (29) |
where,
| (30) |
Although 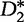 and
and 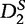 are generally more powerful statistics than
are generally more powerful statistics than 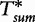 and
and 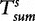 for the common motif model, this is not the case for studies concerning the pattern transfer model. For this reason, the statistics presented by Liu et al. are desirable in pattern transfer model applications when the sequence data are long.
for the common motif model, this is not the case for studies concerning the pattern transfer model. For this reason, the statistics presented by Liu et al. are desirable in pattern transfer model applications when the sequence data are long.
DATA COMPRESSION AND DICTIONARIES
Alignment-free methods, involving data compression and dictionaries, are based on the idea that the more similar two sequences are to each other, then the better one sequence can be created from the parts of another. Inspired by LZ compression technologies [65], we offer an example of sequence comparison, from Otu et al. [34].
For the sequences S1, S2 and SQ, we define 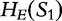 ,
, 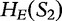 and
and 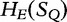 to be the exhaustive sets of all words found using an approach from LZ-compression. We then analyze the sets of sequence histories to determine how much of one sequence can be built out of the sequence histories of another. We define
to be the exhaustive sets of all words found using an approach from LZ-compression. We then analyze the sets of sequence histories to determine how much of one sequence can be built out of the sequence histories of another. We define 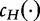 to be the number of components in a history of a sequence S and
to be the number of components in a history of a sequence S and 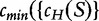 over all histories of S.
over all histories of S.
For S1 and S2, we have 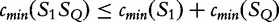 , by the sub-additivity of the LZ-complexity. To compute the closest similarity of S1 and SQ,
, by the sub-additivity of the LZ-complexity. To compute the closest similarity of S1 and SQ, 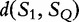 , and S2 to SQ,
, and S2 to SQ, 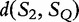 , we take the smallest value of
, we take the smallest value of 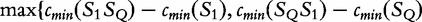 } and
} and 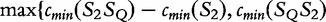
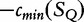 }, respectively.
}, respectively.
Compare the sequence similarity of S1 to SQ and S2 to SQ. We first find the sequence histories to compare distances. We introduce an example to demonstrate how this is performed.

By the author’s method, we conclude that S1 and SQ are more similar, as 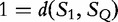
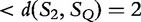 . The authors used this method to populate phylogenetic trees from simulated sequences to show clusterings of ‘related’ sequences.
. The authors used this method to populate phylogenetic trees from simulated sequences to show clusterings of ‘related’ sequences.
Text compression algorithms
Data compression is nearly out of the scope of this article; however, they are worth mentioning because they also provide an alignment-free approach to comparing sequence data. These general purpose compression algorithms may be based on the Ziv and Lempel [65] methods (as seen earlier in the text). Recent advances have been developed in [66, 67] and [68]. Cao et al. [33] proposed a memory-based algorithm called expert model to compress DNA by applying statistical information, gained from previous encounters of a particular symbol.
Average common substring
Ulitsky et al. [35] built on information theoretic tools, such as Kullback–Leibler relative entropy, to find a distance between entire genomes, even if their lengths vary. The average common substring measure that they proposed is based on computing the average lengths of maximum common substrings. They used these average lengths between the sequences to construct phylogenetic trees from an efficient algorithm.
Let S1 and S2 be sequences, of lengths n1 and n2 where, 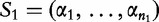 and
and 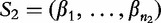 . For any position i, let r(i) be the length of longest substring in S1 that exactly matches a substring in S2 starting at some position j. These lengths r(i) are averaged to get a measure,
. For any position i, let r(i) be the length of longest substring in S1 that exactly matches a substring in S2 starting at some position j. These lengths r(i) are averaged to get a measure, 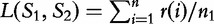 . As
. As 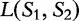 represents a common sequence found in both sequences, then the longer it is, the more similar the sequences are to each other. This value is only a similarity measure and must still be converted to a distance value. The inverse is taken to get the distance, and then a ‘correction term’ is subtracted to ensure that the distance
represents a common sequence found in both sequences, then the longer it is, the more similar the sequences are to each other. This value is only a similarity measure and must still be converted to a distance value. The inverse is taken to get the distance, and then a ‘correction term’ is subtracted to ensure that the distance 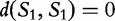 (will always be zero). This allows for,
(will always be zero). This allows for, 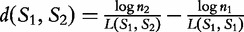 where
where 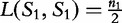 to provide the correctional term,
to provide the correctional term, 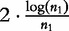 , which converges to 0 as
, which converges to 0 as  . As the measure,
. As the measure,  is not symmetric, the authors compute the final average common substring measurement between the two strings,
is not symmetric, the authors compute the final average common substring measurement between the two strings, 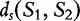 by the following.
by the following.
| (31) |
We now show how to apply this method to determine the distance between two sequences. Let 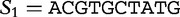 and
and 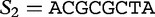 , of lengths
, of lengths 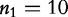 and
and 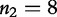 , the method finds all common substrings as shown in Table 2.
, the method finds all common substrings as shown in Table 2.
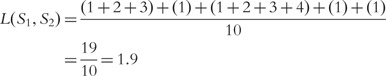 |
and
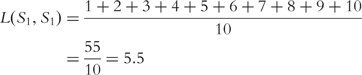 |
Table 2:
The similar and different chunks, taken in order from each sequence
| Sequence | Same | Different | Same | Different |
|---|---|---|---|---|
| S1 |  |
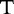 |
 |
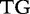 |
| S2 |  |
 |
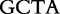 |
Then the distance between the two sequences is
Similarly, we can calculate 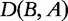 as follows:
as follows:
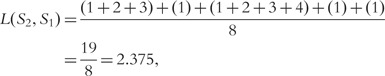 |
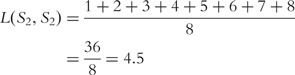 |
and,
For our example aforementioned, where 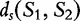 is not symmetric, the symmetric distance is
is not symmetric, the symmetric distance is 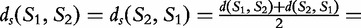
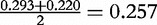 . This value can be used as a weight for a sequence in a phylogenetic tree to show relations between sequences of a set.
. This value can be used as a weight for a sequence in a phylogenetic tree to show relations between sequences of a set.
APPLICATIONS OF ALIGNMENT-FREE METHODS
Biological data and sequence assembly
In genetic sequence assembly work, alignment technologies are important for determining the adjacency of reads (or contigs which are partially combined reads) to reconstruct the original sequence. During a typical de novo assembly task, a sequencing machine may split the genome into many millions (trillions) of reads that must be reassembled like from a jigsaw puzzle. This reconstruction task is computationally intensive, as each piece must be compared with every other piece in the pool to determine adjacency. This task is frustrated when there are foreign reads of other sequences to be assembled in the same data pool. The extra sequence data serve to massively broaden the search space when determining the adjacency of a read, as there are many more comparison operations to perform. To reduce the workload of the assembly project, it is therefore desirable to place all related reads into a unique groups (bins) and apply the main assembly algorithms to each organism separately.
A novel approach, requiring no database support, was introduced by [69, 70] to order the organisms in the pool into separate bins. The authors’ method creates CVs from restriction sites [71] to determine inter-sequence relatedness and place the sequences from the mixed pool into separate groups. This type of proposed alignment is for a global analysis, as it is able to process and compare sequences in a pool of arbitrarily size. They applied their work to the sequence assembly reads and contigs of Bifidobacterium longum, Mycobacterium bovis, Clostridium tetani, Staphylococcus aureus, Burkholderia pseudomallei and Campylobacter jejuni. Based on the similarity of proportional values contained in the CVs, the authors were able to differentiate the sequence material by organism.
The method uses spectrum sets that are lists of motifs made up of permutations of restriction enzymes, which are specific and unique sites in DNA where enzymes are able to cleave. To create a spectrum set from the bacterial restriction site, 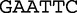 , we observe that the motif contains, two
, we observe that the motif contains, two 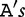 , two
, two 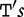 , one
, one  and one
and one  . A spectrum set contains all motifs, which have exactly the same number of each base. For example, for the bacterial restriction site,
. A spectrum set contains all motifs, which have exactly the same number of each base. For example, for the bacterial restriction site, 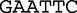 , there are 156 motifs in the spectrum set that have the same base composition. A vector of length-156 is constructed from the proportions of each of these motifs, which are contained in the sequence data. For example, to populate the vector
, there are 156 motifs in the spectrum set that have the same base composition. A vector of length-156 is constructed from the proportions of each of these motifs, which are contained in the sequence data. For example, to populate the vector 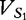 of the motif proportions of wi for
of the motif proportions of wi for  for sequence S1 of length- n1, the following equation is used,
for sequence S1 of length- n1, the following equation is used,
| (32) |
where 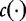 represents the number of occurrences of the motif in the sequence. This equation serves to normalize the proportions so that the values can be compared across diverse data sets. The authors noted that similar sequence data gave rise to similar vectors that they used to organize the sequence data.
represents the number of occurrences of the motif in the sequence. This equation serves to normalize the proportions so that the values can be compared across diverse data sets. The authors noted that similar sequence data gave rise to similar vectors that they used to organize the sequence data.
Chromosomal data and phylogeny
In addition, in [70], it was shown that the method could also be applied to create phylogenetic trees, which were extremely similar to trees created by NCBI’s taxonomy tree making software. In this work, they used chromosomal sequences of arbitrarily chosen organisms (Caenorhabditis elegans, Canis lupus familiaris, Drosophila melanogaster, Mus musculus, Mycoplasma hyorhinis, Oryctolagus cuniculus and Rattus norvegicus) and built a tree that replicated that of NCBI’s taxonomy analysis software (available at http://www.ncbi.nlm.nih.gov/guide/taxonomy/).
HGT
HGT is the phenomenon where genetic material is shared between unrelated organisms. Evolutionary [72] and Phylogenetic studies [73] have observed common material between unrelated bacterial organisms, which suggests a parallel evolutionary history. The discovery of similar regions of DNA between two enormous genomes is not a trivial task, and therefore alignment-free methods have proven to be helpful in this field. In [36], the authors present Alignment-Free Local Homology (alfy), a method to determine HGT by an alignment-free approach. As determining evolutionary distances from word frequency data is a non-trivial task, the authors report that their method is conveniently able to make this determination.
We cite and discuss the method and example presented in [36] where the query sequence, denoted as 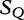 of Table 3, is compared with the subject sequence,
of Table 3, is compared with the subject sequence, 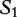 . For each position in the query
. For each position in the query 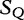 , the alfy algorithm determines the shortest substring that starts in query, which is absent from the subject sequence.
, the alfy algorithm determines the shortest substring that starts in query, which is absent from the subject sequence.
Table 3:
The sequences to compare by the alfy method
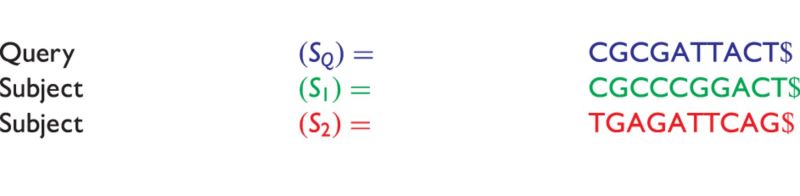 |
To compare sequences, we find the shortest sequence in the query (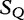 ), which is absent from a subject.
), which is absent from a subject.
In Tables 4 and 5, this comparison task is shown by a string of numbers (match scores), which show the length of the substring starting in (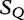 ) that are absent in (
) that are absent in (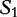 ). If the consecutive intervals created by these matching scores are wide (e.g. long strings of uninterrupted consecutive integers), then the sequences are closely related (similar); however, if the intervals are generally short, then the sequences are not closely related (dissimilar).
). If the consecutive intervals created by these matching scores are wide (e.g. long strings of uninterrupted consecutive integers), then the sequences are closely related (similar); however, if the intervals are generally short, then the sequences are not closely related (dissimilar).
Table 4:
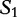 is compared with
is compared with 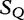 to determine the shortest substring in
to determine the shortest substring in 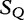 , which is absent from
, which is absent from 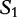
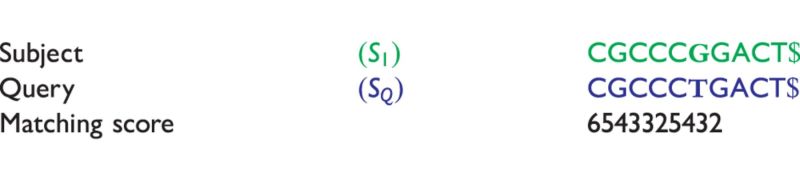 |
The matching numbers indicate the shortest unique substring starting at this position that is absent from the subject.
Table 5:
Sequences 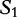 and
and 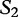 are compared with
are compared with 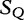
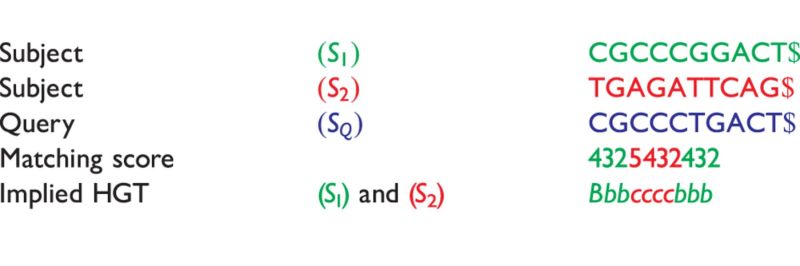 |
The matching numbers indicate the shortest unique substring starting at this position that is absent from the subject. The HGT is described by a string of  and
and  characters to indicate where the subsequences likely originated.
characters to indicate where the subsequences likely originated.
We cite an example from another study concerning HGT by the same authors [13]. This method is applied to locating regions of common genetic material in Escherichia coli and recombinant HIV-1 strains. This method is similar because it locates local regions in subject sequences that are closely related to the query sequence. In Table 6, sequences 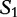 to
to 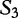 are the subjects and
are the subjects and 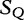 is the query. We find which parts of
is the query. We find which parts of 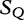 most closely resemble the subject sequences. The sections of sequence material are written in an interval notation:
most closely resemble the subject sequences. The sections of sequence material are written in an interval notation: 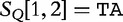 matches
matches 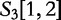 ,
, 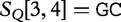 matches
matches 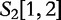 . By this system, we claim that
. By this system, we claim that 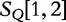 is most closely related to
is most closely related to 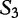 , and
, and 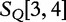 is most closely related to
is most closely related to 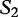 .
.
Table 6:
We wish to determine the sequence relations based on common sequence material
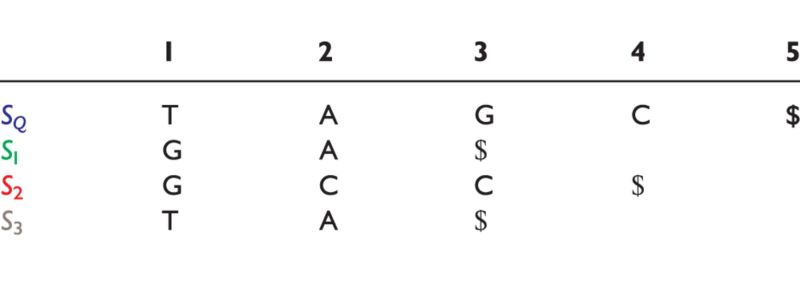 |
The query sequence is SQ and subjects are S1 through S3.
During the sequence comparison task of query-to-subject, in [13], the authors denote the length of the shortest query sequence prefix by 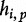 . The query suffix,
. The query suffix, 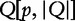 denotes the sequence starting at position p, which is absent in subject sequences. The length of the longest subsequence starting at
denotes the sequence starting at position p, which is absent in subject sequences. The length of the longest subsequence starting at 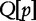 taken over all subject sequences is denoted,
taken over all subject sequences is denoted, 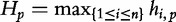 , where hp is bounded by the query length:
, where hp is bounded by the query length: 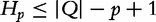 . For example, in Table 6,
. For example, in Table 6, 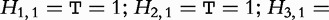
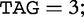 and
and 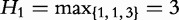 . Conversely, the longest subject subsequences, which start at
. Conversely, the longest subject subsequences, which start at 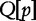 are found in a subject sequence, are denoted by
are found in a subject sequence, are denoted by 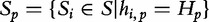 . Based on these properties, the authors note that the longest sequence from Table 6 is S3 (the most similar subject to sequence SQ).
. Based on these properties, the authors note that the longest sequence from Table 6 is S3 (the most similar subject to sequence SQ).
ADVANTAGES AND DISADVANTAGES OF METHODS
The method that an algorithm uses to gain its statistical data for an analysis is an important part of the whole operation. A fault at this stage would travel throughout the comparison task and upset the conclusion. In this section, we describe the generation of the motif frequency distributions, and we discuss how this initial statistical work may not always be appropriate for a particular data set.
The methods of ‘Factor Frequencies’ section are powerful methods to use in sequence comparison tasks, as they do not concern the location of the motifs they analyze. Their algorithms are efficient, as they are generally of a linear complexity. They contrast to the general high complexity of the algorithms that are based on dynamic programming. The results of factor frequency methods are adaptable and can be conveniently applied to an analysis by mutual information (‘A comparison by frequencies and the Jensen–Shannon Divergence test’ section), k-mers (‘Suffix trees by k-mer frequencies’ section) or by CVs (‘Composition vectors based on k-mer frequencies’ and ‘A revised string composition method sections’).
As the factor frequency methods are generated by word occurrences in a sequence, it important to choose words that are not likely to commonly appear in a sequence. As a general rule in DNA, the shorter the word, then the more likely it will appear randomly in a sequence. In ‘BBC by analysis of mutual information’ and ‘A comparison by frequencies and the Jensen–Shannon Divergence test’ section, vectors were created out of pairs of DNA bases. Although this may be an simple way to illustrate the concept, frequencies made up of these short pairs have less meaning than frequencies made up by longer words because any particular DNA pair has a probability of 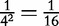 to occur randomly. We note that for sequences that are largely dissimilar, then shorter words (hence shorter CVs) should be used to create the feature frequency distributions. However, longer words, (hence, longer CVs, assuming an exhaustive list of motifs) may be used when the sequences are known to be similar, such as when they are related, [41]. The methods of ‘Factor Frequencies’ section are well suited for this application using both long and short motifs. They also function well when the location of the motif in the sequence is not important, as in the case of synteny.
to occur randomly. We note that for sequences that are largely dissimilar, then shorter words (hence shorter CVs) should be used to create the feature frequency distributions. However, longer words, (hence, longer CVs, assuming an exhaustive list of motifs) may be used when the sequences are known to be similar, such as when they are related, [41]. The methods of ‘Factor Frequencies’ section are well suited for this application using both long and short motifs. They also function well when the location of the motif in the sequence is not important, as in the case of synteny.
Unlike the approaches of ‘Factor Frequencies’ section where the frequency distributions were generated by user-specified motifs, the methods of ‘Data Compression and Dictionaries’ section ‘choose’ their own sizes of words for their sequence comparison task. In the methods proposed by [34] (LZ compression based) and [36] (HGT), the word size is not a parameter set by the researcher. These kinds of algorithms are useful to comparison tasks where it is not clear about the ‘correct’ kinds of motifs to employ. In the case of factor frequency methods, when designing a list of motifs from which to generate a frequency distribution, an exhaustive list is likely used. As we have previously mentioned, the longer the motif, the larger the exhaustive list. Finding the frequencies of these extra motifs may add additional computational time to the task. Therefore, compression-based methods may be more suitable to comparisons where longer motifs are desirable, such as when the sequences are similar. This might be because the words of varying size and composition will be more similar across related sequences.
CONCLUSION
Comparison of sequence data represents a large problem in computational biology research. Discovery is often frustrated by obstacles such as synteny or other forms of genetic recombination, preventing methods of dynamic programming from working effectively. We provide a summary of the methods that we have discussed in Table 7, listed by sections, references and authors. When confronted with a large number of comparison tasks, which are unsuitable for traditional forms of alignment from dynamic programming, these alignment-free methods may be the only feasible approach for completing the tasks to permit discovery. This is because the alignment-free methods do not function based on the location of genes or regions in each sequence. When the location of these regions is not important for the analysis, alignment-free methods like the ones included in the present review may accomplish the goal of comparing genetic sequences.
Table 7:
Summary of the discussed methods in this article
| Section | Method | Author | Alignment | Citation |
|---|---|---|---|---|
| BBC by analysis of mutual information | BBC | Lui et al. | Global | [30] |
| FFP | Oligonucleotide profiling | Arnau et al. | Local | [43] |
| FFP | Feature frequency | Sims et al. | Local | [44] |
| Suffix trees by k-mer frequencies | k-mers frequencies | Soars et al. | Global | [47] |
| Composition vectors based on k-mer frequencies | Composition vectors | Lu et al. | Global | [32] |
| A revised string composition method | Composition vectors | Chan et al. | Global | [31] |
| D2 statistic | 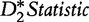 |
Reinert et al. | Global | [60] |
| D2 statistic | Improved D2 statistic | Lui et al. | Global | [64] |
| Data compression and dictionaries | Sequence distance | Otu et al. | Global | [34] |
| Text compression algorithms | DNA compression | Cao et al. | Global | [33] |
| Average common substring | Average common substring | Ulitsky et al. | Global | [35] |
| HGT | ALign. Free local homology | Domazet-Lošo et al. | Local | [13, 36] |
| Biological data and sequence assembly | Sequence assembly | Bonham-Carter et al. | Global | [69] |
| Chromosomal data and phylogeny | Phylogeny | Bonham-Carter et al. | Global | [70] |
The column ‘Alignment’ contains the best suggested use of the method.
As there is more sequence data available today than ever before, there are many more projects that depend on sequence comparison. For discovery to be made, this work will have to be done by other technologies such as those based on dynamic programming, which have obvious limitations. Alignment-free methods generally require less computational resources and use algorithms that are typically of linear complexity. These incorporated elements are appropriate for advancing comparative bioinformatics research.
It is our hope that this review provides useful information for researchers who are studying alignment-free methods and are using them in the analysis of genomic sequences and metagenomes. As the mathematical aspects of the aforementioned tools are themselves an obstacle, it is also our hope that this review helps to introduce the reader to some of the more complicated calculations that are associated with these alignment-free tools for discovery. Furthermore, we envisage that this review will serve as a useful reference in identifying open problems and driving future research in sequence comparison.
Key Points.
Dynamic programming methods are inappropriate for the voluminous.
Statistical methods from information theory and other areas of mathematics are now used to conveniently differentiate sequence data based on extracted motif distributions.
We review popular methods of comparing word distributions between sequences to infer distance.
Application of these sequence comparison methods extend to the following: sequence assembly, phylogeny, HGT and many other areas where sequence separation is necessary.
ACKNOWLEDGEMENTS
The authors thank Joe Fitzpatrick for his work in proof-reading our manuscript. In addition, authors thank Janyl Jumadinova for helping us format the manuscript.
Biographies
Oliver Bonham-Carter is a PhD student in the College of Information Science and Technology at the University of Nebraska at Omaha.
Joe Steele was a part of the application development team at the College of Information Science and Technology at the University of Nebraska at Omaha.
Dhundy Bastola is an assistant professor in Bioinformatics at the School of Interdisciplinary Informatics at the University of Nebraska at Omaha.
FUNDING
UNO-Bioinformatics Core Facility, funded by the grants from the National Center for Research Resources [5P20RR016469] and the National Institute for General Medical Science (NIGMS) [8P20GM103427].
References
- 1.Gusfield D. Algorithms On Strings, Trees, and Sequences: Computer Science and Computational Biology. Cambridge University Press, Cambridge; 1997. [Google Scholar]
- 2.Knuth DE, Morris JH, Pratt VR. Fast pattern matching in strings. SIAM J Comput. 1977;6:323–50. [Google Scholar]
- 3.Boyer RS, Moore SJ. A fast string searching algorithm. Commun ACM. 1977;20:762–72. [Google Scholar]
- 4.Horspool RN. Practical fast searching in strings. Softw Pract Exp. 1980;10:501–6. [Google Scholar]
- 5.Apostolico A, Giancarlo R. The boyer moore galil string searching strategies revisited. Siam J Comput. 1986;15:98–105. [Google Scholar]
- 6.Ukkonen E. Finding approximate patterns in strings. J Algor. 1985;6:132–7. [Google Scholar]
- 7.Navarro G. A guided tour to approximate string matching. J ACM Comp Surv. 2001;33:31–88. [Google Scholar]
- 8.Cheng L-L, Cheung DW, Yiu S-M. Procceedings of the Eighth International Conference on Database Systems for Advance Applications. 2003. Approximate string matching in DNA sequences; pp. pp. 303–10. http://dx.doi.org/10.1109/DASFAA.2003.1192395. [Google Scholar]
- 9.Koonin E. The emerging paradigm and open problems in comparative genomics. Bioinformatics. 1999;15:265–66. doi: 10.1093/bioinformatics/15.4.265. [DOI] [PubMed] [Google Scholar]
- 10.Wooley J. Trends in computational biology: a summary based on a RECOMB plenary lecture. J Comput Biol. 1999;6:459–74. doi: 10.1089/106652799318391. [DOI] [PubMed] [Google Scholar]
- 11.Li H, Homer N. A survey of sequence alignment algorithms for next-generation sequencing. Brief Bioinform. 2010;11:473–83. doi: 10.1093/bib/bbq015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liao B-Y, Chang Y-J, Ho J-M, et al. The unimarker (um) method for synteny mapping of large genomes. Bioinformatics. 2004;20:3156–65. doi: 10.1093/bioinformatics/bth380. [DOI] [PubMed] [Google Scholar]
- 13.Domazet-Lošo M, Haubold B. Alignment-free detection of horizontal gene transfer between closely related bacterial genomes. Mob Genet Elements. 2011;1:230–5. doi: 10.4161/mge.1.3.18065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Berkman PJ, Skarshewski A, Manoli S, et al. Sequencing wheat chromosome arm 7BS delimits the 7BS/4AL translocation and reveals homoeologous gene conservation. Theor Appl Genet. 2012;124:423–32. doi: 10.1007/s00122-011-1717-2. [DOI] [PubMed] [Google Scholar]
- 15.Crameri A, Raillard S-A, Bermudez E, et al. DNA shuffling of a family of genes from diverse species accelerates directed evolution. Nature. 1998;391:288–91. doi: 10.1038/34663. [DOI] [PubMed] [Google Scholar]
- 16.Orobitg M, Cores F, Guirado F, et al. Parallel & Distributed Processing Symposium (IPDPS), 2012 IEEE 26th International. 2012. Enhancing the scalability of consistency-based progressive multiple sequences alignment applications; pp. pp. 71–82. [Google Scholar]
- 17.Eddy SR. What is dynamic programming? Nat Biotechnol. 2004;22:909–10. doi: 10.1038/nbt0704-909. [DOI] [PubMed] [Google Scholar]
- 18.Smith T, Waterman M. Identification of common molecular subsequences. J Mol Biol. 1981;147:195–7. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- 19.Needleman S, Wunsch C. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J Mol Biol. 1970;48:443–53. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- 20.Larkin M, Blackshields G, Brown N, et al. Clustalw and clustalx version 2. Bioinformatics. 2007;23:2947–8. doi: 10.1093/bioinformatics/btm404. [DOI] [PubMed] [Google Scholar]
- 21.Altschul SF, Madden TL, Schäffer AA, et al. Gapped blast and psi-blast: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen C, Rajapakse JC. Grid-enabled blastz: application to comparative genomics. J VLSI Signal Process Syst Signal Image Video Technol. 2007;48:301–9. [Google Scholar]
- 23.Kent WJ. Blatthe blast-like alignment tool. Genome Res. 2002;12:656–64. doi: 10.1101/gr.229202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schadt EE, Linderman MD, Sorenson J, et al. Computational solutions to large-scale data management and analysis. Nat Rev Genet. 2010;11:647–57. doi: 10.1038/nrg2857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chenna R, Sugawara H, Koike T, et al. Multiple sequence alignment with the clustal series of programs. Nucleic Acids Res. 2003;31:3497–500. doi: 10.1093/nar/gkg500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Katoh K, Toh H. Parallelization of the mafft multiple sequence alignment program. Bioinformatics. 2010;26:1899–900. doi: 10.1093/bioinformatics/btq224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hara Y, Imanishi T. Abundance of ultramicro inversions within local alignments between human and chimpanzee genomes. BMC Evol Biol. 2011;11:308. doi: 10.1186/1471-2148-11-308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vinga S, Almeida J. Alignment-free sequence comparison–a review. Bioinformatics. 2003;19:513–23. doi: 10.1093/bioinformatics/btg005. [DOI] [PubMed] [Google Scholar]
- 29.Mantaci S, Restivo A, Sciortino M. Distance measures for biological sequences: some recent approaches. Int J Approx Reason. 2008;47:109–24. [Google Scholar]
- 30.Liu Z, Meng J, Sun X. A novel feature-based method for whole genome phylogenetic analysis without alignment: application to HEV genotyping and subtyping. Biochem Biophys Res Commun. 2008;223:223–30. doi: 10.1016/j.bbrc.2008.01.070. [DOI] [PubMed] [Google Scholar]
- 31.Chan RH, Chan TH, Yeung HM, et al. Composition vector method based on maximum entropy principle for sequence comparison. IEEE/ACM Trans Comput Biol Bioinform. 2011 doi: 10.1109/TCBB.2011.45. Mar 3. [DOI] [PubMed] [Google Scholar]
- 32.Lu G, Zhang S, Fang X. An improved string composition method for sequence comparison. BMC Bioinform. 2008;9:S15. doi: 10.1186/1471-2105-9-S6-S15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cao MD, Dix TI, Allison L, et al. Data Compression Conference. 2007. A simple statistical algorithm for biological sequence compression; pp. pp. 43–52. [Google Scholar]
- 34.Out HH, Sayood K. A new sequence distance measure for phylogenetic tree construction. Bioinformatics. 2003;19:2111–30. doi: 10.1093/bioinformatics/btg295. [DOI] [PubMed] [Google Scholar]
- 35.Ulitsky I, Burstein D, Tuller T, et al. The average common substring approach to phylogenomic reconstruction. J Comp Bio. 2006;13:226–50. doi: 10.1089/cmb.2006.13.336. [DOI] [PubMed] [Google Scholar]
- 36.Domazet-Lošo M, Haubold B. Alignment-free detection of local similarity among viral and bacterial genomes. Bioinformatics. 2011;27:1466–72. doi: 10.1093/bioinformatics/btr176. [DOI] [PubMed] [Google Scholar]
- 37.Shannon C. The mathematical theory of communication. Bell Syst Tech J. 1948;27:379–429. [Google Scholar]
- 38.Kim I, Watada J, Pedrycz W, et al. Pattern clustering with statistical methods using a DNA-based algorithm. IEEE Trans Nanobioscience. 2012;11:100–10. doi: 10.1109/TNB.2012.2190618. [DOI] [PubMed] [Google Scholar]
- 39.Wang J-D. Bioinformatics and Bioengineering (BIBE), 2011 IEEE 11th International Conference. 2011. A comparison study of virus classification by genome sequences; pp. pp. 270–3. [Google Scholar]
- 40.Zhang L, Meng J, Liu H, et al. Genomic Signal Processing and Statistics (GENSIPS), 2011 IEEE International Workshop. 2011. Clustering DNA methylation expressions using nonparametric beta mixture model; pp. pp. 170–3. [Google Scholar]
- 41.Wu T-J, Huang Y-H, Li L-A. Optimal word sizes for dissimilarity measures and estimation of the degree of dissimilarity between DNA sequences. Bioinformatics. 2005;21:4125–32. doi: 10.1093/bioinformatics/bti658. [DOI] [PubMed] [Google Scholar]
- 42.Dai Q, Li L, Liu X, et al. Integrating overlapping structures and background information of words significantly improves biological sequence comparison. PLoS One. 2011;6:e26779. doi: 10.1371/journal.pone.0026779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Arnau V, Gallach M, Marín I. Fast comparison of DNA sequences by oligonucleotide profiling. BMC Res Notes. 2008;1:5. doi: 10.1186/1756-0500-1-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sims GE, Jun SR, Kim SH. Alignment-free genome comparison with feature frequency profiles (ffp) and optimal resolutions. Proc Natl Acad Sci USA. 2008;106:2677–82. doi: 10.1073/pnas.0813249106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lin J. Divergence measures based on the shannon entropy. IEEE Trans Inf Theory. 1991;37:145–51. [Google Scholar]
- 46.Prasad AB, Allard MW, Green ED. Confirming the phylogeny of mammals by use of large comparative sequence data sets. Mol Biol Evol. 2008;25:1795–808. doi: 10.1093/molbev/msn104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Soares I, Goios A, Amorim A. Sequence comparison alignment-free approach based on suffix tree and l-words frequency. Sci World J. 2012;2012:450124. doi: 10.1100/2012/450124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hao B, Qi J, Wang B. Prokaryotic phylogeny based on complete genomes without sequence alignment. Mod Phys Lett B. 2003;2:1–4. [Google Scholar]
- 49.Qi J, Wang B, Hao B-I. Whole proteome prokaryote phylogeny without sequence alignment: a k-string composition approach. J Mol Evol. 2004;58:1–11. doi: 10.1007/s00239-003-2493-7. [DOI] [PubMed] [Google Scholar]
- 50.Wu X, Wan X, Wu G, et al. Phylogenetic analysis using complete signature information of whole genomes and clustered neighbour-joining method. Int J Bioinform Res Appl, 2006;2:219–48. doi: 10.1504/IJBRA.2006.010602. [DOI] [PubMed] [Google Scholar]
- 51.Brendel V, Beckmann JS, Trifonov EN. Linguistics of nucleotide sequences: morphology and comparison of vocabularies. J Biomol Struct Dyn. 1986;4:11–21. doi: 10.1080/07391102.1986.10507643. [DOI] [PubMed] [Google Scholar]
- 52.Hao B, Qi J. Prokaryote phylogeny without sequence alignment: from avoidance signature to composition distance. J Bioinform Comput Biol. 2004;2:1–19. doi: 10.1142/s0219720004000442. [DOI] [PubMed] [Google Scholar]
- 53.Gentleman J, Mullin R. The distribution of the frequency of occurrence of nucleotide subsequences, based on their overlap capability. Biometrics. 1989;45:35–52. [PubMed] [Google Scholar]
- 54.Hua R, Wanga B. Statistically significant strings are related to regulatory elements in the promoter regions of saccharomyces cerevisiae. Physica A. 2001;290:464–74. [Google Scholar]
- 55.Yu Z-G, Zhou L-Q, Anh VV, et al. Phylogeny of prokaryotes and chloroplasts revealed by a simple composition approach on all protein sequences from complete genomes without sequence alignment. J Mol Evol. 2005;60:538–45. doi: 10.1007/s00239-004-0255-9. [DOI] [PubMed] [Google Scholar]
- 56.Forêt S, Wilson SR, Burden CJ. Characterizing the d2 statistic: word matches in biological sequences. Stat Appl Genet Mol Biol. 2009;8:1–21. doi: 10.2202/1544-6115.1447. [DOI] [PubMed] [Google Scholar]
- 57.Waterman M. Introduction to Computational Biology: Maps, Sequences and Genomes. Chapman and Hall; 1995. [Google Scholar]
- 58.Forêt S, Kantorovitz M, Burden CJ. Asymptotic behavior of k-word matches between two uniformly distributed sequences. BMC Bioinform. 2006;7:S21. doi: 10.1186/1471-2105-7-S5-S21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lippert R, Huang H, Waterman M. Distributional regimes for the number of k-word matches between two random sequences. Proc Natl Acad Sci USA. 2002;99:13980–9. doi: 10.1073/pnas.202468099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Reinert G, Chew D, Sun F, et al. Alignment-free sequence comparison (i): Statistics and power. J Comput Biol. 2009;16:1615–34. doi: 10.1089/cmb.2009.0198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kantorovitz MR, Robinson GE, Sinha S. A statistical method for alignment-free comparison of regulatory sequences. Bioinformatics. 2007;23:i249–55. doi: 10.1093/bioinformatics/btm211. [DOI] [PubMed] [Google Scholar]
- 62.Wan L, Reinert G, Sun F, et al. Alignment-free sequence comparison (ii): theoretical power of comparison statistics. J Comput Biol. 2010;17:1467–90. doi: 10.1089/cmb.2010.0056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Song K, Ren J, Zhai Z, et al. Research in Computational Molecular Biology. Springer; 2012. Alignment-free sequence comparison based on next generation sequencing reads; pp. pp. 272–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Liu X, Wan L, Li J, et al. New powerful statistics for alignment-free sequence comparison under a pattern transfer model. J Theor Biol. 2011;284:106–16. doi: 10.1016/j.jtbi.2011.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Ziv J, Lempel A. A universal algorithm for sequential data compression. IEEE Trans Inf Theory. 1977;23:337–43. [Google Scholar]
- 66.Mohammed MH, Dutta A, Bose T, et al. Deliminate–a fast and efficient method for loss-less compression of genomic sequences. Bioinformatics. 2012;28:2527–9. doi: 10.1093/bioinformatics/bts467. [DOI] [PubMed] [Google Scholar]
- 67.Cox AJ, Bauer MJ, Jakobi T, et al. Large-scale compression of genomic sequence databases with the burrows–wheeler transform. Bioinformatics. 2012;28:1415–9. doi: 10.1093/bioinformatics/bts173. [DOI] [PubMed] [Google Scholar]
- 68.Kozanitis C, Saunders C, Kruglyak S, et al. Compressing genomic sequence fragments using slimgene. J Comput Biol. 2011;18:401–13. doi: 10.1089/cmb.2010.0253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Bonham-Carter O, Ali H, Bastola D. In: Bioinformatics and Biomedicine Workshops (BIBMW), 2012 IEEE International Conference on IEEE. 2012. A meta-genome sequencing and assembly preprocessing algorithm inspired by restriction site base composition; pp. pp. 696–703. [Google Scholar]
- 70.Bonham-Carter O, Ali H, Bastola DK. A meta-genome sequencing and assembly preprocessing algorithm inspired by restriction site base composition. BMC Bioinformatics. 2013 doi: 10.1186/1471-2105-14-S11-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Bonham-Carter O, Najjar L, Thapa I, et al. Distributions of palindromic proportional content in bacteria. Short Paper. The 8th International Symposium on Bioinformatics Research and Applications (ISBRA 2012) Dallas, TX, 2012. [Google Scholar]
- 72.Syvanen M. Evolutionary implications of horizontal gene transfer. Annu Rev Genet. 2012;46:341–58. doi: 10.1146/annurev-genet-110711-155529. [DOI] [PubMed] [Google Scholar]
- 73.Moreno-Letelier A, Olmedo G, Eguiarte LE, et al. “Parallel evolution and horizontal gene transfer of the pst operon in firmicutes from oligotrophic environments. Int J Evol Biol. doi: 10.4061/2011/781642. vol. 2011;2011. [DOI] [PMC free article] [PubMed] [Google Scholar]


