SecureMA: protecting participant privacy in genetic association meta-analysis

Abstract

Motivation: Sharing genomic data is crucial to support scientific investigation such as genome-wide association studies. However, recent investigations suggest the privacy of the individual participants in these studies can be compromised, leading to serious concerns and consequences, such as overly restricted access to data.

Results: We introduce a novel cryptographic strategy to securely perform meta-analysis for genetic association studies in large consortia. Our methodology is useful for supporting joint studies among disparate data sites, where privacy or confidentiality is of concern. We validate our method using three multisite association studies. Our research shows that genetic associations can be analyzed efficiently and accurately across substudy sites, without leaking information on individual participants and site-level association summaries.

Availability and implementation: Our software for secure meta-analysis of genetic association studies, SecureMA, is publicly available at http://github.com/XieConnect/SecureMA. Our customized secure computation framework is also publicly available at http://github.com/XieConnect/CircuitService

Contact: b.malin@vanderbilt.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Decreasing costs in sequencing technologies, in combination with large repositories of clinical information, has enabled the discovery of novel associations between genetic variants and disease. These achievements are facilitated by increased collection and reuse of genomic data (Green and Guyer, 2011), as well as broad efforts to obtain larger sample sizes (by sharing and combing data) for increased statistical power (Panagiotou et al., 2013). Meta-analysis is a common solution for aggregating substudy results across large consortia to achieve this goal. In fact, meta-analysis is responsible for ∼37% of the 15 845 genome-trait associations listed in the NHGRI genome-wide association studies (GWAS) Catalog (Welter et al., 2014). At the same time, the sensitive nature of genomic data has led to numerous discussions around the governance of genomic records (Fullerton et al., 2010; Kaye et al., 2009). Currently, policy and advisory groups recommend removing identifying information (e.g. personal names) to uphold the privacy of study participants (Lowrance and Collins, 2007; Presidential Commission for the Study of Bioethical Issues, 2012).

Yet, the efficacy of such protections is increasingly being questioned (Rodriguez et al., 2013). Various studies demonstrate that the identity of participants, as well as sensitive information (such as disease status) can still be inferred from the shared genomic data (Gymrek et al., 2013; Homer et al., 2008; Humbert et al., 2013; Im et al., 2012; Jacobs et al., 2009; Lin et al., 2004; Sankararaman et al., 2009). This can occur by leveraging an individual’s genome sequence or the study summary statistics about associations, such as genotype frequencies and allelic regression coefficients that would be used in meta-analysis. Most recently, it was shown that an individual’s identity could be ascertained through Y-chromosome short tandem repeats (Y-STRs) using public genealogy databases on the internet (Gymrek et al., 2013). While certain privacy attacks may seem non-trivial in the knowledge necessary to be executed, they have already raised serious concerns from scientists, policy makers and the general public. They have also led to reduced sharing of genome sequences and site-level summary statistics. For instance, based on (Homer et al., 2008), the NIH and Wellcome Trust stopped sharing aggregate genomic data directly to the public (Zerhouni and Nabel, 2008). These demonstrations have also influenced proposed regulations [e.g., (European Commission, 2012, 2014)], some of which would designate all biospecimens and their derived data as identifiable (U.S. Department H.H.S., 2011).

To address the privacy concerns on individual genomic information as well as site-level summary statistics, we engineered a practical protocol to securely perform meta-analysis for genotype–phenotype association studies across substudy sites in large consortia (Fig. 1). Our protocol leverages cryptographically secure technology to provide provable security guarantees. Unlike alternative proposals (Kamm et al., 2013), in our protocol, substudy sites retain full control of their respective individual participants’ data and local site analyses. This allows each site to make appropriate adjustments to effect estimates to account for study-specific differences in design, which is pervasive in multisite studies but not supported in (Kamm et al., 2013). Our protocol also allows sites to contribute to meta-analysis without exposing site-level summary statistics. Such comprehensive protections make our protocol impervious to popular privacy attacks over genomic data at both the individual and site level.

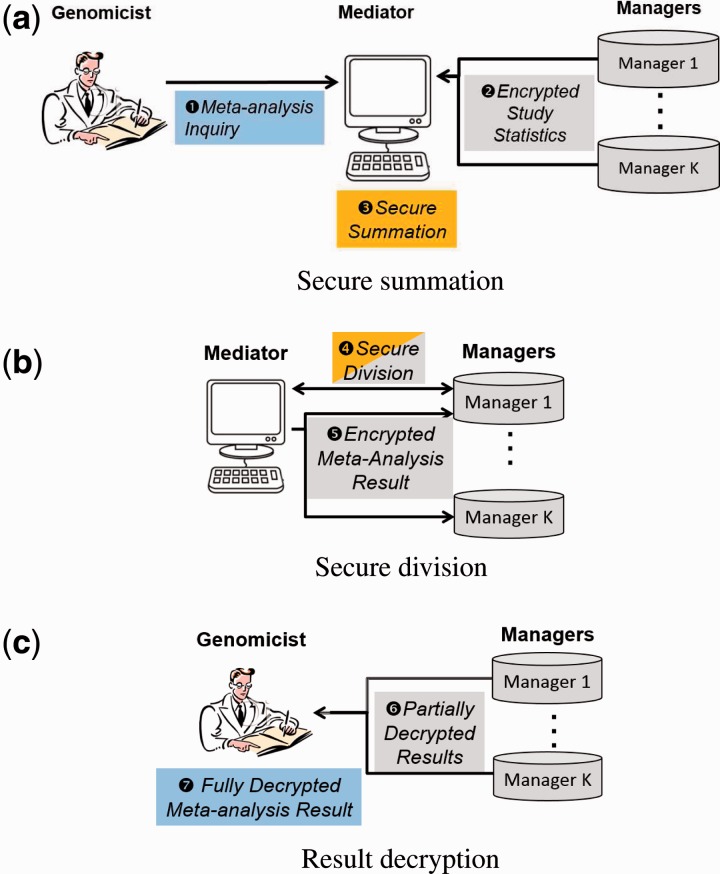
Fig. 1.

The SecureMA protocol (secure computation step). (a) The process begins when a scientist submits a meta-analysis study inquiry. Each data manager in the study submits encrypted local statistics (e.g. effect size and the inverse of its variance) to the Mediator for secure summation. (b) The Mediator then coordinates with one random data manager to securely divide the numerator by the denominator of the meta-analysis function. (c) The results of the meta-analysis are partially decrypted by the data managers, which are composed into the final full decryption of the meta-analysis P-value at the scientist’s computer

In this article, we demonstrate the design and implementation of our secure meta-analysis protocol (called SecureMA), and provide empirical evaluations with three separate multisite genetic association studies.

2 SYSTEM

2.1 Secure meta-analysis protocol

The SecureMA protocol consists of two main steps: (1) Setup and (2) Secure Computation. The Setup initializes the system by (i) generating and distributing the encryption/decryption keys, (ii) encrypting association statistics locally at each study site and (iii) submitting the data encryptions to the data managers (e.g. coordination centers in practice). The Secure Computation step securely performs meta-analysis over the encrypted submissions of site-level association statistics (Fig. 1).

2.2 Setup step of the protocol

To setup the process, a one-time step for generating and disseminating the encryption/decryption keys is coordinated by a trusted authority who is not involved in any data management or computations (Supplementary Fig. S1; Following standard practice in security for cryptographic systems, this authority generates keys and has no further interaction with any of the participants involved in SecureMA). For protection purposes, the decryption key is then split into multiple shares and distributed across the participants of the protocol, as described below. By doing so, to successfully decrypt data, collaboration is required between the majority of key holders. As detailed in Supplementary Section S5.1, the splitting of the key enforces an ‘honest-majority’ to mitigate collusion for illicit decryption.

Optionally, to make the protocol more practical, several intermediate parties, which we call data managers, can be set up to host the (encrypted aggregate) data on behalf of the local sites. Following this scheme, the local sites submit encryptions of their study summary statistics (e.g. effect size and the inverse of its variance) to their entrusted data managers and can then go offline. In doing so, one manager can coordinate for several local sites, such that only a limited number of online participants are required for the protocol to proceed. And, as mentioned, enforcing an honest majority ensures no manager alone can decrypt the data. Further details on this a management model can be found in Supplementary Section S5.1.

2.3 Secure computation step of the protocol

When a scientist issues a study inquiry to the system, encryptions of site-level association statistics are requested from the data managers and then provided to a third party responsible for coordination and computation—the Mediator—who securely sums the encrypted submissions (Fig. 1a).

Next, the mediator coordinates with one randomly selected data manager to perform a secure division to derive the weighted average, the last operation of meta-analysis (Fig. 1b; details in Section 3.1).

At this point, the meta-analysis result is still in an encrypted state. The mediator is then responsible for initiating a final round of collaborative decryption by distributing the encrypted result to a majority of the trusted data managers for partial decryption (Fig. 1c). By collecting a sufficient number of the partially decrypted shares from the data managers, the scientist combines them to reveal the final decryption from which the final result of his/her study query would be derived. Thus, until the scientist requests the final decryption, no individual or site-level aggregate information is ever disclosed because all information remains encrypted throughout the protocol.

A complete activity diagram of the SecureMA protocol is provided in Supplementary Figure S2.

3 METHODS

3.1 Meta-analysis

Meta-analysis (Hedges and Olkin, 1985) is a statistical technique widely used in genetic association studies for synthesizing study results from across consortia to obtain larger sample sizes and gain statistical power. In this work, we focus on the fixed-effects model to perform meta-analysis (Willer et al., 2010), which yields a weighted average of the effect size (e.g. beta coefficient) using the inverse of its variance as the weight:

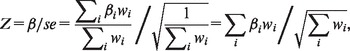(1)

where β is the aggregated effect size, se is the aggregated standard error, ${\beta }_i$ is the effect size of an association for the i-th substudy (i.e. site contributing data to the meta-analysis), weight $w_i=1/s{e}_i^2$ and se_i corresponds to the standard error of the effect for the i^th substudy.

3.2 Secure computation of meta-analysis

To enable direct computation in a cryptographic setting, we square Equation (1) (i.e. Z²; Supplementary Section S5.4). The final square root and conversion from Z-score to P-value is performed by software running on the computer of the scientist who issued the meta-analysis request.

For reference, the core (secure) computations for the proposed SecureMA protocol are summarized in Table 1. For each meta-analysis study, the mediator requests and receives encryptions of site-level association summaries [denoted as $E({\beta }_i{w}_i)$, $E(w_i)$] from the data managers. Then, the mediator leverages the secure summation subprotocol (denoted as ADD, see Supplementary Section S5.4) to compute the sums in the numerator and denominator of Equation (1) without decryption (resulting in encryptions: $E({\displaystyle \sum _i{\beta }_i{w}_i})$ and $E({\displaystyle \sum _i{w}_i})$).

Table 1.

The core variables and computations for SecureMA

Notations	${\beta }_i$—effect size estimate for substudy i
	wi—weight term for substudy i
	$E()$—encrypted data or secure computation
Inputs	$E({\beta }_i{w}_i)$—encrypted statistic for substudy i
	$E(w_i)$—encrypted statistic for substudy i
Intermediate computations	Summations: $E({\displaystyle \sum _i{\beta }_i{w}_i})$, $E({\displaystyle \sum _i{w}_i})$
	Logarithms: $E(\ln {\displaystyle \sum _i{\beta }_i{w}_i}),E(\ln {\displaystyle \sum _i{w}_i})$
	$E(\ln Z^2)=E(2\ln {\displaystyle \sum _i{\beta }_i{w}_i}-\ln {\displaystyle \sum _i{w}_i})$
	Decrypt $E(\ln Z^2)$ to obtain $\ln Z^2$
Overall Z-Score	$Z=\sqrt{\exp (\ln Z^2)}$
Overall P-value	$P=2\Phi (-|Z|)$

The final step of meta-analysis involves a division operation (for deriving the weighted average of effect size), where in our case, both the numerator and the denominator are encrypted. There is no efficient method for directly computing the division of two encryptions. Thus, we convert it into a subtraction problem, which is easier to implement in cryptography, by applying a logarithmic transformation on the squared Equation (1) (e.g. Z²):

$$\ln Z^2=2\ln {\displaystyle \sum _i{\beta }_i{w}_i}-\ln {\displaystyle \sum _i{w}_i}$$ (2)

The logarithmic transformation, $\ln x$ (where x is encrypted), is approximated using secure computation techniques and a Taylor series (Supplementary Section S5.5). The result from this step is still in an encrypted form.

Next, secure subprotocols for multiplication-by-constant and subtraction (e.g. defined as MULC and SUB subprotocols in Supplementary Section S5.4) are used to complete the rest of the operations in Equation (2), yielding encryption $E(\ln Z^2)$. The final Z² can be obtained by decrypting and computing the exponential operation at the study inquiry issuer’s site.

4 IMPLEMENTATION AND RESULTS

We implemented the SecureMA protocol in working software and released it open source. To demonstrate its feasibility and practicality, we reproduced three multisite genetic association meta-analyses. For the purposes of evaluation, we focus on the efficacy of protecting participant privacy, the computational accuracy, the running time efficiency and the sensitivity to certain protocol parameterizations.

4.1 Study data

The Electronic Medical Records and Genomics (eMERGE) hypothyroidism study. The first collection of datasets is from a GWAS on hypothyroidism provided by the eMERGE consortia (Denny et al., 2011). It consists of 6370 study participants across five study sites, and for evaluation, we analyzed 100 single nucleotide polymorphisms (SNPs)—these include the 16 statistically significant SNPs ($P<{10}^{-6}$) reported in their original study and an additional 84 random SNPs for running time efficiency analysis (Supplementary Section S3).

The Population Architecture using Genomics and Epidemiology (PAGE) obesity study. The second collection of datasets is from a genetic association study on obesity and body mass index provided by the PAGE consortia (Fesinmeyer et al., 2013). It consists of 53 238 participants across six study sites, and for evaluation, we analyzed 40 SNPs—these include the 25 statistically significant SNPs (P < 0.05) as identified by their original study, and an additional 15 SNPs (Supplementary Section S3).

The Epidemiologic Architecture for Genes Linked to Environment (EAGLE) diabetes study. The third collection of datasets is from a genetic association study on Type II Diabetes provided by the EAGLE group (Haiman et al., 2012). It contains 14 998 participants across two substudies, and we analyzed 216 SNPs. The published study did not report P-values for all SNPs, and thus, for comparison, we only focus on a controlled benchmark using the standard non-secure meta-analysis as the baseline (reported in Supplementary Section S4) and running time analysis.

4.2 Protection of sensitive information

Throughout the SecureMA protocol, the privacy of the genomic records of the individual participants is ensured. This is because the records are maintained solely at their respective local sites and are never disclosed. This resolves privacy concerns over individual genome sequences [e.g. no risk of unique identifiability based on the uniqueness of SNPs as posed by (Lin et al., 2004)].

Moreover, site-level summaries (e.g. association study statistics of each local site) are protected via strong encryption throughout the process. And the final meta-analysis results (limited to aggregate P-values only) are only made known to the inquiry issuer. Such protections make it impossible to perform inference attacks based on group statistics or allele frequencies or regression coefficients; which are features relied on in various attacks; e.g. (Homer et al., 2008; Im et al., 2012; Jacobs et al., 2009; Sankararaman et al., 2009).

4.3 Accuracy of association results

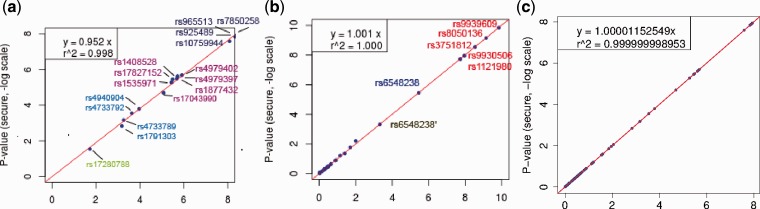
We compared the accuracy of our secure computations with those reported by the original studies associated with these datasets (Denny et al., 2011; Fesinmeyer et al., 2013; EAGLE is excluded from comparison owing to lack of published P-values as baseline). These results are summarized as QQ-plots of the SNP association P-values on a negative logarithmic scale (Fig. 2). The plots for the eMERGE and PAGE genotype–phenotype summary statistics correspond to the 16 and 25 SNPs, respectively, that were reported as significant in the publications. To compare the secure and non-secure estimates of the P-values, we applied a linear regression with the y-intercept forced to zero. The Pearson correlation coefficient was found to be ∼0.998 and ∼1.000 for eMERGE and PAGE, respectively, implying that the secure meta-analysis yielded results directly in line with those in the original publications. The regression slopes for the PAGE and eMERGE datasets were 1.001 and 0.952 respectively, and in both cases the rank order of the significance of the SNPs was retained. These results illustrate that the secure and non-secure meta-analysis approaches produce highly consistent results.

Fig. 2.

Protocol accuracy. The correlation plots correspond to (a) the P-values (secure protocol versus original publication) based on the 16 SNPs from eMERGE; (b) the P-values (secure protocol versus original publication) based on the 25 SNP-ethnicity pairs from PAGE (all SNPs annotated correspond to one ethnicity subpopulation, except for rs6548238’, which corresponds to another); and (c) the P-values (secure protocol versus standard non-secure meta-analysis) based on a controlled comparison of 100 SNPs from eMERGE)

We noticed that certain original studies used different analysis methods (e.g. pooled analysis instead of meta-analysis) and additional data processing, which may introduce replication discrepancy. We thus performed additional controlled experiments with the standard non-secure meta-analysis as the baseline [i.e. we used METAL software (Willer et al., 2010) to compute significance]. The results indicate our secure results are accurate, yielding both a slope and correlation coefficient of ∼1.000 for all datasets evaluated (Fig. 2c and Supplementary Fig. S3).

Overall, these results demonstrate our secure protocol supports genetic association studies with high accuracy. Further details on how to achieve even greater accuracy can be found in the sensitivity analysis (Section 4.5).

4.4 Running time efficiency

To evaluate the running time of the protocol, we performed a series of experiments on a desktop computer (2.4 GHz dual-core, 4 GB memory) running Java 1.7. We simulated the different participants of the protocol using separate system processes. All experiments were performed without parallelization to mitigate interference in the measurement of running time.

On average, the secure meta-analysis for most SNPs completed in 1.20–1.34 s (SD $\le 0.024$ s) and no SNP required more than 1.38 s (Table 2). In comparison with the eMERGE and PAGE datasets, the EAGLE study consumed slightly more time because of the fact that EAGLE consists of much larger numeric values, which leads to longer processing time.

Table 2.

Per-SNP running time for SecureMA and the proportion of the time dedicated to the division process (mean and standard deviation in seconds)

Dataset	Total	Division substep	Proportion of division
eMERGE	1.2028 (0.0169)	1.2017 (0.0169)	0.9991 (0.0002)
PAGE	1.2148 (0.0239)	1.2136 (0.0240)	0.9990 (0.0005)
EAGLE	1.3427 (0.0164)	1.3423 (0.0165)	0.9997 (0.0003)

Sample size. It is important to recognize that the running time of our protocol is weakly dependent on the number of study participants in the study (i.e. sample sizes) because the secure computations occur only on site-level summaries (Individual participant records are used by sites only for their local analyses. These are computed without encryption and, thus, the running time is negligible when compared with secure computations). This implies that our protocol can be efficient even in studies with large sample sizes, which is common for GWAS in large consortia.

Number of sites. We also point out that the majority of the computation time is dedicated to the secure division of the meta-analysis (>99.9%), as opposed to other computations such as secure summation (Table 2). This indicates the protocol is scalable to a large number of data-contributing sites. Specifically, the division operation involves only the mediator and one other participant, and thus its running time is not dependent on the number of sites. While the running time of other computations (e.g. secure summation) may increase linearly with the number of sites, its overall running time (and increase) is negligible.

To demonstrate the scalability of our technology for large consortia, we randomly selected sites from the eMERGE dataset to simulate environments consisting of up to 100 data-contributing sites (e.g. data managers participating in the protocol). For each setting, we computed a meta-analysis for 100 SNPs (Fig. 3). We illustrate that even when the protocol is composed of 100 sites, the time to complete the computation is around 1.22 s, which is approximately the same as the initial case studies.

Fig. 3.

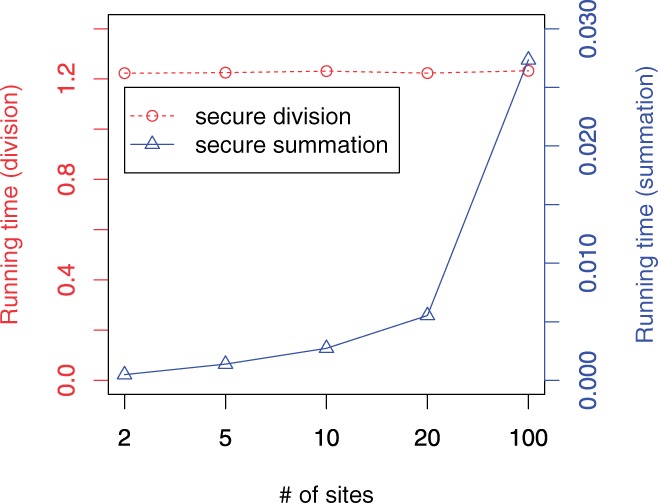
Average running time of SecureMA, per SNP, as a function of the number of sites providing data (all times reported in seconds)

4.5 Sensitivity analysis

The SecureMA protocol incorporates several tunable parameters to allow users to tune the computational accuracy and running time efficiency as necessary. These are introduced because neither decimal values nor division over encryptions are directly supported in cryptographic protocols. Here, we demonstrate their impact both theoretically and empirically (Supplementary Section S5 provides further details on these tunable parameters).

4.5.1 Parameters influencing protocol sensitivity

There are three primary parameters that influence the accuracy and running time of the SecureMA protocol. These parameters were introduced owing to a series of transformations and approximations to the square of Equation (1).

The first parameter corresponds to a scale-up factor ${10}^s$, where the scale s is defined a priori by protocol participants. This is multiplied against every value submitted by the local sites. In doing so, every value is converted from a decimal to an integer.

The next two parameters are associated with the approximation of secure division, which relies on the secure logarithmic transformation [Equation (2)]. Briefly, $\ln x$ can be approximated as follows:

$$\begin{array}{c}\ln x\approx \frac{yln2\times 2^{Nk}·lcm(2,\dots ,k)}{2^{Nk}·lcm(2,\dots ,k)}\\ +\frac{{\displaystyle \sum _{i=1}^k{(-1)}^{i-1}}{2}^{N(k-i)}·\frac{lcm(2,\dots ,k)}{i}·{({\alpha }_{true}+{\alpha }_{rand})}^i}{2^{Nk}·lcm(2,\dots ,k)},\end{array}$$ (3)

where integer y is a rough estimate of the exponent such that $2^y\approx x$, and additional terms such as $2^{Nk}$ and $lcm(2,\dots ,k)$ are for scaling purposes. The first term on the right side of Equation (3) obtains a rough estimate of $\ln x$, while the second term refines the previous approximation using a Taylor series.

Based on the above function, the second tunable parameter corresponds to the maximum exponent (i.e. N, or the upper bound of exponent estimate y) required to roughly estimate $\ln x$. And, the third tunable parameter corresponds to the number of expansions (i.e. k) to perform in a Taylor series when refining the accuracy of approximating $\ln x$.

For evaluation purposes, we randomly selected five significant and five non-significant SNPs from the eMERGE dataset to execute a series of secure meta-analyses.

4.5.2 Evaluation of the scale-up sactor

As mentioned, the scale-up factor ${10}^s$ is used to convert decimal values into integers. Larger factors result in the truncation of a fewer number of trailing digits and, thus, a smaller amount of information loss during computation.

Figure 4 depicts how the computational error and the overall running time, respectively, of the secure meta-analysis are influenced as the factor is varied from 10⁴ to ${10}^{16}$. For context, SecureMA uses a default value of 10⁸.

Fig. 4.

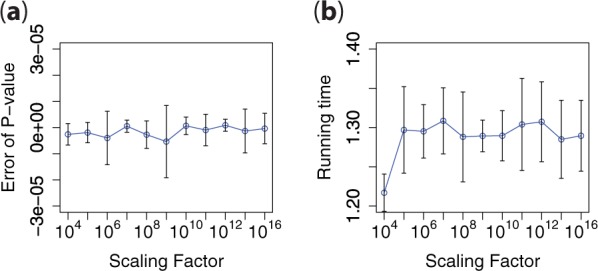
Impact of the scale-up factor on (a) computational accuracy; (b) running time efficiency. Results are based on the 10 SNPs from the eMERGE dataset (mean ± 1 SD)

In Figure 4a, it can be seen that, in general, the computational error of the P-value decreases (approaching 0) as the scale-up factor increases. Overall, the absolute and relative errors are always bounded within the range $[-3.0\times {10}^{-5},8.2\times {10}^{-6}]$ and $[-0.03,0.01\%]$, respectively. However, we note there are several outlying points in the graph, such as at 10⁶ and 10⁹. We note that these occur because, at times, the error of the two logarithms in Equation (2) diverge in opposite directions, which results in a magnification of the total error.

Nonetheless, in Figure 4b it can be seen that the variance of the overall running time is relatively small as the scale-up factor increases. This is an expected result because the change of the scale-up factor has limited influence on the secure division operation, which is the most time-consuming process in the protocol.

4.5.3 Evaluation of the maximum exponent of the logarithm approximation

The secure logarithmic transformation (i.e. $\ln x$ where x is encrypted) involves two phases to the approximation. The first phase aims to find an optimal integer exponent to roughly estimate the number x. The maximum exponent we analyze in this section corresponds to the upper bound for the exponent estimate. The second step corresponds to the application of a Taylor series, which we discuss in further depth below.

Figure 5 shows how the computational error and the overall running time, respectively of the secure meta-analysis (per SNP) are affected as the exponent varies from 64 to 96. For context, SecureMA uses a default value of 80.

Fig. 5.

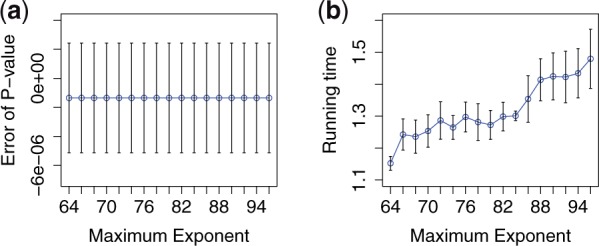
The impact of the maximum exponent on (a) computational accuracy and (b) running time efficiency. The results are based on 10 SNPs from the eMERGE dataset (mean ± 1 SD)

It was expected that a larger exponent would yield better approximation accuracy, with a trade-off in a longer running time. It is confirmed that the overall running time changes almost linearly with the increase of the maximum exponent (Fig. 5b). However, it can be seen that the computational accuracy is almost identical across all test cases (Fig. 5a). This is because, in this particular scenario, the other two protocol parameters are the dominating factors regarding computational accuracy.

4.5.4 Evaluation of the number of steps in the taylor series

A Taylor series is applied in the second phase of the secure logarithm subprotocol to boost the approximation accuracy. Figure 6 shows how the computational error and the overall running time, respectively, of the secure meta-analysis are affected as the number of steps in the series varies from 6 to 12. For context, SecureMA uses a default value of 10.

Fig. 6.

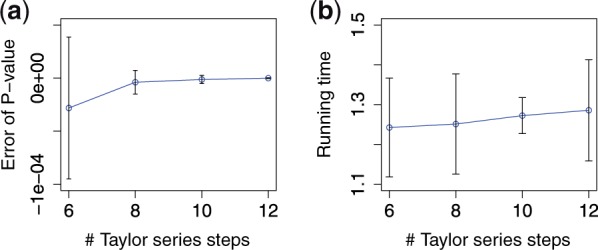
The impact of the number of steps in the Taylor series [i.e., k in Equation (3)] on (a) computational accuracy and (b) running time efficiency. The results are based on 10 SNPs from the eMERGE dataset (mean ± 1 SD)

Figure 6a illustrates that the more steps in the Taylor series, the better the computational accuracy is on average. Figure 6b further demonstrates that there is a slight linear increase in the running time as the number of steps in the Taylor series grows. This result stems from the fact that the number of terms required to compute in secure computation is increasing, which causes a longer running time.

5 DISCUSSION

5.1 Analysis on GWAS scale

As discussed earlier, one of the benefits of the SecureMA protocol is that its running time has only a weak dependence on the sample size. As a result, it can be efficient for studies run over large consortia. This is a notable improvement over alternative cryptographic proposals [e.g., (Kamm et al., 2013; Kantarcioglu et al., 2008)] whose running time is positively correlated, in a linear and sometimes exponential manner, with the number of study participants and sites.

At the same time, the SecureMA protocol can be made more efficient to support analysis on a genome-wide scale. First, the SecureMA protocol can easily be run in parallel on large computer clusters or cloud computing servers because each SNP can be analyzed independently. Thus, the total computation time for a large-scale GWAS would be inversely proportional to the computing resources allocated. As a rough estimate, a GWAS on 2 000 000 SNPs would require around 10 h on 16 eight-core computers without further optimization. Second, from a scientific perspective, it might be permissible to disclose the aggregate effect size of meta-analysis [i.e., the numerator in Equation (1)]. In such a scenario, the time-consuming secure division operation could be avoided entirely, reducing the overall running time per SNP to milliseconds. Third, recent advances in the optimization of secure computations [e.g., (Asharov et al., 2013; Henecka et al. 2013)] may be ready to transition into practice in the near future. This could allow for certain SecureMA subprotocols, such as secure division, to be run on parallel computing frameworks and make significant gains in efficiency.

5.2 Limitations

There are several limitations to the SecureMA protocol as currently designed. First, SecureMA assumes that study data have already been carefully cleaned data and subject to rigorous quality control (QC) [e.g. deposited data in dbGaP (Mailman et al., 2007)]. To support more dirty data in the wild, it will be necessary to embed QC processes for meta-analysis in the protocol (Winkler et al., 2014). Certain procedures may be vulnerable to attacks on privacy, but those which are based on standard algebraic computations should be translatable into secure computations. At the same time, it should be noted that many procedures can be directly applied in the clear because they do not violate privacy [e.g., file-level QC and SE-N plots in (Winkler et al., 2014)]. As QC is a relatively independent and large pipeline, we leave it for future work. Second, the current SecureMA implementation relies on a trusted authority to generate cryptographic keys, which sometimes may not be desirable (alternative solutions are in Supplementary Section S1). Third, in situations when individual-level genomic records need to be processed, it will be necessary to pair secure data management technologies with effective societal controls (e.g. use agreements and mandated limits on investigator behavior) that deter misuse and limit the extent to which genomic information can be abused and cause harm to people [e.g. expansion of laws to prevent utilization of genomic data in life insurance eligibility and support for long term care (Altman et al., 2013)].

5.3 Alternative methods to maintain genomic privacy

To provide context for the contributions of the SecureMA protocol, we take a moment to review other recent developments in the field. There are generally two categories of data protection mechanisms that have been proposed to maintain participant privacy while supporting scientific investigations on genomic data. From a societal and regulatory perspective, it has been suggested that research participants consent to the risk of being reidentified (Lunshof et al., 2008; which may bias participant recruitment), while users of such data contractually agree not to attempt to reidentify the participants (Taylor, 2008). We believe such mechanisms can lower risk and, while data use agreements assign liability, they do not provide any technological deterrent and can only be enforced when violations could be detected.

On the other hand, various technological techniques have been proposed to promise genomic privacy. These include encrypting genomic sequences and supporting simple queries (Kantarcioglu et al., 2008), obfuscating raw (short) genome sequences and allowing for retrieval (Ayday et al., 2014), splitting regression analyses into local-site computations and center-level aggregation (Wolfson et al., 2010) and hosting participant-level genomic data using a cryptographic technique and facilitating genetic association studies (Kamm et al., 2013). The two approaches most similar to ours are hampered by practical limitations. First, Wolfson et al. (2010) may leak sensitive information because local sites inappropriately disclose intermediate summary statistics during computation (Emam et al., 2013); The other recent proposal (Kamm et al., 2013) fails to account for site-specific covariates and other data preprocessing within sites, which is a common practice for multisite genetic association studies. Their solution may also suffer from computational scalability and network trafficking issues in studies with large sample sizes because all individual genomic data must pass through, and be analyzed by, every server.

5.4 Conclusion

This work illustrates that the privacy of individual participants, and site-level summary statistics, in genetic association meta-analysis can be guaranteed without sacrificing the ability to perform analysis that use shared data. Our proposal, SecureMA, is useful for running joint studies over disparate data sites in large consortia, where privacy or confidentiality is a concern. If appropriately implemented, our approach can prevent privacy intrusions posed by the attacks published to date. While there are opportunities to make this protocol more efficient and to incorporate quality control measures, we believe it is possible to enable much broader analytic access to genomic data for the purposes of effect estimation and statistical association via meta-analysis.