Partitioning the Metabolic Cost of Human Running: A Task-by-Task Approach

Abstract

Compared with other species, humans can be very tractable and thus an ideal “model system” for investigating the metabolic cost of locomotion. Here, we review the biomechanical basis for the metabolic cost of running. Running has been historically modeled as a simple spring-mass system whereby the leg acts as a linear spring, storing, and returning elastic potential energy during stance. However, if running can be modeled as a simple spring-mass system with the underlying assumption of perfect elastic energy storage and return, why does running incur a metabolic cost at all? In 1980, Taylor et al. proposed the “cost of generating force” hypothesis, which was based on the idea that elastic structures allow the muscles to transform metabolic energy into force, and not necessarily mechanical work. In 1990, Kram and Taylor then provided a more explicit and quantitative explanation by demonstrating that the rate of metabolic energy consumption is proportional to body weight and inversely proportional to the time of foot-ground contact for a variety of animals ranging in size and running speed. With a focus on humans, Kram and his colleagues then adopted a task-by-task approach and initially found that the metabolic cost of running could be “individually” partitioned into body weight support (74%), propulsion (37%), and leg-swing (20%). Summing all these biomechanical tasks leads to a paradoxical overestimation of 131%. To further elucidate the possible interactions between these tasks, later studies quantified the reductions in metabolic cost in response to synergistic combinations of body weight support, aiding horizontal forces, and leg-swing-assist forces. This synergistic approach revealed that the interactive nature of body weight support and forward propulsion comprises ∼80% of the net metabolic cost of running. The task of leg-swing at most comprises ∼7% of the net metabolic cost of running and is independent of body weight support and forward propulsion. In our recent experiments, we have continued to refine this task-by-task approach, demonstrating that maintaining lateral balance comprises only 2% of the net metabolic cost of running. In contrast, arm-swing reduces the cost by ∼3%, indicating a net metabolic benefit. Thus, by considering the synergistic nature of body weight support and forward propulsion, as well as the tasks of leg-swing and lateral balance, we can account for 89% of the net metabolic cost of human running.

Introduction

In this article, we first review the net metabolic cost of running as a function of speed. Then, we briefly discuss the simple spring-mass model that has been fundamental in conceptualizing the mechanical principles involved in human running as well as inspiring the “cost of generating force” hypothesis. The bulk of our paper provides a chronological account of a task-by-task approach that has identified the biomechanical tasks that comprise the net metabolic cost of running. Unless indicated otherwise, the following data and discussion refer specifically to our experiments on humans.

Metabolic energy and the cost of transport during running

The submaximal rate of oxygen consumption (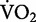) provides a good indication for the rate of metabolic energy consumption (Brooks et al. 2004). In recreational runners, the net 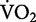for running increases linearly as speed increases (Bøje 1944; Margaria et al. 1963; Menier and Pugh 1968). As a consequence, the net cost of transport for running is independent of speed. As demonstrated in Fig. 1, this relationship emerges from the constant slope that mathematically expresses the linear increase in the net 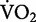as a function of running speed (Margaria et al. 1963). Therefore, the “amount” of metabolic energy used to run a given distance is the same, whether one decides to run at a slow or at a fast speed.

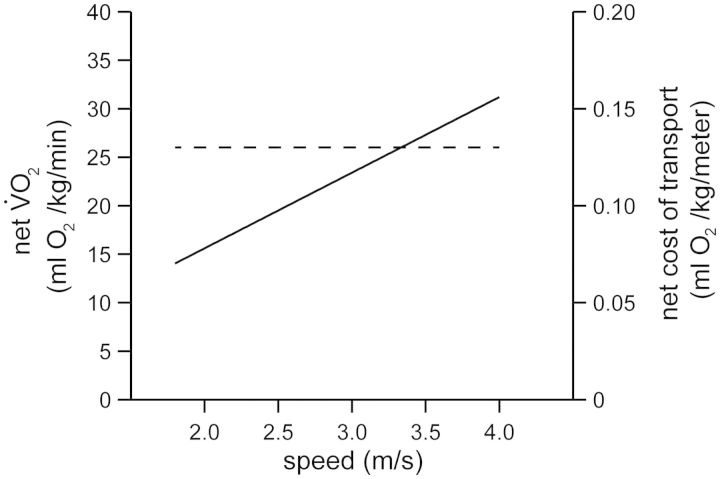
Fig. 1.

The net rate of oxygen consumption increases linearly across human running speed (solid line), and as a consequence, the net cost of transport (dashed line) remains independent of speed (m/s). The lines are developed from the classic data published by Margaria et al. (1963). It is important to note that Margaria et al. (1963) found that the extrapolation of the regression line relating gross 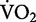and running speed crossed the zero-speed intercept at a value that was similar to his subjects’ resting metabolism. After subtracting this value from gross 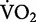, Margaria et al. (1963) referred to this quantity using the term “net”.

In keeping with the original thinking at the time of C.R. Taylor and his colleagues, we express the general idea that the rate of metabolic energy consumption increases linearly with running speed. However, we recognize that there is evidence to suggest that this may not be the case for all human runners (van der Walt and Wyndham 1973; Hagan et al. 1980). Recent evidence suggests that the cost of transport is not independent of running speed (Steudel-Numbers and Wall-Scheffler 2009; Batliner et al. 2013). This trend appears to stem from the changes in 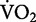at the relatively faster running speeds achieved by high-caliber athletes (Batliner et al. 2013). Thus, we caution that the linear increase in the rate of metabolic energy consumption likely holds only for recreational runners at running speeds for which metabolic energy is provided primarily by aerobic metabolism.

Performing mechanical work?

Initially, researchers attempted to explain the metabolic cost of running by quantifying the mechanical work involved. Fenn (1930a, 1930b), using kinematic data of the moving limbs and force-plate measurements, was the first to relate the rate of total mechanical work, both internal and external, to the rate of metabolic energy consumption during running. Internal mechanical work refers to the movement of the limbs relative to the whole body center of mass (COM). External mechanical work refers to the movement of the whole body‘s COM relative to the ground. These experiments, however, were performed at near maximum running speeds (∼7.5 m/s) and thus are outside the scope of this review. Using similar methods, Cavagna et al. (1964) extended Fenn’s findings by quantifying the changes in the total mechanical work across a range of submaximal running speeds (∼3–6 m/s). Their findings revealed that the rate of total mechanical work increased linearly with speed (Cavagna et al. 1964), similar to the linear relationship observed between net 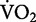and speed (Fig. 1).

Although the changes in the rate of total mechanical work versus speed paralleled the changes in the net 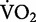versus speed in running, Cavagna et al. (1964) realized that this approach produced efficiency values that far exceeded the maximal mechanical efficiency of skeletal muscle. Muscle mechanical efficiency is defined as the ratio of mechanical power output to the rate of metabolic energy consumption and describes the muscle’s ability to convert metabolic energy into useful mechanical work. Mechanical efficiency of skeletal muscle reaches a maximum value of 25% (Hill 1922; Margaria 1976). Yet, the mechanical efficiency measured in running ranged from 40% to 50% (Cavagna et al. 1964, 1977; Cavagna and Kaneko 1977). Thus, a large portion of the metabolic energy consumed during running could not be explained by the total mechanical work performed by the muscles alone.

Spring-mass model

The observation that the mechanical efficiency of running was much higher than 25% led to the idea that “elastic elements” within the musculoskeletal system store and return mechanical energy. Cavagna et al. (1964) characterized human running as a bouncing ball and this analogy was later extended to a simple spring-mass model whereby the leg acts as a linear spring (McMahon et al. 1987; Blickhan 1989; McGeer 1990; McMahon and Cheng 1990). In this model (Fig. 2), the spring-like behavior of the leg is due to the stretch and recoil of elastic tissue elements such as the muscles, tendons, and ligaments (Alexander 1984; Ker et al. 1987).

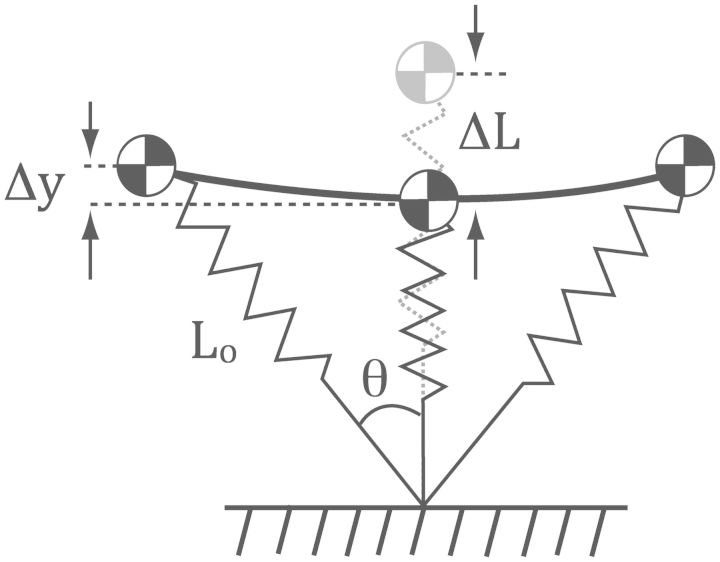
Fig. 2.

Spring-mass model characterizes the mechanics of human running. The model consists of a mass and a single leg-spring that connects the foot (not shown) and COM. This model depicts the runner transversing along the ground from the beginning (left-most position), middle (leg-spring is oriented vertically), and to the end of stance phase (right-most position). The leg-spring has an initial length, L_o, at the beginning, and ΔL represents its maximal compression at mid-stance. The dashed spring-mass model shows the length of the uncompressed leg-spring. Thus, the difference between the length of the dashed leg-spring and maximally compressed leg-spring represents the maximum compression of the leg-spring, ΔL. The downward vertical displacement of the mass during stance is represented by Δy, which is substantially smaller than ΔL. Half of the angle swept by the leg-spring during contact with the ground is denoted by θ. Figure reprinted and caption adapted and modified from Farley and Gonzalez (1996) with permission from Elsevier.

The linear spring in the model compresses and stores mechanical energy during the first half of the stance phase and then recoils and releases the mechanical energy during the second half of the stance phase (Fig. 2). The energy released by the linear leg spring provides the mechanical energy for the acceleration of the body in the upward and forward direction. The elastic property of the linear leg spring is characterized by the leg’s stiffness (k_leg), which is defined as the ratio of the peak force to the maximum compression of the spring (McMahon and Cheng 1990; Farley et al. 1993).

Based on the assumptions of the spring-mass model, several experiments revealed that the stiffness of the legs in a variety of animals, including humans, remains relatively constant over a wide range of running speeds (He et al. 1991; Farley et al. 1993). Humans, like other animals, run faster by increasing the angle swept by the leg spring (θ) and by reducing the vertical excursion (Δy) of the COM during the stance phase. These adjustments allow humans to run faster by bouncing off the ground more quickly.

Despite the simplicity of the spring-mass model for characterizing the overall COM mechanics during running, this analogy presents a paradox for explaining the net metabolic cost of running. If running can be modeled as a simple spring-mass system, why does running demand any metabolic energy at all? Theoretically, the external mechanical work performed on the COM can be supplied by the spring itself. Furthermore, this model assumes that the linear spring is perfectly elastic, meaning that the same amount of mechanical energy is stored and returned during the stance phase of running. Therefore, the simple spring-mass model cannot explain the net metabolic cost of running, but one must realize that the model’s main intention was to describe the mechanics of running and has done so extremely well.

In summary, Cavagna et al. (1964)’s mechanical work approach did not provide a satisfactory explanation for the metabolic cost of running. That approach, however, led to the hypothesis that elastic elements must be involved in the mechanics of running. We now understand that these elastic elements greatly reduce the metabolic cost of running in humans and other animals (Cavagna et al. 1964, 1977; Alexander 1984). Despite these initial efforts, it was not until 25 years later that a more satisfactory explanation for the net metabolic cost of running emerged.

Cost of generating muscular force

Since the transformation of metabolic energy into mechanical work did not explain the metabolic cost of running in humans and other animals (Heglund et al. 1982a, 1982b; Taylor et al. 1982), Taylor et al. (1980) proposed the “cost of generating force” hypothesis. This approach was based on the idea that “muscles transform metabolic energy into force and not necessarily mechanical work”. By measuring rates of oxygen consumption in a variety of small and large animals (0.30–120 kg), including humans, while running with various loads (7–27% of body mass), Taylor et al. (1980) observed that the rate of oxygen consumption increased in direct proportion to the added mass. Thus, they proposed that the metabolic cost of running could be explained by the cost of generating force integrated over time (∫F dt). Taylor (1985) and Heglund and Taylor (1988) further explored this hypothesis by providing evidence that the rate of oxygen consumption at physiologically equivalent speeds (transition between trotting and galloping) did not change in parallel with the mechanical work performed. However, the rate of oxygen consumption per kilogram body mass “per stride” at physiologically equivalent speeds was nearly constant across a wide size-range of animals.

Kram and Taylor (1990) then provided an explicit and quantitative explanation for the net metabolic cost of running. They demonstrated that the net rate of metabolic energy consumption was proportional to the average vertical force applied to the ground (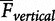) and inversely proportional to the time (t_c) when the foot applies force to the ground (Eq. 1) for a variety of animals ranging in size (30g-140 kg) and speed.

(1)

Over an integral number of complete strides, the average vertical force generated on the ground remains the same across speed and is equal to the animal's body weight, W_b. By introducing a “cost coefficient”, c, the proportionality can be converted to a mathematical equation expressing the relation between mass-specific rate of net metabolic energy consumption and the inverse of t_c (Eq. 2).

(2)

Kram and Taylor (1990) found that the cost coefficient was nearly constant across a wide range of animal size and running speed. This simple equation demonstrates that the net metabolic cost of running can be explained by the cost of how rapidly one generates vertical forces on the ground to support the weight of the body. Experiments on humans and other running bipeds further supported the cost of generating force hypothesis whereby changes in net metabolic rate versus speed paralleled the changes in the rate of generating force (1/t_c) versus speed (Roberts et al. 1998). Furthermore, in-vivo measurements from the lateral gastrocnemius of running turkeys revealed that during stance, the active muscle fibers generate force while performing little or no mechanical work. The majority of the mechanical work is performed by elastic stretch and recoil of the tendon (Roberts et al. 1997). The elastic stretch and recoil of the Achilles tendon play a similar role in human running (Alexander 1984; Alexander and Bennetclark 1977; Ker et al. 1987) and the ability of the Achilles tendon to store and release elastic energy relies upon the active fibers of the soleus and gastrocnemius muscles. Other anatomical structures (e.g., the arch of the foot) also store and return elastic energy (Ker et al. 1987).

The metabolic cost of running: task-by-task

The comparative approach is very powerful for explaining the metabolic cost of running across a wide range of animal sizes and speeds. It is unlikely that the “cost of generating force” hypothesis would have ever been formulated and scientifically tested without broad comparative studies. However, to further investigate the cost of generating force hypothesis, we have found that humans are conducive for a particular set of studies that involve direct manipulations that reduce the metabolic cost of running. Chang and Kram (1999) initiated a task-by-task approach in an attempt to provide a more detailed explanation for the net metabolic cost of running. This methodological approach has been continually refined over the years, and now we have a coherent biomechanical account for the net metabolic cost of running. Based on this task-by-task approach, the net metabolic cost of running can be partitioned into the biomechanical tasks of: 1) body weight support, 2) forward propulsion, 3) leg-swing, 4) lateral balance, and 5) arm-swing. Here, we summarize the relative net metabolic cost required for each biomechanical task as estimated from the cost-of-generating-force approach and the task-by-task approach.

Body weight support

During the foot-ground contact phase of running, muscles are recruited to generate force to support the weight of the body, thus demanding metabolic energy. Although we use the term “body weight support”, it is important to understand that running is a dynamic series of bounces during which the magnitude of the vertical force exerted by the muscles varies as a function of time. For instance, the vertical ground reaction force increases during the first half of the foot-ground contact phase, reaches its maximum at mid-stance, decreases during the second half, and then equals zero during the aerial phase. The development of the vertical ground-reaction force changes dramatically during the time-course of ground-contact. The average vertical force over a complete stride, however, is equal to the weight of the body and remains constant across running speeds (Taylor et al. 1980; Kram 2000).

While the average vertical force remains equal to body weight, it is important to understand that the time available in each step to generate force decreases as running speed increases, thus, the muscles must generate force in a shorter period of time (Kram and Taylor 1990; Kram 2000). Although the storage and return of mechanical energy are primarily performed by the elastic elements of the lower limb, the muscle fibers still consume metabolic energy to generate force that not only supports the weight of the body but is also required to operate the tendinous spring-like behavior of the leg (Taylor et al. 1980). The cost of body weight support in humans can be predicted from Equation (2). Roberts et al. (1998) estimated that between the running speeds of 2 and 4 m/s, 80% of the increase in net metabolic rate could be explained by the changes in the rate at which force is generated along the ground (1/t_c). As outlined below, other experiments on humans that externally support the weight of the body are consistent with these findings.

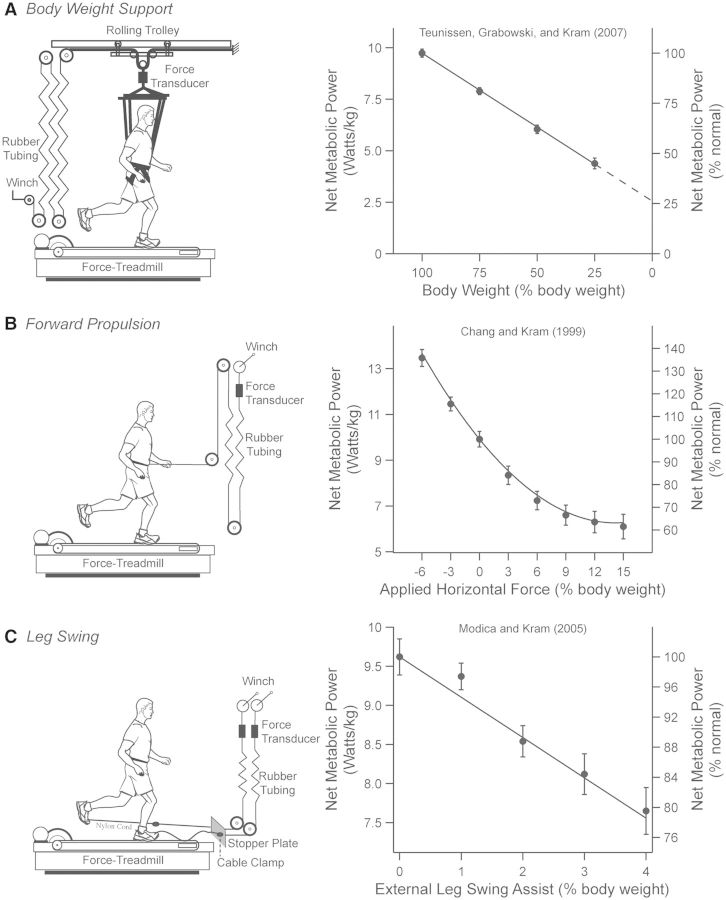
Using methods similar to those of Farley and McMahon (1992), Teunissen et al. (2007) partitioned the metabolic cost of body weight support by utilizing a low-friction rolling trolley system that applied a relatively constant upward force to the whole body’s COM via a modified climbing harness (Fig. 3A). By systematically reducing body weight from 1 to 0.25 g (g is gravity) while subjects ran at 3 m/s, Teunissen et al. (2007) found that the demand for net metabolic energy decreased in less than direct proportion to body weight support. In that study and throughout the rest of this article, we define “net” as gross metabolic power minus standing metabolic power. By extrapolating a regression line fit from their original data, Teunissen et al. (2007) estimated that even running with zero body weight (0 g) would still exact ∼26% of the net metabolic cost of running at normal body weight (1 g). Based on this extrapolation, one can deduce that body weight support comprises ∼74% of the net metabolic cost of running.

Fig. 3.

The individual tasks of body weight support, forward propulsion, and leg-swing exacts a metabolic cost, leading to an overestimation for explaining the net metabolic cost of running. (A) To reduce the amount of body weight than the subject must support, a rolling trolley apparatus applies a relatively constant upward force via a modified climbing harness to the subject’s waist. As a result, the net metabolic cost of running decreased in less than direct proportion to the level of body weight support. When extrapolating to zero body weight support, the regression value suggests that the task of body weight support exacts ∼74% of the net metabolic cost of running. (B) On the left, the apparatus applies a relatively constant horizontal force about the subject’s waist in the forward direction, thus reducing the need to generate forward propulsive forces along the ground. An optimal aiding force of 15% body weight suggests that the task of forward propulsion exacts ∼37% of the net metabolic cost of running. (C) On the left, an external leg-swing-assist apparatus applies anterior pulling forces to each foot to initiate and propagate the leg forward during swing. An optimal, external leg swing-assist force of 4% body weight suggests that the task of leg-swing exacts ∼20% of the net metabolic cost of running. The data (mean ± SEM) and least-squares regression lines are derived from the studies noted on each figure.

Forward propulsion

Although the horizontal ground-reaction forces are much smaller in magnitude compared with the vertical ground-reaction forces, intuition and indirect evidence suggest that generating horizontal forces is an important determinant of the net metabolic cost of running. Performing external work against an impeding load applied at the waist during running exacts a metabolic cost that increases linearly with the magnitude of the load (Lloyd and Zacks 1972; Zacks 1973). Chang and Kram (1999) extended those findings by investigating the metabolic cost of generating horizontal ground-reaction forces while humans ran at 3.3 m/s with horizontal impeding or aiding forces applied at the waist (Fig. 3B). An optimal aiding force of 15% body weight reduced the demand for net metabolic energy by 37% (assuming a standing rate of metabolic energy consumption of 1.85 W/kg). Using essentially the same device in a follow-up study, Moed and Kram (2005) found that forward propulsion comprises ∼42% of the net metabolic cost of running at 3 m/s.

In addition to the cost of generating propulsive forces, there is also a metabolic cost for generating braking forces. Chang and Kram (1999) demonstrated that generating horizontal propulsive forces was more costly than generating horizontal braking forces. When humans ran against a maximum impeding force of −6% body weight, the average braking impulse decreased by 52% while the average propulsive impulse increased by 48%, resulting in a 38% increase in the net metabolic cost of running. When humans ran with a maximum aiding force of +15% body weight, the average braking impulse increased by 173% while the average propulsive impulse decreased by 70%, resulting in a 37% decrease in the net metabolic cost of running. Despite the fact that increase in the braking impulse far exceeded the decrease in propulsive impulse, there was still a decrease in the net metabolic cost of running. Therefore, it seems clear that the cost of generating braking forces is metabolically cheaper than the cost of generating propulsive forces. Although it would be ideal to estimate the cost of braking forces, we put forward evidence to suggest that the tasks of body weight support and forward propulsion should be treated synergistically (see below). This suggests that the individual cost of braking forces is not what is important. Rather, it is the cost of generating force required for the synergistic task of body weight support and forward propulsion.

Leg-swing

In running, muscles are recruited to swing each leg forward during a stride. Such muscular actions presumably incur a metabolic cost. To empirically quantify the metabolic cost of leg-swing during running, Modica and Kram (2005) developed a device that strategically applied external anterior pulling forces to each foot to initiate and propagate the forward motion of the leg during swing (Fig. 3C). Therefore, their external device reduced the need of the muscles to directly swing the leg. Applying a forward pulling assistive force of 4% body weight reduced the net metabolic cost of running by ∼20%. From these data, Modica and Kram (2005) inferred that leg-swing comprises at most 20% of the net metabolic cost of running. Interestingly, using blood flow measurements, Marsh et al. (2004) contemporaneously estimated that leg-swing in guinea fowl incurred 26% of the net metabolic cost of running (for further discussion on this issue, see the section “Where do we stand?”).

Overestimation of the net metabolic cost of running

At this point, an astute reader may realize that the “individual” tasks of body weight support, forward propulsion, and leg-swing sum to 131–136%, an apparent overestimation for the net metabolic cost of running. We suspected that this overestimation occurs because of the interactive nature of the muscular forces generated for these three biomechanical tasks. For example, the ankle extensor muscles have multifunctional roles in contributing to body weight support, forward propulsion, and leg-swing; thus, these interactive effects make it difficult to empirically separate their relative cost. With this in mind, Kram and colleagues (Moed and Kram 2005; Warddrip 2007) continued to refine the task-by-task approach by empirically quantifying the reductions in net metabolic cost when combining the effects of these assistive devices.

Combinations of body weight support, aiding horizontal forces, and leg-swing-assist forces

Building upon Gottschall and Kram’s (2005) walking study, Moed and Kram (2005) applied a combination of horizontal aiding forces at the waist and assistive forces at the feet during running. When an optimal aiding horizontal force (AHF) of 10% body weight was applied at the waist, the net metabolic cost decreased by 42%. When combining the optimal AHF with an optimal leg-swing assistive force of 2% body weight, net metabolic cost further decreased to 49%, suggesting that leg-swing comprises ∼7% of the net metabolic cost of running. This 7% value was found to be nearly constant across a range of running speeds (2–4 m/s).

To further elucidate the possible interactions between these biomechanical tasks, Kram’s student, Warddrip (2007), quantified the reductions in net metabolic cost in response to synergistic combinations of BWS, an AHF, and leg-swing-assist (LSA) forces at each foot (Fig. 4). For clarity, we use the acronym “BWS” to refer to the experimental manipulations implemented by Warddrip (2007) and use the term “body weight support” to represent the biomechanical task required during running throughout the rest of the text. Consistent with the results of Teunissen et al. (2007), Warddrip (2007) found that net metabolic cost decreased in less than direct proportion to body weight support. Extrapolating the regression line to zero body weight, she estimated that body weight support comprises ∼65% of the net metabolic cost of running. In combination with BWS, providing an AHF further reduced the cost of running across the levels of body weight support. By considering the effect that body weight support might have on forward propulsion, the magnitude of the AHF was adjusted for each level of BWS, e.g., at 75% normal body weight, AHF equals 7.5% normal body weight.

Fig. 4.

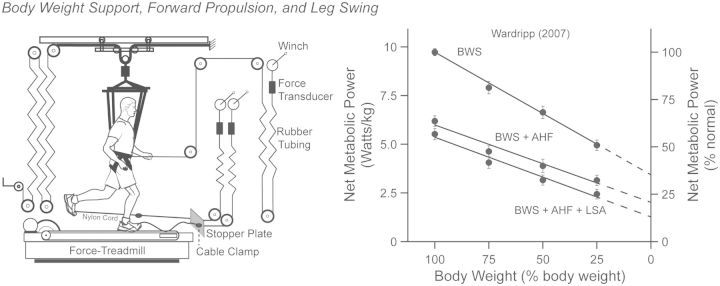
When considering their interactive nature, the synergistic tasks of body weight support, forward propulsion, and leg-swing exact a metabolic cost that is less than physiologically possible, thus providing a more coherent explanation for the metabolic cost of running. The experimental set-up consists of strategic combinations of BWS, an optimal aiding horizontal force about the waist (AHF), and an optimal leg-swing assistive force at the feet (LSA). The regression lines represent changes in the net metabolic cost of running when applying BWS, BWS + AHF, and BWS + AHF + LSA. The BWS condition demonstrates that the net metabolic cost of running decreased in less than direct proportion to the level of BWS. When extrapolating the BWS line to zero body weight, the regression value suggests that the task of body weight support exacts ∼65% of the net metabolic cost of running. When extrapolating the BWS + AHF line to zero body weight, the regression value suggests that the synergistic tasks of body weight support and forward propulsion exacts ∼80% of the net metabolic cost of running. When extrapolating the BWS + AHF + LSW line to zero body weight, the regression value suggests that synergistic tasks of body weight support and forward propulsion along with the independent task of leg-swing exacts ∼87% of the net metabolic cost of running. The data (mean ± SEM) and least-squares regression lines are derived from the study noted in the figure.

Two important observations emerge from the regression line denoting the reductions in net metabolic cost when combining BWS and an AHF. First, the “percent” cost of forward propulsion to the net metabolic cost of running is consistent across the levels of BWS (i.e., % difference between the BWS line and BWS + AHF line). Specifically, a proportional AHF reduced the net metabolic cost of running by 36%, 41%, 41%, and 36% at the 100%, 75%, 50%, and 25% levels of normal body weight. Based on the average value of these percent differences, one can infer that forward propulsion comprises on average ∼39% of the net metabolic cost of running, which is consistent with the findings of Chang and Kram (1999) and Moed and Kram (2005). Second, when extrapolating Warddrip’s (2007) BWS + AHF regression line to zero body weight, the data suggest that the synergistic tasks of body weight support and forward propulsion comprise ∼80% of the net metabolic cost of normal running, which is consistent with the findings of Roberts et al. (1998).

Providing LSA forces of 2% body weight further reduced the net metabolic cost of running (BWS + AHF + LSA). Since the mass and inertia of the leg remain the same under the combination of assistive devices, Warddrip (2007) reasoned that the muscular effort required to swing the leg should be independent of body weight support and forward propulsion, thus keeping the absolute LSA forces constant across all levels of BWS. When extrapolating the BWS + AHF + LSA regression line to zero body weight, the data suggest that the synergistic tasks of body weight support, forward propulsion, and leg swing comprise ∼87% of the net metabolic cost of normal running.

The extrapolations to zero body weight appear to present a paradox in which 13% of the net metabolic cost of running remains unexplained, yet, our previous estimates of body weight support, forward propulsion, and leg-swing “individually” summed to 131–136%. In light of these results, Warddrip (2007) put forward the idea that this paradox suggests that synergies between the tasks of body weight support and forward propulsion act to reduce the net metabolic cost of running. In “absolute” terms, for example, applying an AHF of 10%, 7.5%, 5.0%, and 2.5% normal body weight decreased the net metabolic cost of running by 3.5, 3.3, 2.6, and 1.8 W/kg at the 100%, 75%, 50%, and 25% levels of normal body weight, respectively. From these values, we can see that the absolute cost of forward propulsion decreases as the absolute cost of body weight support decreases, revealing that these tasks act synergistically. In contrast, LSA further decreased the “absolute” cost of running by 0.7, 0.6, 0.7, and 0.7 W/kg at the 100/10%, 75/7.5%, 50/5.0%, and 25/2.5% combinations of percent normal body weight and an AHF. Thus, the absolute cost of leg-swing remained the same across all combination levels, indicating that a synergy does not exist between leg-swing and the synergistic actions of body weight support and forward propulsion.

Considering the interactive nature of body weight support and forward propulsion, we infer that body weight support, forward propulsion, and leg-swing comprise ∼87% of the net metabolic cost of running. Extrapolation of the Wardripp (2007) data to zero body weight yields the synergistic costs of body weight support and forward propulsion as comprising ∼80% of the net metabolic cost of running. In addition, the same extrapolation yields the non-synergistic cost of leg-swing to comprise ∼7% of the net metabolic cost of running. We are careful to note that both Moed and Kram (2005) and Wardripp (2007) independently found that leg-swing comprises just ∼7% of the net metabolic cost of running. Taken together, it appears that the study of Modica and Kram (2005) overestimated the cost of leg-swing. Apparently, the external LSA device used in that study also provided forward propulsive forces, thus we do not include the data of Modica and Kram (2005) in our estimates.

Lateral balance

Maintaining lateral balance is arguably a critical prerequisite for running. Until recently, it was unknown whether maintaining lateral balance during running incurred a net metabolic cost. We performed a series of studies motivated by two simple questions: 1) Why do humans prefer to run with a step width near zero? and 2) Why do humans prefer to swing their arms while running? In our first study, we found that running at target step widths greater than preferred or without arm-swing increased net metabolic cost, which coincided with increases in step width variability—our indicator of lateral balance (Arellano and Kram 2011). From our data, we inferred that humans prefer to run with a step width near zero and to swing their arms so as to minimize metabolic cost and optimize lateral balance. From these insights into lateral balance, we hypothesized that maintaining lateral balance during running would not exact a significant metabolic cost. In other words, when considering body weight support, forward propulsion, and leg-swing, we reasoned that the net metabolic cost of maintaining lateral balance during running would be relatively small.

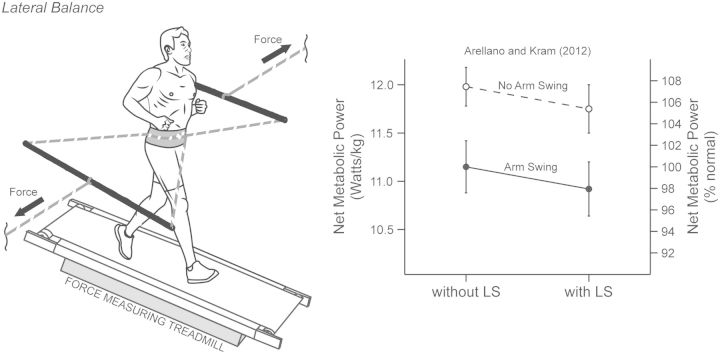
That hypothesis was supported by our subsequent experiment (Arellano and Kram 2012), in which we reduced the muscular effort required to maintain lateral balance by providing external lateral support during running with and without arm-swing (Fig. 5). In brief, our external lateral support system applied lateral forces to the waist with an in-situ effective stiffness of ∼2200 N. When controlling for step width using our real-time visual-feedback method (Arellano and Kram 2012), we found that external lateral support while running with or without arm-swing reduced net metabolic cost and step width variability by 2% and 12%, respectively. We reasoned that the reductions in both net metabolic cost and step width variability reflect the cost of maintaining lateral balance, thus, maintaining lateral balance comprises only ∼2% of the net metabolic cost of running.

Fig. 5.

The task of maintaining lateral balance exacts a net metabolic cost during human running. When provided with external lateral support (LS, solid and dashed lines), the net metabolic cost of running decreased by ∼2% (significant external LS effect, P = 0.032). When eliminating arm-swing (no arm swing, open circles; arm swing, filled circles), the net metabolic cost of running increased by ∼8% (significant arm swing effect, P < 0.001). The lack of a significant interaction effect between external LS and arm-swing indicates that external LS resulted in a similar reduction in net metabolic cost of running with or without arm-swing. The data (mean ± SEM) are derived from the authors noted in the figure.

Furthermore, we found that eliminating arm-swing increased the net metabolic cost of running. However, eliminating arm-swing did not affect step width variability, indicating that arm-swing does not assist with lateral balance. Therefore, we reasoned that arm-swing must help with other aspects of balance control, such as counteracting the angular momentum generating by the swinging legs about the vertical axis (Arellano and Kram 2012).

Arm-swing

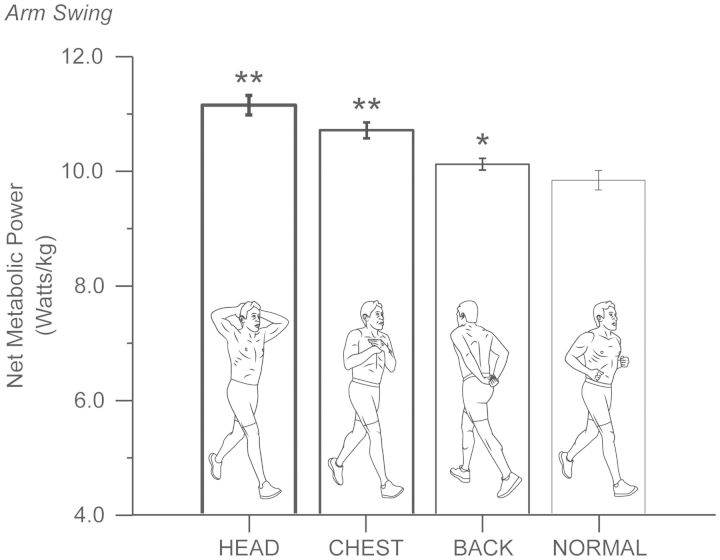
Since swinging the legs incurs a metabolic cost during running, it seems reasonable to imagine that swinging the arms could also incur a metabolic cost. In our previous studies (Arellano and Kram 2011, 2012), we revealed that running without arm-swing “increased” the net metabolic cost of running by ∼8%. We concluded that arm-swing helps to minimize the metabolic cost of running; however, our findings were confounded by the fact that when humans ran without swinging their arms, they held their arms across the chest. This type of restriction perhaps artificially elevated the cost of running due to the extra muscular effort required to hold the arms across the chest. To address this issue as well as to settle the controversy surrounding the metabolic benefit of arm-swing (Arellano and Kram forthcoming 2014), we compared the metabolic cost of running with normal arm-swing to the metabolic cost of running while restricting the arms in three different ways: 1) holding the hands with the arms behind the back in a relaxed position (BACK), 2) holding the arms across the chest (CHEST), and 3) holding the hands on top of the head (HEAD). When compared to running while swinging the arms normally, the net metabolic cost of running in the BACK, CHEST, and HEAD conditions was 3%, 9%, and 13% greater, respectively (Fig. 6). These findings further support our original idea that humans swing their arms to minimize the metabolic cost of running (Arellano and Kram 2011, 2012). While actively swinging the arms might incur a metabolic cost, our data suggest that this action provides other benefits, such as reducing the amplitude of torso motion (Arellano and Kram forthcoming 2014). Indeed, we found that when arm-swing was restricted while running, humans increase the peak-to-peak amplitude of both shoulder and pelvis rotation about the vertical axis, most likely reflecting a compensatory strategy that counteracts the angular momentum of the swinging legs. Overall, actively swinging the arms provides both metabolic and biomechanical benefits during running.

Fig. 6.

Swinging the arms reduces the net metabolic cost of human running. We measured net metabolic cost (mean ± SEM) as subjects ran while holding the hands on top of the head (HEAD), holding the arms across the chest (CHEST), holding the hands with the arms behind the back in a relaxed position (BACK), and while swinging their arms normally (NORMAL). The data demonstrate that running without arm-swing (compared with the control, * indicates P < 0.05 and ** indicates P < 0.01) increases net metabolic cost, indicating that arm-swing provides a small, but significant metabolic benefit during human running.

Task-by-task summary

Even we did not consider the inherent synergy between some tasks, both the “cost of generating force” and the “individual task-by-task” approaches demonstrate that body weight support is the primary determinant of the net metabolic cost of running (Fig. 7A and B). In the individual task-by-task approach, forward propulsion represents the second largest determinant of the net metabolic cost of running while leg-swing and lateral balance exact small relative metabolic costs. If we “individually” sum all the biomechanical tasks, the lower and upper bounds for the metabolic cost of running are paradoxically 111% and 125%, respectively. If we had perfectly partitioned the net metabolic cost of running, the sum of all four tasks would be equal to 100%. The fact that these independent studies (Chang and Kram 1999; Moed and Kram 2005; Teunissen et al. 2007; Warddrip 2007; Arellano and Kram 2012) captured more cost than physiologically possible suggests that the synergistic nature of these tasks requires them to be studied interactively.

Fig. 7.

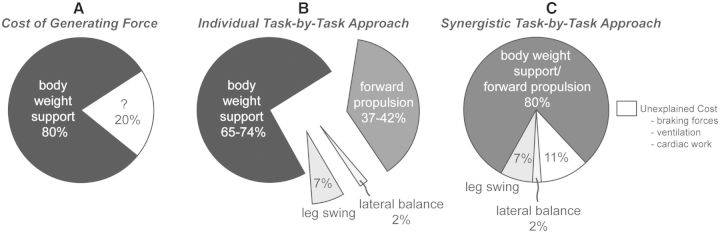
The (A) cost of generating force, (B) individual task-by-task, and (C) synergistic task-by-task approach partition the net metabolic cost of human running into its biomechanical constituents. The cost of generating force approach and the individual task-by-task approach both illustrate that body weight support is the primary determinant of the net metabolic cost of human running. In the individual task-by-task approach, forward propulsion represents the second largest determinant. The individual task-by-task approach leads to an overestimation while the synergistic task-by-task approach suggests that the synergistic tasks of body weight support and forward propulsion are the primary determinant of the net metabolic cost of human running. Note that leg-swing and lateral balance exact a relatively small net metabolic cost. If we sum all the biomechanical tasks, the synergistic task-by-task approach accounts for 89% of the net metabolic cost of human running.

If we consider the interactive nature of body weight support and forward propulsion, the synergistic cost of body weight and forward propulsion comprises ∼80% of the net metabolic cost of running (Fig. 7C). The synergistic task-by-task approach further demonstrates that the task of leg-swing is independent of both body weight support and forward propulsion, comprising ∼7% of the net metabolic cost of running. Although the task of maintaining lateral balance has not been studied with the synergistic task-by-task approach, we reason that the cost of lateral balance (∼2%) is also independent of body weight support, forward propulsion, and leg-swing. Therefore, we infer that body weight support, forward propulsion, leg-swing, and lateral balance comprise ∼89% of the net metabolic cost of running. Actively swinging the arms could also be included in our approach; however, arm-swing provides a small net metabolic savings rather than exacting a net metabolic cost. While the other tasks of body weight support, forward propulsion, leg-swing, and lateral balance incur a net metabolic cost, swinging the arms is the only task that provides a net metabolic benefit during running.

After summing all the costs that comprise the biomechanical tasks of running, the question that comes to mind is: What could account for the 11% of the net metabolic cost of running that is left unexplained by our synergistic task-by-task approach? Increased costs of lung ventilation and cardiac work, as a result of hyperpnea during exercise, surely contribute to the remaining 11%. The relative cost of hyperpnea at moderate exercise intensities (e.g., 70% 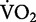max) has been estimated to comprise 3–6% of the total oxygen consumed at 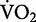max (Aaron et al. 1992a, 1992b). Therefore, the net cost of exercise hyperpnea probably comprises about 3–6% of the overall net cost of running. The net metabolic cost of cardiac work during running is more difficult to estimate, but is likely small.

Where do we stand?

In this review so far, we have explained the biomechanical basis for the metabolic cost of running in humans. Humans are of course only one species among many. Our studies of humans complement the many comparative studies on other biological systems. One advantage of studying humans is that subjects are generally cooperative and can run using our strange mechanical devices without undue agitation. Few other species would be so cooperative and calm. Ethical standards, however, prevent the use of many invasive techniques on human subjects. For such invasive experiments, animal model systems are generally more accepted. In locomotion, the guinea fowl has emerged as an excellent model species. Perhaps most relevant are the studies by Marsh et al. (2004), whom developed unique techniques for measuring the distribution of blood flow to the lower leg muscles of running guinea fowl. Total blood flow to the leg muscles increases linearly with the increase in the rate of oxygen consumption across guinea fowls’ running speeds (Marsh et al. 2004). Based on the electrical activity of the muscles, Marsh et al. (2004) categorized the leg muscles as contributing to either the swing or stance phase. For example, active muscles either 1) generate force on the ground during the stance phase or 2) advance the leg forward during the swing phase. Assuming that the amount of blood flow to the muscles is proportional to the metabolism of oxygen, Marsh et al. (2004) inferred that relative cost of the muscles to generate force during stance and swing exacts 74% and 26% of the total use of energy, respectively. Interestingly, these relative costs remain the same across guinea fowls’ locomotor speeds of 0.5–2.8 m/s, representing up to 90% 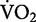max. This finding is analogous to observations on humans that indicate the relative costs of leg-swing and forward propulsion remain constant across running speed (Moed and Kram 2005).

The LiMb model of Pontzer (2005, 2007) predicts the rate of oxygen consumption during human running by taking into account the muscle force generated to support the mass of the body during stance and to swing the leg. Using kinematic variables such as running speed, length of the leg, the angle swept by the leg during stance, and stride frequency, Pontzer (2005, 2007) derived, combined, and summed two simple mathematical models to estimate the mass-specific rate of muscular force production during running. The LiMb model is based on the vertical, horizontal, and leg-swing forces generated by the muscles, thus allowing one to predict the relative cost of each component during running. A modified version (Pontzer 2007) of the LiMb model predicts that generating vertical, horizontal, and leg-swing forces accounts for ∼60%, 17%, and 23% of the net cost of running, respectively.

Considering the different species and methods involved, the findings of Marsh et al. (2004) and Pontzer (2005, 2007) are in general agreement with our synergistic task-by-task approach. The guinea fowl data from Marsh et al. (2004) suggest that the vertical and horizontal forces generated during stance comprise ∼74% of the net cost of running. When summed together, the LiMb model developed by Pontzer (2007) predicts that the cost of generating vertical and horizontal forces during stance comprises ∼77% of the net cost of running. Both of these estimates are in close agreement with our synergistic task-by-task approach, whereby our direct measurements suggest that the synergistic tasks of body weight support and forward propulsion comprise ∼80% of the net metabolic cost of running. The obvious disagreement among these three approaches is the estimated cost of swinging the legs. Marsh et al. (2004) and Pontzer (2007) predicted the net cost of leg-swing as 26% and 23%, respectively, more than three times the 7% cost estimated from our synergistic task-by-task approach. Directly comparing the leg-swing cost estimated from running guinea fowl to running humans is of dubious value given the different design and morphology of the legs between these two species. Indeed, the LiMb model (Pontzer 2007) predicts that the cost of swinging the legs can comprise between 8% and 23% of the net cost of running in dogs, goats, and humans. One explanation for the dramatic difference between our estimate of leg swing cost and the LiMb model’s estimate of leg swing cost is that the LiMb model uses stride-frequency to estimate the mass-specific rate of force production necessary to swing the leg. Swing-time, however, may be a more appropriate parameter in the LiMb model since the rate of muscular force production would be required during the period of leg-swing as suggested by isolated leg swinging experiments on humans (Doke et al. 2005; Doke and Kuo 2007).

The original hypothesis put forward by Taylor et al. (1980) and later supported by Kram and Taylor (1990) was simple and provocative. Over time, many studies have disproved the idea that the cost of generating vertical force to support the weight of the body is the sole determinant that explains the net metabolic cost of running. The net metabolic cost of running primarily reflects the synergistic cost of body weight support and forward propulsion. Other biomechanical tasks such as leg-swing and lateral balance have notable contributions, but exact a small net metabolic cost. Overall, the synergistic task-by-task approach stands as a useful synthesis for explaining the net metabolic cost of human running.

Beyond the task-by-task approach

Although the task-by-task approach is not completely exhausted, we wish to also include a forward-looking perspective in this article by highlighting some exciting and relatively new methods for investigating the metabolic cost of human running. A next level of analysis, beyond a task-by-task approach, is a muscle-by-muscle analysis.

Combining computer simulations of muscle mechanical behavior with models for energy consumption of individual muscles is both a promising and flexible approach (Umberger and Rubenson 2011). A beauty of simulation is that one can ask “what if” questions and thus probe situations that are otherwise impossible in human or comparative studies. However, existing simulations greatly overestimate the metabolic cost of locomotion and it is not clear where the problems are occurring. Thus, before these methods can provide useful information, we need both dramatic improvements in their accuracy and extensive validation of both biomechanical and muscle energetic models.

Another muscle-by-muscle technique that has been used for analyzing the metabolic cost of walking and cross-country skiing is positron emission tomography—known as PET (Oi et al. 2003; Shimada et al. 2007; Bojsen-Moller et al. 2010). While this technique is non-invasive, it does require sophisticated equipment and is expensive. PET only provides information about how much energy is consumed over trials lasting a few minutes or more. Further, data from PET do not provide insight about “when” in a stride the oxygen is being consumed.

Although it is far more invasive, the Fick principle (involving arterial and venous catheters) has been used to measure oxygen consumption rates of various regions such as the lower leg, the upper leg, or the arms (Poole et al. 1992; Calbet et al. 2005). These methods have been used in stationary cycling and treadmill roller skiing, but to our knowledge they have not been applied to running. While oxygen content and oxygen saturation measures are very reliable, measuring cardiac output is less so. Like PET, these techniques also lack temporal resolution. With future advances in technology, perhaps these techniques can be used to discern the rate of metabolic energy consumed at the level of the individual muscles.

Where are we going?

Partitioning force, work, and their interactions at the muscle-tendon level

It is important to note that the task-by-task approach does not attempt to partition the cost of generating force and/or work at the muscle-tendon level. We could attempt to perform calculations of the mechanical work performed on the body, analogous those of Cavagna et al. (1964), but we would be limited by having only indirect estimates of the mechanical work that muscles presumably perform on the body. In other words, the mechanical work approach can reflect the overall behavior of the whole body COM mechanics, but it will not provide us with a direct representation of muscle-tendon dynamics. Understanding muscle-tendon dynamics and their interactions will have to be approached through direct measurements involving experiments on freely-moving, instrumented animals.

For example, in-vivo measurements during bipedal running demonstrate that key muscles of the lower leg primarily generate force isometrically while the tendon stores and returns elastic energy (Roberts et al. 1997). Thus, the tendon performs a majority of the external mechanical work on the body during running. In-vivo and in-situ measurements are also providing insights into the mechanisms that have a direct influence on muscular force production and performance, such as the ability of tendons to act as energy buffers and amplifiers (Roberts and Azizi 2011; Konow et al. 2012; Roberts and Konow 2013). The importance of these mechanisms (and their interactions) in modulating locomotor performance remains to be explored, but it is becoming clear that these in-vivo and in-situ methods provide a tool for linking muscle-tendon performance to locomotor performance.

Conclusion

The task-by-task approach that we have outlined in this article provides a conceptual framework for partitioning the net metabolic cost of human running into its biomechanical constituents. The next question to be answered is: How do muscles and tendons function in-vivo to perform the biomechanical tasks of body weight support, forward propulsion, leg-swing, and lateral balance? Direct measurements of in-vivo muscle-tendon function in animal models are providing valuable insight into the determinants of generating “force” and “work”. If we are to understand the link between metabolic cost and the mechanics of bipedal running, we will need to understand the muscle-tendon mechanical functions that underlie these biomechanical tasks.

Funding

The National Institutes of Health Research Supplement awarded to C.J.A. The National Institutes of Health Research Supplement is under the parent grant awarded to Thomas J. Roberts [AR055295]. Support for participation in this symposium was provided by the Company of Biologists and by the Society for Integrative and Comparative Biology (Divisions of Vertebrate Morphology, Comparative Biomechanics, Neurobiology, and Animal Behavior).