Pulmonary Fluid Flow Challenges for Experimental and Mathematical Modeling

Abstract

Modeling the flow of fluid in the lungs, even under baseline healthy conditions, presents many challenges. The complex rheology of the fluids, interaction between fluids and structures, and complicated multi-scale geometry all add to the complexity of the problem. We provide a brief overview of approaches used to model three aspects of pulmonary fluid and flow: the surfactant layer in the deep branches of the lung, the mucus layer in the upper airway branches, and closure/reopening of the airway. We discuss models of each aspect, the potential to capture biological and therapeutic information, and open questions worthy of further investigation. We hope to promote multi-disciplinary collaboration by providing insights into mathematical descriptions of fluid-mechanics in the lung and the kinds of predictions these models can make.

Introduction

For many decades, mathematicians, physicists, and biomedical and chemical engineers have developed mathematical models of pulmonary fluids to predict mucus flow in airways by single and coordinated cilia, air-drag, and capillary forces. Most of the modeling efforts, both historical and recent, were tested and benchmarked against laboratory or biological experiments (Sleigh 1956; Baba 1972; Blake and Sleigh 1974; Blake 1975; Liron and Mochon 1976; Fulford and Blake 1986; Sleigh et al. 1988; Gaver and Grotberg 1990; Gueron and Liron 1992; Smith et al. 2007, 2008), and their limitations have been fairly represented. Today, it is reasonable to take stock of how far we have come, and what the remaining obstacles are, toward a faithful predictive model of the flow of fluid in the lung’s airways. In this article, we discuss some of the challenges faced by modelers and experimentalists working to provide insight into lung physiology as well as the design and assessment of medical interventions for lung pathologies.

Modeling the flow of fluid in the lungs, even under baseline healthy conditions, presents many challenges. The lung possesses a branching network of airways, which are responsible for conducting air to and from the small respiratory sacs called alveoli (see Fig. 1). Starting from the trachea at generation 0, the network consists of bifurcating tubes that go to generation 23 (Weibel and Gomez 1962), and terminate at alveolar sacs made up of many alveoli. These airways and alveoli are coated on the inside with a thin liquid layer whose thickness is 2–4% of the diameter of the airway under normal conditions (Codd et al. 1994; Yager et al. 1994), but may be 20% in disease (Sackner and Kim 1987). Indeed, complete blockage of the airway is observed in advanced obstructive diseases of airways (Hogg et al. 2004). In the first 15–16 generations, this film is a bilayer consisting of a mucus layer bordered toward the epithelium by a layer of the periciliary fluid that serves as the bath for the carpet of cilia (Widdicombe 1997).

Fig. 1.

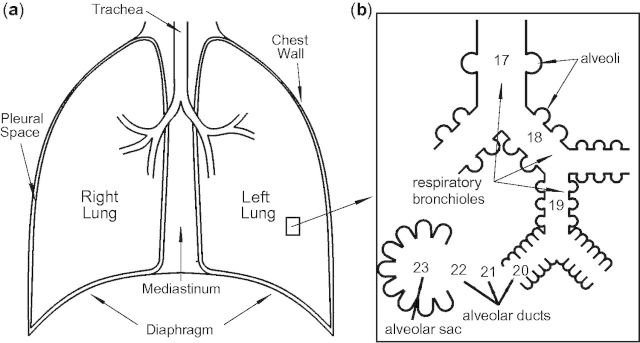
Sketch of a human lung and airways showing insert for generations 17–23 where alveoli appear.

The mucus layer is a non-Newtonian fluid (Yeates 1990), possessing viscoelastic (Lai et al. 2009; Hill et al. 2014) and shear-thinning characteristics and a remarkably low yield stress (Basser et al. 1989; Quraishi et al. 1998). We emphasize, however, that while there is agreement on these qualitative properties of mucus, there is no consensus in the literature either on quantitative values (see Table 1) of linear storage and elastic moduli, or on the stress or strain thresholds versus frequency for nonlinear responses such as shear-thinning and normal generation of stress in shear. For example, see Hill et al. (2014) for dramatic (orders of magnitude) variation of the viscoelastic moduli of human epithelial mucus in cell culture versus concentration of solids by weight. Since weight-percent solids of mucus is considered a proxy for progression of the disease in many pulmonary disorders (asthma, cystic fibrosis, and chronic obstructive pulmonary disease [COPD]), these data on mucus in cell cultures reveal that the large variability in viscoelasticity of human mucus is indeed physiological and not necessarily an artifact of handling or experimental techniques. The extension of these linear-response properties of human mucus to nonlinear properties and their physiological relevance is in a very early stage, with little progress thus far. A direct connection between mucus linear and nonlinear viscoelasticity and efficiency of mucus-transport by cilia and air-drag from breathing or cough is far from being understood. It is therefore an important open problem and a challenge to the broader community studying the biology of lungs to develop tools to assess such quantitative properties of an individual’s pulmonary fluids; to develop correlations of such biophysical properties with healthy versus diseased states; to further link biophysical properties to efficiency of mucus-transport by cilia, tidal breathing, and cough; and finally, to explore physical therapeutic and pharmacological interventions that reinstate more efficient transport of the mucus layer. Such capabilities will require heightened collaborations among clinicians, biomedical engineers, and applied scientists.

Table 1.

Published rheological properties of human mucus and sputum

Reference	η0 (Pa s)	Ginf (Pa)
Human (recurrent bronchitis) (Puchelle et al. 1981)	24.8	6.2
Human (mild chronic bronchitis) (Puchelle et al. 1981)	11.4	0.76
Human (severe chronic bronchitis) (Puchelle et al. 1981)	12.5	0.87
Human (Baconnais et al. 1999)	0.71	N/A
Human (CF) (Baconnais et al. 1999)	0.16	N/A
Human (Puchelle et al. 1983)	24.7	1.7
Human (CF) (Dawson et al. 2003)	60	15.5
2.5% (w/w) cell culture of human mucus (Matsui et al. 2006)	0.12	0.87
8% (w/w) cell culture of human mucus (Matsui et al. 2006)	3.3	4.7

In generations beyond 15 or 16 there are fewer mucin-producing goblet cells and few, or no, ciliated cells. The result of these physiological changes in the types of cells is that lining of the airways transitions deep in the lung from a non-Newtonian or viscoelastic, two-layered fluid (a periciliary liquid [PCL] in which cilia reside and in which mucus occurs between the PCL and air) to a single layer of fluid that is Newtonian and primarily saltwater, yet with significant concentrations of surfactant. The upshot is that rheological and physical properties of pulmonary fluids, such as viscous and elastic moduli, air–liquid surface tension, density and thickness, vary within a single human lung as well as across populations, as noted above, not only during the progression of a disease but also during aging and potentially on much shorter timescales due to diet, environmental conditions, and physical activity. The properties of the mucus layer are affected by the distribution and relative concentrations of mucins, the concentration of surfactants, and a host of proteins, DNA from dead cells, as well as by particles and pathogens deposited by inhalation (Yeates and Aspin 1978; Grotberg 2001; Williams et al. 2006).

In addition to the complexity of fluid flow, the branching of the airways from the trachea to the alveoli constitutes a multi-scale structure. The diameter of the trachea is about 25 mm (2.5 × 10⁻² m), whereas the diameter of one of the 700 million alveoli is two orders of magnitude smaller, about 300 μm (3 × 10⁻⁴ m) (Breatnach et al. 1984). Further, as the branches of the airways become small, the thickness of the layer of fluid also decreases. In these lower airways, fundamental questions about the flow of surfactants in this complicated system motivate new experiments and mathematical modeling. The geometry and airflow of the lungs change over time because of the periodic motion of respiration and episodic events such as coughing and sneezing. During this tidal breathing, airways can close or become fluid-filled and must reopen on inspiration.

We provide a brief overview of approaches used to model three aspects of pulmonary fluid and its flow: the surfactant layer in the deep branches of the lung, the mucus layer in the upper branches of the airway, and closure/reopening of the airway. We discuss models of each aspect, the potential to capture biological and therapeutic information, and several open questions that are worthy of further investigation. We hope to promote collaboration by providing biological communities with insight into mathematical descriptions of fluid mechanics in the lung and the kinds of predictions these models can make. Further, we seek to provide modelers with a glimpse into some of the open problems that remain in the authors’ immediate area of expertise. Each of these issues provides challenges that require multi-disciplinary insights to fully probe the dynamics of the biological processes. We first consider the impact of surfactant on fluid flow in the lungs.

Surfactant dynamics

In the 1950s, biomedical researchers became aware of the role of surfactants in the deep airways of the lung (Avery and Mead 1959). They recognized that naturally occurring surfactants (surface-active-agents) are found in the airway-fluid and reduce the surface tension to approximately 20 dyn/cm (Schurch et al. 1989), much lower than the normal air–water value of approximately 70 dyn/cm. The lower tension facilitates breathing because the pressure differential required to inflate the lungs is lower (Zasadzinski et al. 2001). Insufficient surfactant can lead to alveolar collapse and respiratory distress syndrome. Recognizing the role of surfactants not only helped explain the function of healthy lungs but also provided information critical to the development of therapies for lung pathologies especially in prematurely born infants (Notter 2000).

Surfactant deficiency has many possible causes. General causes include acidosis, hypoxia, hyperoxia, atelectasis, and pulmonary vascular congestion. Specific causes include adult respiratory distress syndrome, infant respiratory distress syndrome, pulmonary edema, pulmonary embolism, pneumonia, excessive pulmonary lavage or hydration, and drowning and extracorporeal oxygenation (Keough 2014). At birth, insufficient production of surfactant can be fatal. This problem is critical in premature infants because the lungs begin to produce surfactant during the 4th month of gestation, but the surfactants may not function well until the 7th month. Artificially produced pulmonary surfactants serve as substitutes for lung surfactants, which contain phospholipids as well as proteins. These therapies have been successful at reducing the rate of infant mortality from respiratory distress syndrome in premature infants as well as acute respiratory distress in adults (Notter 2000).

Modeling the effect of surfactants in the airways has many facets. A lubrication model has been used since the 1980s to describe the motion of a surfactant on the surface of a thin, viscous fluid. Lubrication theory, also called the theory of thin liquid films, models environments in which a fluid is spread thinly enough that the area coated by the fluid (think of that as a characteristic length L) is much larger than the thickness of the film (characteristic film height H). Then the small parameter H/L can allow modelers to derive a more specialized form of the Navier–Stokes equations for fluid flow. The specialized equations are simpler, but still usually require computer simulations to provide solutions.

A recent review paper discusses multiple approaches to modeling (Craster and Matar 2009). The models must account for the chemical structure of surfactants (often a hydrophilic head and hydrophobic tail) that make it energetically preferable for them to gather at the interface between liquid and air. On the surface of the fluid, surfactant is pulled toward areas with less densely packed surfactant molecules because that region has higher surface tension. The motion of the surfactant induces a surface stress, which moves the fluid. As the fluid surface moves, it spreads the surfactant while also dragging the underlying liquid. Models of these dynamics can describe the distribution and motion of naturally produced pulmonary surfactants as well as surfactants introduced in surfactant-replacement therapies.

To model the flow of the liquid-lining and the impact of surfactant on that flow, the liquid is sometimes assumed to be Newtonian. The traditionally cited mathematical model uses two coupled partial differential equations, one describing the height of the film which forms a wave and the other describing the surfactant’s concentration, with both features described as functions of time and two spatial dimensions (Gaver and Grotberg 1990). This model employs material parameters for the fluids involved, and takes different forms, depending on whether the surfactant is immiscible and whether it can collect in high enough concentrations to form micelles (Bull and Grotberg 2003; Warner et al. 2004). As an example of the two-way interaction between mathematics and biology, modeling this spreading wave led to the identification of a new fluid mechanical shock wave, the GBG shock (Borgas and Grotberg 1988; Gaver and Grotberg 1990; Grotberg 2011). Many groups have studied the mathematical properties of this model (Jensen and Grotberg 1992; Renardy 1996, 1997; Stone and Ajdari 1998; Craster and Matar 2009; Zhang et al. 2002; Levy and Shearer 2006; Levy et al. 2007; Peterson et al. 2009; Peterson and Shearer 2011), but until recently there have not been experiments that validate the model with physical data.

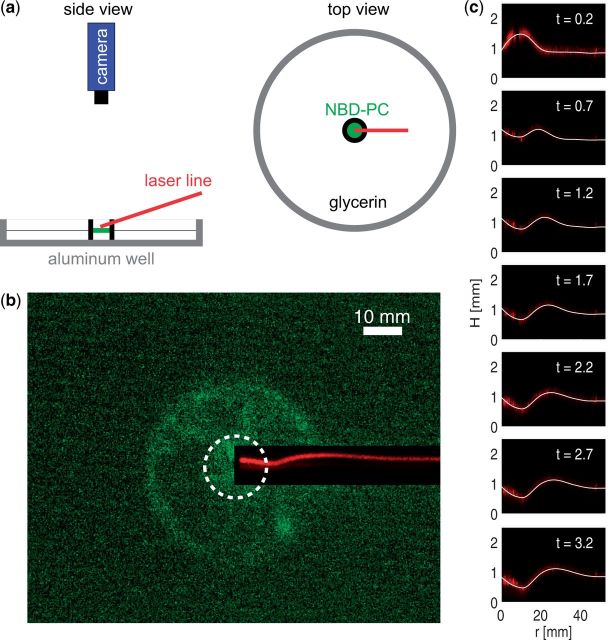
Experiments developed in the Daniels Nonlinear Laboratory and continued in the Levy Laboratory use a surfactant with a fluorescent tag, NBD-PC (Fallest et al. 2010; Strickland et al. 2014). In these experiments, the fluorescence-intensity captured by an overhead camera was used to measure the spatial distribution and motion of the surfactant. However, interactions between particles of surfactant create a non-monotonic relationship between concentration and intensity, which provides an additional challenge when extracting values for concentration of surfactant from fluorescence-intensity profiles. To resolve this issue, additional information about the surfactant’s distribution (using the known distribution at earlier times) can be used. At the same time, laser sheets can be used to track the motion of fluid since the intersection of the sheet with the fluid’s surface produces a curved line. Images of the curve can be used to extract the height of the film in one spatial dimension and time; see Fig. 2 from Fallest et al. (2010). Because the observed spreading in these experiments is approximately radially symmetric (without the fingering instabilities present in other thin-films experiments), the radial film profile provides information about the shape of the fluid’s surface.

Fig. 2.

Setup of experiment (a) designed to simultaneously image the height of the film of fluid (of glycerol via laser line) and concentration of surfactant (of NBD-PC via fluorescence). (b) Initial disc of surfactant spreading out and creating fluid wave to the right. (c) Evolution of the wave shown in b over time. Image reproduced with permission from Figure 1 of Fluorescent visualization of a spreading surfactant by David W Fallest et al. 2010. New J Phys 12:073029. © IOP Publishing & Deutsche Physikalische Gesellschaft.

The primary driving force for fluid motion is change in the surfactant’s concentration at the surface of the viscous fluid, which causes surface stress. In addition, the model includes the effect of gravity, capillarity, and diffusion. An important input to the model is a function relating the surfactant’s concentration to the surface tension of the fluid, which can be empirically determined from experiments (Tsukanova et al. 2002). This measurement becomes more difficult when the Newtonian underlying fluid (such as glycerol) is replaced by a non-Newtonian fluid with rheological properties closer to that of pulmonary mucus. Furthermore, the fluorescent surfactant, NBD-PC, could be replaced with more biologically relevant surfactants, but without the fluorescent tag, the surfactant’s distribution and the dynamics of its spreading are harder to infer.

The current model and experiments still have many significant differences from pulmonary biology but can provide answers about the fundamental dynamics of fluids. Future challenges include imaging the motion of surfactants and fluids on flexible, ciliated substrates with changes in geometry that model breathing cycles and introduce additional complexity. Incorporation of properties such as surface viscosity and surface elasticity can provide more detail about biological fluid-flows. In addition, particulates, such as dust or other contaminants, must be cleared from airways and should be included in a full model of the pulmonary system’s functions. Extending the existing models and computational codes to Marangoni mechanisms in non-Newtonian fluids like mucus is a ripe area for new investigations, and requires knowledge of the rheology of mucus, to which we turn next.

The rheology of mucus: flow and diffusive-transport properties

Physiologically, mucus is the body’s first line of defense from inhaled pathogens and irritants that are deposited onto the air–mucus interface. Protection of the airways from pathogens involves an airway surface liquid (ASL) consisting of a two-phase protective system reaching into the deep branches of the airway. One phase consists of the cilia plus the so-called PCL that covers the cilia except for the ciliary tips during full extension in their power stroke. This phase of cilia plus PCL recently has been described as a complex polymeric brush (Button et al. 2012). The metachronal wave of coordinated cilia is considered to be the dominant mechanism for propulsion of the mucus layer in healthy lungs of humans and animals. The second phase involves mucus, which successfully preserves the health of the lung in homeostasis and under extreme assaults if flow dominates diffusion. Inhaled agents must be trapped and cleared from the trachea by flow of mucus before the agents diffuse across the mucus barrier to the epithelium or colonize into an infection. In healthy lungs, mucus in the upper and mid airways is estimated to flow at a rate of up to approximately 60 μ/s (Chen and Dulfano 1978). The flow profile is very challenging to resolve in vivo yet widely assumed to be a weak shear-flow (almost a plug-flow). As the mucus layer thickens in diseased states, clearance drops toward zero leading to increased infections and inflammation (Donaldson et al. 2007; Fahy and Dickey 2010). To predictively model this two-layered system plus the liquid pumping mechanism of air-drag, one must perform experiments to accurately characterize the viscoelastic properties of mucus, including linear and nonlinear properties and thresholds of nonlinearity. Such viscoelastic-characterization experiments are necessary to identify the correct model-equations for the PCL and mucus layers, so that one can perform simulations that are faithful to physiology. There has been recent work on linear (Hill et al. 2014) viscoelasticity of mucus from cultures of human lungs, but nonlinear characterization remains an open problem, as well as the modeling of single and coordinated cilia to propel mucus. Mucociliary propulsion of mucus using Maxwell-like constitutive laws for mucus and a viscous approximation of the PCL has been considered (Mitran 2007a, 2007b). Presumably, this numerical platform will allow incorporation of more accurate constitutive equations for the PCL and mucus as they become available. Some progress also has been made on modeling and simulating air-drag-driven core-annular flow of highly viscous films to imitate turbulent airflow during expiration in the upper airways (Camassa et al. 2012). The full coupling of cilia, PCL, and mucus layers, in a physiological multi-branched airway, with accurate breathing-induced pressure driving conditions, is a major open challenge for the modeling community.

Pathologically, obstructive lung disorders involve compromises in the flow of mucus (Boucher 2004; Donaldson et al. 2006) which leads to chronic lung infections and significant changes in the passage-times of particles through mucus layers (Matsui et al. 2006). The diffusive properties of particles in lung mucus can offer critical information about particle-inhalation therapies for acute lung infection, asthma, COPD, or lung cancer. All of these disorders can be more accurately treated with predictive tools for diffusion of powder particles or liquid droplets that contain small-molecule drugs. Recent results (Hill et al. 2014) reveal a remarkable dependence of the diffusive behavior of human bronchial epithelial cell-culture mucus on concentration of solids (by weight). In particular, micron-diameter probe-particles, in a wide range of weight-percent, cell-culture mucus, exhibit anomalous diffusion. That is, the scaling of mean-squared displacement (MSD) of particle-position time-series for normal diffusion is linear in time, and the pre-factor is the diffusion coefficient that is related to the viscosity of the fluid. In mucus, however, probe-particles of a micron in diameter exhibit sub-linear scaling of the MSD, which is called sub-diffusion, to reflect a qualitatively different behavior. Formulas that clarify these properties are given just below. Furthermore, it is found that the same micron-diameter probes exhibit progressively more anomalous (more sub-diffusive) behavior with increased concentration of solids. Since many pulmonary diseases are associated with an increase in concentration of solids, the implication is that diffusion of pathogens and particulates is progressively slowed; by the methods of passive microrheology, these data on diffusion also yield linear viscoelastic properties that are important in understanding flow-transport of mucus versus solids’ concentration. Tools to accurately assess the linear and nonlinear viscoelasticity and diffusive properties of mucus provide the capability to test modified properties of a mucus sample due to drugs or physical therapies. Mathematically, the flow of mucus in biologically relevant geometries, volumes, and driving conditions has not been simulated yet with any degree of physiological relevance, nor have passage-times of particles been modeled and computed that are consistent with experimental data. These capabilities are critical for judging whether diffusive or hydrodynamic transport dominates when a pathogen or a drug particle lands on the air–mucus interface.

From a materials and rheological perspective, mucus is a biopolymer-based viscoelastic fluid (Viney et al. 1993). It is pervasive in anatomy, coating epithelial surfaces in the lung, intestines, eyes, nasal tract, and female reproductive tract and serves specific functions in each organ. Viscoelastic fluids, in general, are prone to flow-responses that are sensitive to amplitudes and frequency of applied stress and strain, whereas the diffusion of particles in gels is sensitive to the size of particles relative to the size of the internal structures within the gel. Diffusion of particles in gels is also sensitive to the particle’s surface chemistry due to electrostatic interactions with the gel. Human lung mucus (see Fig. 3) is continually exposed to diverse frequencies ranging from less than 1 Hz for tidal breathing to 10–15 Hz from mucociliary clearance and a wide turbulent frequency spectrum from cough. Further, mucus is characterized by viscoelastic properties that are strongly dependent both on frequency and on amplitude of stress and rate of strain (cf. Hill et al. 2014). Finally, diffusion of nanoparticles within mucus is strongly dependent on the particle’s size and on electrostatic attraction or repulsion of the mucin molecules and other proteins within the mucus. It is no surprise that lung mucus is tuned through physical and chemical structure to respond to diverse pathogens and environmental particulates, but the field of rheology has only recently begun to afford methods to assess these properties.

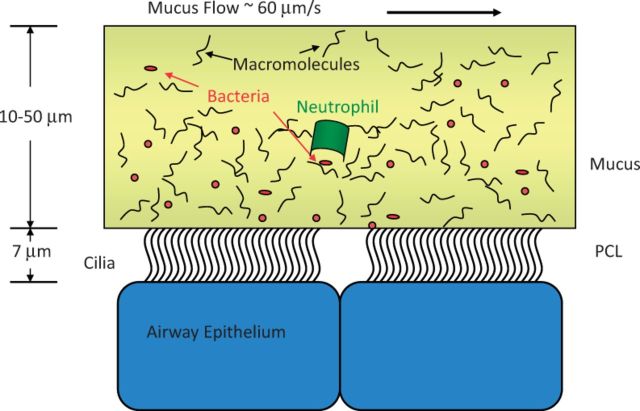
Fig. 3.

The ASL consists of a cellular substrate, cilia beating through a 7-µ PCL, and a viscoelastic mucus layer. Within the mucus layer, mucin glycoproteins and other macromolecules form a gel-like matrix, trapping pathogenic materials such as bacteria.

A further rheological challenge for the characterization of mucus relative to synthetic hydrogels and other well-characterized, homogeneous polymeric fluids is the inherent variability of mucus across populations during progression of a disease, an environmental assault, or normal metabolic cycles. A clinical protocol for the diagnosis and treatment of mucus-transport clearly would have more value if determined in full recognition of these inherent sources of variability. Otherwise, one can be confounded by reported literature values of the viscosity of human mucus that span two orders of magnitude (see Table 1). A comprehensive strategy to determine the particle-specific properties of diffusive barriers, and forcing-specific properties of the flow of lung mucus, could be applied to samples from patients and from cell cultures. Further, studies will rely on mucus that is harvested from cultures of human bronchial epithelium (HBE), thereby allowing the research to be performed on a physiologically relevant mucus (Matsui et al. 1998, 2005, 2006; Hill et al. 2014) that is chemically similar to sputum from healthy patients (Kesimer et al. 2009).

There are several challenges to a comprehensive experimental characterization of mucus rheology. Due to limited availability, we only have access to low volumes (Fahy et al. 2001) on the order of microliters. The samples have low thresholds of yield (Palmer et al. 1970; Powell et al. 1974) due to transitions in viscous and elastic properties (such as shear-thinning or strain-hardening), which occur at very low levels of stress or strain-rate. How the lung exploits the shear-thinning and other nonlinear physical properties of mucus for either cilia-mediated or cough clearance remains an open question. Multi-scale and multifunctional heterogeneity are also common (Sheehan and Carlstedt 1987; Thornton et al. 1991; Kirkham et al. 2002). The thickness of the mucus layer is less than 100 μ and, to flow most efficiently, mucus has to respond to diverse scales of force, time, and length from individual cilia, coordinated waves of cilia, and laminar and turbulent air-drag during normal breathing and cough. An additional challenge is that the exact coupling of cilia to the mucus layer is unknown (Smith et al. 2007, 2008, 2009), and this presents a significant challenge to fluid-structure interaction-algorithms to extend these methods to fluids with memory.

As illustrated in Table 1, the range of viscosity (η₀) and steady-state elasticity (G_inf) from various sources of mucus are quite wide, and it is impossible to associate the variability to the source of mucus versus instrumentation and experimental technique. Careful experimental technique and theory are necessary to determine the properties of mucus viscoelasticity across the range of frequencies and amplitudes of forcing relevant to lung mucus, so that one can be sure properties are measured in the linear viscoelastic-response regime, or at nonlinear forcing levels. The reader is directed to examples of recent literature on new techniques for linear (Waigh 2005) and nonlinear microrheology (Cribb et al. 2013). The results obtained by Cribb et al. (2013) on active magnetic-bead microrheometry applied to lambda DNA solutions in the entanglement regime, which is a reasonable simulant of mucus, indicate that highly entangled biopolymer gels, which includes mucus, can yield at O (5–10 pN) force scales, which are comparable to the forces generated by individual tips of cilia during the power stroke (Hill et al. 2010).

Mucus also serves as a diffusive barrier for inhaled airborne particles of diverse type. Particles above 100 nm routinely are observed to exhibit anomalous sub-diffusive scaling. The degree of sub-diffusivity, for example the scaling of the MSD of tracked particles, is highly variable both across sources of mucus and within one sample across particle diameter and surface chemistry. Fortunately, experiments on passive diffusion of particles are ideally suited for the tools of passive microrheology (MacKintosh and Schmidt 1999; Matsui et al. 2006; Lai et al. 2009). For clinical relevance, experimental methods have to be high throughput. However, the information of most value is the distribution of passage-times of particles through mucus layers, which is extremely time-consuming and data intensive. If the diffusion was normal across the ranges of interest, inference of passage-times from data on the paths of particles would be straightforward since there are rigorous formulas for passage-times and their scaling with fluid viscosity, particle diameter, and thickness of a layer, or dimensions of a volume. However, particles in mucus above 200 μ exhibit sub-diffusion. In sub-diffusion, the mean-squared-displacements of tracked positions of particles scale like a fractional power of time, $t^{\alpha }$ where α is less than 1; see Fig. 4, reproduced from data presented by Hill et al. (2014). The limiting factor for modeling and characterization of diffusive properties is theoretical: a paucity of stochastic models reflects the observed anomalous, sub-diffusive properties. Recent results by McKinley et al. (2009) provide stochastic models, known as generalized Langevin equations, with a tunable MSD sub-diffusive exponent, whereas another model, known as fractional Brownian motion, also has a tunable MSD sub-diffusive exponent. The reader is likewise pointed to a recent text (Meerschaert and Sikorskii 2012) for in-depth treatment of stochastic models. With such models to fit to data, it is then possible to perform direct simulations from fitted models to predict the passage-times of particles (Hill et al. 2014). The implications of these models to the wider biological and medical communities lie in their power to assess how inhaled pathogens, particulates, and drug-carrier particles diffuse in a given sample of mucus, which has to be compared with the mucus’ clearance timescales in order to assess the fate of inhaled particles (cleared to the throat versus passage through the mucus–PCL barrier versus remain in the ASL for an extended period).

Fig. 4.

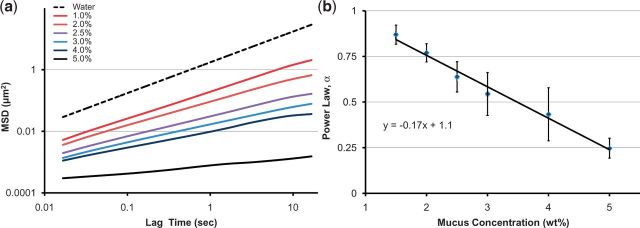
(a) Ensemble-averaged MSD versus lag time for particles 1-µ in diameter in mucus solids concentrations that range from those typified by health (1.5%) through disease-like concentrations (5%). The dashed line represents a viscous fluid; any smaller slope indicates sub-diffusive scaling. (b) Scaling of the MSD versus mucus solids concentration, where <Δr α. Power law exponent. Squares represent the averaged values of α and the Dfbmτ vertical bands represent its range over all paths of the particle. The goodness-of-fit metric for the linear relationship is R₂ ∼ 0:98.

These challenges point to the need to develop models and experiments that are capable of characterizing both the flow of mucus and the diffusive-transport properties under the constraint of microliter volumes. This need includes instruments, experiments, theory, and simulations designed to quantitatively measure and deduce properties from scales of 10⁻⁷ to 10⁻³ m that are relevant to in vivo conditions of lung mucus. The results of integrated protocols, when applied to clinical mucus samples or to controlled simulants, inform the properties of flow and transport across this wide range of lengths. Likewise, drug or physical therapies can be explored using mucus samples to identify which transport properties are modified, by what order of magnitude, and for how long.

In mathematical models of mucociliary clearance, it is critical to understand the boundary condition between the mucus and PCL layers: how the cilia-generated force is communicated to the mucus layer and translated into the flow of mucus. This question was explored by Sleigh, in 1962, and subsequently by many authors (some listed in the Introduction section). Understanding the interaction between cilia and mucus through experiments and modeling is a critical challenge to a predictive model of mucociliary clearance in lung airways. It is almost surely true that cilia and air-drag drive mucus into the nonlinear response regime, triggering both strain-hardening and shear-thinning behavior, as explored by Cribb et al. (2013) with magnetic-bead microrheology applied to lambda DNA solutions. A major open problem that would have a significant impact on modeling the flow of mucus in the lung is the coarse-graining of coordinated cilia into a macroscopic boundary condition. Blake and collaborators have proposed boundary conditions (Smith et al. 2007, 2008, 2009) that are easily analyzed, but not deduced from experimental data. Further, an experimentally verifiable mucus–PCL–cilia boundary condition will enable modeling studies of the debilitating mucus pathology known as mucostatis, which is a result of adhesion of mucus at the interface with the cilia–PCL layer. This condition is a chronic problem in cystic fibrosis (Boucher 2004; Donaldson et al. 2006) and COPD (Bennett et al. 1993, 2006) due to strongly modified viscoelastic properties of mucus and to biochemical interactions of the mucus layer with the PCL and cilia. For modeling purposes, this condition corresponds to a dramatic change in the boundary condition at the mucus–PCL–cilia interface. The HBE cell-culture model can be used to explore this chronic condition and the associated boundary conditions in the cell culture. The application of drugs that diffuse to the interface and reduce adhesion can be explored to reinstate normal flow. In addition to the clinical value of assessing and relieving adhesion, the mucus–PCL boundary condition is also a necessary, and poorly understood, element of all codes of the flow and transport of mucus.

The challenges associated with the modeling of mucus rheology, and the translation of linear and nonlinear characterization to faithful constitutive models and simulations of clearance in lung airways, remain an essentially wide-open area in need of many contributions. Such contributions, if they are to be of physiological relevance, require a multi-disciplinary approach that draws on biochemistry, biophysics, physiology, and mathematical modeling and computation. Collaborations between modelers and experimentalists are essential, since idealized experiments and models will be necessary to address many isolated open problems prior to their integration into a comprehensive model and simulation. We further recommend an upcoming Springer monograph on Complex Fluids in Biological Systems, including an introductory chapter by one of the present authors.

Closure of airways

Our final discussion regards how the fluid, mucus, and surfactants flow within the airway geometry. Airways close near the end of expiration, that is when the airway’s diameters are at, or near, their smallest diameter during normal respiration. Although this closure of airways occurs in healthy adults as well as in children and aging adults (Anthonisen et al. 1969; Mansell et al. 1972), it can be dangerous for individuals with pulmonary problems, for example, premature infants with respiratory distress or individuals with asthma (Idiong et al. 1998; King et al. 1998; Hays and Fahy 2003). Measuring the occurrence of airway closure is one component of a standard pulmonary-function test: the single-breath nitrogen washout test. This test measures the critical lung volume at which closure occurs, called the closing volume. If the test shows early closure of the airway (at higher lung volume), it is often interpreted that there is inhomogeneous distribution of ventilation within the lung, which may be caused by a number of normal and pathological conditions (Frazer et al. 1985; Crawford et al. 1989).

The experimental studies of a model airway by Liu et al. (1991) showed that adding surfactant prevented formation of liquid plugs and allowed air to flow. It is well recognized that the liquid-lining of the lung can close off a small airway (Macklem et al. 1970; Greaves et al. 1986). This can happen either by the formation of a liquid plug (lens) due to capillary (surface tension) instability, known as the Rayleigh instability, or by provoking the collapse of the elastic wall of the airway, that is, a capillary-elastic instability (Kamm and Schroter 1989; Halpern and Grotberg 1992, 1993). Collapse of the tube can have important three-dimensional effects causing non-axisymmetry with corrugations in the azimuthal direction (Hill et al. 1997; Heil 1999a, 1999b; Hazel and Heil 2005).

Figure 5 sketches the stages of progression of closure of the airway based on measurements with and without surfactants (Cassidy et al. 1999; Bian et al. 2010). Prior to any disturbance, this system has a single liquid layer coating a tube uniformly. The ratio of the initial thickness of the liquid layer, a−b, to the radius of the tube, a, is the dimensionless parameter $ϵ=(a-b)/a$. Closure of the airway happens when ε is large enough, that is, $ϵ>ϵ$_c Here, ϵ_c = 0.12 in the absence of surfactant (Everett and Haynes 1972; Hammond 1983; Gauglitz and Radke 1988; Kamm and Schroter 1989; Halpern and Grotberg 1992; Halpern and Grotberg 1993) and ϵ_c = 0.15 with surfactant present (Halpern and Grotberg 1993; Cassidy et al. 1999). Physically this criterion simply states that there needs to be enough liquid on the wall for it to form a liquid plug in the tube. The value of ϵ will be larger at lower lung volumes both because the layer of liquid will be thicker (due to conservation of mass), and the radius of the tube will be smaller. Therefore, closure tends to occur near the end of expiration.

Fig. 5.

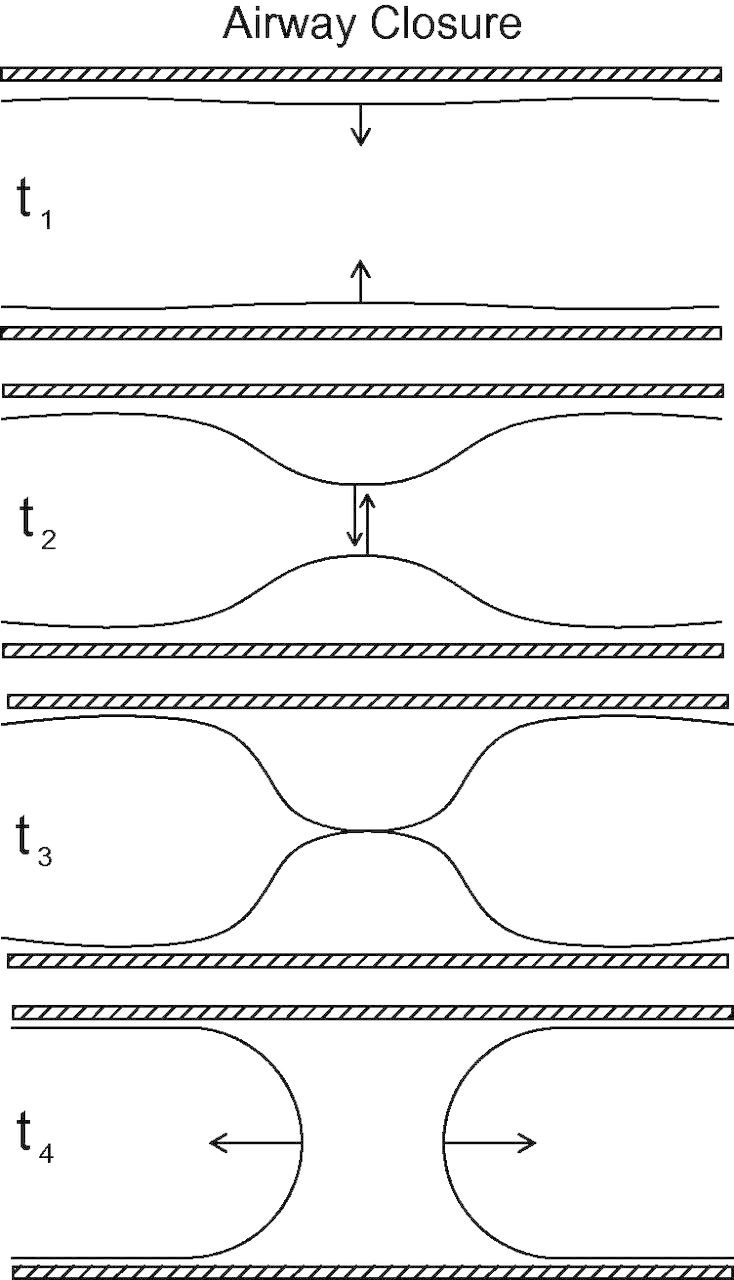
Airway-closure sequence for a rigid tube. Here, t₁ is the beginning of instability; at t₂ the interface forms a liquid bulge; at t₃ the interface meets at the centerline and coalesces; and at t₄ there is post-closure filling flow.

Closure of the airway starts when a small disturbance is applied to the air–liquid interface, which then undergoes a Rayleigh instability due to surface tension and the cross-sectional interfacial curvature, t = t₁ as shown in Fig. 5. At t = t₂, the interface is forming a liquid bulge. The interface meets at the centerline and coalesces at t₃ after which the fluid undergoes a post-closure flow that consists of two receding air fingers moving away from one another in the axial direction and the wall’s liquid layer flowing radially into the space between them as shown at t₄. Related computational studies include calculations of wall-shear and normal stresses, the effects of surfactants, flexibility of the wall, and viscoelasticity (Halpern and Grotberg 1992, 1993; Halpern et al. 2008, 2010).

Reopening an airway

Once a liquid plug is formed, the airway is closed off from gas exchange and getting it to reopen is an important objective. Since closure of an airway is likely at the end of expiration, it is the ensuing inspiration of fresh gas into the lung that can achieve this goal. Propagation of the plug (Fujioka and Grotberg 2004; Fujioka et al. 2008) has been studied under a variety of conditions related to the airway, including the effects of the wall’s flexibility (Howell et al. 2000; Zheng et al. 2009), surfactant (Waters and Grotberg 2002; Fujioka and Grotberg 2005), non-Newtonian fluid properties that arise in mucus (Zamankhan et al. 2011), unsteadiness (Fujioka et al. 2008), and rupture of the plug (Hassan et al. 2011). Based on these results, a sketch of propagation of the plug and the rupture that reopens an airway is shown in Fig. 6. At t₅, the liquid plug is propagating with the inspiratory airflow where the upstream gas pressure is higher than the downstream gas pressure, and pushes the liquid along. This process is in force regardless of the origin of the plug. At t₆, the rear meniscus is catching up with the front meniscus due to net deposit of liquid onto the wall from the plug. This occurs when the trailing thickness of film is larger than the thickness of the precursor film ahead of the plug. At t₇, the rear interface interacts with the front interface and then they rupture, opening the airway. Sometimes this interaction can lead to the formation of satellite droplets. The sudden rupture of the interface at t₈ allows a pressure disturbance in the gas phase due to the pressure jump from gas being suddenly released from upstream to downstream. There is also a wave of fluid stress from the interface and from liquid snapping back to the wall. In addition, if the airway has been partially collapsed, the elastic deformation back to the open state creates its own stress wave in the tissues. Together these can create a crackle sound audible with a stethoscope. Crackles are a well-known clinical finding in various lung diseases with abnormal conditions of the liquid in the airway. Normal and shear fluid stresses on the wall, and their axial gradients, can be significant during both the closure and the reopening of flow and can lead to injury and/or death of epithelial cells (Taskar et al. 1997; D'Angelo et al. 2002; Bilek et al. 2003; Dailey et al. 2007; Huh et al. 2007; Yalcin et al. 2007, 2009; Ghadiali and Gaver 2008; Douville et al. 2011; Tavana et al. 2011). Staining techniques can show cell death following propagation and rupture of a liquid plug (Huh et al. 2007).

Fig. 6.

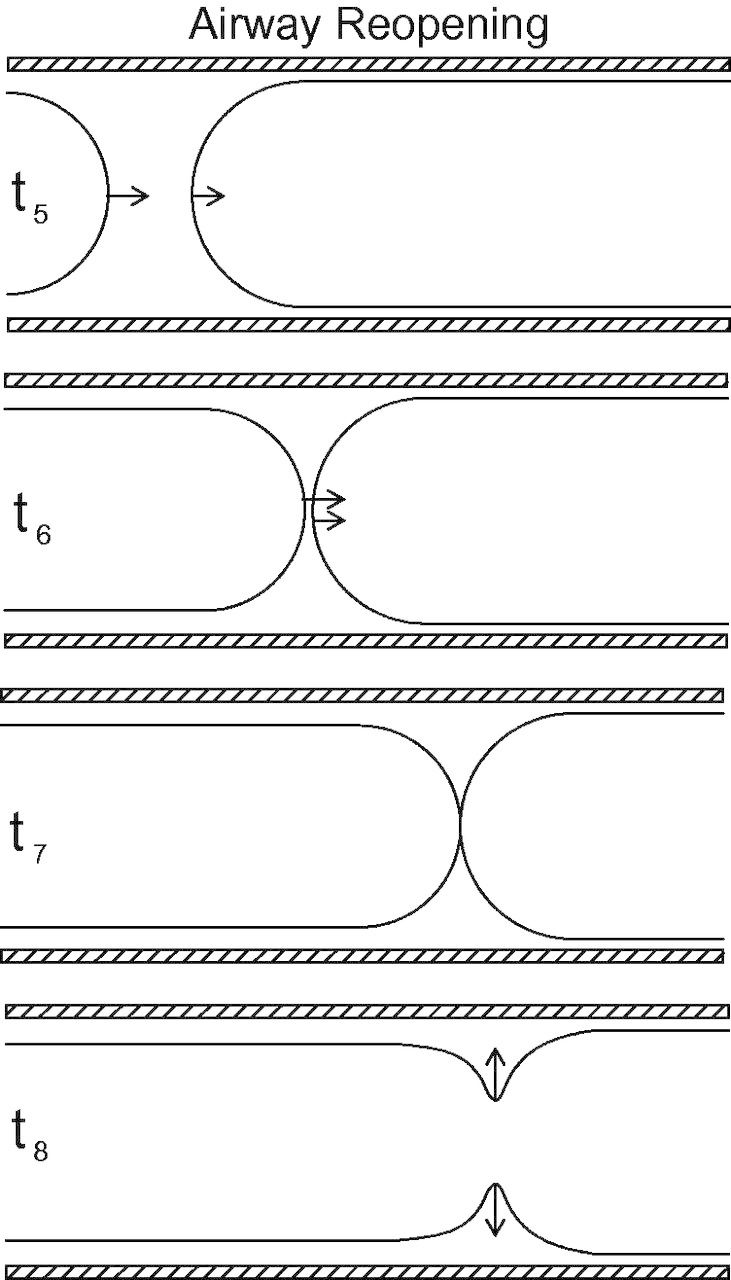
Airway-reopening: t₅ shows liquid plug propagation from airflow; at t₆ the rear meniscus approaches the front meniscus due to net deposit of liquid onto the wall from the plug; t₇ shows coalescence of the film; t₈ shows rupture of the plug and production of crackle sound.

Delivery of liquid and surfactant into the lung

In addition to self-formation from the airway’s own liquid-lining, plugs also can be created by introducing liquid exogenously into the airways. This can occur accidentally, as in partial drowning or aspiration, but also intentionally as in surfactant-replacement therapy (SRT) (Espinosa and Kamm 1999; Halpern et al. 2008). During SRT, a liquid-surfactant mixture is instilled into the trachea of a premature neonate who is surfactant-deficient and suffering from stiff lungs that are difficult to inflate (respiratory distress syndrome of the newborn, also called hyaline membrane disease). When the liquid-surfactant mix is squirted into the trachea through an endotracheal tube it will form plugs that propagate distally into the airway tree. The plug decreases in volume as it deposits liquid on the wall into the trailing film. However, when the plug reaches a bifurcation of the airway, it splits.

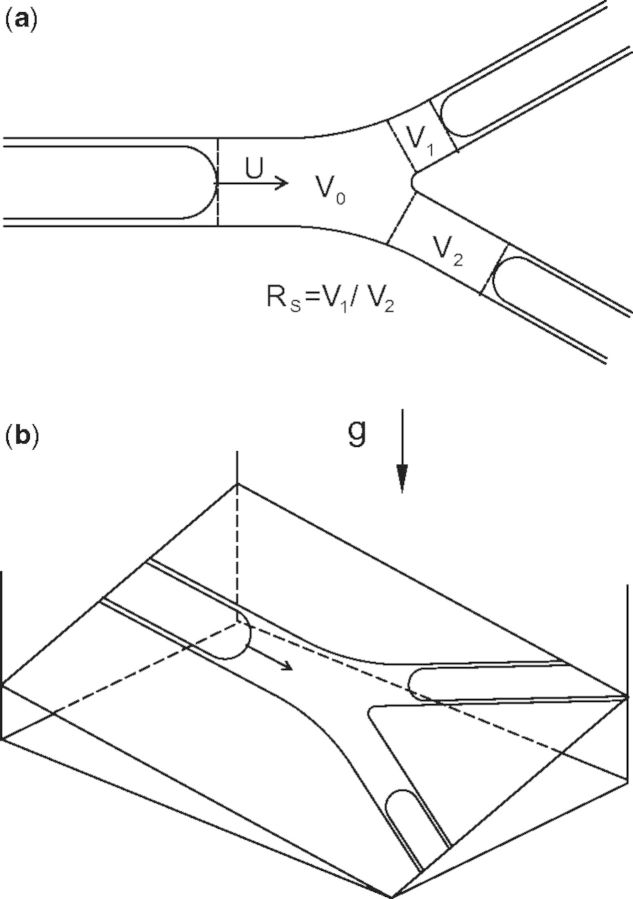
An example of a plug splitting in the plane of the bifurcation is shown in Fig. 7(a). Part of the plug’s volume goes down one daughter airway, V₁, and the rest goes down the other, V₂, in this simple example of a symmetric branching. Once the split of fluid from the single parent branch into the two daughter branches is complete, the volume V₀ of the original parent tube plug becomes zero because all of the liquid is in the two branches. We call the ratio of the volumes in the branches the split ratio, R_S = V₁/V₂, where we make V₁ the smaller volume so that the value of R_S is bounded, $0\le R_{\text{S}}\le 1$. The split ratio depends on the plug’s velocity in the parent tube, U, the branch angle θ, the surface tension, σ, the fluid’s viscosity, µ, and density, ρ, the tube’s geometry, the initial plug’s volume, the precursor film’s thickness, and the orientation to gravity. The direction of gravity with respect to the plane of bifurcation is shown in Fig. 7(b) where there is a roll angle, ϕ, and a pitch angle, γ. For a symmetric bifurcation with no effects of gravity, we expect R_S = 1. Otherwise, more of the volume will tend to split in the gravity-favored, downhill, direction dictated by the roll angle, ϕ.

Fig. 7.

Diagram of the splitting of a plug. (a) Plug splitting in the plane of the bifurcation. (b) Effects of gravity on splitting of the plug.

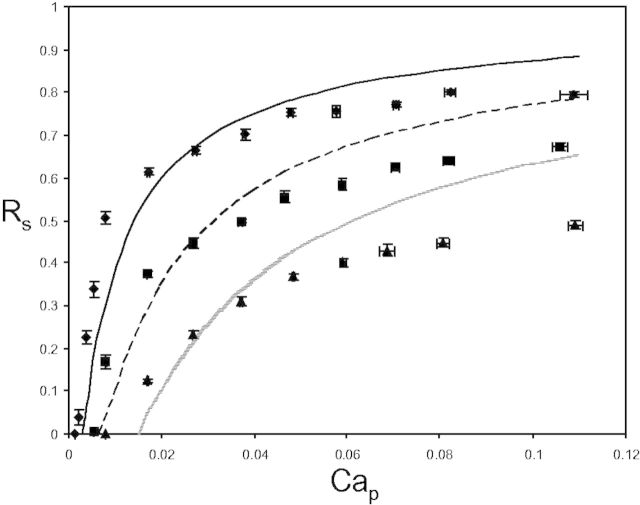
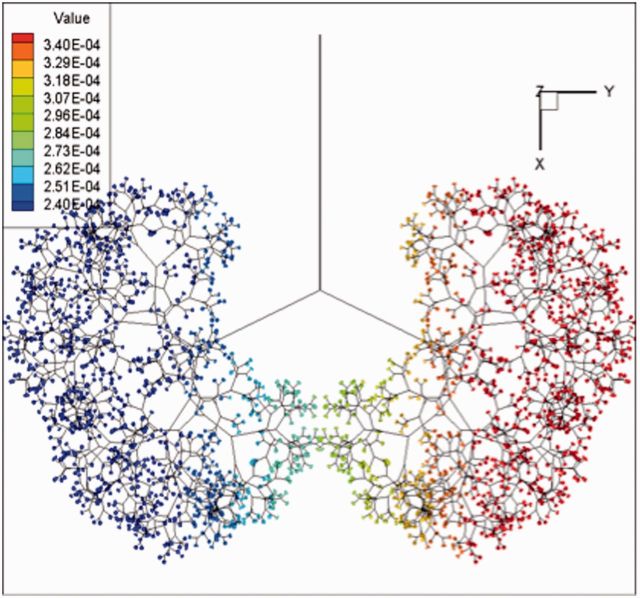
Experiments on model bifurcations and one-dimensional fluid-mechanics theory (Cassidy et al. 2001; Suresh and Grotberg 2005; Zheng et al. 2005, 2006, 2007) showed that R_S behaves similar to the sketches shown in Fig. 8 (from Zheng et al. 2005) with the pitch angle γ = 0. The parent tube’s capillary number is Ca_p = µU/a. Here, µ and U are defined as above and a is the radius of the parent tube. As Ca increases, R_S increases from 0 toward 1. Increasing the roll angle shifts the curves to the right, a higher Ca required to achieve the same R_S. There is a critical value of Ca below which R_s = 0. This feature can be viewed in terms of the pressure at the point of bifurcation. It takes a sufficient pressure in the tube to drive fluid uphill and the increase in Ca is consistent with increasing the driving pressure. Taking into account the splitting ratio at each bifurcation, and the amount of plug volume left on the walls in a trailing film, it is possible to send the plug through an entire airway tree and determine the distribution of the delivery. Figure 9 shows the prediction of surfactant delivery into a neonatal airway tree to the 14th generation. Gravity is directed to the right, as would happen for an infant in the left lateral decubitus posture, which is a clinical setting for SRT. Note the higher amounts in the left lung and lower amounts in the right lung.

Fig. 8.

The split ratio, R_S, as a function of the parent airway’s capillary number, Ca_p, for three values of the roll angle, ϕ = 15° (filled diamond) 30° (filled square) 60° (filled triangle), and the pitch angle γ = 0. Experimental data are the symbols and the curves are theory.

Fig. 9.

Surfactant mixture instilled at trachea; 2 lb neonate, 2.5 cc dose, gravity +y, and 4 cc/s rate of airflow.

Conclusion

We have described several aspects of the modeling of pulmonary airways and fluids that employ a wide variety of mathematical and experimental techniques. Each topic requires a multi-disciplinary approach that draws on biochemistry, biophysics, physiology, and mathematical modeling and computation. To advance the study of surfactant dynamics, we must look closer at the dynamics of particular surfactants and their effect on viscosity and surface tension. In studies of mucus rheology, linking the two fundamental processes of mucus (trapping and clearance) requires models and experiments over multiple scales of space, time, and force. To advance the study of the closure and reopening of the lung, we need more work relating mathematical models to biological and drug-delivery data. These are just some of the rich problems inspired by the complex and dynamic biological system in the lungs. We hope that this review will motivate new research efforts and collaborations with biologists. Further, tight collaborations between modelers and experimentalists will help maximize the potential for growth for both disciplines.

Funding

Levy’s research is supported by NSF-DMS-0968154 and RCSA 19788. Hill’s and Forest’s research was funded by National Science Foundation grants [DMS-1100281 and DMR-1122483], National Institutes of Health grants [NIH/NHLBI 1 P01 HL108808-01A1 and NIH/NHLBI 5 R01 HL 077546-05], a Simons Foundation Collaboration grant [245653], and the Cystic Fibrosis Foundation [HILL08I0]. Grotberg’s research was supported by NIH [HL 41126, HL 85156, and HL 84370] and NSF [MSM-8351494].