Short-Term Bone Formation is Greatest Within High Strain Regions of the Human Distal Radius: A Prospective Pilot Study

Short abstract

Bone adaptation is understood to be driven by mechanical strains acting on the bone as a result of some mechanical stimuli. Although the strain/adaptation relation has been extensively researched using in vivo animal loading models, it has not been studied in humans, likely due to difficulties in quantifying bone strains and adaptation in living humans. Our purpose was to examine the relationship between bone strain and changes in bone mineral parameters at the local level. Serial computed tomography (CT) scans were used to calculate 14 week changes in bone mineral parameters at the distal radius for 23 women participating in a cyclic in vivo loading protocol (leaning onto the palm of the hand), and 12 women acting as controls. Strains were calculated at the distal radius during the task using validated finite element (FE) modeling techniques. Twelve subregions of interest were selected and analyzed to test the strain/adaptation relation at the local level. A positive relationship between mean energy equivalent strain and percent change in bone mineral density (BMD) (slope = 0.96%/1000 με, p < 0.05) was observed within experimental, but not control subjects. When subregion strains were grouped by quartile, significant slopes for quartile versus bone mineral content (BMC) (0.24%/quartile) and BMD (0.28%/quartile) were observed. Increases in BMC and BMD were greatest in the highest-strain quartile (energy equivalent strain > 539 με). The data demonstrate preliminary prospective evidence of a local strain/adaptation relationship within human bone. These methods are a first step toward facilitating the development of personalized exercise prescriptions for maintaining and improving bone health.

Introduction

The relationship between bone adaptation and mechanical loading has been extensively explored using in vivo animal models (e.g., Refs. [1,2]). These studies have shown the importance of specific mechanical stimuli, such as strain magnitude, strain gradient, and strain frequency, for the initiation of bone adaptation, leading to improved bone stiffness and strength. Many believe these mechanical stimuli produce fluid forces in the extracellular matrix of bone that cause shear stress on mechanosensing osteocytes [3,4]. Osteocytes then generate signals to regulate bone turnover through the action of osteoclasts and osteoblasts, the cells responsible for bone resorption and formation, respectively, [5]. An example of such a response is the observed inverse relation, using an in vivo rodent loading model, between strain magnitude and Sclerostin, a protein expressed by osteocytes that inhibits bone formation through the Wnt signaling pathway [6].

Given that applied loads generate strains that are highly nonuniform within a particular bone region, bone remodeling in response to an applied load should be correspondingly nonuniform, with regions of high strain associated with bone formation. Such site-specific behavior has been observed in response to applied mechanical stimuli in animal loading models, wherein the observed adaptive response has been related to local measures of strain or strain energy density. Six weeks of axially loading the mouse tibia illustrated a greater bone formation response at the highly strained proximal corticocancellous region compared to the lower strained cortical midshaft region [7]. More recently, adaptive simulations driven by strain energy density were able to predict local changes in bone microarchitecture in a mouse vertebral loading model [8].

Although it is reasonable to assume that the mechanisms of bone adaptation in humans are similar to that observed in animals, the specific details of this process may differ slightly. Unfortunately, prospective data linking local strain to site-specific bone adaptation in humans are lacking, primarily due to the logistic and technical challenges of measuring bone strain and bone adaptation in living humans. For example, surrogate measures such as force or acceleration are often used in place of strain, and these fail to account for variation in bone strain arising from bone size or structure [9]. To address these challenges, we developed an in vivo loading paradigm for humans that involves leaning onto the palm of the hand in order to apply an axially directed force through the distal radius [10]. This paradigm prevented seasonal bone resorption and resulted in modest increases in bone mass, but the bone strain imparted by the loading was not explicitly quantified or controlled, nor were local changes to bone examined. Our subsequent work focused on the verification and validation subject-specific FE models for the prediction of strains within the distal radius caused by this loading paradigm [11].

The objective of this study was to use our novel in vivo loading paradigm for the human distal radius, combined with our validated subject-specific FE modeling technique to prospectively examine the relationship between localized bone strain and changes to localized bone mineral parameters. We hypothesized that subjects who applied the highest strains to their distal radius would illustrate the greatest increases in whole-bone mineral parameters, and that the greatest increases within-bone would occur in regions experiencing the highest strains.

Methods

Experiment.

Twenty-three healthy women ages 21–35 years with a distal radius BMD t-score > −2.5, height = 156.2 ± 5.7 cm, mass = 61.1 ± 7.6 kg, and regular menstrual activity volunteered for this institutionally approved experiment. Twelve additional women (age 21–30, height = 155 ± 5.7 cm, and mass = 62.6 ± 8.8 kg) participated as a control group. All subjects gave written informed consent prior to their participation. The experiment was previously described in detail [10], and subjects in the present cohort included those reported earlier plus additional volunteers. Briefly, each experimental subject was instructed to apply an axially directed force to the wrist of their nondominant arm by leaning onto the palm of their hand. Subjects applied a pre-assigned force 50 cycles per day, 3 days per week, for 14 weeks. The target forces assigned to these subjects (328.6 ± 101.3 N and range = 154.2–579.5 N) were determined to induce an estimated mean periosteal strain of 1000 με or more at the distal radius of the respective subjects based on subject-specific FE models [11]. This value was chosen based on preliminary data from a subset of this cohort, which indicated it was sufficient to produce an osteogenic response, and is supported by in vivo animal loading studies that showed an osteogenic response above this value (e.g., Ref. [12]). The subjects applied these forces onto a padded load cell, which recorded real time feedback of the applied force by each subject. The average force applied by these subjects was 353.7 ± 48.3 N (range = 225.1–419.5 N), reached over a 0.3–0.6 second period. Compliance with the assigned loading was determined through a combination of load cell recordings and subject-completed log sheets. Control subjects did not participate in the loading activity, but did complete all data collection.

Computed tomography (CT) data were collected on the distal most 12 cm of the nondominant arm of each participant at baseline and after 14 weeks (BrightSpeed; GE Medical Systems, Milwaukee, WI, 120 kV, 180 mA, voxel size: 0.234 mm × 0.234 mm × 0.625 mm). A calibration phantom (QRM, Moehrendorf, Germany) with known calcium hydroxyapatite equivalent concentrations was included in each scan to establish a relationship between CT, Hounsfield units, and calcium hydroxyapatite equivalent density (ρ_ha) in g/cm³. The CT data were segmented and analyzed quantitatively using methods previously described in detail [10] to measure integral bone volume (BV; cm³), volumetric BMD (g/cm³), and BMC (g) for a 9.375 mm ultradistal (UD) section immediately proximal to the subchondral plate. Integral measures included all voxels enclosed within the periosteal surface.

FE Models.

Baseline CT data were used to create subject-specific linear elastic FE models (Fig. 1) with methods previously validated by comparison with experimental cadaveric testing [11]. The FE models included contact between the scaphoid, lunate, and radius, and were meshed using quadratic tetrahedral elements with mean element size of 0.5 mm³, and assigned inhomogeneous linearly isotropic material properties based on the CT data. To simulate the loading task, a quasi-static ramped force was applied to the centroid of the scaphoid (180 N) and lunate (120 N) directed toward the centroid of the proximal most 1 cm of the scanned radius, which was completely constrained [13]. Nodal stress and strain values were then calculated and linearly scaled to correspond to the actual forces applied by the respective subject (obtained from load cell recordings). Energy equivalent strain was calculated as the outcome of interest, as this has been previously related to bone adaptation [14]. Energy equivalent strain ($\overline{\varepsilon }$) is a scalar quantity that represents the total work done on the bone tissue provided by the multi-axial stress–strain state

Fig. 1.

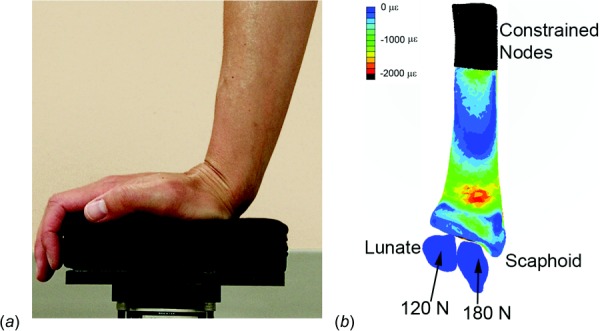
(a) Targeted loading protocol, sagittal view, (b) FE model (cartilage removed) with boundary conditions shown, palmar view. Contours display minimum (compressive) principle strain at the periosteal surface during loading for an example subject.

$$\overline{\varepsilon }=\sqrt{\frac{2U}{E}}$$

where E is the elastic modulus, and U is the strain energy density calculated as

$$U=\frac{1}{2}[{\sigma }_1{\varepsilon }_1+{\sigma }_2{\varepsilon }_2+{\sigma }_3{\varepsilon }_3]$$

where σ_n and ε_n are the principal stress and strain components, respectively. Mean energy equivalent strains were calculated for the UD section (Fig. 2) for each subject based on the baseline data.

Fig. 2.

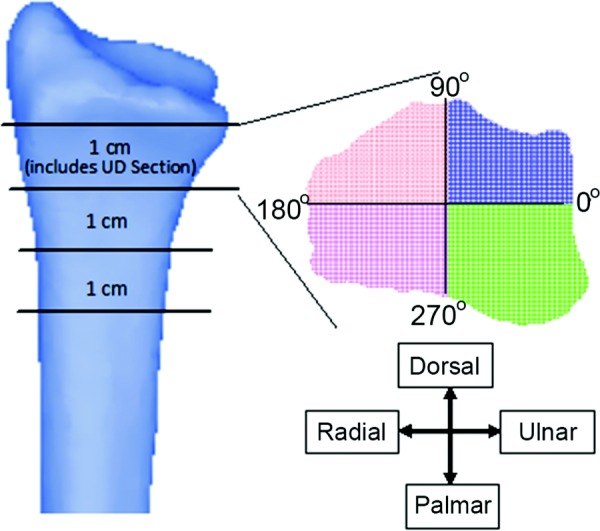
Three 1 cm slices proximal to the subchondral plate, each divided into quadrants about their respective centroid. The distal-most slice includes the entire 9.375 mm UD section. The 12 subregions used for local analysis consisted of the 4 quadrants × 3 slices.

Percent change in UD section BV, BMC, and BMD after 14 weeks were compared between experimental and control groups using Student's t-tests. To test the hypothesis that subjects who applied the highest strains to their distal radius would elicit the greatest changes in whole-bone mineral parameters, Pearson's correlation coefficients were calculated for percent changes in BV, BMC, and BMD after 14 weeks of loading versus mean energy equivalent strain at baseline within the entire UD section. Only the 23 subjects who participated in the loading experiment were included in this analysis.

Localized Strain and Adaptation.

To examine the relationship between localized bone strain and adaptation within subregions of the distal radius, model and image registration methods were developed and evaluated. The segmented CT data from the two serial time points and element data from the baseline FE models for each subject were imported into matlab. A combination of custom algorithms, ICP_GINITE (an iterative closest point registration algorithm for 3D point clouds available through matlab central file exchange), and matlab commands were used to register the CT scans, such that the same local regions were selected between the two serial time points. The localized bone analysis focused on twelve subregions located just proximal to the subchondral plate. The subregions were defined by three consecutive 1-cm transverse cross sections, each divided into quadrants defined by an orthogonal intersection at the cross-sectional centroid (Fig. 2). The quadrants included all voxels (for CT) and elements (for FE) contained within regions between: 1) 0 and 90 deg, 2) 90 and 180 deg, 3) 180 and 270 deg, and 4) 270 and 360 deg. Hereafter, we refer to these quadrants as the dorsal–ulnar (0–90 deg), dorsal–radial (90–180 deg), palmar–radial (180–270 deg), and palmar–ulnar (270–360 deg) sections. These quadrants were chosen a priori because of their anatomical relevance and the fact that they coincided with regions of high and low strain in previous in vitro cadaveric simulations of the loading protocol [10].

A laboratory precision study was performed in which ten CT scans were randomly rotated in four sequences about the x, y, and z axes, and then automatically registered back into their initial unrotated data. FE models based on the registered CT data were created and solved, and BMC, BMD, BV, and energy equivalent strain were calculated for each subregion in the original and the four rotated/registered scans. These methods were highly repeatable, with root mean squared coefficient of variation (CV) of 0.6% for BMC, 0.7% for BMD, 0.7% for BV, and 1.4% for energy equivalent strain. As an additional measure of precision, a tube of packed hydroxyapatite powder was included in 45 scans acquired over a 28 week period, and was found to have a density CV of 1.4%.

The hypothesis that the greatest within-bone increases would be localized to regions experiencing the highest strains was tested by comparing $\overline{\varepsilon }$ with change in bone parameters (BV, BMC, and BMD) in both the experimental and control groups. In experimental subjects, $\overline{\varepsilon }$ was calculated based on load cell recordings from each subject, while those subjects in the control group were assigned an arbitrary external load of 353 N (the mean force applied by the experimental subjects) from which $\overline{\varepsilon }$ was calculated. The purpose of making this comparison with the control group was to rule out the possibility that an observed relationship between bone parameters and $\overline{\varepsilon }$ was due to generalized adaptation patterns. Because the FE models were linear in nature, the arbitrary magnitude of the simulated force in the control subjects would be expected to influence the slope, but not the strength, of any detected relationship.

First, mixed linear models were calculated in which the percent change in bone parameters within each subregion were each considered dependent variables, mean $\overline{\varepsilon }$ was the independent variable, and subject was treated as a repeated measure with random intercept. Next, because the maximum and minimum strain values were not consistent between subjects, all subregions and all subjects were pooled (23 subjects × 12 subregions = 276 data points) and sorted into quartiles (n = 69 points/quartile) by mean $\overline{\varepsilon }$. Then, a second set of mixed linear models, similar to the first set in which subjects were considered a repeated measure, were run using strain quartile as the independent variable. To determine the robustness of all linear models, leave-one-out cross-validations were performed on any significant models. Finally, percent change in bone mineral parameters was compared between the strain quartiles using anova with subject treated as a repeated measure, followed by Bonferroni-corrected posthoc t-tests.

Results

For the subjects who participated in this study, the average self-reported compliance was 81.5 ± 17.1% (range 39.7%–100.0%). As previously shown [10], our mechanical loading protocol was associated with modest improvements to bone mineral parameters. The mechanical loading produced an average energy equivalent strain of 734 ± 278 με (range: 275–1221 με) at the UD radius across subjects in the experimental group. Fifteen of the 23 subjects in the experimental group showed increases in BMC over 0.5%, and the baseline characteristics of these subjects were not significantly different from the eight subjects who did not gain bone mass, or the 12 control subjects (Table 1). The experimental group experienced significant increases in BMC while the control group experienced significant losses in BMC and BMD over the 14 week experimental period.

Table 1.

Mean (SD) baseline and change data for the UD section in experimental versus control subjects. Responders were classified as those experimental subjects with >0.5% increase in BMC. Note that the control group did not participate in the loading activity; force was assigned 353 N and strains were calculated based on this value to facilitate comparisons.

	Experimental group
	Responders	Nonresponders	All	Control group
Number of subjects	15	8	23	12
Force (N)	354 (97)	352 (62)	353 (48)	353
Energy equivalent strain (με)	783 (349)	641 (221)	734 (278)	852 (293)
Compliance (%)	75.7	87.2	81.7	—
Baseline BV (cm3)	3.7 (0.4)	3.9 (0.4)	3.8 (0.4)	4.0 (0.4)
Baseline BMC (g)	0.92 (0.24)	1.07 (0.25)	0.97 (0.25)	0.98 (0.15)
Baseline BMD (g/cm3)	0.25 (0.05)	0.28 (0.04)	0.26 (0.05)	0.25 (0.04)
Change in BV (#voxels)	1602 (2106)	−1014 (1415)	692 (2275)	965 (2080)
Percent change in BV (%)	1.5 (1.9) a	−0.9 (1.3)	0.6 (2.0)	0.7 (1.8)
Percent change in BMC (%)	2.7 (1.8) a	−1.3 (1.7)	1.3 (2.6) a b	−1.9 (2.8) a
Percent change in BMD (%)	1.3 (1.9) a	−0.4 (1.9)	0.7 (2.0) b	−2.6 (2.6) a

^a p < 0.05 for change versus zero.

^b p < 0.05 for experimental versus control groups.

The mean energy equivalent strain within the UD section was significantly correlated with changes in BV (r = 0.483 and p = 0.042), but not BMC (r = 0.34 and p = 0.10), or BMD (r = 0.35 and p = 0.09) in the experimental group. When subregions were examined, the mixed linear models showed that mean $\overline{\varepsilon }$ was related to percent change in BMD (slope: 0.96%/1000 με and 95% CI: [0.42,1.50]), but not BMC or BV (Fig. 3). Every leave-one-out cross-validation model of BMD versus mean $\overline{\varepsilon }$ was significant (largest p = 0.044), supporting the robustness of this relationship. When subregion strains were examined by quartile in the experimental group, mixed linear models showed significant slopes for quartile versus percent change in BMD (slope: 0.28%/quartile and 95% CI: [0.06,0.49]) and BMC (slope: 0.24%/quartile and 95% CI: [0.05,0.44]), but not BV (slope: 0.02%/quartile and 95% CI: [−0.15,0.19]). There was a significant effect of strain quartile on change in BMD (p < 0.001), BMC (p < 0.001), and BV (p = 0.02). Increase in BMC was significantly larger in the highest-strain quartile compared to the other three (p ≤ 0.001 for all posthoc comparisons; Table 2) and increase in BMD was greater in the highest-strain quartile compared to the lowest (p ≤ 0.001). The control group showed no relationship between subregion mean $\overline{\varepsilon }$ and change to bone in any analysis (p > 0.25 for all statistical tests).

Fig. 3.

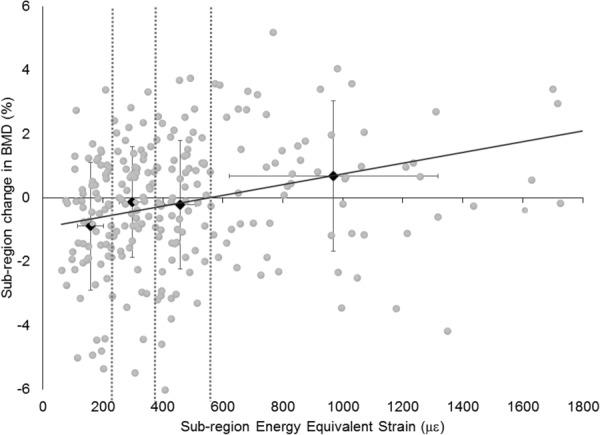
Energy equivalent strain versus percent change in BMD for all subregions of subjects in the experimental group. Black diamonds and error bars represent the quartile means and standard deviations, and dashed vertical lines show the strain quartile divisions. Regression slope: 0.28%/quartile.

Table 2.

Mean (SD) of energy equivalent strain and percent change in bone mineral parameters for the quartiles of strain values across the experimental group (n = 69/quartile)

Quartile	Energy equivalent strain (με)	Percent change in BV	Percent change in BMC	Percent change in BMD
Q1	159 (43)	1.1 (2.3)	0.2 (1.9) a	−0.9 (2.0) a
Q2	299 (43)	0.4 (1.9)	0.2 (1.6) a	−0.1 (1.7)
Q3	458 (52)	0.3 (1.7)	0.1 (2.0) a	−0.2 (2.0)
Q4	969 (346)	1.0 (1.5)	1.7 (2.5)	0.7 (2.4)

^a p < 0.05 versus Q4.

Discussion

The purpose of this study was to examine the relationship between FE-predicted bone strain and changes to bone mineral at the distal radius following a novel loading task. Our hypothesis that subjects with higher average bone strains would experience a greater osteogenic response was only supported when examining changes to BV. However, our hypothesis that, within experimental subjects, regions of high-strain would be associated with the greatest osteogenic response was supported. To our knowledge, this represents the first prospective evidence of a local strain/adaptation relationship within human bone, and is an important first step in defining a quantitative relationship between bone adaptation and mechanical loading in humans. Such a quantitative relationship would facilitate the development of personalized exercise prescriptions for bone health and fracture avoidance.

These changes to bone in the experimental and control groups after 14 weeks are consistent with our previous observations at 28 weeks in a subset of this cohort [10] and suggest that the loading protocol was mildly osteogenic and effective at preventing seasonal bone loss. BMD has been observed to fluctuate by 1.4% at the lumbar spine, declining between August and February [15]. Baseline measurements for subjects in the present analysis were performed between late June and early October, with the majority in late September; thus, a modest loss over the 14 week period would not be unexpected. The significant and positive relationship between UD BV and $\overline{\varepsilon }$ indicates that periosteal expansion may be a primary mechanism by which bone initially adapts to novel loads. Although the changes observed were small and may not have significantly impacted bone strength, they are consistent with observations of increased humerus cross-sectional area in long-term racquet sports players compared to nonplaying controls [16]. There are several explanations for why we did not detect a relationship between strain and BMC or BMD at the macro-level. Although the group was relatively homogeneous in terms of age, sex, and body mass index, the sample was relatively small (n = 23) and the range of strain achieved may not have been sufficient to separate this factor from other between-subject factors that affect bone adaptation. In addition to strain magnitude and compliance with the experimental intervention, dietary intake of calcium and Vitamin D, sun exposure [17,18], physical activity, genetics [19], and bone structure at baseline all modulate the osteogenic response. These factors, many of which cannot be controlled, may have contributed to our inability to detect a strain/adaptation relationship at the macro-level. Here we examined changes to bone mineral after 14 weeks of loading, which is near to the 100 day expected lifespan of a basic multicellular unit [20]. Although trabecular turnover may occur more rapidly than this, some of the observed intersubject variability could be attributed to incomplete remodeling at this time point.

Within this group of subjects the local regions experiencing the highest strains did indeed illustrate the largest increases in BMC and BMD, supporting our second hypothesis. The wide range of strains occurring within the subregions of the distal radius (average within-subject range: 134–1147 με) highlights the complexity of the physiological strain environment that poses a challenge to predicting whole-bone adaptation from a single strain value. Indeed, the notion that one could use external force transducers, accelerometers, or place a single strain gauge on the periosteal surface of a bone and obtain a measure that predicts whole-bone adaptation may be overly simple.

Although the loading task was simulated in the same manner for all FE models, the strain distribution within each bone was highly variable between subjects due to differences in bone size, shape and mineral distribution. Despite this variability, the subregions experiencing the highest strain within each experimental subject were associated with the largest increases in bone mineral, although the exact magnitude of both the stimulus and response varied substantially. In the experimental group changes to BMC and BMD in the highest strain quartile were significantly different from the lower three quartiles (Table 2), suggesting that there might exist a threshold above which mechanical stimuli result in bone formation at this anatomic site. Our data suggest this threshold may be near an energy equivalent strain of 539 με, the lower bound of the highest quartile. This value is somewhat lower than the diaphyseal surface strain thresholds reported in other in vivo loading models [2,7,12], but it must be noted that 539 με represents the mean strain throughout the region, and not the peak periosteal value. Other factors, such as strain rate, number of loading cycles, and time interval between loading bouts may influence this threshold and are the topic of future investigations.

This study had several limitations, most notably the small sample size and short duration of mechanical loading investigated. Although 35 subjects were recruited for this study, our loading protocols were osteogenic in only 15 of the 23 subjects in the experimental group. Even so, the relationship between local changes in BMD and energy equivalent strain was significant across all experimental subjects and remained significant with cross-validation. Additionally, this relationship was not detected in control subjects, further supporting the validity of the observations. Although not significant, the 15 responders experienced larger strains and had slightly lower baseline BMC and BMD compared to the nonresponders (Table 1). Identifying the characteristics of individuals who are most likely to benefit from bone loading interventions is an important public health priority, and is one focus of our ongoing research.

The voxel size of the CT scans used in this study was 0.234 mm × 0.234 mm × 0.625 mm, and the average volume of the each subregion was 0.95 ± 0.1 cm³ or 27,760 voxels. Although strain and bone mineral parameters were highly repeatable within these relatively small subregions, the continuum models may not reflect the true conditions within the trabecular microarchitecture. Our ongoing research using high resolution CT data coupled with micro-FE models should provide additional insight into the nature of the link between external loads, trabecular bone strain, and the resulting bone adaptation.

The boundary conditions for our FE models were adopted to mimic the loading task, under the assumption that the subjects positioned their wrists in such a way so as to apply an axial load to the distal radius. Although uniform instructions were provided to all subjects to position their wrists to apply loads axially, the exact position used by the subjects during each bout of loading could not be controlled, though it is known to strongly influence bone strain [21]. The boundary conditions modeled represent the mean of an assumed Gaussian distribution in terms of both loading magnitude and direction. Future prospective studies using this loading task may benefit from the use of wrist braces to reduce variability in wrist positioning, a probabilistic approach to modeling strain, or consideration of the entire distribution of boundary conditions imposed in vivo.

In conclusion, despite the limitations of this study, significant relationships were observed between short-term changes in bone mineral parameters and energy equivalent strain. BMC and BMD increased in regions of the radius experiencing energy equivalent strains over 539 με, both compared to low-strain regions and control subjects. To our knowledge, this is the first prospective report of localized bone adaptation behavior in humans. The methods established here provide a framework within which other factors related to bone adaptation may be explored noninvasively. In the future, these methods may serve as an important tool to facilitate the development of personalized exercise prescriptions for bone health and identify likely responders.